Investigations on Spray Characteristics and Self-Pulsation of a Gas-Centered Shear Coaxial Injector

The spray characteristics of a gas-centered shear coaxial injector under different conditions and recess ratios (RR) were studied through experiments and numerical simulations. The numerical study was carried out based on the coupled level set and volume-of-fluid (CLSVOF) method and the adaptive mesh refinement (AMR) method. The results indicated that without recess, the spray angle first stayed almost constant and then dropped linearly with an increase in the gas mass flow rate $\left({\dot{m}}_g\right)$ when holding the liquid mass flow rate $\left({\dot{m}}_l\right)$ constant. In contrast, with recess, the spray angle was found to increase with ${\dot{m}}_g$, which could be attributed to the secondary expansion of the central gas flow. Under specific conditions, self-pulsation occurred and was accompanied by a loud scream. The frequency of the self-pulsation increased with both ${\dot{m}}_g$ and ${\dot{m}}_l$. Moreover, the self-pulsation frequency decreased with RR. Meanwhile, the mechanism of self-pulsation was initially explored through numerical simulation. It was concluded that self-pulsation was caused by the surface tension and the pressure difference between the inside and outside of the liquid sheet, together with the central airflow impact extrusion.

1 Introduction

Liquid rocket engines are the heart of liquid propellant rockets and are highly valued in many countries. The interaction between gases and liquids significantly enhances the atomization performance of gas–liquid coaxial injectors; therefore, these injectors are widely used in bipropellant liquid rocket engines (Kang et al., 2018).

In an experimental study of liquid-centered shear coaxial injectors, Hardalupas and Whitelaw (1994) found that atomization could be enhanced by reducing the diameter of the liquid injector. Yang and Fu (2012) found that recession could confine the airflow to limited space and enhance the gas–liquid interaction and thus could significantly improve the atomization performance. Hautman et al. (1993) conducted an experimental study on liquid-centered swirl coaxial injectors and found that the spray angle decreased with ${\dot{m}}_g$ and ambient pressure and subsequently increased with ${\dot{m}}_l$. The droplet Sauter mean diameter (SMD) demonstrated a single-peak distribution along the radial direction while decreasing along the axial direction downstream. Yang et al. (2006) investigated the effect of recess lengths on the SMD of a liquid-centered swirl coaxial injector. They also proposed the concept of recessed angle. Accordingly, the flow inside the recess chamber was classified into three modes: external mixing, critical mixing, and internal mixing flows. SMD was minimized when the flow was in the critical mixing flow mode. Kulkarni et al. (2010) found that a low Weber number (We) liquid sheet was more sensitive to gas than a high We number liquid sheet for a gas-centered swirl coaxial injector, with a more obvious variation in the spray angle and breakup length of the low We number liquid sheet. Based on experimental data, Siddharth et al. (2017) found that: 1) the addition of swirl flow in the gas contributed to the breakage of the liquid sheet and 2) the breakup length of the liquid sheet in the counter-swirl air flow (opposite to the direction of liquid sheet rotation) was shorter than that in the co-swirl air flow.

Despite the numerous advantages of a gas-liquid coaxial injector, it can generate self-pulsation under certain structures and conditions, and the accompanying periodic pulsations of spray flow and pressure (Bazarov and Yang, 1998; Eberhart et al., 2012) may cause combustion instability in the thrust chamber, which could further result in combustion instability in liquid rocket engines. Nunome et al. (2007) and (Nunome et al., 2009) experimentally investigated the change in the liquid-centered shear coaxial injector spray from the stable to self-pulsation state and concluded that the recess of the inner injector was the key parameter to inducing injector self-pulsation. They found that there was a critical parameter F_cr, at which, when Re_l/(Re_g)^0.5 < F_cr, self-pulsation could occur. Tsohas and Heister (2011) studied the internal flow of a recessed chamber during injector self-pulsation using two-dimensional simulation. They found that vortex shedding at the injector, the acoustic instability of the liquid injector, and vortex shedding at the injector outlet could result in self-pulsation. (Kim and Heister (2004) and Kim et al. (2005) conducted a three-dimensional simulation study of the flow inside the injector recess chamber and found that the pulsation frequency and amplitude could be increased by increasing the gas-liquid density and velocity ratios; the amplitude could also be increased by decreasing the jet diameter and increasing the recess length. Kelvin–Helmholtz (K-H) instability on the jet surface was assumed to cause self-pulsation of the injector. Self-pulsation of liquid-centered swirl coaxial injectors was first studied experimentally and theoretically by Bazarov et al. (1995), Bazarov (1998), and Bazarov and Yang (1998). It was concluded that self-pulsation was caused by the time-lag feedback between the rotating liquid sheet and the annular airflow and that self-pulsation can enhance the effect of atomization and mixing to a certain extent. The most important parameter affecting self-pulsation was the recess length. Eberhart et al. (2013) and Eberhart and Frederick (2017) found that the unstable frequency and wave velocity measured at a steady spray were consistent with those measured at self-pulsation in an analysis of proper orthogonal decomposition. Therefore, it was speculated that the occurrence of self-pulsation could be attributed to K-H instability. Chu et al. (2021) investigated the effect of backpressure on the self-pulsation of an injector using three-dimensional numerical simulation and found that: 1) with an increase in the backpressure, the mass flow rate distribution in the radial direction changed from a double peak to a single peak and 2) the central mass flow rate was increased by backpressure and ${\dot{m}}_g$, while the peripheral mass flow rate decreased. The increase in backpressure could suppress the self-pulsation effect and accelerate the breakage of the liquid sheet; the frequency of self-pulsation increased with an increase in back pressure (or ${\dot{m}}_g$). Xu. (2016) conducted experiments to further study the phenomenon of self-pulsation in gas-centered swirl coaxial injectors and summarized the conditions of self-pulsation and the range of ${\dot{m}}_g$ and ${\dot{m}}_l$. They concluded that self-pulsation was generated by the increase in gas momentum to overcome the inertial potential energy of the liquid sheet, which could further cause periodic aggregation and expansion of the liquid sheet in the outlet.

In recent decades, the study of the gas-liquid coaxial injector spray and self-pulsation characteristics has gradually intensified. The influences of injector structural parameters, injection conditions, back pressure, and other factors on the spray angle, breakage length, droplet SMD, and other spray characteristics were studied using theoretical, experimental, and simulated methods. However, few studies have been published that report on the spray and self-pulsation characteristics of gas-centered shear coaxial injectors. Therefore, in this study, the spray characteristics and self-pulsation of gas-centered shear coaxial injectors under different conditions and recess ratios were investigated by experiments and numerical simulations based on CLSVOF and AMR. Due to the limitation of experimental equipment, the SMD of droplets in this study was not measured. The latest results of particle measurement by Huang et al. (2022) and Wu et al. (2022) provide a reference for the follow-up work.

2 Experimental Methods

2.1 Experimental System

The experimental system was composed of four parts: 1) a propellant feed system, 2) a measurement and control system, 3) an image acquisition system, and 4) a bench system, as shown in Figure 1A. The propellant feed system was composed of a high-pressure gas source, gas conduit, liquid conduit, propellant tank, and other components. To achieve a smooth flow supply to the liquid injector, the propellant (water) storage tank was pressurized with compressed air. Meanwhile, the air was delivered by a high-pressure gas source to the gas injector through the conduit via the pressure-reducing valve. The pressure of the liquid and gas manifolds was measured and recorded using a pressure sensor: OHR-M2G-2-L-C-0-1.6 MPa with an accuracy of 0.5% FS. The mass flow rates of the water and pressurized air were measured and recorded using an LWGY turbine flowmeter and a Coriolis mass flowmeter (MFC608), with an accuracy of 0.5% FS, respectively. The in-line image acquisition system was composed of a high-speed camera, shading plate, and rectangular LED background light source (HLS-30, power: 250 W). The distance of each component could be adjusted to ensure a fine spray transient image. During the experiments, the recording rate of the camera was set as 31,862 fps, the exposure time was 1/95,586 s, and the resolution of the transient image was 800 × 600 pixels.

FIGURE 1

FIGURE 1. Experimental system and geometries of the gas-centered shear coaxial injector.

2.2 Geometries of the Injector and Experimental Operating Conditions

A gas-centered shear coaxial injector was studied in the experiment, as shown in Figure 1B, in which the outer injector was a coaxial annular aperture, and the inner injector was a central circular hole. The liquid fuel entered the injector through the coaxial annular aperture, and the gaseous oxidizer was fed through the central hole. They interacted with each other after spraying out from the injector. For the recessed injector, the gaseous oxidizer was ejected from the inner injector and expanded to compress the liquid fuel; thus, the oxidizer and fuel were initially mixed inside the recess chamber. The liquid fuel was jetted from the outer injector to form a liquid sheet near the injector outlet and then was broken into liquid blocks and droplets after a certain distance (breakup length) downstream. Recess is an important parameter which determines propellants’ mixing efficiency and even flame stability (Xu, 2016). Three injectors with different recess lengths were applied in the experiment. The recess length was the distance from the outlet section of the inner injector to the outlet section of the outer injector (Chu et al., 2021), as shown in Figure 1. The key geometrical parameters of the injector are listed in Table 1, and the RR is defined as follows:

$RR=\frac{L_r}{d_g}.$

TABLE 1

TABLE 1. Geometrical parameters of the injector.

In this study, the spray characteristics and self-pulsation of the gas-centered shear coaxial injector under different working conditions and recess ratios were mainly explored. To ensure the comprehensiveness of the experimental study, the operating conditions in the present experiments were denser, as shown in Table 2, whereas the errors of the gas and liquid mass flow rates were less than 4.2 and 6.7%, respectively. The ${\dot{m}}_l$ is set from 30 g/s to 120 g/s with a step of 10 g/s, and ${\dot{m}}_g$ increased from 4 g/s to 25 g/s with a step of 1 g/s.

TABLE 2

TABLE 2. Parameters of working conditions.

2.3 Image Processing

To obtain the spray angle, self-pulsation frequency, and other information, 2000 images were taken for each working condition and processed by the in-home code.

2.3.1 Acquisition of the Spray Angle

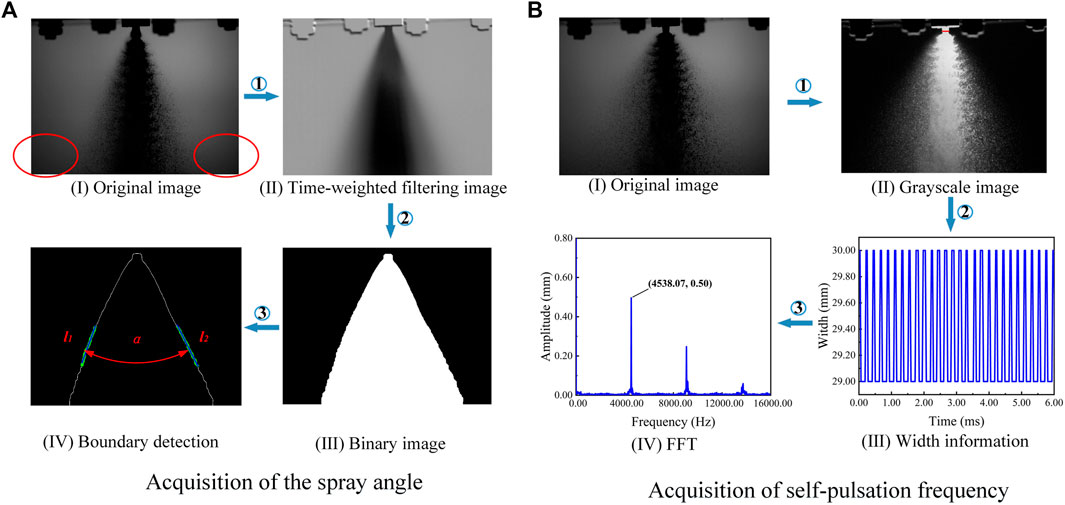
The extraction of the spray angle was performed using the clustering method. First, all the spray images were processed to obtain the time-averaged image; second, the weighted image was obtained by the background, and a time-averaged image was multiplied with the weighted image to eliminate the effect of uneven illumination; third, the time-weighted filtering image was obtained by Gaussian filtering, which was followed by the calculation of the average grayness of each class based on the K-means segmentation algorithm (Arthur and Vassilvitskii, 2007) to obtain the background image classification, and moreover, the background binary image was obtained by morphological filtering. The boundary coordinates were found to extract the spray boundaries, calculating the left and right boundaries of the spray to fit the straight lines l₁ and l₂. Due to the spray being completely broken and unfolded only in the downstream direction and to avoid the interference of the background (as marked by the red circle in Figure 2A), the fitted straight line was taken in the 50–75% interval downstream of the spray. Finally, the included angle between the two fitting lines was calculated by the program formula to obtain the spray angle, as shown in the following equation:

$l_1:y_1=k_{1}x+b_1,{\alpha }_1=\mathit{arctan}{k}_1,(1)$

$l_2:y_2=k_{2}x+b_2,{\alpha }_2=\mathit{arctan}{k}_2,(2)$

$\alpha ={180}^{\circ }-|{\alpha }_1-{\alpha }_2|.(3)$

FIGURE 2

FIGURE 2. Acquisition of the spray angle and self-pulsation frequency.

2.3.2 Acquisition of the Self-Pulsation Frequency

The self-pulsation frequency was obtained by first subtracting the background to obtain the grayscale image after background removal, followed by the binarization of the image after background removal, which was then processed to obtain the binarized image. At a certain distance from the injector outlet, a measurement line was selected (which is 2 mm below the injector for this study), and the spray width information reflected by the white area on the measurement line was extracted to obtain the spray width of each image. Finally, the frequency involved in the self-pulsation of the spray was obtained by the time series of the spray width subjected to a fast Fourier transform (FFT) (Xu, 2016), as shown in Figure 2B.

3 Theory and Model of Numerical Simulation

3.1 Governing Equations

The governing equations include the mass, momentum, and energy conservation equations, which are described by the governing equations of fluid motion. Incompressible fluid treatment should be conducted if the flow velocity of the liquid is low. Moreover, the incompressible gas treatment should be conducted when the flow velocity of the gas is lower. However, the density change can no longer be neglected if the flow velocity of the gas is larger (M_a > 0.15) (Luo, 2017). In that case, it should be treated as a compressible fluid, that is, the energy equation should be considered.

Conservation of mass equation: $\frac{\partial \rho }{\partial t}+\mathit{\nabla }\cdot \left(\rho U\right)=0.$

Conservation of momentum equation: $\frac{\partial }{\partial t}\left(\rho U\right)+\mathit{\nabla }\cdot \left(\rho UU\right)=-\mathit{\nabla }p+\mathit{\nabla }\cdot \left(\stackrel{\text{=}}{\tau }\right)+\rho g+F.$

Conservation of energy equation: $\frac{\partial }{\partial t}\left(\rho E\right)+\mathit{\nabla }\cdot \left[U\left(\rho E+p\right)\right]=\mathit{\nabla }\cdot \left(k_{eff}\mathit{\nabla }T-{\displaystyle \sum _j{h}_j{J}_j}+\left({\stackrel{\text{=}}{\tau }}_{eff}\cdot U\right)\right)+S_h.$Whereas:

$\stackrel{\text{=}}{\tau }=\mu \left[\left(\mathit{\nabla }U+\mathit{\nabla }{U}^T\right)-\frac{2}{3}\mathit{\nabla }\cdot UI\right],$

$E=h-\frac{p}{\rho }+\frac{U^2}{2}.$

3.2 Turbulence Model and the Gas–Liquid Interface Capturing Method

The realizable k-ε model was chosen as the turbulence model, for which the constraint on the Reynolds stress was satisfied. Therefore, it can be kept consistent with the real turbulent flow in terms of the Reynolds stress. One of the advantages of this feature in the calculation is that the diffusion velocity of planar and circular jets can be simulated more accurately. Meanwhile, the calculated results could be more consistent with the real situation in problems such as the calculation of rotating flow, calculation of the boundary layer with a directional pressure gradient, and separation flow calculation.

The volume-of-fluid (VOF) method can 1) easily calculate complex phase interface change processes, 2) capture the particularly sharp phase interfaces, and 3) have good volume conservation and other advantages. Its disadvantages are that it may have difficulty in accurately calculating the curvature and physical quantities related to curvature, which results in an increase in the use of computational cost to capture the phase interface location in detail if the encryption of the grid at the phase interface becomes necessary. The level set method has the following advantages: 1) it can accurately calculate the curvature and curvature-related physical quantities, which does not need to reconstruct the interface; 2) it has stronger topological description ability, and 3) the phase interface calculated based on the level set method is smoother than that using the VOF method. Its disadvantage is that it faces difficulty in accurately simulating sharp interfaces with relatively poor volume conservation. CLSVOF combined the VOF method with the level set method, which has the advantages of those two methods. CLSVOF has an excellent capture of the phase interface in two-phase flow simulations (Wang et al., 2016).

The realizable k-ε model and the controlling equations of the CLSVOF are described in detail in the literature (Chu et al., 2020).

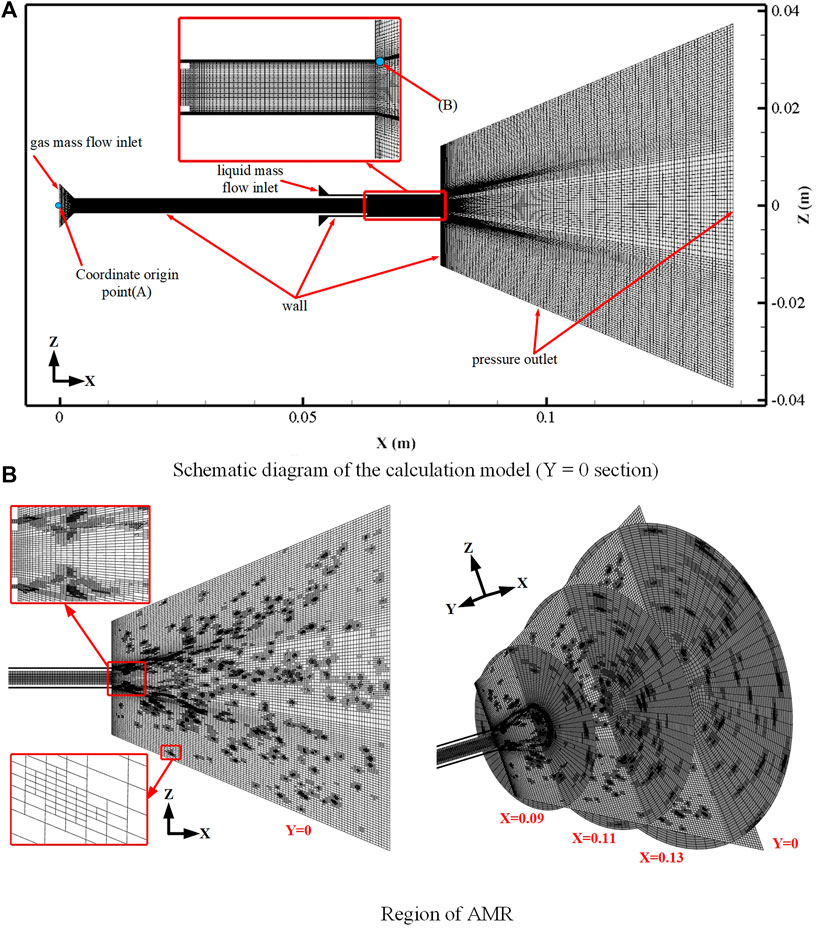
Owing to the multiscale characteristics of the atomization phenomenon, to fully collect the motion and breakage details of the liquid film and reduce the numerical errors in the numerical solution, the AMR method, which was based on the gradient of the liquid volume fraction (α), was used in this study to encrypt the mesh to accurately track the gas–liquid interface (Wang et al., 2021), as shown in Figure 3B. Refinement is realized when the following conditions are satisfied:

$h\left|\nabla \alpha \right|>{\epsilon }^{\prime },$

where h is the grid scale, and ${\epsilon }^{\prime }$ is a constant with a small value. Here, ${\epsilon }^{\prime }=0.05$. In other words, the grids at the gas–liquid interface are refined. The mesh refinement interval was 10 time steps with three refinement levels.

FIGURE 3

FIGURE 3. Schematic diagram of the calculation model and region of AMR.

3.3 Computational Model

A schematic representation of the calculation model is illustrated in Figure 3A. It has a gas injector bore diameter of 3 mm and a liquid injector bore diameter of 4.5 mm, among which the vertically downward direction was the positive X-axis, the coordinate origin was located at the center A (0, 0, 0) of the gas injector inlet, and the pressure monitoring point was located at Point B (80.2, 2.25, 0).

The inlet boundary condition of the mass flow rate was applied to the inlet of the gas and liquid, the outlet boundary was set as the pressure outlet boundary, and the wall surface was a non-slip wall boundary. The gas was simulated using air, and the liquid was simulated using water. The pressure discretization method (PRESTO) and the pressure-velocity coupling method (PISO) were applied. Furthermore, the second-order upwind scheme discretization was applied in the momentum and other equations, and the phase interface reconstruction technique (Geo-Reconstruct) was used. Moreover, the simulation accuracy of the wall part was improved by non-equilibrium wall functions. At the initial moment, all the fluid in the calculation region was air. The compressibility of air was considered, and its viscosity was calculated using the Sutherland method, as shown in the following equation:

$\frac{\mu }{{\mu }_0}={\left(\frac{T_L}{T_{L0}}\right)}^{3/2}\frac{T_{L0}+B}{T_L+B},$

where B ≈ 110.4 K. The equation is applicable to air over a fairly large range $\left(T_L<2000\mathrm{K}\right)$.

For the acquisition of the self-pulsation frequency in the simulation, first, the pressure pulsation curve of monitoring point B (Case 0-80-5) was monitored, and then, its frequency was obtained through FFT (Chu et al., 2021), as shown in Figure 4A.

FIGURE 4

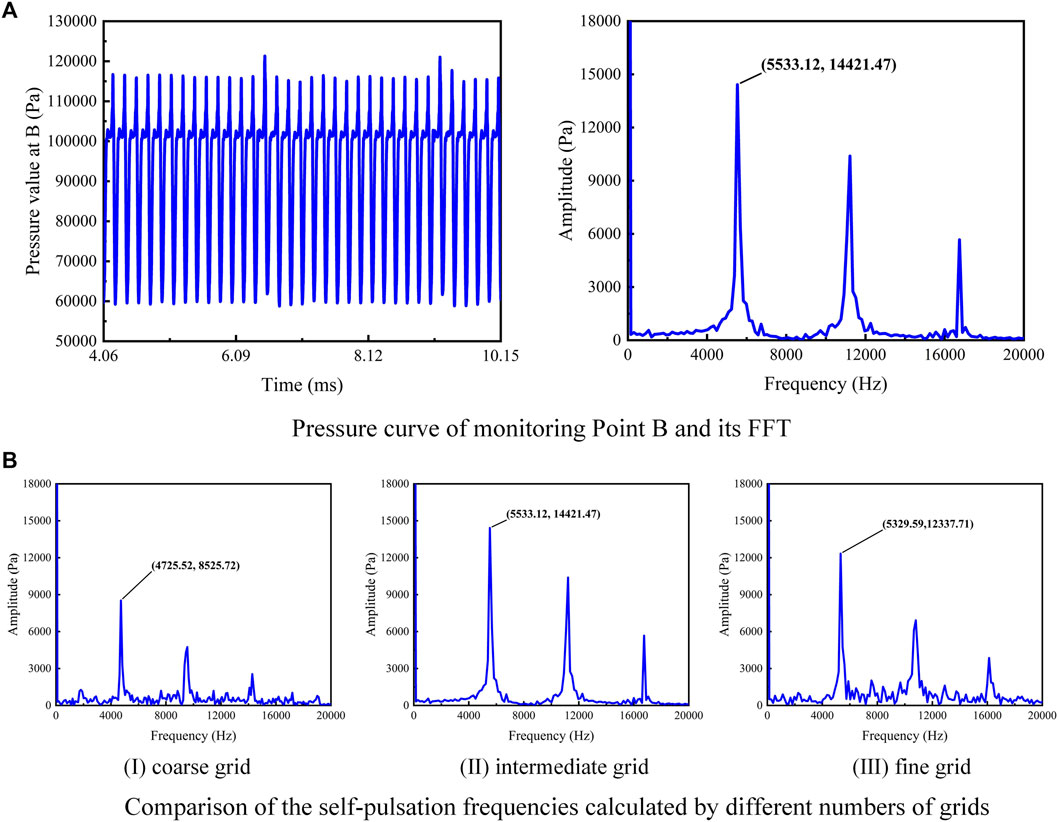
FIGURE 4. Pressure curve of the monitoring point B and its FFT and comparison of the self-pulsation frequencies calculated by different grids.

3.4 Simulation Working Condition

The effects of different recess ratios and gas-liquid mass flow rates on the spray characteristics were studied. The simulation working conditions are listed in Table 3.

TABLE 3

TABLE 3. Simulation working conditions.

3.5 Grid Independence

Case 0-80-5 was selected for the grid independence study. Three different grids, which initially (before AMR) contain 330,000 (coarse), 630,000 (intermediate), and 930,000 (fine) grids, respectively, were utilized to check the dependence of the grid size. The pressure pulsation frequency at the monitoring point B on basis of those three grids is plotted in Figure 4B. Compared with the self-pulsation frequency based on experimental data (5,286 Hz), the frequency errors obtained from the coarse grid calculation (10.6%) were greater than those obtained from the intermediate (4.7%) and fine grid calculations (0.8%). To reduce the calculation cost and ensure its accuracy, an intermediate grid was used for the calculation in this study.

4 Results and Discussion

4.1 Spray Angle

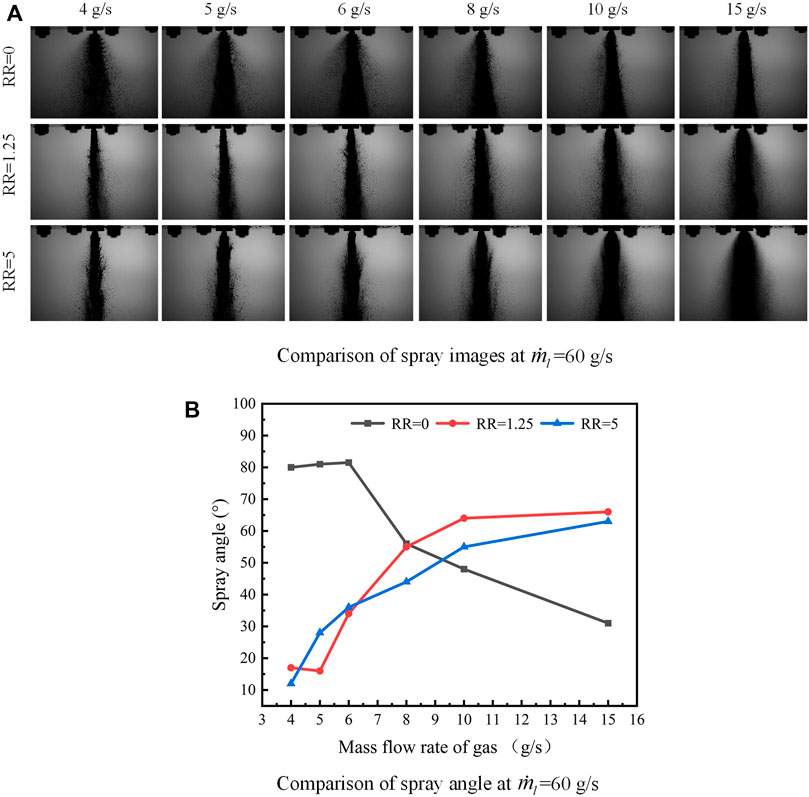
For injector without recess, the spray angle first stayed almost constant with the variation of ${\dot{m}}_g$ (4 $\le {\dot{m}}_g\le$ 6). However, as ${\dot{m}}_g$ continued to increase, the spray angle dropped linearly. On the other hand, for injectors with recess (RR = 1.25 and RR = 5), the spray angle got larger with ${\dot{m}}_g$. Holding ${\dot{m}}_l=60g/s$, spray images and the changes of spray angles versus ${\dot{m}}_g$ are shown in Figures 5A,B, respectively. Here, the gas–liquid ratio (GLR) of mass flow rates is defined as follows:

$GLR=\frac{{\dot{m}}_g}{{\dot{m}}_l}.$

FIGURE 5

FIGURE 5. Comparison of spray images and the spray angle at ${\dot{m}}_l=60\mathrm{g}/\mathrm{s}$.

For an injector without recess, self-pulsation occurred at a low GLR (the details of self-pulsation are described in section 4.2). The spray pulsations in the radial direction led to an increase in the radial distribution of the droplets, resulting in an enlarged spray angle. The self-pulsation phenomenon of the spray was enhanced with the increasing GLR (0.07 ≤ GLR≤0.10). However, because the spray pulsations were very intense, the increase in the spray angle was not particularly significant. In other words, the spray angles stayed almost constant. When the GLR continued to increase, the axial velocity of the central airflow increased sharply, and the strong ejecting effects of the central airflow made the liquid film outlet completely broken. At the same time, the strong ejecting effects made the liquid converge toward the axis, which resulted in the spray angle dropping linearly. Even though there were still self-pulsations in the first working conditions (0.10 < GLR≤0.17), the promotion effect of spray pulsation on the spray angle was inferior to the weakening effect of ejecting effects on the spray angle. Meanwhile, the promotion effect of the expansion of the central airflow outlet on the spray angle was inferior to the weakening effect of ejecting effects on the spray angle. A larger GLR led to a stronger ejecting effect of the central airflow and hence minimizes the spray angle.

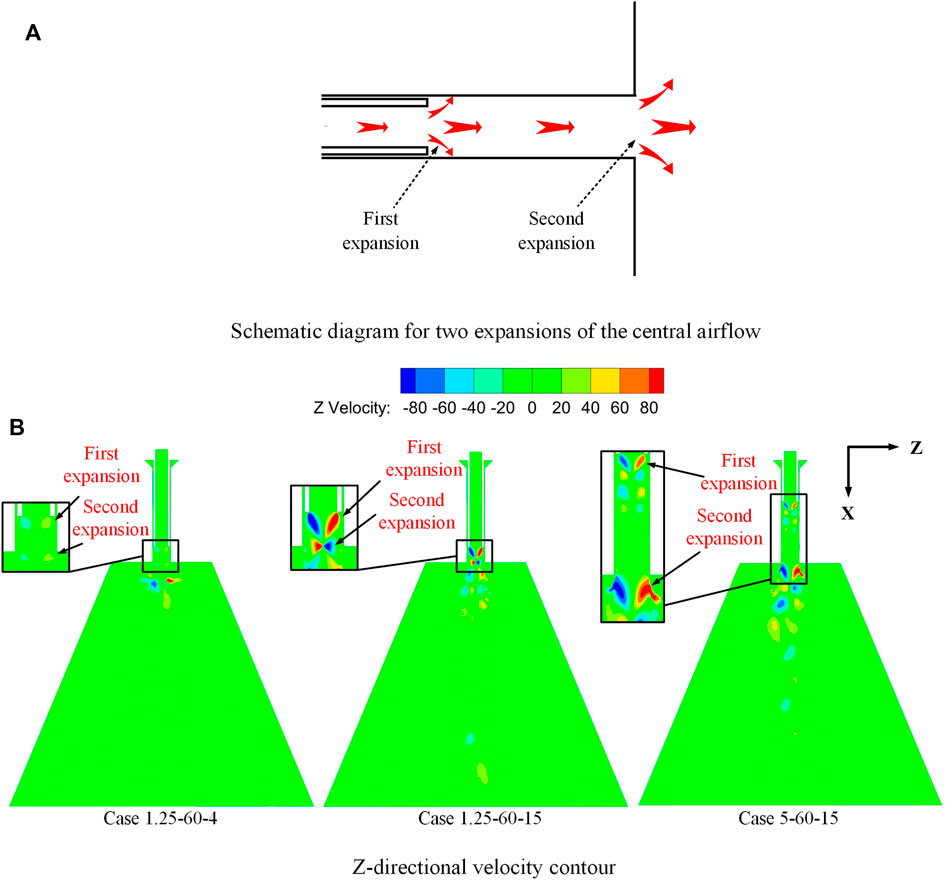
In the current study, the Mach numbers at the outlet of the gas injector were greater than 0.15. In other words, the gas could not be treated as an incompressible flow. The gas expanded at the injector outlet, and the liquid sheet was directly affected by the gas flow. For the injector with recess, the center gas experienced two expansions, as shown in Figure 6A. The first expansion occurred in the recess chamber after the center gas flowed out of the inner injector. Thereafter, the gas got expanded once more downstream of the outlet of the outer injector. However, for the injector without recess, the center gas flow experienced only one expansion at the outlet of the inner injector.

FIGURE 6

FIGURE 6. Schematic diagram for two expansions and the Z-directional velocity contour.

Under conditions with a low GLR (0.07 ≤ GLR<0.13), spray self-pulsation was found for injectors with recess. However, spray angles for those injectors were relatively smaller than those for injectors without recess. It was concluded that the radial diffusion of the liquid film is limited by the recess chamber wall. At the same time, recess can lead to a strong gas–liquid interaction. In other words, the central airflow has strong momentum transfer to the liquid film in the recess chamber. These reduced the radial velocity of the liquid film at the injector outlet, which resulted in a reduction in the spray angle. With the increase in RR, the recess chamber wall limited the radial diffusion of the liquid film for a longer time, and the acting time of the central airflow with the liquid sheet was longer. The radial velocity of the liquid sheet was reduced more significantly, thus further reducing the spray angle. However, with an increase in the GLR, the secondary expansion of the central airflow at the outlet of the outer injector became more and more significant. The expansion gas transferred a greater radial velocity to the liquid sheet, which resulted in an increase in the radial velocity of the liquid sheet and a subsequent increase in the spray angle. However, under a low GLR, the secondary expansion of the central airflow was insignificant and contributed little to the radial velocity of the liquid sheet. Moreover, the above-mentioned observations were confirmed through simulation. The Z-directional velocity contours for case 1.25-60–4, case 1.25-60–15, and case 5-60–15 are shown in Figure 6B. The two airflow expansions related to case 1.25-60-4 were minimal, whereas the two airflow expansions related to case 1.25-60-15 and case 5-60-15 were significant.

4.2 Self-Pulsation Phenomenon Without Recess

When conducting the experiment under specific working conditions, the injector produced a self-pulsation phenomenon, accompanied by a loud scream, and the self-pulsation frequency increased with ${\dot{m}}_g$, as shown in Figure 7A. However, for a constant ${\dot{m}}_l$ (such as ${\dot{m}}_l=80\mathrm{g}/\mathrm{s}$ = 80 g/s), when ${\dot{m}}_g$ reached a critical value (here ${\dot{m}}_g=8\mathrm{g}/\mathrm{s}$), the self-pulsation phenomenon disappeared.

FIGURE 7

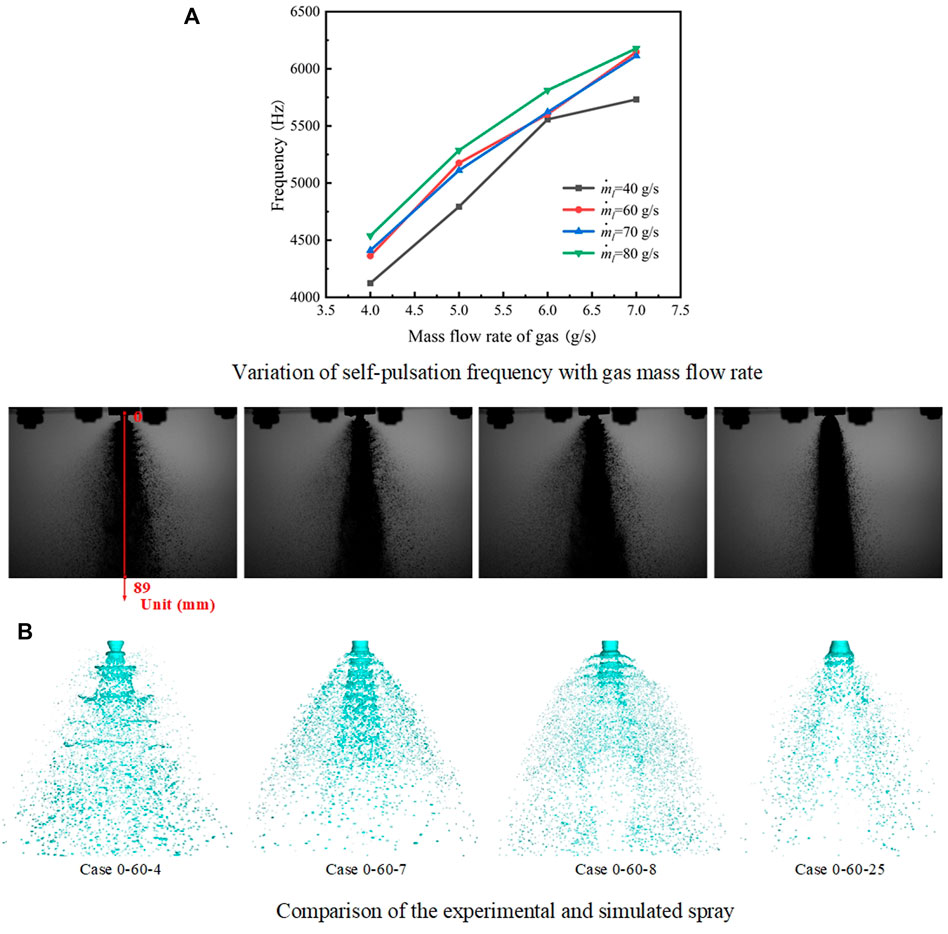
FIGURE 7. Variation of the self-pulsation frequency with ${\dot{m}}_g$ and comparison of the experimental and simulated spray.

Similar results were obtained from the simulation calculations. As shown in Figure 7B, under ${\dot{m}}_l=60g/s$ and the gas mass flow rates at 4, 7, 8, and 15 g/s, the experimental images are compared with the simulated spray images. A comparison between the experimental and simulated frequencies is shown in Table 4. The error between the simulated and experimental frequencies was relatively small, verifying the reliability of the simulation model. The gas–liquid interface in the simulation was represented by the iso-surface with α= 0.25 (Li et al., 2019).

TABLE 4

TABLE 4. Comparison of experimental and simulation frequencies.

When ${\dot{m}}_g$ was small, the self-pulsation phenomenon was caused by the gas–liquid interaction at the injector outlet. The self-pulsation spray was formed in the shape of a “Christmas tree”. Moreover, the structure of the spray comprised “shoulder” and “neck” sections, which appeared alternately to form the self-pulsation phenomenon of the spray. As shown in Figure 7B, the spray pulsations were violent near the injector outlet, whereas the downstream pulsation was weakened. In other words, the self-pulsation phenomenon had a greater impact on the spray characteristics near the injector outlet and less impact on the downstream. With an increase in ${\dot{m}}_g$, the central airflow of the ejector function was enhanced, the spray gradually gathered toward the axis, and the intensity of the pulsations and breakages of the liquid sheet increased. When ${\dot{m}}_g$ reached a certain value and above, the self-pulsation phenomenon disappeared, and strong aerodynamic fragmentation of the annular aperture liquid sheet was observed.

Meanwhile, a consistent pattern was observed in the experimental and simulation results; the frequency of self-pulsation increased with ${\dot{m}}_l$ at a constant ${\dot{m}}_g$. The variation in the self-pulsation frequency with ${\dot{\mathit{m}}}_{\mathit{l}}$ for fixed gas mass flow rates and the comparison between the experimental and simulated frequencies are shown in Figure 8A. A comparison between the experimental and simulated spray images for ${\dot{m}}_g=4g/s$ and liquid mass flow rates of 40, 60, 80, and 120 g/s is shown in Figure 8B. The minimum error between the simulated and experimental frequencies was 0.80%, and the maximum error was 9.79%.

FIGURE 8

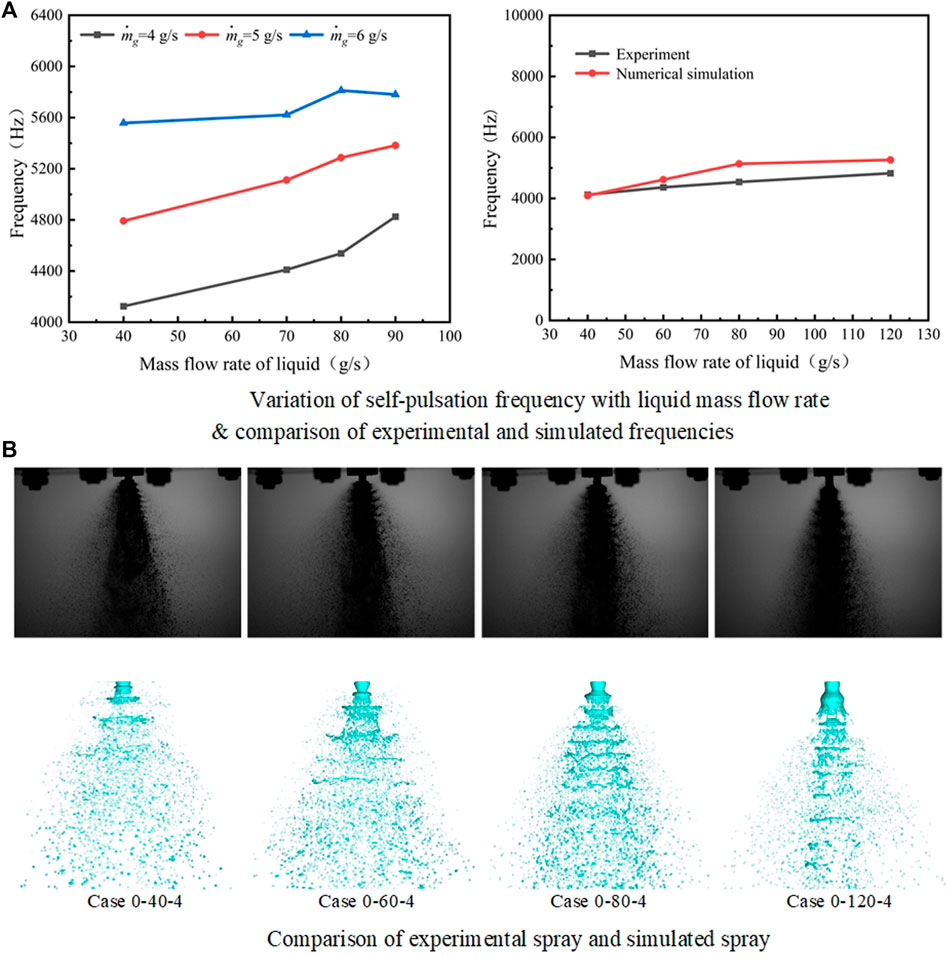
FIGURE 8. Variation of the self-pulsation frequency with ${\dot{m}}_l$ and comparison of experimental and simulated frequencies and spray images.

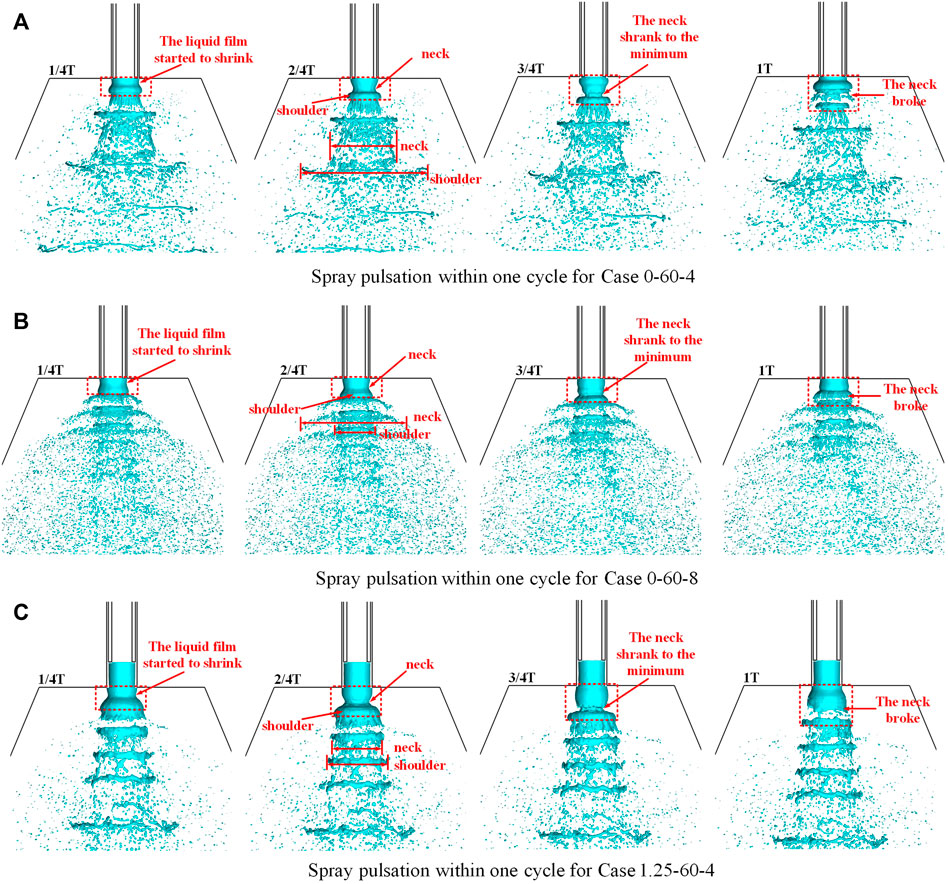
Analysis suggests that the injector self-pulsation resulted from the combined action of the pressure difference between the inside and outside of the liquid sheet, the surface tension of the liquid sheet, and the impact extrusion of the central airflow. For example, in case 0-60-4, the liquid sheet flowed out from the outer annular aperture injector outlet at 1/4T. The airflow in the center of the annular liquid film was fast, while the airflow outside the annular liquid film was approximately in a static state, as shown in Figure 9A. In accordance with the Bernoulli equation, the outer pressure of the liquid sheet was demonstrably higher than the inner pressure. Owing to the action of the pressure difference between the inside and outside of the liquid sheet, the liquid film of the annular aperture injector tended to shrink toward the central axis shortly after it flowed out of the injector outlet. As the liquid sheet underwent contraction, the “neck” and “shoulder” sections of the spray formed gradually at 2/4T. As the “neck” section blocked the central gas channel, gas accumulation occurred in the inner side of the annular liquid film and caused the pressure inside the annular liquid film to rise. The pressure difference between the inside and outside of the liquid film began to reverse. When the “neck” section shrank to its minimum size, the pressure difference between the inside and outside of the liquid sheet attained the maximum value (as shown in Figure 10B at 3/4T). Concurrently, the effect of surface tension of the liquid film during contraction caused the downstream liquid film of the “neck” section to become weak. Subsequently, under the combined action of the pressure difference and the impact extrusion of the central gas flow, the “neck” broke, and the gas channel opened (the process was also caused by the combined action of the K-H instability and R-T instability). Then, the spray entered the next pulsation cycle. Substantial momentum was transferred at the “neck” fracture owing to the “breaking out of the liquid film” of the central airflow (as shown in Figure 9A at 1T) such that the droplet and liquid block gained a large radial velocity, thus increasing the spray angle. The self-pulsation spray was formed in the shape of a “Christmas tree”. The droplet clusters were periodically produced and moved downstream with the spray.

FIGURE 9

FIGURE 9. Spray pulsation within one cycle for cases 0-60-4, 0-60-8, and 1.25-60-4.

FIGURE 10

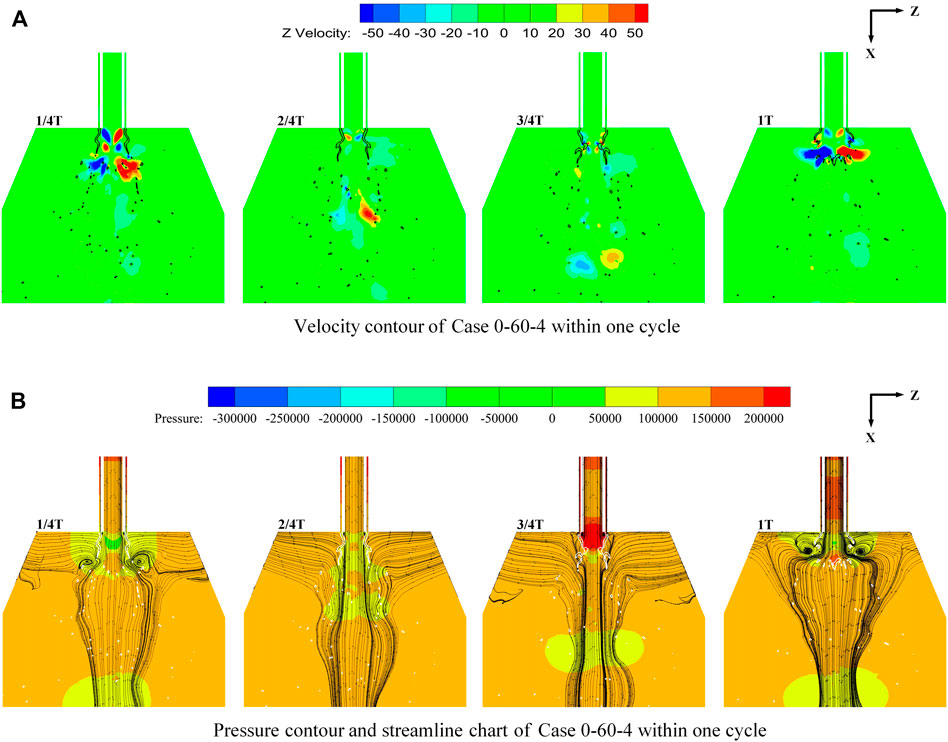
FIGURE 10. Velocity contour, pressure contour, and streamlines of case 0-60-4 within one cycle (the thick solid line indicates the isoline of the liquid phase volume fraction of 0.25).

Meanwhile, the flow characteristics during the cycle were evident, as shown in Figure 10, which shows the velocity contour, pressure contour, and streamline chart during one cycle of case 0-60-4. As the liquid sheet began to contract, the gas channel at the contraction narrowed at 1/4T, which resulted in an increase in the velocity of the airflow. However, the velocity of the central airflow and the inner part of the liquid film of the annular aperture was reduced by shearing. This resulted in the formation of two counter-swirl reflux zones at the gas injector outlet, with two vortices in opposite directions. The “neck” formation began at 2/4T, and the increasing length of the shearing effect between the central airflow and the inner side of the annular aperture liquid sheet resulted in an increase in the counter-swirl reflux zones. Thus, the two opposite vortices formed between the outlet of the gas injector and the inside of the liquid film increased, and this growth was apparent at 3/4T. Finally, when the “neck” section broke at 1T, the central airflow “broke out of the liquid film” with the opened gas channel. The two vortices in opposite directions formed in the inner part of the “neck” section dissipated rapidly. At the same time, two larger opposing vortices at the “broken” section owing to gas-liquid entrainment and some small and complex vortex systems were generated simultaneously.

When the ${\dot{m}}_g$ increased, the central airflow was accelerated. The iterative speed of the above-mentioned processes, such as the contraction of the liquid sheet, was accelerated. This resulted in an enhanced frequency of self-pulsations, and a stronger momentum was transferred when the central airflow “broke out of the liquid film”. The spray pulsation within one cycle for case 0-60-8 is shown in Figure 9B, and its spray pulsation is similar to that of case 0-60-4. However, compared to case 0-60-4, when the “neck” broke at 1T, the action of “breaking out of the liquid film” provided a greater radial velocity to the droplets and liquid blocks at the “neck” for the increase in ${\dot{m}}_g$. It resulted in the spray width of the “neck” being larger than that of the “shoulder”. In other words, compared to case 0-60-4, the comparison of the spray width values for the two above-mentioned values was reversed.

4.3 Self-Pulsation Phenomenon With Recess

The experimental results revealed similar changes in behavior for the injector with and without recess. In other words, when ${\dot{m}}_g$ was low for a constant ${\dot{m}}_l$, the phenomenon of self-pulsation occurred and was accompanied by a scream, and the frequency of self-pulsation increased with ${\dot{m}}_g$ until it subsided. However, for injectors with recess, the frequency of self-pulsation significantly decreased compared to those without recess. The variations in the self-pulsation frequency at different gas mass flow rates for ${\dot{m}}_l=40g/s$ are illustrated in Figure 11A.

FIGURE 11

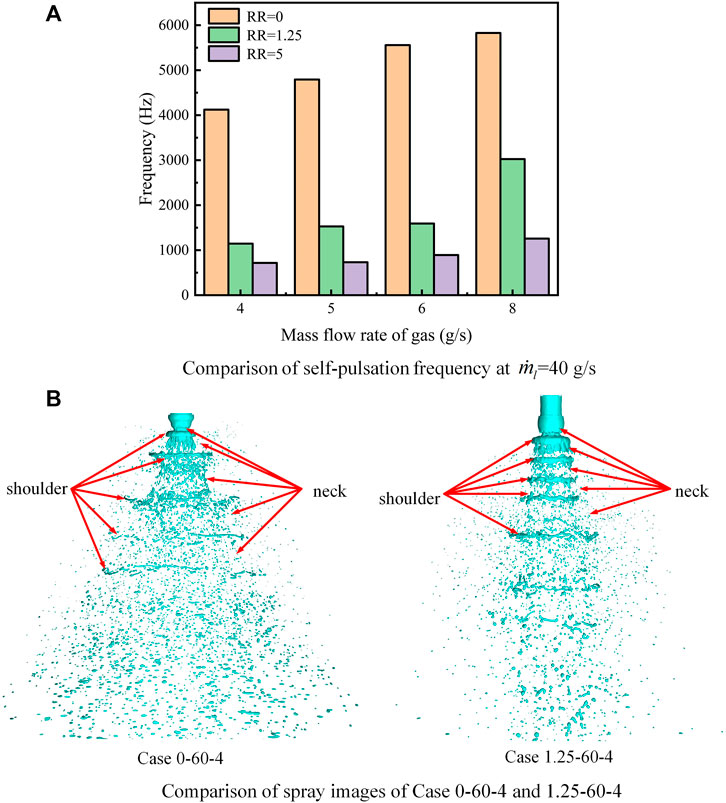
FIGURE 11. Comparison of the self-pulsation frequency at ${\dot{m}}_l$ = 40 g/s and comparison of spray images of cases 0-60-4 and 1.25-60-4.

The central gas flow in the recess chamber was assumed to have produced the entrainment and ejection functions on the annular aperture liquid sheet. On the one hand, the friction between the gas and liquid hindered the flow of the liquid sheet, which prolonged the period of liquid sheet pulsation, that is, the frequency of self-pulsation decreased. On the other hand, the wall limited the radial velocity of the liquid sheet, which reduced the amplitude of radial pulsation downstream of the outlet, that is, the intensity of self-pulsation decreased. When RR increased, the friction between the gas and liquid further hindered the flow of the liquid sheet. Therefore, the frequency of self-pulsation was further reduced.

Numerical simulations of the injector with recession showed that it also underwent a similar self-pulsation cycle as the injector without a recession, as shown in Figure 11B, for the comparison of the spray images of cases 0-60-4 and 1.25-60-4. However, as mentioned earlier, as the recess chamber wall also limited the radial velocity of the liquid sheet, the radial pulsations downstream of the exit amplitude were reduced. This demonstrated that the width difference between the “shoulder” and “neck” of the spray decreased, that is, the spray angle decreased. The spray pulsation process in one cycle of the working condition (frequency of 4,354 Hz obtained from the simulation) is depicted in Figure 9C. In this period, the spray pattern was more distinguishable as a “string” shape than a “Christmas tree” shape.

5 Conclusion

In this study, the spray characteristics of gas-centered shear coaxial injectors under different operating conditions and RRs were investigated through experiments and numerical simulation methods based on CLSVOF and AMR. The results demonstrated the following.

1) In the case of a constant ${\dot{m}}_l$, the spray angle showed an opposite variation law for injectors with and without recess. For an injector without recess, the spray angle first stayed almost constant with the variation of ${\dot{m}}_g$ $\left(4\le {\dot{m}}_g\le 6\right)$. However, as ${\dot{m}}_g$ continued to increase, the spray angle dropped linearly. But the spray angle increased with ${\dot{m}}_g$ for injectors with recess. Moreover, the change in the spray angle with recess was attributed to the second expansion of the central gas flow by the numerical simulation analysis.

2) The experimental results revealed that under certain conditions, the injector without recess produced a self-pulsation phenomenon accompanied by a loud scream, and the self-pulsation frequency increased with ${\dot{m}}_g$ and ${\dot{m}}_l$ within a certain range. Moreover, the “Christmas tree”-shaped spray with the alternating “shoulder” and “neck” sections was obtained in the simulation results in addition to the small error of the frequency between numerical simulation and experiment.

3) The changes of self-pulsation in the injector with recession exhibited a pattern similar to that without recess. However, the self-pulsation frequency for an injector with recess was significantly lower than that without recess. It can be concluded from the analysis results that the friction between the gas and liquid inside the recess chamber hindered the flow of the liquid sheet, which extended the liquid sheet pulsation period, that is, the frequency of self-pulsation decreased. Meanwhile, the radial velocity of the liquid sheet would be restricted by the wall such that its radial pulsations downstream of the outlet amplitude would decrease, that is, the intensity of self-pulsation would be weakened.

4) The self-pulsation mechanism was initially explored through the numerical simulation. The self-pulsation of the injector was possibly the result of the combined action of the pressure difference between the inside and outside of the liquid sheet, the surface tension of the liquid sheet, and the impact extrusion of the central airflow. The self-pulsation spray was shaped like a “Christmas tree” for the injector without recess, whereas the spray was shaped like a “string” for the injector with recess. It was caused by the recess chamber wall to limit the radial velocity of the liquid sheet, and then, the width difference between the “shoulder” and “neck” of the spray and the radial pulsations downstream of the exit amplitude could be further reduced.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author Contributions

GY mainly contributed to experiments, data processing, and writing; CW and XY were the main contributors to the experiment; JC and XB contributed primarily to data processing; Su and Tong provided financial support for the experiment.

Funding

The study was supported by the National Natural Science Foundation of China (No. 12002386).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to express their sincere acknowledgment for support from the National Natural Science Foundation of China (No. 12002386).

References

Arthur, D., and Vassilvitskii, S. (2007). “K-means++: The Advantages of Careful Seeding, SODA '07,” in Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms (Philadelphia, PA: Society for Industrial and Applied Mathematics).

Google Scholar

Bazarov, V. G., and Yang, V. (1998). Liquid-propellant Rocket Engine Injector Dynamics. J. Propuls. Power 14, 797–806. doi:10.2514/2.5343

CrossRef Full Text | Google Scholar

Bazarov, V. (1998). “Non-linear Interactions in Liquid-Propellant Rocket Engine Injectors,” in 34th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit (Cleveland, OH: AIAA).

CrossRef Full Text | Google Scholar

Bazarov, V. (1995). “Self-pulsations in Coaxial Injectors with Central Swirl Liquid Stage,” in 31st AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit (San Diego, CA: AIAA).

CrossRef Full Text | Google Scholar

Chu, W., Li, X., Tong, Y., and Ren, Y. (2020). Numerical Investigation of the Effects of Gas-Liquid Ratio on the Spray Characteristics of Liquid-Centered Swirl Coaxial Injectors. Acta Astronaut. 175, 204–215. doi:10.1016/j.actaastro.2020.05.050

CrossRef Full Text | Google Scholar

Chu, W., Ren, Y., Tong, Y., Li, X., Jiang, C., and Lin, W. (2021). Numerical Study of Effects of Backpressure on Self-Pulsation of a Liquid-Centred Swirl Coaxial Injector. Int. J. Multiph. Flow 139, 103626. doi:10.1016/j.ijmultiphaseflow.2021.103626

CrossRef Full Text | Google Scholar

Eberhart, C. J., and Frederick, R. A. (2017). Details on the Mechanism of High-Frequency Swirl Coaxial Self-Pulsation. J. Propuls. Power 33, 1418–1427. doi:10.2514/1.b36216

CrossRef Full Text | Google Scholar

Eberhart, C. J., Lineberry, D. M., and Jr Frederick, R. A. (2013). “Detailing the Stability Boundary of Self-Pulsations for a Swirl-Coaxial Injector Element,” in 49th AIAA/ASME/SAE/ASEE Joint Propulsion Conference (San Jose, CA: AIAA).

Google Scholar

Eberhart, C., Lineberry, D., and Frederick, R. (2012). “Propellant Throttling Effects on Self-Pulsation of Liquid Rocket Swirl-Coaxial Injection,” in 48th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit (Atlanta: AIAA). doi:10.2514/6.2012-4204

CrossRef Full Text | Google Scholar

Hardalupas, Y., and Whitelaw, J. H. (1994). Characteristics of Sprays Produced by Coaxial Airblast Atomizers. J. Propuls. Power 10, 453–460. doi:10.2514/3.23795

CrossRef Full Text | Google Scholar

Hautman, D. J. (1993). Spray Characterization of Liquid/gas Coaxial Injectors with the Center Liquid Swirled. At. Spr. 3, 373–387. doi:10.1615/atomizspr.v3.i4.20

CrossRef Full Text | Google Scholar

Huang, J., Cai, W., Wu, Y., and Wu, X. (2022). Recent Advances and Applications of Digital Holography in Multiphase Reactive/nonreactive Flows: a Review. Meas. Sci. Technol. 33, 022001. doi:10.1088/1361-6501/ac32ea

CrossRef Full Text | Google Scholar

Kang, Z. T., Li, X. D., Mao, X. B., and Li, Q. L. (2018). Review on Gas Liquid Shear Coaxial Injector in Liquid Rocket Engine. Acta Aeronautica Astronautica Sinica 39, 6–25. doi:10.7527/S1000-6893.2018.22221

CrossRef Full Text | Google Scholar

Kim, B.-D., Heister, S. D., and Collicott, S. H. (2005). Three-dimensional Flow Simulations in the Recessed Region of a Coaxial Injector. J. Propuls. Power 21, 728–742. doi:10.2514/1.12651

CrossRef Full Text | Google Scholar

Kim, B.-D., and Heister, S. D. (2004). Two-phase Modeling of Hydrodynamic Instabilities in Coaxial Injectors. J. Propuls. Power 20, 468–479. doi:10.2514/1.10378

CrossRef Full Text | Google Scholar

Kulkarni, V., Sivakumar, D., Oommen, C., and Tharakan, T. J. (2010). Liquid Sheet Breakup in Gas-Centered Swirl Coaxial Atomizers. J. Fluids Eng. 132, 011303. doi:10.1115/1.4000737

CrossRef Full Text | Google Scholar

Li, J. N., Lei, F. P., Zhou, L. X., and Yang, A. L. (2019). Effects of Misaligned Impingement on Atomization Characteristics of Impinging Jet Injector. J. Aerosp. Power 34, 2280–2293.

Google Scholar

Luo, T. Q. (2017). Fluid Mechanics. Beijing: China Machine Press, 224.

Google Scholar

Nunome, Y., Sakamoto, H., Tamura, H., Kumakawa, A., Amagasaki, S., and Inamura, T. (2007). “An Experimental Study of Super-pulsating Flow on a Shear Coaxial Injector with a Recessed Inner Post,” in 43rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit (Cincinnati, OH: AIAA).

CrossRef Full Text | Google Scholar

Nunome, Y., Tamura, H., Onodera, T., Sakamoto, H., and Inamura, T. (2009). “Effect of Liquid Disintegration on Flow Instability in a Recessed Region of a Shear Coaxial Injector,” in 45th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit (Denver, CO: AIAA).

CrossRef Full Text | Google Scholar

Siddharth, K. S., Panchagnula, M. V., and Tharakan, T. J. (2017). Effect of Gas Swirl on the Performance of a Gas-centered Swirl Co-axial Injector. At. Spr. 27, 741–757. doi:10.1615/atomizspr.2017019923

CrossRef Full Text | Google Scholar

Tsohas, J., and Heister, S. D. (2011). Numerical Simulations of Liquid Rocket Coaxial Injector Hydrodynamics. J. Propuls. Power 27, 793–810. doi:10.2514/1.47761

CrossRef Full Text | Google Scholar

Wang, K., Yang, G. H., Li, P. F., Zhang, M. Q., and Zhou, L. X. (2016). Numerical Simulation of Internal Flow Process in Pressure Swirl Injector. J. Rocket Propuls. 42, 14–20. doi:10.3969/j.issn.1672-9374.2016.04.003

CrossRef Full Text | Google Scholar

Wang, L., Fang, B., and Wang, G. C. (2021). Process of Pressure Swirl Injector Atomization Based on Large Eddy Simulation. J. Propuls. Technol. 42, 1855–1864. doi:10.13675/j.cnki.tjjs.190392

CrossRef Full Text | Google Scholar

Wu, Y. C., Zhao, X. X., Zhang, H. Y., Lin, X. D., and Wu, X. C. (2022). Discrimination and Measurement of Droplet and Ice Crystal by Combining Digital Inline Holography with Interferometric Particle Imaging with Single Color Camera. IEEE Trans. Instrum. Meas., 0018–9456. doi:10.1109/tim.2022.3147333

CrossRef Full Text | Google Scholar

Xu, S. (2016). Experimental Study on Spray Characteristic of Gas-Liquid Centred Coaxial Swirling Injectors. Changsha: National University of Defense Technology.

Google Scholar

Yang, L.-J., and Fu, Q.-F. (2012). Stability of Confined Gas-Liquid Shear Flows in Recessed Shear Coaxial Injectors. J. Propuls. Power 28, 1413–1424. doi:10.2514/1.b34560

CrossRef Full Text | Google Scholar

Yang, L. J., Ge, M. H., Zhang, M. Z., Fu, Q. F., and Cai, G. B. (2006). Spray Characteristics of Recessed Gas-Liquid Coaxial Swirl Injector. J. Propuls. Power 2, 1332–1339. doi:10.13675/j.cnki.tjjs.2006.04.001

CrossRef Full Text | Google Scholar

Nomenclature

d_o inner diameter of the outer injector (unit: mm)

d_g inner diameter of the inner injector (unit: mm)

d_t outer diameter of the inner injector (unit: mm)

L_r recessed length (unit: mm)

RR recess ratio

$\dot{m}$ mass flow rate (unit: g/s)

μ viscosity coefficient (unit: Pa·s)

p pressure (unit: Pa)

ρ density (unit: Kg/m³)

g gravitational acceleration vector (unit: m/s²) gas

F additional volume force vector (unit: N)

U velocity vector (unit: m/s)

T_L temperature (unit: K)

T symbol of period

k_eff effective heat transfer coefficient (unit: W/m·K)

I unit tensor

J_j diffusive flow of the component j

S_h volumetric heat source term

h_j enthalpy of the component j (unit: J)

T_L0 reference temperature (unit: K)

μ₀ reference viscosity coefficient (unit: Pa·s)

Subscripts

g gas

l liquid