A Meandering-Capturing Wake Model Coupled to Rotor-Based Flow-Sensing for Operational Wind Farm Flow Prediction

The development of new wake models is currently one of the key approaches envisioned to further improve the levelized cost of energy of wind power. While the wind energy literature abounds with operational wake models capable of predicting in fast-time the behavior of a wind turbine wake based on the measurements available (e.g., SCADA), only few account for dynamic wake effects. The present work capitalizes on the success gathered by the Dynamic Wake Meandering formulation and introduces a new operational dynamic wake modeling framework aimed at capturing the wake dynamic signature at a low computational cost while relying only on information gathered at the wind turbine location. In order to do so, the framework brings together flow sensing and Lagrangian flow modeling into a unified framework. The features of the inflow are first inferred from the turbine loads and operating settings: a Kalman filter coupled to a Blade Element Momentum theory solver is used to determine the rotor-normal flow velocity while a Multi-Layer Perceptron trained on high-fidelity numerical data estimates of the transverse wind velocity component. The information recovered is in turn fed to a Lagrangian flow model as a source condition and is propagated in a physics-informed fashion across the domain. The ensuing framework is presented and then deployed within a numerical wind farm where its performances are assessed. The computational affordability of the proposed model is first confirmed: 7 × 10⁻⁴ wall-clock seconds per simulation second are required to simulate a small 12 turbines wind farm. Large Eddy Simulations of wind farm using advanced actuator disks are then used as a baseline and a strong focus is laid on the study of the wake meandering features. Comparison against the Large Eddy Simulation baseline reveals that the proposed model achieves good estimates of the flow state in both low and high Turbulence Intensity configurations. The model distinctly provides additional insight into the wake physics when compared to the traditional steady state approach: the wake recovery is consistently accounted for and the wake meandering signature is captured as far as 12D downstream with a correlation score ranging from 0.50 to 0.85.

1 Introduction

Wind turbine wakes are notoriously hard to study owing the inherent complexity of the interactions between wind turbines and the Atmospheric Boundary Layer (ABL) physics. Yet, enhancing our understanding and modeling capabilities of wind turbine wakes is paramount to improving the performances of existing wind power plants controllers. Indeed, wakes induce strong delayed interactions between neighboring turbines which degrade the performances of the wind farm taken as a whole. Designing new global wind power plant control schemes accounting for wake effects is thus expected to have a strong impact on the overall power production and life time expectancy of wind farms and hence on the levelized cost of energy of wind energy globally.

To this end, a large number of control schemes has been proposed in the literature. They fall within two categories: model-free or model-based controllers. Model-based control (e.g., Doekemeijer et al., 2019) aims at selecting the optimal control action based on the information provided by an underlying simplified model of the wind farm dynamics which predicts the turbines-wakes interactions. Model-free control (e.g., Park and Law, 2016), on the other hand, alleviates the need for wake understanding: the flow is essentially considered as a black box and the wind turbines select their control policy based on their observed states. However, this approach struggles with the extended convective time scales observed in wind farms which induce large delays between a control input change and its impact on downstream wind turbines (Doekemeijer et al., 2019). Model-based control schemes have thus been gaining a significant amount of traction recently.

Developing such a control scheme is however not straightforward. It requires an adequate level of understanding of the flow field at the scale of the wind farm as the accuracy of the underlying surrogate wake model always bounds the performances of the synthesized control scheme. Some key criteria should therefore be matched by the surrogate wake model in order to make it suitable for the control-based approach: it should be fast enough to be usable online and yet guarantee a sufficient degree of fidelity to reality. This latter criterion, along with the unsteady nature of wind wakes and their high sensitivity to the local wind characteristics, makes the development of accurate surrogate models one of the remaining pivotal challenges faced by the model-based strategy.

While significant insight into wind farm wake flows has been gained thanks to modern computer technology and high-fidelity numerical simulation techniques such as Large Eddy Simulation (LES), the porting of these approaches to real time control has been hindered by their prohibitive computational cost along with the uncertainty of real time conditions. In order to overcome this limitation, a number of medium- to low-fidelity wake models have been successively introduced in the literature. Low-fidelity wake models typically rely on a simplified description of the flow derived from the mass and/or momentum conservation equations. They most often provide a steady-state analytical description of the mean flow field and are thus computationally affordable. To this day, the wake model introduced by Jensen (1983) remains one of the most popular low-fidelity model examples. Other examples include the analytical Gaussian model proposed by Bastankhah and Porté-Agel (2014) based on momentum conservation as well as its variants including near wake correction (Blondel et al., 2020; Schreiber et al., 2020). These models offer a great robustness at the cost of a low degree of accuracy. Furthermore, owing to their steady-state assumption, they are unable to capture some of the key features of wakes such as their meandering. They essentially consider the wake as static and wide and assimilate wake meandering to the wake expansion (Thøgersen et al., 2017; Braunbehrens and Segalini, 2019). This approximation works relatively well for slow wind farm control but leads to inconsistent results if finer time scales are considered. It further fails to correctly account for meandering-induced fatigue loads (Reinwardt et al., 2020). Medium-fidelity wake models aim to bridge the gap between the two ends of the model spectrum: they provide a dynamic reasonably-faithful description of the flow while remaining computationally tractable. The most common medium-fidelity wake model is the Dynamic Wake Model (DWM) introduced by Larsen et al. (2007) and its FAST-Farm implementation by Jonkman and Shaler (2021) though other models such as the dynamic control-oriented version of Floris proposed (Becker et al., 2022) also fall within that category.

The framework presented here aims at developing an online physics-based medium-fidelity model able to capture the main dynamic features of the wake. As this model is intended for operational use (i.e., real time control of wind farm), it should only rely on information that is available to the turbine: the features of the incoming flow field can not be determined a priori but should be inferred from the measurements available. This implies that both the incoming turbulent flow field and the wake shed by the wind turbine should be reconstructed from the information gathered at the wind turbine location. Furthermore, the flow reconstruction procedure should run in fast time in order to be deployable in the context of model-based control.

This work extends some previous works toward the formulation of an online operational wake model (Lejeune et al., 2020). It brings flow sensing and Lagrangian flow modeling together into a unified framework where information gathered at the wind turbine location is propagated across the wind farm thereby reconstructing an estimated snapshot of the flow state at a low computational cost. Consistent with the turbine as a sensor approach (Bottasso et al., 2018; Bertelè and Bottasso, 2020), we first deploy a flow sensing module that estimates the inflow features from the wind measurements. The estimation of the rotor-normal component is handled through a Kalman filter coupled with a Blade Element Momentum (BEM) code (Bottasso et al., 2018) while the transverse velocity component is computed using an Artificial Neural Network (ANN) regressor trained on high-fidelity LES data. Based on the inflow features acquired through the flow sensing module, the Lagrangian flow model then reconstructs the farm flow field in terms of two coupled fields: a freestream velocity field and a wake velocity deficit one. Both fields are modeled as series of information-carrying particles propagated across the wind farm in a physics-informed fashion thereby capturing the dynamic wake signature at a low computational cost. The resulting framework captures the relevant dynamic features of the wake (i.e., wake meandering and wake convection) as well as from the freestream field (i.e., inflow heterogeneities). The implemented information propagation procedure, in a fashion akin to a Particle Filter (Notter et al., 2020; Le Provost and Eldredge, 2021), enables the prediction of the main flow features at a downstream turbine at a time horizon set by the turbine separation. This should, in turn, allow to select the optimal control policy for the impinged rotor. Furthermore, as discrepancies between the estimated flow state and its real counterpart are inevitable, strong focus is laid on providing a concise description of the flow based on few tuning parameters in order to make the model usable within a state-correction framework (Doekemeijer et al., 2019; Dong et al., 2021).

We leverage LESs of wind farms to support the development, tuning and testing of this operational model. Specifically, the LES flow solver (Section 2.1) is used to aggregate a database of high-fidelity results that includes several wind farm layouts and inflow conditions. These data sets then serve as reference for 1) the calibration of the flow model (Section 2.2), 2) training the neural network based flow sensing module (Section 2.2.1) and 3) assessing the performances of the whole operational model (Section 3). The wake behind isolated wind turbines is first investigated (Section 3.2.1): the LES are compared to the Lagrangian flow model prediction in terms of their meandering signature and speed deficit characteristics. These results are finally confirmed by the analysis of a small wind farm (Section 3.2.2) consisting of 12 turbines operating under strong wake effects.

2 Materials and Methods

2.1 Reference High-Fidelity Simulation

As mentioned above, the present work will rely exclusively on numerical simulations to develop the wake model. This section succinctly highlights the main features of the LES simulation framework.

The flow solver is an in-house fourth-order finite difference LES solver coupled with an advanced actuator disk featuring improved tip-loss correction (Moens et al., 2018). The wind turbine model is the NREL 5MW (Jonkman et al., 2009), implemented with its torque and collective blade pitch controllers. Accordingly, the rotor diameter, D, is set to D = 126 m. The wind turbine operating settings are directly extracted from the simulation data while the blade loads are obtained by projecting the total disk loads over virtual wind turbine blades (Moens et al., 2022).

The wind turbines are arranged in farm configurations within the numerical simulation domain whose physical dimensions are 32D × 8D × 16D for the streamwise $({\widehat{\mathbf{e}}}_{x,WT})$, vertical $({\widehat{\mathbf{e}}}_{y,WT})$ and transverse $({\widehat{\mathbf{e}}}_{z,WT})$ directions respectively. For this work, the resolution is set to 16 points per rotor diameter in the horizontal directions. This results from a compromise between efficiency and accuracy in the representation of the wind turbine behavior and wake phenomena. The mesh is refined in the y-direction, from the ground to a height slightly above the highest point of the disk, in order to have a few points between the lowest disk position and the height where the velocity is sampled for the wall modelling procedure. The final mesh is a N_x × N_y × N_z = 512 × 128 × 256 grid that is uniform in the wall-parallel directions (Δx = Δz = 7.875 m) and that is partially stretched in the vertical direction. This stretching leads to a uniform vertical grid below 200 m, with Δy_min = 3.975 m. Above that, Δy increases, to reach Δy_max ≃ 10 m at the top of the domain.

A rough wall law is enforced on the bottom boundary along with a no-through condition on the top boundary. The transverse direction is considered periodic while a inflow-outflow condition is applied in the streamwise direction: a convective boundary condition is used at the outflow and a concurrent precursor simulation with no wind turbine provides the inflow condition.

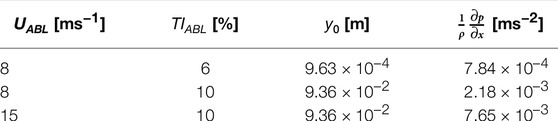
The parameters of this precursor simulation, namely its roughness length, y₀ and forcing pressure gradient, $\frac{1}{\rho }\frac{\partial p}{\partial x}$, determine the features of the inflow. The parameters of the different simulation precursors are summed up in Table 1. Each set of parameters is selected in order to obtain the desired mean wind velocity, U_ABL, and turbulence intensity, TI_ABL, at the hub location.

TABLE 1

TABLE 1. ABL configuration used.

Finally, the wake centroid position is computed using a wake tracking algorithm developed by Coudou (2021). This algorithm evaluates the position of the wake centroid by finding the minimum of a convolution product between a masking function and the available flow power density retrieved from the LES velocity field. In this context, a 3D Gaussian masking function allowing a smooth wake centerline tracking, f_G, is applied:

$f_G\left(x,y,z\right)=-\exp \left(-\left(\frac{x^2}{2{\sigma }_x^2}+\frac{y^2}{2{\sigma }_y^2}+\frac{z^2}{2{\sigma }_z^2}\right)\right)(1)$

with σ_x = σ_y = σ_z = D/2, values that consistent with the scales targeted by the wake model. Though this broad mask parametrization partially filters out the influence of the low speed external eddies on the wake centerline computation, it sometimes also leads to an unrealistic smoothing of the latter. A narrower mask, i.e., σ_x = σ_y = D/4 and σ_z = D/2, is therefore also used to provide a sensitivity information in the form of a wake centerline position envelope. A representative numerical setup is illustrated in Figure 1 by means of an instantaneous velocity field together with the extracted wake centerlines.

FIGURE 1

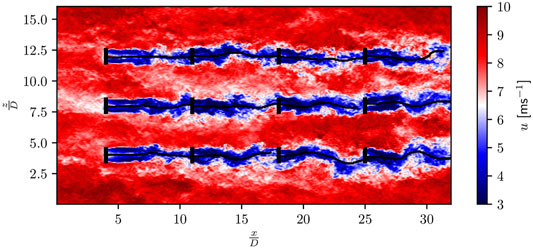
FIGURE 1. Streamwise velocity field at hub height extracted from the reference LES for for U_ABL = 8 ms⁻¹; position of the wake center as computed by the wake tracking algorithm (continuous black line).

2.2 Flow Sensing

The first step toward developing an online wake model deployable in the context of wind farm control is to accurately estimate the inflow features from the wind turbine measurements. However, as typical hub-mounted sensors (e.g., wind vane or anemometers) suffer from a number of disturbances ranging from the presence of the nacelle or blades to the wake-induced flow deformations, their measurements are often considered unreliable (Bertelè and Bottasso, 2020). The turbine as a sensors approach is thus chosen in order to provide robust estimates of the inflow velocity field, ${\widehat{\mathbf{u}}}_{\text{WT}}=[{\widehat{u}}_{\text{WT}},{\widehat{w}}_{\text{WT}}]$. The remainder of this section presents these rotor-normal (Section 2.2.1) and transverse (Section 2.2.2) velocity estimators that infer the wind characteristics from the specific turbine responses they trigger.

2.2.1 Rotor-Normal Velocity Component

Following Bottasso et al. (2018), a Kalman filter coupled with a BEM code is first implemented in order to estimate the inflow features. This method essentially considers the wind turbine blades as moving sensors whose out-of-plane bending loads, m_f, are strictly connected to the local wind speed at the blade position.

In order to retrieve an accurate local snapshot of the flow azimuthal features, the rotor is divided into N_S sectors over which the local sector effective rotor-normal velocities, u_s(t), are evaluated (Bottasso et al., 2018):

$u_s\left(t\right)=\frac{1}{{\theta }_{s,1}-{\theta }_{s,0}}{\int }_{{\theta }_{s,0}}^{{\theta }_{s,1}}u\left(\theta ,t\right)\text{d}\theta (2)$

where θ denotes the azimuthal coordinate and θ_s,0 and θ_s,1 are the sector s upper and lower bounds, respectively.

At every blade sweep, a Kalman filter computes the new sector effective wind speed estimation, ${\widehat{u}}_s$, from the measured bending loads averaged over the crossing time window. The resulting local wind speed estimations are, in turn, combined into ${\widehat{u}}_{\text{WT}}=\mathrm{\Sigma }{\widehat{u}}_s/N_S$, the estimated rotor effective rotor-normal wind speed.

Finally, an estimation of the wind turbine thrust coefficient, ${\widehat{C}}_{T,\text{WT}}$, and flow turbulence intensity, ${\widehat{TI}}_{\text{WT}}$ are recovered based on the estimated sectors effective rotor-normal velocities. The latter are eventually fed as inputs to the flow model and read:

${\widehat{C}}_{T,\text{WT}}\left(t\right)=\frac{8T\left(t\right)}{\rho \pi D^2{\widehat{u}}_{\text{WT}}^2\left(t\right)}(\mathrm{3a})$

$\widehat{T}{I}_{\text{WT}}\left(t\right)=\sqrt{\frac{\sum {\left(u_s\left(t\right)-{\bar{\widehat{u}}}_{\text{WT}}\left(t\right)\right)}^2}{N_S-1}}\frac{1}{{\bar{\widehat{u}}}_{\text{WT}}\left(t\right)}(\mathrm{3b})$

with ρ the air density. The $\bar{\varphi }$ operator applied to a flow quantity ϕ indicates its averaging over a prescribed time window.

2.2.2 Transverse Velocity Component

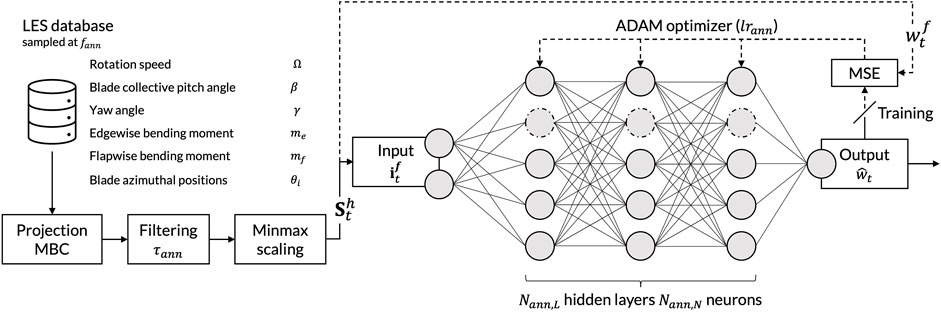
Extending the model presented in the previous paragraph to account for the effect of the transverse velocity component on the rotor dynamic is not trivial as it falls beyond the classical BEM theory assumptions. Bertelè and Bottasso (2020) propose a similar wind turbine state estimator based on the loads harmonics. Even though their estimator leads to accurate instantaneous flow shear angles and rotor-averaged streamwise velocity, it is not able to capture the instantaneous fluctuations of the yaw angle. This difference in sensitivity between the streamwise and transverse velocity components is largely due to the difference in rotor aerodynamic response as demonstrated by Bertelè et al. (2017) who analysed the airflow around a simplified wind turbine airfoil section. In light of this, we elect to base our transverse velocity regressor not upon a physics-based model (i.e., an underlying flow-rotor model), but rather upon an ANN trained on a high-fidelity data set.

The training of the transverse velocity regressor is thus formulated as a supervised-learning problem. Learning is performed by iteratively feeding the ANN labeled data of the operation settings of the turbine as well as with the transverse velocity directly retrieved from the LES thereby providing the algorithm with corrective information (Brunton et al., 2020). Once the ANN has been trained, it is tested against never-seen data for which it has no knowledge of the expected output. This section first explains the labeled data formatting step (Section 2.2.2.1) before moving on to the presentation of the structure of the ANN used and subsequent learning procedure (Section 2.2.2.2).

2.2.2.1 Data Preparation

The neural network is supplied with data extracted from the high-fidelity LES which allows it to predict the rotor effective transverse velocity, w_WT(t). The corresponding ANN input consists of the instantaneous rotation speed of the wind turbine, Ω(t) as well as its projected yaw, γ(t), and global pitch angles, β(t). Finally, following Bertelè and Bottasso (2020), the reconstructed blade loads harmonics are also appended to this input state vector:

$\begin{array}{ll}\hfill \left[\begin{array}{c}\hfill \bar{m}\left(t\right)\hfill \\ \hfill m_{\text{c}}\left(t\right)\hfill \\ \hfill m_{\text{s}}\left(t\right)\hfill \end{array}\right]& =\left[\begin{array}{ccc}\hfill \frac{1}{3}\hfill & \hfill \frac{1}{3}\hfill & \hfill \frac{1}{3}\hfill \\ \hfill \frac{2}{3}\cos \left(,\theta ,\left(t\right)\right)\hfill & \hfill \frac{2}{3}\cos \left(\theta \left(t\right)-\frac{2\pi }{3}\right)\hfill & \hfill \frac{2}{3}\cos \left(\theta \left(t\right)+\frac{2\pi }{3}\right)\hfill \\ \hfill \frac{2}{3}\sin \left(,\theta ,\left(t\right)\right)\hfill & \hfill \frac{2}{3}\sin \left(\theta \left(t\right)-\frac{2\pi }{3}\right)\hfill & \hfill \frac{2}{3}\sin \left(\theta \left(t\right)+\frac{2\pi }{3}\right)\hfill \end{array}\right]\hfill \\ \hfill & \times \left[\begin{array}{c}\hfill m_1\left(t\right)\hfill \\ \hfill m_2\left(t\right)\hfill \\ \hfill m_3\left(t\right)\hfill \end{array}\right]\hfill \end{array}(4)$

with θ(t), the instantaneous azimuthal position of blade 1. In this expression, a Multi-Blade Coordinate (MBC) transform derived by Coleman and Feingold (1958) is applied in order to map the edgewise, m_e,b and flapwise bending moments, m_f,b of the blades, b = 1, 2, 3 to their 1-P harmonics.

The resulting state vector fed to the neural network thus comprises 11 different fields:

${\mathbf{i}}_t=\left[\mathrm{\Omega }\left(t\right),{\gamma }_{c/s}\left(t\right),{\beta }_{c/s}\left(t\right),m_{e/f,0}\left(t\right),m_{e/f,c}\left(t\right),m_{e/f,s}\left(t\right)\right](5)$

where t is the temporal index and ϕ_c/s denotes the projected cos(ϕ) and sin(ϕ) components, respectively. Data is sampled at a frequency f_ann and the input and output state vectors are eventually concatenated into a single data base entry:

${\mathbf{S}}_t=\left[{\mathbf{i}}_t^f;w_t^f\right](6)$

where (⋅)^f denotes that an Exponential Moving Average filter with time constant τ_ann has been applied (here both to the input and output data).

We finally introduce some information about the past history by concatenating several input filtered states into a single data base entry:

${\mathbf{S}}_t^h=\left[{\mathbf{i}}_{t-T_{ann}}^f,\dots ,{\mathbf{i}}_{t-1}^f,{\mathbf{i}}_t^f;w_t^f\right].(7)$

T_ann determines the number of successive time indices considered: the larger T_ann, the longer the neural network memory. We should however note that, in this configuration, each data base entry is considered as an independent data sample, this may very rapidly increase the complexity of the input data.

The different date base entries are then collected inside one large data base whose different fields, ϕ, are normalized using a minmax scaler:

${\varphi }_{norm}=\frac{\varphi -\min \left(\varphi \right)}{\max \left(\varphi \right)-\min \left(\varphi \right)}(8)$

which casts all the database values into the interval [0, 1] thereby facilitating the neural network convergence.

This data formatting procedure is then applied in order to aggregate a LES data base. The latter is splitted into three subsets: a training, a validation and a testing set. The training set provides never-seen data against which the performances of the trained neural network can be validated. The testing set on the other hand constitutes the bulk of the data base and is used for training purposes. Finally, the validation set provides a metric to avoid overfitting: the optimization procedure should be stopped when the loss metric evaluated on the validation set has reached its minimum. This procedure ensures that the calibrated neural network generalizes well to other data sets.

Different LES are performed in order to assemble the LES database. Their results are uniformly sampled at a f_ann = 0.25 Hz and then appended to the data base. The description of the simulation setup used for each data base subset (i.e., validation, training and testing sets) is presented hereunder.

• The wind farm layout from which the training and validation data set are extracted consists of 19 turbines with a random spacing ranging from 4D to 10D thereby accounting for both waked and unwaked conditions. 6,250 s long simulations are carried for each of the ABL precursors resulting in a total 89,000 data base entries. 20% of this data is used for validation purposes while the remaining 80% are fed to the ANN as part of its learning. Within both subsets, the data is shuffled so that the neural network does not overfit the last wind turbine of the data set. Indeed, if no shuffling was applied, the ANN would converge toward an optimum representative of the last wind turbine encountered as part of its training which may not be corresponding to the global optimum.

• The test set, on the other hand, is obtained by simulating a farm of 12 evenly spaced (7D) turbines during 1,250 s. Once again, three simulations are carried: one for each ABL settings. The test set thus comprise a total of roughly 11,000 data base entries.

2.2.2.2 Neural Network Structure and Training

A Multi-Layer Perceptron (MLP) is used to learn the mapping between the input state vector consisting of the 11 original inputs, ${\mathbf{i}}_t^f$, and the target effective transverse velocity output, $w_{\text{WT},t}^f$. As illustrated on Figure 2, MLPs are a class of ANNs consisting of at least three fully-connected layers of nodes: an input, a hidden and an output layers. Both the hidden and outputs layers use non-linear activation functions thereby allowing this class of neural networks to capture non-linear behaviors.

FIGURE 2

FIGURE 2. Transverse velocity sensing: data preparation and Neural Network structure.

The different layers are connected through weight matrices whose values are updated as part of the training procedure until convergence is reached. Learning is performed through the back-propagation of the reference loss function through the network during the training step. The complete training data set is first split into mini-batches each consisting of N_ann,b randomly picked data base samples. At each iteration, a new mini-batch is fed to the MLP and the network weights are updated using the standard Adam optimizer algorithm with learning rate lr_ann in order to minimize the target loss function, L_MSE:

$L_{\text{MSE}}=\sum _t{\left({\widehat{w}}_{\text{WT},t}-w_{WT,t}^f\right)}^2(9)$

which corresponds to the Mean Square Error (MSE) with ${\widehat{w}}_{\text{WT},t}$ and $w_{\text{WT},t}^f$ the estimated and reference rotor effective transverse velocities, respectively.

The MLP used here comprises N_ann,L hidden layers of N_ann,N neurons. The latter use Rectified Linear Unit (ReLU) activation functions preceded by a Normalization Layer in order to reduce the training time (Ba et al., 2016). Finally, the Adam optimization algorithm is used to update the layers weight matrices during the training procedure. The resulting neural network architecture is implemented and trained using PyTorch, an open source machine learning framework for deep neural networks (Paszke et al., 2019). A heuristic approach was adopted in order to compute the hyperparameters. Different configurations were tested and only the set of hyperparameters achieving the lowest MSE on the validation set was conserved. We should therefore note that a more exhaustive hyperparameters search may lead to improved performances of the ANN. However, it would inevitably inflate the computational cost. The neural network training and subsequent hyperparameters tuning are not discussed in more details here. The optimized network hyperparameters are: N_ann,L = 3, N_ann,N = 64, T_ann = 1, τ_ann = 8s, lr_ann = 3.5 × 10⁻⁵ and N_ann,b = 64.

2.3 Lagrangian flow Model

Information is gathered where it is available, at the wind turbine, and then propagated in a physics-informed fashion across the domain. The estimated inflow velocity field, ${\widehat{\mathbf{u}}}_{\text{WT}}=[{\widehat{u}}_{\text{WT}},{\widehat{w}}_{\text{WT}}]$, and its associated states, ${\widehat{C}}_{T,\text{WT}}$ and ${\widehat{T}I}_{\text{WT}}$, are fed to the Lagrangian flow model which, in turn, uses them to infer flow quantities at arbitrary locations throughout the wind farm.

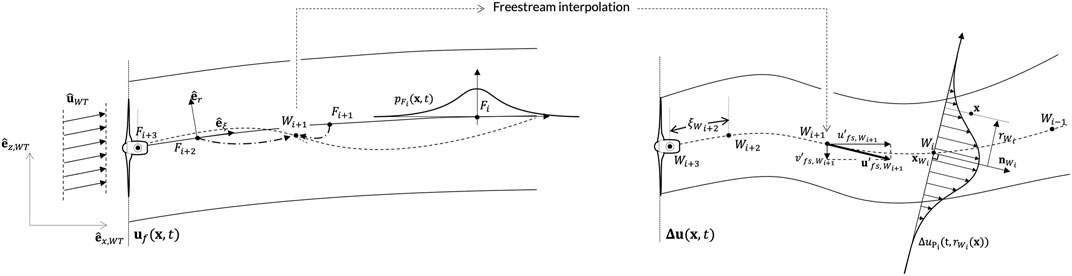
The two-dimensional wake model introduced in this section follows the standard DWM hypothesis. Consistent with Taylor’s frozen turbulence hypothesis, the wake is discretized as a series of wake particles behaving as passive tracers advected by the background flow (Larsen et al., 2007; Jonkman and Shaler, 2021). As illustrated in Figure 3, one of the key features of this model is that this background flow is also modeled using a particle-based discretization which makes it similar to (and actually compatible with) Particle Filter approaches for the estimation of flow information, see e.g., Notter et al. (2020) or Le Provost and Eldredge (2021) for very similar applications in an operational context.

FIGURE 3

FIGURE 3. Flow model: discretization strategy.

The Lagrangian flow model is thus decomposed into two main coupled fields: the freestream velocity field, u_f(x, t), and the speed deficit one, Δu(x, t):

${\mathbf{u}\left(\mathbf{x},t\right)=\mathbf{u}}_f\left(\mathbf{x},t\right)-\mathbf{\Delta }\mathbf{u}\left(\mathbf{x},t\right).(10)$

The freestream velocity field is understood as the velocity field that would be observed without any wake effect: it corresponds to the LES precursor velocity field. The speed deficit field on the other hand is obtained by superposing the speed deficit shed by all the turbines of the wind farm.

A source condition for both fields is provided by the wind turbine measurements through flow sensing. This information is then propagated downstream at its own characteristic velocity and contributes incrementally to the estimation of the flow field throughout the wind farm.

This section presents how both fields are modeled and how they interact together. The freestream particle discretization is first discussed (Section 2.3.1) after which a description of the wake parametrization is provided (Section 2.3.2).

2.3.1 Freestream Module

The wake features are directly dictated by the wind turbine geometry, operating settings and the characteristic of the ambient flow, u_f(x, t). The first step necessary to estimate the complete farm flow is therefore to reconstruct the background, unperturbed flow. Classically, this field would be retrieved from a Mann turbulence box or a precursor simulation (Larsen et al., 2007; Jonkman and Shaler, 2021). The resulting background velocity field would then be advected across the wind farm simulation domain at its own characteristic advection speed assuming frozen turbulence. However, focus is here laid on developing a model that can be used in the context of online control where the incoming turbulent flow field is obviously not available. Advection is thus handled in a Lagrangian fashion where the freestream measurements, ${\widehat{\mathbf{u}}}_{\text{WT}}(t)$, gathered at the wind turbine locations, x_WT, are propagated downstream along the mean flow streaklines

$\frac{\partial {\widehat{\mathbf{u}}}_{\text{WT}}}{\partial t}\left(\mathbf{x},t\right)+{\tilde{\mathbf{u}}}_f\left(\mathbf{x},t\right)\cdot \frac{\partial {\widehat{\mathbf{u}}}_{\text{WT}}}{\partial \mathbf{x}}\left(\mathbf{x},t\right)=0(11)$

with ${\tilde{\mathbf{u}}}_f(\mathbf{x},t)$, the effective freestream advection velocity. This equation derives from the frozen turbulence hypothesis: it neglects the contribution of both the molecular and effective turbulent viscosities. The validity of this assumption should consequently remain limited to eddies whose characteristic timescale is larger than the convective timescale.

2.3.1.1 Freestream Particle Discretization

The freestream flow field is represented by a series of freestream particles, F_i, shed at successive timesteps t_i, and described by a position, ${\mathbf{x}}_{F_i}(t)$ and a characteristic velocity, ${\mathbf{u}}_{F_i}(t)$. The source state of a given particle is provided by the measurements of the wind turbine it emanates from:

${\mathbf{x}}_{F_i}\left(t_i\right)={\mathbf{x}}_{\text{WT}}(\mathrm{12a})$

${\mathbf{u}}_{F_i}\left(t_i\right)={\alpha }_w{\mathbf{u}}_{F_{i-1}}\left(t_i\right)+\left(1-{\alpha }_w\right){\widehat{\mathbf{u}}}_{\text{WT}}\left(t_i\right)(\mathrm{12b})$

where α_w is the Exponential Moving Average parameter computed from its filtering timescale, τ_w.

2.3.1.2 Spatio-Temporal Interpolation

The discrete information conveyed by the freestream particles is interpolated using a radial basis function based spatio-temporal interpolation scheme similar to Rott et al. (2020):

${\mathbf{u}}_f\left(\mathbf{x},t\right)=\frac{{\sum }_i{\mathbf{u}}_{F_i}{p}_{F_i}\left(\mathbf{x},t\right)}{{\sum }_i{p}_{F_i}\left(\mathbf{x},t\right)}(13)$

where the interpolation weights, $p_{F_i}$, are computed as follows:

$p_{F_i}\left(\mathbf{x},t\right)=\exp \left(-\left(\frac{r{\left(\mathbf{x},t\right)}^2}{2{\sigma }_r^2}+\frac{\xi {\left(\mathbf{x},t\right)}^2}{2{\sigma }_{\xi }^2}\right)\right)\exp \left(-\frac{{\left(t-t_i\right)}^2}{2{\sigma }_t^2}\right).(14)$

ξ(x, t) and r(x, t) are the local streamwise and radial curvilinear coordinates of the point considered in the particle frame of reference. The weight relative to a particle thus fades out as the particle gets further away from the point of evaluation for the field u_f(x, t). Furthermore, the information contained by a particle is considered less relevant as the particle progressively gets older, i.e., t ≫ t_i. This temporal decay is tuned by σ_t, the scaling constant of the temporal distance. The σ_r and σ_ξ parameters, on the other hand, govern how localized the information should be in the streamwise and radial directions: a low value means the particles have a small trust zone. Far away from the particles sources, the weights collapse and the mean average flow features are recovered.

We note that this framework allows different values of the spatio-temporal scheme weighting parameters to be selected depending on the nature of the phenomenon studied. Indeed, frozen turbulence demands the freestream velocity field to be advected as smoothly as possible whereas the coherence with the self-induced velocity of the wake requires a narrower interpolation kernel. A distinction is thus made for the interpolation of the advection velocities for the large-scale freestream field, u_f, and the local wake, ${{\mathbf{u}}^{\prime }}_f$; those are evaluated using the weighting parameters [σ_r, σ_ξ, σ_t] and [σ_r, ${\sigma }_{\xi }^{\prime },{\sigma }_t$], respectively, with ${\sigma }_{\xi }^{\prime }<{\sigma }_{\xi }$.

2.3.1.3 Freestream Field Advection

Following Eq. 11, particle positions are transported by an effective freestream convection velocity ${\tilde{\mathbf{u}}}_f$:

${\mathbf{x}}_{F_i}\left(t+\mathrm{\Delta }t\right)={\mathbf{x}}_{F_i}\left(t\right)+{\tilde{\mathbf{u}}}_f\left({\mathbf{x}}_{F_i},t\right)\mathrm{\Delta }t(15)$

while their characteristic velocity, ${\mathbf{u}}_{F_i}$, is assumed to remain unchanged. The effective freestream convection velocity is obtained by subtracting the speed deficit from the freestream velocity field itself:

${\tilde{\mathbf{u}}}_f\left({\mathbf{x}}_{F_i},t\right)={\mathbf{u}}_f\left({\mathbf{x}}_{F_i},t\right)-\frac{C_f}{\pi R_W^2}{\int }_S\mathbf{\Delta }\mathbf{u}\left(\mathbf{x},t\right)\mathrm{d}s(16)$

where C_f is a tuning constant and S denotes the circular area of radius $R_W=2\frac{D}{2}$ centered at ${\mathbf{x}}_{F_i}$ and normal to the time-averaged flow streaklines defined by Eq. 15.

2.3.2 Wake Model Module

Once the estimated freestream flow has been reconstructed, the wake model integration can be performed in order to retrieve the global speed deficit field, Δu(x, t). The wake is subsequently discretized as a series of information-carrying particles advected by the reconstructed freestream velocity field.

2.3.2.1 Wake Particle Discretization

A wake particle, W_i, shed at time t_i, is described by a position, ${\mathbf{x}}_{W_i}(t)$, an orientation, ${\mathbf{n}}_{W_i}(t)$, a curvilinear coordinate along the wake centerline, ${\xi }_{W_i}(t)$ and finally a thrust coefficient, $C_{T,W_i}(t)$, and a rotor-effective turbulence intensity, $T{I}_{W_i}$(t).

The position of the particle, ${\mathbf{x}}_{W_i}=x_{W_i}{\widehat{\mathbf{e}}}_{x,\text{WT}}+z_{W_i}{\widehat{\mathbf{e}}}_{z,\text{WT}}$, is measured in the wind farm inertial frame and initially coincides with that of the wind turbine hub. Its remaining states are directly retrieved from the wind turbine state at shedding time. The subsequent source state of the wake particle is therefore similar to equation and reads:

${\xi }_{W_i}\left(t_i\right)=0(\mathrm{17a})$

${\mathbf{x}}_{W_i}\left(t_i\right)={\mathbf{x}}_{\text{WT}}(\mathrm{17b})$

${\mathbf{n}}_{W_i}\left(t_i\right)=\left[\cos \left(\gamma \left(t_i\right)\right),-\sin \left(\gamma \left(t_i\right)\right)\right](\mathrm{17c})$

$T{I}_{W_i}\left(t_i\right)={\alpha }_{w}T{I}_{W_{i-1}}\left(t_i\right)+\left(1-{\alpha }_w\right){\widehat{T}I}_{\text{WT}}\left(t_i\right)(\mathrm{17d})$

$C_{T,W_i}\left(t_i\right)={\alpha }_w{C}_{T,W_{i-1}}\left(t_i\right)+\left(1-{\alpha }_w\right){\widehat{C}}_{T,\text{WT}}\left(t_i\right)(17e)$

where the orientation of the wake particle is computed based on the turbine yaw angle at shedding time, γ(t_i).

2.3.2.2 Speed Deficit Parametrization

Each wake particle, W_i, is associated to a relative speed deficit field: $\mathrm{\Delta }{u}_{W_i}(t,r_{W_i}(\mathbf{x}))$ where $r_{W_i}(\mathbf{x})$ and t denote the radial position of x relative to the wake particle and the time considered, respectively. The orientation of the particle, ${\mathbf{n}}_{W_i}$, is introduced in order to allow the computation of the radial position of an arbitrary point, x, in the wake particle frame:

$r_{W_i}\left(\mathbf{x}\right)=‖\left(\mathbf{x}-{\mathbf{x}}_{W_i}\right)-\left(\left(\mathbf{x}-{\mathbf{x}}_{W_i}\right)\cdot {\mathbf{n}}_{W_i}\right){\mathbf{n}}_{W_i}‖.(18)$

The speed deficit field relative to the wake particle is assumed quasi-steady and then paramatrized based on the analytical expression proposed by Bastankhah and Porté-Agel (2014) unlike most DWM implementations (Larsen et al., 2007; Jonkman and Shaler, 2021) that rather rely on the tuning-intensive Ainslie viscosities wake model. Indeed, even though both models were shown to predict accurately the far-wake speed deficit (Zhan et al., 2020), the former overall demonstrates improved computational time and facilitated tuning due to its limited set of parameters.

The Bastankhah (Bastankhah and Porté-Agel, 2014) wake model is derived through the momentum conservation equation assuming a negligible pressure term. Consistent with the thin shear layer assumption, the speed deficit is then parametrized as a Gaussian whose characteristics are expressed as functions of the thrust coefficient and turbulent intensities:

$\begin{array}{ll}\hfill \mathrm{\Delta }{u}_{W_i}\left(\mathbf{x},t\right)& ={\widehat{u}}_{\text{WT}}\left(t_i\right)\left(1-\sqrt{1-\frac{C_{T,W_i}}{8{\left({\sigma }_{W_i}\left(t\right)/D\right)}^2}}\right)\hfill \\ \hfill & \times \exp \left(-\frac{1}{2{\left({\sigma }_{W_i}\left(t\right)/D\right)}^2}{\left(\frac{r_{W_i}\left(\mathbf{x}\right)}{D}\right)}^2\right).\hfill \end{array}(19)$

The width of the Gaussian, ${\sigma }_{W_i}(t)$, grows linearly with the material coordinate ${\xi }_{W_i}(t)$ through a growth rate k that is itself assumed to be a linear function of the turbulent intensity, $T{I}_{W_i}$ (Doekemeijer et al., 2019; Duc et al., 2019):

${\sigma }_{W_i}\left(t\right)=k\left(T{I}_{W_i}\right){\xi }_{W_i}\left(t\right)+{\epsilon }_{W_i}D=\left(a_k+b_{k}T{I}_{W_i}\right){\xi }_{W_i}\left(t\right)+{\epsilon }_{Wi}D(20)$

with a_k and b_k tuning constants. The initial value of the width is σ_Wi,0 = ɛ_WiD and determines the characteristic diameter of the streamtube at the outlet of the near-wake region:

${\epsilon }_{Wi}=\epsilon \frac{1}{2}\frac{1+\sqrt{1-C_{T,W_i}}}{\sqrt{1-C_{T,W_i}}}(21)$

with ɛ = 0.2 (Bastankhah and Porté-Agel, 2014). The value of these constants has been extensively studied in the literature (e.g., Niayifar and Porté-Agel, 2015). Most of these studies have however targeted the development of time-averaged models where k captures the time-averaged effects of both wake expansion and wake meandering. The value used here should therefore be lower than the traditional values of the expansion constant as wake meandering is already accounted for through our Lagrangian framework.

The speed deficit estimated by Eq. 19 is however not valid in the near wake region. Other analytical field models introducing various near-field wake correction strategies such as the ones proposed by Blondel et al. (2020) or Keane (2021) were thus investigated. They were eventually dismissed as, in the near-wake, only the effective convective velocity scale is important. The exact shape of the speed deficit is not pertinent as no wind turbine is generally located within this wake region. Following Bastankhah and Porté-Agel (2016), the characteristic speed deficit within the near wake is thus recovered using the potential core theory. This theory is consistent with the present framework because it provides coherent estimates of the wake velocity while requiring minimal tuning even though it largely overlooks the near-wake physics. The wake potential core is described as a region of uniform wake speed deficit, $\mathrm{\Delta }{u}_{W_i}^{NW}\left(t,r_{W_i}(\mathbf{x})\right)$, whose inlet is located at the wind turbine location. Due to its interactions with the ambient flow, it gradually gets smaller until ${\xi }_{W_i,0}={\xi }_{W_i}(t)$ where the Gaussian self similarity solution is recovered:

$\begin{array}{ll}\hfill \mathrm{\Delta }{u}_{W_i}^{NW}\left(\mathbf{x},t\right)& ={\widehat{u}}_{\text{WT}}\left(t_i\right)\left(1-\sqrt{1-C_{T,W_i}}\right)\hfill \\ \text{for}\frac{2r_{W_i}\left(\mathbf{x}\right)}{D}\hfill & \hfill <1-\frac{{\xi }_{W_i}\left(t\right)}{{\xi }_{W_i,0}}.\end{array}(22)$

2.3.2.3 Wake Interpolation

For isolated wakes, the global speed deficit field, Δu(x, t), is obtained by projecting the local speed deficit, $\mathrm{\Delta }{u}_{W_j}$, along the wake particle orientation, ${\mathbf{n}}_{W_j}$ (Jonkman and Shaler, 2021):

$\mathrm{\Delta }\mathbf{u}\left(\mathbf{x},t\right)=\mathrm{\Delta }{u}_{W_j}\left(t,r_{W_j}\left(\mathbf{x}\right)\right){\mathbf{n}}_{W_j}.(23)$

W_j is the particle whose plane is the closest to x. In the context of multiple superposing wakes, an altered version of the standard root-sum-square weighting superposition strategy (Gebraad and van Wingerden, 2014; Duc et al., 2019; Jonkman and Shaler, 2021) is applied:

$\begin{array}{ll}\hfill \mathrm{\Delta }\mathbf{u}\left(\mathbf{x},t\right)& =\sum _{k\in \left[x,z\right]}\left(\mathcal{R}\left(\sum _{j\in \mathcal{S}}\left(\mathrm{\Delta }{u}_{W_j}^2\left(t,r_{W_j}\left(\mathbf{x}\right)\right)\right.\right.\right.\hfill \\ \hfill & \times \left(n_{W_j,k}|n_{W_j,k}|\right)\left.\right){\widehat{\mathbf{e}}}_{k,WT}\left.\right).\hfill \end{array}(24)$

$\mathcal{R}(\varphi )=\mathrm{sign}(\varphi )\sqrt{|\varphi |}$ is the sign preserving square root operator and $\mathcal{S}$ denotes the set of the closest wake particles for each superposing wake. This procedure allows for an efficient merging of both streamwise and transverse components of the speed deficit.

2.3.2.4 Wake Advection

The interpolated wake field can then be used to update the wake particles states using a Lagrangian advection scheme as in Eq. 15:

${\mathbf{x}}_{W_i}\left(t+\mathrm{\Delta }t\right)={\mathbf{x}}_{W_i}\left(t\right)+{\tilde{\mathbf{u}}}_w\left({\mathbf{x}}_{W_i},t\right)\mathrm{\Delta }t.(25)$

The wake curvilinear coordinate, ${\xi }_{W_i}$, is updated accordingly:

${\xi }_{W_i}\left(t+\mathrm{\Delta }t\right)={\xi }_{W_i}\left(t\right)+‖{\tilde{\mathbf{u}}}_w\left({\mathbf{x}}_{W_i},t\right)‖\mathrm{\Delta }t.(26)$

Consistent with Hill’s vortex theory and experimental investigations (Machefaux et al., 2014; Larsen et al., 2020), the wake advection velocity is assumed to be directly related to the maximum speed deficit observed. Following Eq. 24, the effective wake convection velocity, ${\tilde{\mathbf{u}}}_{W_i}(t)$, is thus readily computed from the superposition of the local reconstructed freestream field and local speed deficit:

${\tilde{\mathbf{u}}}_w\left(t\right)={{\mathbf{u}}^{\prime }}_f\left({\mathbf{x}}_{W_i},t\right)-C_w\mathbf{\Delta }\mathbf{u}\left({\mathbf{x}}_{W_i},t\right)(27)$

where C_w is a tuning constant.

The remaining particle states used to compute the local speed deficit, $T{I}_{W_i}$ and $C_{T,W_i}$, are conserved as the particle moves downstream.

2.3.3 Calibration

The present operational wake model involves on a total of 9 parameters: a_k, b_k, C_f/w, τ_w, σ_r/ξ/t and finally ${\sigma }_{\xi }^{\prime }$. a_k and b_k describe the wake expansion while C_w and C_f govern the wake deficit and freestream velocity transports, respectively. τ_w is the time-filtering constant used to compute the rotor quantities and σ_r, σ_ξ, ${\sigma }_{\xi }^{\prime }$ and σ_t parametrize the spatio-temporal interpolation of the freestream velocity field. These parameters are fitted manually and tabulated in Table 2. A fine calibration was not deemed necessary, as this framework is intended toward an operational context where a runtime calibration of the parameters is performed through data assimilation (e.g., Doekemeijer et al., 2018b).

TABLE 2

TABLE 2. Lagrangian flow model parameters used for the wind farm simulations.

2.3.3.1 Freestream Advection

The identified constant for the wake convective velocity, C_w, is in line with the values reported in the literature. Larsen et al. (2020) found C_w = 0.4 by exploiting the wake/ring-vortex analogy along Hill’s vortex theory to approximate the wake self-induction. This theory is investigated in more details by Machefaux et al. (2014) who report slightly higher values (0.63 and 0.51) based on LES and experimental data. Keck et al. (2014), on the other hand, did not directly account for wake-induced velocity and adopted the wake transport velocity at 80% of free-stream velocity.

2.3.3.2 Speed Deficit Parametrization

An initial guess for the wake expansion constants is retrieved from the high-fidelity data. The value of the precursor velocity field is first subtracted from the wind farm one thereby isolating the speed deficit from the ambient flow. The wake centerline is then extracted from the wind farm LES through the algorithm introduced by Coudou (2021). This allows to translate the speed deficit, initialy in the inertial LES frame, to the meandering frame of reference. A Gaussian speed deficit is finally fitted on the profiles obtained for various time windows and ambient conditions. Even so, the wake expansion constant obtained (ɛ = 0.2, a_k = 0.022 and b_k = 0.14) still overestimated wake recovery due to the inaccuracies introduced by the wake tracking algorithm and by the flow asymmetry. As expected, the calibrated constants are lower than the ones presented in the literature (Niayifar and Porté-Agel, 2015).

2.3.3.3 Wake Advection

Following the frozen turbulence hypothesis, the freestream convective constant, C_f, is traditionally set to zero: this is equivalent to postulating a one-way coupling between the freestream velocity field and the wake. While a uniform convective velocity was indeed observed for freestream flow, the analysis of the reference LES rotor-averaged quantities indicates a reduction of the effective freestream convection speed for waked conditions (Figure 4). The cross-correlation between the histories of the rotor-scale flow quantities and the rotor measurements is evaluated at several downstream locations, ξ_f. The time offset, T_f, which achieves the maximum cross-correlation, and ξ_f are then combined to define the velocity scale, $U_f=\frac{{\xi }_f}{T_f}$. This analysis is repeated for different wind farm configurations and demonstrates a drop in U_f in the near wake while the freestream convection speed is progressively recovered as one considers positions further downstream.

FIGURE 4

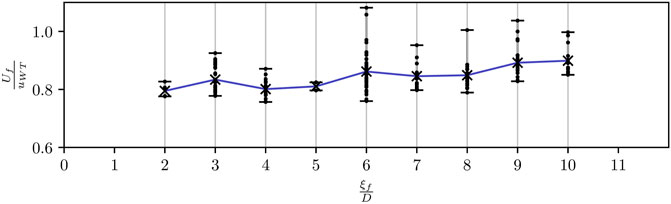
FIGURE 4. Lagrangian flow model calibration: evolution of the mean convection velocity scale (blue), U_f, of the rotor-effective transverse velocity component as a function of the normalized downstream distance; each dot indicates an individual U_f value obtained using the cross-correlation maximization approach.

3 Results

3.1 Flow Sensing

The performances of the proposed Lagrangian flow model are highly contingent on those of the embedded flow sensing module (Section 2.2); we therefore first assess the performances of this module in isolation. To that end, we compare the flow characteristics inferred by the flow sensing module with those retrieved directly from the LES, see Figure 5. Several freestream ABL configurations have been studied for an eight turbines farm visible in Figure 6; all its turbines operate in essentially non-waked conditions (wakes impacting the third row are quite dissipated). The LES velocities are sampled and then averaged over fictitious rotors located 2D upstream of the actual wind turbines and time shifted accordingly. For an estimator ${\widehat{\varphi }}_{WT}$, different performance metrics are evaluated, namely the correlation score, ${\rho }_{{\widehat{\varphi }}_{WT}}$, mean relative error, $e_{{\widehat{\varphi }}_{WT}}$, and mean relative bias, $b_{{\widehat{\varphi }}_{WT}}$. The mean error and bias of the streamwise and TI estimators are made dimensionless using the time-averaged value of ϕ_WT while metrics associated with the transverse velocity use the Root Mean Square of ϕ_WT.We hereunder discuss the performances of each estimator: rotor-normal velocity, transverse velocity and TI.

FIGURE 5

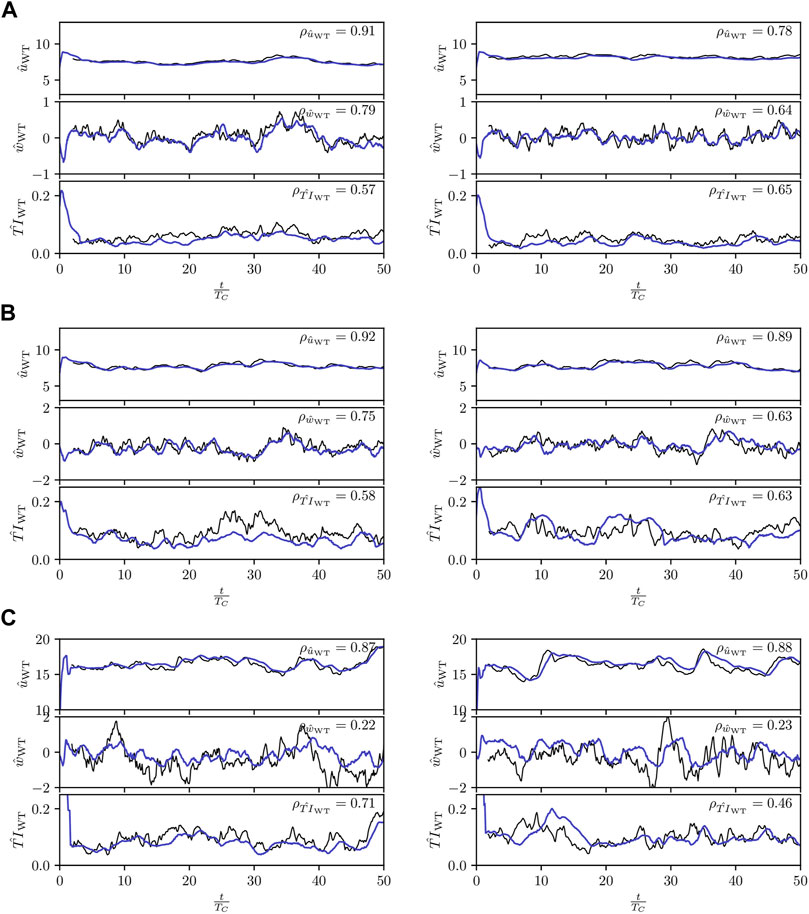
FIGURE 5. Flow sensing: comparison of the temporal evolutions of the rotor-effective inferred flow quantities (blue) against the LES data (black) for WT0 (left) and WT3 (right); (A) U_ABL = 8 ms⁻¹ and TI_ABL = 6%; (B) U_ABL = 8 ms⁻¹ and TI_ABL = 10%; (C) U_ABL = 15 ms⁻¹ and TI_ABL = 10%.

The BEM-based rotor-normal velocity estimator provides accurate estimates which translate into high correlations (${\rho }_{{\widehat{u}}_{WT}}=0.88$ on average) and low relative error ($e_{{\widehat{u}}_{WT}}=2.4$% on average) irrespective of the ABL configuration studied. Its estimations are further characterized by a negligible bias ($b_{{\widehat{u}}_{WT}}=-0.071$% on average). The Kalman filtering process however induces a slight smoothing and time offset of the output signal.

The transverse velocity estimator does not achieve such high levels of accuracy ($e_{{\widehat{w}}_{WT}}=61$% on average). This large error nonetheless does not fully characterizes the performances of this estimator. Indeed, it is able to predict the main features of the transverse velocity signal for low values of U_ABL as indicated by the good correlation score achieved for wind turbine below rated conditions (i.e., ${\rho }_{{\widehat{w}}_{WT}}=0.71$ on average for U_ABL = 8 ms⁻¹). The agreement deteriorates for turbines above rated conditions thereby leading to low correlations values: ${\rho }_{{\widehat{w}}_{WT}}=0.29$ on average for U_ABL = 15 ms⁻¹. Above rated conditions, a collective pitch is applied to the blades. This pitch varies according to the incoming wind fluctuations, which presumably makes the mapping between the blade loads and the transverse velocities more complex (e.g., through the dynamics of the collective pitch controller). A mean bias, $b_{{\widehat{w}}_{WT}}=-7.2$%, is observed across all three ABL configurations: the ANN systematically underestimates the transverse velocity component. As no notable asymmetry is observed in the training data set, the estimator bias likely arises from the neural network training itself. In addition, the selected MLP hyperparameters only allow to consider the current wind turbine state (T_ann = 1): the network has no knowledge of the past wind turbine state. However, no significant improvement of the neural network performances was observed when providing the neural network with more temporal data (T_ann > 1). This may arise from the structure of the neural network itself which considers each temporal state as an individual input. More temporal information then just leads to a more complex ANN, which hinders its training and its handling of the present time-varying phenomenon. Other network architectures accounting explicitly for time (e.g., Long Short Term Memory Recursive Neural Network) should therefore be considered as part of future investigations. One could also envision to employ different ANNs depending on the wind speed or pitch angle and then merge their predictions in order to obtain a more robust transverse velocity estimate better accounting for blade pitching. Finally, enriching the data base with more data extracted from above rated condition may also contribute to improving the overall performances of the neural network.

The last plot depicts the temporal evolution of the turbulence intensity. After the initial settling period, similar performances are obtained across all three simulations with correlations of around ${\rho }_{{\widehat{T}I}_{WT}}=0.61$. The flow sensing module captures most of the turbulence intensity signal patterns but underestimates the predictions by about $b_{{\widehat{T}I}_{WT}}=-17$% with ensuing error of $e_{{\widehat{T}I}_{WT}}=25$%. This is to be expected as ${\widehat{T}I}_{WT}$ is computed from the sector effective streamwise velocities which by definition neglects the influence of the small-scale velocity fluctuations.

3.2 Lagrangian flow Model

Let us now assess the Lagrangian flow model through a comparison against data retrieved from the reference LES. The case of isolated wind turbines (Section 3.2.1) is first considered and the performances of the model in the context of a small wind farm are then investigated (Section 3.2.2).

3.2.1 Isolated Wind Turbines

We use the same wind farm layout as in Section 3.1. The loads and operating settings recovered from the high-fidelity simulation are first processed by the flow sensing module and then fed to the Lagrangian flow model. The model runs much faster than real time: a 2,500 s wind farm simulation runs in around 12 s on a single laptop core (5 × 10⁻⁴ wall-clock second per simulation second). The freestream and wake particles update and shedding frequencies are, respectively, $\frac{4}{T_C}$ and $\frac{1}{T_C}$ with T_C, the convective time scale defined as T_C = D/U_ABL. The particle discretization strategy is illustrated in Figure 7 for wind turbine 1 (WT1). 50 wake particles and 25 freestream ones suffice to capture the development of one wind turbine wake across the full domain (28D downstream of WT0). For the wind farm layout studied, fewer freestream particles are required to capture the freestream field. Indeed, as freestream particles shed by WT0 reach WT5 their interpolation weight have collapsed due to their age and the info they convey is thus largely disregarded. It is therefore not pertinent for the freestream particles to span more than 20D in the current configuration. The same would not be true if the wind was not aligned with the wind turbines.

FIGURE 6

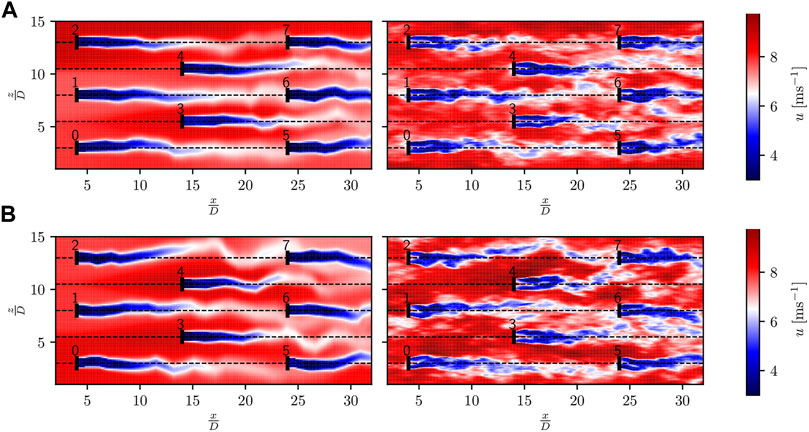
FIGURE 6. Isolated wind turbines: instantaneous streamwise velocity field (t = 1,000 s) predicted by the flow model (left) and retrieved from the LES (right); (A) U_ABL = 8 ms⁻¹ and TI_ABL = 6%; (B) U_ABL = 8 ms⁻¹ and TI_ABL = 10%.

Figure 6 compares the full flow fields of the model and the LES in terms of the hub-height velocity field. Both low-TI (TI_ABL = 6%) and high-TI (TI_ABL = 10%) configurations are studied at U_ABL = 8 ms⁻¹. This comparison confirms the good potential of the approach: the Lagrangian flow model captures an array of phenomena that classical steady-state models simply cannot capture.

FIGURE 7

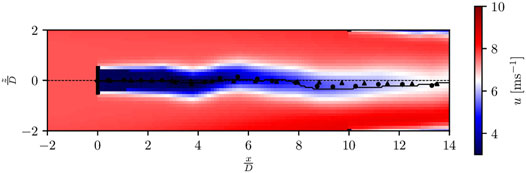
FIGURE 7. Isolated wind turbines: instantaneous streamwise velocity field (t = 1,000 s) predicted by the flow model for U_ABL = 8 ms⁻¹ and TI_ABL = 6%; wake particle (•) and freestream particle (▴); wake position extracted from the LES (full black line).

A first qualitative comparison indicates a good agreement between the meandering patterns, particularly for the low-TI case. While the high-TI near-wake is reconstructed in a satisfactory manner, the far-wake estimate deviates from the expected value significantly. Indeed, the information collected at the rotor becomes less pertinent as one travels downstream. Accordingly, the deterioration of particle information is expected to increase with the turbulent intensity of the inflow.

If one now considers the freestream information, the corresponding particle discretization appears to capture the flow heterogeneity at farm scales: the reconstructed freestream velocity is not uniform across the domain and reflects the large-scale velocity fluctuations present in the LES. The reconstructed flow field can however only provide a smoothed out representation of the instantaneous LES one. The influence of small-scale eddies (typically $<2D$) is ignored since only rotor-effective information is fed to the model. Moreover, since information is gathered and processed where it is relevant (around the wake centerline), some blindspots may appear between the wind turbines rows. The use of Lidar data could therefore potentially be investigated in order to better account for the small-scale structures (Rott et al., 2020). Accounting for these small-scale structures may however fall outside the hypothesis of frozen turbulence hypothesis as suggested by Bossanyi (2013).

The wake model also suffers from the same limitation: for both TI cases, the model depicts the wakes as smooth representations of their LES counterparts. It is not able to capture asymmetry nor the loss in coherence of the wake particularly for high-TI configurations. Nevertheless, one notes the good overall agreement between the speed deficit widths and intensities. This is better demonstrated by the instantaneous streamwise velocity profiles of Figure 8A. Despite its simple form, the near wake correction introduced by Bastankhah and Porté-Agel (2016) leads to coherent estimates for the near wake profiles. These profiles definitely underline the need to account for wake meandering in dynamic models of wind turbine wakes: meandering clearly manifests itself in the instantaneous flow fields, even away from the rotors.

FIGURE 8

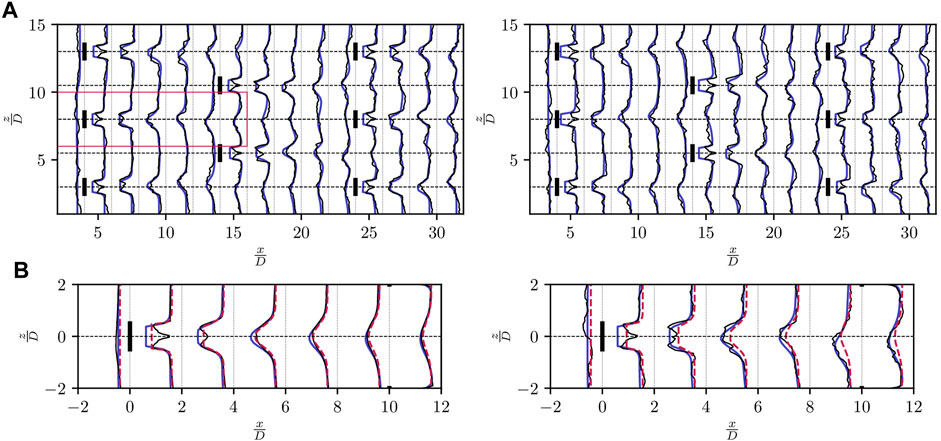
FIGURE 8. Isolated wind turbines: instantaneous streamwise velocity profiles (A) Instantaneous streamwise velocity profiles at different streamwise locations (t = 1,000 s) predicted by the model (blue) and retrieved from the LES (black) for U_ABL = 8 ms⁻¹ and TI_ABL = 6% (left); U_ABL = 8 ms⁻¹ and TI_ABL = 10% (right); (B) Time averaged (left) and instantaneous (right - t = 1,000 s) streamwise velocity profiles for WT1; flow model (blue); LES (black); optimally fitted steady-state Gaussian Bastankhah wake model - ɛ = 0.2 and k = 0.028 (dashed red) for U_ABL = 8 ms⁻¹ and TI_ABL = 6%.

Figure 8B presents time-averaged and instantaneous streamwise velocity fields at hub height, which confirm the observations hereabove. A Gaussian steady-state wake model is fitted over the time-averaged LES data: it corresponds to a model that would be optimally tuned by exploiting state feedback in a fashion similar to Doekemeijer et al. (2019). The tuned parameters obtained, ɛ = 0.2 and k = 0.028, are in line with the values reported by Niayifar and Porté-Agel (2015). Excellent agreement is obtained between all three approaches regarding the steady-state profiles especially in the far wake $(\frac{x}{D}>4)$ where the self-similarity of the Gaussian profile is recovered. This is however not true for the instantaneous flow field: the calibrated Gaussian model over-estimates the width of the wake whereas the Lagrangian flow model better predicts the speed deficit downstream of the turbine.

3.2.1.1 Wake Centerline Statistics

A quantitative analysis of wake centerline characteristics is now performed for WT0 and WT3. Figure 9 shows the histories of their transverse location, z_C, evaluated at several downstream positions (6D, 9D and 12D). As differences in tracked wake centerline positions will likely occur depending on the size of the mask considered for the LES post-processing, different mask sizes are evaluated and used to define the so-called wake centerline envelope. Highly asymmetric or incoherent wakes are logically harder to track and hence tend to lead to larger differences in wake centerline position depending on the size of the mask selected. A wider wake envelope is therefore indicative of an asymmetric or incoherent wake. In both the high- and the low-TI case, less agreement is obtained between the different wake tracking masks for WT3 than for WT0 resulting in broader wake envelopes on average. The reference mask is then chosen quite wide, i.e., σ_x = σ_y = σ_z = D/2, in order to prevent the spurious numerical behaviors of the wake centerline detection.

FIGURE 9

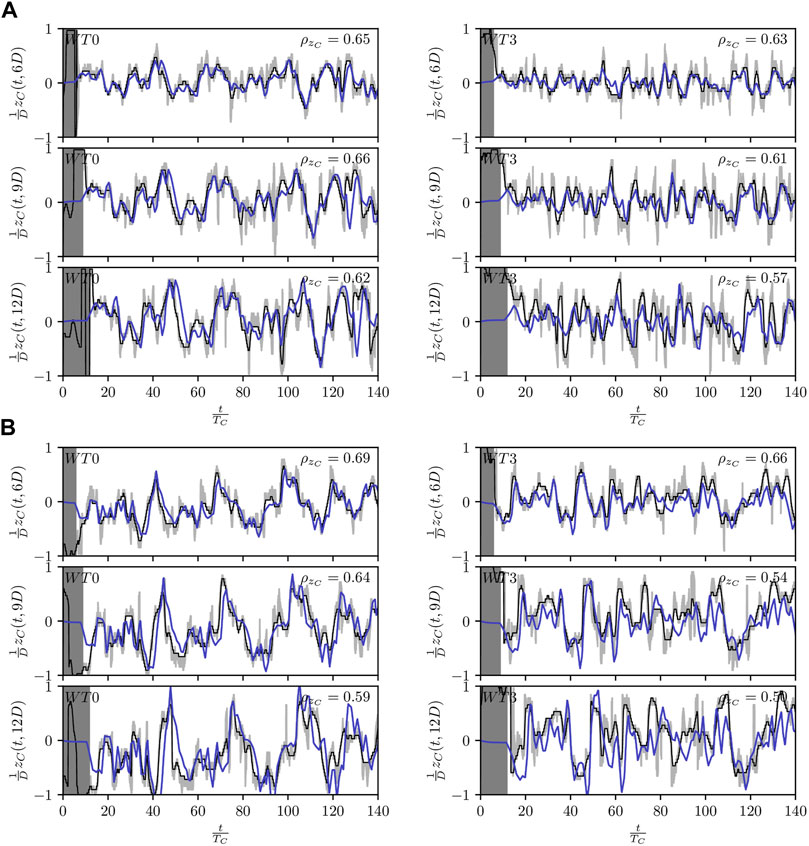
FIGURE 9. Isolated wind turbines: temporal evolutions of the wake centerline position estimated by the model (blue) against the one retrieved from the LES (black) at locations 6D, 9D and 12D downstream of WT0 (left) and WT3 (right); settling period (dark grey); LES wake centerline envelope (light grey).(A) U_ABL = 8 ms⁻¹ and TI_ABL = 6%; (B) U_ABL = 8 ms⁻¹ and TI_ABL = 10%.

The wake centerline computed by the model is in good overall agreement with the wake centroid extracted from the LES. The model appears to correctly advect the large wake features and to reproduce consistent wake deflection amplitudes. The accuracy of the wake centerline prediction is however limited by that of the underlying flow estimator. The transverse velocity estimations for WT0 clearly outperform those obtained for WT3 (Figure 5) which directly translates into a better tracking of the wake center downstream of WT0. This increased mismatch also reflects the higher complexity of the wake downstream of WT3 as indicated by the broader wake envelope. Moreover, the performances of the Lagrangian flow model degrade as the wavelength of the meandering mode considered decreases. As noted previously, this may be partially explained by the reduced turnover time of small-scale eddies. Small eddies quickly evolve as they travel downstream thereby making the information conveyed by the particles less relevant as they age. As a result, the signal cross-correlations, ${\rho }_{z_C}$, tend to decrease with the downstream distance.

The wake centerlines are further compared in terms of their statistics on the basis of the work of Foti et al. (2018). Each wake centerline is first low-pass filtered spatially with a cut-off length of 1D. The maxima and minima of the subsequent signals are then tracked and the statistics are evaluated. The amplitude, A, is defined as half the transverse distance between two consecutive maxima-minima while the wavelength, λ, is computed as the streamwise distance between two successive maxima or minima. Finally the Strouhal number is introduced as:

$St=\frac{{\tilde{u}}_W}{U_{ABL}}\cdot \frac{D}{\lambda }(28)$

where ${\tilde{u}}_W$ is the wake convection speed. These quantities are then binned, with respect to the downwind distance from the rotor. The resulting wake statistics are finally averaged over the turbines WT0 to WT4 and the results are plotted in Figure 10. The greyed areas (i.e., $\frac{x}{D}<3$ and $11<\frac{x}{D}$) denote areas that are not exploitable owing to the method used for the computation of the wake statistics. It is nonetheless plotted for the sake of transparency.

FIGURE 10

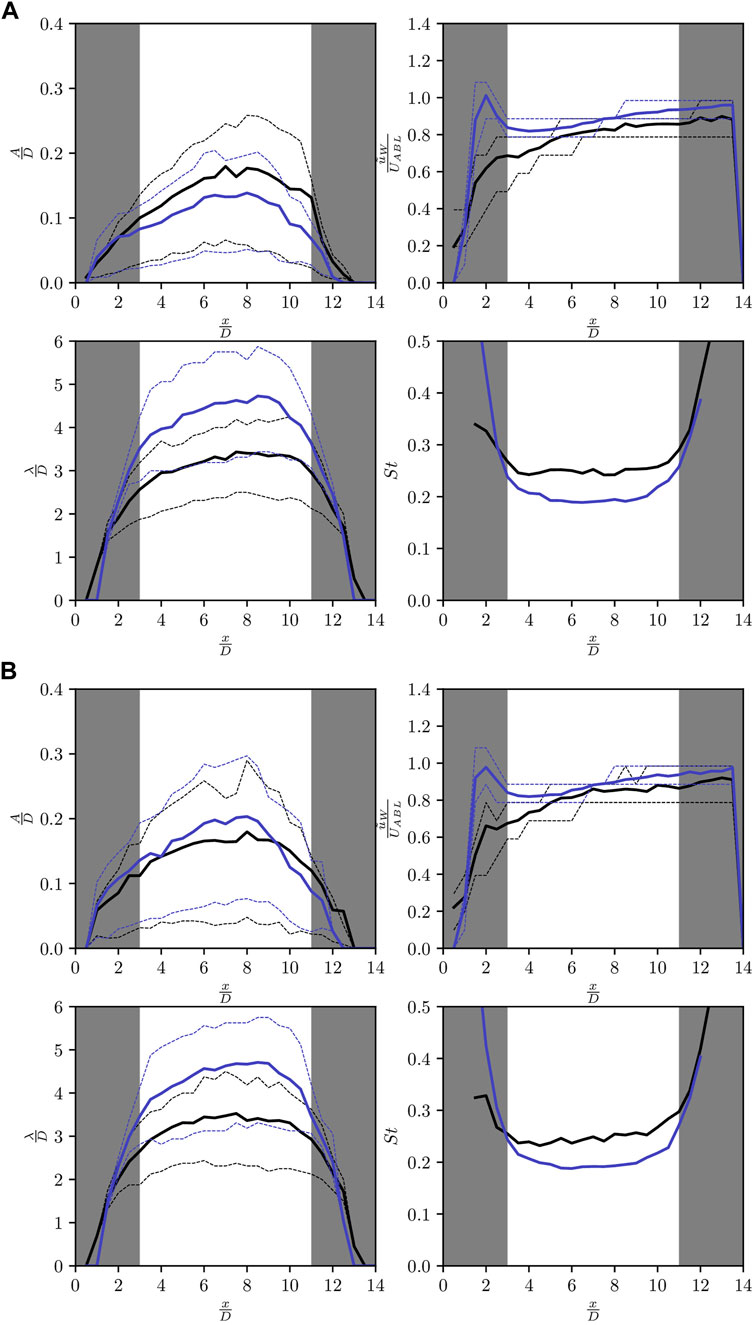
FIGURE 10. Isolated wind turbines: mean binned statistics computed from the reconstructed flow field (full blue) against the one retrieved from the LES (full black); wake centerline amplitudes (A); wavelengths (λ); convective speeds $({\tilde{\mathrm{u}}}_W)$; Strouhal numbers (St); 25 and 75% confidence bounds of the binned quantities (dashed); (A) U_ABL = 8 ms⁻¹ and TI_ABL = 6%; (B) U_ABL = 8 ms⁻¹ and TI_ABL = 10%.

The method is first applied to the wake centerline time series extracted from the LES using a Gaussian mask with ${\sigma }_x={\sigma }_y=\frac{D}{2}$ and σ_z = D. The LES results demonstrate good agreement with previous experimental investigations by Coudou (2021). However, while they report strong influence of the ABL characteristics on the wake meandering statistics, we do no distinguish such a trend in the current context: the wake statistics exhibit a similar behavior for the low- and high-TI configurations.

When comparing the Lagrangian flow model statistics to that of the LES, reasonable match is obtained regarding the predicted binned amplitudes. Both approaches result in a drop in amplitude beyond 8D and the binned amplitude probability distributions look similar.

The wake convection speed is slightly overestimated by the Lagrangian flow model even though both curves present similar trends. The wake recovery leads to higher ${\tilde{u}}_w$ in the far wake. We however note that wake convection speed behavior in the near wake $(\frac{x}{D}<4)$ is not consistent with that of LES. A more consistent behavior is obtained when the near wake correction is disabled. This however leads to a significant time offset between the LES and the flow model time responses.

We finally investigate the mean wavelength: this metric is roughly constant across all downstream distances but appears inflated by the model while the LES produces values in line with the ones obtained by Coudou et al. (2018) (i.e., $2.5<\frac{\lambda }{D}<3.25$ for isolated wind turbines). This in turn results into an underestimation of the Strouhal number. Wake lengths under 3D are mostly overlooked by the model. Improving the resolution (i.e., the particle shedding frequency) can substantially improve this match but does not translate into a better correspondence of the time series. If a wider Gaussian mask σ_x = σ_y = σ_z = D/2 is employed for the LES wake centerline extraction, better agreement is recovered regarding the binned wavelengths while similar agreement is conserved for the other statistics.

3.2.1.2 Rotor Effective Wind Speed

The rotor-effective streamwise velocity, u_RE, describes how the rotor-averaged velocity of a fictive wind turbine placed at some location downstream would evolve with time. The 2D flow field inferred by the Lagrangian Flow model is extrapolated outside the reference x − z plane assuming wake axi-symmetry and neglecting the flow shear while the reference u_RE value is simply extracted from the LES using a circular mask. Both curves are plotted on Figure 11.

FIGURE 11

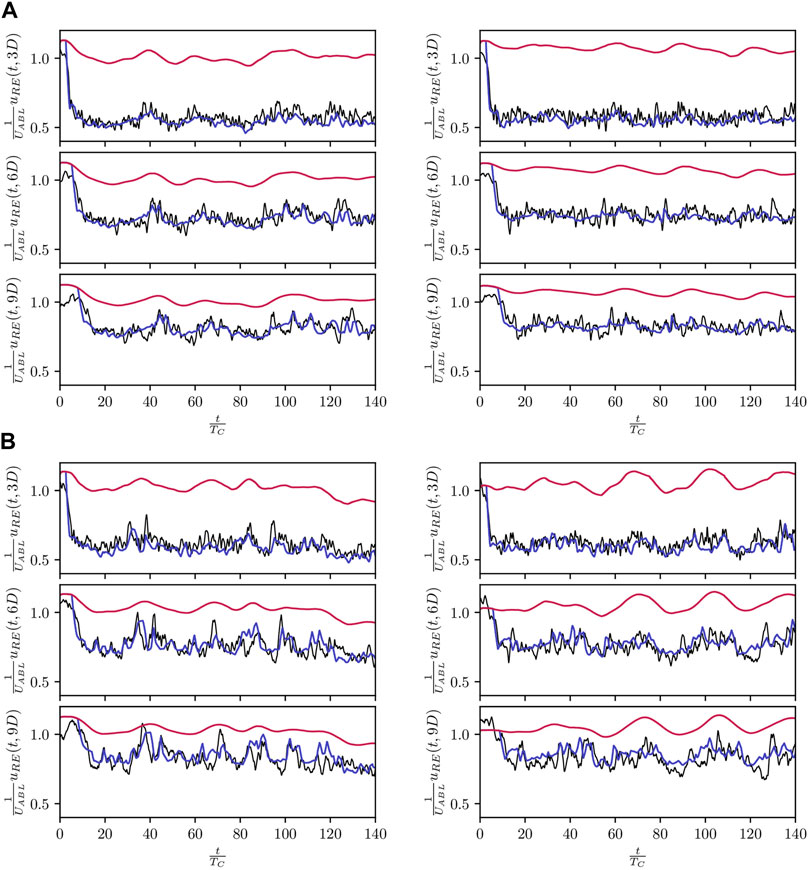
FIGURE 11. Isolated wind turbines: temporal evolution of the fictive streamwise rotor effective velocities at different downstream station (3D, 6D and 9D) downstream WT0 (left) and WT3 (right); flow model (blue) and LES (black); estimated freestream rotor effective velocities (red) (A) U_ABL = 8 ms⁻¹ and TI_ABL = 6%; (B) U_ABL = 8 ms⁻¹ and TI_ABL = 10%.

The rotor effective velocity can be considered as the superposition of the freestream velocity and of the speed deficit. The former dictates the slow velocity fluctuations caused by the heterogeneous inflow and the latter, strongly influenced by the meandering phenomenon, leads to the marked drops in velocity observed within the wake. Specifically, wake meandering deviates the wake into or away from the fictious downstream rotors, thus successively decreasing and increasing the rotor effective wind speed. This phenomena is remarkably well captured downstream of WT0 for the low-TI configuration (and to some more limited extent for the high-TI one). In the low-TI case, the extreme wake centerline deflection occurring 9D behind WT0 at times 45T_C, 65T_C and 105T_C coincides with a sharp increases in u_RE. Similar peaks can be found in the high-TI case for times 40T_C, 45T_C and 105T_C. Still, most small-scale velocity fluctuations are overlooked by the rotor as they corresponds the eddies whose characteristic dimensions fall beyond the model resolution. The model performances regarding this metric are however not consistent across all wind turbines: turbines whose meandering is poorly captured are obviously less likely to produce accurate predictions u_RE. Nevertheless, in all cases, the initial drop in streamwise velocity as well as the slow dynamics of the deficit recovery are well captured by the Lagrangian flow model.

3.2.2 Small Wind Farm

Let us now assess the model in a configuration quite close to an operational use with wake impingement. We consider a small wind farm operating inside a weakly turbulent ABL (U_ABL = 8 ms⁻¹ and TI_ABL = 6%); 12 turbines, initially at rest, are distributed across three rows with a uniform streamwise spacing of 7D. The resulting wind farm layout is illustrated in Figure 12A at t = 1,000 s.

FIGURE 12

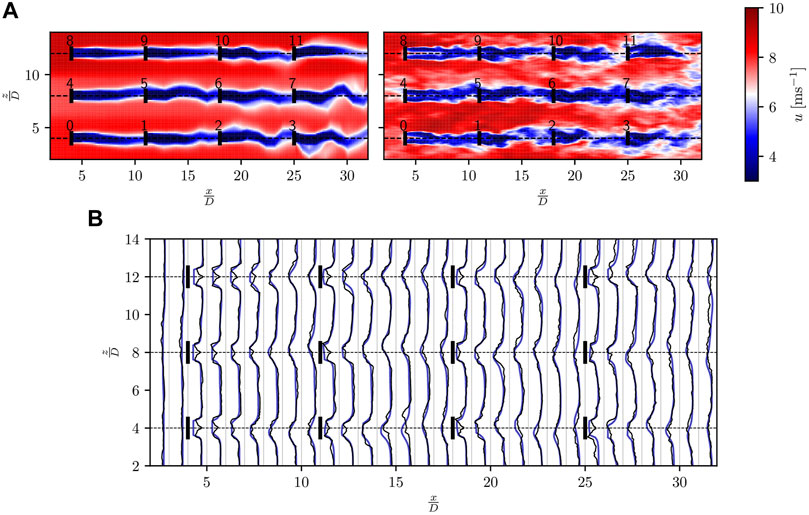
FIGURE 12. Small wind farm: instantaneous (t = 1,000 s) streamwise velocity field across the 12 wind turbines farm for U_ABL = 8 ms⁻¹ and TI_ABL = 6%; (A) full flow field predicted by the flow model (left) and retrieved from the LES (right); (B) velocity profiles at different streamwise locations predicted by the model (blue) and retrieved from the LES (black).

For the sake of conciseness, the validation of the flow sensing module is not presented in the context of waked wind turbines. The MLP training database nevertheless includes both waked and freestream wind turbines while the BEM-Kalman based estimator does not differentiate between waked and unwaked settings. The framework developed can therefore be extended to waked rotor as demonstrated in this section.

Each wake is discretized using 25 wake particles and 15 freestream ones while the update and shedding frequencies are kept unchanged ($\frac{4}{T_C}$ and $\frac{1}{T_C}$, respectively). The reconstruction of the 1,250 s-long flow field requires a wall-clock time of 8 s on the same hardware as for Section 3.2.1.

A satisfactory match is obtained between the LES data and the reconstructed flow field. The instantaneous streamwise velocity profiles appear similar in both cases as illustrated in Figure 12B. The estimated wake intensities, widths and deflections are globally well captured by the model even though the increasing levels of wake asymmetry and incoherence observed for turbine deeper in the array are not reflected by the wake model. The smoothing introduced by the model is particularly apparent for WT3, WT7 and WT11 whose wakes are pictured as much more coherent than what they really are.

The Lagrangian flow model allows to capture most of the large-scale freestream flow heterogeneities. The wind turbines of the center row experience a slower freestream than that of the upper and lower row. Some blindspots nonetheless exist between the wind turbines rows where no information is available. As a result, the large high-velocity gust propagating between the first and second row remains completely unnoticed by the model.

Figure 13 provides a comparison of the history of the transverse wake deflection. In accordance with the non-waked studies of Section 3.2.1, high correlations are reported for the freestream wind turbines (${\rho }_{z_C}=0.85$ and 0.76). After the wakes have propagated throughout the farm (t ≫ 32T_C), broader wake envelopes indicative of a more pronounced asymmetry are observed for wind turbines deep into the wind farm. The wake centerline dynamics predicted by the wake model nonetheless remain in relatively good agreement with the LES data with a minimum score of ${\rho }_{z_C}=0.55$ for WT7. Remarkably, they even exhibit an amplification of the meandering process within turbines rows reported by Coudou (2021) and Muller et al. (2015). For an identical downstream position, the amplitude of wake meandering increases for wind turbine deeper into the row (e.g., WT0 and WT1). The meandering amplitudes however seem to be overestimated for wind turbines deep into the array (WT2 - WT3 - WT6 - WT7). Finally, no significant loss in accuracy with respect to the LES-fed flow model is obtained when using the flow sensing approach. This confirms the good performances of the flow sensing module in the context of Lagrangian flow modeling.

FIGURE 13

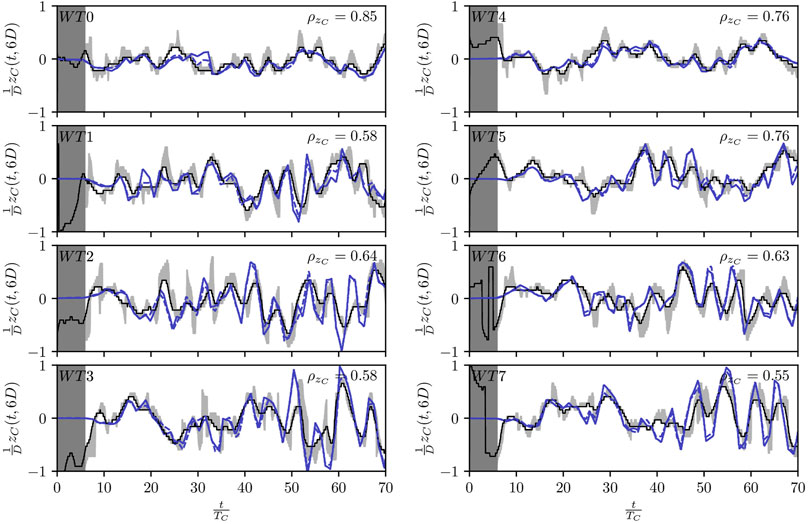
FIGURE 13. Small wind farm: history of the wake centerline position 6D downstream WT0-WT7 estimated by the model (blue) against the one retrieved from the LES (black); bottom row WT0-WT3 (left); middle row WT4-WT7 (right); model fed with the flow sensing data (full blue); model fed with LES data (dashed blue); settling period (dark grey); LES wake centerline envelope (light grey).

4 Discussion

The presented work introduces a particle-based wind farm flow modeling framework aimed at wind farm control. It reconstructs the farm flow field in terms of a freestream velocity field and of a wake velocity deficit field based on information recovered at the wind turbines through a flow sensing module. The wakes are modeled using simplified speed deficits and this information is propagated across the wind farm in a physics-informed fashion thereby capturing the dynamic wake signature at a low computational cost: 5 × 10⁻⁴ to 7 × 10⁻⁴ wall-clock seconds are required per simulation second on a single core laptop depending on the configuration studied.

The resulting surrogate wake model can, to some extent, be regarded as a flow sensing-based hybrid approach between the FAST-farm implementation (Jonkman and Shaler, 2021) of the DWM and the standard, steady-state speed deficit formulation introduced by Bastankhah and Porté-Agel (2016). Its wake-particle formulation is analogous to the FLORIDyn observations-points approach proposed by Becker et al. (2022) which also allows to account for heterogeneous inflow in its latest version.

This particle-based discretization is particularly in-line with the particle filter approach as investigated by Le Provost and Eldredge (2021) or Notter et al. (2020). Moreover, another notable aspect for the further development of this framework is its limited number of input parameters and the reduction of the state space size in order to facilitate the tuning procedure. This should allow to extend the presented formalism to joint state-space correction scheme in a ensemble manner akin to Doekemeijer et al. (2018b) or Howland et al. (2020). Similar configurations have already been successfully investigated by Dong et al. (2021) or Lio et al. (2020) in an attempt to improve the DWM operational performances by assimilating loads or Lidar measurements.

Simulation results demonstrate that the proposed Lagrangian flow model achieves good estimates of the flow state in both low- and high-TI configurations when compared to LES results. The analysis is first oriented toward the modelization of isolated turbines and the ensuing findings are then corroborated by the study of a small 12 turbines wind farm with strong wake interactions. The main dynamic features of the flow are captured: both the deflection and shape of the speed deficit and the heterogeneous flow field features are consistent with the LES. The model distinctly provides additional insight into the wake physics when compared against the traditional steady state approaches. Great agreement is observed regarding wake meandering: the Lagrangian flow model is indeed able to capture the distinctive wake meandering signature across large downstream distances while being fed with limited and localized flow information. The lowest correlation score between the predicted wake centerline and its LES counterpart is observed 12D downstream the wind turbine with a value of 0.50 while correlation scores as high as 0.85 are obtained closer to the rotor (i.e., 6D), where the information gathered by the wind turbine is more pertinent. The model however introduces a strong smoothing of LES field since its resolution is limited by the rotor-averaged nature of the information collected. This is reflected by an overprediction of the averaged meandering wavelength: in line with past investigations (e.g., Coudou, 2021) the LES provides a mean wavelength of around $2.75<\frac{\lambda }{D}<3.25$ while, for the flow model, a value around $3.5<\frac{\lambda }{D}<4.5$ is recovered. Feeding the model with Lidar data could therefore allow the model to boost its spatial resolution thereby improving its overall performances. Moreover, it is not clear whether or not the ANN transverse velocity estimator will generalize well to other wind turbines geometries or ABL characteristics. This is problematic as we observe a strong influence of the accuracy of the transverse velocity estimator on the performances of the flow model as a whole. As mentioned previously, one way the robustness of the transverse velocity estimator could be improved is by taking advantage of more advanced ANN architecture that explicitly account for time (e.g., Long Short Term Memory Recursive Neural Network). They should result in a better ability of the neural network to deal with the transverse velocity history thereby improving its accuracy. The use of Lidar data is yet another tool that could also potentially alleviate the need for such a error-prone flow estimator thereby making this framework more robust. Notable efforts toward reconstructing the ambient flow from Lidar have been performed by various authors including Bauweraerts and Meyers (2021) and could provide valuable additional insight into the ambient flow physics. One could also envision to merge both the transverse velocity measurements and the ANN inside a unified framework relying on a Kalman filter in a similar fashion as for the BEM-based rotor-normal velocity estimator.

Clearly, this model is part of a more general recent trend toward the development of operational dynamic surrogate wake models aimed at model-based wind farm control (Doekemeijer et al., 2018b; Becker et al., 2022) and that rely on valuable corrective information provided by state feedback to enhance their robustness (Doekemeijer et al., 2018a; Howland et al., 2020). We believe that such an operational meandering-capturing model could prove invaluable for the mitigation of fatigue loads in wind farms. This is supported by recent studies (e.g., Reinwardt et al., 2020; Moens and Chatelain, 2022) that clearly demonstrate that the meandering behavior definitely governs fatigue loads; this clearly pleads for the capture of the phenomenon by an operational model if one targets fatigue alleviating model-predictive control of wind farms. Further work toward evaluating the dynamic response of the flow model to a control step input change is also under progress (Lejeune et al., 2022) and shall further demonstrate the applicability of the presented framework to operational wind farm control.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

The theoretical bases were laid down by PC and ML. ML assembled the LES data base used in this work. He also implemented and validated the flow sensing module and the Lagrangian flow model. MM developed the LES wind turbine model and provided technical support for it. She further implemented the wake tracking algorithm with the in-house flow solver. PC and ML analyzed the results and authored the manuscript.

Funding

This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement no. 725627). Simulations were performed using computational resources provided by the Consortium des Équipements de Calcul intensif (CÉCI), funded by the Fonds de la Recherche Scientifique de Belgique (F.R.S.-FNRS) under Grant No. 2.5020.11, and computational resources made available on the Tier-1 supercomputer of the Fédération Wallonie-Bruxelles, infrastructure funded by the Walloon Region under the Grant Agreement No. 1117545.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We acknowledge the contributions of Marion Coquelet (UCLouvain/UMons) toward the development of the rotor-normal sensing tool.

References

Ba, J. L., Kiros, J. R., and Hinton, G. E. (2016). Layer Normalization. arXiv [Preprint]. Available at: https://arxiv.org/abs/1607.06450 (Accessed December 15, 2021).

Google Scholar

Bastankhah, M., and Porté-Agel, F. (2014). A New Analytical Model for Wind-Turbine Wakes. Renew. Energy 70, 116–123. doi:10.1016/j.renene.2014.01.002

CrossRef Full Text | Google Scholar

Bastankhah, M., and Porté-Agel, F. (2016). Experimental and Theoretical Study of Wind Turbine Wakes in Yawed Conditions. J. Fluid Mech. 806, 506–541. doi:10.1017/jfm.2016.595

CrossRef Full Text | Google Scholar

Bauweraerts, P., and Meyers, J. (2021). Reconstruction of Turbulent Flow Fields from Lidar Measurements Using Large-Eddy Simulation. J. Fluid Mech. 906, A17. doi:10.1017/jfm.2020.805

CrossRef Full Text | Google Scholar

Becker, M., Ritter, B., Doekemeijer, B., van der Hoek, D., Konigorski, U., Allaerts, D., et al. (2022). The Revised Floridyn Model: Implementation of Heterogeneous Flow and the Gaussian Wake. Wind Energy Sci. Discuss. 2022, 1–25. doi:10.5194/wes-2021-154

CrossRef Full Text | Google Scholar

Bertelè, M., Bottasso, C. L., Cacciola, S., Daher Adegas, F., and Delport, S. (2017). Wind Inflow Observation from Load Harmonics. Wind Energy Sci. 2, 615–640. doi:10.5194/wes-2-615-2017

CrossRef Full Text | Google Scholar

Bertelè, M., and Bottasso, C. (2020). Non-deterministic Wind Observation from Wind Turbine Loads. J. Phys. Conf. Ser. 1618, 062022. doi:10.1088/1742-6596/1618/6/062022

CrossRef Full Text | Google Scholar

Blondel, F., and Cathelain, M. (2020). An Adaptation of the Super Gaussian Wake Model for Yawed Turbine. Wind Energy Sci. Discuss. 5, 1–16. doi:10.5194/wes-2019-99

CrossRef Full Text | Google Scholar

Bossanyi, E. (2013). Un-freezing the Turbulence: Application to Lidar-Assisted Wind Turbine Control. Renew. Power Gener. IET 7, 321–329. doi:10.1049/iet-rpg.2012.0260

CrossRef Full Text | Google Scholar

Bottasso, C. L., Cacciola, S., and Schreiber, J. (2018). Local Wind Speed Estimation, with Application to Wake Impingement Detection. Renew. Energy 116, 155–168. doi:10.1016/j.renene.2017.09.044

CrossRef Full Text | Google Scholar

Braunbehrens, R., and Segalini, A. (2019). A Statistical Model for Wake Meandering behind Wind Turbines. J. Wind Eng. Indust. Aerodyn. 193, 103954. doi:10.1016/j.jweia.2019.103954

CrossRef Full Text | Google Scholar

Brunton, S. L., Noack, B. R., and Koumoutsakos, P. (2020). Machine Learning for Fluid Mechanics. Annu. Rev. Fluid Mech. 52, 477–508. doi:10.1146/annurev-fluid-010719-060214

CrossRef Full Text | Google Scholar

Coleman, R. P., and Feingold, A. M. (1958). Theory of Self-Excited Mechanical Oscillations of Helicopter Rotors with Hinged Blades. Tech. rep.,. Langley, Virginia: NACA.

Google Scholar

Coudou, N., Moens, M., Marichal, Y., Beeck, J. V., Bricteux, L., and Chatelain, P. (2018). Development of Wake Meandering Detection Algorithms and Their Application to Large Eddy Simulations of an Isolated Wind Turbine and a Wind Farm. J. Phys. Conf. Ser. 1037, 072024. doi:10.1088/1742-6596/1037/7/072024

CrossRef Full Text | Google Scholar

Coudou, N. (2021). Numerical and Experimental Investigations of the Meandering Phenomenon in Wind Turbine Wakes. Belgium: UMons/UCLouvain/VKI, Sint-Genesius-Rode. Ph.D. thesis.

Google Scholar

Doekemeijer, B. M., Boersma, S., Pao, L., and van Wingerden, J. (2018a). Joint State-Parameter Estimation for a Control-Oriented LES Wind Farm Model. J. Phys. Conf. Ser. 1037, 032013. doi:10.1088/1742-6596/1037/3/032013

CrossRef Full Text | Google Scholar

Doekemeijer, B. M., Boersma, S., Pao, L. Y., Knudsen, T., and van Wingerden, J.-W. (2018b). Online model calibration for a simplified les model in pursuit of real-time closed-loop wind farm control. Wind Energy Sci. 3, 749–765. doi:10.5194/wes-3-749-2018

CrossRef Full Text | Google Scholar

Doekemeijer, B. M., Van Wingerden, J., and Fleming, P. A. (2019). “A Tutorial on the Synthesis and Validation of a Closed-Loop Wind Farm Controller Using a Steady-State Surrogate Model,” in 2019 American Control Conference (ACC) (2019 American Control Conference (ACC)), 2825–2836. doi:10.23919/ACC.2019.8815126

CrossRef Full Text | Google Scholar

Dong, L., Lio, W. H., and Meng, F. (2021). Wake Position Tracking Using Dynamic Wake Meandering Model and Rotor Loads. J. Renew. Sustain. Energy 13, 023301. doi:10.1063/5.0032917

CrossRef Full Text | Google Scholar

Duc, T., Coupiac, O., Girard, N., Giebel, G., and Göçmen, T. (2019). Local Turbulence Parameterization Improves the Jensen Wake Model and its Implementation for Power Optimization of an Operating Wind Farm. Wind Energy Sci. 4, 287–302. doi:10.5194/wes-4-287-2019

CrossRef Full Text | Google Scholar

Foti, D., Yang, X., and Sotiropoulos, F. (2018). Similarity of Wake Meandering for Different Wind Turbine Designs for Different Scales. J. Fluid Mech. 842, 5–25. doi:10.1017/jfm.2018.9

CrossRef Full Text | Google Scholar

Gebraad, P. M. O., and van Wingerden, J. W. (2014). A Control-Oriented Dynamic Model for Wakes in Wind Plants. J. Phys. Conf. Ser. 524, 012186. doi:10.1088/1742-6596/524/1/012186

CrossRef Full Text | Google Scholar

Howland, M. F., Ghate, A. S., Lele, S. K., and Dabiri, J. O. (2020). Optimal Closed-Loop Wake Steering, Part 1: Conventionally Neutral Atmospheric Boundary Layer Conditions. Wind Energy Sci. Discuss. 2020, 1–38. doi:10.5194/wes-2020-52

CrossRef Full Text | Google Scholar

Jensen, N. (1983). A Note on Wind Generator Interaction. Tech. rep. Roskilde, Denmark: Risø National Laboratory.

Google Scholar

Jonkman, J., Butterfield, S., Musial, W., and Scott, G. (2009). Definition of a 5mw Reference Wind Turbine for Offshore System Development. Golden, CO: National Renewable Energy Laboratory NREL. doi:10.2172/947422

CrossRef Full Text | Google Scholar

Jonkman, J., and Shaler, K. (2021). FAST.Farm User’s Guide and Theory Manual. Tech. rep. Golden, CO: National Renewable Energy Laboratory.

Google Scholar

Keane, A. (2021). Advancement of an Analytical Double-Gaussian Full Wind Turbine Wake Model. Renew. Energy 171, 687–708. doi:10.1016/j.renene.2021.02.078

CrossRef Full Text | Google Scholar

Keck, R., de Maré, M., Churchfield, J. M., Lee, S., Larsen, G., and Madsen, H. (2014). On Atmospheric Stability in the Dynamic Wake Meandering Model. Wind Energy 17, 1689–1710. doi:10.1002/we.1662

CrossRef Full Text | Google Scholar

Larsen, G., Madsen Aagaard, H., Bingöl, F., Mann, J., Ott, S., Sørensen, J., et al. (2007). Dynamic Wake Meandering Modeling. Roskilde, Denmark: Risø National Laboratory.

Google Scholar

Larsen, G., Ott, S., Liew, J., van der Laan, M., Simon, E., Thorsen, G., et al. (2020). Yaw Induced Wake Deflection-A Full-Scale Validation Study. J. Phys. Conf. Ser. 1618, 062047. doi:10.1088/1742-6596/1618/6/062047

CrossRef Full Text | Google Scholar

Le Provost, M., and Eldredge, J. D. (2021). Ensemble Kalman Filter for Vortex Models of Disturbed Aerodynamic Flows. Phys. Rev. Fluids 6, 050506. doi:10.1103/physrevfluids.6.050506

CrossRef Full Text | Google Scholar

Lejeune, M., Moens, M., and Chatelain, P. (2022). Extension and Validation of an Operational Dynamic Wake Model to Yawed Configurations. J. Phys. Conf. Ser. 2265, 022018. doi:10.1088/1742-6596/2265/2/022018

CrossRef Full Text | Google Scholar

Lejeune, M., Moens, M., Coquelet, M., Coudou, N., and Chatelain, P. (2020). Data Assimilation for the Prediction of Wake Trajectories within Wind Farms. J. Phys. Conf. Ser. 1618, 062055. doi:10.1088/1742-6596/1618/6/062055

CrossRef Full Text | Google Scholar

Lio, W. H., Larsen, G. C., and Poulsen, N. K. (2020). Dynamic Wake Tracking and Characteristics Estimation Using a Cost-Effective LiDAR. J. Phys. Conf. Ser. 1618, 032036. doi:10.1088/1742-6596/1618/3/032036

CrossRef Full Text | Google Scholar

Machefaux, E., Larsen, G. C., Troldborg, N., Gaunaa, M., and Rettenmeier, A. (2014). Empirical Modeling of Single-Wake Advection and Expansion Using Full-Scale Pulsed Lidar-Based Measurements. Wind Energy 18, 2085–2103. doi:10.1002/we.1805

CrossRef Full Text | Google Scholar

Moens, M., and Chatelain, P. (2022). Correlations Between Wake Phenomena and Fatigue Loads Within Large Wind Farms: A Large-Eddy Simulation Study. Front. Energy Res. 10, 881532. doi:10.3389/fenrg.2022.881532

CrossRef Full Text | Google Scholar

Moens, M., Duponcheel, M., and Chatelain, P. (2022). Assessment of an Actuator Disk-Based Approach for the Prediction of Fatigue Loads in Wind Turbine Rotors. Wind Energy. in press.

Google Scholar

Moens, M., Duponcheel, M., Winckelmans, G., and Chatelain, P. (2018). An Actuator Disk Method with Tip-Loss Correction Based on Local Effective Upstream Velocities. Wind Energy 21, 766–782. doi:10.1002/we.2192

CrossRef Full Text | Google Scholar

Muller, Y.-A., Aubrun, S., and Masson, C. (2015). Determination of Real-Time Predictors of the Wind Turbine Wake Meandering. Exp. Fluids 56, 53. doi:10.1007/s00348-015-1923-9

CrossRef Full Text | Google Scholar

Niayifar, A., and Porté-Agel, F. (2015). A New Analytical Model for Wind Farm Power Prediction. J. Phys. Conf. Ser. 625, 012039. doi:10.1088/1742-6596/625/1/012039

CrossRef Full Text | Google Scholar

Notter, S., Groß, P., Schrapel, P., and Fichter, W. (2020). Multiple Thermal Updraft Estimation and Observability Analysis. J. Guid. Control, Dyn. 43, 490–503. doi:10.2514/1.G004205

CrossRef Full Text | Google Scholar

Park, J., and Law, K. H. (2016). A Data-Driven, Cooperative Wind Farm Control to Maximize the Total Power Production. Appl. Energy 165, 151–165. doi:10.1016/j.apenergy.2015.11.064

CrossRef Full Text | Google Scholar

Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J., Chanan, G., et al. (2019). “Pytorch: An Imperative Style, High-Performance Deep Learning Library,” in Advances in Neural Information Processing Systems (Curran Associates, Inc.), 32, 8024–8035.

Google Scholar

Reinwardt, I., Schilling, L., Dalhoff, P., Steudel, D., and Breuer, M. (2020). Extension of the DWM Model towards a Static Model for Site-specific Load Simulations. J. Phys. Conf. Ser. 1618, 062007. doi:10.1088/1742-6596/1618/6/062007

CrossRef Full Text | Google Scholar

Rott, A., Petrović, V., and Kühn, M. (2020). Wind Farm Flow Reconstruction and Prediction from High Frequency SCADA Data. J. Phys. Conf. Ser. 1618, 062067. doi:10.1088/1742-6596/1618/6/062067

CrossRef Full Text | Google Scholar

Schreiber, J., Balbaa, A., and Bottasso, C. L. (2020). Brief Communication: A Double-Gaussian Wake Model. Wind Energy Sci. 5, 237–244. doi:10.5194/wes-5-237-2020

CrossRef Full Text | Google Scholar

Thøgersen, E., Tranberg, B., Herp, J., and Greiner, M. (2017). Statistical Meandering Wake Model and its Application to Yaw-Angle Optimisation of Wind Farms. J. Phys. Conf. Ser. 854, 012017. doi:10.1088/1742-6596/854/1/012017

CrossRef Full Text | Google Scholar

Zhan, L., Letizia, S., and Iungo, G. V. (2020). Optimal Tuning of Engineering Wake Models through Lidar Measurements. Wind Energy Sci. Discuss. 5, 1–28. doi:10.5194/wes-2020-72

CrossRef Full Text | Google Scholar