
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
BRIEF RESEARCH REPORT article
Front. Energy Res. , 20 May 2022
Sec. Smart Grids
Volume 10 - 2022 | https://doi.org/10.3389/fenrg.2022.878810
This article is part of the Research Topic Advanced Anomaly Detection Technologies and Applications in Energy Systems View all 64 articles
The slime mold algorithm (SMA) is a novel meta-heuristic search that replicates the characteristics of slime mold during oscillation. This is presented in a novel mathematical formulation that employs changeable weights to modify the sequence of both negative and positive propagation waves in order to build a mechanism for linking food availability with intensive exploration capacity and exploitation affinity. The study demonstrates how to solve a non-convex and cost-effective load dispatch issue (ELD) in an electric power system using the SM method. The efficacy of SMA is explored for a single-area economic load dispatch on small-scale power systems, using 3-, 5-, and 6-unit test systems, and the results are validated by comparing the results to those of other well-known meta-heuristic algorithms.
In the actual functioning of power systems, economic load dispatch (ELD) is a crucial problem to solve. The role of the power system is to deliver continuous power to the consumers at an affordable price which is its main feature (Panigrahi et al., 2006), (Jadoun et al., 2015). The objective is to reduce energy-generating costs while fulfilling load needs and ensuring equality and in-quality constraints. This fact results in a higher degree of pollution awareness in thermal plants and a lower cost of diagnosing the problem. Because they operate in conjunction with a collection of viable alternatives, evolutionary methods are now perfectly suited for discovering answers to optimization problems. All optimization approaches, including evolutionary ones, are known to be influenced by constraints (Salcedo-Sanz, 2009). Since the traditional procedure of an evolutionary approach, employing operators for individuals in a population may violate the constraint rules. The way evolutionary approaches deal with constraint rules of challenges is a significant aspect that is directly connected to the quality of solutions created for such problems. By converting the present solution that opposes the constraints into a viable one, a redesigned method eliminates unattainable solutions.
Wind, solar, thermal, nuclear, renewable, hydro, and other power-producing facilities are used in most power generation systems. In the case of renewable energy systems, the operational cost will not change as much as the production. In thermal systems, however, the running cost varies with the total power output. As a result, the ELD issue, which includes the use of thermal systems as generators, is considered a critical optimization issue in electric power systems. Maintaining an economical operation is a difficult challenge for both traditional and smart grid systems. When power systems are exposed to operational and a transmission imperative, the ELD limits the optimal outcome for an electric power generation to sustain the load demand with a minimum generation price. The ELD problem is usually solved by sophisticated computerized approaches that meet the operational and power system imperatives via minute-to-minute monitoring. A little increase in the ELD demonstrates its long-term reaction to the declining price of the total power output. As a result, a variety of optimization methods have been developed to address cost-effective load dispatch issues while producing high-quality results. Traditional optimization approaches were the sole option to address ELD concerns for many years. Because of the limitations of conventional methods, system operators have a chance to fail to notice the realistic and technological imperatives of the system’s units. There are two types of simplifications in this category: first, combined with the accuracy of the generating unit’s pricing model, particularly for different types of fuels or taking the valve-point loading impact into account (Cai et al., 2012; Zhong et al., 2013). Multi-valve steam turbines are widely seen in real-world generating units. The valve point of the generating unit is drawn when the steam turbine’s intake valve opens abruptly, pushing the energy consumption curve upward.
The economic load dispatch problem is a major concern for the cost-effective operation of electric power systems as it concentrates on basically assembling the power outputs of the units by establishing time intervals to decrease generating costs while still meeting other system requirements. In general, the traditional ELD problem is reduced to solve the convex quadratic programming problem (Reid and Hasdorff, 1973), which may now be handled effectively using MOSEK (Babonneau et al., 2019). Furthermore, the system becomes non-smoothed, non-convex, and non-continuous when the valve-point loading effect, transmission loss, and prohibited operating zones are considered. The objective function arises as multiples of the local minimum because of these features, making global minima exceedingly difficult to attain. Aside from that, the non-smooth nature of the function makes the derivate-based mathematical programming technique challenging to apply directly.
Traditional optimization techniques often look at linear, piece-wise linear, and price functions of generators in quadratic functions, with just network loss being considered. These classic techniques include lambda iteration (Zhan et al., 2014), gradient descent method (Dibangoye et al., 2015), linear programming (Torreglosa et al., 2016), Newton’s technique (Wang et al., 2014), dynamic programming (Al-Kalaani, 2009), gradient search (Subathra et al., 2015), and the Lagrangian relaxation algorithm (Li et al., 2013; Mohammadi-Ivatloo et al., 2013). Because of the persistence of severe non-linear characteristics in real-world practical networks, while dealing with high-dimensional economic dispatch difficulties, these suffer disadvantages such as failure to meet imperatives and lengthy time calculations.
This time-consuming calculation in optimization methods prompted researchers to develop meta-heuristic optimization strategies to solve large-scale problems. The meta-heuristic method (Gjorgiev and Čepin, 2013) takes into consideration non-convex pricing functions and non-smooth operating functions as well as other imperatives. This includes techniques such as synergic predator–prey optimization (SPPO) (Singh et al., 2016), seeker optimization algorithm (SOA) (Shaw et al., 2012), genetic algorithm (GA) (Amjady and Nasiri-Rad, 2010), (Elsayed et al., 2014), evolutionary programming (EP) (Sinha et al., 2003), firefly algorithm (FA) (Yang et al., 2012), particle swarm optimization (PSO) (Neyestani et al., 2010), (Safari and Shayeghi, 2011), (Wang and Singh, 2009), artificial bee colony (ABC) (Aydın and Özyön, 2013), colonial competitive differential algorithm (CCDE) (Ghasemi et al., 2016), bacterial foraging algorithm (BFA) (Farhat and El-Hawary, 2010), improved Tabu search algorithm (ITS) (Whei-Min Lin et al., 2002), ant colony optimization (ACO) (Pothiya et al., 2010), group search optimizer (GSO) (Zare et al., 2012), harmony search algorithm (HAS) (Jeddi and Vahidinasab, 2014), biogeography-based optimization (BBO) (Bhattacharya and Chattopadhyay, 2010), and differential evolution (DE) (Jiang et al., 2013). Many researchers used slime mould algorithm to bring better results and few such algorithms are Dispersed Foraging Slime Mould Algorithm (DFSMA) (Hu et al., 2022), Chaos-opposition-enhanced slime mould algorithm (CO-SMA) (Rizk, 2022), Opposition based learning slime mould algorithm (OBLSMA) (Houssein et al., 2022), Multi-objective slime mould algorithm (MOSMA) (Houssein et al., 115870), Equilibrium optimizer slime mould algorithm (EOSMA) (Yin et al., 2022). In this work, SMA is used to identify solutions to economic load dispatch problems on a variety of test systems. Other new and popular approaches outcomes are compared to analyze the results.
The goal of the ELD problem is to lower the entire fuel cost of power systems by finding the optimum combination of power outputs from all generating units while congregating load demand and operational constraints (Dubey et al., 2013).
The fuel cost for unit generation is represented as a quadratic function, with the assumption that the collective cost curves of the generating units develop as linear functions over time. The mathematical equation for the single-area ELD for an hour is as follows in Eq. 1:
where n
The dispatching of power-generating units for “Hr” hours can be represented as follows:
where n
The right mathematics for ED is Eq. 2. Because the load demand changes over time, “hr” is changed from a single hour to “Hr” hours.
The aforementioned objective functions are subjected to the following equality and inequality constraints:
The total power generation is equal to total power demand plus system power loss.
where
In presence of loss coefficients
The extension of Eq. 5 is as follows:
The true power output of each generator is controlled by the upper and lower operational limits.
where
The output power of the generating unit is boosted between the lower and higher limits of active power generation.
1) By increasing the generated power,
2) By reducing the amount of generated power
Therefore, the generator ramp rate is shown in the following equation:
where n = 1,2, 3, …, ng, and
Prohibited operating zones (POZ) are allocated to the graph for input–output powers in the generating unit, which may be discontinuous due to functional constraints of the generator produced by a defective mistake in the machine parts or the machine itself. The discontinuous input–output power limitations are as follows in Eq. 11:
It is known that the behavior of the organism can be imitated and molded to tackle the mathematics of unconstrained and non-convex characteristics. Researchers have framed to imitate the guiding principles to develop computations and algorithms. The slime molds have received significant courteousness for the past few years. Scientifically, slime mold is titled as Physarum polycephalum (Howard, 1931). The slime mold undergoes few changes in its structure, that is, it repositions its front position into a fan-shaped model, and its interconnected venous network allows the cytoplasm to flow inside at some level in relocation series. This stretchable venous network helps in searching for food in multiple places and grabs the food from food points. The slime mold has the ability to creep up to 900 sq.m if it finds rich food points in the environment.
The mathematical modeling of SMA is discussed in three stages, namely, approaching food, wrapping food, and food grabble (Li et al., 2020).
Step 1: The slime mold identifies the food based on the smell present in the air. The mathematics to explicate the contraction phase and update its position during the food search process is presented in the following expression which depends on x and p:
where
The maximum limit
where t = 1, 2,.n,
The equation
where
The slime mold’s updated location is numerically given as follows:
The upper and lower bounds of search ranges are given as
The slime mold’s location gets upgraded in the search process and the value varies within the limits and fluctuates between [-1, 1] and falls to zero. The flowchart of the proposed optimizer is shown in Figure 1.
In this section of the article, the IEEE bus systems in small size test systems were considered, and comparison was done with other methods, to see how well the slime mold optimization algorithm performed on the ELD issue.
The input test data and loss coefficient matrices were obtained from Sharma and Moses (2016), which shows a three-generator test system with a power requirement of 150 MW assessed. The input test data are displayed in appendix. In this case, the ELD issue was cracked without a valve-point effect. Table 1 indicates that the slime mold algorithm’s fuel price is 1590.627083 Rs./h, which was the lowest of all the algorithms satisfying the system constraints. The convergence curve of the SMA obtained by simulation which was stable is shown in Figure 2A.
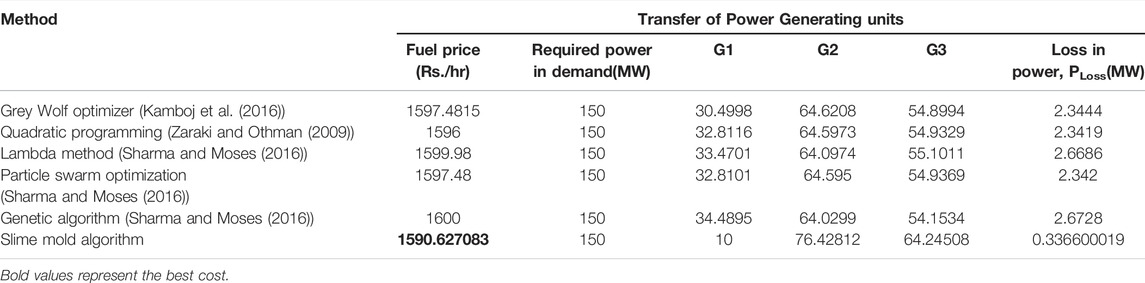
TABLE 1. (Case I) Slime mold algorithm results for economic dispatch of 3-unit system (without valve-point effect).
With a power demand of 730MW, a five-unit test system with a valve-point loading effect was used, and its input test information was taken from Coelho and Lee (2008) with the loss coefficient matrix set to zero, which is given in appendix. Table 2 shows that the slime mold algorithm obtained a fuel price of 2034.972427 R/h, satisfying all the constraints and was the best fuel price among all algorithms. The convergence curve of SMA obtained by simulation which was stable is shown in Figure 2B.
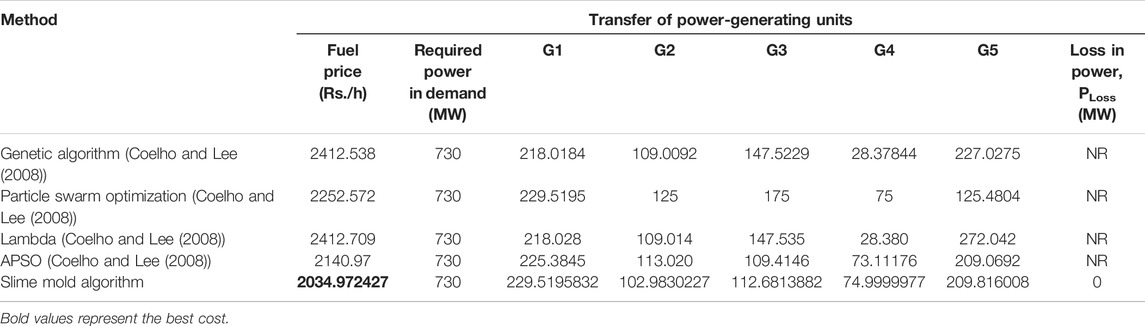
TABLE 2. Slime mold algorithm results for economic dispatch of 5-unit system (with valve-point effect).
In order to intuitively analyze the location and fitness changes of the slime mold during foraging, the qualitative analysis findings of the SMA in lowering the fuel cost in ELD are provided in Figures 2A,B. During the iteration phase, the convergence curve reveals the ideal fitness value of the slime mold. The convergence curve shows how the average fitness of the slime mold’s ideal fitness value changes over time. We can see the slime mold’s convergence rate and the moment when it transitions between exploration and exploration gradation by looking at the decline of the curve.
In this study, the slime mold optimization approach was used to solve economic load dispatch problems in electric power networks. This method’s effectiveness was tested on conventional IEEE bus systems with 3 and 5 producing units in small, medium, and large power systems. According to the statistics, the slime mold optimizer was clearly the best choice for dealing with economic load dispatch issues since it contributes reduced fuel costs and less transmission loss. It has a higher rate of convergence than other well-known optimizers. By establishing a balance between exploration and exploitation, the slime mold optimizer achieved maximal avoidance in the local optimum. As a result, this algorithm provided improved solutions for load dispatch difficulties that were cost-effective.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
The author confirms being the sole contributor of this work and has approved it for publication.
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Al-Kalaani, Y. (2009). Power Generation Scheduling Algorithm Using Dynamic Programming. Nonlinear Anal. Theor. Methods Appl. 71 (12), e641–e650. doi:10.1016/j.na.2008.11.082
Amjady, N., and Nasiri-Rad, H. (2010). Solution of Nonconvex and Nonsmooth Economic Dispatch by a New Adaptive Real Coded Genetic Algorithm. Expert Syst. Appl. 37 (7), 5239–5245. doi:10.1016/j.eswa.2009.12.084
Aydın, D., and Özyön, S. (2013). Solution to Non-convex Economic Dispatch Problem with Valve point Effects by Incremental Artificial Bee colony with Local Search. Appl. Soft Comput. 13 (5), 2456–2466. doi:10.1016/j.asoc.2012.12.002
Babonneau, F., Corcos, G., Drouet, L., and Vial, J.-P. (2019). Neatwork: A Tool for the Design of Gravity-Driven Water Distribution Systems for Poor Rural Communities. INFORMS J. Appl. Analytics 49 (3), 129–136. doi:10.1287/inte.2018.0983
Bhattacharya, A., and Chattopadhyay, P. K. (2010). Solving Complex Economic Load Dispatch Problems Using Biogeography-Based Optimization. Expert Syst. Appl. 37 (5), 3605–3615. doi:10.1016/j.eswa.2009.10.031
Cai, J., Li, Q., Li, L., Peng, H., and Yang, Y. (2012). A Hybrid CPSO-SQP Method for Economic Dispatch Considering the Valve-point Effects. Energ. Convers. Manag. 53 (1), 175–181. doi:10.1016/j.enconman.2011.08.023
Coelho, L. d. S., and Lee, C.-S. (2008). Solving Economic Load Dispatch Problems in Power Systems Using Chaotic and Gaussian Particle Swarm Optimization Approaches. Int. J. Electr. Power Energ. Syst. 30 (5), 297–307. doi:10.1016/j.ijepes.2007.08.001
Dibangoye, J., Doniec, A., Fakham, H., Colas, F., and Guillaud, X. (2015). Distributed Economic Dispatch of Embedded Generation in Smart Grids. Eng. Appl. Artif. Intelligence 44, 64–78. doi:10.1016/j.engappai.2015.05.007
Dubey, H. M., Pandit, M., Panigrahi, B. K., and Udgir, M. (2013). Economic Load Dispatch by Hybrid Swarm Intelligence Based Gravitational Search Algorithm. Ijisa 5 (8), 21–32. doi:10.5815/ijisa.2013.08.03
Elsayed, S. M., Sarker, R. A., and Essam, D. L. (2014). A New Genetic Algorithm for Solving Optimization Problems. Eng. Appl. Artif. Intelligence 27, 57–69. doi:10.1016/j.engappai.2013.09.013
Farhat, I. A., and El-Hawary, M. E. (2010). Dynamic Adaptive Bacterial Foraging Algorithm for Optimum Economic Dispatch with Valve-point Effects and Wind Power. IET Gener. Transm. Distrib. 4 (9), 989–999. doi:10.1049/iet-gtd.2010.0109
Ghasemi, M., Taghizadeh, M., Ghavidel, S., and Abbasian, A. (2016). Colonial Competitive Differential Evolution: An Experimental Study for Optimal Economic Load Dispatch. Appl. Soft Comput. 40, 342–363. doi:10.1016/j.asoc.2015.11.033
Gjorgiev, B., and Čepin, M. (2013). A Multi-Objective Optimization Based Solution for the Combined Economic-Environmental Power Dispatch Problem. Eng. Appl. Artif. Intelligence 26 (1), 417–429. doi:10.1016/j.engappai.2012.03.002
Houssein, E. H., Mahdy, M. A., Shebl, D., Manzoor, A., Sarkar, R., and Mohamed, W. M. (1158). An Efficient Slime Mould Algorithm for Solving Multi-Objective Optimization Problems. Expert Syst. Appl. 187, 2022. doi:10.1016/j.eswa.2021.115870
Houssein, E. H., Helmy, B. E.-d., Rezk, H., and Nassef, A. M. (2022). An Efficient Orthogonal Opposition-Based Learning Slime Mould Algorithm for Maximum Power point Tracking. Neural Comput. Applic 34 (5), 3671–3695. doi:10.1007/s00521-021-06634-y
Howard, F. L. (1931). The Life History Ofphysarum Polycephalum. Am. J. Bot. 18 (2), 116–133. doi:10.1002/j.1537-2197.1931.tb09577.x
Hu, J., Gui, W., Heidari, A. A., Cai, Z., Liang, G., Chen, H., et al. (2022). Dispersed Foraging Slime Mould Algorithm: Continuous and Binary Variants for Global Optimization and Wrapper-Based Feature Selection. Knowledge-Based Syst. 237, 107761. doi:10.1016/j.knosys.2021.107761
Jadoun, V. K., Gupta, N., Niazi, K. R., Swarnkar, A., and Bansal, R. C. (2015). Improved Particle Swarm Optimization for Multi-Area Economic Dispatch with Reserve Sharing Scheme. IFAC-PapersOnLine 48 (30), 161–166. doi:10.1016/j.ifacol.2015.12.371
Jeddi, B., and Vahidinasab, V. (2014). A Modified harmony Search Method for Environmental/economic Load Dispatch of Real-World Power Systems. Energ. Convers. Manag. 78, 661–675. doi:10.1016/j.enconman.2013.11.027
Jiang, X., Zhou, J., Wang, H., and Zhang, Y. (2013). Dynamic Environmental Economic Dispatch Using Multiobjective Differential Evolution Algorithm with Expanded Double Selection and Adaptive Random Restart. Int. J. Electr. Power Energ. Syst. 49 (1), 399–407. doi:10.1016/j.ijepes.2013.01.009
Kamboj, V. K., Bath, S. K., and Dhillon, J. S. (2016). Solution of Non-convex Economic Load Dispatch Problem Using Grey Wolf Optimizer. Neural Comput. Applic 27 (5), 1301–1316. doi:10.1007/s00521-015-1934-8
Li, S., Chen, H., Wang, M., Heidari, A. A., and Mirjalili, S. (2020). Slime Mould Algorithm: A New Method for Stochastic Optimization. Future Generation Comp. Syst. 111, 300–323. doi:10.1016/j.future.2020.03.055
Li, Z., Wu, W., Zhang, B., Sun, H., and Guo, Q. (2013). Dynamic Economic Dispatch Using Lagrangian Relaxation with Multiplier Updates Based on a Quasi-Newton Method. IEEE Trans. Power Syst. 28, 4516–4527. doi:10.1109/TPWRS.2013.2267057
Mohammadi-Ivatloo, B., Rabiee, A., and Soroudi, A. (2013). Nonconvex Dynamic Economic Power Dispatch Problems Solution Using Hybrid Immune-Genetic Algorithm. IEEE Syst. J. 7 (4), 777–785. doi:10.1109/JSYST.2013.2258747
Neyestani, M., Farsangi, M. M., and Nezamabadi-Pour, H. (2010). A Modified Particle Swarm Optimization for Economic Dispatch with Non-smooth Cost Functions. Eng. Appl. Artif. Intelligence 23 (7), 1121–1126. doi:10.1016/j.engappai.2010.06.006
Panigrahi, C. K., Chattopadhyay, P. K., Chakrabarti, R. N., and Basu, M. (2006). Simulated Annealing Technique for Dynamic Economic Dispatch. Electric Power Components Syst. 34 (5), 577–586. doi:10.1080/15325000500360843
Pothiya, S., Ngamroo, I., and Kongprawechnon, W. (2010). Ant colony Optimisation for Economic Dispatch Problem with Non-smooth Cost Functions. Int. J. Electr. Power Energ. Syst. 32 (5), 478–487. doi:10.1016/j.ijepes.2009.09.016
Reid, G., and Hasdorff, L. (1973). Economic Dispatch Using Quadratic Programming. IEEE Trans. Power Apparatus Syst. PAS-92 (6), 2015–2023. doi:10.1109/TPAS.1973.293582
Rizk, M.Rizk-Allah, Aboul Ella Hassanien, Dongran Song, “Chaos-Opposition-Enhanced Slime Mould Algorithm for Minimizing the Cost of Energy for the Wind Turbines on High-Altitude Sites”. ISA Trans. 121, 2022191–2022205. doi:10.1016/j.isatra.2021.04.011
Safari, A., and Shayeghi, H. (2011). Iteration Particle Swarm Optimization Procedure for Economic Load Dispatch with Generator Constraints. Expert Syst. Appl. 38 (5), 6043–6048. doi:10.1016/j.eswa.2010.11.015
Salcedo-Sanz, S. (2009). A Survey of Repair Methods Used as Constraint Handling Techniques in Evolutionary Algorithms. Comp. Sci. Rev. 3 (3), 175–192. doi:10.1016/j.cosrev.2009.07.001
Sharma, U., and Moses, B. (2016). Analysis and Optimization of Economic Load Dispatch Using Soft Computing Techniques. Int. Conf. Electr. Electron. Optim. Tech. ICEEOT, 4035–4040. doi:10.1109/ICEEOT.2016.7755472
Shaw, B., Mukherjee, V., and Ghoshal, S. P. (2012). Solution of Economic Dispatch Problems by Seeker Optimization Algorithm. Expert Syst. Appl. 39 (1), 508–519. doi:10.1016/j.eswa.2011.07.041
Singh, N. J., Dhillon, J. S., and Kothari, D. P. (2016). Synergic Predator-Prey Optimization for Economic thermal Power Dispatch Problem. Appl. Soft Comput. 43, 298–311. doi:10.1016/j.asoc.2016.02.042
Sinha, N., Chakrabarti, R., and Chattopadhyay, P. K. (2003). Evolutionary Programming Techniques for Economic Load Dispatch. IEEE Trans. Evol. Computat. 7 (1), 83–94. doi:10.1109/TEVC.2002.806788
Subathra, M. S. P., Selvan, S. E., Victoire, T. A. A., Christinal, A. H., and Amato, U. (2015). A Hybrid with Cross-Entropy Method and Sequential Quadratic Programming to Solve Economic Load Dispatch Problem. IEEE Syst. J. 9 (3), 1031–1044. doi:10.1109/JSYST.2013.2297471
Torreglosa, J. P., García-Triviño, P., Fernández-Ramirez, L. M., and Jurado, F. (2016). Control Based on Techno-Economic Optimization of Renewable Hybrid Energy System for Stand-Alone Applications. Expert Syst. Appl. 51, 59–75. doi:10.1016/j.eswa.2015.12.038
Wang, L., and Singh, C. (2009). Reserve-constrained Multiarea Environmental/economic Dispatch Based on Particle Swarm Optimization with Local Search. Eng. Appl. Artif. Intelligence 22 (2), 298–307. doi:10.1016/j.engappai.2008.07.007
Wang, M. Q., Gooi, H. B., Chen, S. X., Lu, S., Lu, S., and Variables, A. (2014). A Mixed Integer Quadratic Programming for Dynamic Economic Dispatch with Valve Point Effect. IEEE Trans. Power Syst. 29 (5), 2097–2106. doi:10.1109/APPEEC.2014.706614710.1109/tpwrs.2014.2306933
Whei-Min Lin, W., Fu-Sheng Cheng, F., and Ming-Tong Tsay, M. (2002). An Improved Tabu Search for Economic Dispatch with Multiple Minima. IEEE Trans. Power Syst. 17 (1), 108–112. doi:10.1109/59.982200
Yang, X.-S., Sadat Hosseini, S. S., and Gandomi, A. H. (2012). Firefly Algorithm for Solving Non-convex Economic Dispatch Problems with Valve Loading Effect. Appl. Soft Comput. 12 (3), 1180–1186. doi:10.1016/j.asoc.2011.09.017
Yin, S., Luo, Q., and Zhou, Y. (2022). EOSMA: An Equilibrium Optimizer Slime Mould Algorithm for Engineering Design Problems. Arab. J. Sci. Eng.doi:10.1007/s13369-021-06513-7
Zaraki, A., and Othman, M. F. B. (2009). Implementing Particle Swarm Optimization to Solve Economic Load Dispatch Problem. SoCPaR 2009 - Soft Comput. Pattern Recognit, 60–65. doi:10.1109/SoCPaR.2009.24
Zare, K., Haque, M. T., and Davoodi, E. (2012). Solving Non-convex Economic Dispatch Problem with Valve point Effects Using Modified Group Search Optimizer Method. Electric Power Syst. Res. 84 (1), 83–89. doi:10.1016/j.epsr.2011.10.004
Zhan, J. P., Wu, Q. H., Guo, C. X., and Zhou, X. X. (2014). Fast $\lambda$-Iteration Method for Economic Dispatch with Prohibited Operating Zones. IEEE Trans. Power Syst. 29 (2), 990–991. doi:10.1109/TPWRS.2013.2287995
Keywords: slime mold algorithm, non-convex optimization, electric power system, metaheuristic algorithms, load dispatch
Citation: Zhu Z (2022) An Improved Solution to Generation Scheduling Problem Using Slime Mold Algorithm. Front. Energy Res. 10:878810. doi: 10.3389/fenrg.2022.878810
Received: 18 February 2022; Accepted: 08 March 2022;
Published: 20 May 2022.
Edited by:
Xun Shen, Tokyo Institute of Technology, JapanReviewed by:
Surya Deo Choudhary, Aryabhatta Knowledge University, IndiaCopyright © 2022 Zhu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zixuan Zhu, Mjk0NTE5NjYwNUBxcS5jb20=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.