An Approach for the Dynamic Reliability Assessment of the Digital Power Control System for Nuclear Reactor

The digital power control system for nuclear reactor (DPCSNR) for a nuclear power plant has dynamic characteristics including dynamic interaction, time dependence, and causal relationship uncertainty, and it is of great significance to assess its dynamic reliability. This study aimed to propose an approach for the dynamic reliability assessment of the DPCSNR with dynamic characteristics. First, the dynamic fault tree analysis (DFTA) method was used to establish a DFT characterizing the dynamic interaction for the DPCSNR. Then, the dynamic Bayesian network (DBN) method was used to transform the DFT into the initial DBN (IDBN) model characterizing the dynamic interaction and time dependence for the DPCSNR. Furthermore, the fuzzy mathematics (FM) method was used to modify the conditional probability table (CPT) characterizing the causal relationship uncertainty in the IDBN model and to establish the DBN model characterizing the dynamic interaction, time dependence, and causal relationship uncertainty for the DPCSNR. Finally, DBN reasoning was applied to assess the dynamic reliability of the DPCSNR. The results showed that the system reliability under conditions of periodic tests and predictable maintenance was 99.959%, and the computer system was the most critical event of the DPCSNR failure.

Introduction

The digital power control system for nuclear reactor (DPCSNR) for a nuclear power plant (NPP) consists of hardware, software, and human operations, which uses the redundancy design and digital control, and it is a complex system with dynamic interaction, time dependence, and causal relationship uncertainty (Zhou et al., 2014; Ibrahim, 2015; Shukla and Arul, 2017; Ding et al., 2021). Its functions are to realize the normal startup and shutdown and power regulation of the nuclear reactor and to ensure the safe and stable operation of the NPP (Lu et al., 2015). Therefore, it is of great significance to assess its dynamic reliability.

Previous studies have dealt with the reliability assessment of the DPCSNR. Vinod et al. (2008) used the fault tree (FT) analysis (FTA) method to analyze the influence of software failure on the system reliability and calculate the system failure probability. Tao and Lu (2013) applied the FTA method to obtain the risk importance measures, which were used to identify the system’s weak points. Wang et al. (2016) used the dynamic flowgraph method to describe the interactions between system hardware and software and analyze the system reliability. Durga Rao et al. (2009) used the dynamic FTA method to calculate the system reliability, but they ignored the effect of loss of power supply on the system. These studies have made contributions to the reliability assessment of the DPCSNR, but they have only been preliminary studies on dynamic interaction, time dependence, and causal relationship uncertainty for the DPCSNR.

Recently, investigators proposed that the dynamic characteristics of a complex system should be analyzed and characterized in terms of its dynamic interaction, time dependence, and causal relationship uncertainty. Nie et al. (2020) believed that only when the complex systems in the NPP used the dynamic reconfiguration technology, their components, functions, processes, and behavior correlated, which indicates that the system failure is closely related to the dynamic interaction between hardware, software, and human factors. Shukla et al. (2020) believed that due to the influences from the external environment and hardware aging, the performance and reliability of the complex system would decrease with time, which implies that the periodic test and predictive maintenance should be carried out for the systems’ hardware. Yazdi et al. (2019) and Jafari et al. (2020) argued that since the FT structure for a complex system was artificially designed, this could lead to causal relationship uncertainty between upper and lower events.

In order to characterize the dynamic interaction, investigators introduced the priority AND (PAND) gate, functional dependency (FDEP) gate, sequence enforcing (SEQ) gate, and spare gate into the FT and established the dynamic FT (DFT) expressing the dynamic logic relationship between events (Chiacchio et al., 2011a; Manno et al., 2014). This method solved the problem of how to characterize the dynamic interaction that the traditional static FT method could not characterize (Chiacchio et al., 2011b; Gascard and Simeu-Abazi, 2018). But when the Markov model was used to analyze the DFT, it was difficult to deal with the state space explosion (Marquez et al., 2008; Chiacchio et al., 2013) and to assess the system reliability under test and maintenance conditions (Nguyen et al., 2015).

The latest studies show that the dynamic Bayesian network (DBN) method can be applied to determine the conditional independence relationship among non-parent–child nodes in the DBN model so as to greatly reduce the computational complexity (Neil and Marquez, 2012) and to introduce the maintenance parameters into the state transition probability formula to express the test and maintenance information (Jiang et al., 2020). Thus, the DBN method can make up for the two aforementioned deficiencies of the dynamic DFT analysis (DFTA) method. Meanwhile, this method can use the directed arc between time slice nodes to characterize the time dependence (Marquez et al., 2010; Khakzad, 2015), and it has strong forward and backward reasoning capability. Therefore, it should be well suited for the reliability assessment of a complex system (Kabir and Papadopoulos, 2019).

Furthermore, the latest studies have shown that the fuzzy mathematics (FM) method is feasible in dealing with the causal relationship uncertainty. Zarei et al. (2019) and Wang et al. (2021) used the FM method to study the problems with causal relationship uncertainty.

Therefore, in this study, the DFTA method was used to establish the DFT for the DPCSNR, which can characterize the hardware–software–human dynamic interaction; the DBN method was used to establish the initial DBN (IDBN) model based on the transformation strategy from the DFT to the DBN model, which can characterize the dynamic interaction and time dependence; the FM method was used to modify the CPT in the IDBN model to characterize the causal relationship uncertainty in the IDBN model and to establish the DBN model, which can characterize the dynamic interaction, time dependence, and causal relationship uncertainty; and the Monte Carlo (MC) method was to be used to verify the effectiveness of the DBN model. The objective of this study was to propose an approach for dynamic reliability assessment of the DPCSNR with respect to its dynamic characteristics including dynamic interaction, time dependence, and causal relationship uncertainty.

Brief Description of the Digital Power Control System for Nuclear Reactor

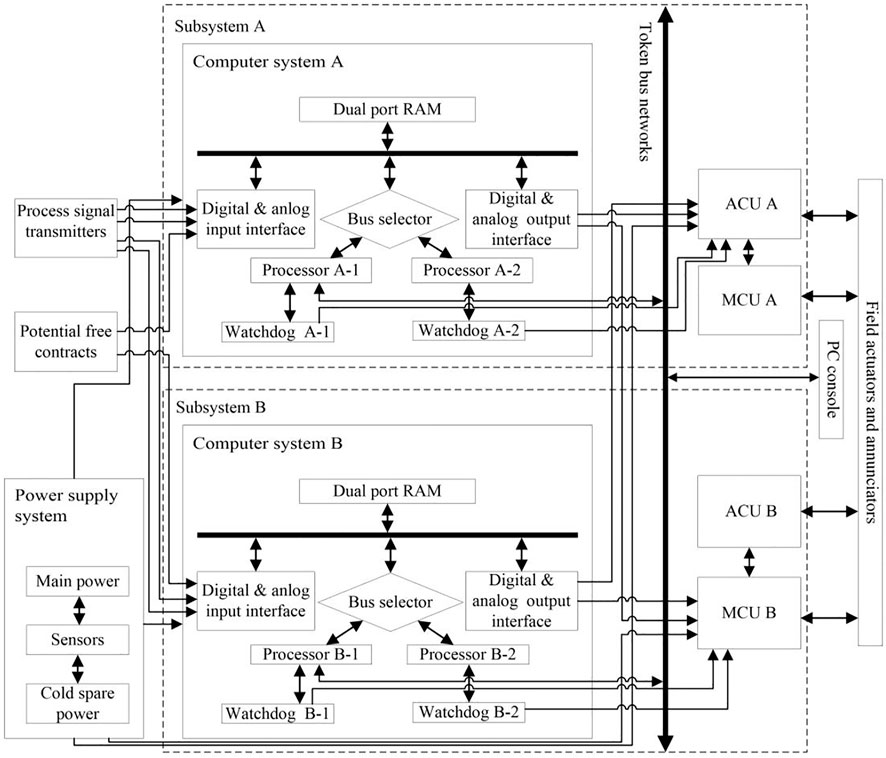
DPCSNR is a computer-based feedback control system, and its function is to control the reactor power within the range of 10⁻⁷ FP−100% FP according to the demand for NPP. Computer systems and various sensors are integrated to measure the reactor power and monitor the actuation of reactivity devices in the DPCSNR. The structure of the DPCSNR is shown in Figure 1 (Vinod et al., 2008). It contains subsystem A and subsystem B and a power supply system (PSS). The two subsystems have the same configuration and structure, and each one of the subsystems including the computer system, automatic conversion unit (ACU), and manual conversion unit (MCU) can control the reactor power. If one computer system fails, the ACU or MCU can transfer the control to another normal computer system. The PSS, which includes main power, cold spare power, and sensors, supplies power to the subsystems.

FIGURE 1

FIGURE 1. Structure of the DPCSNR.

Proposed Approach

Theoretical Framework

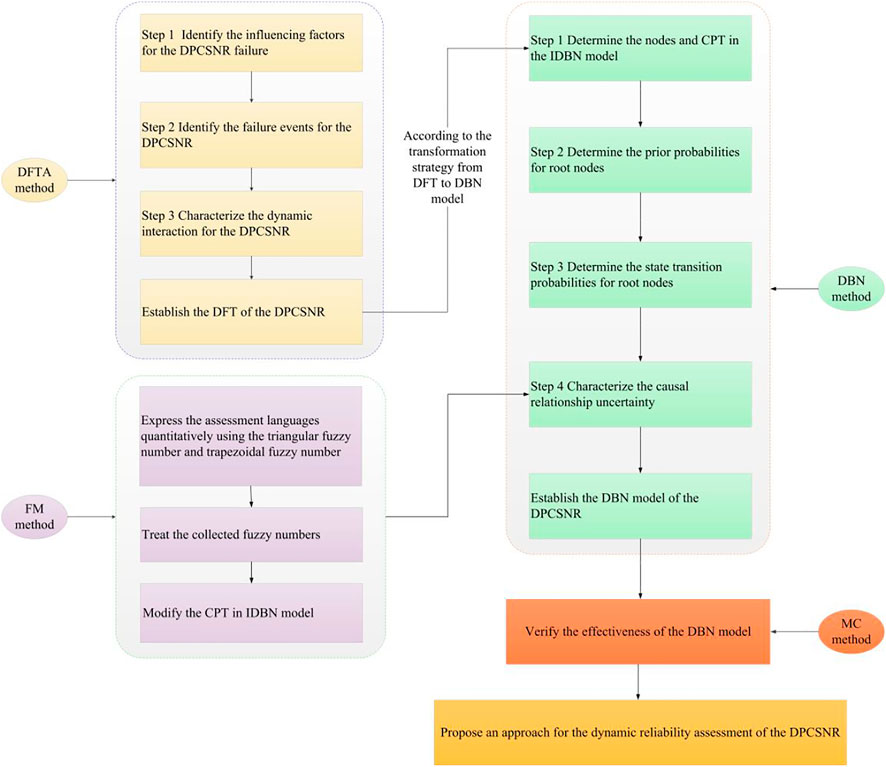
The theoretical framework of the approach for dynamic reliability assessment of the DPCSNR was established by using DFTA, DBN, FM, and MC methods, and it is shown in Figure 2.

FIGURE 2

FIGURE 2. Theoretical framework for the approach.

Establishment of the Dynamic Fault Tree for the Digital Power Control System for Nuclear Reactor

The DFT for the DPCSNR was established by using the DFTA method, and the steps were as follows:

Step 1Identify the factors influencing the DPCSNR failure.The structure and function of the DPCSNR were investigated, and the factors influencing its failure were identified in terms of hardware, software, and human operations.

Step 2Identify the failure events resulting in the DPCSNR failure.The failure events including failure causes, failure modes, and failure consequences of the DPCSNR were identified by using the failure mode and effect analysis method, and the failure causes, failure modes, and failure consequences were defined as the basic events, intermediate events, and top events in the DFT for the DPCSNR.

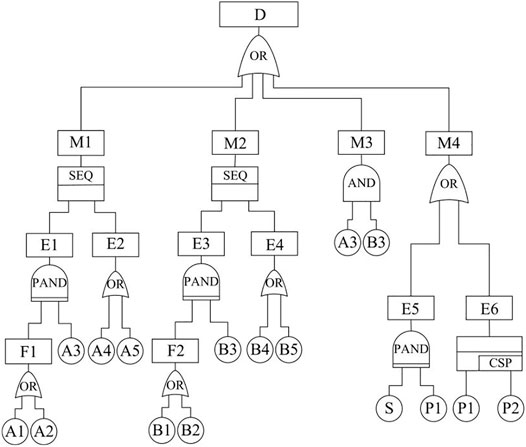
Step 3Characterize the dynamic interaction for the DPCSNR.The dynamic and static logic gates were introduced to analyze the hardware–software–human interactive behavior for the DPCSNR, and the dynamic interaction for the DPCSNR was characterized. After the analyses, the introduced dynamic logic gates included the PAND gate, FDEP gate, and cold spare (CSP) gate in spare gates, and the introduced static logic gates included AND gate and OR gate.By using the three aforementioned steps, the DFT for the DPCSNR was established, as shown in Figure 3, and the symbols and their descriptions in the figure are given in Table 1.

FIGURE 3

FIGURE 3. DFT for the DPCSNR.

TABLE 1

TABLE 1. Symbols and their descriptions in Figure 3.

Establishment of the Dynamic Bayesian Network Model for the Digital Power Control System for Nuclear Reactor

In the BN model, a node X_i is given, and it is conditionally independent of all the other nodes, except its parent and child nodes. For a two-state system with n nodes, its joint probability distribution can be determined from the following equation (Khakzad et al., 2017; Sundaramoorthy et al., 2021):

$P\left(X_1,X_2,\cdots ,X_n\right)={\displaystyle \prod _{i=1}^{n}P\left(X_i|Pa\left(X_i\right)\right)},(1)$

where $\mathit{Pa}\left({\mathit{X}}_{\mathit{i}}\right)$ represents the parent set of X_i and $\mathit{P}\left({\mathit{X}}_{\mathit{i}}|\mathit{Pa}\left({\mathit{X}}_{\mathit{i}}\right)\right)$ is the conditional probability distribution.

The DBN is an extension of the static BN in time (Hearty et al., 2009; Khakzad, 2019). By combining the static BN with time information, the transition model between two neighboring time slices for the DBN model can be established as follows (Maldonado et al., 2019):

$P\left(X_t|X_{t-1}\right)={\displaystyle \prod _{i=1}^{N}P\left(X_{t,i}|Pa\left(X_{t,i}\right)\right)},(2)$

where X_t and X_t-1 represent the nodes at time slice t and t-1, respectively; X_t,i is the i-th node in time slice t; and Pa(X_t,i) is its parent node set.

In the DBN model, the joint probability distribution of multiple time slices can be calculated from the following equation (Khakzad et al., 2016; Guo et al., 2021):

$P\left(X_{1:T}\right)={\displaystyle \prod _{i=1}^T{\displaystyle \prod _{i=1}^{N}P\left(X_t^i|pa\left(X_t^i\right)\right)}},(3)$

where $X_{1:T}=\left\{X_1,X_2,\cdots ,X_T\right\}$.

Based on the established DFT and by using the DBN and FM methods, the DBN model for the dynamic reliability assessment of the DPCSNR was established, and the steps were as follows (Mamdikar et al., 2021):

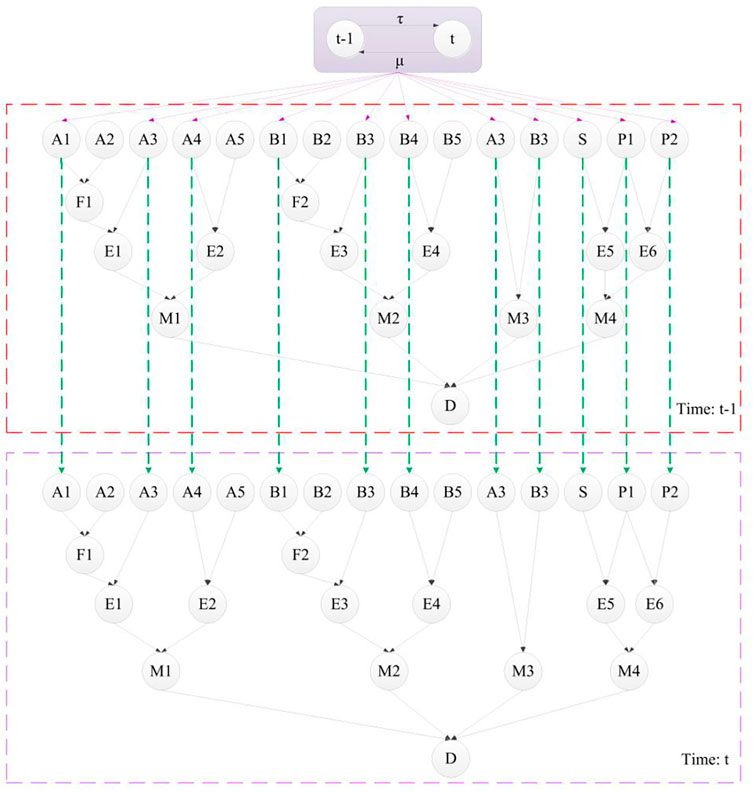
Step 1Determine the nodes and CPT in the IDBN model.Using the transformation strategy from the DFT to the DBN model, the basic events, intermediate events, and top events in the DFT for the DPCSNR were transformed as root nodes, intermediate nodes, and leaf nodes (Cai et al., 2013; Yazdi and Kabir, 2017), and the static logic gates and dynamic logic gates were transformed as CPT in the IDBN model (Liang et al., 2017).

Step 2Determine the prior probabilities for root nodes.At the initial moment, t = 0, it can be assumed that hardware for the DPCSNR was completely reliable, which indicates that their prior probabilities were 0. By referring to the probabilistic safety analysis report for the NPP (U.S. Nuclear Regulatory Commission, 2017; Gertman et al., 2005), the prior probabilities of software failures and human failures were assumed to be 0.0001 and 0.1, respectively.

Step 3Determine the state transition probabilities for root nodes.There is lack of failure rates of hardware for the DPCSNR. By referring to the probabilistic safety analysis report for the NPP (Durga Rao et al., 2009; U.S. Nuclear Regulatory Commission, 2017; Gertman et al., 2005), the operation and maintenance and reliability data for the DPCSNR, the expert experience, and the failure rates of hardware for the DPCSNR were determined, which were used to calculate the state transfer probabilities in the DBN model, as given in Table 2.It was assumed that the hardware of the DPCSNR had two states including work (W) and failure (F); they were independent, and their failure probabilities followed the exponential distribution. The probability density for hardware failures can be calculated from the following equation (Oh and Lee, 2020):

$f\left(t\right)=\tau e^{-\tau t},(4)$

where τ denotes the failure probability.The time interval between two neighboring time slices was set to 1 day (24 h). Taking the hardware failure of the MCU as an example, its state transition probabilities were calculated as follows:

$\{\begin{array}{l}P\left(X\left(t+1\right)=W|X\left(t\right)=W\right)=e^{-\tau \Delta t}=0.993064,\\ P\left(X\left(t+1\right)=F|X\left(t\right)=W\right)=1-e^{-\tau \Delta t}=0.006936,\\ P\left(X\left(t+1\right)=F|X\left(t\right)=F\right)=1,\\ P\left(X\left(t+1\right)=W|X\left(t\right)=F\right)=0,\end{array}(5)$

Similarly, the state transition probabilities for other hardware were calculated.Due to the complexity and uncertainty of software and human failures for the DPCSNR, it was assumed that their state transition probabilities were 0.

Step 4Characterize the causal relationship uncertainty.The IDBN model transformed from the DFT cannot characterize the causal relationship uncertainty for the DPCSNR. The CPT in the IDBN model should be modified.The senior experts on operation, maintenance, equipment management, reliability assessment, and probabilistic safety assessment for NPP were invited to participate in the assessment. They used their risk knowledge and experience and gave the assessment language for the causal relationship uncertainty. The triangular fuzzy number and trapezoidal fuzzy number were used to quantitatively present the assessment languages (Yazdi, 2020). The corresponding fuzzy number form and λ-cut set for the assessment language are given in Table 3.In order to eliminate the subjective influence from expert judgments as much as possible, the collected fuzzy numbers were treated using the following equations (Deng et al., 2018; Yuan et al., 2021):

$I=\frac{f_1^{\lambda }\oplus f_2^{\lambda }\oplus \cdots \oplus f_{e-1}^{\lambda }\oplus f_e^{\lambda }}{e},(6)$

${\mu }_L\left(I\right)=\frac{1}{2}\left[{\displaystyle \sum _{\lambda =0.1}^1{m}^{\lambda }\Delta \lambda }+{\displaystyle \sum _{\lambda =0}^{0.9}{m}^{\lambda }\Delta \lambda }\right],(7)$

${\mu }_R\left(I\right)=\frac{1}{2}\left[{\displaystyle \sum _{\lambda =0.1}^1{n}^{\lambda }\Delta \lambda }+{\displaystyle \sum _{\lambda =0}^{0.9}{n}^{\lambda }\Delta \lambda }\right],(8)$

$P_M=\left(1-\alpha \right){\mu }_L\left(I\right)+\alpha {\mu }_R\left(I\right),(9)$

where I denotes the average fuzzy number; e denotes the number of experts; $f_e^{\lambda }$ denotes the corresponding fuzzy number for the e-th expert assessment language; ${\mu }_L\left(I\right)$ and ${\mu }_R\left(I\right)$ denote the integral value of the inverse function of the left and right membership functions, respectively; $m^{\lambda }$ and ${\mathit{n}}^{\mathit{\lambda }}$ denote the upper and lower bounds of the λ-cut set for the fuzzy number, respectively; λ = 0, 0.1, 0.2,…, 1 and $\mathit{\Delta \lambda }$ = 0.1; $P_M$ denotes the modified conditional probability; and α denotes the optimistic coefficient. In this study, α = 0.The assessment languages given by the invited experts were collected and transformed into the form of the corresponding fuzzy numbers in Table 3, then Eqs. 6–9 were applied to obtain the modified conditional probabilities. The CPT was further modified, as given in Table 4.Through the four aforementioned steps, the DBN model for the dynamic reliability assessment of the DPCSNR was established as shown in Figure 4.

TABLE 2

TABLE 2. Failure rates of hardware for the DPCSNR.

TABLE 3

TABLE 3. Fuzzy number form and λ-cut set.

TABLE 4

TABLE 4. Modified CPT in the DBN model.

FIGURE 4

FIGURE 4. DBN model for the dynamic reliability assessment of the DPCSNR.

Monte Carlo Simulation of the Digital Power Control System for Nuclear Reactor Reliability

Previous studies show that the MC method is feasible in verifying the effectiveness of the DBN model (Lee and Choi, 2020). In this section, the MC method was used to simulate the DPCSNR reliability with MATLAB simulation software, and the steps were as follows (Abdo and Flaus, 2016):

1) Based on the failure probability distributions of root nodes (hardware) in the DBN model in Figure 4, their failure times were randomly generated. Then, the causal relationships between the nodes in the DBN model were used to judge whether the DPCSNR failed or not and to achieve its failure time.

2) The previous process was repeated until the preset number of iterations was reached.

3) The simulation results were statistically analyzed, and the reliability curve of the DPCSNR was obtained.

Results and Discussion

Reliability Calculation

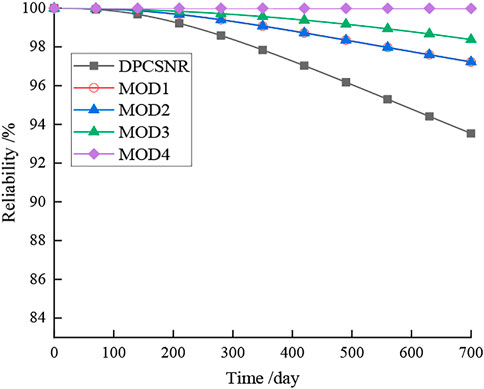
Subsystem A, subsystem B, computer systems A and B, and the power supply system were set as module 1 (MOD1), module 2 (MOD2), module 3 (MOD3), and module 4 (MOD4), respectively. GeNIe software was used to conduct the forward reasoning, and the reliability curves for the DPCSNR and its four MODs were obtained, as shown in Figure 5.

FIGURE 5

FIGURE 5. Reliability curves for the DPCSNR and its four MODs.

Figure 5 shows that the hardware failure or damage to the DPCSNR would partially reduce the reliability of the DPCSNR. Therefore, periodic test and predictive maintenance should be carried out for the DPCSNR. To be conservative, it was assumed that the cycle for the periodic test and predictive maintenance was 60 days, which indicates that the hardware maintenance rate $\mu$ was 6.94 × 10⁻⁴. Under these conditions, Eq. 5 can be modified to the following equation:

$\{\begin{array}{l}P\left(X\left(t+1\right)=W|X\left(t\right)=W\right)=e^{-\tau \Delta t}=0.993064,\\ P\left(X\left(t+1\right)=F|X\left(t\right)=W\right)=1-e^{-\tau \Delta t}=0.006936,\\ P\left(X\left(t+1\right)=F|X\left(t\right)=F\right)=e^{-\mu \Delta t}=0.98347145,\\ P\left(X\left(t+1\right)=W|X\left(t\right)=F\right)=1-e^{-\mu \Delta t}=\mathrm{0.01652855.}\end{array}(10)$

The reliability curve for the DPCSNR was further determined, as shown in Figure 6.

FIGURE 6

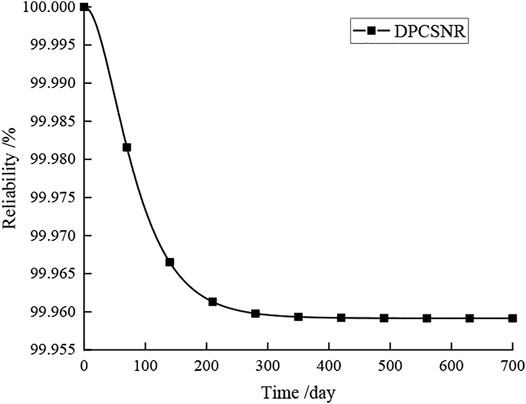
FIGURE 6. Reliability curve for the DPCSNR with the cycle for periodic test and predictive maintenance of 60 days.

In response to the requirements of the operation technical specification for the DPCSNR, it is necessary to carry out the periodic test within the specified time to check whether the system and its components are available or not. Meanwhile, the predictive maintenance for the components, which have been determined to be invalid or have potential failure through the test, is conducted. Figure 6 indicates that through the periodic test and predictive maintenance, the hardware failure or damage can be effectively avoided, and the reliability of the DPCSNR was significantly improved.

Sensitivity Analysis

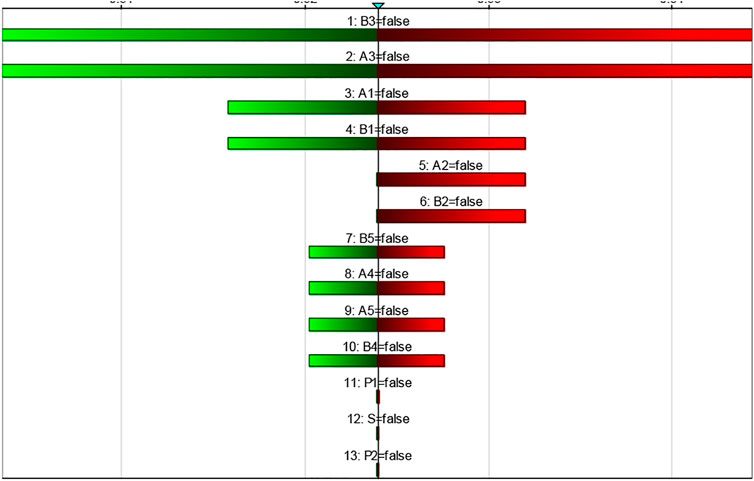
GeNIe software was used to conduct the backward reasoning, and the sensitivity analysis results for the DPCSNR were obtained, as shown in Figure 7.

FIGURE 7

FIGURE 7. Sensitivity analysis results for the DPCSNR.

It can be seen from Figure 7 that the critical events leading to the DPCSNR failure were sorted as follows in terms of their impact degrees: computer system (A3 and B3) > ACU hardware (A1 and B1) > ACU software (A2 and B2) > MCU hardware (A4 and B4) > MCU software (A5 and B5) > other hardware programs (P1, S, P2, etc.). Thus, NPP should pay attention to the critical events, in turn, so as to ensure the safety and reliability of the DPCSNR.

Analysis of Dynamic Characteristics

The first dynamic characteristic of the DPCSNR is the dynamic interaction. As shown in Figure 3, the dynamic and static logic gates were introduced to characterize this dynamic interaction. The computer system in the DPCSNR is a special component. It contains a bus selector, processor, watchdog, RAM, and digital and analog signal processing software, and they interact with each other to realize the function of the computer system. The ACU hardware and its software interact, and MCU hardware interacts with the human operation. The ACF failure in subsystems is linked with ACU failure and computer system failure through the PAND gates. The subsystem failure is connected with the ACF failure and MCU failure through the SEQ gates. The sensor failure prior to main power failure or main power and cold spare power failures will result in the loss of power supply.

The second dynamic characteristic of the DPCSNR is the time dependence. A node in the DBN model at time slice t is affected not only by its parent node but also by its parent node or itself at time slice t-1, which is presented in the joint probability distribution function in Eq. 3 (Adumene et al., 2021). In the established DBN model, the nodes of hardware failures were defined as the dynamic nodes, as shown in Figure 4. The rates of hardware failures were used to calculate their state transition probabilities, as shown in Eq. 5, and the cycle of the periodic test and predictive maintenance was used to determine the maintenance rate so as to correct the state transition probabilities, as shown in Eq. 10. The lines with arrows represent the time dependencies between neighboring time slices.

The third dynamic characteristic of the DPCSNR is the causal relationship uncertainty. The analysis of the OR gate in Figure 3 shows that when an input event occurs, the corresponding output event still has a certain probability of not occurring. For example, when the MCU hardware failure or human error occurs, MCU failure still has a certain probability of not occurring. In order to reduce the causal relationship uncertainty for the DBN model, the FM method was used to modify the CPT, as given in Table 4.

Verification of the Effectiveness of Dynamic Bayesian Network Model

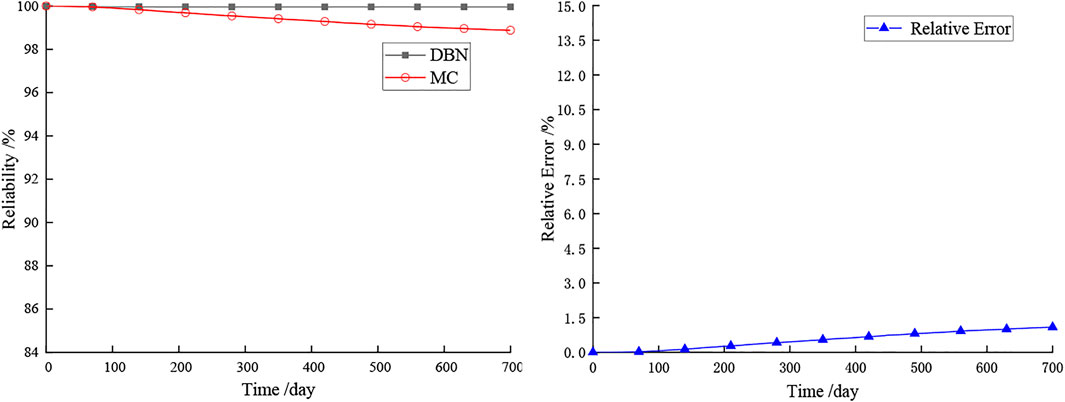
The two reliability curves of the DPCSNR were obtained by using the DBN model and MC simulation (1 × 10⁵ times), respectively. Their relative error curve was drawn in the rectangular coordinate system, and the aforementioned results are shown in Figure 8. The figure indicated that the maximum relative error was only 1.08%, and the effectiveness of the DBN model was verified.

FIGURE 8

FIGURE 8. Comparison between DBN calculation and MC simulation results.

Conclusion

This study proposed an approach for the dynamic reliability assessment of the DPCSNR with respect to its dynamic interaction, time dependence, and causal relationship uncertainty based on DFTA, DBN, FM, and MC methods.

GeNIe software was used to conduct the failure probability calculation and sensitivity analysis of the DPCSNR. The results show that without periodic tests and predictive maintenance, the reliability value of the DPCSNR is 93.531% when it runs for 700 days, and with the periodic test and predictive maintenance, the reliability value is 99.959%. In addition, the critical events for the DPCSNR were identified.

The main contributions of this study were as follows: 1) the dynamic reliability assessment approach of the DPCSNR was for proposed the first time with respect to its dynamic characteristics including dynamic interaction, time dependence, and causal relationship uncertainty; 2) the periodic test and predictive maintenance were proved to be the effective measures to improve reliability for the DPCSNR; and 3) the effectiveness of the DBN model was verified by MC simulation.

In this study, the computer system was simplified as hardware. But in practice, it is a complex system, which makes its failure rate uncertain and results in the causal relationship uncertainty between the events in the DFT. In addition, the DPCSNR has a redundant configuration, and its common causes of failures are also worthy of study. Therefore, in future work, the operation and maintenance and reliability data for the DPCSNR will be collected and analyzed, and the Dempster–Shafer evidence theory will be applied to calculate the accurate failure rate of the computer system so as to eliminate its influence on the causal relationship uncertainty. Investigation of possible common causes of failures and failure in one component that makes failure in another more likely will be carried out.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author Contributions

MG: conceptualization, methodology, and writing-review and editing. YS: supervision. RD: validation and software. SX: conceptualization and writing-review and editing. TY: financial support. JX: investigation, formal analysis, and software. BY and FM: data curation.

Conflict of Interest

YS and BY were employed by Fujian Fuqing Nuclear Power Co., Ltd. FM was employed by Hainan Nuclear Power Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors wish to acknowledge the National Natural Science Foundation of China (Nos. 52174189 and 11805094) and the Science and Technology Innovation Program of Hunan Province (No. 2020RC4053).

References

Abdo, H., and Flaus, J.-M. (2016). Monte Carlo Simulation to Solve Fuzzy Dynamic Fault Tree*. IFAC-PapersOnLine 49, 1886–1891. doi:10.1016/j.ifacol.2016.07.905

CrossRef Full Text | Google Scholar

Adumene, S., Khan, F., Adedigba, S., Zendehboudi, S., and Shiri, H. (2021). Dynamic Risk Analysis of marine and Offshore Systems Suffering Microbial Induced Stochastic Degradation. Reliability Eng. Syst. Saf. 207, 107388. doi:10.1016/j.ress.2020.107388

CrossRef Full Text | Google Scholar

Cai, B., Liu, Y., Zhang, Y., Fan, Q., Liu, Z., and Tian, X. (2013). A Dynamic Bayesian Networks Modeling of Human Factors on Offshore Blowouts. J. Loss Prev. Process Industries 26, 639–649. doi:10.1016/j.jlp.2013.01.001

CrossRef Full Text | Google Scholar

Chiacchio, F., Compagno, L., D’Urso, D., Manno, G., and Trapani, N. (2011a). “An Open-Source Application to Model and Solve Dynamic Fault Tree of Real Industrial Systems,” in 5th International Conference on Software, Knowledge Information, Industrial Management and Applications (SKIMA 2011) (Benevento, Italy: IEEE), 1–8.

CrossRef Full Text | Google Scholar

Chiacchio, F., Cacioppo, M., D'Urso, D., Manno, G., Trapani, N., and Compagno, L. (2013). A Weibull-Based Compositional Approach for Hierarchical Dynamic Fault Trees. Reliability Eng. Syst. Saf. 109, 45–52. doi:10.1016/j.ress.2012.07.005

CrossRef Full Text | Google Scholar

Chiacchio, F., Compagno, L., D'Urso, D., Manno, G., and Trapani, N. (2011b). Dynamic Fault Trees Resolution: A Conscious Trade-Off between Analytical and Simulative Approaches. Reliability Eng. Syst. Saf. 96, 1515–1526. doi:10.1016/j.ress.2011.06.014

CrossRef Full Text | Google Scholar

Deng, Y., Song, L., Zhou, J., and Wang, J. (2018). Evaluation and Reduction of Vulnerability of Subway Equipment: An Integrated Framework. Saf. Sci. 103, 172–182. doi:10.1016/j.ssci.2017.10.017

CrossRef Full Text | Google Scholar

Ding, R., Liu, Z., Xu, J., Meng, F., Sui, Y., and Men, X. (2021). A Novel Approach for Reliability Assessment of Residual Heat Removal System for HPR1000 Based on Failure Mode and Effect Analysis, Fault Tree Analysis, and Fuzzy Bayesian Network Methods. Reliability Eng. Syst. Saf. 216, 107911. doi:10.1016/j.ress.2021.107911

CrossRef Full Text | Google Scholar

Durga Rao, K., Gopika, V., Sanyasi Rao, V. V. S., Kushwaha, H. S., Verma, A. K., and Srividya, A. (2009). Dynamic Fault Tree Analysis Using Monte Carlo Simulation in Probabilistic Safety Assessment. Reliability Eng. Syst. Saf. 94, 872–883. doi:10.1016/j.ress.2008.09.007

CrossRef Full Text | Google Scholar

Gascard, E., and Simeu-Abazi, Z. (2018). Quantitative Analysis of Dynamic Fault Trees by Means of Monte Carlo Simulations: Event-Driven Simulation Approach. Reliability Eng. Syst. Saf. 180, 487–504. doi:10.1016/j.ress.2018.07.011

CrossRef Full Text | Google Scholar

Gertman, D., Blackman, H., Marble, J., Byers, J., and Smith, C. (2005). The SPAR-H Human Reliability Analysismethod, NUREG/CR-6883. Washington, DC: US Nuclear Regulatory Commission.

Google Scholar

Guo, X., Ji, J., Khan, F., Ding, L., and Tong, Q. (2021). A Novel Fuzzy Dynamic Bayesian Network for Dynamic Risk Assessment and Uncertainty Propagation Quantification in Uncertainty Environment. Saf. Sci. 141, 105285. doi:10.1016/j.ssci.2021.105285

CrossRef Full Text | Google Scholar

Hearty, P., Fenton, N., Marquez, D., and Neil, M. (2009). Predicting Project Velocity in XP Using a Learning Dynamic Bayesian Network Model. IIEEE Trans. Softw. Eng. 35, 124–137. doi:10.1109/tse.2008.76

CrossRef Full Text | Google Scholar

Ibrahim, W. Z. (2015). Assessment of Signals Reliability for Instrumentation and Control System for Nuclear Power Plants. Am. J. Sci. Technol. 2, 98–105.

Google Scholar

Jafari, M. J., Pouyakian, M., khanteymoori, A., and Hanifi, S. M. (2020). Reliability Evaluation of Fire Alarm Systems Using Dynamic Bayesian Networks and Fuzzy Fault Tree Analysis. J. Loss Prev. Process Industries 67, 104229. doi:10.1016/j.jlp.2020.104229

CrossRef Full Text | Google Scholar

Jiang, Q., Gao, D.-c., Zhong, L., Guo, S., and Xiao, A. (2020). Quantitative Sensitivity and Reliability Analysis of Sensor Networks for Well Kick Detection Based on Dynamic Bayesian Networks and Markov Chain. J. Loss Prev. Process Industries 66, 104180. doi:10.1016/j.jlp.2020.104180

CrossRef Full Text | Google Scholar

Kabir, S., and Papadopoulos, Y. (2019). Applications of Bayesian Networks and Petri Nets in Safety, Reliability, and Risk Assessments: A Review. Saf. Sci. 115, 154–175. doi:10.1016/j.ssci.2019.02.009

CrossRef Full Text | Google Scholar

Khakzad, N. (2015). Application of Dynamic Bayesian Network to Risk Analysis of Domino Effects in Chemical Infrastructures. Reliability Eng. Syst. Saf. 138, 263–272. doi:10.1016/j.ress.2015.02.007

CrossRef Full Text | Google Scholar

Khakzad, N., Landucci, G., and Reniers, G. (2017). Application of Dynamic Bayesian Network to Performance Assessment of Fire protection Systems during Domino Effects. Reliability Eng. Syst. Saf. 167, 232–247. doi:10.1016/j.ress.2017.06.004

CrossRef Full Text | Google Scholar

Khakzad, N. (2019). Modeling Wildfire Spread in Wildland-Industrial Interfaces Using Dynamic Bayesian Network. Reliability Eng. Syst. Saf. 189, 165–176. doi:10.1016/j.ress.2019.04.006

CrossRef Full Text | Google Scholar

Khakzad, N., Reniers, G., Abbassi, R., and Khan, F. (2016). Vulnerability Analysis of Process Plants Subject to Domino Effects. Reliability Eng. Syst. Saf. 154, 127–136. doi:10.1016/j.ress.2016.06.004

CrossRef Full Text | Google Scholar

Lee, D., and Choi, D. (2020). Analysis of the Reliability of a Starter-Generator Using a Dynamic Bayesian Network. Reliability Eng. Syst. Saf. 195, 106628. doi:10.1016/j.ress.2019.106628

CrossRef Full Text | Google Scholar

Liang, X. F., Wang, H. D., Yi, H., and Li, D. (2017). Warship Reliability Evaluation Based on Dynamic Bayesian Networks and Numerical Simulation. Ocean Eng. 136, 129–140. doi:10.1016/j.oceaneng.2017.03.023

CrossRef Full Text | Google Scholar

Lu, J.-J., Huang, H.-H., and Chou, H.-P. (2015). Evaluation of an FPGA-Based Fuzzy Logic Control of Feed-Water for ABWR under Automatic Power Regulating. Prog. Nucl. Energ. 79, 22–31. doi:10.1016/j.pnucene.2014.10.010

CrossRef Full Text | Google Scholar

Maldonado, A. D., Uusitalo, L., Tucker, A., Blenckner, T., Aguilera, P. A., and Salmerón, A. (2019). Prediction of a Complex System with Few Data: Evaluation of the Effect of Model Structure and Amount of Data with Dynamic Bayesian Network Models. Environ. Model. Softw. 118, 281–297. doi:10.1016/j.envsoft.2019.04.011

CrossRef Full Text | Google Scholar

Mamdikar, M. R., Kumar, V., and Singh, P. (2021). Dynamic Reliability Analysis Framework Using Fault Tree and Dynamic Bayesian Network : A Case Study of NPP. Nucl. Eng. Technol. 54, 1213. doi:10.1016/j.net.2021.09.038

CrossRef Full Text | Google Scholar

Manno, G., Chiacchio, F., Compagno, L., D'Urso, D., and Trapani, N. (2014). Conception of Repairable Dynamic Fault Trees and Resolution by the Use of RAATSS, a Matlab Toolbox Based on the ATS Formalism. Reliability Eng. Syst. Saf. 121, 250–262. doi:10.1016/j.ress.2013.09.002

CrossRef Full Text | Google Scholar

Marquez, D., Neil, M., and Fenton, N. (2008). “Solving Dynamic Fault Trees Using a New hybridBayesian Network Inference Algorithm,” in Proceeding of IEEE the 16th med-iterranean conference on control and automation, Ajaccio, France, 609–614. doi:10.1109/med.2008.4602222

CrossRef Full Text | Google Scholar

Marquez, D., Neil, M., and Fenton, N. (2010). Improved Reliability Modeling Using Bayesian Networks and Dynamic Discretization. Reliability Eng. Syst. Saf. 95, 412–425. doi:10.1016/j.ress.2009.11.012

CrossRef Full Text | Google Scholar

Neil, M., and Marquez, D. (2012). Availability Modelling of Repairable Systems Using Bayesian Networks. Eng. Appl. Artif. Intelligence 25, 698–704. doi:10.1016/j.engappai.2010.06.003

CrossRef Full Text | Google Scholar

Nguyen, T. P. K., Beugin, J., and Marais, J. (2015). Method for Evaluating an Extended Fault Tree to Analyse the Dependability of Complex Systems: Application to a Satellite-Based Railway System. Reliability Eng. Syst. Saf. 133, 300–313. doi:10.1016/j.ress.2014.09.019

CrossRef Full Text | Google Scholar

Nie, G., Yang, H., Pan, Y., Liu, Y., and Zhe, L. (2020). “Research on the Technology to Build Safety Integration Model of Complex System Based on Relevant Failure,” in 2020 Asia-Pacific International Symposium on Advanced Reliability and Maintenance Modeling (APARM), 1–7.

Google Scholar

Oh, C., and Lee, J. I. (2020). Real Time Nuclear Power Plant Operating State Cognitive Algorithm Development Using Dynamic Bayesian Network. Reliability Eng. Syst. Saf. 198, 106879. doi:10.1016/j.ress.2020.106879

CrossRef Full Text | Google Scholar

Shukla, D. K., and Arul, A. J. (2017). “Development of Smart Component Based Framework for Dynamic Reliability Analysis of Nuclear Safety Systems,” in Int Conf Fast React Relat Fuel Cycles Next Gener Nucl Syst Sustain Dev, 603.

Google Scholar

Shukla, D. K., and John Arul, A. (2020). “A Review of Recent Dynamic Reliability Analysis Methods and a Proposal for a Smart Component Methodology,” in Reliability, Safety and Hazard Assessment for Risk-Based Technologies. Editors P. V. Varde, R. V. Prakash, and G. Vinod (Singapore: Springer), 267–291. doi:10.1007/978-981-13-9008-1_22

CrossRef Full Text | Google Scholar

Sundaramoorthy, A. S., Valluru, J., and Huang, B. (2021). Bayesian Network Approach to Process Data Reconciliation with State Uncertainties and Recycle Streams. Chem. Eng. Sci. 246, 116996. doi:10.1016/j.ces.2021.116996

CrossRef Full Text | Google Scholar

Tao, Y., and Lu, L. (2013). Risk-informed Maintenance for Non-coherent Systems. Proc. Annu. Reliab Maintainab Symp. 10, 1–6. doi:10.1109/rams.2013.6517648

CrossRef Full Text | Google Scholar

U.S. Nuclear Regulatory Commission (2017). Industry-average Performance for Components and Initiating Events at U.S. Proceedings of the Commercial Nuclear Power Plants, NUREG/CR-6928, Initiating Event Data Sheets (2015 Update). Washington, DC: US Nuclear Regulatory Commission.

Google Scholar

Vinod, G., Santosh, T. V., Saraf, R. K., and Ghosh, A. K. (2008). Integrating Safety Critical Software System in Probabilistic Safety Assessment. Nucl. Eng. Des. 238, 2392–2399. doi:10.1016/j.nucengdes.2008.02.028

CrossRef Full Text | Google Scholar

Wang, C., Xia, Y., Wang, D., Niu, Z., Liu, Y., and Yu, C. (2021). Dynamic Risk Assessment of Deep-Water Dual Gradient Drilling with SMD System Using an Uncertain DBN-Based Comprehensive Method. Ocean Eng. 226, 108701. doi:10.1016/j.oceaneng.2021.108701

CrossRef Full Text | Google Scholar

Wang, H., Tian, C., Zhou, S., Liu, Y. Y., and Shahroze, A. (2016). Reliability Analysis of the Automatic Control System of Reactor Power in Nuclear Power Plant Based on DFM. Int. Conf. Nucl. Eng. 4, 1–9.

Google Scholar

Yazdi, M. (2020). A Question on Using Fuzzy Set. Theor. Its Extensions Saf. Reliability 06, 203–209.

Google Scholar

Yazdi, M., and Kabir, S. (2017). A Fuzzy Bayesian Network Approach for Risk Analysis in Process Industries. Process Saf. Environ. Prot. 111, 507–519. doi:10.1016/j.psep.2017.08.015

CrossRef Full Text | Google Scholar

Yazdi, M., Kabir, S., and Walker, M. (2019). Uncertainty Handling in Fault Tree Based Risk Assessment: State of the Art and Future Perspectives. Process Saf. Environ. Prot. 131, 89–104. doi:10.1016/j.psep.2019.09.003

CrossRef Full Text | Google Scholar

Yuan, C., Hu, Y., Zhang, Y., Zuo, T., Wang, J., and Fan, S. (2021). Evaluation on Consequences Prediction of Fire Accident in Emergency Processes for Oil-Gas Storage and Transportation by Scenario Deduction. J. Loss Prev. Process Industries 72, 104570. doi:10.1016/j.jlp.2021.104570

CrossRef Full Text | Google Scholar

Zarei, E., Yazdi, M., Abbassi, R., and Khan, F. (2019). A Hybrid Model for Human Factor Analysis in Process Accidents: FBN-HFACS. J. Loss Prev. Process Industries 57, 142–155. doi:10.1016/j.jlp.2018.11.015

CrossRef Full Text | Google Scholar

Zhou, S. L., Jiang, R. T., and Liu, Y. Y. (2014). “Reliability Assessment of Nuclear Power Plant Digital Instrumentation and Control System I: Challenges and Research Status of Reliability Assessment Methodology,” in Control and Decision Conference (2014 CCDC) (Changsha, China: IEEE), 1773–1778.

Google Scholar