Robust Unit Commitment for Minimizing Wind Spillage and Load Shedding With Optimal DPFC

The distributed power flow controller (DPFC) has a positive effect of UC problem on the network side based on its ability to manage capacity of power flow. This study presents a novel two-stage robust model to optimize the status of the generator and location–allocation of the DPFC, while simultaneously considering wind and load uncertainties. The column-and-constraint generation (CCG) method is utilized to solve the two-stage problem into the master problem and the subproblem iteratively. The optimal status of the generator and location of the DPFC can be easily obtained with the master problem, and the dispatch solution and compensation level of the DPFC are solved in the subproblem. We conduct the IEEE 24 bus system to verify the performance of the proposed procedure. There are effects on wind spillage/load shedding and generator dispatch scheduling planning once the DPFC is injected. Detailed simulation results illustrate the effect of the proposed approach.

1 Introduction

Over the last decade, the penetration of wind power is gradually increasing as the load diversity changes (Yang et al., 2021a). However, the inherent fluctuation of wind power and load also constrains the operating economy and safety of the unit commitment problem (UC) with the long-distance power transmission (Milligan et al., 2009). On the other hand, the flexible AC transmission system (FACTS) device can enhance the flexibility of the network side, which also affects the operating conditions (Yuan et al., 2010). The DPFC is derived from the UPFC, which will be the most powerful tools in the FACTS. It has the same external characteristics as that of the UPFC and has advantage over the transmission corridors, investment, and replaceability (Khanchi and Garg, 2013; Dai et al., 2019; Tang et al., 2020).

Generally, the flexible operating principle of the major UC problem is divided into three categories: source side, demand side, and network side. In the source and demand sides, various research methods have been studied in the UC problem to enhance the operating flexibility by tackling uncertain parameters such as stochastic optimization (SO), robust optimization (RO), and information gap decision theory (IGDT). All these methods focus on tackling the uncertainty parameters such as wind or load uncertainties. The SO optimizes the dispatch problem with various scenarios considering uncertainty samples, which can enforce the dispatch scheduling feasibility. Wang et al. (2012) and Nandi et al. (2022a) present a stochastic UC model considering the uncertainty of demand response (DR) to improve the overall social welfare, where the uncertainty of DR is functioned as the chance constrained form. Zhao et al. (2014); Nandi and Kamboj (2021); Nandi et al. (2022b); and Kamboj et al. (2022) evaluate the wind utilization in the UC problems, where the wind uncertainty is also solved by the stochastic chance constraint. Wu et al. (2019) formulated a two-stage dispatch model considering network congestion with the chance-constrained forms of wind and DR uncertainties. Dvorkin et al. (2014) presented a stochastic rolling UC model to evaluate the operating cost, considering wind spillage and load not served, where the wind is constrained by the chance-constrained form and the load is depicted as its stochastic interval form. Obviously, there are two drawbacks: the computational efficiency decreases rapidly as the scenarios increase, and the probability distribution function (PDF) is hard to obtain accurately (Shen and Raksincharoensak, 2021a; Shen and Raksincharoensak, 2021b; Shen et al., 2021; Shen et al., 2022). There is no need to obtain the exact PDF of uncertain parameters in the RO method, and only its uncertainty boundary is offered to describe the fluctuation of the uncertain parameters. An and Zeng (2014) explore the wind uncertainty by formulating a “min–max–min” robust model to research the dispatch problem, and the result verifies the effectiveness of optimal scheduling to incorporate the wind. In the work carried out by Gangammanavar et al. (2015), the worst scenarios of uncertain wind is well-distinguished with the deterministic load. In the study by Zhang et al. (2017), the authors researched the coordination of DG and elastic-price DR scheduling with uncertainty in the microgrid, which is solved by the CCG algorithm. Wang et al. (2016) propose an adjustable robust model of the building energy system to optimize the social welfare, where the PV output and load demands are uncertain. Zhao et al. (2013) assumed that the connection between elastic electricity price and load demand fluctuates within a certain range, derived the uncertainty set for demand response, and then proposed a two-stage robust model with interval sets to depict the uncertain parameters. Zhang et al. (2016) developed a robust model coordinating the energy storage system and direct-load control (DLC) considering uncertainties, which the generation/wind/PV/ESS and DLC scheduling planning satisfy for any realization of uncertainty. Based on the aforementioned research, the two-stage model for the RO method to deal with the uncertainty is mainly important in two directions. On the one hand, the reserve capacity in the first stage is optimized to adapt to the fluctuation of the uncertain parameters in the second stage, and on the other hand, the uncertain parameters are directly optimized in the second stage to ensure power balance. The conservation of the RO method challenges the operating cost of the system dispatch, where the extreme worst scenario hardly appears (Yang et al., 2021a; Yang et al., 2021b; Li et al., 2021; Yang et al., 2022a; Yang et al., 2022b). The IGDT method aims to search for the adjustable bound of uncertain parameters based on its stochastic model and robust model, which satisfy the objective function in the predefined interval. The IGDT overcomes the difficulties of acquiring distribution function in the SO problem and reduces the conservation of the RO problem. Thus, the computational time of IGDT is much lower than that of the RO and SO methods, and the conservation is also improved obviously. This approach is widely used in dealing with the uncertainty of renewable energy (Nikoobakht and Aghaei, 2017; Ahmadi et al., 2018), energy system (Ahmadi et al., 2019; Khajehvand et al., 2021), electrical vehicles (Rabiee et al., 2014), and other loads (Ahrabi et al., 2021). Nikoobakht and Aghaei (2017 present a robust model to solve the SCUC problem considering wind uncertainty; the wind absorption is optimized with flexible resources. Ahmadi et al. (2019) formulate the UC problems with the ESS uncertainty to improve the optimal capacity of ESS. A linear model by Rabiee et al. (2014); Ahrabi et al. (2021) is established to evaluate the effect of load uncertainty to the dispatch scheduling based on its stochastic model.

Although the FACTS has an advantage over the flexibility of the network side, few studies have been proposed to investigate its impacts on operating performance. Ziaee et al. (2017) optimized the TCSC device to improve the absorption of wind based on the stochastic method, evaluating the positive effect of wind spillage and considering optimal location and allocation of TCSC simultaneously. Nasri et al. (2014) formulate a two-stage model to minimize wind spillage and load shedding considering optimal TCSC with a fixed scenario. All these research studies focus on a single-time phase sample, which only indicates the aspects of improving operating safety considering the optimization of the FACTS. There are several studies which focus on the areas of the UC problem, where the FACTS location is predefined. Li et al. (2018) investigate the effect of the UPFC to the operating cost with a fixed wind scenario. Sang et al. (2017) reduced the wind spillage by optimizing the location–allocation of TCSC considering various wind scenarios. Considering the past research studies, there is no evidence of evaluating the inter-connection between the generator status and optimal FACTS. At the same time, there is no research study on the robust UC problem considering the optimal FACTS, which may be the best way to locate the FACTS successfully.

This study develops a two-stage robust model with optimal DPFC based on its PIM model considering wind and load uncertainties, which can not only hold the internal characteristics of multiple DPFCs but also enforce the feasible horizon with the uncertain parameters. We solve the status of generators and location of the DPFC in the master problem and obtain the dispatch solution and compensation level of the DPFC in the subproblem. The main contribution in this study can be summarized as follows:

1) The DPFC scheduling planning maintains the consistence, which is easy to adopt for the uncertain environments based on the proposed model.

2) A robust UC model with a flexible FACTS on the network side is presented, which is solved by the CCG algorithm.

3) A detailed experiment with different numbers of DPFCs has been presented to evaluate the impacts of the DPFC to the generator scheduling, wind absorption, and load supplies.

We demonstrate the effectiveness of the proposed two-stage robust dispatch problem in the IEEE 24 bus system and provide insight into the influence on the performance of the DPFC. This article is organized as follows: Section 2 introduces the power injection model of the DPFC and a relaxed AC-SOCP power flow model. Section 3 presents the two-stage robust model of the optimal location–allocation problem. Section 4 describes the procedure of the CC&G method. Section 5 shows the results and discussion, while the conclusion is represented in Section 6.

2 Power Injection Model of Distributed Power Flow Controller

2.1 Distributed Power Flow Controller Configuration and Principle

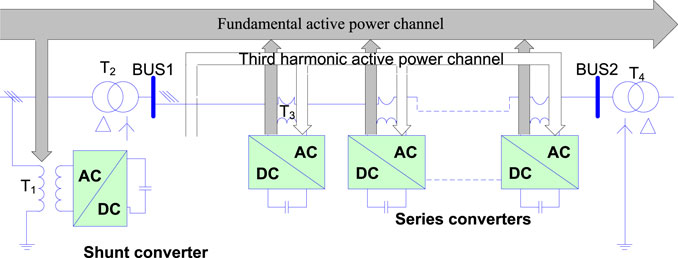
The general structure of the DPFC device includes the series side and shunt side. In the series side, there are many distributed converters cascaded to offer its control capabilities to manage the power flow on the network side. There are huge capacity shunt converters injected in the bus. There is power flow exchange by the fundamental wave and third harmonic wave through the series/shunt converters. The structure and operating principle is shown in Figure 1.

FIGURE 1

FIGURE 1. Configuration and principle of the DPFC

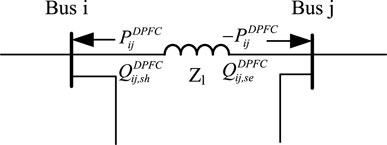
There is high similarity in the external characteristics between the UPFC and DPFC. However, the DPFC involves only active power transferable from the shunt side to the series side, which can reduce the power loss. Thus, a power injection model (PIM), which is introduced by the UPFC, can be modified as depicted in Figure 2

$\begin{array}{l}{P}_{ij}^{\ast }=P_{ij}-P_{ij}^{DPFC},\\ P_{ij,rev}^{\ast }=P_{ij,rev}+P_{ij}^{DPFC},\\ Q_{ij,sh}^{DPFC}=0;Q_{ij,se}^{DPFC}=0;\end{array}(1)$

where $P_{ij},P_{ij,rev}$ is the line power or reverse line power and $P_{ij}^{DPFC}$ is the DPFC compensation level.

FIGURE 2

FIGURE 2. PIM model of the DPFC.

2.2 Relaxed AC-SOCP Model

The traditional line flow (Le et al., 2021; Toyoda and Wu*, 2021; Wu et al., 2021) is modeled as shown in Eq. 2. Obviously, the nonlinear model is nonconvex.

$\begin{array}{l}{P}_{ij}\left(\theta ,V\right)=V_i^2{g}_{ij}-V_i{V}_j(g_{ij}\cos ({\theta }_i-{\theta }_j)+b_{ij}\sin ({\theta }_i-{\theta }_j)).\\ Q_{ij}(\theta ,V)=-V_i^2{b}_{ij}-V_m{V}_n(g_{ij}\sin ({\theta }_i-{\theta }_j)-b_{ij}\cos ({\theta }_i-{\theta }_j)).\end{array}(2)$

To tackle the nonconvex and nonlinear difficulties of the traditional model, we introduce several relax variables to the convex model, which are shown in Eqs 3–5

$U_i=V_i^2;U_j=V_j^2.(3)$

$R_{ij}=U_i{U}_{j}cos({\theta }_i-{\theta }_j);R_{ij}\ge 0.(4)$

$T_{ij}=U_i{U}_{j}sin({\theta }_i-{\theta }_j).(5)$

Hence, the traditional model can be rewritten as shown in Eq. 6, which is a linear model and easily solved.

$\begin{array}{l}{P}_{ij}=g_{ij}{U}_i-g_{ij}{R}_{ij}-b_{ij}{T}_{ij}\\ Q_{ij}=-b_{ij}{U}_i-g_{ij}{T}_{ij}+b_{ij}{R}_{ij}\\ P_{ij,rev}=g_{ij}{U}_j-g_l{R}_{ij}+b_{ij}{T}_{ij}\\ Q_{ij,rev}=-b_{ij}{U}_j+g_{ij}{T}_{ij}+b_{ij}R{.}_{ij}\end{array}(6)$

However, there are connections between $R_{ij}$ and $T_{ij}$ in the original model, which can represented as

$R_{ij}^2+T_{ij}^2=V_i^2{V}_j^2=U_i{U}_j.(7)$

There are bilinear variable terms in the aforementioned equation, which is still nonlinear. By relaxing the tight equality constraint into an inequality one, we can transform the representation into an SOCP form.

${\Vert \begin{array}{c}2R_{ij}\\ 2T_{ij}\\ U_i-U_j\end{array}\Vert }_2\le U_i+U_j.(8)$

An SOCP power flow model can be easily constructed by Eqs 6, 8, which can be easily solved by CPLEX due to its convexity.

3 Robust Model With the Optimal Distributed Power Flow Controller

The power system planners aim to determine the location–allocation of the DPFC considering wind and load uncertainties, which can enhance the management efficiency of power flow and decrease the investment of the DPFC. However, the operators desire to minimize the operation cost of injected DPFCs and improve the operating level of the system. Therefore, optimal location–allocation of the DPFC in the power system must consider the operational cost, investment of installing the DPFC, curtailment of wind spillage, and load shedding. The optimal model is represented by Eqs 9–23

$\begin{array}{l}min{\displaystyle \sum _t{\displaystyle \sum _{i\in G_i}[S{U}_i+S{D}_i+c_{g,i}{P}_{i,t}^G]}}+{\displaystyle \sum _t{\displaystyle \sum _{ij\in G_{ij}}{\pi }^{DPFC}{P}_{ij}^{DPFC}}}\\ +{\displaystyle \sum _t{\displaystyle \sum _{i\in G_w}{M}^{Curt}{P}_{i,t}^{W,curt}}}+{\displaystyle \sum _t{\displaystyle \sum _{i\in G_{nb}}{M}^{shed}{P}_{i,t}^{D,shed}}}\end{array}(9)$

$\{\begin{array}{l}S{U}_i\ge C_i^{su}{u}_{i,t}\\ S{D}_i\ge C_i^{sd}{v}_{i,t}\end{array}(10)$

$\{\begin{array}{l}{u}_{i,t}-v_{i,t}=I_{i,t}-I_{i,t-1}\\ u_{i,t}+v_{i,t}\le 1\end{array}(11)$

$\{\begin{array}{l}{\displaystyle \sum _{h=0}^{T_i^{on}+h-1}{I}_{i,t}}\ge T_i^{on}(I_{i,t}-I_{i,t-1})\\ {\displaystyle \sum _{h=0}^{T_i^{off}+h-1}{I}_{i,t}}\ge T_i^{off}(I_{i,t-1}-I_{i,t})\end{array}(12)$

$\begin{array}{l}{I}_{i,t}{P}_{i,t}^{G,min}\le P_{i,t}^G\le I_{i,t}{P}_{i,t}^{G,max}\\ I_{i,t}{Q}_{i,t}^{G,min}\le Q_{i,t}^G\le I_{i,t}{Q}_{i,t}^{G,max}\end{array}(13)$

$\begin{array}{l}{P}_{i,t}^G-P_{i,t-1}^G\le (2-I_{i,t}-I_{i,t-1})I_{i,t}{P}_{i,t}^{G,min}+(1+I_{i,t-1}-I_{i,t})R{U}_i\\ P_{i,t-1}^G-P_{i,t}^G\le (2-I_{i,t}-I_{i,t-1})I_{i,t}{P}_{i,t}^{G,min}+(1-I_{i,t-1}+I_{i,t})R{D}_i\\ \end{array}(14)$

$\begin{array}{l}{P}_{i,t}^G-{\displaystyle \sum _{j\in \psi \left(i\right)}{P}_{ij}}-{\displaystyle \sum _{j\in \varphi \left(i\right)}{P}_{ij,rev}}+{\displaystyle \sum _{l\in \psi \left(i\right)}{P}_{ij}^{DPFC}}-{\displaystyle \sum _{l\in \varphi \left(i\right)}{P}_{ij}^{DPFC}}-P_{i,t}^{W,shed}+P_{i,t}^{D,curt}=P_{i,t}^D+P_{i,t}^{D,u}-P_{i,t}^W\\ Q_{i,t}^G-{\displaystyle \sum _{j\in \psi \left(i\right)}{Q}_{ij}}-{\displaystyle \sum _{j\in \varphi \left(i\right)}{Q}_{ij,rev}}-Q_{i,t}^{W,curt}+Q_{i,t}^{D,curt}=Q_{i,t}^D+Q_{i,t}^{D,u}-Q_{i,t}^W\end{array}(15)$

$\begin{array}{l}0\le P_{i,t}^{D,shed}\le P_{i,t}^D+P_{i,t}^{D,u}\\ 0\le Q_{i,t}^{D,shed}\le Q_{i,t}^D+Q_{i,t}^{D,u}\\ \end{array}(16)$

$\begin{array}{l}0\le P_{i,t}^{W,curt}\le P_{i,t}^W\\ 0\le Q_{i,t}^{W,curt}\le 0.95\ast P_{i,t}^W\\ \end{array}(17)$

$\begin{array}{l}0\le P_{ij,t}^{DPFC}\le {\delta }_{ij,t}{P}_{DPFC}^{max}\\ {\displaystyle \sum _{ij}{\delta }_{ij,t}\le }{\alpha }_L\end{array}(18)$

${\Vert \begin{array}{c}{P}_{ij}-P_{ij}^{DPFC}\\ Q_{ij}\end{array}\Vert }_2\le S_{ij}(19)$

${\Vert \begin{array}{c}{P}_{ij,rev}+P_{ij}^{DPFC}\\ Q_{ij,rev}\end{array}\Vert }_2\le S_{ij}(20)$

$\begin{array}{l}{T}_{ij}\approx {\theta }_i-{\theta }_j\\ \{\begin{array}{l}{P}_{ij}=g_{ij}{U}_i-g_{ij}{R}_{ij}-b_{ij}{T}_{ij}\\ Q_{ij}=-b_{ij}{U}_i-g_{ij}{T}_{ij}+b_{ij}{R}_{ij}\\ P_{ij,rev}=g_{ij}{U}_j-g_l{R}_{ij}+b_{ij}{T}_{ij}\\ Q_{ij,rev}=-b_{ij}{U}_j+g_{ij}{T}_{ij}+b_{ij}{R}_{ij}\end{array}\\ {\Vert \begin{array}{c}2R_{ij}\\ 2T_{ij}\\ U_i-U_j\end{array}\Vert }_2\le U_i+U_j\end{array}(21)$

$\begin{array}{l}{\theta }_i^{min}\le {\theta }_i\le {\theta }_i^{max}\\ \end{array}(22)$

${\left(V_i^{min}\right)}^2\le U_i\le {\left(V_i^{max}\right)}^2.(23)$

The objective function is to minimize the generation cost, investment cost of the DPFC, and curtailment of wind spillage and load shedding as shown in Eq. 9. Eq. 10 constrains the start-up and shut down cost of the thermal unit; Eq. 11 distinguishes the operating state from the start-up and shut down state of generators. The minimum ON/OFF time limits are shown in Eq. 12, the active and reactive output of generators is limited in Eqs 13, 14 and shows the ramp-up and ramp-down limitation of thermal units. The active and reactive power balance is depicted in Eq. 15. Eqs 16–18 constrain wind spillage, load shedding, and location–allocation of the DPFC. The transmission network security constraint is formulated in Eqs 19–20 with line forward and reverse power flow. The relaxed AC-SOCP power flow model is introduced in Eqs 21–23.

The formulated MISOCP problem aims to improve the operating level with optimal location and ratings of the DPFC. However, there are uncertainties of wind and load, as shown in Eqs 24–25.

$P_{i,t}^{DR}=\left\{P_{i,t}^{DR}|P_{i,t}^{DR}\in [P_{i,t}^{DR,F}-{\mu }_{i,t}^{DR}△P_{i,t}^{DR},P_{i,t}^{DR,F}+{\mu }_{i,t}^{DR}△P_{i,t}^{DR}],{\mu }_{i,t}^{DR}\in \left\{\mathrm{0,1}\right\}\right\}.(24)$

$P_{i,t}^W=\left\{P_{i,t}^W|P_{i,t}^W\in [P_{i,t}^{W,F}-{\mu }_{i,t}^W△P_{i,t}^W,P_{i,t}^{W,F}+{\mu }_{i,t}^W△P_{i,t}^W],{\mu }_{i,t}^W\in \left\{\mathrm{0,1}\right\}\right\}.(25)$

Once the DPFC is injected into the grid, the device should offer its functions considering the uncertainty circumstance of wind-load with fixed locations. We developed a two-stage robust approach to obtain the robust dispatch solutions with the PIM model of the DPFC, which can easily adapt to the uncertain environment. The robust model is shown as

$\begin{array}{l}min{\displaystyle \sum _t{\displaystyle \sum _{i\in G_i}[S{U}_{i,t}+S{D}_{i,t}]}}+maxmin[{\displaystyle \sum _t{\displaystyle \sum _{i\in G_i}{c}_{g,i}{P}_{i,t}^G}}+{\displaystyle \sum _t{\displaystyle \sum _{i\in G_i}{\pi }^{DPFC}{P}_{ij}^{DPFC}}}.\\ +{\displaystyle \sum _t{\displaystyle \sum _{i\in G_i}{M}^{Curt}{P}_{i,t}^{W,curt}}}+{\displaystyle \sum _t{\displaystyle \sum _{i\in G_i}{M}^{shed}{P}_{i,t}^{D,shed}}}].\\ s.t.\{\begin{array}{l}\left(10\right)-\left(23\right)\\ \left(24\right)-\left(25\right)\end{array}\end{array}(26)$

4 Two-Stage Robust Unit Commitment and Column-and-Constraint Generation Method

The column-and-constraint generation method is introduced to solve the proposed two-stage robust problem (Zeng and Zhao, 2013). For simplicity, the robust problem can be reformulated in the following compact matrix form:

$\begin{array}{l}\underset{x}{min}{c}^{T}x+\underset{\lambda }{max}\underset{y}{min}{d}^{T}y+e^T\lambda .\\ s.t.Ax\le b,x\in \left\{\mathrm{0,1}\right\}.\\ Y=\left\{y|\begin{array}{l}Cy\le f\\ Gx+Dy\le g\\ Ey=\lambda \\ {\Vert Q_{i}y+q_i\Vert }_2\le h_{i}y+d_i,i=1,\mathrm{...},n\end{array}\right\}.\end{array}(27)$

The objective described in (27) corresponds to constraint (26), which is modeled in a “min–max–min” optimization form. The outer “min” is to minimize the start-up and shut down costs of generators considering the optimal locations of the DPFC; the decision variable $\left\{x\right\}$ is a binary variable, which represents the state variables including the thermal generator operating state and optimal locations of the DPFC. The “max” is to find the worst uncertainty scenario under the uncertainty circumstance; the decision variable $\left\{\lambda \right\}$ refers the wind and load operating level, which is shown in Eqs 24–25. The inner “min” is to obtain the solutions under the worst uncertainty case; the decision variable $\left\{y\right\}$ represents the continuous variables in the second stage, which is described in Eqs 13–23. It can be observed that the decision variable $\left\{\lambda \right\}$ is optimized in the second stage by maximizing the minimal second stage costs, which can easily improve the robustness.

The details of the CC&G method are shown as follows:

Master Problem

$\begin{array}{l}\underset{x}{min}{c}^{T}x+\eta .\\ \{\begin{array}{l}Ax\le b\\ \eta \ge d^T{y}_l^{\ast }+e^T{\lambda }_l^{\ast }\text{. }\\ C{y}_l^{\ast }\le f\\ D{y}_l^{\ast }\le g-G{x}^{\ast }\\ E{y}_l^{\ast }={\lambda }_l^{\ast }\\ {\Vert Q_i{y}_l^{\ast }+q_i\Vert }_2\le h_{i}y+d_i,i=1,\mathrm{...},n\\ l\in \left\{1,\mathrm{...},m\right\}\end{array}\end{array}(28)$

The master problem is optimized to obtain the first-stage decision under various worst-case scenarios, which is duplicated from the subproblem. Obviously, the master problem provides the lower bound of the original problem.

For a given first-stage decision variable $\left\{x\right\}$, the subproblem can be formulated as follows. The SP is aimed to obtain the optimal dispatch solutions with uncertainty. This can provide an upper bound of the original problem.

Subproblem

$\begin{array}{l}\underset{\lambda }{max}\underset{y}{min}{d}^{T}y+e^T\lambda .\\ \{\begin{array}{l}Cy\le f\left({\gamma }_1\right)\\ Gx+Dy\le g\left({\gamma }_2\right)\\ Ey=\lambda \left({\gamma }_3\right)\\ {\Vert Q_{i}y+q_i\Vert }_2\le h_{i}y+d_i,i=1,\mathrm{...},n({\gamma }_4,{\gamma }_5)\end{array}.\end{array}(29)$

The aforementioned “max–min” problem can be transformed by the dualization method, which can be easily solved. The convert procedure is shown in Eq. 30.

$\begin{array}{l}\max f^T{\gamma }_1+(g^T-G^T{x}^{\ast }){\gamma }_2+{\lambda }^T{\gamma }_3-{\displaystyle \sum _{i=1}^n(q_i^T{\gamma }_4+d_i^T{\gamma }_5)}.\\ \{\begin{array}{l}{C}^T{\gamma }_1+D^T{\gamma }_2+E^T{\gamma }_3+{\displaystyle \sum _{i=1}^n(Q_i^T{\gamma }_4+h_i^T{\gamma }_5)}=d\\ {\Vert {\gamma }_4\Vert }_2\le {\gamma }_5\\ {\gamma }_1\le 0;{\gamma }_2\le 0;{\gamma }_4\le 0;{\gamma }_3:free;{\gamma }_5\ge 0;\\ \lambda \in \left\{\begin{array}{c}{d}_{i,t}\\ g_{i,t}\end{array}|\begin{array}{c}{d}_{i,t}^{min}\le d_{i,t}\le d_{i,t}^{max}\\ g_{i,t}^{min}\le g_{i,t}\le g_{i,t}^{max}\end{array}\right\}\end{array}.\end{array}(30)$

It is clearly observed that there is a bilinear term $\left\{{\lambda }^T{\gamma }_3\right\}$ in the subproblem, which is hard to solve. According to Li et al. (2018), all the optimal solutions with uncertainties can be obtained at its extreme points. This reminds us to convert the bilinear term to linear ones by introducing the Big-M method. We can introduce a binary variable, which can easily convert the uncertainty interval optimization into boundary point optimization.

The extreme points of uncertainty can be formulated as follows:

${\lambda }^T{\gamma }_3={\lambda }_{i,t}^{min}{\gamma }_3+({\lambda }_{i,t}^{max}-{\lambda }_{i,t}^{min}){\mu }_{i,t}{\gamma }_3.(31)$

We introduce a dummy variable $\left\{{\omega }_{i,t}={\mu }_{i,t}{\gamma }_3\right\}$ and based on the Big-M method, we can obtain the following linear constraints:

$\begin{array}{c}({\lambda }_{i,t}^{max}-{\lambda }_{i,t}^{min}){\omega }_{i,t}=({\lambda }_{i,t}^{max}-{\lambda }_{i,t}^{min}){\mu }_{i,t}{\gamma }_3.\\ -M{\mu }_{i,t}\le {\omega }_{i,t}\le M{\mu }_{i,t}\\ -M(1-{\mu }_{i,t})+{\gamma }_3\le {\omega }_{i,t}\le {\gamma }_3+M(1-{\mu }_{i,t}).\end{array}(32)$

Combining Eqs 30–32, a linear single-stage model is successfully reformulated to obtain its maximum solution, which is easily solved by commercial software such as CPLEX.

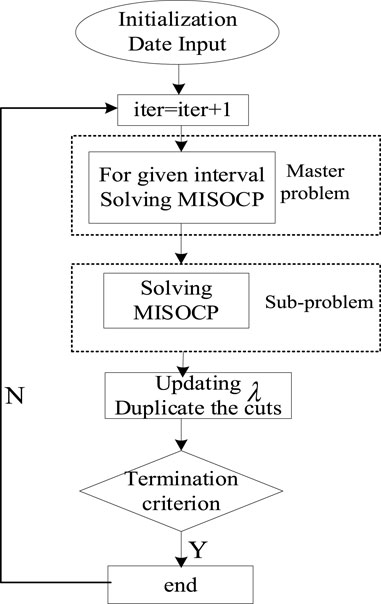
The flowchart of two-stage robust optimization is depicted in Figure 3.

FIGURE 3

FIGURE 3. Flowchart of CCG procedure.

For a given gap $\epsilon$ , the complete procedure of CCG can be described as

Step 1: Let ${\text{Φ}}^{down}=-\infty$, ${\text{Φ}}^{up}=+\infty$, iter = 0;

Step 2: Solve the MP which is modeled in Eq. 28,

Obtain the status of generators $I_{i,t}$ and location of the DPFC ${\delta }_{ij,t}$ with the uncertainty ${\lambda }^{\ast }$,

Update the lower bound ${\text{Φ}}^{down}$;

Step 3: Fix the location of the DPFC and status of thermal units. Solve the SP considering wind-load uncertainties.

Obtain decision variable solution $P_{i,t}^G/Q_{i,t}^G/P_{i,t}^{W,curt}/P_{i,t}^{D,shed}/P_{ij,s}^{DPFC}$ and uncertainty parameters ${\alpha }^L,{\alpha }^W$under each scenario.

Update the upper bound ${\mathrm{\Phi }}^{up}$;

Step 4: If $\frac{\left|{\text{Φ}}^{up}-{\text{Φ}}^{down}\right|}{\left|{\text{Φ}}^{down}\right|}\le \epsilon$, return the optimal solutions and stop. Otherwise, duplicate the cuts into the master problem, update the uncertainty parameters, and go to step.

5 Case Study

5.1 Verification of the Relaxed AC-SOCP Model

In this section, three cases are presented to check the characteristics of the power flow to illustrate the effectiveness of the proposed model. All cases are conducted on the IEEE-118 bus system.

Case 1: DC power flow

Case 2: the nonlinear power flow model

Case 3: the proposed model in Eq. 27

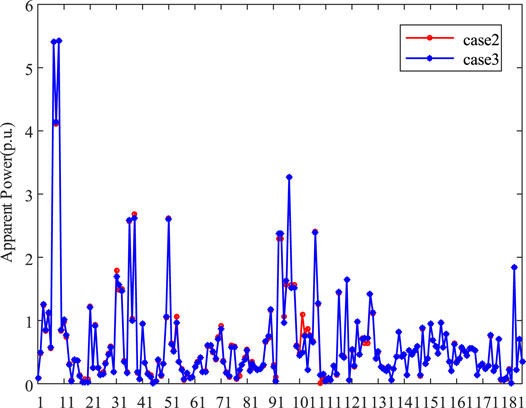
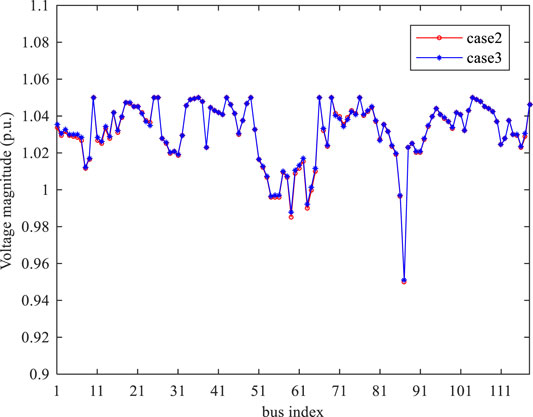
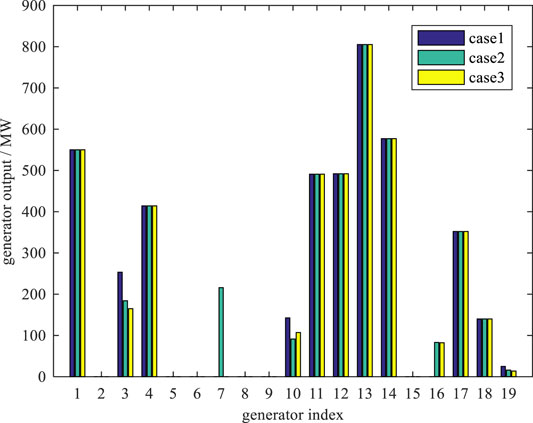
To evaluate the performance of the three power flow models, we conducted the simulation on apparent power of lines, generator outputs, and voltage magnitude, as is shown in Figures 4, 5, 6. We can easily find that the apparent power of lines has little difference in case 2 and case 3; only four lines have a little fluctuation. Similarly, voltage magnitude also conforms to the trend. In the aspect of generator output, there is an obvious difference between case 1 and case 2/3 on the G3/G7/G19, which is due to the absence of reactive power. Comparing the output of generators in case 2 and case 3, the dispatch solutions show highly consistent characteristics (Figures 4, 5, 6, 7).

FIGURE 4

FIGURE 4. Comparison of apparent power.

FIGURE 5

FIGURE 5. Comparison of voltage.

FIGURE 6

FIGURE 6. Comparison of generator output.

FIGURE 7

FIGURE 7. Derivation performance.

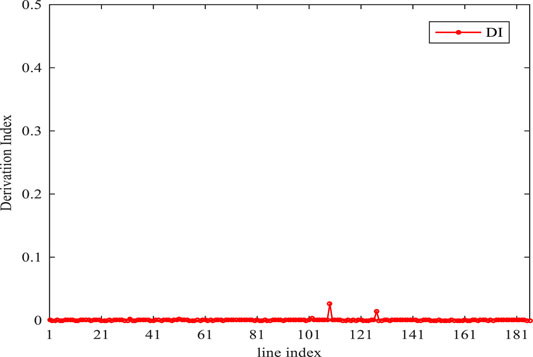
To quantify the exactness of the relaxed AC-SOCP model, a deviation index stated in (39) is introduced to describe the gap difference between case 2 and case 3, as shown in Figure 7. It is clearly shown that the gap difference is almost zero for the system.

$DI=U_i{U}_j-R_{ij}^2-T_{ij}^2.(39)$

5.2 Effects of the Optimal Distributed Power Flow Controller With High Penetration of Wind Power

To verify the proposed method, we conducted case studies on the modified IEEE-24 bus system. The wind power is located at bus 6/8. The rating of wind power is 4 MW. There are three loads with uncertainties, which are located at bus 4/5/6. The interval of wind and load is 0.2 and 0.1, respectively. The proposed method is solved by GAMS/CPLEX. The threshold values of the stop criterion are set to be 1e-4.

In order to evaluate the impacts of optimal DPFC planning, four cases have been set up to quantify the specific control effects of the DPFC to the scheduling of the thermal generator.

Case (a): the proposed robust model with no DPFC.

Case (b): the proposed robust model with one optimal DPFC.

Case (c): the proposed robust model with two optimal DPFC.

Case (d): the proposed robust model with three optimal DPFC.

A. Comparison of Unit States With Different Optimal Distributed Power Flow Controller Solutions

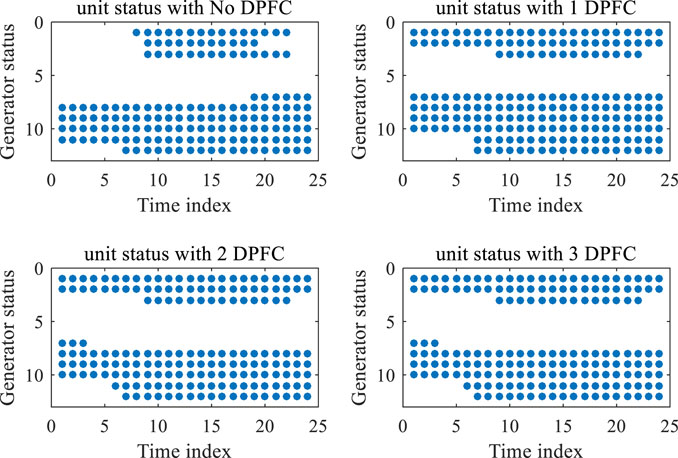
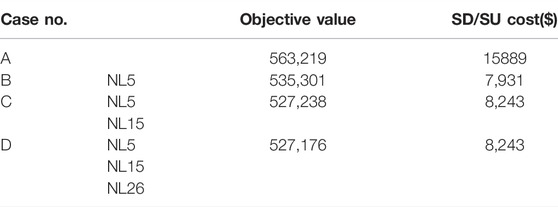
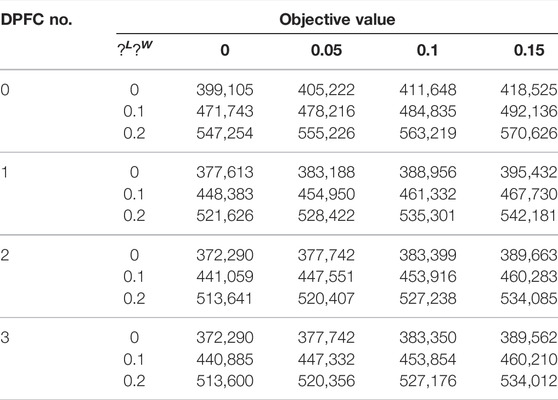
As shown in Figure 8, there is a huge difference in the start–stop scheduling planning of the units. Compared to the generator statuses of case (a), there are huge differences of scheduling planning with four units; the SD/SU costs have decreased from 15,889$ to 7,931$, which is shown in Table 1. Once 2/3 DPFC devices are injected into the system, the unit state is exactly the same, which illustrates that the control capacity of the DPFC has reached its extreme effects on the scheduling state of the system. Furthermore, the status of G7 and G11 show a different planning solution between case (b) and case (c)/(d); the SD/SU costs have a little increment from 7,931$ to 8,243$. Hence, there is a positive trend of dispatch state scheduling considering the optimal DPFC injected.

FIGURE 8

FIGURE 8. Thermal generator state with different numbers of the DPFC.

TABLE 1

TABLE 1. Dispatch performance with different numbers of the DPFC.

Table 1 shows the objective performance with different numbers of the DPFC; the value keeps decreasing as the number of DPFCs increase. Comparing the performance between case (c) and case (d) , the objective values change very little, which indicates that the management of power flow is approaching its limit.

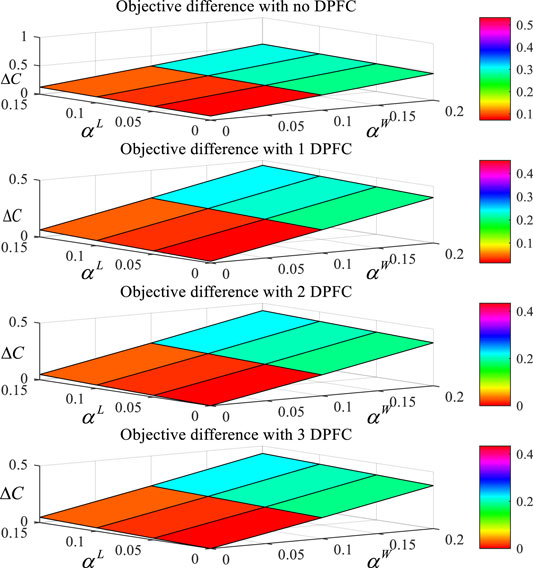
In order to more clearly depict the performance difference between the robust model and deterministic model considering the optimal DPFC, we introduce an index $\Delta C$, which denotes the objective difference.

$\text{Δ}C=\frac{C_{RO}-C_{DM,3}}{C_{DM,3}},(40)$

where $C_{RO}$ is the objective value of the robust model and $C_{DM,3}$ is the objective value for the deterministic model with three DPFCs injected. The differences of objective values for the IEEE 24 bus system under different wind and load intervals are shown in Figure 9.

FIGURE 9

FIGURE 9. Objective difference with different numbers of the DPFC.

As shown in Table 2 and Figure 9, it is easily observed that the robust model has a high property improvement, which is due to the robust conversation of dispatch solution. The system operators only sacrifice the economy effects to tackle with the uncertainties of wind/load. Furthermore, the difference $\text{Δ}C$ shows the downward directions as the numbers of DPFC increased. There is a similar trend with Figure 9. The objective difference $\mathrm{\Delta }C$ is almost the same when comparing the 2 and 3 DPFCs injected, which indicates that optimal location and allocations of 2 DPFC has reached its limitation for the IEEE 24 bus system.

TABLE 2

TABLE 2. Objective values under different intervals considering the optimal DPFC.

B. Comparison of the Last Worst Wind-Load Scenario with Different Optimal Distributed Power Flow Controller Solutions

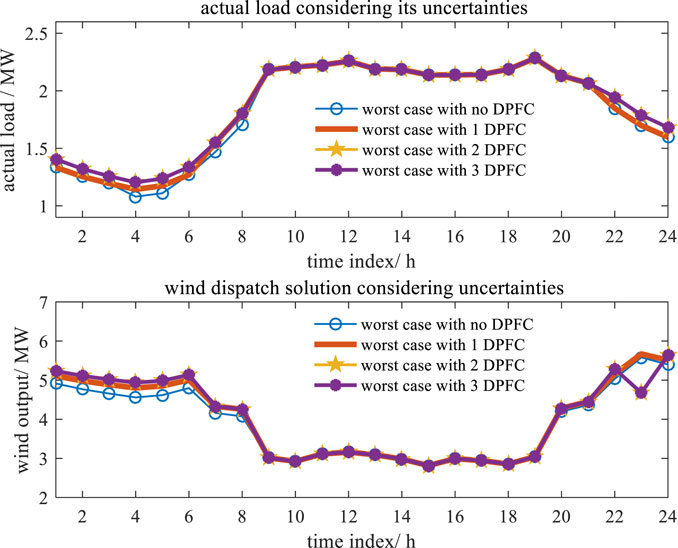
With the uncertainties of wind and load, the optimal solution is obtained at the extreme points of uncertain parameters. However, there is an inconsistent trend while the uncertain parameters reach its extreme values with different numbers in the last worst case scenario, as shown in Figure 10. Obviously, there is only one difference of wind extreme values at a single time phase (t = 23). However, it can be easily found that the load reaches its upper values once 1/2/3 DPFC is injected, which indicates that optimal DPFC planning can enforce the resistance level of power supply considering the uncertainty.

FIGURE 10

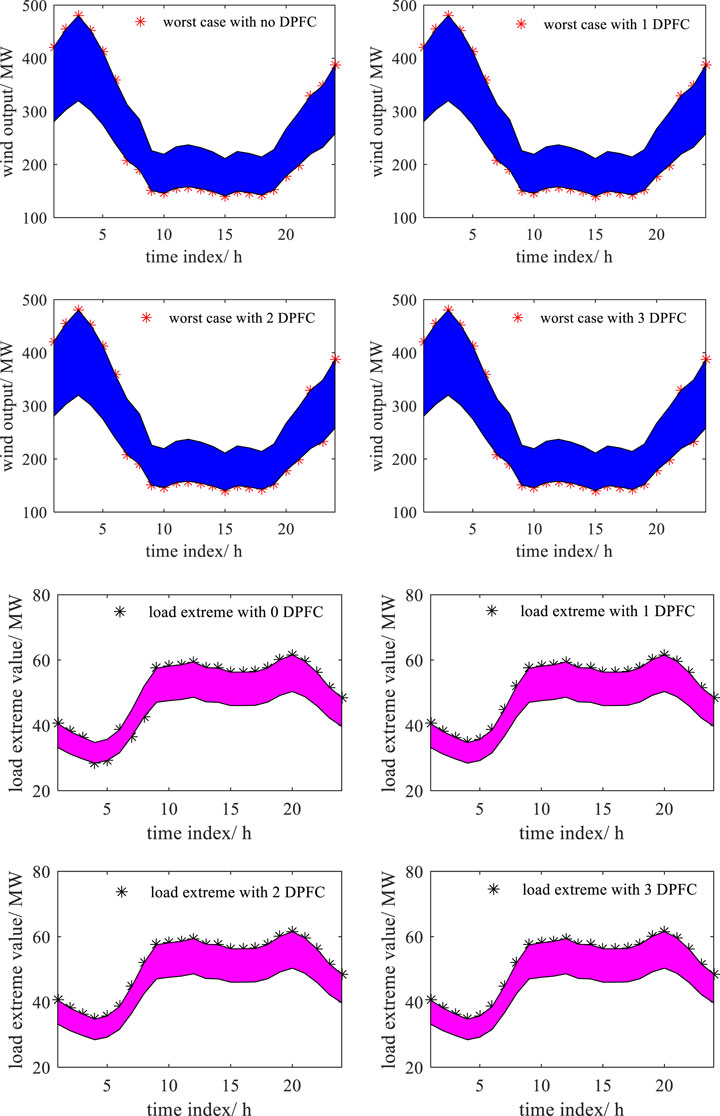
FIGURE 10. Wind/load upper/lower bound and its worst-case scenario with different numbers of the DPFC.

To evaluate the effects of wind spillage and load shedding with the optimal DPFC in the last worst-case scenario, considering its extreme value inconsistence with wind/load uncertainties, we conducted the simulation of wind absorption and actual load supplies, which is shown in Figure 11. For the wind aspect, the overall trend of wind absorption is positive, and the amount outputs of wind absorption are 94.06/96.24/96.32/96.32 MW as the numbers of DPFC are 0/1/2/3, respectively. For the actual load aspect, there is a drop difference at time phase (t = 23 h) considering different numbers of the DPFC optimized. However, the amounts of actual load supplies are 43.89/44.20/45.13/45.13 MW from case (a) to case (d). Hence, the dispatch effects with the DPFC optimized the wind spillage and load shedding move in a positive direction.

FIGURE 11

FIGURE 11. Wind upper/lower bound and its worst-case scenario with different numbers of the DPFC.

For the consistence of DPFC optimal scheduling planning, Table 3 shows advantages of the location and allocation of the optimized DPFC simultaneously. Once the DPFC is injected, the unit cost has a great positive effect, and the wind spillage and load shedding also conform to the positive trend with the increased numbers of the DPFC. In cases (c) and (d), the amounts of load shedding are 0, and the wind spillage also has no changes, which indicates that the robust planning of the DPFC has reached its extreme repeatedly.

TABLE 3

TABLE 3. Optimal dispatch performance with the optimal DPFC under the worst-case scenario.

6 Conclusion

This work presents a two-stage robust dispatch method with optimal location–allocations of the DPFC considering wind-load uncertainties. In the model, we mainly optimize the scheduling state of thermal units and location–allocation of the DPFC to tackle the uncertainties. Case studies are performed to demonstrate the effectiveness of the proposed method. The conclusions are summarized as follows:

1) The relaxed AC-SOCP model can easily simulate the nonlinear AC power flow and has an advantage of solving speed and difficulties.

2) The robust dispatch with the optimal DPFC has an economic advantage and load supplies, which also reduce the wind spillage and load shedding.

3) The proposed model can be easily solved by the CCG method, which efficiently checks the worst-case scenario, optimizes the dispatch solution, and DPFC consistent scheduling planning with uncertainties.

However, the robust dispatch with the optimal DPFC may face a conservative challenge because of the overall intervals of uncertainties. Some studies have developed a distributed robust optimization to overcome the conservation, which combine the priorities between stochastic and robust optimization. In addition, the DPFC has shown great advantages over the management on the network side. We will conduct more research studies on the control capabilities of the DPFC in the future. Such advantages may be effective in dispatching and operating the principle of integrated energy system (IES) due to the electric characteristics; we can relieve the couple conjunction in the gas turbine (GT) and CCHP with the energy storage system (ESS) by optimal coordination of the control capabilities of the DPFC. Another coordinate research on the TEP and DPFC has been in process to tackle the high wind-load conditions to improve robustness and flexibilities in the network side, which render more capability of available transfer power. Obviously, there is an advantage of the DPFC to be adopted in N-k contingency analysis, which may be the best performance in the application areas of the DPFC.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

XZ contributed to the simulation and writing. JW contributed to the model and method. DL offered financial support.

Funding

This study received funding from the State Grid Corporation of China (No. 52150016000Y) and National Key Research and Development Program of China (No.2018YFB0904800). The funders were not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahmadi, A., Nezhad, A. E., and Hredzak, B. (2018). Security-constrained Unit Commitment in Presence of Lithium-Ion Battery Storage Units Using Information-gap Decision Theory[J]. IEEE Trans. Ind. Inform. 15 (1), 148–157.

Google Scholar

Ahmadi, A., Nezhad, A. E., Siano, P., Hredzak, B., and Saha, S. (2019). Information-gap Decision Theory for Robust Security-Constrained Unit Commitment of Joint Renewable Energy and Gridable Vehicles[J]. IEEE Trans. Ind. Inform. 16 (5), 3064–3075.

Google Scholar

Ahrabi, M., Abedi, M., Nafisi, H., Mirzaei, M. A., Mohammadi-Ivatloo, B., and Marzband, M. (2021). Evaluating the Effect of Electric Vehicle Parking Lots in Transmission-Constrained AC Unit Commitment under a Hybrid IGDT-Stochastic Approach. Int. J. Electr. Power Energ. Syst. 125, 106546. doi:10.1016/j.ijepes.2020.106546

CrossRef Full Text | Google Scholar

An, Y., and Zeng, B. (2014). Exploring the Modeling Capacity of Two-Stage Robust Optimization: Variants of Robust Unit Commitment Model[J]. IEEE Trans. Power Syst. 30 (1), 109–122.

Google Scholar

Dai, J., Tang, Y., Liu, Y., Ning, J., Wang, Q., Zhu, N., et al. (2019). Optimal Configuration of Distributed Power Flow Controller to Enhance System Loadability via Mixed Integer Linear Programming. J. Mod. Power Syst. Clean. Energ. 7 (6), 1484–1494. doi:10.1007/s40565-019-0568-8

CrossRef Full Text | Google Scholar

Dvorkin, Y., Pandžić, H., Ortega-Vazquez, M. A., and Kirschen, D. S. (2014). A Hybrid Stochastic/interval Approach to Transmission-Constrained Unit Commitment[J]. IEEE Trans. Power Syst. 30 (2), 621–631.

Google Scholar

Gangammanavar, H., Sen, S., and Zavala, V. M. (2015). Stochastic Optimization of Sub-hourly Economic Dispatch with Wind Energy[J]. IEEE Trans. Power Syst. 31 (2), 949–959.

Google Scholar

Kamboj, V. K., Kumari, C. L., Bath, S. K., Prashar, D., Rashid, M., Alshamrani, S. S., et al. (2022). A Cost-Effective Solution for Non-convex Economic Load Dispatch Problems in Power Systems Using Slime Mould Algorithm. Sustainability 14 (5), 2586. doi:10.3390/su14052586

CrossRef Full Text | Google Scholar

Khajehvand, M., Fakharian, A., and Sedighizadeh, M. (2021). A Risk-Averse Decision Based on IGDT/stochastic Approach for Smart Distribution Network Operation under Extreme Uncertainties. Appl. Soft Comput. 107, 107395. doi:10.1016/j.asoc.2021.107395

CrossRef Full Text | Google Scholar

Khanchi, S., and Garg, V. K. (2013). Unified Power Flow Controller (FACTS Device). A. Review[j]. System 5, 6.

Google Scholar

Le, S., Wu, Y., Guo, Y., and Vecchio, C. D. (2021). Game Theoretic Approach for a Service Function Chain Routing in NFV with Coupled Constraints. IEEE Trans. Circuits Syst. 68, 3557–3561. doi:10.1109/TCSII.2021.3070025

CrossRef Full Text | Google Scholar

Li, J., Liu, F., Li, Z., Mei, S., and He, G. (2018). Impacts and Benefits of UPFC to Wind Power Integration in Unit Commitment. Renew. Energ. 116, 570–583. doi:10.1016/j.renene.2017.09.085

CrossRef Full Text | Google Scholar

Li, Z., Jiang, W., Abu-Siada, A., Li, Z., Xu, Y., and Liu, S. (2021). Research on a Composite Voltage and Current Measurement Device for HVDC Networks. IEEE Trans. Ind. Electron. 68 (9), 8930–8941. doi:10.1109/tie.2020.3013772

CrossRef Full Text | Google Scholar

Milligan, M., Porter, K., DeMeo, E., Denholm, P., Holttinen, H., Kirby, B., et al. (2009). Wind Power Myths Debunked. IEEE Power Energ. Mag. 7 (6), 89–99. doi:10.1109/mpe.2009.934268

CrossRef Full Text | Google Scholar

Nandi, A., and Kamboj, V. K. (2021). A Meliorated Harris Hawks Optimizer for Combinatorial Unit Commitment Problem with Photovoltaic Applications[J]. J. Electr. Syst. Inf. Technol. 8 (1), 1–73. doi:10.1186/s43067-020-00026-3

CrossRef Full Text | Google Scholar

Nandi, A., Kamboj, V. K., and Khatri, M. (2022). Hybrid Chaotic Approaches to Solve Profit Based Unit Commitment with Plug-In Electric Vehicle and Renewable Energy Sources in winter and Summer[J]. Mater. Today Proc. doi:10.1016/j.matpr.2021.12.525

CrossRef Full Text | Google Scholar

Nandi, A., Kamboj, V. K., and Khatri, M. (2022). Metaheuristics Approaches to Profit Based Unit Commitment for GENCOs[J]. Mater. Today Proc. doi:10.1016/j.matpr.2021.12.526

CrossRef Full Text | Google Scholar

Nasri, A., Conejo, A. J., Kazempour, S. J., and Ghandhari, M. (2014). Minimizing Wind Power Spillage Using an OPF with FACTS Devices. IEEE Trans. Power Syst. 29 (5), 2150–2159. doi:10.1109/tpwrs.2014.2299533

CrossRef Full Text | Google Scholar

Nikoobakht, A., and Aghaei, J. (2017). IGDT‐based Robust Optimal Utilisation of Wind Power Generation Using Coordinated Flexibility Resources. IET Renew. Power Generation 11 (2), 264–277. doi:10.1049/iet-rpg.2016.0546

CrossRef Full Text | Google Scholar

Rabiee, A., Soroudi, A., and Keane, A. (2014). Information gap Decision Theory Based OPF with HVDC Connected Wind Farms[J]. IEEE Trans. Power Syst. 30 (6), 3396–3406.

Google Scholar

Sang, Y., Sahraei-Ardakani, M., and Parvania, M. (2017). Stochastic Transmission Impedance Control for Enhanced Wind Energy Integration[J]. IEEE Trans. Sustain. Energ. 9 (3), 1108–1117.

Google Scholar

Shen, X., Ouyang, T., Khajorntraidet, C., Li, Y., Li, S., and Zhuang, J. (2022). Mixture Density Networks-Based Knock Simulator. Ieee/asme Trans. Mechatron. 27, 159–168. doi:10.1109/TMECH.2021.3059775

CrossRef Full Text | Google Scholar

Shen, X., Ouyang, T., Yang, N., and Zhuang, J. (2021). Sample-based Neural Approximation Approach for Probabilistic Constrained Programs. IEEE Trans. Neural Netw. Learn. Syst., 1–8. doi:10.1109/TNNLS.2021.3102323

CrossRef Full Text | Google Scholar

Shen, X., and Raksincharoensak, P. (2021). Pedestrian-aware Statistical Risk Assessment. IEEE Trans. Intell. Transport. Syst., 1–9. doi:10.1109/TITS.2021.3074522

CrossRef Full Text | Google Scholar

Shen, X., and Raksincharoensak, P. (2021). Statistical Models of Near-Accident Event and Pedestrian Behavior at Non-signalized Intersections. J. Appl. Stat., 1–21. doi:10.1080/02664763.2021.1962263

CrossRef Full Text | Google Scholar

Tang, A., Lu, Z., Yang, H., Zou, X., Huang, Y., and Zheng, X (2020). Digital/analog Simulation Platform for Distributed Power Flow Controller Based on ADPSS and dSPACE[J]. CSEE J. Power Energ. Syst. 7 (1), 181–189.

Google Scholar

Toyoda, M., and Wu*, Y. (2021). Mayer-type Optimal Control of Probabilistic Boolean Control Network with Uncertain Selection Probabilities. IEEE Trans. Cybern. 51, 3079–3092. doi:10.1109/tcyb.2019.2954849

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, C., Jiao, B., Guo, L., Tian, Z., Niu, J., and Li, S. (2016). Robust Scheduling of Building Energy System under Uncertainty. Appl. Energ. 167, 366–376. doi:10.1016/j.apenergy.2015.09.070

CrossRef Full Text | Google Scholar

Wang, Q., Wang, J., and Guan, Y. (2012). Stochastic Unit Commitment with Uncertain Demand Response[J]. IEEE Trans. Power Syst. 28 (1), 562–563.

Google Scholar

Wu, J., Zhang, B., Jiang, Y., Bie, P., and Li, H. (2019). Chance-constrained Stochastic Congestion Management of Power Systems Considering Uncertainty of Wind Power and Demand Side Response. Int. J. Electr. Power Energ. Syst. 107, 703–714. doi:10.1016/j.ijepes.2018.12.026

CrossRef Full Text | Google Scholar

Wu, Y., Guo, Y., and Toyoda, M. (2021). Policy Iteration Approach to the Infinite Horizon Average Optimal Control of Probabilistic Boolean Networks. IEEE Trans. Neural Netw. Learn. Syst. 32 (6), 2910–2924. doi:10.1109/TNNLS.2020.3008960

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, N., et al. (2021). A Comprehensive Review of Security-Constrained Unit Commitment. J. Mod. Power Syst. Clean Energ., 1–14. doi:10.35833/MPCE.2021.000255

CrossRef Full Text | Google Scholar

Yang, N., Qin, T., Wu, L., Huang, Y., Huang, Y., Xing, C., et al. (2022). A Multi-Agent Game Based Joint Planning Approach for Electricity-Gas Integrated Energy Systems Considering Wind Power Uncertainty. Electric Power Syst. Res. 204, 107673. doi:10.1016/j.epsr.2021.107673

CrossRef Full Text | Google Scholar

Yang, N., Yang, C., Wu, L., Shen, X., Jia, J., Li, Z., et al. (2022). Intelligent Data-Driven Decision-Making Method for Dynamic Multisequence: An E-Seq2Seq-Based SCUC Expert System. IEEE Trans. Ind. Inf. 18, 3126–3137. doi:10.1109/TII.2021.3107406

CrossRef Full Text | Google Scholar

Yang, N., Yang, C., Xing, C., Ye, D., Jia, J., Chen, D., et al. (2021). Deep Learning‐based SCUC Decision‐making: An Intelligent Data‐driven Approach with Self‐learning Capabilities. IET Generation Trans. Dist 16, 629–640. doi:10.1049/gtd2.12315

CrossRef Full Text | Google Scholar

Yuan, Z., de Haan, S. W. H., Ferreira, J. B., and Cvoric, D. (2010). A FACTS Device: Distributed Power-Flow Controller (DPFC). IEEE Trans. Power Electron. 25 (10), 2564–2572. doi:10.1109/tpel.2010.2050494

CrossRef Full Text | Google Scholar

Zeng, B., and Zhao, L. (2013). Solving Two-Stage Robust Optimization Problems Using a Column-And-Constraint Generation Method. Operations Res. Lett. 41 (5), 457–461. doi:10.1016/j.orl.2013.05.003

CrossRef Full Text | Google Scholar

Zhang, C., Xu, Y., Dong, Z. Y., and Wong, K. P. (2017). Robust Coordination of Distributed Generation and price-based Demand Response in Microgrids[J]. IEEE Trans. Smart Grid 9 (5), 4236–4247.

Google Scholar

Zhang, C., Xu, Y., Dong, Z. Y., and Ma, J. (2016). Robust Operation of Microgrids via Two-Stage Coordinated Energy Storage and Direct Load Control[J]. IEEE Trans. Power Syst. 32 (4), 2858–2868.

Google Scholar

Zhao, C., Wang, J., Watson, J.-P., and Guan, Y. (2013). Multi-Stage Robust Unit Commitment Considering Wind and Demand Response Uncertainties. IEEE Trans. Power Syst. 28 (3), 2708–2717. doi:10.1109/tpwrs.2013.2244231

CrossRef Full Text | Google Scholar

Zhao, C., Wang, Q., Wang, J., and Guan, Y. (2014). Expected Value and Chance Constrained Stochastic Unit Commitment Ensuring Wind Power Utilization. IEEE Trans. Power Syst. 29 (6), 2696–2705. doi:10.1109/tpwrs.2014.2319260

CrossRef Full Text | Google Scholar

Ziaee, O., Alizadeh-Mousavi, O., and Choobineh, F. F. (2017). Co-optimization of Transmission Expansion Planning and TCSC Placement Considering the Correlation between Wind and Demand Scenarios[J]. IEEE Trans. Power Syst. 33 (1), 206–215.

Google Scholar

Glossary

Indices

$\raisebox{1ex}{$i$}\!\left/ \!\raisebox{-1ex}{$j$}\right.$ Indices of buses Indices of lines

$ij$ Indices of buses Indices of lines

Sets

$G_i$ Sets of generators

$G_w$ Sets of wind generator

$G_{ij}$ Sets of lines

$G_{nb}$ Sets of buses

Constants

$g_{ij}/b_{ij}$ Line parameters

$C_i^{su}/C_i^{sd}$ Coefficients of start-up/shut down cost of generator i

$c_{g,i}$ Cost coefficient of generator

${\pi }^{DPFC}$ Cost coefficients of DPFC investment

$\raisebox{1ex}{$T_i^{on}$}\!\left/ \!\raisebox{-1ex}{$T_i^{off}$}\right.$ Minimum up-time and down time of generator

$P_i^{G,min}/P_i^{G,max}$ Lower and upper bound of generator active output

$Q_i^{G,min}/Q_i^{G,max}$ Lower and upper bound of generator reactive output

$R{U}_i/R{D}_i$ Ramp-up and ramp-down values of generator

$S{U}_i/S{D}_i$ Start-up/shut down cost of generator i

$S_{ij}$ Apparent power limitation of line ij

${\theta }_i^{min}/{\theta }_i^{max}$ Lower and upper bound of voltage angle

$V_i^{min}/V_i^{max}$ Lower and upper bound of voltage magnitude

$M^{Curt}$ Curtailment coefficient of wind spillage

$M^{shed}$ Curtailment coefficient of load shedding

Variables

$P_{ij}/Q_{ij}$ Active/reactive power flow of line ij

$P_{ij,rev}/Q_{ij,rev}$ Reverse active/reactive power flow of line ij

$V_i$ Voltage magnitude

${\theta }_i$ Voltage angle

$R_{ij}/T_{ij}$ Slack variables

$P_{i,t}^G/Q_{i,t}^G$ Active/reactive power of generator

$P_{ij}^{DPFC}$ Compensation level of the DPFC on line ij

${\delta }_{ij,t}$ Binary variables indicating the location of the DPFC

$\alpha$ Scalar indicating the amount of DPFC numbers

$P_{i,t}^{W,curt}$ Wind spillage value

$P_{i,t}^{D,shed}$ Load shedding value

$u_{i,t}/v_{i,t}/I_{i,t}$ Binary variable indicating start-up/shut down/operating state.

$P_{i,t}^{W,curt}/Q_{i,t}^{W,curt}$ Active/reactive power spillage of wind

$P_{i,t}^{D,shed}/Q_{i,t}^{D,shed}$ Active/reactive load shedding

$P_{i,t}^{D,u}/Q_{i,t}^{D,u}$ Active/reactive power of load considering uncertainty.