Numerical and Experimental Study on Mode Identification Error Characteristics of Fan Noise

The influence of different test methods on the accuracy of mode identification is not clear, and it is necessary to explore the error transfer characteristics in mode decomposition of fan noise. Numerical and experimental research studies are carried out on the advantages and disadvantages of radial rake and axial microphone array and error transmission characteristics in mode decomposition. In the numerical study, the error transmission characteristics of different arrays are investigated by adding random disturbances to the artificial sound field, so as to evaluate the applicability and limitations of the two typical arrays in mode identification based on the error analysis theory. The mode recognition error of the single-stage axial flow fan is investigated experimentally using the designed radial rakes and axial arrays. The results show that although the radial rake can directly measure the radial distribution of the modal amplitude, it has a large error in the mode identification at low frequencies. Compared with the radial rake, axial array will take more priority in practical applications. The accuracy of the axial microphone array in mode recognition strongly depends on the axial spacing of the array measuring sensors. The small deviations in the mode identification when applying the two typical arrays are caused by the different signal-to-noise ratio of the sound pressure signals acquired by the two arrays and their discriminative sensitivities to the duct airflow. Based on the obtained modal identification error characteristics, an effective mode identification method can be proposed to help fan noise reduction design.

1 Introduction

The acoustic wave propagates in the form of modal waves in the duct, and the number of cut-on modal waves depends on the duct geometry, sound wave frequency, the airflow velocity, and the acoustic boundary conditions of the duct. Aero-engine noise includes tonal noise (such as rotor self-noise, buzzer, and rotor-static interference noise) and broadband noise (Qiao, 2010). The method of mode decomposition is widely used to investigate the generation mechanism of tonal noise and broadband noise in the flow duct. For radial modal analysis in tonal noise, starting in the 1960s, a number of experimental measurement methods have been developed (Bolleter and Crocker, 1972; Bolleter et al., 1973; Moore, 1979; Holste and Neise, 1997; Enghardt et al., 1999; Lan et al., 2002). These methods have different limitations considering the solvable modal order range, the accuracy of analysis results, and the complexity of method application. Ideally, radial mode decomposition is achieved by far-field measurements (Farassat et al., 2001), as this is easy to achieve in practical measurements and is not limited by size. However, considering the errors introduced by the analytical model when applied to the real engine geometry and the time-consuming in numerical calculation of the transfer function between the inlet (or outlet) and the far field, nowadays, the radial mode decomposition of the sound field at low frequencies is usually performed by arranging a large number of sensors in the duct (Tapken and Enghardt, 2006), and the radial mode distribution results in the duct are obtained by inversely processing the measured sound pressure data. The German Aerospace Academy (DLR) successfully used this method to measure tonal noise in the ducts of fans (Enghardt et al., 2002), low-pressure compressors (Enghardt et al., 2005), and low-pressure turbines (Enghardt et al., 2001).

There are two types of commonly used microphone arrays: radial rakes and axial arrays. The radial rake can directly measure the distribution of modal waves in the radial direction, and it is easier to realize the modal sound power in terms of numerical solution. Enghardt et al. (2001), Sutliff, (2005), Dahl et al. (2013), and Heidelberg and Hall, (1996) used a rotating rake array to measure the sound field in the flow duct, but when placed upstream, its wake will interfere with the original flow field and pollute the sound field. Joppa, (1987) developed a practical method to measure the sound pressure using an array of equally spaced axial microphones flush-mounted on the duct wall, and the distribution of the fan discrete tonal noise can be obtained by using the axial microphones (Wang et al., 2014; Xu et al., 2018), which can perform circumferential modal analysis of compressor rotational instability (Zhou et al., 2015) and compressor fault diagnosis (Cheng et al., 2019). Zillmann and Tapken, (2009) and Tapken et al. (2009) used a circumferentially rotatable axial array to measure fan noise with very large bypass ratios. Yardley (Yardley, 1974) suggested that the microphones should be installed on the duct wall and pointed out that the mode identification of fan duct noise can be carried out by sound pressure measurement at multiple axial positions, and the duct acoustic performance analysis can be carried out according to the acoustic modal amplitude (Wagih Nashed et al., 2018) and sound field reconstruction (Liu et al., 2018). For both radial rakes and axial arrays, the mode identification is achieved by inverting the coefficient matrix between the sound pressure at the measuring sensors and the radial modal amplitudes. Acoustic mode identification is also closely related to the airflow turbulence in the duct (Kan et al., 2021). Under the measured modal coherence characteristics, the accuracy in acoustic mode identification can be effectively improved. However, the influence of different testing methods on mode identification accuracy is not clear, and the error transmission characteristics of different microphone arrays in mode identification are not analyzed in detail.

Based on the modal decomposition theory, the error transfer characteristics of two typical kinds of arrays in turbomachinery noise measurement is investigated in this study. The influence of different microphone arrays on the accuracy of acoustic mode identification is numerically studied, and the design criteria of the axial microphone array are established. Based on the error characteristics shown in the results, acoustic mode identification of a single-stage axial flow fan is investigated experimentally through the processing of rotating radial rakes and axial arrays. Accordingly, effective measures to reduce the mode identification error are proposed.

2 Measurement Theory

2.1 Acoustic Mode Recognition Method

For acoustic propagation in an incompressible circular/annular duct, the acoustic propagation equation in a circular/annular duct can be written as follows:

$\frac{1}{c^2}\frac{D^{2}p}{D{t}^2}-\frac{{\partial }^{2}p}{\partial x^2}-\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial p}{\partial r}\right)-\frac{1}{r^2}\frac{{\partial }^{2}p}{\partial {\theta }^2}=0(1)$

where c is the speed of sound and $p$ is the sound pressure. For the propagation of the sound field in a cylindrical or annular hard-walled duct, a numerical solution can be obtained from the formula (Eq. 1), which can be obtained by linear superposition of modal waves for a certain frequency (Qiao, 2010).

$p\left(x,r,\phi ,t\right)={\displaystyle \sum }_{m=-\infty }^{\infty }{\displaystyle \sum }_{n=0}^{\infty }\left(A_{mn}^{+}{e}^{i{k}_{mn}^{+}x}+A_{mn}^{-}{e}^{i{k}_{mn}^{-}x}\right){\psi }_{mn}\left(r\right)e^{im\phi }{e}^{i\omega t}(2)$

The axial wavenumber $k_{mn}^{\pm }$ depends on the eigenvalues ${\sigma }_{mn}$ of the mode (m,n) and the wavenumber in the free field $k=\omega /c$; the modal wave can cut-on along the duct when axial wavenumber $k_{mn}^{\pm }$ is a real number and is defined as follows:

$k_{mn}^{\pm }=k\frac{-M_a\pm {\alpha }_{mn}}{1-M_a^2}(3)$

${\alpha }_{mn}=\sqrt{1-{\left(\frac{\sqrt{1-M_{\text{a}}^2}{\sigma }_{mn}}{kR}\right)}^2}(4)$

The modal characteristic functions satisfy the following:

$\frac{1}{\pi R^2}{\displaystyle \underset{0}{\overset{2\pi }{\int }}{e}^{i\left(m-\mu \right)\phi }}{\displaystyle \underset{\eta R}{\overset{R}{\int }}{\psi }_{mn}\left(r\right){\psi }_{\mu \nu }}\left(r\right)rdrd\phi ={\delta }_{m\mu }{\delta }_{n\nu }(5)$

In which $\mu ,\nu$ represents mode $\left(\mu ,\nu \right)$, and assuming that there are K measuring points in the duct for synchronous acquisition of sound pressure data, the sound pressure at the measuring points can be written as follows:

$\mathrm{p}=\mathrm{\Phi a}(6)$

In the formula, $\mathrm{p}\in {ℂ}^K$ represents the complex sound pressure vector at the measured frequency $\omega$, $a\in {ℂ}^L$ represents the complex modal amplitude $A_{mn}^{\pm }$, in which m represents the modal circumferential order and n represents modal radial order, the size of L depends on the total number of cut-on modes in the flow duct, and the values in the matrix $\mathrm{\Phi }\in {ℂ}^{K\times L}$ are determined by the measuring point position of the microphone array and the modal order. The cross-spectral matrix of the sound pressure signals at the two measuring points can be defined as ${\mathrm{S}}_{pp}\triangleq E\left(\mathrm{p}{\mathrm{p}}^H\right)$, where E represents the expectation. Based on the formula (Eq. 6), the cross-spectrum of the two sound pressure measuring points can be written as follows:

${\mathrm{S}}_{pp}=\mathrm{\Phi }{\mathrm{S}}_{aa}{\mathrm{\Phi }}^H(7)$

Therefore, the cross-spectrum of the modal amplitudes can be written as follows:

${\mathrm{S}}_{aa}={\mathrm{\Phi }}^{†}{\mathrm{S}}_{pp}{\left({\mathrm{\Phi }}^{†}\right)}^H(8)$

where $†$ represents the pseudo-inverse of the matrix. In actual experimental measurements, the number of measurement points K of the microphone array is usually larger than the size L of the modal amplitude vector, and the coefficient matrix may be singular. When solving the matrix with the singular coefficient matrix and the overdetermined equation, singular value decomposition (SVD) (Nelson and Yoon, 2000; Kim and Nelson, 2004) was used in this study to solve the following:

$\mathrm{Gp}=\widehat{\mathrm{a}}\iff \mathrm{V}\cdot \left[diag\left(\frac{1}{w_j}\right)\right]\cdot {\mathrm{U}}^T\mathrm{p}=\widehat{\mathrm{a}}(9)$

In the formula, $\mathrm{U}$ and $\mathrm{V}$ are both transformation matrices and orthogonal matrices, which satisfy $\mathrm{U}\cdot {\mathrm{U}}^T=1$ and $\mathrm{V}\cdot {\mathrm{V}}^T=1$, but $\mathrm{W}$ is a diagonal matrix, and the elements are all positive values and values tending to zero (i.e., singular values). Appropriately discarding smaller singular values can improve the accuracy of the algorithm. Its optimal estimate can be obtained by the following:

$p={\left[G^{H}G\right]}^{-1}{{\displaystyle G}}^H\widehat{\mathrm{a}}={{\displaystyle G}}^{+}\widehat{\mathrm{a}}(10)$

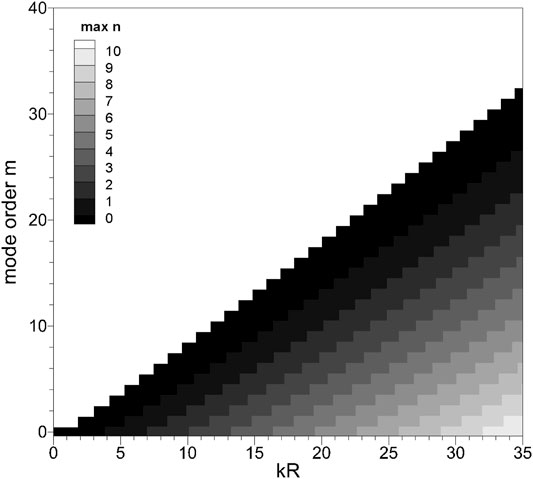
The solvability and stability of Eq. 10 and the error transfer characteristics of the system are closely related to the condition number of the square matrix. The condition number depends on many factors: the number of cut-on modes, frequency, hub-to-shroud ratio, airflow parameters, and the shape of the design array. Therefore, it becomes necessary to evaluate the quality of mode decomposition by condition number analysis.

2.2 Error Analysis Theory

In order to explore the limitations of different array schemes in mode identification measurement, the numerical method is used to study the error characteristics of radial rakes and axial arrays in mode identification. By analyzing the coefficient matrix condition number, the influence of the axial spacing in the array design on the mode identification is studied and the error transfer characteristics of different arrays during mode decomposition are investigated by superimposing random disturbances in the artificial sound field, which thus provides theoretical guidance for mode identification of duct noise.

The accuracy of the calculation results in the mode identification is related to the condition number of the matrix. It determines the upper bound of the error transfer coefficient of the system of Eq. 10:

$\frac{\Vert {\tilde{A}}_{mn}\Vert }{\Vert A_{mn}\Vert }\le \kappa \left(w\right)\frac{\Vert {\tilde{A}}_m\Vert }{\Vert A_m\Vert }(11)$

The tilde character ∼ represents the perturbation of the circumferential modal amplitude $A_m$ and radial modal amplitude $A_{mn}$, respectively, and the circumferential modal amplitude can be calculated by reference (Moore, 1979), in which $A_m=W_m\cdot A_{mn}$ and $A_{mn}={\left[W_m^H{W}_m\right]}^{-1}{W}_m^H{A}_m=W_m^{+}{A}_m$. $\Vert \ast \Vert$ represents the Euclidean norm. As shown in the formula (Eq. 11), if the condition number is $\kappa \left(w\right)=1$, that is to say, when a small disturbance in the input signal is transmitted to the output signal through the system, the magnitude of the disturbance is basically unchanged. When the input amplitude error is 10%, the maximum error of the output signal amplitude after passing through the system can reach 10%. But when the condition number is greater than 1, the small disturbance in the input signal will be amplified after passing through the system, and its amplification rate depends on the condition number of the coefficient matrix in the system, as shown in the formula (Eq. 11). Therefore, the error characteristics of different arrays in mode identification can be qualitatively analyzed by calculating the condition numbers of the coefficient matrices constructed by different microphone arrays, and furthermore, their distribution law can be grasped.

The matrix condition number $\kappa \left(w\right)$ can only reflect the upper limit of the overall error of the modal recognition system but cannot reflect the error characteristics of a single internal mode. In order to further study the reliability of mode identification, the formula (Eq. 11) is used to derive the relative accuracy expression in mode identification, which is defined as follows:

$\left|\right|{\tilde{A}}_{mn}|{|}_{rel}:=\frac{\left|\right|{\tilde{A}}_{mn}\left|\right|}{\left|\right|A_{mn}\left|\right|}\frac{\left|\right|A_m\left|\right|}{\left|\right|{\tilde{A}}_m\left|\right|}(12)$

It is easy to know that the larger the relative accuracy value, the larger the relative error in mode identification.

2.3 Error Analysis Process

Numerical simulation is used to investigate the influence of the measurement error on the final output of the system in the experimental test. Generally speaking, measurement error is divided into systematic error and random error, but only the influence of random measurement error is considered here, and the random error added in the simulation satisfies the Gaussian distribution.

The numerical simulation process is mainly divided into four steps: 1) based on the given radial modal amplitude $A_{mn}^{}$, the circumferential modal amplitude at different measuring points $\left(x_j,r_l\right)$ can be constructed, where $j$ and $l$ are integers and the ranges are 1∼ $N_x$ and 1∼ $N_r$, respectively; 2) for the $n{i}^{th}$ measurement, the perturbation superimposed to circumferential modal amplitude at position $\left(x_j,r_l\right)$ is defined as follows:

${\tilde{A}}_m\left(x_j,r_l,\left[ni\right]\right)={\sigma }_{A_m}{a}_{jl}\left[ni\right]e^{i{b}_{jl}\left[ni\right]2\pi }(13)$

where ${\sigma }_{A_m}$ is the standard deviation of the circumferential modal amplitude, and $a_{jk}\left[i\right]$ and $b_{jk}\left[i\right]$ are real numbers and their time dependence obeys Gaussian distribution; 3) for each measurement, the radial modal amplitude $A_{mn}\left[i\right]$ can be obtained by solving the pseudo-inverse matrix $W_m^{+}$; 4) after $N_{avg}$ times averaging, the accuracy of the calculation can be determined by solving the formula (Eq. 13) or calculating the standard deviation of each radial mode, which is defined as follows:

${\sigma }_{A_{mn}}=\sqrt{\frac{1}{N_{avg}}{\displaystyle \sum _{i=1}^{N_{avg}}{\left(A_{mn}\left[i\right]-{\overline{A}}_{mn}\right)}^2}}(14)$

The modal amplitude $A_{mn}^{+}$ propagating downstream is set as 85 dB, and $A_{mn}^{-}$ in the upstream direction is set as 75 dB. The average number of times in the calculation is set to 50.

2.4 Array Design Scheme

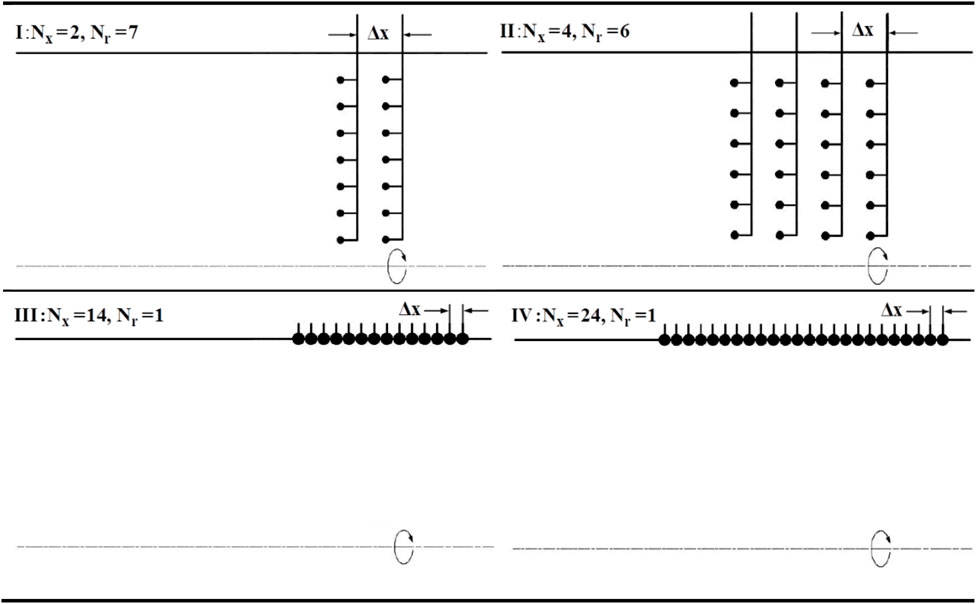
Radial rakes and axial microphone arrays have been mainly developed for acoustic mode identification of engine noise. Therefore, four array design schemes shown in Figure 1 are investigated in this section, the array is represented by prefix A, and different schemes are distinguished by Roman numbers. Generally, the experimental measurement section is arranged in the fan inlet section, so the hub ratio of the four arrays is set as $\eta =\mathrm{0}$. The total number of microphones in the A-I and A-III schemes is $N_x\cdot N_r=14$ and the total number of microphones in the A-II and A-IV schemes is $N_x\cdot N_r=24$. The details are as follows:

FIGURE 1

FIGURE 1. Sensor array schemes A-I to A-VI: $N_x{N}_r=14$ in the left column; $N_x{N}_r=24$ in the right column.

I: Array scheme A-I consists of radial rakes at $N_x=2$ axial measurement positions. Each radial rake consists of $N_r$ microphones arranged at equal radial spacing, and the radial spacing $\Delta r$ and radial position $r_j$ are defined as follows:

$r_j=j\Delta r,j=\left(1\sim N_r\right),\Delta r=\frac{R}{N_r+1}(15)$

II: The array scheme A-II consists of four radial rakes at $N_x=4$ equally spaced axial measurement positions. Each radial rake contains $N_r$ equally distributed sensors, and the radial position and space $\Delta r$ definitions are the same as those of A-I according to the formula (Eq. 15).

III: The array scheme A-III consists of an axial array mounted on the duct wall. There are $N_x$ measuring points arranged at equal intervals in the axial direction. The axial spacing is $\Delta x$.

IV: The array scheme A-IV is similar to A-III, in which the microphones are arranged on the duct wall, but the total number of microphones is different.

A-I and A-III consist of the same number of microphones $N_x\cdot N_r=14$, while A-II and A-IV both have $N_x\cdot N_r=24$ microphones. A-I and A-II are radial rakes, while A-III and A-IV are axial microphone arrays arranged on the duct wall. Therefore, the only common parameter—$\Delta x$—is left. The effect of the array spacing on the matrix condition number and the optimal arrangement will be investigated below.

Considering the number of measuring points $N_{\varphi }$ in the circumferential direction, it is assumed in the simulation that the arrays are all installed on the rotating measuring section, which can accomplish sound pressure collection with enough circumferential measuring points. In all simulations, it is ensured that there are enough measuring points in the circumferential direction, so that the identification of any circumferential mode can meet the sampling requirements. Based on mathematical principles, the modal amplitudes collected by different radial positions in the radial rakes are different, and they will be distributed in the form of Bessel functions along the radial direction, so the modal decomposition can be achieved by using this fixed phase difference appearing between different measurement sensors. In experimental measurements, the measurement of the duct sound field at the fan inlet section, the wake of one or more sensors in the radial microphone array can interfere with noise sources such as the rotor. This changes the original sound field structure and excites additional noise sources. Especially in smaller diameter test benches, the radial rakes can cause airflow blockage, which will essentially change the working point of the turbomachinery. For axial arrays such as A-III and A-IV, both of these drawbacks can be circumvented.

The frequency range for the numerical study is $0\le kR\le 35$, where $k=2\pi f/c$ represents the wavenumber of the sound wave in the free field. The modal cut-on function calculated using Eq. 3 is shown in Figure 2. It can be seen that up to 11 radial modes can be cut on at $kR=35$, and these modes propagate in the downstream and upstream directions, respectively. It can be seen from the figure that the (0,1) mode is cut on at $kR\approx 3.8$, and then at kR, approximately equal to 6.9, 10.1, and 13.3, more radial modes in the duct begin to cut on. The cut-off frequency difference between different radial modes is approximately equal to kR = 3.2. This rule helps to observe the error characteristics of different array design schemes in mode identification and their sensitivity to radial modal cut-off characteristics in the spectrogram.

FIGURE 2

FIGURE 2. Modal cut-on function up to kR = 35.

3 Mode Identification Error Simulation

3.1 Mode Identification Relative Accuracy

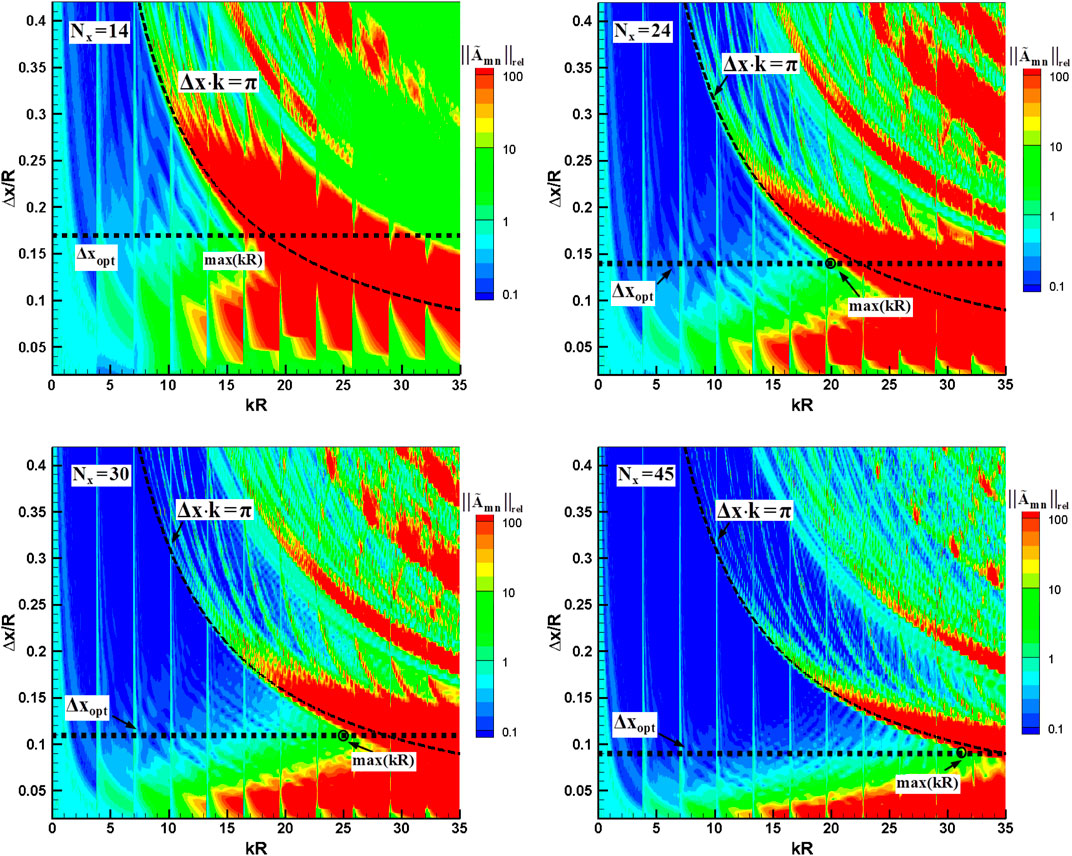
Figure 3 shows the condition number results of the four array schemes at m = 0 circumferential mode; m = 0 mode is selected for analysis because more radial modes can be cut on at m = 0. The results show that the condition number is very sensitive to the axial spacing of the array as well as the frequency. Comparing the relative accuracy results of the four arrays, it can be found that the corresponding frequencies appearing with poor relative accuracy are roughly the same, while the A-I array is better than the other three arrays initially. It can be found that the poor relative accuracy is caused by insufficient sampling of the phase information of the acoustic wave in the axial direction by the array schemes. Unlike the orthogonality of the radial modal eigenfunctions, the axial wavenumbers are not orthogonal, so frequencies with poor relative accuracy in mode identification appear at the following:

$\{\begin{array}{l}\left({\alpha }_{mn}-{\alpha }_{m\nu }\right)k\Delta x=s\cdot 2\pi \left(a\right)\\ \left({\alpha }_{mn}+{\alpha }_{m\nu }\right)k\Delta x=s\cdot 2\pi \left(b\right)\end{array}(16)$

where $s$ is an integer. In principle, as the frequency increases, the number of combinations ( $kR$ and $\Delta x/R$) corresponding to the formula (Eq. 16) will also increase. This is because the number of cut-on radial modal waves continues to increase and the modal cut-off factor approaches 1 with increasing frequency. However, the correlation with respect to the formula (Eq. 16) of the four arrays is different; it depends on the ratio of the radial measurement points to the number of radial modes $N_r/N_{rad}$. When the frequency is close to the mode cut-off frequency, the axial wavenumber $k_{mn}^{\pm }$ is approximately equal to 0, at which the wavelength of the mode approaches infinity. For this condition, it is theoretically necessary to arrange microphones far apart in the axial direction to perform modal measurements. For the A-I and A-II schemes, the number of axial measuring points is small, which can cause the condition numbers of A-I and A-II to surge at $kR\approx f_{c,mn}$ as shown in Figure 3. After a given threshold value $\max \left(\text{|| }{\tilde{A}}_{mn}{\text{||}}_{rel}\right)$, the optimal axial spacing $\Delta x_{opt}$ of each array and the corresponding upper limit of the solvable frequency $\max \left(kR\right)$ can be calculated. According to the numerical study results, the axial array is more suitable for mode identification of airflow noise in ducts because this type of array can maintain a small coefficient matrix condition number and excellent relative accuracy over a wide frequency range. This characteristic is more pronounced in axial arrays with relatively small axial spacing. For all axial arrays, there is an upper limit of the solvable frequency $\max \left(kR\right)$ after a given relative accuracy threshold value, and it can be seen from Figure 3 that for all microphone arrays, the minimum solution frequency satisfies $\min \left(kR\right)\approx 0$, and $\text{|| }{\tilde{A}}_{mn}{\text{||}}_{rel}$ is affected by the $n\ne \nu$ modal combination. The upper frequency limit represented by the black long dashed line in Figure 3 satisfies the law $\Delta x\cdot k=\pi$, which corresponds to the situation in (11(b)) $s=1$ and $n=\nu =0$ (${\alpha }_{\mathrm{0,0}}\equiv 1$ at this time). The lower limit of the axial spacing will decrease with the increase in $N_x{N}_r/N_{rad}$. When the relative accuracy threshold value is set to $\max \left(\text{|| }{\tilde{A}}_{mn}{\text{||}}_{rel}\right)=10$, the optimal spacing of each array and the corresponding upper limit of frequency can be obtained, and the exact values are shown in Table 1. It can be seen that the optimal axial spacing continues to decrease with more axial measuring points being applied in the simulation. It should be noted that when the number of axial measuring points is determined, smaller axial spacing between the measuring sensors is not better, especially when the number of axial measuring points is small, such as $N_x=14$ as shown in Figure 3. Moreover, the upper limit of frequency $\max \left(kR\right)$ that can be solved precisely cannot be obtained simply by $\Delta x\le \lambda /2$, where $\lambda =c/f$, that is to say, the frequency range of mode identification cannot be determined simply using the Nyquist sampling theorem. In experimental measurements, the frequency range that can be accurately solved in mode identification is much smaller than the range calculated using the Nyquist sampling theorem after a given upper error limit.

FIGURE 3

FIGURE 3. Relative accuracy of the four axial arrays.

TABLE 1

TABLE 1. Optimal axial spacing and upper limit of solvable frequency.

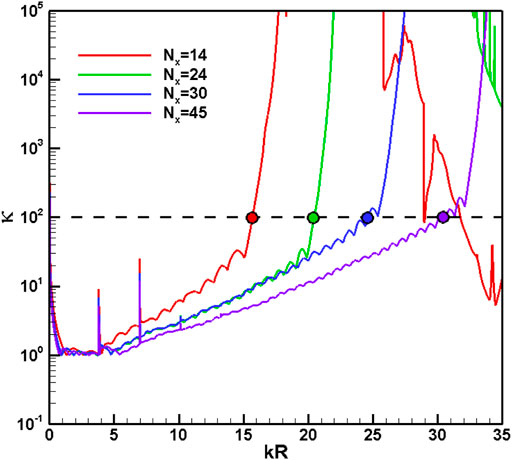
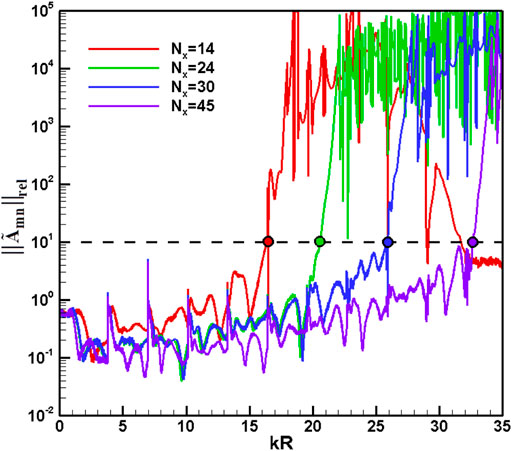
Figures 4, 5 present the condition number and relative accuracy results for the four axial arrays at the optimum spacing, respectively. As the frequency increases, the condition number of the axial array presents a monotonically and steadily increasing trend, and the greater the number of axial measuring points in the array, the slower the increasing trend. Different from the spectral characteristics of the condition number, the relative accuracy results show an upward trend of oscillation as the frequency increases. When the threshold values of the condition number and the relative accuracy are given, it can be found by comparing Figures 4, 5 that the upper limit of frequency $\max \left(kR\right)$ determined by the condition number is basically consistent with that determined by the relative accuracy.

FIGURE 4

FIGURE 4. Condition numbers at optimal spacing for the four axial arrays.

FIGURE 5

FIGURE 5. Relative accuracy of the four axial arrays at optimal spacing.

3.2 Sensitivity of Relative Accuracy of Mode Identification to Modal Order

The previous section only studied the relationship between the axial spacing $\Delta x$ and the upper limit of the solution frequency $\max \left(kR\right)$ during the $m=0$ mode identification process. When the optimum axial spacing $\Delta x_{opt}$ is determined, it is necessary to investigate the relative accuracy during the mode identification process of each circumferential mode. Figure 6 shows the solution accuracy results of circumferential modes of different orders after setting the axial spacing of the four arrays to $\Delta x_{opt}$, and it is necessary to relate the results of the modal cut-off function shown in Figure 2 in the comparative analysis. It can be seen that with the increase in the circumferential mode order m, the change trend of the relative accuracy of each circumferential mode is not the same due to the change of the modal cut-off frequency $f_{c,mn}$ and the modal cut-off factor ${\alpha }_{mn}$. At high frequencies, the identification operation of the low-order circumferential modes is more likely to become unstable because the eigenvalues ${\sigma }_{mn}$ of the low-order circumferential modes are smaller than those of high-order circumferential modes, so that the cut-off factors of the low-order circumferential modes tend to approach 1 more easily, resulting in different modes becoming indistinguishable due to the similar axial wave numbers. This situation will be improved with the increase in axial measuring points. It can also be found in the figure that for any axial array, $m=0$ mode is always the first to appear as the solution instability phenomenon, which indicates that $m=0$ mode is the dominant mode restricting the accuracy of the mode identification method and the upper limit of the solvable frequency, which is consistent with the research conclusion in the previous chapter.

FIGURE 6

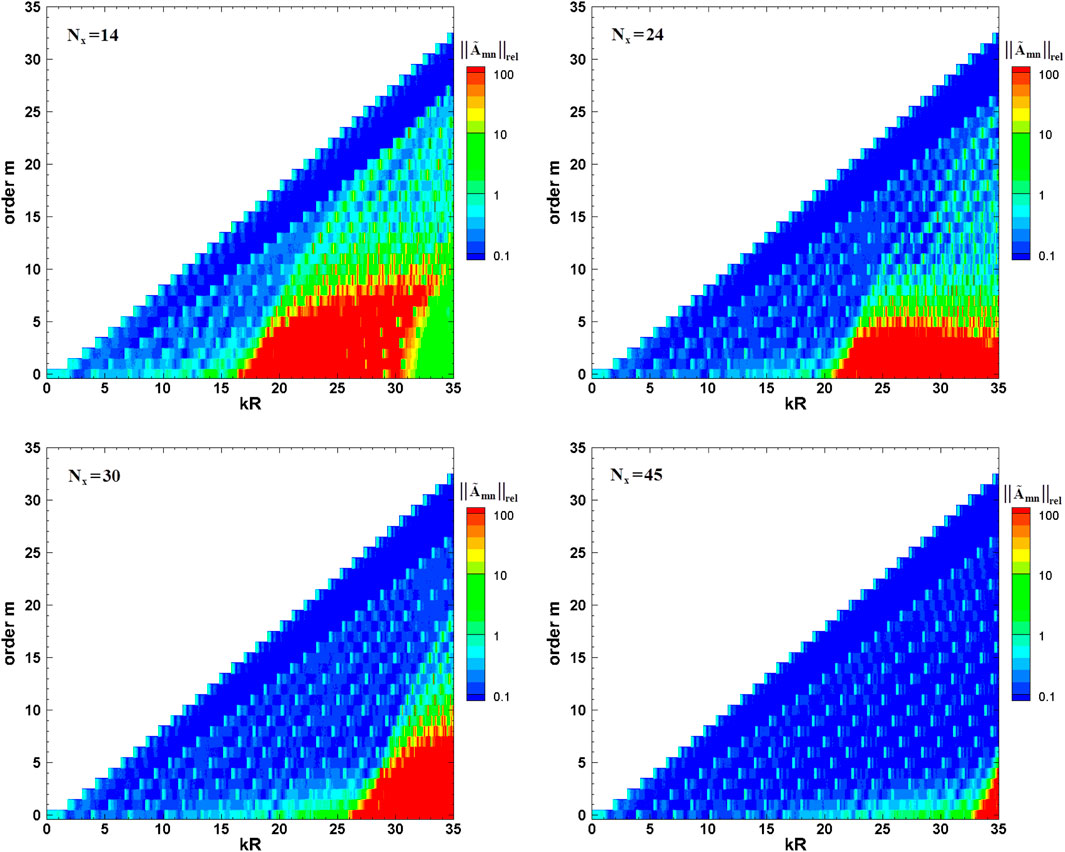
FIGURE 6. Relative accuracy of the four axial arrays under optimum spacing in different circumferential mode decompositions.

4 Array Design Method in Mode Decomposition

4.1 Standard Deviation in Mode Decomposition

In the turbomachinery noise mode identification experiment, the amplitude of each radial mode is what everyone cares about most. The investigations in the previous chapter can only predict the overall accuracy of each radial mode. In this section, modal standard deviation is used to investigate the accuracy of different microphone arrays in mode identification.

Figure 7 shows the standard deviation ${\sigma }_{Amn}/{\sigma }_{Am}$ results when $m=0$ mode is decomposed into each radial mode; the axial spacing of the four arrays is set to $\Delta x=\Delta x_{opt}$. When the flow is uniform in the duct, the modal ${\sigma }_{Amn}$ values are the same for mode propagating upstream and downstream. The simulation results of the artificial sound fields show that when the coefficient matrix condition number is within the range $\kappa \left(w\right)<500$ (or relative accuracy $\text{|| }{\tilde{A}}_{mn}{\text{||}}_{rel}<100$), ${\sigma }_{Amn}/{\sigma }_{Am}$ is independent of the initial modal amplitude $A_{mn}^0$ in the simulated sound source. Therefore, it can also prove that the law in Figure 6 can be applied to any modal amplitude $A_0(x_j,r_k)$. The relative standard deviations of the radial modes are very similar, especially for the modes with radial mode order $n=0$ and $\nu =1$, and their relative standard deviations are in good agreement. It should be noted that the difference between the relative standard deviations of each radial mode ($n\ne \nu$) is not affected by the new cut-on mode, which makes it possible to measure the individual radial modes more accurately when relative accuracy is poor.

FIGURE 7

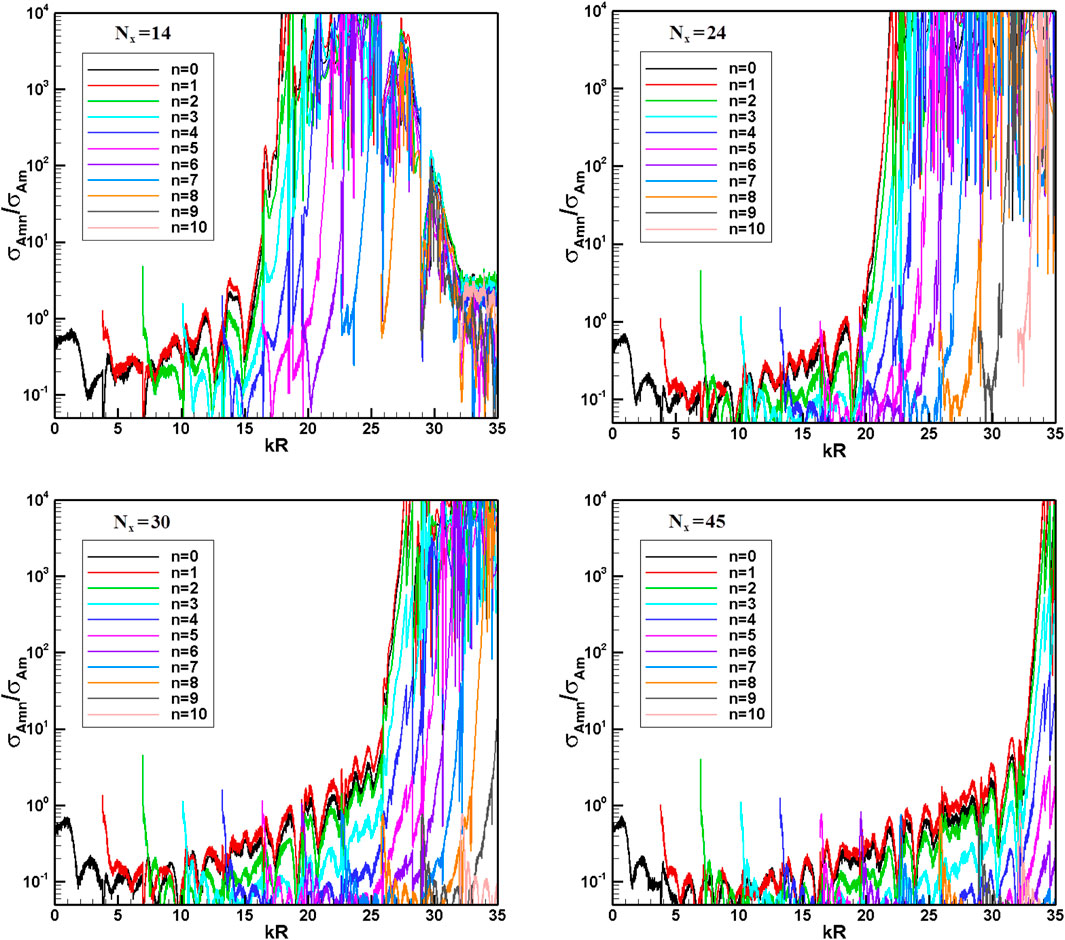
FIGURE 7. Relative standard deviations ${\sigma }_{A_{mn}}/{\sigma }_{A_m}$ in the m = 0 mode decomposition of the four axial arrays with optimal spacing.

4.2 Guidelines for Microphone Array Design

The previous section presents the upper frequency limit of the four axial arrays for mode identification and the optimal spacing in array scheme design. In general, as the number of measuring points increases, the frequency range that can be accurately solved in mode identification also increases. However, the array design scheme will seriously affect the solution accuracy in the mode identification, so it is necessary to investigate the design criteria of the axial array.

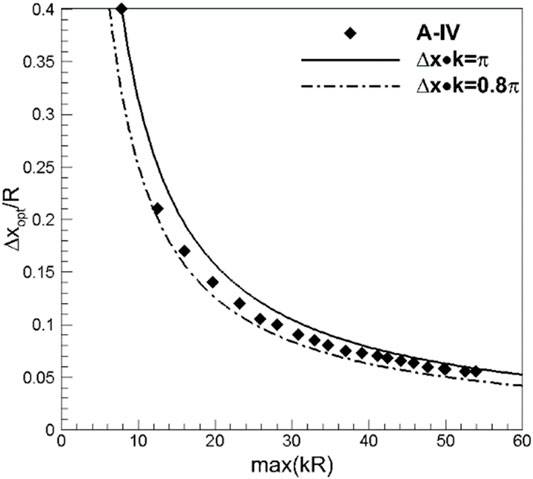
In the process of array design, two main problems need to be solved: (a) when the number of measuring sensors is given, how to quickly determine the distance between the measuring sensors, so that the mode identification measurement in a wider frequency range can be realized within a certain error limit; (b) how to quickly determine the number of measuring sensors required by the array design when the frequency of interest is given. For the first problem, it can be achieved by calculating the optimal axial spacing $\Delta x_{opt}$ and the upper frequency limit $\max \left(kR\right)$ under different numbers $N_x{N}_r$ of measuring sensors in mode identification. Figure 8 presents the optimal spacing results of the axial arrays at different frequencies, where the frequency range increases from $kR=8$ to $kR=56$. In order to describe its distribution law more clearly, two auxiliary curves are given in Figure 8, $\Delta x=\pi /k$ and $\Delta x=0.8\pi /k$, respectively. It can be seen that the optimal spacing satisfies the following:

$\frac{0.8\pi }{kR}\le \frac{\Delta x_{opt}}{R}\le \frac{\pi }{kR}(17)$

FIGURE 8

FIGURE 8. Law of optimal axial spacing applied in array scheme design.

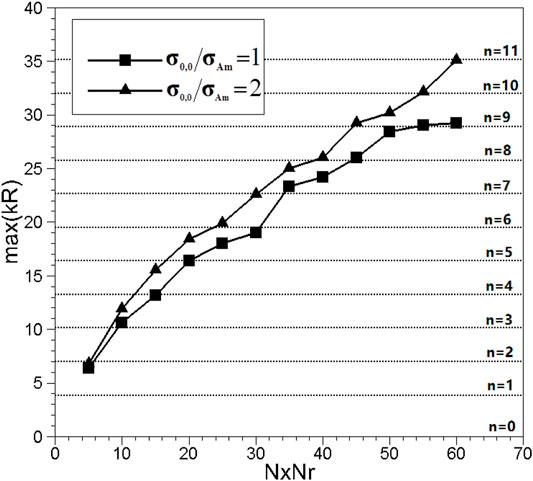
For the second problem, this section investigates the dependence of the frequency upper limit $\max \left(kR\right)$ in mode identification on the number $N_x{N}_r$ of measuring sensors by giving the upper limit of the relative standard deviation ${\sigma }_{A_{0,0}}/{\sigma }_{A_m}$. The calculation of relative standard deviations allow the relative accuracy of individual modes to be determined. From the research in the previous section, it can be seen that the m = 0 mode contains most cut-on radial modes. Therefore, this mode is more sensitive to the measurement device, that is to say, the ${\sigma }_{A_{0,0}}/{\sigma }_{A_m}$ value can be used to identify the accuracy of the entire mode measurement. For a given ${\sigma }_{A_m}$, the signal-to-noise ratio of the mode can be easily obtained. This section examines two relative standard deviation upper limits: ${\sigma }_{A_{0,0}}/{\sigma }_{A_m}=1$ and ${\sigma }_{A_{0,0}}/{\sigma }_{A_m}=2$. The upper limit selected in this section is actually relatively conservative, because when the relative standard deviation is relatively high, the signal-to-noise ratio in mode identification can be improved using the adaptive resampling method (re-sampling technique). Figure 9 shows the required measuring sensors for mode identification as the frequency increases under the two upper limit conditions of the relative standard deviation mentioned above, and the cut-on frequency of each radial order is marked with a dotted line. It can be clearly seen from the figure that with the increasing number of radial modes, the ratio $N_x{N}_r/N_{rad}$ of the number of measuring sensors to that of radial modes for mode identification is not fixed, that is to say, the growth rates of the two numbers are different. For example, at $n=2$, the ratio needs to satisfy $N_x{N}_r/N_{rad}\ge 1.67$; at $n=9$, the ratio needs to satisfy $N_x{N}_r/N_{rad}\ge 4.5$. When given an upper relative standard deviation, it is difficult to determine a parameter that satisfies all modes unless it is set to a large value.

FIGURE 9

FIGURE 9. Required sensors under a given threshold value of relative standard deviation.

5 Experimental Analysis of Mode Identification Error

Regarding the influence of different microphone arrays on the mode identification accuracy, after numerical investigation of error variation, this section will conduct an experimental measurement based on the axial fan test bench. The main purpose of the research is to conduct an experimental study on the differences in mode identification between axial arrays (Axial Arrays, AA) and radial rakes (Radial Rakes, RR) installed, respectively, in the fan inlet section.

5.1 Acoustic Test Bench

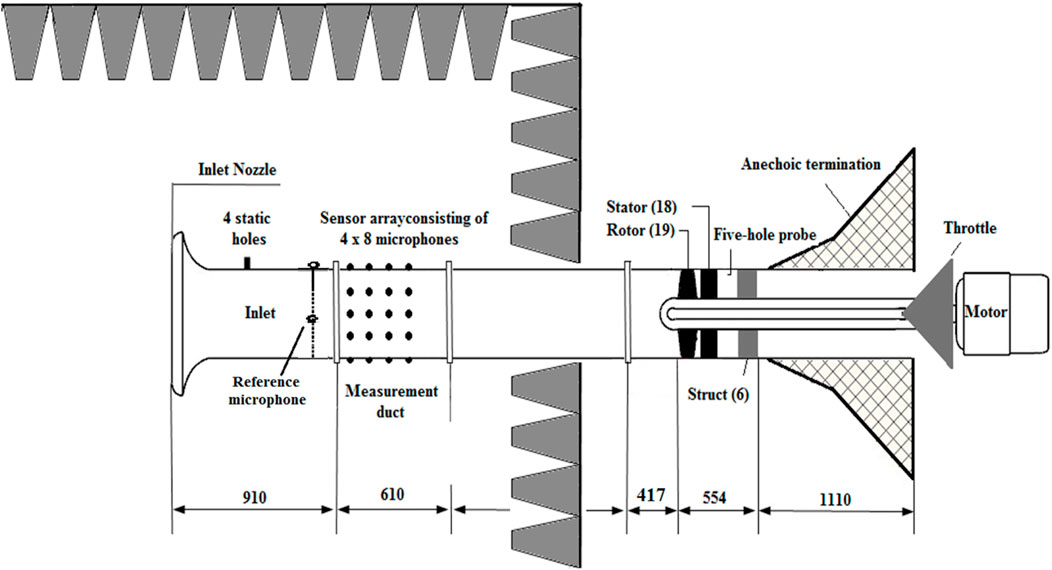
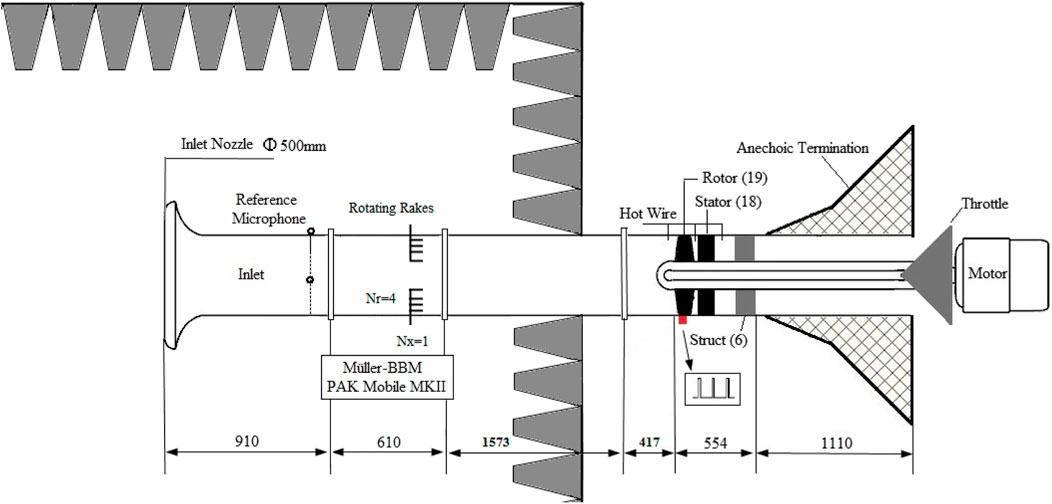
The experimental test scheme of the axial microphone array is shown in Figure 10. The acoustic measurement device is installed in the inlet section of the fan, 1.50 m away from the leading edge of the rotor blade tip. The entire acoustic measurement section and the fan inlet are placed in a semi-anechoic chamber. Four rows of microphones were installed on the acoustic measurement section with an axial spacing of 10 cm. Each row consists of 8 flush-mounted microphones with equal angles.

FIGURE 10

FIGURE 10. Schematic diagram of the axial microphone array in experimental investigation.

Radial rakes are designed and fabricated in this study in order to compare the influence of different microphone arrays on fan noise measurement. The radial rakes are also installed in the acoustic measurement section at the same location as the axial microphone array, and multi-angle measurement is achieved by installing the radial rakes on the casing that can rotate around the axis. A total of 60 circumferential positions are measured in the experimental test. As shown in Figure 11, two radial rakes are installed at the same axial position and separated by 180° in the circumferential direction. Figure 12 shows the actual photo and three-dimensional design of the radial rakes. Each rake has a total of $N_r=4$ measuring points in the radial direction.

FIGURE 11

FIGURE 11. Schematic diagram of rotating radial rakes in experimental investigation.

FIGURE 12

FIGURE 12. Photo and 3D design drawing of radial rakes.

Applying radial rakes to the mode decomposition test of fan noise needs to pay attention to two issues: (1) since the measuring device penetrates deep into the cross section in the duct, it will inevitably affect the original flow field, and its wake may interfere with the rotor and then generate a new interference mode, which may eventually affect the original fan noise field and (2) the microphone is located inside the flow field, and the measured sound pressure will be affected by the airflow velocity and pressure pulsation, which thereby can reduce the signal-to-noise ratio in acoustic test.

This study adopts two ways to deal with the first issue: on one hand, the outer wall of the pipeline wrapping the signal line is designed to be streamlined, so as to ensure that the radial rake is not a blunt trailing edge structure; on the other hand, the axial position of the radial rake is nearly 2 m away from the rotor leading edge. According to the research of Chong (Chong et al., 2015), the turbulent intensity will decay approximately with a regularity ${(x_l-x_0)}^{-5}$, where $x_l$ is the observation point and $x_0$ is the initial position, Therefore, the turbulence intensity 2 m apart will decay to 1/32 of the turbulent intensity at the initial position, which can be approximately ignored. For the second issue, a windshield is installed for each microphone in the experimental measurement to reduce the influence of airflow on the sound pressure test.

5.2 Signal-to-Noise Ratio

In order to analyze the accuracy of sound pressure acquisition data, the concept of signal-to-noise ratio (SNR) is used here, which can be defined as follows (Joseph et al., 2003; Tapken et al., 2008):

$SN{R}_p=20\times \log \left(P_{RMS}/s_p\right)(18)$

where $P_{RMS}$ is the root mean square (RMS) result of the complex sound pressure amplitudes (frequency domain results after fast Fourier transform) of all measuring points at a single frequency, but $s_p$ is the random pulsation amplitude of the complex sound pressure amplitudes $p$. The measured sound pressure time series signal is processed by sub-window truncation, and the truncated data are processed by FFT, respectively, where $p\left[k\right]$ represents the complex pressure value calculated from the k’th window truncated data. The component of the sound pressure at the measurement point at this frequency is represented by the mean of multiple Fourier transforms, namely,

$\overline{p}=\frac{1}{N_{total}}{\displaystyle \sum _{k=1}^{N_{total}}p\left[k\right]}(19)$

For a single sound pressure measurement point, starting from time $i$, a single subset consists of $N_{win}$ data, where the mean of $N_{win}\ll N_{total}$ is defined as follows:

$p_{N_{win}}\left[i\right]=\frac{1}{N_{win}}{\displaystyle \sum _{j=1}^{N_{win}}p\left[i-1+j\right]}(20)$

When repeated $p_{N_{win}}\left[i\right]$ such that $i=\mathrm{1,2},\mathrm{...},N_{means}$, the $s_p$ of sound pressure is defined as follows:

$s_p=\sqrt{\frac{1}{N_{means}}{\displaystyle \sum _{i=1}^{N_{means}}{\left(p_{N_{win}}\left[i\right]-\overline{p}\right)}^2}}(21)$

It represents the predicted magnitude of random noise superimposed on the valid signal during the measurement.

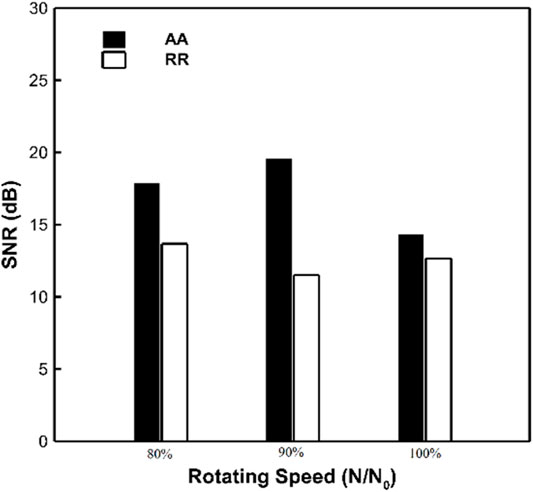
Figure 13 shows the signal-to-noise ratio results of the sound pressure data measured by the two arrays at different operation conditions. It can be seen that the SNR values at all operation conditions are higher than 10 dB, which indicates that the quality of the sound pressure data during the entire measurement process is good. The signal-to-noise ratio of the axial array increases as the rotational speed increases because the aerodynamic interference between the rotor and stator becomes stronger with higher rotational speed. However, the signal-to-noise ratio of the radial rakes decreases with increasing rotational speed; this may be because when the air velocity increases, the influence of the air pressure pulsation on the radial rake is also intensified. In order to further investigate this phenomenon, Figure 14A presents the RMS and $s_p$ results for radial rakes and axial arrays, respectively. It can be seen that as the rotational speed increases, the RMS of the sound pressure data shows an overall upward trend, although at 80% and 90% design rotational speed, the RMS value of the sound pressure measured by the axial array is lower than that of the radial rake, and the signal-to-noise ratio of the measured signal of the axial array is higher than that of the radial array as shown in Figure 13 because the random noise of the axial array is smaller. At 100% design speed, although the RMS value of sound pressure has increased, the final signal-to-noise ratio result is smaller than those of the first two operation conditions because of the larger margin increase in random noise at this operation condition. This is the intrinsic reason for the reduction in the SNR of the sound pressure signal at 100% rotational speed in Figure 13. Figure 14B shows the RMS and $s_p$ difference results of the radial rake array and the axial array, respectively, where the black bar chart represents the RMS difference $\mathrm{RM}{\mathrm{S}}^{\left(\mathrm{RR}\right)}-\mathrm{RM}{\mathrm{S}}^{\left(\mathrm{AA}\right)}$ of all measuring points, and the green histogram represents the amplitude difference of $\mathrm{S}{\mathrm{p}}^{\left(\mathrm{RR}\right)}-\mathrm{S}{\mathrm{p}}^{\left(\mathrm{AA}\right)}$. It can be seen that as the fan rotational speed increases, the RMS value of the sound pressure measured by the axial array increases faster than the result of the radial rake. In terms of random noise, the results of radial rake are larger than those of the axial array at the three operation conditions because the microphones of the axial array are all wall-mounted, which are much less affected by airflow velocity or pressure pulsation than the radial rakes exposed to the airflow.

FIGURE 13

FIGURE 13. Results of signal-to-noise ratio at different operation conditions.

FIGURE 14

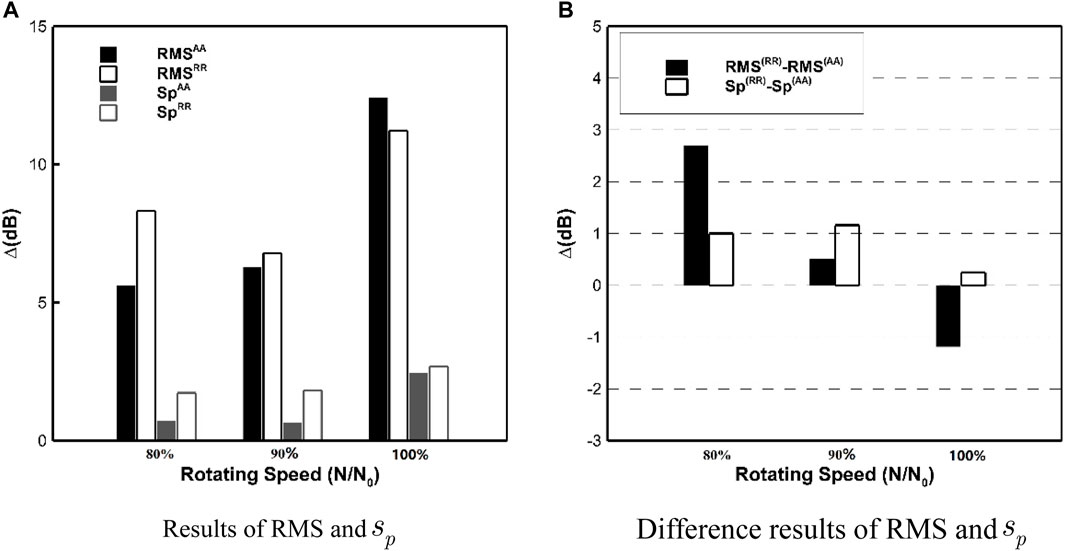
FIGURE 14. RMS and $s_p$ of sound pressure measurement signals measured by radial rakes and axial arrays. (A) Results of RMS and $s_p$. (B) Difference results of RMS and $s_p$.

5.3 Mode Decomposition Results

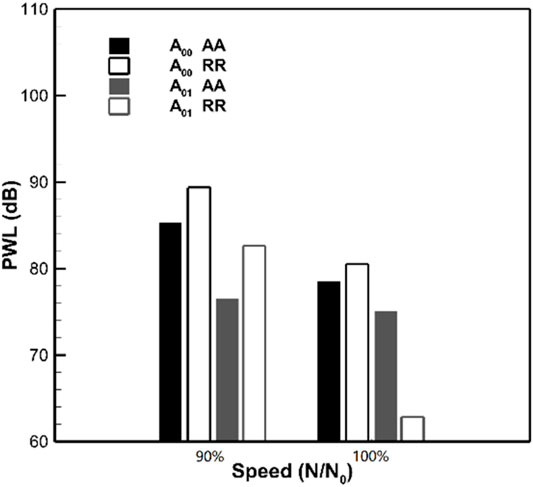
Based on the two measurement devices designed in the above sections, this section conducts experimental measurements on the fan inlet noise. Figure 15 presents the sound power results for each circumferential mode measured by the axial array (AA) and radial rake (RR) at 1 BPF. Figure 15A shows the results of circumferential sound power at 90% design speed condition. It can be seen that the modal sound power calculated by the radial rakes is generally larger than that of the axial arrays, the difference between the dominant mode m = 1 is 3 dB, and the difference between the non-dominant modes is even greater. It can be seen that the results measured by the two arrays are in good agreement on the whole at 100% design speed condition as shown in Figure 15B. The difference in the sound power results of the m = 1 dominant mode measured using the two devices is less than 1 dB, and the test results of the two devices are also in good agreement in the low-order circumferential mode range (m = −2 to m = +1). The sound power results of the high-order circumferential mode measured by different arrays have large deviations, which may be caused by the non-dominant modes being “buried” into random noise in the calculation. Referring to Figure 13, the SNR of the measured signal at 90% design speed condition is only 11 dB, but the non-dominant mode (m≠1) in Figure 15A is at least 13 dB lower than that of the dominant mode, and the difference is greater than the acquisition signal-to-noise ratio of the signal, which makes the estimation results of these non-dominant modes heavily influenced by random noise and eventually unreliable. At 100% design speed condition, although the signal-to-noise ratio of the two arrays is relatively small, the measurement results of the two devices have high consistency. In order to better investigate the influence of random noise during measurement on mode identification, it is necessary to derive the transfer relationship between the mode identification error and the random noise of sound pressure measurement. For the sound pressure measured at a single location, it can be expressed as a superposition of the actual value and random noise, namely,

$p_l=p_l^0+{\tilde{p}}_l(22)$

FIGURE 15

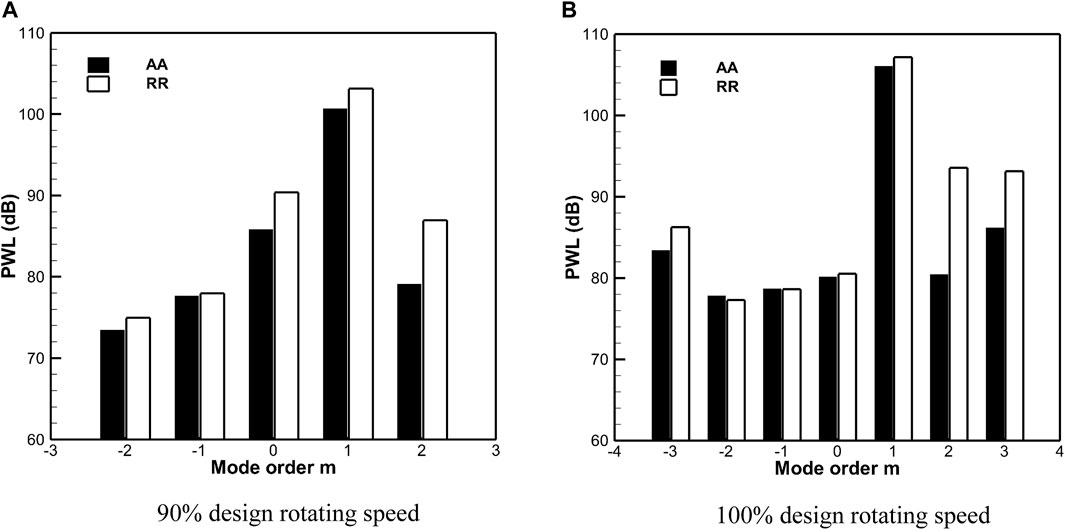
FIGURE 15. Comparison of modal sound power applying radial rakes and axial microphone arrays. (A) 90% design rotating speed. (B) 100% design rotating speed.

In the formula, the random noise amplitude satisfies the Gaussian distribution. If the random noise collected at different measuring points is incoherent, then the expected value of random noise satisfies the following:

$\langle {\tilde{p}}_l\rangle =0\langle {\tilde{p}}_l{\tilde{p}}_{l\mathrm{’}}^{\ast }\rangle =s_p^2{\delta }_{ll\mathrm{’}}(23)$

If it is further assumed that all measuring points and the signal transfer function are the same, then the amplitude of the circumferential mode can be written as follows:

$A_m=\frac{1}{N_{\varphi }}{\displaystyle \sum _{l=0}^{N_{\varphi }-1}{p}_l^0\cdot e^{-iml2\pi /N_{\varphi }}}+\frac{1}{N_{\varphi }}{\displaystyle \sum _{l=0}^{N_{\varphi }-1}{\tilde{p}}_l\cdot e^{-iml2\pi /N_{\varphi }}}(24)$

The first part of Eq. 19 is denoted as $A_m^0$ , and the second part is denoted as ${\tilde{A}}_m$ ; then the error amplitude of the circumferential mode is equal to the following:

$\langle {\tilde{A}}_m{\tilde{A}}_{m\mathrm{’}}^{\ast }\rangle =\frac{1}{N_{\varphi }^2}{\displaystyle \sum _l{\displaystyle \sum _{l^{\prime }}\langle {\tilde{p}}_l{\tilde{p}}_{l^{\prime }}^{\ast }\rangle }}\cdot e^{-i\left(ml-m\mathrm{’}l\mathrm{’}\right)2\pi /N_{\varphi }}=\frac{s_p^2}{N_{\varphi }^2}{\displaystyle \sum _l{e}^{-i\left(m-m\mathrm{’}\right)l2\pi /N_{\varphi }}}=\frac{s_p^2}{N_{\varphi }^2}{\delta }_{mm\mathrm{’}}(25)$

Therefore, the standard deviation in mode identification is as follows:

$s_{A_m}=\frac{s_p}{\sqrt{N_{\varphi }}}(26)$

That is to say, the standard deviation of mode identification is smaller than the standard deviation of sound pressure measurement, and the two values are proportional. This shows that random noise during measurement will have a linear effect on the accuracy of mode identification.

The modal acoustic powers calculated by the radial rakes in Figure 15 are generally greater than the results of the axial arrays because the random noise measured by the radial rake is larger than that of the axial array. As shown in Figure 14, $\mathrm{S}{\mathrm{p}}^{\left(\mathrm{RR}\right)}-\mathrm{S}{\mathrm{p}}^{\left(\mathrm{AA}\right)}$ is a positive value at each operation condition. The physical mechanism of this phenomenon is easy to understand; in experimental measurements, although the microphones on the radial rake are equipped with windshields, the airflow velocity and pressure pulsations in the airflow will still affect the sound pressure data measured by the microphones. In contrast, the microphones arranged on the duct wall are relatively less affected by the airflow velocity or pressure pulsation during the signal acquisition process, that is to say, the two arrays have different sensitivities to the airflow in the duct. In order to analyze the error characteristics of the two microphone arrays in the identification of different radial modes, Figure 16 shows the (0, 0) and (0, 1) modes measured by the axial array and the radial rakes. At 90% design rotational speed, modal results measured by radial rakes are larger than those identified by the axial arrays, which results in the sound power of the m = 0 mode decomposed by radial rakes being higher than that decomposed by axial arrays as shown in Figure 15A. For 100% design rotational speed, the two arrays have high consistency in the identification of the n = 0 radial mode. The main difference is in the identification of the n = 1 radial mode, which may be caused by the low accuracy in mode identification with high cut-on ratios induced by the small angle between the main lobe of modal radiation and the axis.

FIGURE 16

FIGURE 16. Comparison of results for radial modes n = 0 and n = 1.

Although the mode decomposition results of different radial modes are different, this effect is negligible for circumferential mode recognition, for example, the sound power of the m = 0 mode measured by the two arrays matches very well as shown in Figure 15B. The above content mainly focuses on the influence of random noise in sound pressure measurement on modal recognition, but as Taddei et al. (2013) stated, the accuracy of the acoustic model used in mode decomposition is another main factor affecting mode identification. Distortion of the airflow in the duct, other noise sources, errors in the aerodynamic parameters of the airflow, etc. will affect the accuracy of the mode identification, and the two typical arrays have different sensitivities to the acoustic models used in the mode identification. This study uses an equally spaced axial array and radial rakes to test the fan noise. For non-equidistant or compressed sensing arrays, finding out whether the error transfer characteristics obtained in this study are applicable requires further research. How to use the obtained error characteristics in modal decomposition to design a new test method or a new array scheme needs further research, especially for large ventilation facilities.

6 Conclusion

Based on the error analysis theory, the influence of different microphone arrays on the accuracy of acoustic mode identification is studied, and the design criteria for axial microphone arrays are established. Through the processing of rotating radial rakes and axial arrays, the experimental analysis of the acoustic mode identification error applying different arrays is carried out.

Although radial rakes can directly measure the radial distribution of the modal amplitude, this type of array has a large error in the mode identification at low frequencies. As the frequency approaches the cut-on frequency of the mode, the condition number of the coefficient matrix increases by about two orders of magnitude. Compared with the axial arrays, the radial rakes are more suitable for mode identification at high frequencies. At low frequencies, the condition number of the coefficient matrix is less than 10 when applying axial arrays. Therefore, the axial microphone arrays will become more advantageous than the radial rakes in practice. The design criterion of axial microphone array is established: (a) m = 0 mode is the dominant mode that restricts the mode identification accuracy and the upper limit of the frequency that can be solved; (b) the accuracy of the axial microphone array in mode identification strongly depends on the axial spacing of the array measuring points, and when $0.8\pi /kR\le \Delta x/R\le \pi /kR$ is satisfied, the frequency range of the mode identification investigation can be broadened; (c) the upper frequency limit for mode identification cannot be estimated by means of $\Delta x\le \lambda /2$, and when the error threshold value is given in the experimental measurement, the frequency range of mode identification is much smaller than that calculated using the Nyquist sampling theorem; and (d)when given an upper limit of relative standard deviation, it is difficult to determine a $N_x{N}_r/N_{rad}$ parameter that satisfies all modes unless it is set to a large value.

The experimental test results show that the modal sound power values calculated with axial arrays and radial rakes are in good agreement, especially for the rotor–stator interference mode determination. The small deviations in the mode identification when applying the two typical arrays are caused by the different signal-to-noise ratios of the sound pressure signals acquired by the two arrays and their discriminative sensitivities to the duct airflow.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

KX is responsible for the whole article, CL is responsible for the experimental investigation and also the data processing, FT is responsible for the error analysis, and WQ is responsible for the article scheme and the idea to investigate the difference of modal sound power when using the two typical arrays.

Funding

This work was financially supported by the National Natural Science Foundation of China (Grant No. 12002150), The Ministry of Education of Humanities and Social Science Project (Grant No. 20YJCZH196), the Natural Science Foundation of Jiangsu Province, China (Grant No. BK20201041), the Key Laboratory of Aerodynamic Noise Control of China Aerodynamics Research and Development Center (Grant No. ANCL20190306), and the Scientific Research Fund of High-Level Talents in Nanjing Institute of Technology (Grant No. YKJ201906).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bolleter, U., Cohen, R., and Wang, J. (1973). Design Considerations for an In-Duct Soundpower Measuring System. J. Sound Vibration 28 (4), 669–685. doi:10.1016/s0022-460x(73)80142-7

CrossRef Full Text | Google Scholar

Bolleter, U., and Crocker, M. J. (1972). Theory and Measurement of Modal Spectra in Hard‐Walled Cylindrical Ducts. The J. Acoust. Soc. America 51, 1439–1447. doi:10.1121/1.1912994

CrossRef Full Text | Google Scholar

Cheng, L., Yang, W. K., and Liang, T. (2019). Failure Diagnosis on Gas Path of Fan/compressor Based on Acoustic Mode[J]. J. Mech. Eng. 55 (13), 38–44. doi:10.3901/JME.2019.13.038

CrossRef Full Text | Google Scholar

Chong, T. P., Vathylakis, A., and Mcewen, A. (2015). “Aeroacoustic and Aerodynamic Performances of an Aerofoil Subjected to Sinusoidal Leading Edges [C],” in 21th AIAA/CEAS Aeroacoustics Conference. Dallas TX. AIAA 2015-2200.

Google Scholar

Dahl, M. D., Hixon, R., and Sutliff, D. L. (2013). “Further Development of Rotating Rake Mode Measurement Data Analysis [C],” in 19th AIAA/CEAS Aeroacoustics Conference. AIAA-2013-2246.

Google Scholar

Enghardt, L., Tapken, U., Kornow, O., and Kennepohl, F. (2005). “Acoustic Mode Decomposition of Compressor Noise under Consideration of Radial Flow Profiles[C],” in 11th AIAA/CEAS Aeroacoustics Conference, Monterey, United States, 2005–2833.

Google Scholar

Enghardt, L., Tapken, U., Neise, W., Kennepohl, F., and Heing, K. (2001). “Turbine Blade/vane Interaction Noise: Acoustic Mode Analysis Using In-Duct Sensor Rakes[C],” in 7th AIAA/CEAS Aeroacoustics Conference. Maastricht, Netherlands, 2001–2153.

Google Scholar

Enghardt, L., Tapken, U., Neise, W., Schimming, P., Maier, R., et al. (2002). Active Control of Fan Noise from High-Bypass Aeroengines: Experimental Results[J]. Aeronaut. J. R. Aeronaut. Soc. 106, 501–506. doi:10.1017/S0001924000092356

CrossRef Full Text | Google Scholar

Enghardt, L., Zhang, Y., and Neise, W. “Experimental Verification of a Radial Mode Analysis Technique Using wall-flush Mounted Sensors[C],” in Joint Meeting”Berlin 99” TU-Berlin, March 1999, 137th Regular Meeting of the Acoustical Society of America.

Google Scholar

Farassat, F., Nark, D. M., and Thomas, R. H. (2001). “The Detection of Radiated Modes from Ducted Fan Engines[C],” in 7th AIAA/CEAS Aeroacoustics Conference. Maastricht, Netherlands, 2001–2138.

Google Scholar

Heidelberg, L., and Hall, D. G. (1996). Inlet Acoustic Mode Measurements Using a Continuously Rotating Rake [J]. AIAA J. Aircraft. 32 (4), 761–767. doi:10.2514/3.46788

CrossRef Full Text | Google Scholar

Holste, F., and Neise, W. (1997). Noise Source Identification in a Propfan Model by Means of Acoustical Near Field Measurements. J. Sound Vibration 203 (4), 641–665. doi:10.1006/jsvi.1996.0890

CrossRef Full Text | Google Scholar

Joppa, P. D. (1987). Acoustic Mode Measurements in the Inlet of a Turbofan Engine. J. Aircraft 24 (9), 587–593. doi:10.2514/3.45482

CrossRef Full Text | Google Scholar

Joseph, P., Morfey, C. L., and Lowis, C. R. (2003). Multi-mode Sound Transmission in Ducts with Flow. J. Sound Vibration 264 (3), 523–544. doi:10.1016/s0022-460x(02)01205-1

CrossRef Full Text | Google Scholar

Kan, K., Yang, Z., and Lyu, P. (2021). Numerical Study of Turbulent Flow Past a Rotating Axial-Flow Pump Based on a Level-Set Immersed Boundary Method[J]. Renew. Energ. 168, 960–971. doi:10.1016/j.renene.2020.12.103

CrossRef Full Text | Google Scholar

Kim, Y., and Nelson, P. A. (2004). Estimation of Acoustic Source Strength within a Cylindrical Duct by Inverse Methods [J]. J. Sound Vibration 275 (1-2), 391. doi:10.1016/j.jsv.2003.06.032

CrossRef Full Text | Google Scholar

Lan, J. H., Premo, J. W., and Sutliff, D. L. (2002). “Inlet Mode Measurements with an Inflow Control Device Microphone Array[C],” in 8th AIAA/CEAS Aeroacoustics Conference, Breckenridge, United States, 2002–2563.

Google Scholar

Liu, J., Liu, Y., and Bolton, J. S. (2018). Acoustic Source Reconstruction and Visualization Based on Acoustic Radiation Modes. J. Sound Vibration 437, 358–372. doi:10.1016/j.jsv.2018.08.030

CrossRef Full Text | Google Scholar

Moore, C. J. (1979). Measurement of Radial and Circumferential Modes in Annular and Circular Fan Ducts. J. Sound Vibration 62 (2), 235–256. doi:10.1016/0022-460x(79)90024-5

CrossRef Full Text | Google Scholar

Nelson, P., and Yoon, S. (2000). Estimation of Acoustic Source Strength by Inverse Method: Part I, Conditioning of the Inverse Problem [J]. J. Sound Vibration 233 (4), 643–668. doi:10.1006/jsvi.1999.2837

CrossRef Full Text | Google Scholar

Qiao, W. Y. (2010). Aero-engine Aeroacoustics [M]. Beijing: Beijing University of Aeroacoustics & Astronautics Press, 1–8.

Google Scholar

Sutliff, D. L. (2005). Rotating Turbofan Duct Mode Measurement system[R]. NASA-TM-213828. Cleveland, OH: Glenn Research Center.

Google Scholar

Taddei, F., Lucia, M. D., Torzo, D., and Spano, E. (2013). “A Comparison between Radial Rakes of Sensors and Axial Arrays of Microphones for the Experimental Investigation of Tone Noise in LPTs [C],” in 19th AIAA/CEAS Aeroacoustics Conference. Berlin.

Google Scholar

Tapken, U., Bauers, R., and Enghardt, L. (2008). “Turbomachinery Exhaust Noise Radiation Experiments-Part 2: In-Duct and Far-Field Mode Analysis [C],” in 14th AIAA/CEAS Aeroacoustics Conference (Vancouver, British Columbia Canada. AIAA-2008-2858.

Google Scholar

Tapken, U., and Enghardt, L. (2006). “Optimization of Sensor Arrays for Radial Mode Analysis in Flow Ducts[C],” in 12th AIAA/CEAS Aeroacoustics Conference (Cambridge, MA. UK, 2006–2638.

Google Scholar

Tapken, U., Raitor, T., and Enghardt, L. (2009). “Tonal Noise Radiation from an UHBR Fan- Optimized In-Duct Radial Mode Analysis[C],” in 15th AIAA/CEAS Aeroacoustics Conference. AIAA-2009-3288.

Google Scholar

Wagih Nashed, M., Elnady, T., and Åbom, M. (2018). Modeling of Duct Acoustics in the High Frequency Range Using Two-Ports. Appl. Acoust. 135, 37–47. doi:10.1016/j.apacoust.2018.01.009

CrossRef Full Text | Google Scholar

Wang, L. F., Qiao, W. Y., and Ji, L. (2014). In-duct Circumferential Acoustic Mode Measurement of Axial fan/Compressor[J]. J. Aerospace Power 29 (4), 917–926. doi:10.13224/j.cnki.jasp.2014.04.024

CrossRef Full Text | Google Scholar

Xu, K. B., Qiao, W. Y., and Huo, S. Y. (2018). Research of Mode Identification and Error Transfer Property on Fan Tonal Noise [J]. J. Propulsion Technology 39 (1), 185–195. doi:10.13675/j.cnki.tjjs.2018.01.021

CrossRef Full Text | Google Scholar

Yardley, P. D. (1974). Measurement of Noise and Turbulence Generated by Rotating Machinery [D]. PhD Thesis. Southampton: University of Southampton.

Google Scholar

Zhou, D., Wang, X. Y., and Chen, J. (2015). Investigation of Sound Generation by Non-synchronously Vibrating Rotor Blades[J]. Acta Aeronautica et Astronautica Sinica 36 (3), 737–748. doi:10.7527/S1000-6893.2015.0029

CrossRef Full Text | Google Scholar

Zillmann, J., and Tapken, U. (2009). “Tonal Noise Radiation from UHBR Fan- Active Control of Radiation Characteristic [C],” in 15th AIAA/CEAS Aeroacoustics Conference. AIAA-2009-3226.

Google Scholar