- 1Department of Mathematics, Mohi-ud-Din Islamic University, Nerian Sharif, Pakistan
- 2Department of Mathematics and Statistics, Hazara University, Mansehra, Pakistan
- 3Department of Mathematics, Faculty of Sciences, HITEC University, Taxila Cantt, Pakistan
- 4Department of Mathematics, College of Science Al-Zulfi, Majmaah University, Al-Majmaah, Saudi Arabia
- 5Research Centre, Future University in Egypt, New Cairo, Egypt
- 6Department of Mechanical Engineering, College of Engineering at Al Kharj, Prince Sattam bin Abdulaziz University, Al-Kharj, Saudi Arabia
- 7Department of Mechanical Engineering, University of Tunis EI Manar, Tunis, Tunisia
This analysis is concerned about the thermal performance of [(MgZn6Zr)/C8H18]nf by incorporating the essential concept of non-linear thermal radiations. The flow is configured over a 3D stretchable surface which is heated convectively and the surface boundaries updated with slip effects; uniform suction is applied. The proper mathematical modeling is performed by exercising the nanofluids’ empirical correlations and similarity equations. Thereafter, the RK scheme is utilized to execute the problem solution. The influences of imperative flow constraints are furnished and discussed deeply. The results revealed that [(MgZn6Zr)/C8H18]nf motion decays against suction (
Introduction
Nanotechnology is the most progressive and potential research area in the modern technological world. The nanoparticles of various metallic/non-metallic ferrites, CNTs, oxides, and alloys are the key ingredients in nanotechnology. In this loop, nanofluids are also imperatively contributed in the nanotechnological world. These are fluids that contain the components of solid nanosized particles of aforesaid nanomaterials with base solvents such as EO (engine oil), SO (syltherm oil), water, EG (ethylene glycol), and PG (propylene glycol). The addition of these solid components in the base solvents enhances thermal conductivity of the resultant liquids which makes them more effective for nanotechnological purposes.
Nanofluids are extensively utilized for nanotechnological purposes, aerodynamics, paint industries, manufacturing of electronic parts, mechanical engineering, chemical engineering, applied thermal engineering, manufacturing of home appliances, and biomedical engineering. In recent times, biomedical nanotechnologists have directed their attention to induct nanofluids in the field of biomedical engineering. The nanoparticles and nanofluids are utilized to target many diseases in the human body. A milestone that biomedical technologists have achieved is the induction of nanoparticles for targeting cancer cells and tumors in different parts of the human body. More specifically, oxide and silver nanoparticles are used to target the tumor cells. The modern chemotherapy treatment is also based on injecting nanoparticles in human parts to signify the tumor cells (Zhao et al., 2011; Ganau et al., 2018; Khan et al., 2020a; Ray and Bandyopadhyay, 2021). Furthermore, the interaction of nanoparticles with blood as the base solvent is an important research zone in the field of biomedical sciences. Figure 1A presents the role of nanoparticles in nanotechnology used in biomedical engineering.
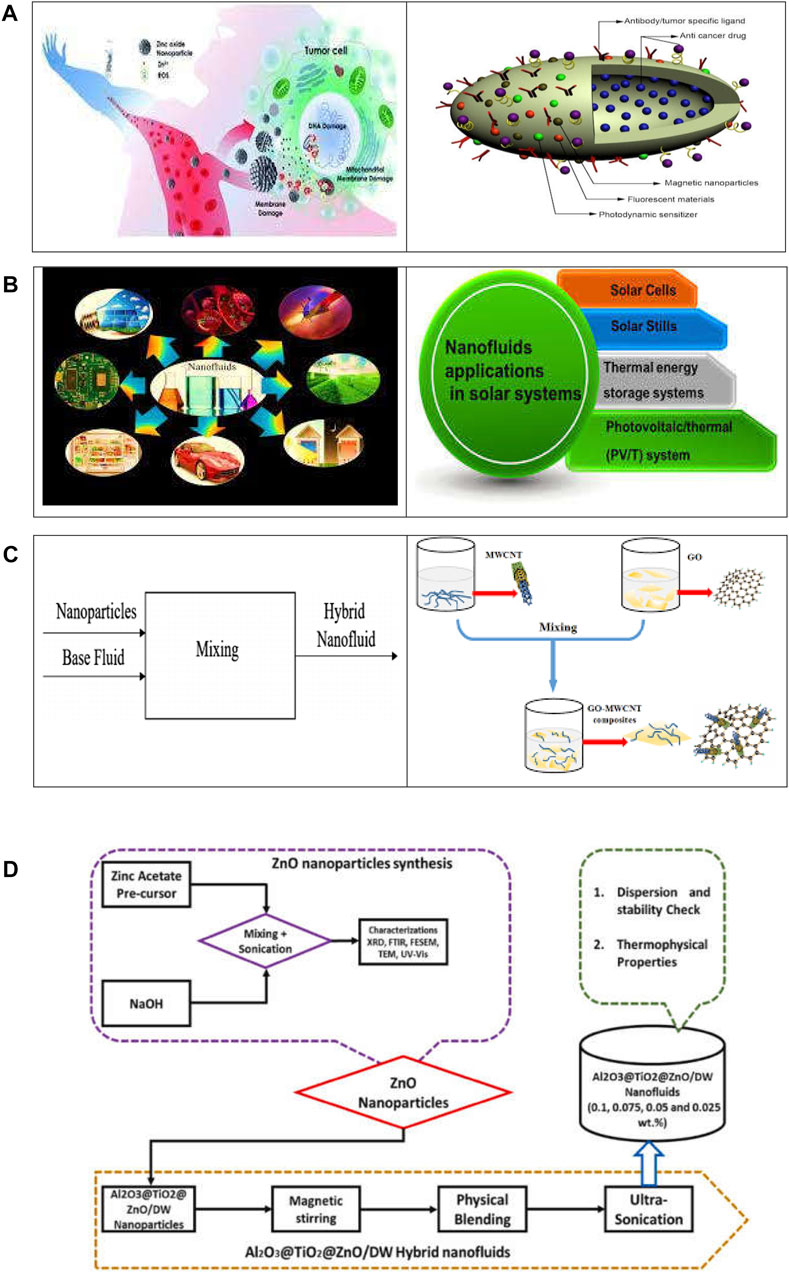
FIGURE 1. (A) Nanotechnology and the field of biomedical engineering. (B): Applications of nanofluids in different zones. (C): Hybrid nanofluids’ synthetization process. (D): Schematic representation of the synthetization process of ternary hybrid nanofluids.
World-renowned researchers did not stop their effects, and they worked on the modifications of nanoparticles and synthesized various nanofluids by combining metallic nanoparticles under various base solvents. They introduced two new classes called hybrid and ternary hybrid nanofluids. Therefore, modern effective heat transport fluids can be characterized in the following three classes:
• Regular liquids such as EG, EO, SO, water, and KS have very restricted applications in nanotechnology because of a very low thermal performance.
• Nanofluids (Zhao et al., 2015; Ahmed et al., 2018; Khan et al., 2018; Ali et al., 2019; Ahmed et al., 2020; Prasad et al., 2020) (1st generation thermal transport fluids) such as Al2O3/EG, AA7072/EO, SWCNTs/SO, CNTs/water, and MgZn6Zr/KS have better heat performance and are more suitable for broad uses than regular liquids.
• Hybrid nanofluids (Ilyas et al., 2021; Ijaz, 2021; Mohyud-Din et al., 2020; Imran et al., 2020; Khashi’ie et al., 2022; Said et al., 2021; Khan et al., 2020b) (2nd generation thermal transport fluids) such as MWCNTs-Al2O3/EG, AA7075-AA7072/H2O, magneto-nanofluid (Abbasi et al., 2017 andKhan et al., 2017), MWCNTs-SWCNTs/SO, Ag-CoFe3O4/water, and MgZn6Zr-MnZnFe3O4/KS have improved heat transport and are effectively used for different nanotechnology purposes than the preceding two classes of the fluids.
• Tri-hybrid nanofluids (Ramadhan et al., 2019; Muzaidi et al., 2021; Palanisamy et al., 2021; Ramadhan et al., 2021; Hou et al., 2022) (3rd generation of thermal transport fluids; addition of a third nanoparticle (Adnan et al., 2022) in the hybrid nanoparticles) are a very recently developed class and exhibit an ultra-high thermal performance which makes it superior to the preceding three classes of the fluids. In these fluids, two metallic/non-metallic or other nanoparticles are induced in the host solvent to synthesize the resultant tri-hybrid nanofluids [SWCNTs-MWCNTs-Al2O3/EG, MgZn6Zr-AA7075-AA7072/EO, MWCNTs-SWCNTs-Ag/SO, MnZnFe3O4-Ag-CoFe3O4/water, and NiZnFe3O4-MgZn6Zr-MnZnFe3O4/KS]. Induced tri-nanoparticles enhance thermal conductivity at a high level, which improves its heat transport capability.
Figures 1B–D elaborate the applications or the synthetization procedure of nano, hybrid, and ternary hybrid nanofluids which have extensive uses in the modern world.
Recently, Ali et al. (2021) disclosed the influences of 1st order activation energy phenomena on thermal transportation in the nanoliquid known as Oldroyd-B nanofluid. The problem is taken over a UHSPR and handled numerically. The disclosed results revealed that the fluid motion rises due to stronger thickness effects and the thermal performance of the fluid improved by the index parameter. The imperative studies regarding heat transfer in bio-convection Carreau fluid and magnetized Williamson fluids are examined in the studies by Shahid et al. (2022) and Bhatti et al. (2022), respectively. The authors observed fascinating results regarding the dynamics of the fluids under various physical circumstances that would be beneficial for industrial applications.
The significance of thermal transport is one of the paramount ingredients in new innovations in the world of nanotechnology. Therefore, investigation of the heat transport mechanism attracts the world-renowned scientists and engineers. Thus, they knocked the door of the modern world and initiated the analysis of nanofluids under various constraints because the significance of the heat transport study strengthens its roots not only in the industrial and engineering zone but also in biomedical engineering, aerodynamics, chemical and mechanical engineering, etc. (Alqahtani et al., 2020; AdnanKhan et al., 2021). Detection of cancer cells by allowing interaction of oxide nanoparticles with blood as the base solvent is one of the latest milestones achieved by biotechnologists. The most fascinating applications of the nanofluids’ heat transfer lies in the solar thermal plates which increases the capability of the plants to store solar energy. Similarly, there exists a lot of potential applications of nanofluids which are of huge interest of the current world. The conducted research convinced us to disclose the answer to the following questions in front of the modern world’s scientists and engineers.
• How to enhance the efficiency of the nanofluids?
• What are the impacts of non-linear thermal radiations on the thermal performance of the nanofluids?
• What is the role of suction and stretching parameters on the velocity and temperature behavior of the nanofluids over a 3D surface?
• What is the significance of convective heat condition in thermal enhancement of the nanofluids?
All the aforementioned issues will be addressed in the extended study and hopefully would be beneficial for applied thermal engineering, biomedical engineering, aerodynamics, more specifically in mechanical engineering and many other purposes that use nanotechnology.
Model Development
Model Statement and Geometry
The flow of the [(MgZn6Zr)/C8H18]nf steady incompressible nanofluid is configured over a 3D stretchable surface. The velocities are organized as
In light of the boundary layer approximation theory (BLAT), the flow is constituted by the following mathematical form:
With associated BCs, it is expressed as follows:
The associated similarity equations are designed as follows:
Thermophysical Attributes of Nanofluids
For a particular nanofluid, the following correlations are adopted:
Here;
Furthermore, the particular values are described in Table 1 for base solvent engine oil and the nanomaterial:
Final [(MgZn6Zr)/C8H18]nf Model
After endorsing the empirical correlations and other related characteristics, the following system is achieved:
The related BCs are reduced in the following version:
The physical constraints appearing in the model are
Furthermore, trends of shear drags are estimated through the following expressions:
Mathematical Analysis of [(MgZn6Zr)/C8H18]nf
The resultant nanofluid model [(MgZn6Zr)/C8H18]nf is tedious in nature and almost impossible to solve it explicitly for a closed form solution. Therefore, the numerical algorithm is applied which works as described subsequently:
• First, the model is written in its appropriate form.
• Substitutions are made, according to the order of the model.
• Using those substitutions, the higher order model should be transformed into first order IVP.
• The BCs are adjusted accordingly, and the conditions are set equal to unknowns which will be determined later.
• Finally, the code is allowed to run, and the results are plotted for various physical constraints.
Now, the following transformations are assigned:
Utilization of the aforementioned transformations leads to the following version of the model:
Thereafter, the code is executed for the results.
Results and Discussion Against the Physical Constraints
The velocities (
The Velocity
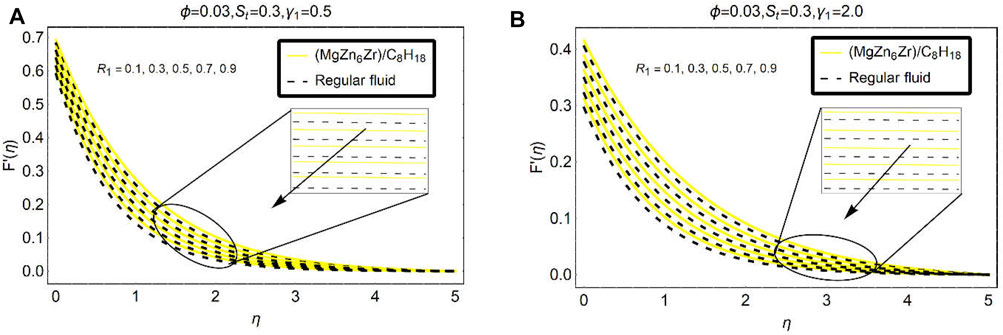
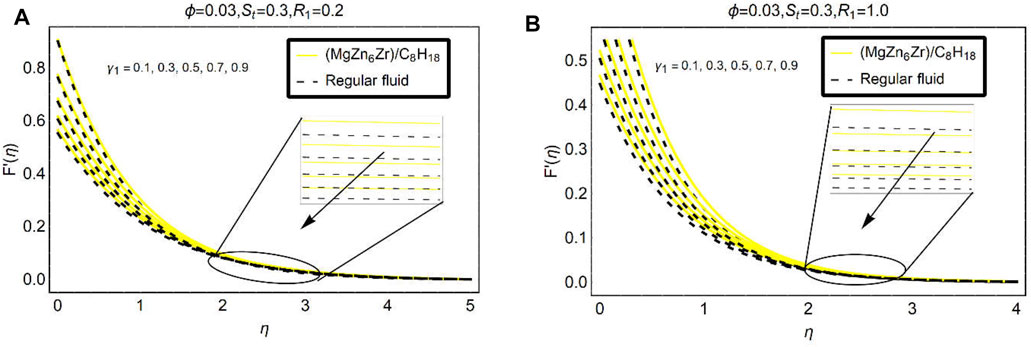
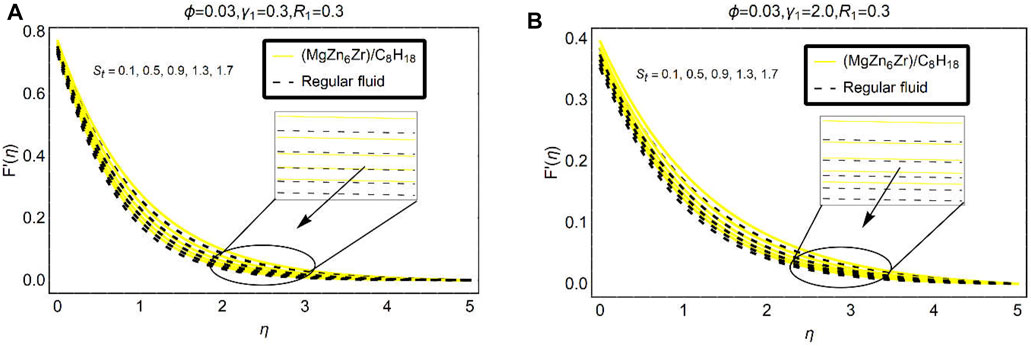
The influences of suction, velocity slip, and stretching parameter on the velocity
The slip parameter effects on
The stretching effects (
The Velocity
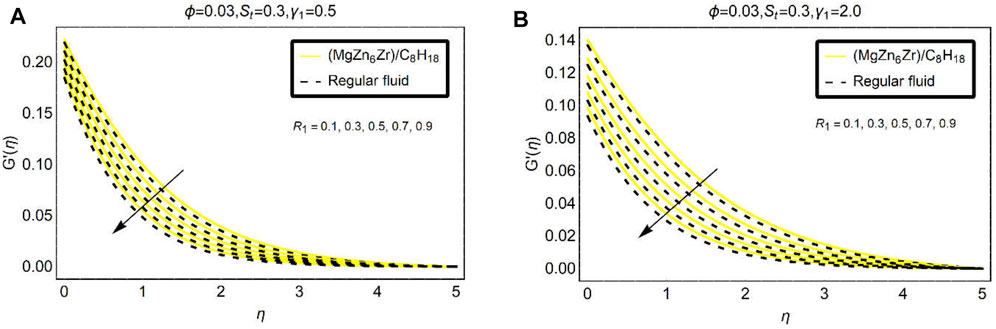
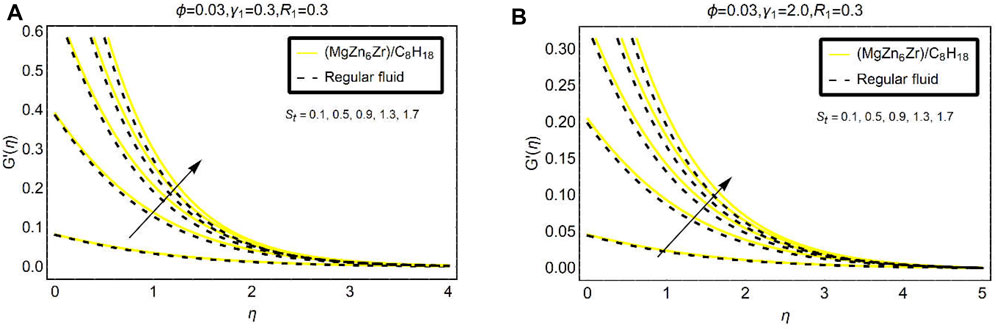
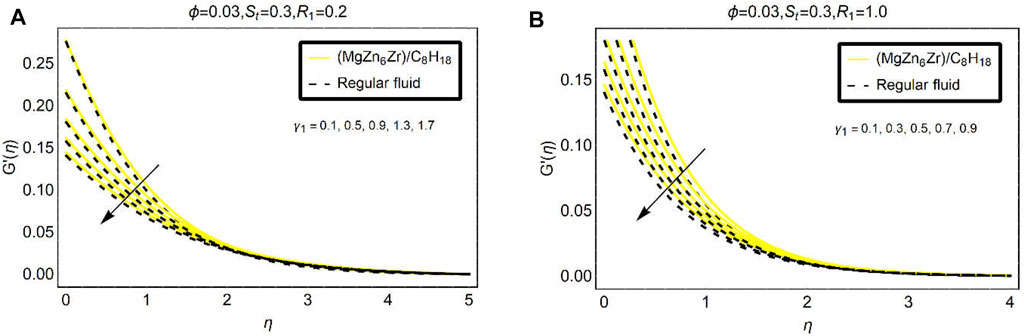
Figures 6–8 explain to analyze the behavior velocity gradient
The suction parameter opposes the fluid motion
Very fascinating trends in the velocity gradient
Figure 8 is associated with the variations in
Thermal Behavior of [(MgZn6Zr)/C8H18]nf
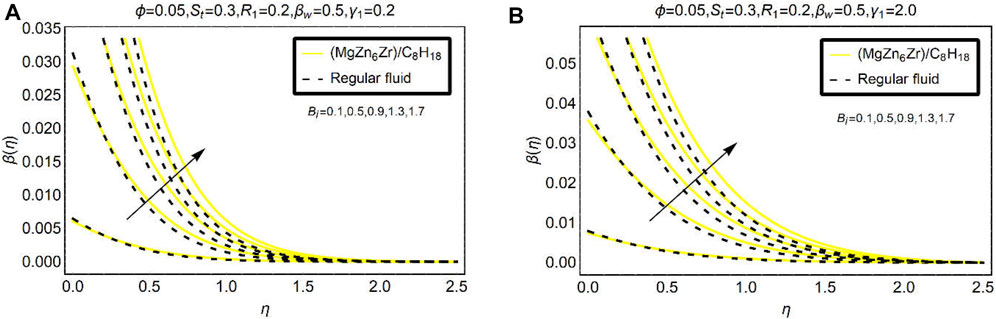
Figure 9 elucidates the temperature enhancement in [(MgZn6Zr)/C8H18]nf for various convectively heated surface values. From the results’ inspection, it discloses that the temperature enhances by increasing surface convection. The imposed heat convection condition at the surface contributes to the energy transfer. Physically, the applied convection condition transfers energy to the neighboring particles at the surface. When these particles gain energy to some extent, these provide the energy to the next particles. In a similar way, the fluid temperature enlarges. In the surface surroundings, these effects are dominant due to stronger convection. The temperature vanishes ambiently for
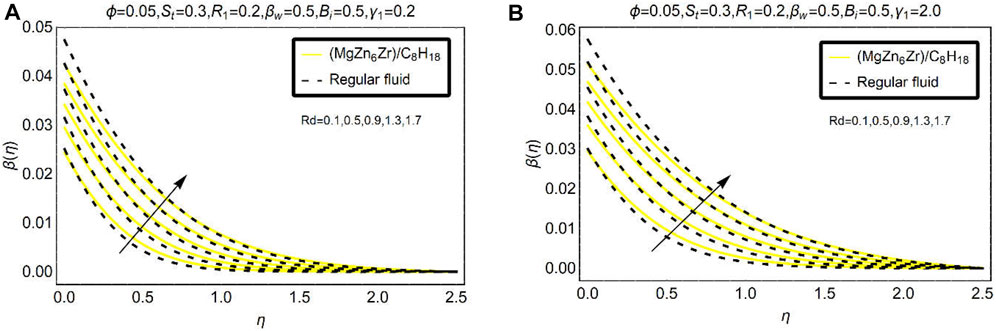
Thermal radiation is an imperative physical phenomenon to improve thermal efficiency of the nanofluids and regular liquids to some limit. Thermal radiations in the existence of the convective heat condition imperatively contribute to thermal enhancement of the nanofluid. Imposed thermal radiations provide energy to the fluid particles that upsurge the ability of the temperature. High thermal radiations are a better heat transport source in the study of nanofluids. Furthermore, high thermal conductance of the nanofluid plays an important role in the energy transport. These effects are displayed in Figure 10.
Figures 11 and 12 highlight the temperature variations for suction and stretching effects, respectively. It is inspected that temperature
Skin Friction, Streamlines, and Isotherms
Figures 14 and 15 present the shear stress trends along both directions (
Reliability of the Study
This subsection is organized to align the conducted study with previously reported work. Therefore, a graphical comparison is provided by restricting the involved physical constraints (
Conclusion
A study of [(MgZn6Zr)/C8H18]nf was conducted over a three-dimensional surface by encountering the influences of thermal radiations and the convective heat condition. The boundaries of the surface are modified with velocity slip, suction, and stretching effects. The governing flow model of [(MgZn6Zr)/C8H18]nf is solved numerically, and the results are provided against the physical constraints. From the study, it is summarized that
• The velocities of [(MgZn6Zr)/C8H18]nf reduce by strengthening suction (
• The velocity
• The convective heat condition provides extra energy to the fluid particles from the surface which enhanced [(MgZn6Zr)/C8H18]nf temperature.
• Thermal radiations are also significantly contributed for thermal enhancement in [(MgZn6Zr)/C8H18]nf.
• The study of [(MgZn6Zr)/C8H18]nf will be more effective in applied thermal engineering and heat transport problems in the modern world.
Data Availability Statement
The study was based on numerical computations and data required for the study. The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
Adnan and UK investigated the research gap and performed mathematical modeling; Adnan and UK wrote the original draft; NA and IK coded the model and methodology; Adnan, NA and IK contributed to results and discussion; AM and SM validated the study; Adnan, AM and SM revised the manuscript.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abbasi, A., Ahmed, N., and Mohyud-Din, S. T. (2017). Flow of Magneto-Nanofluid over a Thermally Stratified Bi-directional Stretching Sheet in the Presence of Ohmic Heating: A Numerical Study of Particle Shapes. Eng. Computations 34 (8), 2499–2513.
Adnan, W. A., Alghtani, A. H., Khan, I., and Andualem, M. (2022). Thermal Transport in Radiative Nanofluids by Considering the Influence of Convective Heat Condition. J. Nanomater. 2022, 1854381. doi:10.1155/2022/1854381
AdnanKhan, U., KhanMohyud-Din, U. S. T., Ahmed, N. D. B., Tauseef Mohyud-Din, S., Khan, I., Baleanu, D., et al. (2021). Al2O3 and γAl2O3 Nanomaterials Based Nanofluid Models with Surface Diffusion: Applications for Thermal Performance in Multiple Engineering Systems and Industries. CMC-Computers Mater. Continua 66 (2), 1563–1576. doi:10.32604/cmc.2020.012326
Ahmed, N., Abbasi, A., Saba, F., Khan, U., and Mohyud-Din, S. T. (2018). Flow of Ferro-Magnetic Nanoparticles in a Rotating System: a Numerical Investigation of Particle Shapes. Indian J. Phys. 92, 969–977. doi:10.1007/s12648-018-1186-4
Ahmed, N., Adnan, , Khan, U., Mohyud-Din, S. T., Khan, I., Hussain, R. I., et al. (2020). A Novel Investigation and Hidden Effects of MHD and Thermal Radiations in Viscous Dissipative Nanofluid Flow Models. Front. Phys. 8. doi:10.3389/fphy.2020.00075
Ali, A., Shehzadi, K., Sulaiman, M., and Asghar, S. (2019). Heat and Mass Transfer Analysis of 3D Maxwell Nanofluid over an Exponentially Stretching Surface. Phys. Scr. 94 (6), 065206. doi:10.1088/1402-4896/ab07cf
Ali, Z., Zeeshan, A., Bhatti, M. M., Hobiny, A., and Saeed, T. (2021). Insight into the Dynamics of Oldroyd-B Fluid over an Upper Horizontal Surface of a Paraboloid of Revolution Subject to Chemical Reaction Dependent on the First-Order Activation Energy. Arab J. Sci. Eng. 46, 6039–6048. doi:10.1007/s13369-020-05324-6
Alqahtani, A. M., Adnan, , Khan, U., Ahmed, N., Mohyud-Din, S. T., and Khan, I. (2020). Numerical Investigation of Heat and Mass Transport in the Flow over a Magnetized Wedge by Incorporating the Effects of Cross-Diffusion Gradients: Applications in Multiple Engineering Systems. Math. Probl. Eng. 2020, 2475831. doi:10.1155/2020/2475831
Bhatti, M. M., Arain, M. B., Zeeshan, A., Ellahi, R., and Doranehgard, M. H. (2022). Swimming of Gyrotactic Microorganism in MHD Williamson Nanofluid Flow between Rotating Circular Plates Embedded in Porous Medium: Application of thermal Energy Storage. J. Energ. Storage 45, 103511. doi:10.1016/j.est.2021.103511
Devi, S. S. U., and Devi, S. P. A. (2016). Numerical Investigation of Three-Dimensional Hybrid Cu-Al2O3/water Nanofluid Flow over a Stretching Sheet with Effecting Lorentz Force Subject to Newtonian Heating. Can. J. Phys. 94, 490–496. doi:10.1139/cjp-2015-0799
Ganau, M., Paris, M., Syrmos, N., Ganau, L., Ligarotti, G., Moghaddamjou, A., et al. (2018). How Nanotechnology and Biomedical Engineering Are Supporting the Identification of Predictive Biomarkers in Neuro-Oncology. Medicines 5, 23. doi:10.3390/medicines5010023
Hou, E., Wang, F., Nazir, U., Sohail, M., Jabbar, N., and Thounthong, P. (2022). Dynamics of Tri-hybrid Nanoparticles in the Rheology of Pseudo-plastic Liquid with Dufour and Soret Effects. Micromachines 13, 201. doi:10.3390/mi13020201
Ijaz, M. (2021). Transportation of Hybrid Nanoparticles in Forced Convective Darcy-Forchheimer Flow by a Rotating Disk. Int. Commun. Heat Mass Transfer 122 (ID), 105177.
Ilyas, H., Ahmad, I., Raja, M. A. Z., Tahir, M. B., and Shoaib, M. (2021). Neuro-intelligent Mappings of Hybrid Hydro-Nanofluid Al2O3-Cu-H2o Model in Porous Medium over Rotating Disk with Viscous Dissolution and Joule Heating. Int. J. Hydrogen Energ. 46 (55), 28298–28326. doi:10.1016/j.ijhydene.2021.06.065
Imran, A., Akhtar, R., Zhiyu, Z., Shoaib, M., and Raja, M. A. Z. (2020). Heat Transfer Analysis of Biological Nanofluid Flow through Ductus Efferentes. AIP Adv. 10, 035029. doi:10.1063/1.5135298
Khan, A. S., Nie, Y., Shah, Z., Dawar, A., Khan, W., and Islam, S. (2018). Three-Dimensional Nanofluid Flow with Heat and Mass Transfer Analysis over a Linear Stretching Surface with Convective Boundary Conditions. Appl. Sci. 8, 2244. doi:10.3390/app8112244
Khan, U., Abbasi, A., Ahmed, N., and Mohyud-Din, S. T. (2017). Particle Shape, thermal Radiations, Viscous Dissipation and Joule Heating Effects on Flow of Magneto-Nanofluid in a Rotating System. Ec 34 (8), 2479–2498. doi:10.1108/ec-04-2017-0149
Khan, U. A., Adnan, , Ahmed, N., Mohyud-Din, S. T., Baleanu, D., Khan, I., et al. (2020). A Novel Hybrid Model for Cu-Al2O3/H2O Nanofluid Flow and Heat Transfer in Convergent/Divergent Channels. Energies 13, 1686–1687. doi:10.3390/en13071686
Khan, U. A., Adnan, , Ahmed, N., Mohyud-Din, S. T., Chu, Y.-M., Khan, I., et al. (2020). γ-Nanofluid Thermal Transport between Parallel Plates Suspended by Micro-cantilever Sensor by Incorporating the Effective Prandtl Model: Applications to Biological and Medical Sciences. Molecules 25, 1777. 8. doi:10.3390/molecules25081777,
Khashi'ie, N. S., Arifin, N. M., Rosca, N. C., Rosca, A. V., and Pop, I. (2022). Three-dimensional Flow of Radiative Hybrid Nanofluid Past a Permeable Stretching/shrinking Sheet with Homogeneous-Heterogeneous Reaction. Hff 32 (2), 568–588. doi:10.1108/hff-01-2021-0017
Mohyud-Din, S. T., Adnan Khan, U., Ahmed, N., Khan, I., Abdeljawad, T., et al. (2020). Thermal Transport Investigation in Magneto-Radiative GO-MoS2/H2O-C2h6o2 Hybrid Nanofluid Subject to Cattaneo-Christov Model. Molecules 25, 2592. doi:10.3390/molecules25112592
Muzaidi, N. A. S., Fikri, M. A., Wong, K. N. S. W. S., Sofi, A. Z. M., Mamat, R., Adenam, N. M., et al. (2021). Heat Absorption Properties of CuO/TiO2/SiO2 Trihybrid Nanofluids and its Potential Future Direction towards Solar thermal Applications. Arabian J. Chem. 14 (4), 103059. doi:10.1016/j.arabjc.2021.103059
Palanisamy, R., Parthipan, G., and Palanic, S. (2021). Study of Synthesis, Characterization and Thermo Physical Properties of Al2O3-SiO2-TiO2/H2O Base Tri-hybrid Nanofluid. Dig. J. Nanomater. Biostructures 16 (3), 939–949.
Prasad, K. V., Vaidya, H., Vajravelu, K., Manjunatha, G., Rahimi-Gorji, M., and Basha, H. (2020). Heat Transfer Analysis of Three-Dimensional Mixed Convective Flow of an Oldroyd-B Nanoliquid over a Slippery Stretching Surface. Ddf 401, 164–182. doi:10.4028/www.scientific.net/ddf.401.164
Ramadhan, A. I., Azmi, W. H., Mamat, R., Hamid, K. A., and Norsakinah, S. (2019). Investigation on Stability of Tri-hybrid Nanofluids in Water-Ethylene Glycol Mixture. Mater. Sci. Eng. 469, 012068. doi:10.1088/1757-899X/469/1/012068
Ramadhan, A. I., Azmi, W. H., and Mamat, R. (2021). Stability and Thermal Conductivity of Tri-hybrid Nanofluids for High Concentration in Water-Ethylene Glycol (60:40). Nanoscience & Nanotechnology-Asia 11 (4), e270421184600. doi:10.2174/2210681210999200806153039
Ray, S. S., and Bandyopadhyay, J. (2021). Nanotechnology-enabled Biomedical Engineering: Current Trends, Future Scopes, and Perspectives. Nanotechnology Rev. 10, 728–743. doi:10.1515/ntrev-2021-0052
Said, Z., Sharma, P., Syam Sundar, L., Afzal, A., and Li, C. (2021). Synthesis, Stability, Thermophysical Properties and AI Approach for Predictive Modelling of Fe3O4 Coated MWCNT Hybrid Nanofluids. J. Mol. Liquids 340, 117291. doi:10.1016/j.molliq.2021.117291
Shahid, A., Bhatti, M. M., Ellahi, R., and Mekheimer, K. S. (2022). Numerical experiment to Examine Activation Energy and Bi-convection Carreau Nanofluid Flow on an Upper Paraboloid Porous Surface: Application in Solar Energy. Sustainable Energ. Tech. Assessments 52 (ID), 102029. doi:10.1016/j.seta.2022.102029
Zhao, Q., Xu, H., and Fan, T. (2015). Analysis of Three-Dimensional Boundary-Layer Nanofluid Flow and Heat Transfer over a Stretching Surface by Means of the Homotopy Analysis Method. Boundary Value Probl. 2015, 64. doi:10.1186/s13661-015-0327-3
Keywords: heat transfer, (MgZn6Zr)/C8H18 nanofluid, thermal radiation, velocity slip, convective heat
Citation: Adnan , Khan U, Ahmed N, Khan I, Mohamed A and Mehrez S (2022) Heat Transfer Evaluation in MgZn6Zr/C8H18 [(Magnesium–Zinc–Zirconium)/Engine Oil] With Non-linear Solar Thermal Radiations and Modified Slip Boundaries Over a 3-Dimensional Convectively Heated Surface. Front. Energy Res. 10:867734. doi: 10.3389/fenrg.2022.867734
Received: 01 February 2022; Accepted: 10 March 2022;
Published: 26 April 2022.
Edited by:
Hsien-Yi (Sam) Hsu, City University of Hong Kong, Hong Kong SAR, ChinaReviewed by:
M. M. Bhatti, Shandong University of Science and Technology, ChinaIskander Tlili, Monastir, Tunisia
Copyright © 2022 Adnan, Khan, Ahmed, Khan, Mohamed and Mehrez. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Adnan, YWRuYW5fYWJiYXNpODlAeWFob28uY29t
 Adnan
Adnan Umar Khan
Umar Khan Naveed Ahmed3
Naveed Ahmed3 Ilyas Khan
Ilyas Khan