An iDTMC-based Monte Carlo depletion of a 3D SMR with intra-pin flux renormalization

Improved deterministic truncation of the Monte Carlo (iDTMC) solution method has been applied to neutronic depletion analyses of a nuclear reactor in this work. The theoretical background on the iDTMC method and material depletion calculation is briefly discussed, and the concept of an intra-pin renormalization scheme is presented to determine the detailed power and flux profiles with the pin-wise homogenized iDTMC solutions. The iDTMC method is applied and evaluated in a 100 MWth 3-dimensional small modular reactor (SMR) problem. Burnup-dependent multiplication factors, pin power distributions, and material densities are estimated by the iDTMC method and compared with the reference and standard Monte Carlo solutions. Numerical performance is investigated in terms of real standard deviation, root-mean-square and relative errors, computing time, and figure-of-merit. The numerical results demonstrate that the iDTMC method is superior to the standard MC method in estimating the burnup-dependent reactor eigenvalue and 3D pin-wise power distribution.

Introduction

A depletion calculation in nuclear reactor analyses is essential for evaluating burnup-dependent reactor parameters and material compositions of nuclear fuels. Recently, the Monte Carlo (MC) method has been extended to the depletion analysis in response to the demand for high-fidelity physics solutions (Romano et al., 2021; Haeck and Verboomen 2007; Ebiwonjumi et al., 2020; Davidson et al., 2018; A. Isotalo 2015). For a practical application of the MC method in commercial reactor problems, a whole core depletion calculation should be affordable in terms of memory and computing time. Despite of advances in computational resources, an intra-pin level burnup calculation in large-scale whole core problems is still excessively demanding.

Many research groups have studied to enhance the efficiency of the MC-based depletion calculation. Fission and surface source iteration algorithm has been suggested to efficiently utilize the given memory storage based on a domain decomposition approach (Y. G. Jo et al., 2020). In a multi-core cluster, each group of processors independently simulates particle sources within local domains evenly decomposing a whole core and corrects the fission and surface sources by a non-blocking communication between the groups. The predictor-corrector method has been applied in the depletion analysis to improve the accuracy and stability of the established burnup calculation (A. E. Isotalo and Aarnio 2011; Dufek et al., 2013; Cosgrove, Shwageraus, and Parks 2020). This method solves multiple neutronic calculations at every depletion time step, and then it can provide corrected material compositions and neutron fluxes by considering continuously changing reaction rates over an interval. The Chebyshev rational approximation method (CRAM) has been popularly used in solving the exponential matrix to enhance the computational accuracy and efficiency by examining the characteristics of the eigenvalues of the burnup matrix (Pusa and Leppänen 2010; A. E. Isotalo and Aarnio 2011; Pusa 2016).

In the meantime, the amount of computational burden in Monte Carlo burnup calculation is largely consumed in the neutronic transport calculation than in the material depletion calculation in large-scale whole core problems. Reducing the numerical cost for the neutronic simulation is still strongly required for the practical and affordable whole core depletion analyses.

The improved deterministic truncation of the Monte Carlo solution (iDTMC) method has been previously developed to decrease the computing time and stochastic uncertainties for the steady-state MC eigenvalue analysis (Kim and Kim 2020; Kim, Kim, and Kim 2020; Kim and Kim 2022). It was shown that the iDTMC method can improve the accuracy and reliability of the pin-wise power and flux profiles compared to the conventional MC method. Recently, preliminary studies were carried out for the application of the iDTMC method to lattice (fuel assembly) depletion calculations (Kim and Kim, 2021a; 2021b).

In this study, the iDTMC method is applied to the depletion calculation in a small modular reactor (SMR) whole core problem. First, an overview of the iDTMC method and material depletion calculation is briefly presented, and the concept of an intra-pin flux renormalization scheme is provided. In numerical analysis, burnup-dependent criticalities, pin power distributions, and material densities through the burnup are estimated by an in-house MC code called iMC (Kim 2021) for both the standard MC and iDTMC approaches. Moreover, computational performance is evaluated by examining the real standard deviation (SD), root-mean-square (RMS) and relative errors, computing time, and figure-of-merit (FOM).

Methods

Improved deterministic truncation of Monte Carlo solution method

The iDTMC method is a numerical algorithm to reduce statistical uncertainty and computing time in the MC transport simulation by maximizing the utilization of deterministic solutions (Kim and Kim 2020; Kim and Kim 2021a; Kim and Kim 2022). The MC method can provide high-fidelity neutronic solutions, while the deterministic method is numerically cheap. Therefore, the accurate reactor solutions can be quickly calculated by strategically combining the deterministic and MC methods and employing the advantages of each method.

In the iDTMC method, the deterministic solutions are calculated by the partial-current coarse mesh finite difference (p-CMFD) method (Cho, 2012). The p-CMFD method is a nonlinear iterative acceleration scheme popularly used in neutronic analyses. This method can give MC-equivalent high-fidelity solutions by solving a one-group diffusion-like neutron balance equation with surface current correction. The one-group neutron balance equation can be simply expressed in the Cartesian coordinate:

${\displaystyle \underset{i}{\Sigma }\frac{A}{V_i}\left(J_{i+1/2}-J_{i-1/2}\right)}+{\displaystyle {\Sigma }_a^i{\varphi }_i}=\frac{1}{k_{eff}}\nu {\displaystyle {\Sigma }_f^i{\varphi }_i}(1)$

where $i$ is the node index, $A$ is surface area, $V$ is the volume of the node, $J$ is the net current, ${\Sigma }_a$ is the absorption cross section, $\nu {\Sigma }_f$ is the fission cross section times the number of neutrons per fission, $k_{eff}$ is the effective multiplication factor, and $\varphi$ is the neutron flux. The net current can be represented by the partial currents, and the partial currents can be expressed by the neighboring neutron fluxes:

$J_{i+1/2}=J_{i+1/2}^{+}-J_{i+1/2}^{-}=-{\tilde{\mathit{D}}}_{i+1/2}({\varphi }_{i+1}-{\varphi }_i)+{\widehat{\mathit{D}}}_{i+1/2}^{+}{\varphi }_i-{\widehat{\mathit{D}}}_{i+1/2}^{-}{\varphi }_{i+1},(2)$

where ${\tilde{\mathit{D}}}_{i+1/2}$ is the interface diffusion coefficient, and ${\widehat{\mathit{D}}}_{i+1/2}$ are the correction factors:

${\tilde{\mathit{D}}}_{i+1/2}=\frac{2D_i{D}_{i+1}}{\left(D_i+D_{i+1}\right)\mathrm{\Delta }},\text{and}(3)$

${\widehat{\mathit{D}}}_{i+1/2}^{\pm }=\frac{J_{i+1/2}^{\pm }\pm 0.5\cdot {\tilde{\mathit{D}}}_{i+1/2}({\varphi }_{i+1}-{\varphi }_i)}{{\varphi }_{i+1/2\mp 1/2}}.(4)$

The group constants for equation formation and the currents and fluxes for the correction factors are obtained from the MC simulation. Then, the subset of the eigenvalue equation can be derived in reference to the MC simulation. By solving the matrix equation, deterministic solutions such as the multiplication factor and neutron flux distribution can be obtained with a convergence tolerance of 1E-9 for the relative errors between criticalities.

In the iDTMC method, these deterministic solutions are used not only to accelerate the convergence of the fission source distribution but also to predict the system solutions. The assembly-wise p-CMFD calculation is implemented during inactive cycles coupled with the MC simulation. In this stage, the deterministic solutions update the fission source of the MC simulation by adjusting particles’ weight. In the meantime, the pin-wise p-CMFD calculation is carried out during active cycles to solely acquire the reactor solutions like the eigenvalue and detailed power distribution.

Depletion analysis

The isotopic changes can be characterized by the Bateman depletion equation taking into account neutron-induced reactions and spontaneous radioactive decay:

$\frac{d{N}_i}{dt}={\displaystyle \sum _{i\ne j}{\lambda }_{ij}{N}_j}-\left({\lambda }_i+\varphi {\sigma }_i\right)N_i,(5)$

where $i$ and $j$ are the indices for the nuclides, $N_i$ is the concentration of nuclide $i$, ${\lambda }_{ij}$ is the coefficient characterizing the production of the nuclide $i$ from the nuclide $j$ through decay, transmutation, and fission reactions, ${\lambda }_i$ is the decay constant of the nuclide $i$, and ${\sigma }_i$ is the disappearance cross section.

The first-order linear differential equations for the isotopes can be represented in a matrix form assuming the coefficients are constant in a time:

$\mathbf{n}\prime =\mathbf{An},(6)$

where $\mathbf{A}$ is the burnup matrix including the transmutation and decay coefficients of the nuclides and $\mathbf{n}$ is the isotope concentration vector. This equation can be solved by the matrix exponential method having the simple solution:

$\mathbf{n}\left(t\right)={\mathit{e}}^{\mathbf{A}\mathit{t}}{\mathbf{n}}_0,(7)$

where ${\mathbf{n}}_0=\mathbf{n}\left(t=0\right)$. In our study, the CRAM is applied to compute the matrix exponential solutions using the constant extrapolation method. Meanwhile, the burnup matrix is determined based on ORIGEN and ACE-formatted libraries (Rearden and Jessee 2018). The libraries contain one-group fission yields and decay characteristics for 1,306 nuclides, and the transmutation cross-section is tallied for 301 nuclides during the MC transport calculation.

In general, the burnup calculation of nuclear fuels in reactor cores is performed by sequentially solving the steady-state neutronics and changes of material compositions in a quasi-static manner. From the MC simulation, the one-group effective cross sections for each isotope are calculated and the one-group neutron flux is updated via the iDTMC method at every time step. These are used for the input parameters in the depletion calculation. The Bateman equation gives the material compositions and isotopic concentrations. Then, the MC simulation is again implemented with the changed materials. This process is repeated over a fuel depletion cycle.

Intra-pin renormalization scheme

In the neutronic depletion calculation, the material compositions and neutron flux are considered spatially constant within each burnup zone. However, in reality, nuclear fuels are pretty heterogeneous due to the spatial self-shielding effect particularly in a radial direction in terms of both the materials and neutron flux. Neutrons are mainly absorbed at the outer periphery of a fuel pellet resulting in the highest thermal flux at the rim and lowest one at the center, and this flux gradient also affects the distribution of fission products and fissionable nuclides. Therefore, fuel rods are generally divided into several rings for a reliable computer simulation of fuel depletion.

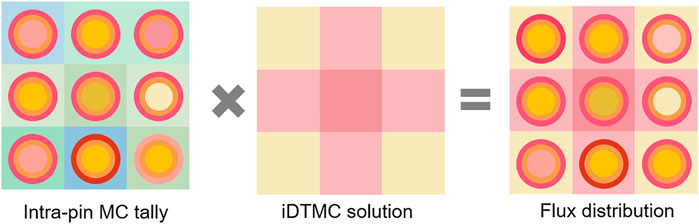
However, the iDTMC method only can provide the homogenized pin-cell flux distribution. The detailed flux distribution inside the fuel pin is essential to apply the iDTMC method to the neutronic depletion calculation. In this study, the intra-pin flux distribution on the designated geometry of the pin interior is reproduced with the iDTMC solutions by the intra-pin renormalization scheme (Nguyen and Kim 2018; Kim and Kim 2021b). A form function upon pin cells is calculated from the MC simulation, and then the intra-pin flux and power distributions are renormalized by adjusting the magnitude with the iDTMC solutions.

The form function is generated based on the MC flux distribution, and normalized for the summation to be unity at each pin cell:

$f{f}_{i,r}=\frac{{\varphi }_{i,r}^{MC}}{{\displaystyle \sum _r^{N_r}{\varphi }_{i,r}^{MC}}},(8)$

where $i$ and $r$ are the indices for the pin and ring nodes respectively, and $N_r$ is the number of rings. When it comes to the number of rings, the fuel rod is generally divided into 1 to 5 rings and the burnable absorber rods are divided into 3 to 10 concentric rings. The flux distribution is normalized to the actual reactor power:

${\mathit{\varphi }}_i^{iDTMC\prime }=\mathit{C}\cdot {\mathit{\varphi }}_i^{iDTMC},(9)$

where $C$ is the normalization factor

$\mathit{C}=\frac{P\left[\text{MW}\right]}{{\displaystyle \sum _i\kappa {\mathrm{\Sigma }}_f^i{\varphi }_i^{iDTMC}{V}_i\left[\text{MeV}\right]\times 1.602\text{E}-19}}$

Then, the intra-pin flux distribution on each pin cell can be finally calculated by multiplying the pin homogenized flux and form function as follows (see Figure 1):

${\mathit{\varphi }}_{i,r}=\mathit{f}{f}_{i,r}\times {\mathit{\varphi }}_i^{iDTMC\prime }(10)$

FIGURE 1

FIGURE 1. Intra-pin renormalization with the MC tally and iDTMC solution.

The neutron balance can be exactly preserved by the iDTMC method on each pin cell as well as the whole core.

Numerical results

Problem description

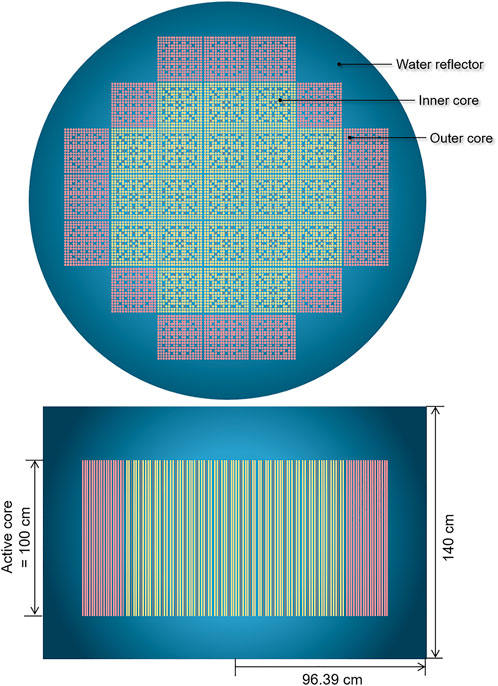
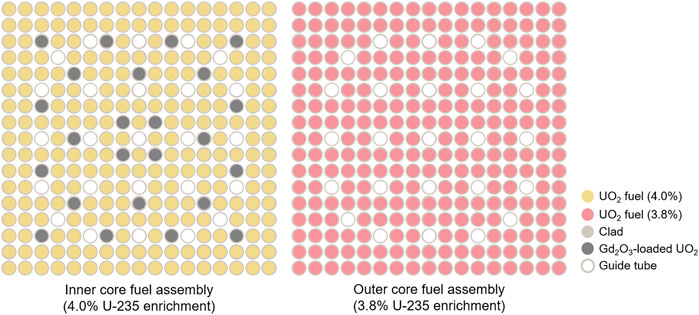
A small modular reactor (SMR) core has been considered for numerical analysis. The detailed configurations of the reactor core are presented in Figures 2A,B. Total 37 fuel assemblies are loaded in the core. There are two different types of fuel assembly. One fuel assembly contains higher-enriched U fuel rods and Gadolinia (Gd₂O₃) burnable absorber pins, while the other one solely consists of lower enriched fuel rods. The fuel rods are arranged in a 17 by 17 array and the fuel assembly includes 25 guide tubes and 264 fuel rods. Among them, 24 fuel rods contain Gadolinia burnable absorbers as shown in Figure 3. The core is surrounded by a water reflector. The diameter and height of the core are 192.78 cm and 140 cm, respectively. The reactor power is 100 MW thermal. The detailed specifications of the SMR core can be found in Table 1.

FIGURE 2

FIGURE 2. Configuration of SMR core; (A) radial (B) axial.

FIGURE 3

FIGURE 3. Detailed configuration of fuel assemblies.

TABLE 1

TABLE 1. Specifications of the SMR core.

The reactor core was depleted over 650 effective full power days (EFPDs) with a power level of 100 MWth. For the burnup calculation, the fuel pins are axially divided into 10 subdivisions by 10 cm. The fuel rods without the Gd₂O₃ burnable absorber are not divided radially in the standard MC and iDTMC calculations, while they are radially divided into 2 rings in the reference calculation for a more accurate solution. In the meantime, since the flux gradient is larger in the Gadolinia-loaded fuel rods due to the strong spatial self-shielding, those are radially divided into equivolumetric 5 rings to account for the spatial self-shielding effect.

Neutronic analysis has been implemented by an in-house MC code named iMC (Kim 2021) with ENDF/B-VII.1 nuclear data library (Chadwick et al., 2011). A reference solution was calculated with 30 inactive cycles, 200 active cycles, and 1,500,000 histories per cycle. For the standard MC and iDTMC methods, 30 inactive cycles, 10 active cycles, and 1,500,000 histories per cycle were used at every time step. For the estimation of the real SD of the reactor parameters, 20 independent batches were simulated with the different random seeds. All the calculations were carried out with a total of 112 cores of Xeon E5-2697.

Source convergence

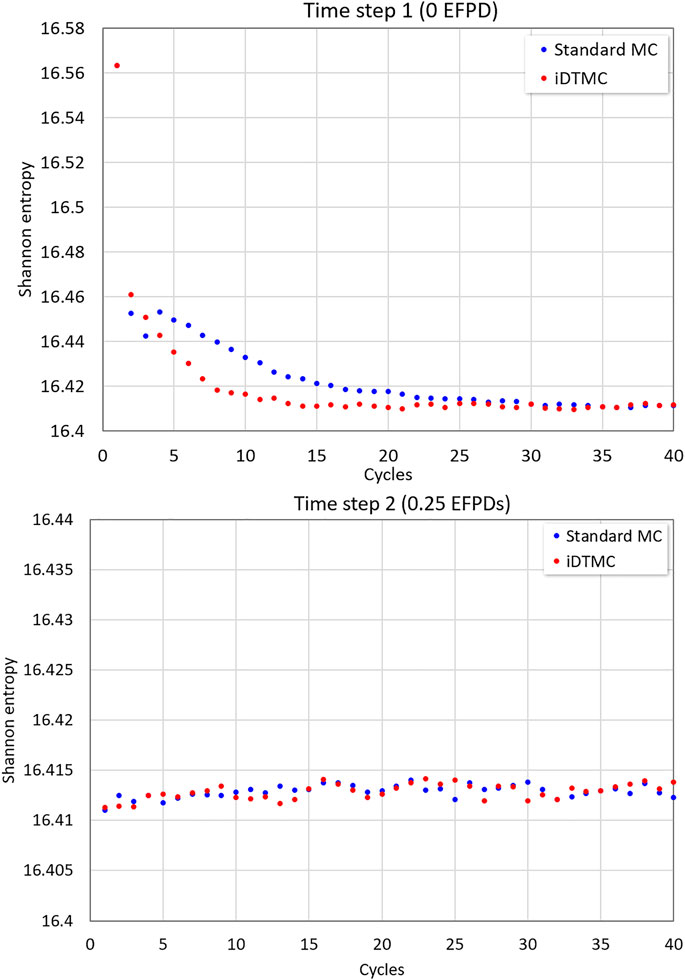
The convergence of the fission source distribution has been characterized by the Shannon entropy. Figures 4A,B show the behavior of the Shannon entropy at the first (0 EFPD) and second (0.25 EFPD) time steps, respectively. The entropy value is highest at the first transport cycle because of uniformly distributed particles and gradually decreases along with the simulation at the first time step. The entropy in the standard MC method reaches a stationary state at around cycle 25, while the iDTMC method more quickly attains the source convergence at around cycle 15 due to the CMFD acceleration. The fission source distribution does not change significantly with the fuel burnup, so the entropy values are already close to the stationary state from the initial transport cycle after the first time step as shown in Figure 4B.

FIGURE 4

FIGURE 4. Shannon entropies at the different time steps; (A) 0 EFPD (B) 0.25 EFPD

Burnup dependent criticality

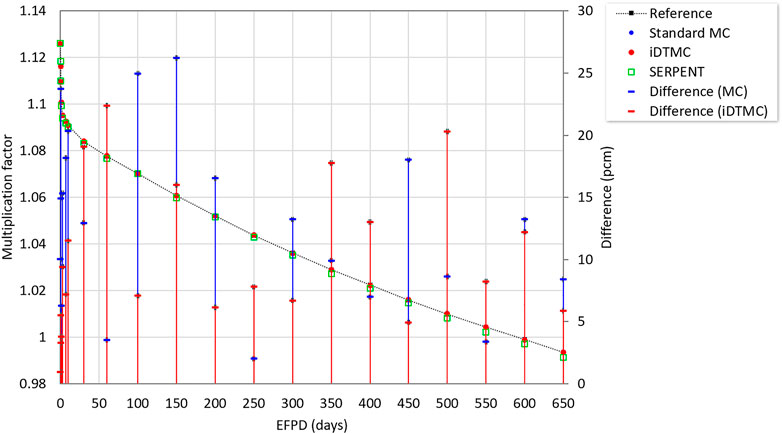
The multiplication factors were calculated at certain time steps over 650 EFPDs. The SMR core was depleted with the short time bin at the beginning of the cycle to properly take into account the depletion of the burnable absorber and the buildup of the neutron-absorbing fission products. Figure 5 describes the burnup-dependent criticalities and the differences compared to the reference solution. The criticality quickly decreases over the early depletion steps due to Xe build-up, and gradually decreases after 10 EFPDs. The RMS error for the burnup dependent criticalities is estimated to be 12.8 pcm for the iDTMC method and 17.1 pcm for the standard MC method. In short, the iDTMC method shows a better agreement with the reference solution compared to the standard MC method.

FIGURE 5

FIGURE 5. Burnup dependent criticalities of the SMR core problem.

The same reactor problem was also analyzed by Serpent 2.1.29 code (A. Isotalo and Sahlberg 2015; A. Isotalo 2015) for comparison, and the results are also given in Figure 5. For the Serpent calculation, 100 inactive cycles, 10 active cycles, and 1,500,000 particles per cycle were simulated. Although Serpent uses different fission yield and decay libraries from iMC and deals with a lot more nuclides including meta-stable isotopes, the iMC results are quite close to the Serpent values. The difference of criticalities between iMC and Serpent is 17.4 pcm for the initial condition. Since the one standard deviation of the multiplication factor is 5.6 pcm for the iMC reference and 20 pcm for the Serpent results, their results agree well within the stochastic uncertainty. The largest discrepancy between the iMC and Serpent through the depletion is only about 220 pcm.

Figure 6 shows the standard deviations of the burnup dependent multiplication factor. The reference solution provides the apparent SDs, while the standard MC and iDTMC methods give the real SDs estimated by the batch calculation. The apparent SD for the reference solution is estimated to be around 5 pcm on average. According to the figure, the iDTMC method clearly shows smaller stochastic uncertainties throughout the simulation than the standard MC. The average of values at each time step is estimated to be 9.4 pcm in the iDTMC method and 21.6 pcm in the standard MC method.

FIGURE 6

FIGURE 6. Standard deviations for burnup dependent criticality (active cycle 10)

Meanwhile, the iDTMC method has shown the effectiveness of the early truncation of the MC solutions in many steady-state neutronic analyses (Kim, Kim, and Kim 2020; Kim and Kim 2022). It means that the iDTMC method can provide accurate and reliable solutions even within 3 active cycles. This characteristic also has been evaluated in this depletion calculation by assessing the statistical errors at the different active cycles. Figure 7 describes the real SDs of the criticality at the specific active cycle 1, 3, 5, and 10, respectively. The standard MC method shows higher SDs at the earlier active cycles. On the other hand, the iDTMC method has consistently smaller SDs even from the early active cycles and seems not significantly affected by the number of active cycles. This implies that the computational burden for the active cycles can be possibly reduced by decreasing the number of cycles.

FIGURE 7

FIGURE 7. Real standard deviations for burnup dependent criticality at different active cycles.

Power distribution

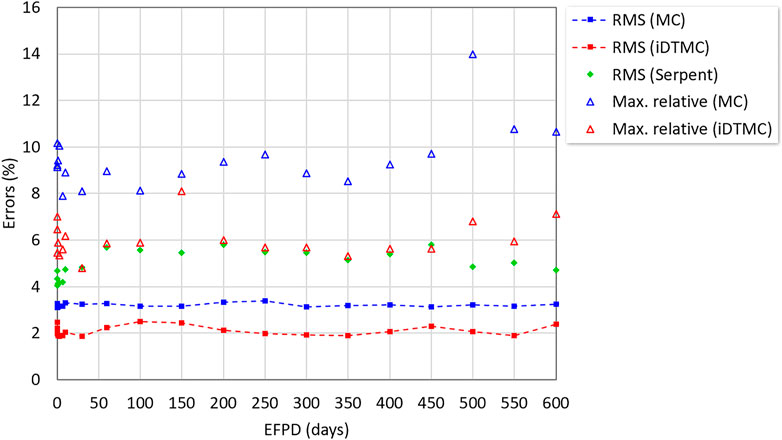
A 2-D pin power distribution has been evaluated and compared with each other. The original 3D powers were axially summed up and normalized for the average to be unity. Figure 8 describes the RMS and relative errors of the 2-D pin power profile. The RMS error is 3.2% in the standard MC and 2.1% in the iDTMC method. The maximum errors were reduced by 40% in the iDTMC method compared to the standard MC method. The pin power distribution was also calculated with the Serpent for comparison. The Serpent solution shows a 4% discrepancy from the iMC-based reference distribution in terms of the RMS errors.

FIGURE 8

FIGURE 8. Errors for pin power distribution (active cycle 10)

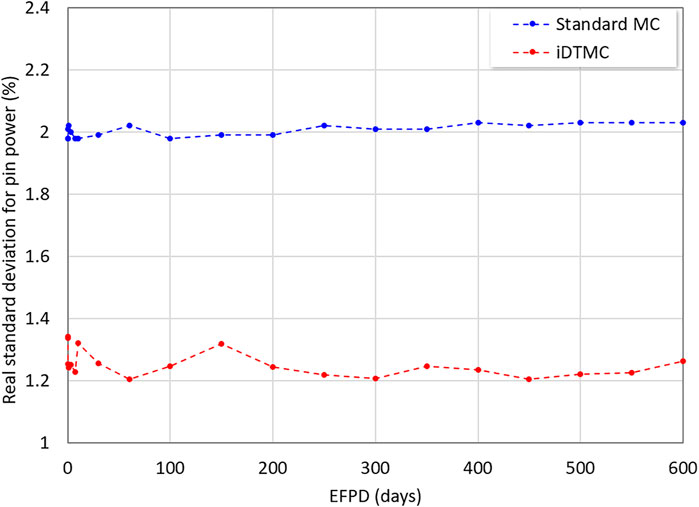
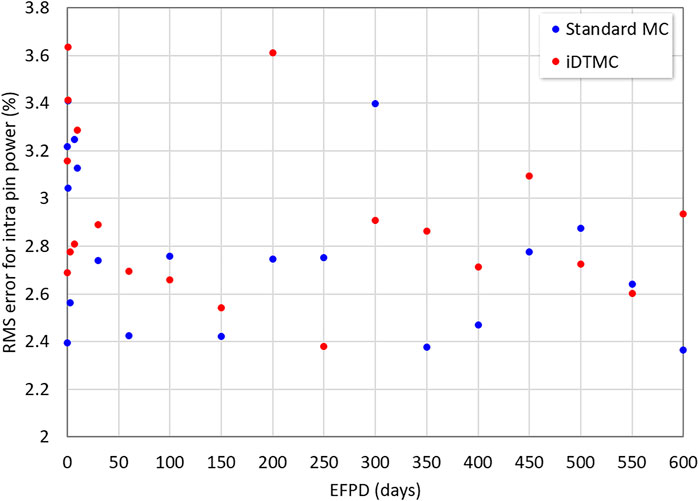
Figure 9 shows the average of real standard deviations of the 2-D pin power distribution at each burnup step. The real standard deviation for the pin power was also calculated with 15 independent runs. The iDTMC method shows smaller stochastic uncertainties for the pin power distribution. The iDTMC method reduces the real standard deviation by 40% compared to the standard MC method with the same calculation condition. Figure 10 shows the RMS errors for the 2-D intra-pin power distribution. The ring-wise intra-pin power distribution was normalized for the average to be unity. The iDTMC method has similar RMS errors with the standard MC method, indicating that the intra-pin power profile was properly determined by the intra-pin renormalization scheme.

FIGURE 9

FIGURE 9. Average of real standard deviations for pin power (active cycle 10)

FIGURE 10

FIGURE 10. RMS errors for intra-pin power distribution (active cycle 10)

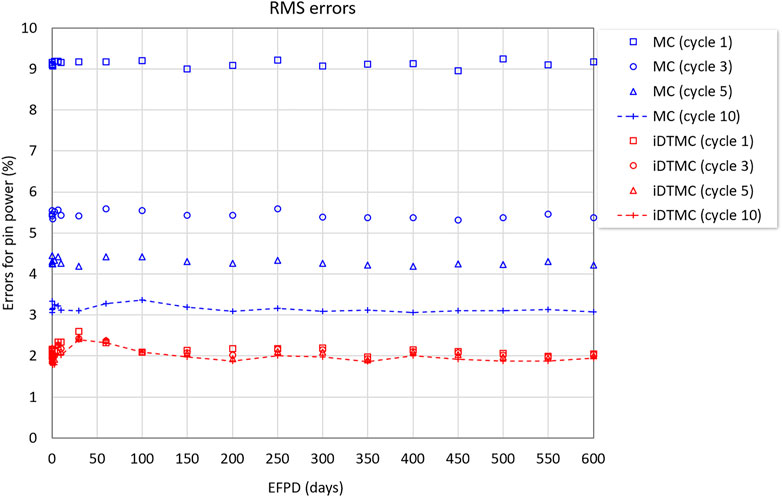
The effectiveness of the early truncation of the MC solutions also has been assessed with the pin power profile. The RMS errors were estimated at the different active cycles (i.e. 1, 3, 5, and 10 cycles) in Figure 11. The RMS errors of the standard MC were more than 9% at the first active cycle and gradually decreased with the cycle accumulation. On the other hand, the RMS errors of the iDTMC method were already low from the first active cycle and slowly decreases with the active cycles. The iDTMC RMS errors of the pin-power profile are consistently lower than in the standard MC case in all active cycles and the difference gets smaller with active cycles.

FIGURE 11

FIGURE 11. Cycle-wise RMS errors for the pin power profile.

Material density

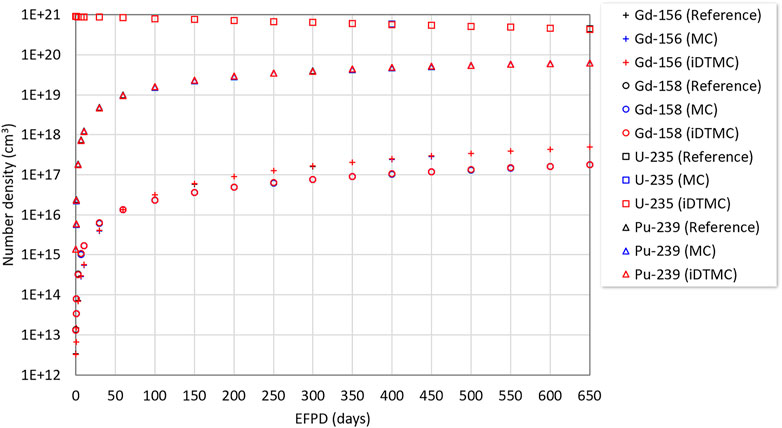
Figure 12 presents the change of the total number density of all the low-enriched uranium fuel rods for several nuclides. The number densities of the gadolinium, uranium, and plutonium isotopes were estimated and compared. U-235 was steadily depleted, while Pu-239 was quickly produced and reaches an equilibrium state. Gadolinium isotopes were also quickly produced as fission products. The nuclide number densities are basically identical within the statistical uncertainties for the two schemes. The results prove that the production and loss of the nuclides in the reactor core have been correctly modeled by the standard MC and iDTMC calculations.

FIGURE 12

FIGURE 12. Number densities of the several isotopes in the fuel.

Numerical performance

Table 2 compares the computing time consumed during the transport and depletion calculations. The standard MC took 16.8 h, while the iDTMC method took 17.3 h. The iDTMC method requires a slightly more running time due to the additional deterministic calculations, but it can be reckoned that the numerical overhead for the iDTMC calculation accounting for ∼3% of the total time is affordable when considering the more accurate and reliable solutions. The computing time of the Serpent calculation is also included only for information, but the Serpent depletion calculation has not been optimized for the large-scale burnup problem involving more than 20,000 depletion zones, and a lot more nuclides are handled in the Serpent depletion.

TABLE 2

TABLE 2. Total computing time for the whole core depletion calculation.

The iDTMC method requires more memory for the deterministic calculation. The additional memory size necessary for the iDTMC calculation considerably depends on the problem size. In this SMR problem, the iDTMC method utilized 17.7 MB more memory than the standard MC method.

Lastly, numerical performance has been measured in view of the FOM for the multiplication factor and pin power as shown in Figure 13. The FOM was calculated with the real variance (${\sigma }^2$) at the active cycle 10 and corresponding total transport computing time ($T$).

$\mathit{FOM}=\frac{1}{{\mathit{\sigma }}^2\mathit{T}}.(11)$

FIGURE 13

FIGURE 13. Figure of merits for the multiplication factor and pin power profile.

Although the computing time is longer in the iDTMC method, the iDTMC method significantly reduces the stochastic uncertainties. Therefore, the iDTMC method shows much bigger FOMs. The FOM of the iDTMC method is 5.2 times higher for the multiplication factor and 2.5 times higher for the pin power distribution.

The FOM of the multiplication factor is also calculated at the first active cycle to demonstrate the effectiveness of the early truncation in the iDTMC method. The iDTMC shows even higher FOM from the beginning of the active cycle. The FOM of the iDTMC method at the first active cycle is shown to be comparable to that at the active cycle 10. On the other hand, the FOM of the standard MC at the first active cycle is clearly lower than that of the 10th active cycle. The average FOM of the standard MC for the multiplication factor is 8.6E+2 at the first cycle and 3.5E+4 at the last cycle, while it is 7.6E+3 at the 1st cycle and 4.3E+4 at the 10th cycle for the iDTMC method, respectively. The iDTMC FOM is ∼40 times higher at the 1^st active cycle and ∼6 times higher at the 10th cycle than that of the standard MC.

Conclusion

Improved deterministic truncation of the Monte Carlo solution (iDTMC) method has been applied to the neutronic depletion calculation in a small modular reactor core problem. The intra-pin flux distribution has been properly determined by the renormalization scheme combined with the iDTMC solutions. From numerical analyses, the iDTMC method showed better agreement with the reference solution and superior numerical performance compared to the standard MC method. For the burnup dependent multiplication factors, the iDTMC method showed the smaller discrepancy on average and reduced the real standard deviation almost by 50%. In particular, the iDTMC method produced reliable solutions even from the first active cycle having consistently smaller stochastic uncertainties regardless of the number of active cycles. When it comes to the pin power distribution, the iDTMC method achieved a 40% reduction both in the stochastic uncertainties and errors. The average real standard deviations for the pin power distribution have been estimated to be 1.3% in the iDTMC method but 2.0% in the standard MC method. Moreover, the RMS error for the iDTMC method was shown to be 2.1%, while that for the standard MC method was shown to be 3.2%. In the meantime, the computing time is marginally longer in the iDTMC method due to the additional deterministic calculation. As a result, the iDTMC method provides quite larger FOMs in terms of the multiplication factor and pin power distribution.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

IK (1st author) and YK developed the theoretical basis. IK (1st author) performed the numerical simulations and IK (2nd author) helped performing the simulations. Both IK (1st author) and IK (2nd author) contributed to the final version of the manuscript with consultation of YK. YK supervised the project.

Funding

This work was supported by the National Research Foundation of Korea Grant funded by the Korean government NRF-2016R1A5A1013919.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Reference

Chadwick, M. B., Herman, M., Obložinský, P., Dunn, M. E., Danon, Y., Kahler, A. C., et al. (2011). ENDF/B-VII.1 nuclear data for science and Technology: Cross sections, covariances, fission product yields and decay data. Nucl. Data Sheets 112 (12), 2887–2996. doi:10.1016/j.nds.2011.11.002

CrossRef Full Text | Google Scholar

Cho, N. Z. (2012). “The partial current-based CMFD (p-CMFD) method revisited,” in Transactions of the Korean Nuclear Society, Gyeongju, Republic of Korea, October 25–26.

Google Scholar

Cosgrove, P., Shwageraus, E., and Parks, G. T. (2020). Stability analysis of predictor-corrector schemes for coupling neutronics and depletion. Ann. Nucl. Energy 149, 107781. doi:10.1016/j.anucene.2020.107781

CrossRef Full Text | Google Scholar

Davidson, Gregory G., Pandya, Tara M., Johnson, Seth R., Evans, Thomas M., Isotalo, Aarno E., Gentry, Cole A., et al. (2018). Nuclide depletion capabilities in the shift Monte Carlo code. Ann. Nucl. Energy 114, 259–276. doi:10.1016/j.anucene.2017.11.042

CrossRef Full Text | Google Scholar

Dufek, Jan, Kotlyar, Dan, Shwageraus, Eugene, and Leppänen, Jaakko (2013). Numerical stability of the predictor-corrector method in Monte Carlo burnup calculations of critical reactors. Ann. Nucl. Energy 56, 34–38. doi:10.1016/j.anucene.2013.01.018

CrossRef Full Text | Google Scholar

Ebiwonjumi, Bamidele, Lee, Hyunsuk, Kim, Wonkyeong, and Lee, Deokjung (2020). Validation of nuclide depletion capabilities in Monte Carlo code MCS. Nucl. Eng. Technol. 52, 1907–1916. doi:10.1016/j.net.2020.02.017

CrossRef Full Text | Google Scholar

Haeck, W., and Verboomen, B. (2007). An optimum approach to Monte Carlo burnup. Nucl. Sci. Eng. 156 (2), 180–196. doi:10.13182/NSE07-A2695

CrossRef Full Text | Google Scholar

Isotalo, Aarno (2015). Comparison of neutronics-depletion coupling schemes for burnup calculations-continued study. Nucl. Sci. Eng. 180 (3), 286–300. doi:10.13182/NSE14-92

CrossRef Full Text | Google Scholar

Isotalo, Aarno, and Sahlberg, Ville (2015). Comparison of neutronics-depletion coupling schemes for burnup calculations. Nucl. Sci. Eng. 179 (4), 434–459. doi:10.13182/NSE14-35

CrossRef Full Text | Google Scholar

Isotalo, A. E., and Aarnio, P. A. (2011). Higher order methods for burnup calculations with bateman solutions. Ann. Nucl. Energy 38, 1987–1995. doi:10.1016/j.anucene.2011.04.022

CrossRef Full Text | Google Scholar

Jo, Yu Gwon, Kim, Hyeon Tae, Kim, Yonghee, and Cho, Nam Zin (2020). Whole-core depletion calculation using domain decomposed continuous-energy Monte Carlo simulation via McBOX with p-CMFD acceleration and inline feedback. Ann. Nucl. Energy 139, 107245. doi:10.1016/j.anucene.2019.107245

CrossRef Full Text | Google Scholar

Kim, Inhyung (2021). “Development of a deterministic truncation of Monte Carlo solution for a pin-resolved nuclear reactor analysis,”. KAIST, Ph.D. Dissertation.

Google Scholar

Kim, Inhyung, Kim, Hyeon Tae, and Kim, Yonghee (2020). Deterministic truncation of the Monte Carlo transport solution for reactor eigenvalue and pinwise power distribution. Nucl. Sci. Eng. 194 (1), 14–31. doi:10.1080/00295639.2019.1654815

CrossRef Full Text | Google Scholar

Kim, Inhyung, and Kim, Yonghee (2020). “A new deterministic truncation of Monte Carlo solution using decoupled fine-mesh finite difference method,” in Proceedings of American Nuclear Society Winter Meeting, November 16–19. Online.

CrossRef Full Text | Google Scholar

Kim, Inhyung, and Kim, Yonghee (2021a). “A study on reconstruction of intra fuel pin power and flux distribution with the IDTMC method in the Monte Carlo reactor analyses,” in Transactions of the Korean Nuclear Society Spring Meeting, Jeju, Korea, May 13–14.

Google Scholar

Kim, Inhyung, and Kim, Yonghee (2022). An improved deterministic truncation of Monte Carlo solution for pin-resolved nuclear reactor analysis. Ann. Nucl. Energy 166, 108723. doi:10.1016/j.anucene.2021.108723

CrossRef Full Text | Google Scholar

Kim, Inhyung, and Kim, Yonghee (2021b). “Depletion analysis of fuel assembly with the IDTMC method,” in Transactions of the Korean Nuclear Society Autumn Meeting, Changwon, Korea, October 21–22.

Google Scholar

Nguyen, Xuan Ha, and Kim, Yonghee (2018). A study on reconstruction of intrapin power distribution in pinwise two-group diffusion analysis. Nucl. Sci. Eng. 189 (3), 224–242. doi:10.1080/00295639.2017.1394086

CrossRef Full Text | Google Scholar

Pusa, Maria (2016). Higher-order Chebyshev rational approximation method and application to burnup equations. Nucl. Sci. Eng. 182 (3), 297–318. doi:10.13182/NSE15-26

CrossRef Full Text | Google Scholar

Pusa, Maria, and Leppänen, Jaakko (2010). Computing the matrix exponential in burnup calculations. Nucl. Sci. Eng. 164 (2), 140–150. doi:10.13182/NSE09-14

CrossRef Full Text | Google Scholar

Rearden, B. T., and Jessee, M. A. (2018). SCALE code system. Ornl/Tm-2005/39.

Google Scholar

Romano, Paul K., Josey, Colin J., Johnson, Andrew E., and Liang., Jingang (2021). Depletion capabilities in the OpenMC Monte Carlo particle transport code. Ann. Nucl. Energy 152, 107989. doi:10.1016/j.anucene.2020.107989

CrossRef Full Text | Google Scholar