Multivariate Time Series Prediction for Loss of Coolant Accidents With a Zigmoid-Based LSTM

Post-LOCA prediction is of safety significance to NPP, but requires a processing coverage of non-linearity, both short and long-term memory, and multiple system parameters. To enable an ability promotion of previous LOCA prediction models, a new gate function called zigmoid is introduced and embedded to the traditional long short-term memory (LSTM) model. The newly constructed zigmoid-based LSTM (zLSTM) amplifies the gradient at the far end of the time series, which enhances the long-term memory without weakening the short-term one. Multiple system parameters are integrated into a 12-dimension input vector to the zLSTM for a comprehensive consideration based on which the LOCA prediction can be accurately generated. Experimental results show both accuracy evaluations and LOCA progression produced by the proposed zLSTM, and two baseline methods demonstrating the superiority of applying zLSTM to LCOA predictions.

1 Introduction

Loss of coolant accident (LOCA) is a severe accident that causes safety threat to nuclear power plants (NPPs). Obviously, it is of great importance to systematically analyze, prevent, and predict LOCAs such that effective decision-making support can be offered to the emergency response strategy. The prediction of the LOCA progression trends, as one of the significant emergency measures, provides evaluation of safety threats ahead of their physical occurrence and allows the emergency response strategy to plan accordingly before worse scenarios emerge. However, the non-linearity of LOCAs and associated complex system factors prevent accurate LOCA predictions. As a coupling result influenced by multiple system parameters, the prediction for LOCA progression also faces multivariant processing challenges, which makes the system modeling more complicated.

In the past decades, various attempts have been taken for process predictions in NPPs. A series of assumptions based on statistical methods and mathematical equations are applied for process predictions such as 1) monitoring the real-time condition of LOCA via time–frequency domain reflectometry (TFDR) (Lee et al., 2017) and 2) using RELAP5/MOD3.3 code to predict the LOCA of the main stream break on generation III reactor (Yang et al., 2019). The aforementioned research studies rely on effort-consuming system modeling and have made feasible progress on LOCA prediction, but the challenges of multivariate processing/coupling remain for further investigation.

Using data-based artificial intelligence (AI) approaches has become an effective way to solve the non-linearity problem with the progress of machine learning, especially when enormous simulated NPP data from previous research studies have founded a firm database for AI applications.

A variety of traditional machine learning algorithms have been applied to NPPs. An abnormal operation state detection method of NPP based on an unsupervised deep generative model is established by using variational auto encoders (VAE) and isolation forest (iForest) (Li et al., 2021). Moshkbar-Bakhshayesh and Ghafari (2022) used support vector machine (SVM) as a machine learning–based method to predict the vessel water level. Xiang et al. (2020) proposed a clustering algorithm for the transient detection in NPPs. Furthermore, Wang et al. (2021a) utilized the clustering algorithm together with SVM and principal component analysis (PCA) for the sensor anomalies in NPPs, which is also reviewed in Hu et al. (2021).

By stacking multiple hidden layers, deep neural network (DNN) has stronger non-linear feature extraction ability. It was utilized to predict the vessel water level (Koo et al., 2018) as well as to identify the fault diagnosis scheme (Santos et al., 2019).

Convolutional neural network (CNN) is a variant of DNN and is usually used for image processing. Viewing NPP sensor data as images, CNN was applied to event identification (Lin et al., 2021; Pantera et al., 2021) and break size estimation (Lin et al., 2022). The mentioned traditional machine learning algorithms (SVM) and deep learning methods (DNN and CNN) can deal with non-linearity, while the sequential data-dependency and multiple physical factors are not taken into account.

Recurrent neural network (RNN), as a classical example, has been successfully applied to sequential data modeling in former explorations. Several long short-term memory (LSTM)–based models cover both the non-linearity and time correlation of LOCAs. For example, the LSTM-based expert system was adopted to predict LOCA behaviors (Mira et al., 2020; Santhosh et al., 2010; Chen et al., 2021) and to evaluate abnormal operation conditions in NPPs (She et al., 2020; Wang et al., 2021b). The coolant flowrate variation was analyzed by She et al. (2021) using a combination of CNN and LSTM. PCA and LSTM were used to identify the fault diagnosis scheme Saeed et al. (2020).

It is necessary to consider modeling non-linearity, multivariate processing, and long-term memory for accurate prediction of LOCA. The aforementioned literatures ignored that LSTM cannot model longer time series. To fully cover the non-linearity, time correlation, and multivariate processing for LOCA predictions, this study proposes an improved LSTM model in which a new gate function called ‘zigmoid’ is constructed. With rigorous experimental verifications conducted on simulated LOCA datasets, the zLSTM is proved to be more accurate and efficient for post-LOCA predictions.

This article starts with Section 1 as the introduction and illustrates the zigmoid function in Section 2. After the presentation of the verification experiments in Section 3, this article is then concluded in Section 4.

2 Zigmoid Method

2.1 Zigmoid for Better Long-Term Memory

Established for the sequential processing problems, RNN obtained preliminary short-term memory. To enable the long-term memory, Hochreiter and Schmidhuber (1997) made a gate-level innovation on RNN and created LSTM that is capable for both short and long-term processing. Nevertheless, the contribution of x_t in LSTM will decay in k timesteps by $f_t^k$ when f_t is a constant (Tallec and Ollivier, 2018). This gives the unit an effective decay period timescale of $O(\frac{1}{1-f_t})$. In case the LSTM is required to have a memory of 1,000 steps, the forget gate parameter f_t has to reach 0.999 since the effective decay period timescale = 1/(1 − f_t). However, it is very challeging to achieve this, according to the following analysis of LSTM.

The standard LSTM process is defined as follows:

$i_t=sigmoid\left(W_{ix}{x}_t+W_{ih}{h}_{t-1}+b_i\right)(1)$

${\mathit{f}}_{\mathit{t}}=\mathit{s}\mathit{i}\mathit{g}\mathit{m}\mathit{o}\mathit{i}\mathit{d}\left({\mathit{W}}_{\mathit{f}\mathit{x}}{\mathit{x}}_{\mathit{t}}+{\mathit{W}}_{\mathit{f}\mathit{h}}{\mathit{h}}_{\mathit{t}-\mathit{1}}+{\mathit{b}}_{\mathit{f}}\right)(2)$

$o_t=sigmoid\left(W_{ox}{x}_t+W_{oh}{h}_{t-1}+b_o\right)(3)$

${\widehat{c}}_t=\tanh \left(W_{cx}{x}_t+W_{ch}{h}_{t-1}+b_c\right)(4)$

$c_t=f_t\odot c_{t-1}+i_t\odot {\widehat{c}}_t(5)$

$h_t=o_t\odot \tanh \left(c_t\right)(6)$

where W_ix, W_ih, b_i, W_fx, W_fh, b_f, W_ox, W_oh, b_o, W_cx, W_ch, and b_c are trainable parameters.

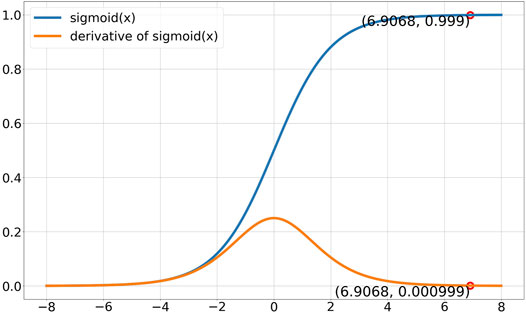
However, the derivative of sigmoid is 0.000999 when f_t = 0.999, as shown in Figure 1, which causes LSTM to be untrainable at this stage. In other words, the LSTM’s long-term memory ability is weakened at the far end of the time series and cannot guarantee accurate prediction in LOCAs.

FIGURE 1

FIGURE 1. Sigmoid properties.

Since the sigmoid function in the forget gate determines the long-term memory of LSTM, a natural idea is to amplify the derivative of the sigmoid function such that model training is still feasible for LSTM even when f_t reaches 0.999. For this purpose, zigmoid is constructed by embedding a transfer function within the original sigmoid.

$zigmoid\left(x\right)=sigmoid\left(trans\left(x\right)\right)(7)$

$trans\left(x\right)=\left\{\begin{array}{cc}{e}^{\beta \ast x}-1\hfill & x\ge 0\hfill \\ 1-e^{-\beta \ast x}\hfill & x<0\hfill \end{array}\right.(8)$

where β is a hyper-parameter.

The derivative of zigmoid is

$\frac{dzigmoid\left(x\right)}{dx}=\frac{dsigmoid\left(x\right)}{dtrans\left(x\right)}*\frac{dtrans\left(x\right)}{dx}(9)$

$\frac{dtrans\left(x\right)}{dx}=\left\{\begin{array}{cc}\beta \ast e^{\beta \ast x}\hfill & x\ge 0\hfill \\ \beta \ast e^{-\beta \ast x}\hfill & x<0\hfill \end{array}\right.(10)$

When β is a large value, that is, $\max (\frac{dzigmoid(x)}{dx})\ge 1.0$, this may lead to gradient explosion. The numerical experiments in PyTorch show that such a case can be avoided when β ≤ 2.5402. On the other hand, the lower bound of β is set to 1.0 because a small value of β cannot achieve effective gradient amplification. Therefore, β is ranged to [1.0, 2.5402] to ensure the system stability.

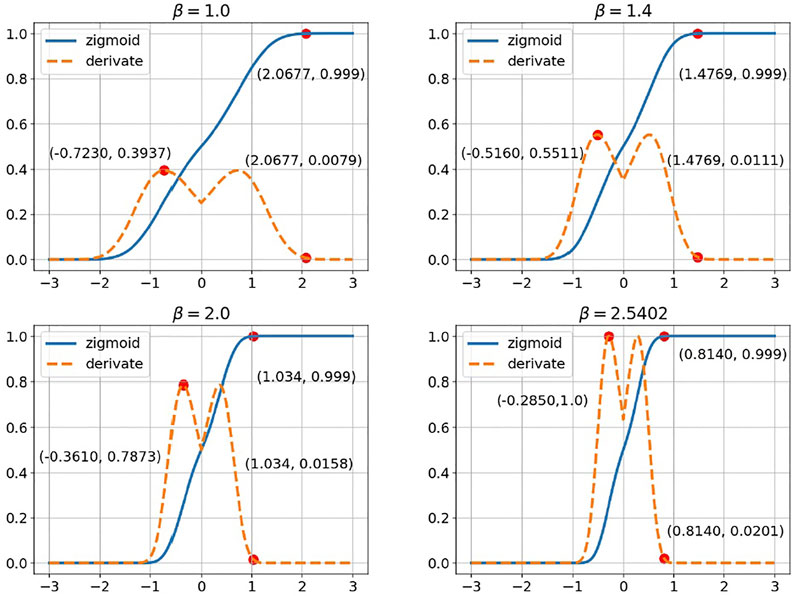
As shown in the comparison of Figures 1, 2, zigmoid amplifies the derivate at the far end of the time axis where sigmoid failed to do so.

FIGURE 2

FIGURE 2. Zigmoid properties.

2.2 zLSTM

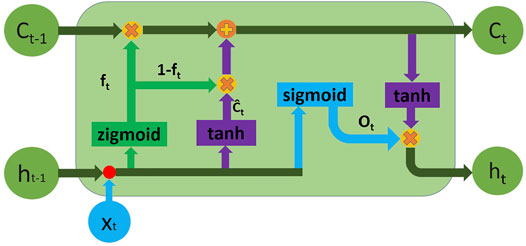
The aforementioned defined zigmoid with ranged β is expected to alleviate the gradient problem for long time series. The following attempts are then conducted to build a new variant of LSTM using the proposed zigmoid (zLSTM) as shown in Figure 3:

1. Replace sigmoid function in the forget gate with zigmoid such that the gradient can be effectively amplified (Figure 3).

2. Replace i_t with (1 − f_t) (Cho et al., 2014) in order to reduce the trainable parameters.

$f_t=\mathit{z}\mathit{i}\mathit{g}\mathit{m}\mathit{o}\mathit{i}\mathit{d}\left(W_{fx}{x}_t+W_{fh}{h}_{t-1}+b_f\right)(11)$

$o_t=sigmoid\left(W_{ox}{x}_t+W_{oh}{h}_{t-1}+b_o\right)(12)$

${\widehat{c}}_t=\tanh \left(W_{cx}{x}_t+W_{ch}{h}_{t-1}+b_c\right)(13)$

$c_t=f_t\odot c_{t-1}+\left(1-f_t\right)\odot {\widehat{c}}_t(14)$

$h_t=o_t\odot \tanh \left(c_t\right)(15)$

where W_ix, W_ih, b_i, W_fx, W_fh, b_f, W_ox, W_oh, b_o, W_cx, W_ch, and b_c are trainable parameters.

FIGURE 3

FIGURE 3. Structure of zLSTM.

2.3 Hyper-Parameter β

An appropriate hyper-parameter β is of great significance for controlling the intensity of the derivative amplification. β should be a value that amplifies the gradient enough for the network to learn long-term information.

Further information to be learned is that the smaller gradient is in zigmoid. For an input sequence with length L:

$\frac{1}{1-f_t}=L(16)$

$f_t=zigmoid\left(x\right)(17)$

Therefore,

$\frac{dzigmoid\left(x\right)}{dx}=\frac{L-1}{L^2}\beta \left(1+log\left(L-1\right)\right)(18)$

The gradient has to be greater than a certain value g_min such that the networks can continue the learning. The g_min is observed and suggested in this study as 0.01.

$\frac{L-1}{L^2}\beta \left(1+log\left(L-1\right)\right)\ge g_{min}(19)$

yields

$\beta \ge \frac{g_{min}{L}^2}{\left(L-1\right)\left(1+log\left(L-1\right)\right)}(20)$

Thus, the β value can be calculated as

$\beta =\left\{\begin{array}{cc}1.0\hfill & {\beta }_{lim}<1.0\hfill \\ {\beta }_{min}\hfill & 1.0\le {\beta }_{lim}\le 2.5402\hfill \\ 2.5402\hfill & {\beta }_{lim}>2.5402\hfill \end{array}\right.(21)$

where ${\beta }_{lim}=\frac{g_{min}L}{(L-1)(1+log(L-1))}$.

2.4 Capabilities of zLSTM

zLSTM obtained by the aforementioned procedure has the following capabilities:

1. zLSTM contains basic properties of LSTM:

 a. Non-linearity: As a variant of RNN, zLSTM inherits the non-linearity processing ability.

 b. Short-term memory: Zigmoid maintains LSTM’s short-term memory ability.

2. As an improved version of LSTM, zLSTM has advantages such as

 a. Long-term memory: Compared with sigmoid, zigmoid has a greater gradient with the same output. This enhances the long-term performance by allowing the model to conduct learning over the full length of the time series. Longer inputs are then allowed to be fed into the model, enriching the information used for predictions.

 b. Reduced trainable parameters: Given that the sum of forget gate and input gate is 1, the input gate can be omitted to deduct parameters. Gate reduction brings reduced trainable parameters such that the computing time and resource are less than traditional models.

With the properties and advantages mentioned previously, this work proposes zLSTM as a better solution for LOCA prediction due to the following considerations:

1. Compared to traditional machine learning algorithms, such as the ones mentioned in Moshkbar-Bakhshayesh and Ghafari (2022), and feed-forward neural network (Santos et al., 2019), zLSTM can achieve better feature extraction with its LSTM kernel that performs the calculation along timesteps. It is then suggested for the non-linear LOCA process, whose variation features are hard to capture.

2. Long term features can be captured by a combination of existing models, such as CNN + LSTM (Wang et al., 2021c), with a sacrifice of more hyper-parameters and more tuning tricks, which burdens the model hyper-parameter processing and deployment. zLSTM, on the contrary, avoids such process by using an improved structure without additional hyper-parameters.

3. The training process of zLSTM is more executable due to reduced gate and parameters, allowing it to generate training/predicting results with less time and efforts.

4. Compared to those baseline models, the LOCA prediction from zLSTM has better credibility and enhanced generalization performance due to zLSTM’s lower overfitting probability and fewer trainable parameters.

3 Experiments

3.1 Datasets

The datasets are obtained from LOCA simulations using an industry-grade NPP simulation platform (Sun et al., 2017). The simulations are carried out at 100% reactor power for LOCA cases, that is, break sizes of 0.9, 0.95, 1.0, 1.5, and 2.0 cm².

There are a total of twelve crucial system parameters selected as the modeling features:

1. pressurizer water level;

2. coolant average temperature;

3. steam generator No. 1 water level;

4. steam generator No. 2 water level;

5. loop 1 coolant flowrate;

6. loop 2 coolant flowrate;

7. pressurizer pressure;

8. stream generator No. 1 output pressure;

9. stream generator No. 2 output pressure;

10. reactor power;

11. cold leg temperature;

12. hot leg temperature.

3.2 Data Preprocessing

To reduce the influence of multiple dimensions, the dataset is preprocessed using the z-score method such that fast convergency can be achieved during the model training process.

$x_{scaled}=\frac{x-\bar{x}}{\sigma }(22)$

where $\bar{x}$ and σ denote mean and variance of x, respectively.

3.3 Metrics

As common metrics for regression task evaluation, mean squared error (MSE) and mean absolute error (MAE) are chosen as the performance judgment for the proposed zLSTM model.

$MSE=\frac{1}{n}\sum _{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2(23)$

$MAE=\frac{1}{n}\sum _{i=1}^n|y_i-{\widehat{y}}_i|(24)$

where y_i and ${\widehat{y}}_i$ are the original value and predicted value, respectively.

3.4 Hyper-Parameter Setting

The zLSTM structure consists of one input layer, two hidden layers, and one output layer. Details are provided in Table 1.

TABLE 1

TABLE 1. Hyper parameters of zLSTM model.

3.5 Baseline Methods

There have been two similar investigations performed by She et al. (2020) and She et al. (2021). However, their major purpose was to verify the feasibility and effects of applying deep learning methods to the LOCA predictions. Neither of them covers the multivariate processing performance that requires theoretical innovation on the NN itself, such as defining a new zigmoid function for the LSTM model. To demonstrate the superiority of using the zigmoid method for multivariate processing, these two previous cases are selected as the baseline, and the prediction accuracy represented by MSE and MAE is compared among all the three methods. The mentioned two previous works, LSTM and CNN-LSTM, are compared with zLSTM to demonstrate its superiority on post-LOCA predictions.

3.6 Model Training

All datasets are randomly split into three subsets, that is, a training set (60%), a validation set (20%), and a test set (20%). Multivariate time series data needed for model training are derived by applying the rolling update method. Following the previous work, the window sizes for LSTM and CNN-LSTM remain 5 and 50. zLSTM uses the same window size as the compared baseline, which means that it uses window size 5 when comparing with LSTM and 50 for CNN-LSTM. The training parameters are optimized using Adam algorithm (Kingma and Adam, 2014) with a learning rate 10^–3 for all models. When the training starts, a sliding window moves from the first row of the training dataset and provides a series of training input data describing the parameter variation during the period limited by the window size. The model learns and memorizes the variations such that it can reproduce similar ones once the test data is fed to it. The model is trained during such iterations until desired loss value is reached. More training process details are provided in She et al. (2020).

3.7 Model Verification Experiments

The performance of the proposed zLSTM is verified through experiments designed to predict crucial parameters of LOCA, in which both univariate scenario and multivariate scenario are tested using zLSTM and the two baseline methods.

The first crucial parameter chosen as the prediction feature is loop 1 flowrate since it is the most impacted parameter during a LOCA. Flowrate data from the test dataset are the so called “single input” for the univariate scenario. As for the multivariate scenario, all the twelve system parameters are integrated into a vector x_t and fed into the zLSTM for a coupled prediction processing. A single output (loop 1 flowrate prediction) is generated by zLSTM’s single-cell output layer that merges the processing results of the 12-dimension vector. The multivariate experiment is only for zLSTM since both baseline methods are originally single-input models without parameter-coupling capability. With a diversity consideration, similar univariate and multivariate experiments are conducted to predict the pressurizer water level as well.

The univariate test is necessary since the two baseline methods are oriented to only one system parameter prediction. During this experiment, the memorizing performance of the models for long- and short-term information is tested, allowing the zLSTM to present its long-term memory advantage with the amplified gradient. For a fair play, zLSTM used for this experiment takes the same single input as the baseline methods. Such univariate-input zLSTM is named zLSTM-univariate (zLSTM-U).

The multivariate test, on the other hand, is to confirm a lower loss value when the prediction is generated with an algorithm (zLSTM) that takes all associated parameters into account. In this case, system parameters associated to the predicted feature are fed to zLSTM as multivariate inputs, naming it zLSTM-multivariate (zLSTM-M).

3.7.1 Prediction of Loop 1 Coolant Flowrate

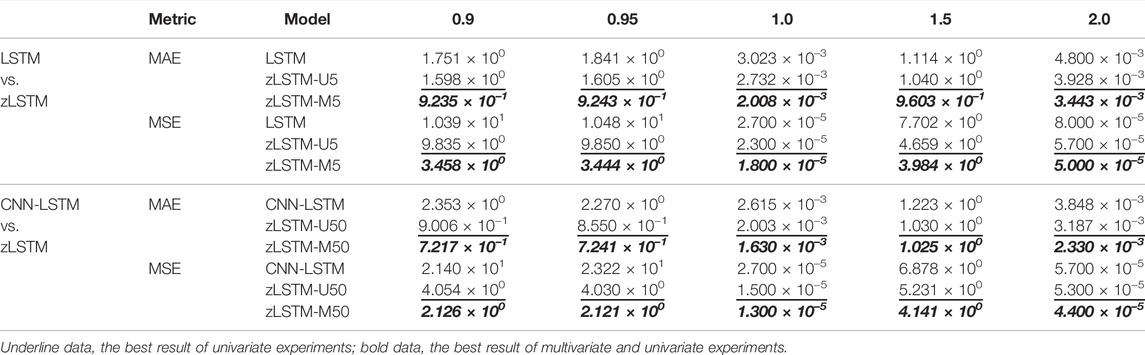
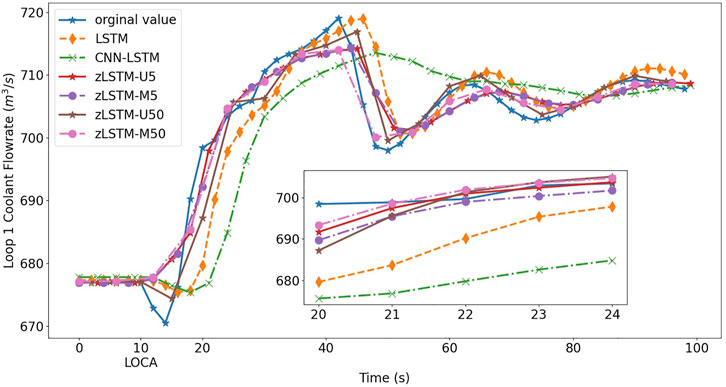
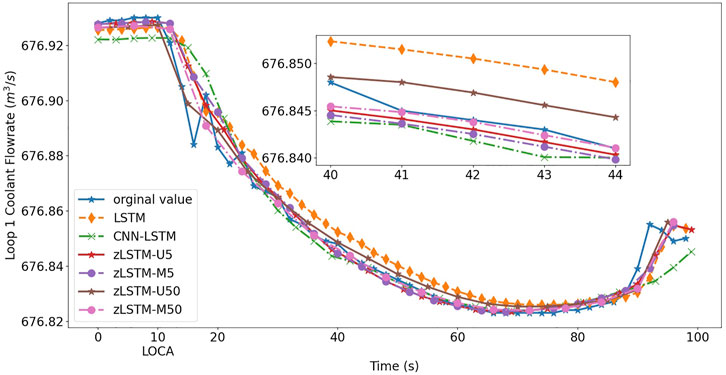
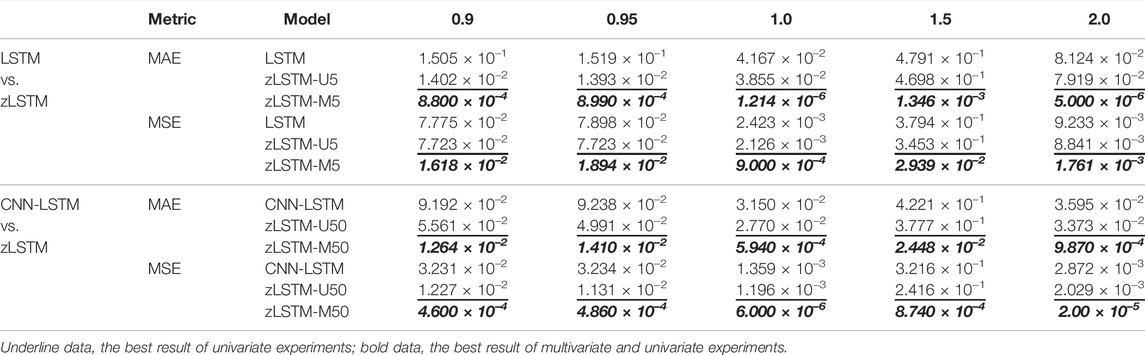
As mentioned in the verification process introduction, the univariate experiment uses the single input value for LSTM, CNN-LSTM, and zLSTM-U. The multivariate experiment, which is for zLSTM-M only, yields a single predicted feature (flowrate or water level) using a 12-dimension vector containing all the key system parameters. The experiments in this subsection focus on the variation of the loop 1 coolant flowrate during LOCAs of five different break sizes. Regarding the discussion in Section 3.6, both zLSTM-U and zLSTM-M select window size 5 to run the univariate and multivariate tests against LSTM, which forms a test group {LSTM, zLSTM-U5, zLSTM-M5}. When comparing to CNN-LSTM that has window size 50, the test group becomes {CNN-LSTM, zLSTM-U50, zLSTM-M50}. Model performance is evaluated using MSE and MAE for each of the six models, providing twelve accuracy evaluation results for each of the five LOCA cases. Table 2 shows all these 60 results for the loop 1 flowrate predictions. The predicted LOCA trends are plotted in Figures 4, 5.

TABLE 2

TABLE 2. Prediction accuracy evaluations for loop 1 flowrate.

FIGURE 4

FIGURE 4. Prediction of loop 1 coolant flowrate on break size 0.9 cm².

FIGURE 5

FIGURE 5. Prediction of loop 1 coolant flowrate on break size 1.0 cm².

3.7.2 Prediction of Pressurizer Water Level

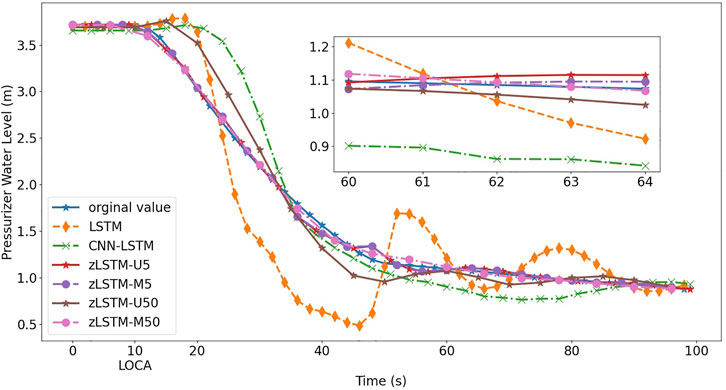
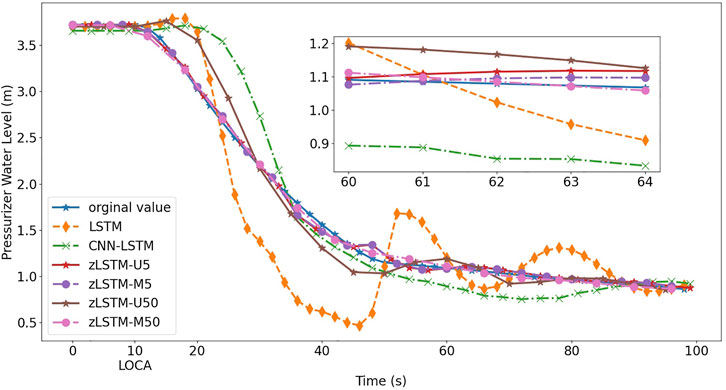
As another crucial system parameter describing the LOCA behavior, the pressurizer water level is predicted in this subsection by experiments same as in Section 3.7.1. Table 3 presents the 60 MSE/MAE data as the accuracy evaluations of the two test groups. Meanwhile, the water level variation illustrated by all the models is presented in Figures 6, 7.

TABLE 3

TABLE 3. Prediction accuracy evaluations for pressurizer water level.

FIGURE 6

FIGURE 6. Prediction of pressurizer water level on break size 0.9 cm².

FIGURE 7

FIGURE 7. Prediction of pressurizer water level on break size 0.95 cm.²

3.7.3 Result Analysis

The prediction accuracy metrics listed in Tables 2, 3 describe the prediction performance of the tested models. The upper half of each table presents the prediction errors from zLSTM (both U and M) against those from LSTM. It can be seen that zLSTM achieves lower errors than LSTM on both MAE and MSE. For instance, the average MAE difference between LSTM and zLSTM-U5 for flowrate prediction is 0.26 in Table 2, giving a 28.7% improvement on prediction accuracy. Additionally, zLSTM working on multivariate mode also beats its univariate mode due to the advantages brought by the 12-dimension parameter vector. The average MAE difference between zLSTM-U5 and zLSTM-M5 is 0.24, giving an accuracy improvement of 28.8%. Similar comparison is reflected by the lower half of each table, where zLSTM once again proves its superiority over CNN-LSTM with accuracy improvements such as 29.52% for pressurizer water level prediction (MSE in Table 3, CNN-LSTM vs. zLSTM-U50).

Figure 4 to Figure 7 visually illustrate the predicted LOCA trends in different LOCA cases. The mini graphs within the figures amplify chosen segments of the trends, offering a better view to the model performance. After the LOCA occurs at t = 10s, the loop 1 flowrate and the pressurizer water level experience dramatical variations, and then approach a stable state with help from the emergency response system. During the entire process, the zLSTM group {U5, M5, U50, M50} represents a more precise prediction performance. At the beginning of the LOCA, it is the zLSTM that grasps the suddenly inserted non-linear variation using its efficient short-term memory, producing a prediction close to the actual trend. How the zigmoid function can enhance the model’s long-term memory is well verified when the zLSTM models generate better predictions at the far end of the time axis. zLSTM-M50 is the one that grasps the progression trends most accurately and persistently, which demonstrate the importance and effect of using multivariate processing (12-dimension vector) and wide data window (size 50).

The analysis conducted to investigate further explanations is presented as follows:

1. The multivariate mode of zLSTM (zLSTM-M) allows the prediction to be generated based on the coupling of system parameters, that is, the prediction comprehensively considers all the 12 critical system parameters relevant to LOCA progression. Sufficient information provided by such a 12-variable input vector guarantees improved prediction accuracy.

2. LOCA predictions for small breaks received higher loss values than those for big ones. They confirm the difficulties of learning and simulating a process with dramatical variations, for example, a small LOCA. Inflect points shorten the time period necessary for information gathering, preventing the model from sufficient evaluation of the progression process. The loss values rise along with the number of inflect points, showing that more inflect points cause more missing information during learning and prediction.

3. It is observed that a larger input window size gives the zLSTM model a better performance since the window size determines the coverage of critical information. More accurate results are generated when the model is capable of learning comprehensively by capturing more useful information from the predicted process.

To summarize, the application of zigmoid function to LSTM has enhanced the short and long-term memory of the model. With the input vector integrated using 12 system parameters, the zLSTM-M model can be even more comprehensive to the multivariate environment of LOCA, allowing the predicted feature to be more accurate.

4 Conclusion

A new gate function zigmoid is raised as a solution to the far-end gradient problem of RNN class models, which is proposed to cover the non-linearity, time correlation, and multivariate processing for LOCA predictions. Proved through theoretical analysis, the zigmoid function is embedded into traditional LSTM to form zLSTM that is capable of effectively memorizing both short- and long-term information. Its multivariate processing is enabled by using a 12-dimension input vector that integrates 12 system parameters. The multivariate mode gathers all-sided system information that eliminates blind spots during the prediction process. The verification experiments successfully demonstrate the aforementioned advantages of the zLSTM model. The accuracy metrics (MAE/MSE) of zLSTM is kept lower than traditional models for both univariate and multivariate scenarios. During the LOCA progression, the parameter trends are followed by zLSTM’s prediction, with the smallest deviation according to the experiment figures. All these findings confirm zLSTM to be a better method for LOCA predictions.

In addition to the achievements, there are a few issues remaining for future investigation. First, zLSTM is constructed by replacing only the forget gate in LSTM. Possible further enhancement could be obtained with more applications of the zigmoid function. The next is the model training process that may be improved using more actual NPP data. Last but not least, inflect points in the LOCA trend cannot be well followed by the prediction curve generated from the deep learning models, which implies alternative solutions in future explorations.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

SG proposed the idea of using zLSTM methods for LOCA prediction and established the main structure of the deep learning models used in this work. SY performed the data preprocessing and model training task. JS drafted most parts of the article and coordinated the cooperation of all the co-authors. WL was responsible for the experiment results analysis as well as preparing the tables and figures. SL provided key instructions to the group members to ensure accurate and efficient research methodologies. All authors contributed to the article and approved the submitted version.

Funding

The authors would like to acknowledge the financial and technical support received from the following research projects and institutions, including but not limited to, National Key Research and Development Project (2020YFB1713400), and The Industrial Internet Innovation and Development Project of China (TC19084DY).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2022.852349/full#supplementary-material

References

Chen, Y., Lin, M., Ren, Y., and Wang, T. (2021). Research on Simulation and State Prediction of Nuclear Power System Based on Lstm Neural Network. Sci. Technology Nucl. Installations 2021, 8839867. doi:10.1155/2021/8839867

CrossRef Full Text | Google Scholar

Cho, K., van Merriënboer, B., Gulcehre, C., Bahdanau, D., Bougares, F., Schwenk, H., et al. (2014). “Learning Phrase Representations Using RNN Encoder–Decoder for Statistical Machine Translation,” in Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, October 25 and 29, 2014 (Doha, Qatar: Association for Computational Linguistics), 1724–1734.

Google Scholar

Hochreiter, S., and Schmidhuber, J. (1997). Long Short-Term Memory. Neural Comput. 9 (8), 1735–1780. doi:10.1162/neco.1997.9.8.1735

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, G., Zhou, T., and Liu, Q. (2021). Data-driven Machine Learning for Fault Detection and Diagnosis in Nuclear Power Plants: A Review. Front. Energ. Res. 9, 663296.

CrossRef Full Text | Google Scholar

Kingma, D., and Adam, J. B. (2014). A Method for Stochastic Optimization. San Diego, CA USA: Computer Science.

Google Scholar

Koo, Y. D., Man, G. N., Kim, K. S., and Kim, C. H. (2018). “Prediction of Nuclear Reactor Vessel Water Level Using Deep Neural Networks,” in 2018 International Conference on Electronics, Information, and Communication (ICEIC), Honolulu, HI, USA, 24-27 Jan. 2018 (IEEE). doi:10.23919/elinfocom.2018.8330616

CrossRef Full Text | Google Scholar

Lee, C.-K., Kwon, G.-Y., Chang, S. J., Jung, M. K., Park, J. B., Kim, H.-S., et al. (2017). Real-Time Condition Monitoring of LOCA via Time-Frequency Domain Reflectometry. IEEE Trans. Instrum. Meas. 66, 1864–1873. doi:10.1109/tim.2017.2664578

CrossRef Full Text | Google Scholar

Li, X., Huang, T., Cheng, K., Qiu, Z., and Tan, S. (2021). Research on Anomaly Detection Method of Nuclear Power Plant Operation State Based on Unsupervised Deep Generative Model. Ann. Nucl. Energ. 167, 108785.

Google Scholar

Lin, T.-H., Chen, C., Wu, S.-C., Wang, T.-C., and Ferng, Y.-M. (2022). Localization and Size Estimation for Breaks in Nuclear Power Plants. Nucl. Eng. Technology 54 (1), 193–206. doi:10.1016/j.net.2021.07.007

CrossRef Full Text | Google Scholar

Lin, T.-H., Wang, T.-C., and Wu, S.-C. (2021). Deep Learning Schemes for Event Identification and Signal Reconstruction in Nuclear Power Plants with Sensor Faults. Ann. Nucl. Energ. 154, 108113. doi:10.1016/j.anucene.2020.108113

CrossRef Full Text | Google Scholar

Mira, B., Pigg, C., Kozlowski, T., Deng, Y., and Qu, A. (2020). Neural-based Time Series Forecasting of Loss of Coolant Accidents in Nuclear Power Plants - Sciencedirect. Expert Syst. Appl. 160.

Google Scholar

Moshkbar-Bakhshayesh, K., and Ghafari, M. (2022). Prediction of Steam/water Stratified Flow Characteristics in Npps Transients Using Svm Learning Algorithm with Combination of thermal-hydraulic Model and New Data Mapping Technique. Ann. Nucl. Energ. 166, 108699.

CrossRef Full Text | Google Scholar

Pantera, L., Stulík, P., Vidal-Ferràndiz, A., Carreño, A., Ginestar, D., George, I., et al. (2021). Localizing Perturbations in Pressurized Water Reactors Using One-Dimensional Deep Convolutional Neural Networks. Sensors 22 (1), 113.doi:10.3390/s22010113

PubMed Abstract | CrossRef Full Text | Google Scholar

Saeed, H. A., Peng, M.-j., Wang, H., and Zhang, B.-w. (2020). Novel Fault Diagnosis Scheme Utilizing Deep Learning Networks. Prog. Nucl. Energ. 118, 103066. doi:10.1016/j.pnucene.2019.103066

CrossRef Full Text | Google Scholar

Santhosh, M. K., Thangamani, I., Mukhopadhyay, D., Verma, V., Rao, V. V. S. S., Vaze, K. K., et al. (2010). “Neural Network Based Diagnostic System for Accident Management in Nuclear Power Plants,” in 2010 2nd International Conference on Reliability, Safety and Hazard - Risk-Based Technologies and Physics-of-Failure Methods (ICRESH), Mumbai, India, 14-16 Dec. 2010 (IEEE), 572–578. doi:10.1109/icresh.2010.5779613

CrossRef Full Text | Google Scholar

Santos, M. C. d., Pinheiro, V. H. C., Desterro, F. S. M. d., Avellar, R. K. d., Schirru, R., Santos Nicolau, A. d., et al. (2019). Deep Rectifier Neural Network Applied to the Accident Identification Problem in a Pwr Nuclear Power Plant. Ann. Nucl. Energ. 133, 400–408. doi:10.1016/j.anucene.2019.05.039

CrossRef Full Text | Google Scholar

She, J. K., Xue, S. Y., Sun, P. W., and Cao, H. S. (2020). “The Application of LSTM Model to the Prediction of Abnormal Condition in Nuclear Power Plants,” in Nuclear Power Plants: Innovative Technologies for Instrumentation and Control Systems, the Fourth International Symposium on Software Reliability, Industrial Safety, Cyber Security and Physical Protection of Nuclear Power Plant (ISNPP). doi:10.1007/978-981-15-1876-8_46

CrossRef Full Text | Google Scholar

She, J., Shi, T., Xue, S., Zhu, Y., Lu, S., Sun, P., et al. (2021). Diagnosis and Prediction for Loss of Coolant Accidents in Nuclear Power Plants Using Deep Learning Methods. Front. Energ. Res. 9, 665262. doi:10.3389/fenrg.2021.665262

CrossRef Full Text | Google Scholar

Sun, P., Zhao, H., Liao, L., Zhang, J., and Su, G. (2017). Control System Design and Validation Platform Development for Small Pressurized Water Reactors (Spwr) by Coupling an Engineering Simulator and Matlab/simulink. Ann. Nucl. Energ. 102 (APR), 309–316. doi:10.1016/j.anucene.2016.12.034

CrossRef Full Text | Google Scholar

Tallec, C., and Ollivier, Y. (2018). Can Recurrent Neural Networks Warp Time? Arxiv.

Google Scholar

Wang, H., Peng, M. J., Ayodeji, A., Xia, H., Wang, X. K., and kang, Z. (2021). Advanced Fault Diagnosis Method for Nuclear Power Plant Based on Convolutional Gated Recurrent Network and Enhanced Particle Swarm Optimization. Ann. Nucl. Energ. 151, 107934. doi:10.1016/j.anucene.2020.107934

CrossRef Full Text | Google Scholar

Wang, H., Peng, M. J., Yue, Y., Saeed, H., Cheng, M. H., and Liu, Y. K. (2021). Fault Identification and Diagnosis Based on Kpca and Similarity Clustering for Nuclear Power Plants. Ann. Nucl. Energ. 150, 107786.

CrossRef Full Text | Google Scholar

Wang, M-D., Lin, T-H., Jhan, K-C., and Wu, S-C. (2021). Abnormal Event Detection, Identification and Isolation in Nuclear Power Plants Using Lstm Networks. Prog. Nucl. Energ. 140, 103928. doi:10.1016/j.pnucene.2021.103928

CrossRef Full Text | Google Scholar

Xiang, L., Fu, X. M., Xiong, F. R., and Bai, X. M. (2020). Deep Learning-Based Unsupervised Representation Clustering Methodology for Automatic Nuclear Reactor Operating Transient Identification. Knowledge-Based Syst. 204, 1061782020.

Google Scholar

Yang, J., Yang, Y., Deng, C., and Ishii, M. (2019). Best Estimate Plus Uncertainty Analysis of a Large Break Loca on Generation Iii Reactor with Relap5. Ann. Nucl. Energ. 127 (MAY), 326–340. doi:10.1016/j.anucene.2018.12.019

CrossRef Full Text | Google Scholar