
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res. , 12 May 2022
Sec. Nuclear Energy
Volume 10 - 2022 | https://doi.org/10.3389/fenrg.2022.852325
This article is part of the Research Topic Artificial Intelligence Applications in Nuclear Energy View all 13 articles
The asymmetric deformation of glass-to-metal seals is an important defect that would lead to the failure of the pressure boundary in nuclear reactors. In this research, an efficient approach to measure the asymmetric deformation and prevent the potential failure was proposed based on the spectrum characterization of fiber Bragg grating (FBG) sensors. The asymmetric deformation was induced from small-size large-gradient nonuniform strain in sealing materials; as a result, it could be monitored through the spectra of embedded FBGs affected by strain variations. The theoretical analysis of the FBG spectrum was carried out using the transfer matrix model (TMM) to validate the measuring feasibility and reliability. Based on the theoretical results, the asymmetric deformation was measured by the distributed embedded FBG experimentally. By combining the reconstructed spectrum and the experimental results, the asymmetric deformation of glass-to-metal was proved to be monitored, and the defect was able to be prevented during the manufacturing process effectively via the proposed method.
The glass-to-metal seal has played an important role in the hermeticity of pressure boundaries applied in nuclear and renewable energy industries. The compressive strain generated in sealing glass during the manufacturing process with the compaction of the steel shell was the main factor for maintaining good hermeticity in glass-to-metal at harsh environments. Defects such as asymmetric deformation would be induced by the special model design, which would lead to the hermetic failure of glass-to-metal seals. Many advanced techniques [digital image correlation (Van Lancker et al., 2016) and photoluminescence spectroscopy (Li S et al., 2022)] were carried out recently to monitor the strain/stress in real-time; however, it was difficult for these methods to be applied in remote sensing under harsh nuclear environments. Based on our previous research studies (Fan et al., 2019; Fan et al., 2020), the embedded fiber sensing technique is demonstrated in this research. Fiber Bragg grating (FBG) sensors have been developed in the past 40 years, and they have been applied in various sensing schemes (Zaghloul et al., 2018; Fan et al., 2019; Morana et al., 2019). FBG has emerged as a reliable, in situ, nondestructive tool for monitoring, diagnosing, and controlling civil structures, and the versatility of FBG sensors represents a key advantage over other technologies in the structural health monitoring (SHM) field (Majumder et al., 2008).
Generally, asymmetric deformation would cause the local strain distribution to vary significantly, so the measurement of strain distribution was essential in this research. Strain measurement has attracted research interest for its important role in SHM. The strain distribution of large equipment (bridges, composite structures, etc.) is regarded as being uniform in the measuring region of small sensors, so the strain signals would be stable and clear, as shown in Figure 1 (Ling et al., 2006; Chen et al., 2017; Goossens et al., 2019; Xiong et al., 2019; Li J et al., 2022). However, for small-size equipment such as glass-to-metal seals, the strain distribution was nonuniform with a large gradient to guarantee hermeticity, so it would be challenging to realize accurate strain measuring because the spectrum would be broadened and distorted by nonuniform strain (Kersey et al., 1997). Previous results showed that it was feasible to characterize the properties of strain distributions with a chirped spectrum (Fan et al., 2019). This phenomenon was widely applied to identify nonuniform strain induced by defects [crack locations in composites (Okabe et al., 2004), crack propagations (Jin et al., 2019), and transverse loads detection (Rajabzadeh et al., 2019)], and the results demonstrated its feasibility.
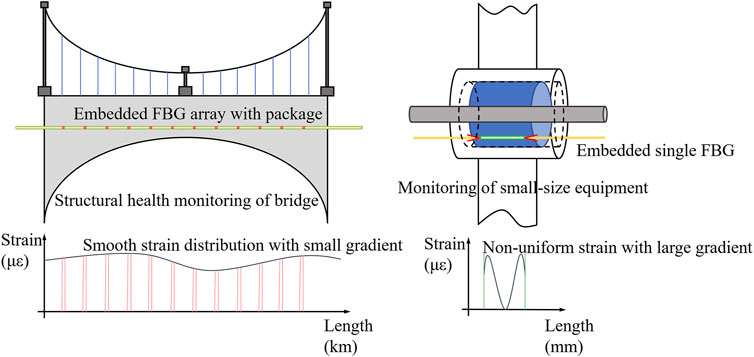
FIGURE 1. Sensing scheme of sizable and small-size equipment with the related measuring strain distribution.
This research performed a practical monitoring method for the hermetic material of glass-to-metal seals, which could realize the discrimination of nonuniform strain distribution and prevention of asymmetric deformation with a high measuring resolution. The spectrum reconstruction of FBG under nonuniform strain was studied using the combined transfer matrix model (TMM) and finite element method (FEM). The relationship between the gradient parameter of strain distribution and the full width at half maximum (FWHM) of the FBG spectrum was obtained. The characteristic parameters (Bragg wavelength shift and FWHM) of the chirped spectrum were proved to monitor asymmetric deformation efficiently through the in situ monitoring experiments, and the accuracy was verified by the numerical simulations.
According to the index modulation depth distribution of the grating region, FBG can be divided into apodized FBG (AFBG) and uniform FBG (UFBG). The feasibility of AFBG to measure the strain was verified in the previous research. UFBG was also applied to monitor the small-size nonuniform strain distributions because its spectrum was more sensitive and would generate appreciable distortions with the nonuniform strain (Jin et al., 2019). The parameters of applied UFBG in this article are shown in Table 1.
FBG is similar to a wavelength-selective reflection filter. A narrow band of the incident optical field is reflected by coherent scattering from the index variations with a wavelength λB given by (Hill and Meltz, 1997)
where Λ is the grating period and neff is the modulation index. The neff perturbation in the core for UFBG is described by
where
The grating forces couple between propagating modes since they impose a dielectric perturbation to the waveguide. The coupled mode theory is effective to describe this behavior. A set of coupled first-order differential equations is used to describe the propagation:
where R(z) and S(z) represent the amplitude of forward- and backward-propagation, respectively.
where
This equation represents the uniform grating with a constant average refractive index change. However, the strain distribution of glass-to-metal was nonuniform with a large gradient, and it would cause a chirp in the grating period. If roughly treated as a uniform strain distribution, the measuring results would generate notable deviations. In this paper, the transmission and reflection spectra from the two-mode coupling can be reconstructed using the transfer matrix method (TMM), whereby the grating is divided into finite discrete uniform sections represented by a 2 × 2 matrix. The matrix for the whole FBG can be obtained by multiplying all the discrete matrices (Figure 2).
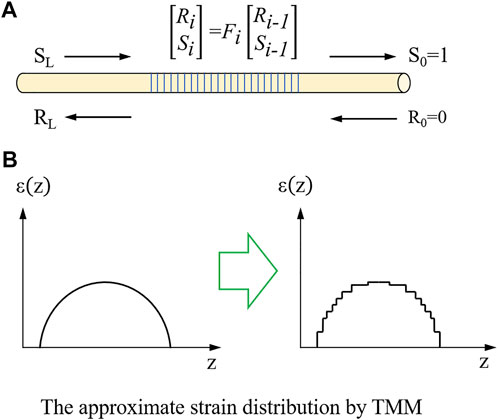
FIGURE 2. (A) Propagation of a waveguide in an optical fiber. (B) Discrete strain distribution by the TMM.
The calculation accuracy of the TMM depends on the section number N, and when
The components of the transfer matrix Fi are defined subsequently, where
The limits of the grating were defined as
where
In addition, substituting Eq. 10 in Eq. 9 results in
Thus, reflectivity as a function of wavelength can be calculated by
Similarly, the transmitted spectrum can be found as
The finite element model of glass-to-metal seals was built to obtain the strain distributions in glass. The thickness of the metal shell was a main factor determining the distribution of compressive strain, so it was designed in a rectangular shape to induce asymmetric deformation defect. The length and width were set to 6 and 0.5 mm (Figure 3), respectively, which could generate remarkable asymmetric strain along the circumference of the hermetic material. The geometrical parameters of the model are shown in Table 2.
To prove the feasibility and measuring resolution of the FBG spectrum, the TMM and FEM were combined to reconstruct the spectrum response with specific nonuniform strain in glass-to-metal seals. This spectrum reconstruction method combined the advantages of both FEM and TMM, and it has been applied by many researchers to predict spectrum variations under large-gradient strain distribution (Kakei et al., 2018; Rajabzadeh et al., 2019; Fazzi et al., 2019; Stathopoulos et al., 2019). The strain of the fiber core transferred directly to the surface of the sealing glass to simplify the simulation (Wang et al., 2019) because the bare fiber was well-fused with molten glass during the manufacturing process and there was little difference between the mechanical properties of fiber and sealing glass (the main component for both was SiO2).
AFBG and UFBG were embedded in the hermetic material to monitor the nonuniform strain distribution. The experimental setup is shown in Figure 4. The FBGs used in this research were type II gratings inscribed by femtolaser provided by Femtofibertech. The previous results showed that FBG had good endurance at high temperature (1000 °C) (Fan et al., 2020). The experimental model was consistent with the finite element model (Table 1). The experimental model was manufactured with FBGs by a gasket. To achieve distributed strain and asymmetric deformation monitoring, four sensors (including 3 AFBGs and 1 UFBG) were embedded simultaneously as shown in Figure 4A, which were located at the same distance (3 mm) with varied metal thickness. The shell thickness of path 1 to path 4 was 6 mm, 5.5 mm, 1 mm, and 0.5 mm, respectively, which ensured the spectra of FBGs would be affected by different strain distributions.
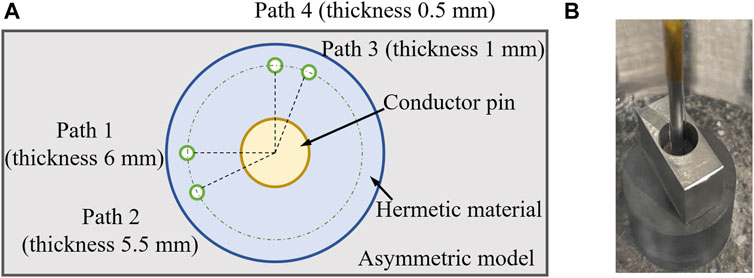
FIGURE 4. Experimental setup for the asymmetric model with distributed FBGs: (A) the schematic diagram and (B) the photograph.
The model was designed under a specific heating process (20°C to 450°C, 10°C/min) to make the hermetic material fuse well with the metal shell and FBGs (Figure 4B). After cooling down to room temperature, the glass-to-metal model with embedded FBGs was obtained, and the hermetic reliability was guaranteed by the compressive strain formed in the sealing glass. The FBGs embedded in four paths were connected to the interrogator to record the real-time spectrum and characteristic parameters. The experimental results were analyzed and compared with the reconstructed spectra obtained by the TMM. The accuracy and feasibility of the proposed method to measure the large-gradient nonuniform strain and prevent the asymmetric deformation defect were demonstrated.
The axial strain distributions in the hermetic material were extracted along the measuring path of FBG. A total of 16 groups of strain with different gradients were obtained under different working conditions from 20°C to 300°C (Figure 5). The sine function was applied to fit the strain distributions with different gradient parameters a, as shown in Figure 5. The gradient parameter a changed from 680 to 2400 with the increase in the amplitude. All the fitting functions were close to the original strain distributions with a deviation of less than 5%.
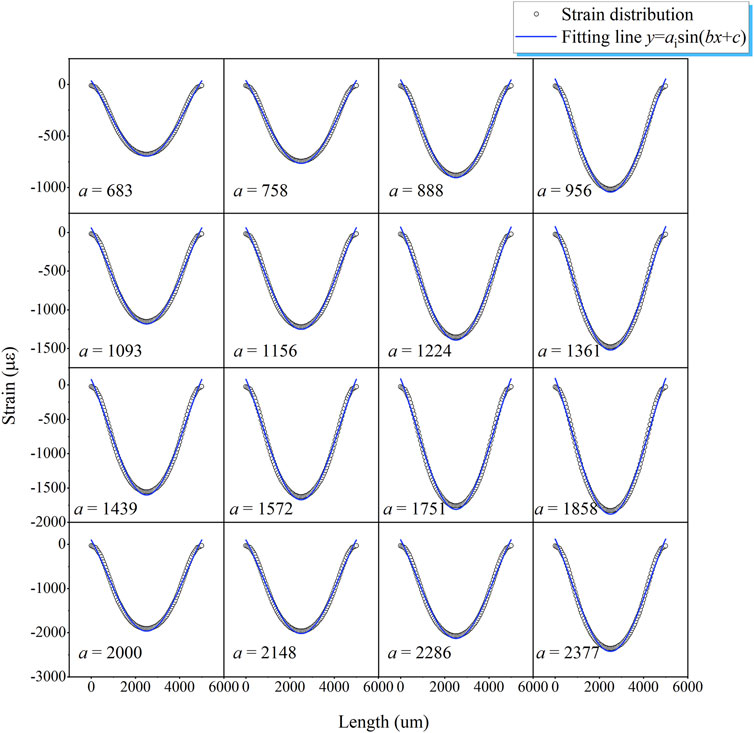
FIGURE 5. Fitting curve of the large-gradient nonuniform strain distributions in glass-to-metal with gradient parameters a.
The strain distributions along the measuring paths and their variation range are summarized in Figure 6. It was shown that those axial strains could be fitted by the sine curve method, and the following three features could be obtained as a conclusion:
1) When the length z = 0 and z = 5,000, the strain was 0.
2) All the distributions could be summarized by the sine curve y = a*sin (bx + c).
3) b = 6.7e-4, and c = 3.028 (based on features 1 and 2).
According to the features, all the axial strain distributions in the hermetic material could be described by the sine curve fitting method with an appropriate parameter a, which represented the difference between the maximum and the minimum value of the distribution. The strain distributions could be assigned to the grating region by the TMM.
A total of 16 groups of sine curve fitting functions were imposed to FBG through the coupling parameters of the transfer matrix, and the spectra were reconstructed as shown in Figure 7. The FWHM tended to broaden (from 0.78 to 2.81 nm) with increasing a, and the relationship between these two parameters is defined in Figure 8. Considering that the resolution of the interrogator was 0.05 nm, consequently, the measuring resolution of the nonuniform strain distribution in the hermetic material was about 70 με. The deviation between the fitting curve and the origin data was around 8%. As a result, the FWHM was proved to characterize the variation in axial strain in the hermetic material. The gradient and distribution of nonuniform strain could be calculated by the spectrum based on the defined relationship. The combined FEM and TMM method was feasible to reconstruct the spectrum response in the hermetic material under different operating conditions.
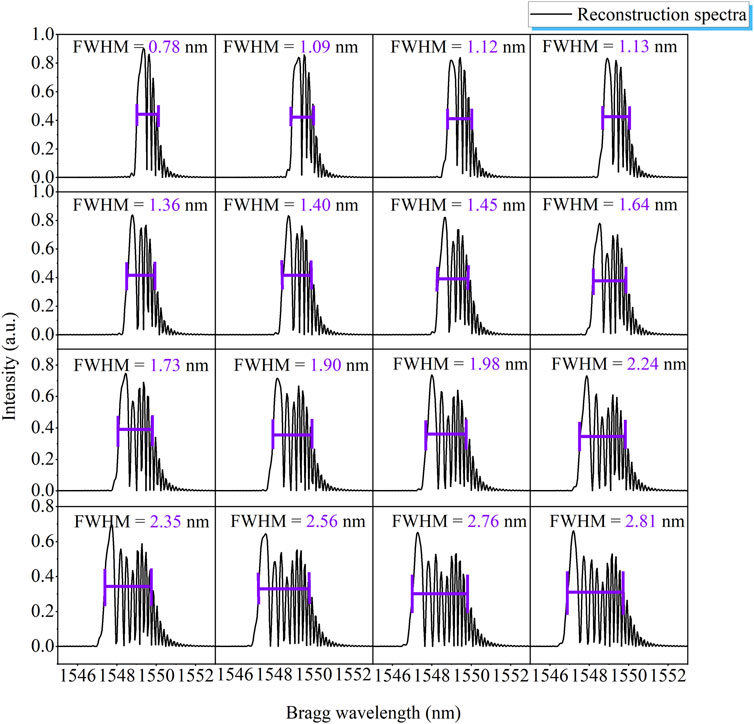
FIGURE 7. Related spectra variations of FBG induced by different nonuniform strain distributions in glass-to-metal.
The deformation and strain contour of the designed model were obtained by the finite element method. The temperature of the model changed from 380°C to 20°C to simulate the manufacturing process of glass-to-metal. The deformation was extracted along two radial paths, as shown in Figure 9A. It was shown that the deformation was extremely asymmetric along radial path 1 and path 2, of which the difference Δl was about 0.008 mm (Figure 9B), which was about 10% compared with the origin radius. The asymmetric deformation would be induced in the hermetic material. Then the strain was extracted along axial path 1 and 2 (Figure 10A), which were related to experimental path 1 and path 4 (Figure 5A), respectively. The gradient of the strain distribution increased with the thickness of the metal shell. Based on the theoretical measuring resolution in Section 4.1, the asymmetric deformation was feasible to be monitored by the distributed FBG sensors embedded in the hermetic material.
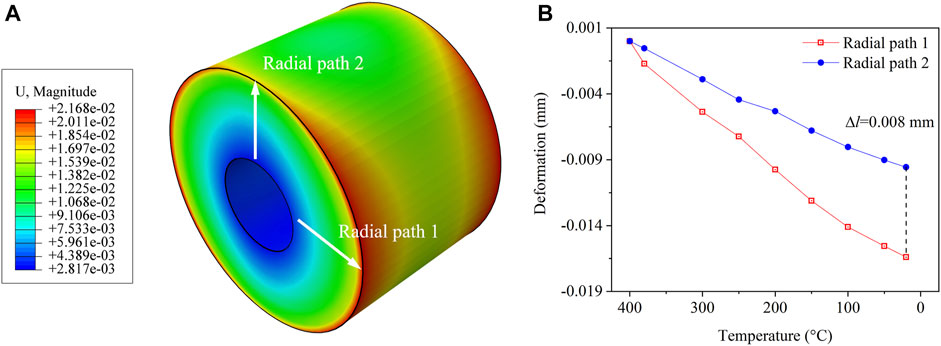
FIGURE 9. (A) Contour of the asymmetric deformation of the designed model; (B) deformation along two radial paths in glass with the thickest and the thinnest metal shell.
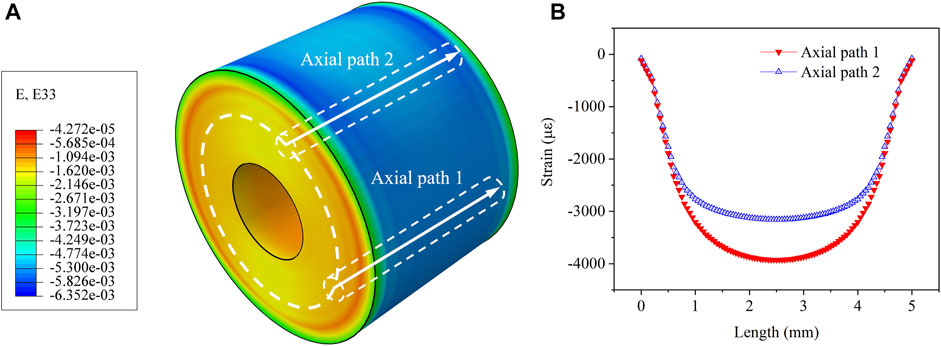
FIGURE 10. (A) Contour of the compressive strain of the designed model; (B) large-gradient nonuniform strain distribution along two radial paths in glass with the thickest and the thinnest metal shell.
A total of four FBGs were embedded simultaneously to monitor the asymmetric deformation during the experiment. The details of four FBGs are shown in Table 3. The AFBGs were embedded in paths 1∼3, and the single UFBG was located in path 4. The two kinds of FBGs were arranged to provide comparisons of the chirped spectrum with nonuniform strain distribution. The distributed monitoring results are shown in Figure 11. The spectra signified with a purple frame were FBGs located in the hermetic material, which generated obvious distortions influenced by the strain variations. The spectra with a yellow frame were FBGs settled near the hermetic material, and the Bragg wavelength shifted as the temperature cooled down without the broadening of the FWHM.
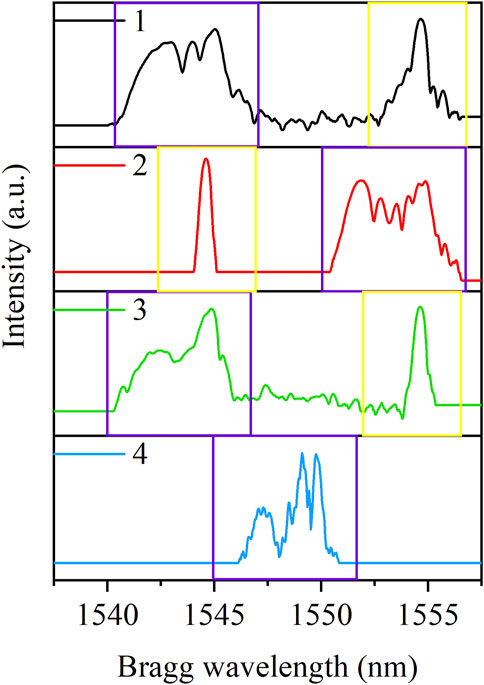
FIGURE 11. Spectral characterization of the asymmetric deformation in glass-to-metal obtained by an interrogator.
The distortions of spectra in the purple frame tended to vary with the thickness of the metal shell, and the feature parameters were extracted as shown in Figure 12. The Bragg wavelength of four FBGs in the hermetic material generated an obvious shift due to the induced compressive strain. However, because the strain distribution was nonuniform with a large gradient, the relationship between the Bragg wavelength shift and the average strain was not linear. In Figure 12, the Bragg wavelength of paths 1 and 2 (the thickness of the metal shell >5.5 mm) was considerably larger than those of paths 3 and 4 (the thickness of the metal shell <1 mm), of which the shift was 0.94 nm, so the asymmetric deformation of the hermetic material was characterized effectively via the Bragg wavelength shift. The FWHM increased with increasing metal shell thickness, and the bandwidth variation induced by the asymmetric deformation was up to 1.16 nm. Therefore, the broadening of the FWHM was feasible to monitor the distributed nonuniform strain distribution in the hermetic material.
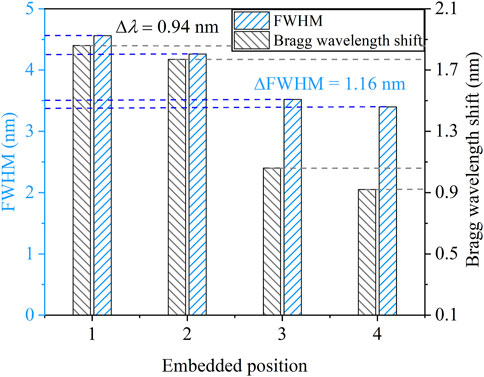
FIGURE 12. Monitoring and discrimination of the asymmetric deformation reflected by the FWHM and Bragg wavelength shift of FBGs.
To verify the accuracy and reliability of the experimental results, the combined TMM and FEM method was carried out to reconstruct the spectrum variation of embedded FBGs in paths 1 and 4. The strain distribution along the special paths was obtained by numerical results in Figure 13, and then the spectra were reconstructed by the transfer matrix with the nonuniform strain distribution as shown in Figure 10B. The theoretical Bragg wavelength shift of FBGs in paths 1 and 4 was 0.70 nm, and the FWHM variation was about 0.91 nm. Compared with the experimental results, the deviation was around 20%, which was induced by the approximate strain distribution of the TMM and the boundary conditions of the FEM. The experimental results proved to remain consistent with the simulations in different paths of the asymmetric model. Thus, in summary, the spectrum would generate obvious distortions when the asymmetric deformation developed in glass-to-metal, and the Bragg wavelength and FWHM would increase as the deformation becomes more severe. Because the FBG spectrum remained stable under consistent operating conditions, the asymmetric deformation could be characterized with the variations in the spectrum distortion, Bragg wavelength, and FWHM. Therefore, the glass-to-metal sample produced with such defect would be replaced promptly to prevent hermetic failure under operating conditions.
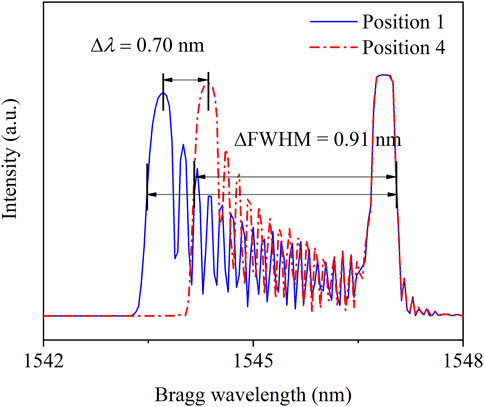
FIGURE 13. Reconstruction spectrum by the TMM in position 1 and position 4 of the experimental model.
This research investigated the spectrum characterization of FBG to non-uniform strain distribution and the derived monitoring and prediction method of the asymmetric deformation defect.
1) The TMM was demonstrated to be a feasible approach to reconstruct the FBG spectra with large-gradient nonuniform strain distributions in glass-to-metal equipment. The FWHM of the reconstructed spectrum tended to increase linearly with the gradient parameter a of strain distributions. The measuring resolution of strain variation in this research was 70 με.
2) The spectrum was feasible to monitor the asymmetric deformation defect of the special model by the distributed FBG array. The embedded FBGs generated distortions affected by the large-gradient nonuniform strain, and the outer FBGs remained as origin spectra with individual Bragg wavelength shift.
3) The FBG spectrum showed distinct variations in different paths of the experimental model. Both the Bragg wavelength shift and the variations in the FWHM proved that the distributed FBGs could measure the asymmetric deformation effectively during the manufacturing process.
Based on the proposed approach, the potential defect in the hermetic material was able to be monitored and prevented, and the quality of products could be inspected and improved after the manufacturing of glass-to-metal equipment.
The original contributions presented in this study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
YH conceived and supported the study. FZ fabricated the experimental models and carried out the defect-monitoring experiments and the theoretical analysis. FZ, YH, and HZ prepared the manuscript. FZ, YH, HZ, and LJ contributed toward revising the manuscript.
This work was supported by the National S&T Major Project of China (ZX069), the project supported by the Science Foundation of Jimei University, China (ZQ2021053), and the Fujian Provincial Department of Education, China (JAT210222).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Chen, S.-Z., Wu, G., and Xing, T. (2017). Deflection Monitoring for a Box Girder Based on a Modified Conjugate Beam Method. Smart Mater. Struct. 26, 085034. doi:10.1088/1361-665x/aa7973
Fan, Z., Diao, X., Liu, M., Zhang, Y., Huang, Z., and Yan, H. (2019). On-line Monitoring of Sealing Glass in Electrical Penetration Assembly Based on Femto-Laser Inscribed Fiber Bragg Grating Sensors. Opt. Express 27, 608–620. doi:10.1364/oe.27.000608
Fan, Z., Diao, X., Hu, K., Zhang, Y., Huang, Z., Kang, Y., et al. (2020). Structural Health Monitoring of Metal-To-Glass-Ceramics Penetration during Thermal Cycling Aging Using Femto-Laser Inscribed FBG Sensors. Sci. Rep. 10, 12330–12413. doi:10.1038/s41598-020-69282-7
Fazzi, L., Rajabzadeh, A., and Milazzo, A. (2019). “Analysis of FBG Reflection Spectra under Uniform and Non-uniform Transverse Loads,” in Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems 2019 (SPIE), 109701, 589–597. doi:10.1117/12.2513795
Goossens, S., De Pauw, B., Geernaert, T., Salmanpour, M. S., Sharif Khodaei, Z., Karachalios, E., et al. (2019). Aerospace-grade Surface Mounted Optical Fibre Strain Sensor for Structural Health Monitoring on Composite Structures Evaluated against In-Flight Conditions. Smart Mater. Struct. 28, 065008. doi:10.1088/1361-665x/ab1458
Hill, K. O., and Meltz, G. (1997). Fiber Bragg Grating Technology Fundamentals and Overview. J. Light. Technol. 15, 1263–1276. doi:10.1109/50.618320
Jin, X., Yuan, S., and Chen, J. (2019). On Crack Propagation Monitoring by Using Reflection Spectra of AFBG and UFBG Sensors. Sensors Actuators A Phys. 285, 491–500. doi:10.1016/j.sna.2018.11.052
Kakei, A., Epaarachchi, J. A., Islam, M., and Leng, J. (2018). Evaluation of Delamination Crack Tip in Woven Fibre Glass Reinforced Polymer Composite Using FBG Sensor Spectra and Thermo-Elastic Response. Measurement 122, 178–185. doi:10.1016/j.measurement.2018.03.023
Kersey, A. D., Davis, M. A., Patrick, H. J., Leblanc, M., Koo, K. P., Askins, C. G., et al. (1997). Fiber Grating Sensors. J. Light. Technol. 15, 1442–1463. doi:10.1109/50.618377
Li S, S., Zhu, Q., Hu, K., Cai, Y., Liu, Z., Chen, F., et al. (2022). Determination of Compressive Stress in Glass-To-Metal Seals Using Photoluminescence Spectroscopy Technique. Ceram. Int. 48, 13379. doi:10.1016/j.ceramint.2022.01.219
Li J, J., Yan, J., Zhu, J., and Qing, X. (2022). K-BP Neural Network-Based Strain Field Inversion and Load Identification for CFRP. Measurement 187, 110227. doi:10.1016/j.measurement.2021.110227
Ling, H.-y., Lau, K.-t., Cheng, L., and Jin, W. (2006). Viability of Using an Embedded FBG Sensor in a Composite Structure for Dynamic Strain Measurement. Measurement 39, 328–334. doi:10.1016/j.measurement.2005.11.011
Majumder, M., Gangopadhyay, T. K., Chakraborty, A. K., Dasgupta, K., and Bhattacharya, D. K. (2008). Fibre Bragg Gratings in Structural Health Monitoring-Present Status and Applications. Sensors Actuators A Phys. 147, 150–164. doi:10.1016/j.sna.2008.04.008
Morana, A., Baghdasaryan, T., Girard, S., Marin, E., Geernaert, T., Thienpont, H., et al. (2019). Radiation-Induced Effects on Fiber Bragg Gratings Inscribed in Highly Birefringent Photonic Crystal Fiber. IEEE Trans. Nucl. Sci. 66, 120–124. doi:10.1109/tns.2018.2886167
Okabe, Y., Tsuji, R., and Takeda, N. (2004). Application of Chirped Fiber Bragg Grating Sensors for Identification of Crack Locations in Composites. Compos. Part A Appl. Sci. Manuf. 35, 59–65. doi:10.1016/j.compositesa.2003.09.004
Rajabzadeh, A., Heusdens, R., Hendriks, R. C., and Groves, R. M. (2019). Characterisation of Transverse Matrix Cracks in Composite Materials Using Fibre Bragg Grating Sensors. J. Light. Technol. 37, 4720. doi:10.1109/jlt.2019.2919339
Stathopoulos, N. A., Savaidis, S. P., Simos, H., Rigas, E., Correia, R., James, S. W., et al. (2019). Transmission Line Method for the Simulation of Fiber Bragg Gratings. Appl. Opt. 58, 353–360. doi:10.1364/ao.58.000353
Van Lancker, B., Hertelé, S., De Corte, W., Dispersyn, J., De Waele, W., and Belis, J. (2016). “Application of Digital Image Correlation in Linear Structural Adhesive Glass-Metal Connection Testing,” in GlassCon Global (FCA Conferences, LLC), 305–313.
Wang, H., Xiang, P., and Jiang, L. (2019). Strain Transfer Theory of Industrialized Optical Fiber-Based Sensors in Civil Engineering: A Review on Measurement Accuracy, Design and Calibration. Sensors Actuators A Phys. 285, 414–426. doi:10.1016/j.sna.2018.11.019
Xiong, L., Guo, Y., Jiang, G., Jiang, L., and Zhou, X. (2019). Fiber Bragg Grating Displacement Sensor with High Measurement Accuracy for Crack Monitoring. IEEE Sensors J. 19, 1. doi:10.1109/jsen.2019.2930761
Keywords: glass-to-metal seal, fiber Bragg grating (FBG), transfer matrix method (TMM), non-uniform strain distribution, nuclear power plant
Citation: Fan Z, Yan H, Huang Z and Liu J (2022) Measurement and Discrimination of Asymmetric Non-uniform Strain Distribution Based on Spectrum Characterization of FBG Sensors. Front. Energy Res. 10:852325. doi: 10.3389/fenrg.2022.852325
Received: 11 January 2022; Accepted: 12 April 2022;
Published: 12 May 2022.
Edited by:
Xianping Zhong, University of Pittsburgh, United StatesCopyright © 2022 Fan, Yan, Huang and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhichun Fan, ZmFuemhpY2h1bkBqbXUuZWR1LmNu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.