Effects of Matrix Creep Properties on Effective Irradiation Swelling of U-10Mo/Zr Dispersion Nuclear Fuels

A meso-mechanical model is established for the homogenized irradiation swelling of U-10Mo/Zr dispersion fuels, with an equivalent sphere chosen as the representative volume element (RVE). In the simulation, a mechanistic model for the fission gas swelling of U-10Mo particles and the creep model for Zr matrix with different values of the creep amplification factor are included. Based on the developed method, the results of effective irradiation swelling of U-10Mo/Zr dispersion fuels are obtained by finite element simulation. Additionally, the effects of matrix creep properties on the effective irradiation swelling are investigated. The numerical results indicate that 1) the Zr matrix has the function of restraining and compensating the irradiation swelling of fuel particles by the mechanical interactions between the fuel particles and the matrix; 2) with the increase in the creep amplification factor of the matrix, the effective irradiation swelling increases while the stresses in the fuel particles and the matrix decrease. The enhanced creep rate of the matrix is apt to result in less restraint of the effective irradiation swelling, but reduces the risk of radial crack initiation and propagation in the matrix; 3) based on the results of finite element simulation, a mathematic model for the effective irradiation swelling of U-10Mo/Zr dispersion fuels is fitted to correlate the effective irradiation swelling with different values of the matrix creep amplification factor under the considered irradiation conditions. The creep property of the matrix should be optimized because of its evident effects on the effective irradiation swelling and stresses of the U-10Mo/Zr dispersion fuels.

Introduction

Dispersion nuclear fuels, with fissionable fuel particles dispersed in the non-fissionable matrix (Ding et al., 2018), are widely used in research and test reactors, advanced nuclear systems, and disposal of nuclear wastes (Duyn, 2003; Carmack et al., 2006; Lombardi et al., 2008; Gong et al., 2013). Tri-structural isotropic particle–based dispersion fuels have been used in high-temperature gas-cooled reactors and have a promising application prospect in advanced pressurized water reactors (Xiang et al., 2014; Zhang T. et al., 2021; Lou et al., 2022). With the non-fissionable matrix encompassing fuel particles, dispersion nuclear fuels possess a more stable swelling behavior and allow higher burnup than traditional homogeneous fuels (Neeft et al., 2003a; Savchenko et al., 2006). Moreover, certain properties of dispersion fuels such as high strength, high thermal conductivity, good corrosion resistance, and good performances under transient conditions can be designed by a proper choice of fuel and matrix materials (Holden, 1967; Savchenko et al., 2007; Savchenko et al., 2010).

In the 1980s, the US Department of Energy Office launched the Reduced Enrichment for Research and Test Reactors (RERTR) program to reduce the threat of nuclear proliferation worldwide, through the conversation of research and test reactors from highly enriched uranium to low-enriched uranium fuels (Meyer et al., 2002; Liu et al., 2011). With the development of the RERTR program, U-Mo/Al dispersion fuels have attracted numerous attention as the low-enriched uranium fuels for research and test reactors (Van den Berghe and Lemoine, 2014), due to their advantages of high uranium density, low neutron capture cross sections, good irradiation stability, and high thermal conductivity (Meyer et al., 2002; Jian et al., 2019a). Early experimental results demonstrated that U-Mo/Al dispersion fuels have good irradiation performance under low power and low burnup (Kim et al., 2002; Meyer et al., 2002). However, excessive local swelling occurred in U-Mo/Al dispersion fuels under high power and high burnup irradiation conditions (Leenaers et al., 2004; Van den Berghe and Lemoine, 2014), due to the formation of an amorphous interaction layer (IL) between U-Mo fuel particles and the Al alloy matrix (Van den Berghe et al., 2008; Oh et al., 2016). Under the irradiation conditions, the IL grows and shows poor fission gas solubility and high diffusivity of fission gas atoms, leading to large bubbles, which induces excessive irradiation swelling (Lee et al., 1997; Huber et al., 2018; Saoudi et al., 2022). To prevent the growth of the IL, some methods were implemented, such as modifying the Al matrix by adding Si (Leenaers et al., 2011; Keiser et al., 2014), coating U-Mo fuel particles with Si or ZrN, and developing monolithic fuels with a Zr layer inserted between U-Mo fuel foil and Al alloy clad (Leenaers et al., 2013; Keiser et al., 2015; Leenaers et al., 2015). An alternative method to eliminate the IL of U-Mo/Al is replacing the Al alloy matrix with some other inert alloys. Zirconium alloys are promising alternative matrixes for U-Mo–based fuels because they have a low reactivity with U and Mo, high melting point, high strength, good corrosion resistance, and low neutron capture cross-section for thermal neutrons (Cox, 2005; Nakamura et al., 2007; Gonzalez et al., 2015). Moreover, zirconium alloys have long been used as fuel matrix and cladding in nuclear reactors (Moorthy, 1969; Savchenko et al., 2007; Savchenko et al., 2010) with extensive knowledge of their material properties and processing technologies, so they would be a good choice to minimize the qualification testing required to introduce a new matrix material for U-Mo–based dispersion fuels (Hagrman et al., 1995; Hayes and Kassner, 2006; Hales et al., 2016; Pasqualini et al., 2016).

Under the irradiation conditions, U-Mo fuel particles undergo irradiation swelling due to the accumulation of solid and gaseous fission products, namely, fission solid swelling and fission gas swelling (Kim and Hofman, 2011). As irradiation swelling is considered the important factor dominating the behavior and service life of nuclear fuels, it is necessary to investigate and model the swelling behavior of U-Mo/Zr dispersion fuels to evaluate its serviceability. Varied knowledge of irradiation swelling behavior of U-Mo alloy has been accumulated through experimental investigation (Kim and Hofman, 2011; Van den Berghe et al., 2012). The fission solid swelling of U-Mo alloy is proportional to the fission density (Kim and Hofman, 2011). The fission gas swelling is complex and related to the fission density, the grain size, the temperature, the external hydrostatic pressure, and the progression of irradiation-induced recrystallization. Kim and Hofman built an empirical model for fission gas swelling by fitting the experiment data (Kim and Hofman, 2011). The empirical model is simple, but it could not reflect the critical influencing parameters mentioned above. Rest built a mechanistic model reflecting the influence of those parameters except the external hydrostatic pressure (Rest, 2005). Cui et al. modified the mechanistic model with consideration of external hydrostatic pressure and re-solution of intergranular gas atoms (Cui et al., 2015). Jian et al. (Jian et al., submitted) further developed the fission gas swelling mechanistic model for U-10Mo fuels, which has been validated by comparing the model results, including the fission gas swelling, the evolution rules of the bubble density, and the bubble size with the experimental results. The newly developed fission gas swelling model could reflect the dependence of external hydrostatic pressure more reasonably. To better understand and study the irradiation swelling behavior of U-Mo/Zr dispersion fuels, it is necessary to adopt the improved mechanistic model of fission gas swelling for fuel particles. For dispersion fuels with numerous fuel particles, it is difficult and expensive to establish a finite element model for the whole fuel element with all particles involved (Schappel et al., 2018). An effective way is to homogenize the thermal-mechanical performances of the dispersion fuels based on homogenization theory, including its effective irradiation swelling behavior (Rest and Hofman, 1997; Zhao et al., 2014; Liu et al., 2018). Zhang J. et al. established an equivalent spherical model to investigate the effective irradiation swelling of PuO₂/Zr dispersion fuels (Zhang J. et al., 2021). The simulation results indicate that the creep behavior of the Zr matrix has an evident influence on the effective irradiation swelling of PuO₂/Zr dispersion fuels. As the creep properties of zirconium alloys are related to alloy compositions, microstructure, process conditions, and service conditions (Krishnan and Asundi, 1980; Hayes and Kassner, 2006; Kim et al., 2021), it is essential and necessary to investigate the effects of Zr matrix creep properties on the effective irradiation swelling of U-Mo/Zr dispersion fuels and provide a reference for the optimization design and advanced manufacture. Meanwhile, the relative research studies are currently limited.

In this study, the three-dimensional finite element simulation for the developed equivalent spherical model is performed for the further homogenization of the effective irradiation swelling of U-10Mo/Zr dispersion fuels. The newly improved mechanistic model of fission gas swelling (Jian et al., submitted) is adopted, which could reflect the significant influences of external hydrostatic pressure. The effects of Zr matrix creep properties on the effective irradiation swelling of U-10Mo/Zr dispersion fuels are investigated with different creep amplification factors imposed on a typical creep model. The irradiation swelling model and creep model are given in Material Properties. The three-dimensional finite element model and the validity of the fission gas swelling model are presented in Results and Discussion. The effective irradiation swelling results are obtained by finite element simulation, and the influence mechanisms are analyzed in Finite Element Modelling. Based on the simulated results, a mathematical model of effective irradiation swelling is described with different values of creep amplification factors.

The acronyms and symbols used in the paper are summarized in Appendix A for better readability.

Material Properties

In this section, the irradiation swelling model for U-10Mo fuel particles and the creep strain rate model for the Zr matrix correlated with the creep amplification factor are given. The other material property models for U-10Mo and the Zr matrix, such as the elastic constants and plasticity model are described in Refs. (Zhao et al., 2014; Jian et al., 2019b). The mechanical constitutive relations for fuel particles and the matrix are introduced to commercial software ABAQUS through user-defined subroutines, based on the stress update algorithms in our previous studies (Zhao et al., 2015; Kong et al., 2018).

The Irradiation Swelling Model for U-10Mo Fuels

The irradiation swelling of U-10Mo consists of fission solid swelling and fission gas swelling, expressed as follows:

$\frac{\mathrm{\Delta }V}{V_0}=\frac{\mathrm{\Delta }{V}_{solid}}{V_0}+\frac{V_{bubble}}{V_0}(1)$

The fission solid swelling is proportional to the fission density, expressed as follows (Kim et al., 2015):

$\frac{\mathrm{\Delta }{V}_{solid}}{V_0}=4.0\times {10}^{-29}\cdot F_d(2)$

where V₀ is the initial fuel volume in m³, $F_d$ depicts the fission density in fission/m³, and $\mathrm{\Delta }{V}_{solid}$ is the absolute volume change caused by solid fission products in m³.

The fission gas swelling is measured by the fraction of identified inter-granular bubbles through SEM, while the intra-granular bubbles are invisible (Kim and Hofman, 2011). Thus, the fission gas swelling is only regarded as the contribution of inter-granular bubbles in the newly developed model (Jian et al., submitted). The fission gas swelling is described as follows:

$\frac{V_{bubble}}{V_0}=\frac{N_{bubble}\times 4/3\pi {\overline{R}}^3}{V_0}(3)$

where $V_{bubble}$ is the total volume of inter-granular bubbles in m³; $N_{bubble}$ is the total number of inter-granular bubbles in the recrystallized and un-recrystallized areas with a new description by Jian et al. (Jian et al., submitted), which could reflect the significant influence of external pressure, and the obtained evolution results of the bubble density and the bubble size have been demonstrated in the same magnitude order as the related experimental results; $\overline{R}$ is the average radius of inter-granular bubbles.

The average radius of inter-granular bubbles is determined using the modified van der Waals gas law (Jian et al., submitted) as follows:

$\left(\frac{2\gamma }{\overline{R}}+P_h\right)\left(\frac{4}{3}\pi {\overline{R}}^3-h_s{b}_v\overline{N}\right)=\overline{N}kT(4)$

where $\frac{2\gamma }{\overline{R}}$ is the surface tension–induced pressure, in Pa; $P_h$ is the external hydrostatic pressure in Pa, involved when positive; $h_s$ is the fitting parameter to make the van der Waals equation equivalent to the hard-sphere equation of state in the value of 0.6; $b_v=8.5\times {10}^{-29}$ m³/atom is the van der Waals gas constant of Xe; $\overline{N}$ is the average number of fission gas atoms in each inter-granular bubble; $k=1.38\times {10}^{-23}$ J/K is the Boltzmann constant and T is the temperature in K.

The numbers of inter-granular bubbles in the recrystallized and un-recrystallized areas are defined as $N_{bubble1}$ and $N_{bubble2}$, respectively, expressed as follows (Jian et al., submitted):

$N_{\text{bubble}1}=2\pi r_{gr}^2\cdot C_b\cdot {\eta }_{F_d}(5)$

$N_{\text{bubble}2}=\frac{2\pi r_{gr0}^3\cdot {\eta }_r}{r_{grx}}\cdot C_{bx}\cdot {\eta }_{F_d}(6)$

${\eta }_{F_d}=\{\begin{array}{cc}1& F_d<F_{d0}\\ {\left(\frac{F_{d0}}{F_d}\right)}^2& F_d\ge F_{d0}\end{array}(7)$

where $C_b$ and $C_{bx}$ are the defined grain-boundary bubble concentration of the un-recrystallization region and the fine grain region in Refs. (Rest, 2005; Cui et al., 2015), respectively; ${\eta }_{F_d}$ is the modified factor for the gas bubble number; $F_{d0}$ = 4.7 × 10²⁷ fissions/m³.

The Creep Model of Zr Matrix

The effects of different creep properties are investigated based on the creep model of Zircaloy-2 alloy (Macdonald and Thompson, 1976). The creep model of the Zr matrix consists of thermal creep and irradiation creep, expressed as follows:

${\dot{\epsilon }}_m^{cr}=\beta \left({\dot{\epsilon }}^{ss}+{\dot{\epsilon }}^{ir}\right)(8)$

where β is the creep amplification factor in the values of 0.01, 0.1, 1, 10, and 100; ${\dot{\epsilon }}^{ss}$ and ${\dot{\epsilon }}^{ir}$ are the thermal creep strain rate and the irradiation creep strain rate, respectively, in 1/s.

The thermal creep strain rate is described as follows:

${\dot{\epsilon }}^{ss}=A_0{\left(\frac{{\mathrm{\sigma }}_m}{G}\right)}^n{e}^{\left(\frac{-Q}{RT}\right)}(9)$

where R is the gas constant in J/(mol·K) with a value of 8.314 J/(mol·K); T is temperature in K; ${\sigma }_m$ is the Mises equivalent stress in Pa and G is the shear modulus in Pa; Q = 27,000 J/mol is the activation energy; A₀ = 3.14 × 10²⁶ s⁻¹ and n = 5 are the used material constants in this study.

The irradiation creep strain rate is described as follows:

${\dot{\epsilon }}^{ir}=K\varphi \left(\sigma +B{e}^{C{\sigma }_m}\right)\exp \left(-10000/RT\right)t^{-0.5}(10)$

where ${\dot{\epsilon }}^{ir}$ is the irradiation creep strain rate in 1/s; ${\sigma }_m$ is the Mises equivalent stress in Pa and $\varphi$ is the fast neutron flux in n/(m²·s), with the constants K = 5.129 × 10^–27, B = 7.252 × 10², and C = 4.967 × 10^–8 in this study.

Figure 1 displays the creep curves of the Zr matrix with different values of β under the condition of 373 K, with a Von Mises stress of 50 MPa and a fast neutron flux of 1.9128 × 10¹⁸ n/(m²·s). It can be found that the creep strain rate decreases with time. For cases of β = 100 and β = 0.01, the effective creep strains after irradiation of 160 days reach 0.5 and 5 × 10^–5, respectively.

FIGURE 1

FIGURE 1. Creep curves for the Zr matrix with β = 0.01, 0.1, 1 (A) and β = 10, 100 (B).

Finite Element Modeling

In this section, the FE (finite element) model for a respective volume element (RVE) of U-10Mo/Zr dispersion fuels with the fuel particle, matrix part, and the applied boundary conditions are presented. The irradiation conditions are chosen according to those of RERTR programs. The effective irradiation swelling of U-10Mo/Zr dispersion fuels is defined and presented in a formula form. To validate the fission gas swelling model, the fission gas swelling results calculated by the model used in this study are compared with the experiment results in the references.

Finite Element Model

The equivalent spherical model has been adopted to study the irradiation swelling behavior of polycrystalline nuclear fuels (Wood and Kear, 1983; Rest, 2010) and the effective irradiation swelling of dispersion fuels (Zhang J et al., 2021). In this study, an equivalent spherical model containing the fuel particle and the matrix is selected as the RVE to obtain the effective irradiation swelling of U-10Mo/Zr dispersion fuels. The initial particle volume fraction of the equivalent spherical model is set as 30% in this study. According to the symmetry in geometry and loading, 1/8 part of the equivalent spherical model is ultimately selected as the FE model shown in Figure 2, including the particle part with a radius of 50 μm and a matrix-shell part.

FIGURE 2

FIGURE 2. FE model of an equivalent sphere.

The bonding between the fuel particle and the matrix is assumed to be perfect with continuous displacements and interfacial stresses. Symmetrical boundary conditions are applied to the surfaces of x = 0, y = 0, and z = 0, which are the symmetrical surfaces of the 1/8 part of the RVE. Constant pressure in a magnitude of 2.5 MPa is applied to the outer surface of the RVE, according to the pressure of the reactor coolant for RERTR (Salvato et al., 2018). A uniform steady-state temperature of 373 K is set. The fission rate in the fuel particle is set as 6 × 10²⁰ fission/(m³·s) and the fast neutron flux is set as 1.9128 × 10¹⁸ n/(m²·s) in this study, according to irradiation conditions of research and test reactors (Perez et al., 2011). The total irradiation time is 160 days, on which the recrystallization process is completed.

To ensure the computation precision and efficiency, three mesh cases are adopted with 1472, 4,147, and 7,868 elements, respectively. The obtained effective irradiation swelling results of the RVE and Mises stress of the matrix for the case of β = 1 are shown in Figure 3. The maximum relative error of the effective irradiation swelling results and Mises stress between Mesh 2 and Mesh 3 is less than 0.11 and 0.14%, respectively. So the effective irradiation swelling and stress results of Mesh 2 have converged, and Mesh 2 is adopted in the following studies.

FIGURE 3

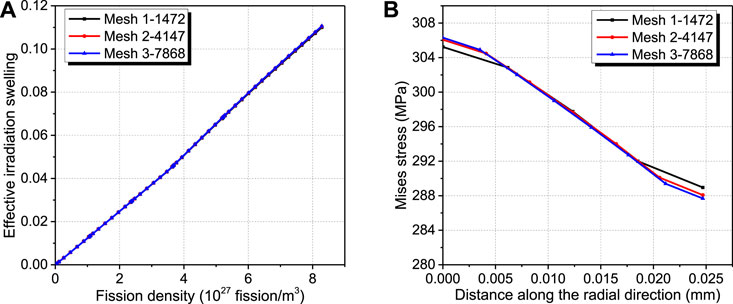
FIGURE 3. Convergence of effective irradiation swelling of the RVE (A) and Mises stress of the matrix (B) to meshes.

The effective irradiation swelling of U-10Mo/Zr dispersion fuels is calculated as follows:

$\frac{\mathrm{\Delta }V}{V_0}=\frac{V-V_0}{V_0}=\frac{r^3-r_0^3}{r_0^3}(11)$

where V is the calculated post-irradiation volume of the equivalent sphere; V₀ is the initial spherical volume; r is the post-irradiation outer spherical radius, obtained from the FE model displacement results; r₀ is the initial outer spherical radius.

Verification of the Used Fission Gas Swelling Model

The irradiation swelling model for the fuel particles is vitally important for calculating the effective irradiation swelling of U-10Mo/Zr dispersion fuels. The fission solid swelling model is directly obtained from the reference (Kim and Hofman, 2011). Meanwhile, the fission gas swelling model considering the critical physical mechanisms will be validated with the experiment results. The plate elements, consisting of Al-alloy cladding and the fuel meat with U-Mo particles dispersed in the aluminum matrix, were irradiated in the advanced test reactor for the test campaigns of RERTR-1∼5 (Kim et al., 2013). The fuel temperature during the test was in the range of 339–431 K, and the achieved fission density was in the range of 2.0 × 10²⁷–5.7 × 10²⁷ fission/m³. The post-irradiation samples were punched out at the plate center to measure the fission gas swelling by scanning electron microscopy. Ignoring the constraint of the IL on U-10Mo particles, the subjected hydrostatic pressure of the fuel particles in the middle zone of fuel plates could be considered as that of the reactor coolant. So, the temperature is ultimately set as 373 K and the hydrostatic pressure is set as 2.5 MPa in this study. The results of the calculated fission gas swelling are compared with the experimental results of RERTR1∼5, shown in Figure 4. It can be seen that the predictions agree well with the experimental results. So, the fission gas swelling model used in this study is effective.

FIGURE 4

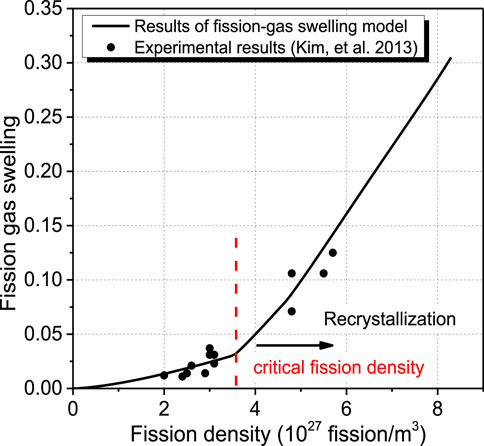
FIGURE 4. Comparison of the simulation results with the experimental results for the fission gas swelling of U-10Mo fuel particles in U-10Mo/Al dispersion fuels.

Results and Discussion

Adopting the FE model in Figure 2, numerical simulation of the irradiation-induced mechanical behavior is implemented, considering different values of β of the Zr matrix. Here, the deformations and stresses of the FE model and the effective irradiation swelling for cases with different values of β are obtained, and the influence mechanisms for effective irradiation swelling are analyzed. A mathematical model correlating the effective irradiation swelling with different values of β is fitted at last.

Deformation and Effective Irradiation Swelling of RVE

The Deformation and Stress Analysis

Due to the irradiation swelling of U-10Mo fuel particles under the irradiation environments, the intensive mechanical interactions are aroused between the fuel particles and the matrix. These mechanical interactions could result in creep and plastic deformations of the matrix. The value of β has a direct influence on the creep deformation of the matrix. Figure 5 gives the contour plots of effective creep strain and equivalent plastic strain of the matrix at the fission density of 8.3 × 10²⁷ fission/m³ for the cases of β = 0.01 and β = 1. It is noted that the other cases with different values of β have similar effective creep strain distributions. The effective creep strain field of the matrix is spherically symmetric on the whole, and the largest effective creep strain occurs at the interface of the matrix with the fuel particle. The plastic deformation of the matrix only occurs in the case of β = 0.01, with the maximum value of 0.055%, excluding the other cases with β ranged from 0.1 to 100. Figure 6 compares the distributions of effective creep strain of the matrix along the radial direction at the fission density of 8.3 × 10²⁷ fission/m³, for different values of β. One can see that the effective creep strain of the matrix decreases along the radial direction for all cases and grows with the increase in β. For the cases with β in the range of 0.01–10, the effective creep strain of the matrix has a small difference with a relative deviation of less than 1.2%. When β is amplified to 100, the maximum effective creep strain of the matrix is about 21%, with a relative increase of ∼20% compared to the result of β = 0.01.

FIGURE 5

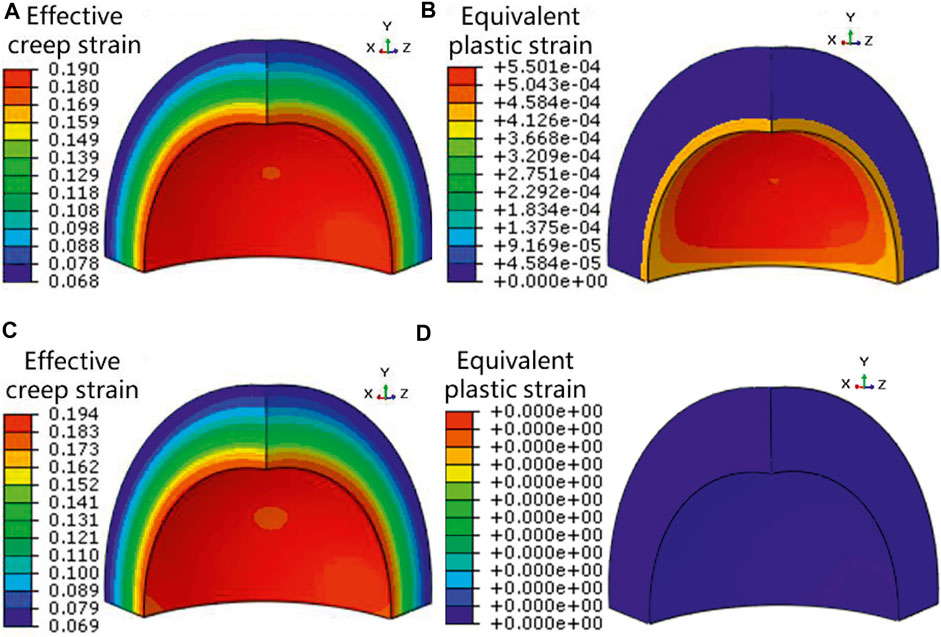
FIGURE 5. Effective creep strain contour plot (A), the equivalent plastic strain contour plot (B) of the matrix for the case of β = 0.01 and the effective creep strain contour plot (C), and the equivalent plastic strain contour plot (D) of the matrix for the case of β = 1 at the fission density of 8.3 × 10²⁷ fission/m³.

FIGURE 6

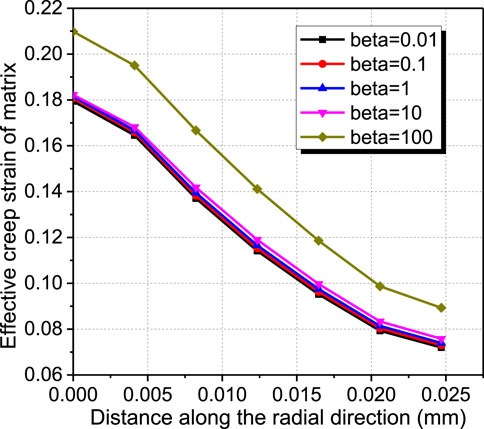
FIGURE 6. Distributions of matrix effective creep strain along the radial direction at the fission density of 8.3 × 10²⁷ fission/m³ for the cases with different values of β

Figure 7 gives the contour plots of Mises stress and the first principal stress of the matrix at a fission density of 8.3 × 10²⁷ fission/m³ for the case of β = 0.01. The largest Mises stress occurs at the interface of the matrix with the fuel particle, while the largest first principal stress occurs at the outer surface of the matrix. Figure 8 compares the evolution results of Mises stress of Element 2 and the first principal stress of Element 3 for the cases with different values of β. It can be found that the stresses of the matrix increase quickly in the preliminary stage of irradiation and tend to be stable at higher burnup levels. As β increases from 0.01 to 100, the maximum Mises stress decreases from 402 to 40 MPa, with a relative reduction of 90%, and the maximum first principal stress decreases from 366 to 16 MPa, with a relative reduction of 96%. As neutron radiations will result in the loss of ductility of the matrix and the formation of the fission fragment damage zone (Duyn, 2003), there is a possibility for the brittle fracture of the matrix. Thus, the increase in β has the positive consequence that the stresses of the matrix decrease, which could reduce the risk of stress-induced failure. To further predict the possible form of crack initiation and propagation, Figure 9 compares the distributions of tangential and radial stress of the matrix along the radial direction at the fission density of 8.3 × 10²⁷ fission/m³, for different values of β. One can see that the radial stress of the matrix is compressive, while the tangential stress is tensile stress approximately equal to the first principal stress. The tangential stress of the matrix decreases with the increase in β. Thus, radial cracks are susceptible to generating and propagating in the matrix, and the enhanced creep rate could prevent the stress-induced cracks of the matrix, similar to the conclusion from the experimental investigation (Neeft et al., 2003b).

FIGURE 7

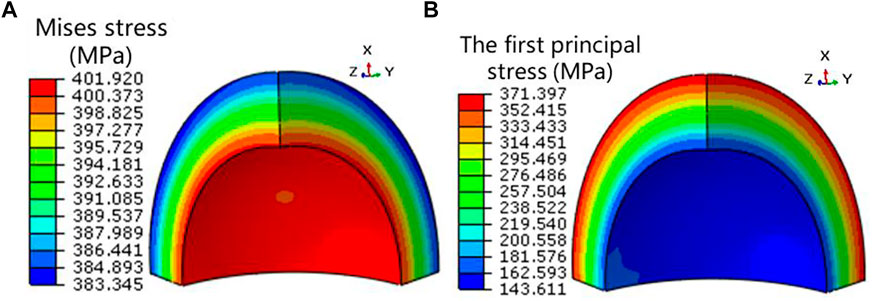
FIGURE 7. Mises stress contour plot (A) and the first principal stress contour plot (B) of the matrix for the case of β = 0.01 at the fission density of 8.3 × 10²⁷ fission/m³.

FIGURE 8

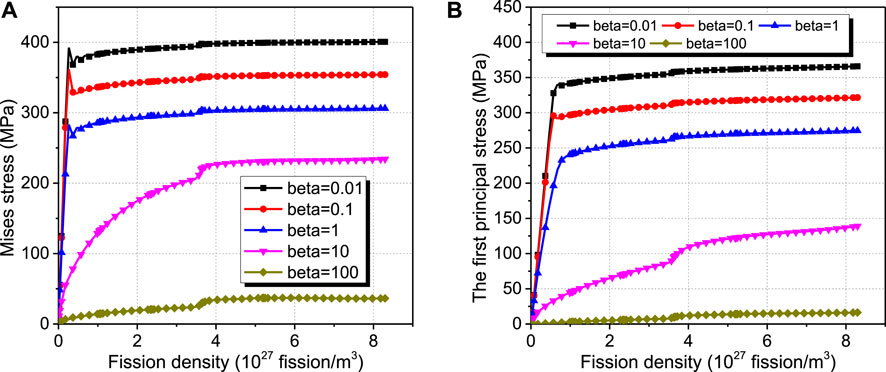
FIGURE 8. Evolution results of (A) Mises stress of Element 2 and (B) the first principal stress of Element 3.

FIGURE 9

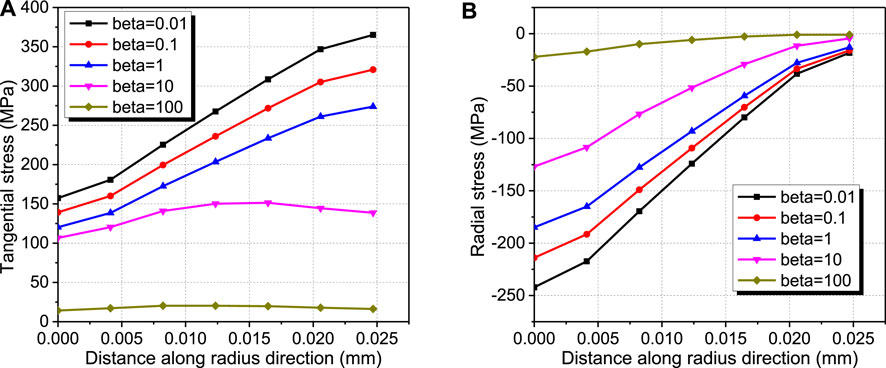
FIGURE 9. Distributions of matrix (A) tangential stress and (B) radial stress along the radial direction at the fission density of 8.3 × 10²⁷ fission/m³ for the cases with different values of β.

The Radial Displacement Analysis

Under the irradiation conditions, U-10Mo fuel particles undergo irradiation swelling, presented as positive radial displacements. Figure 10 displays the radial displacement contour plot of the FE model at a fission density of 8.3 × 10²⁷ fission/m³ for the cases of β = 0.01 and β = 100. It is noted that similar displacement contour plots appear for the other cases with different values of β. The radial displacements of the fuel particle increase along the radial direction. As β increases from 0.01 to 100, the maximum radial displacement, located at the particle surface to be connected with the matrix, increases from 5.5 to 6.4 μm, with a relative increase of ∼18%. The radial displacements of the matrix part are smaller than the maximum of the particle. Figure 11 compares the distributions of radial displacement along Path 1 at the fission density of 8.3 × 10²⁷ fission/m³, for the cases with different values of β and the case without the constraint of the matrix condition. The case without the matrix part means that the original matrix part in Figure 2 is occupied by the particle material. The radial displacements of the FE model along path1 keep increasing for the case without the matrix. Meanwhile, those of the other cases display a decreasing trend along the radial direction across the matrix part, due to the through-thickness shrinking of the matrix. It demonstrates that the Zr matrix has the effects of restraining and compensating the irradiation swelling of U-10Mo fuel particles, and the effects are promoted with the decrease in β. As analyzed in The Deformation and Stress Analysis, the matrix with lower values of β is susceptible to be fractured, which will result in the reduced restraint effect after failure. So, a compromise should be determined in the actual design and fabrication.

FIGURE 10

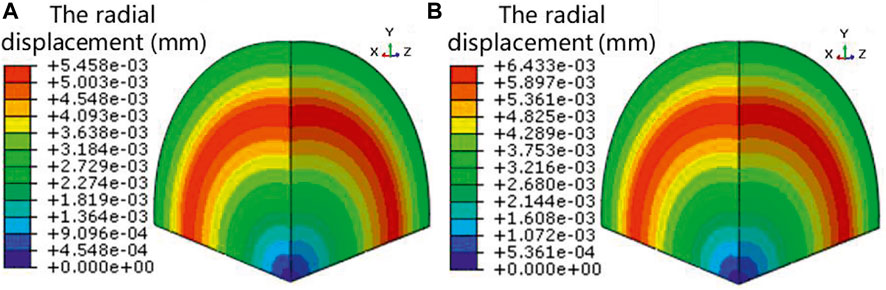
FIGURE 10. Radial displacement contour plot of the FE model at the fission density of 8.3 × 10²⁷ fission/m³for the case of β = 0.01 (A) and the case of β = 100 (B).

FIGURE 11

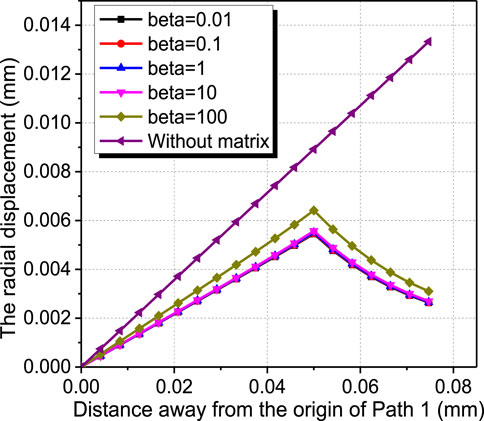
FIGURE 11. Distributions of the radial displacement along Path 1 at the fission density of 8.3 × 10²⁷ fission/m³ for the cases with different values of β and the case without the matrix.

The Irradiation Swelling Analysis

Irradiation swelling of nuclear fuels proceeds with the increase in fission density (Kim and Hofman, 2011; Cui et al., 2015). Figure 12 depicts the effective irradiation swelling evolutions of dispersion fuels, calculated using Eq. 11 for the cases with different values of β. The curve of effective irradiation swelling can be divided into two parts with the critical fission density F_dx. Beyond F_dx, the effective irradiation swelling is accelerated. One can also see that the effective irradiation swelling increases with the rise of β. For the cases with β ranged in 0.01–10, the differences of effective irradiation swelling at the fission density of 8.3 × 10²⁷ fission/m³ are small, not more than 2.5%. For the case of β = 100, the effective irradiation swelling is 13%, with a relative increase of 18% compared to that of the case with β = 0.01.

FIGURE 12

FIGURE 12. Evolution results of effective irradiation swelling of RVE with different values of β

The effective irradiation swelling of dispersion fuels is driven by the irradiation swelling of fuel particles and is approximately equal to the product of the initial particle volume fraction and the sum of fission solid swelling and fission gas swelling, as shown in Figure 13. The evolutions of fission solid swelling and fission gas swelling of Element 1 in the part of the fuel particle are shown in Figure 14. The fission solid swelling in Figure 14A linearly increases with the fission density independent of β, as expressed in Eq. 2. The results of fission gas swelling in Figure 14B rise with the increase in β. The fission gas swelling at the fission density of 8.3 × 10²⁷ fission/m³ for β = 0.01 is 3.44%, becoming 10.2% for β = 100, and they are both less than the fission solid swelling of 33%. So, the discrepancies of effective irradiation swelling for U-10Mo/Zr dispersion fuels are mainly dependent on the difference of fission gas swelling for various values of β. The obtained fission gas swelling predictions here are less than the measured results for U-10Mo/Al dispersion fuels in Ref. (Kim et al., 2013). It is mainly due to the occurrence of the IL between the U-10Mo fuel particles and the Al matrix, which weakens the restraint effect of the matrix and can be interpreted as the high creep rate of the IL (Jeong et al., 2020). Moreover, according to our previous studies, the fission gas swelling increases with the decrease in hydrostatic pressure in fuel particles (Cui et al., 2015; Jian et al., 2019a; Zhang J. et al., 2021). The particles selected to measure the fission gas swellings (Kim et al., 2013) are near the middle region of U-10Mo/Al dispersion fuel plates, and the hydrostatic pressures of these particles are close to the coolant pressure of ∼2.5 MPa, which are much lower than the experienced hydrostatic pressure of the particles in U-10Mo/Zr dispersion fuels, as presented in Fission Gas Swelling of Fuel Particles and the Influencing Mechanisms.

FIGURE 13

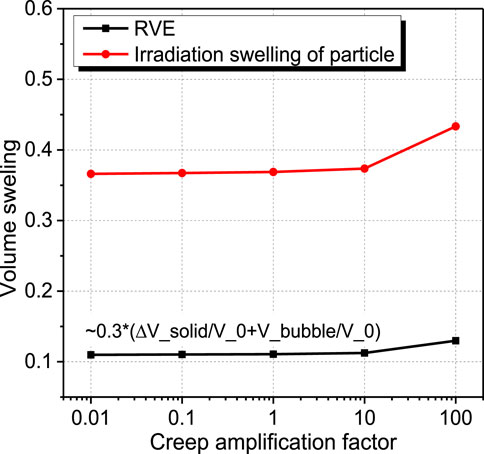
FIGURE 13. Comparison of effective irradiation swelling of RVE with the irradiation swelling of fuel particles for the cases with different values of β.

FIGURE 14

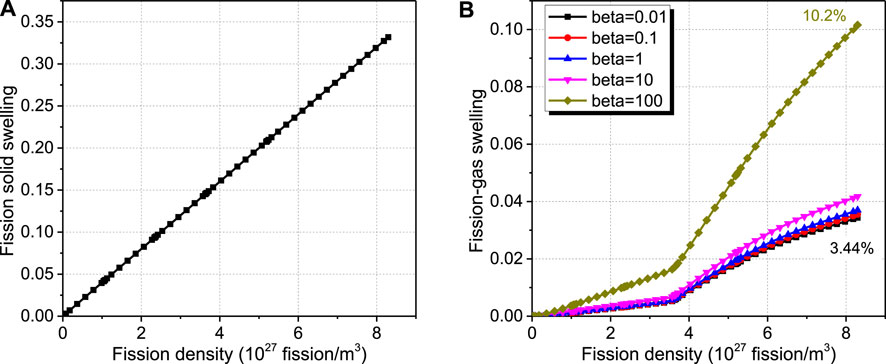
FIGURE 14. Evolution results of (A) fission-solid swelling and (B) fission-gas swelling of Element 1.

Fission Gas Swelling of Fuel Particles and the Influencing Mechanisms

It can be known from The Irradiation Swelling Model for U-10Mo Fuels that the fission gas swelling behavior of nuclear fuels is influenced by the external hydrostatic pressure. Figure 15 displays the evolution results of hydrostatic pressure of Element 1 for the cases with different values of β. It can be found that the hydrostatic pressure of the fuel particle increases quickly in the preliminary stage of irradiation and tend to be stable at higher burnup levels. As β increases from 0.01 to 100, the maximum hydrostatic pressure decreases from 299 to 24 MPa, with a relative reduction of ∼92%. Creep deformation of the matrix could relax the mechanical interactions between the fuel particles and the matrix (Zhang J. et al., 2021). A larger value of β will result in enlarged matrix creep deformations, as shown in Figure 6, and the stress relaxation effect will be enhanced to result in lower hydrostatic pressure in the fuel particle, as shown in Figure 15.

FIGURE 15

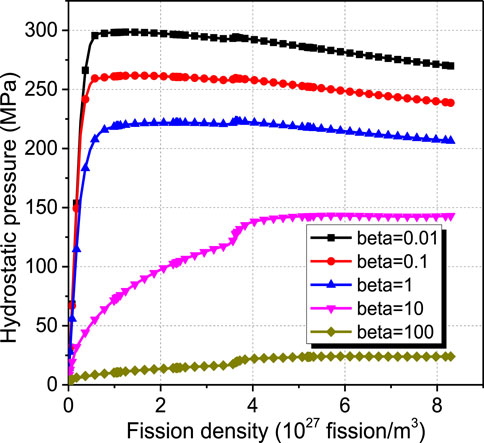
FIGURE 15. Evolution results of hydrostatic pressure of Element 1 for the cases with different values of β.

According to Eq. 4, the average radius of inter-granular bubbles is correlated with hydrostatic pressure and the average number of fission gas atoms in each inter-granular bubble. Figure 16 depicts the average radius predictions of the inter-granular bubbles of Element 1 for the cases with different values of β. One can observe that the average radius of inter-granular bubbles increases with the fission density overall, due to the increase in fission gas atoms. As β increases, the average radius of inter-granular bubbles increases because of the lowered hydrostatical pressure. The predicted radius of inter-granular bubbles is in the same magnitude order with experimental results of U-7Mo fuels (Salvato et al., 2018), so that the external hydrostatical pressure effects could be well reflected.

FIGURE 16

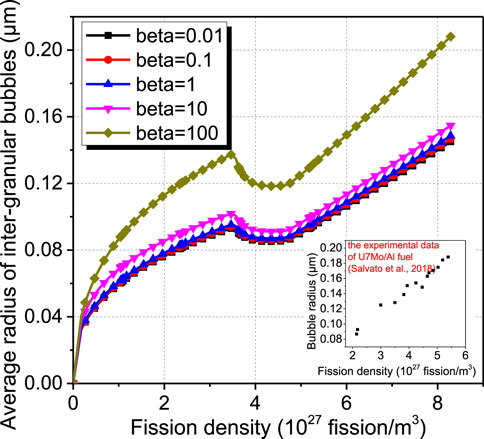
FIGURE 16. Evolution results of the average radius of inter-granular bubbles of Element 1 for the cases with different values of β.

According to Eq. 3, the fission gas swelling also depends on the number of inter-granular bubbles or the bubble density $\frac{N_{bubble}}{V_0}$. The cases with different values of β have the same results of the bubble density. One can find from Figure 17 that the number of inter-granular bubbles does not show significant changes before recrystallization. After recrystallization, the number of inter-granular bubbles increases sharply, due to the increased grain-boundary area per unit volume (Rest, 2005). As the fission density increases further, the inter-granular bubbles begin to coalesce (Meyer et al., 2002) and the predicted number of inter-granular bubbles decreases. The predictions of bubble density match the evolution traits of the experimental results (Salvato et al., 2018). The different fission gas swelling results in Figure 14B for the varied cases of β can be known to stem mainly from the discrepancy of inter-granular bubble size influenced by hydrostatic pressure.

FIGURE 17

FIGURE 17. Evolution results of bubble density of Element 1 for all the considered cases.

Fitted Mathematic Model for the Effective Irradiation Swelling

The effective irradiation swelling is defined as the relative volume variation to the initial volume of the RVE, calculated using Eq. 11. Considering the temperature of RVE as 373 K and the subjected homogenization pressure as 2.5 MPa, a mathematic model for the effective irradiation swelling of U-10Mo/Zr dispersion fuels is fitted as follows:

$S{W}_{eff}=\{\begin{array}{ll}\left(-1.1858\times {10}^{-7}{\beta }^2+2.1160\times {10}^{-5}\beta +1.2375\times {10}^{-2}\right)F_d,\hfill & F_d<3.54\hfill \\ \begin{array}{l}\left(3.6481\times {10}^{-5}\beta +1.3978\times {10}^{-2}\right)F_d\\ -9.8148\times {10}^{-5}\beta -5.0011\times {10}^{-3},\end{array}\hfill & F_d\ge 3.54\hfill \end{array}(12)$

where $S{W}_{eff}$ is the effective irradiation swelling; β is the creep amplification factor in the range of 0.01–100; $F_d$ is fission density in 10²⁷ fission/m³; The critical fission density of 3.54 × 10²⁷ fission/m³ is dependent on fission rate $\dot{f}$, calculated as $4\times {10}^{24}{\left(\dot{f}\right)}^{2/15}$.

The comparison of finite element simulation results and the fitted model results is shown in Figure 18, for the cases with different values of β. The relative error is less than 0.8% at the fission density of 8.3 × 10²⁷ fission/m³. So the fitted model is acceptable and could be used to obtain the effective irradiation swelling for U-10Mo/Zr dispersion fuels with the values of β ranged in 0.01–100, under the irradiation condition mentioned in Finite Element Model.

FIGURE 18

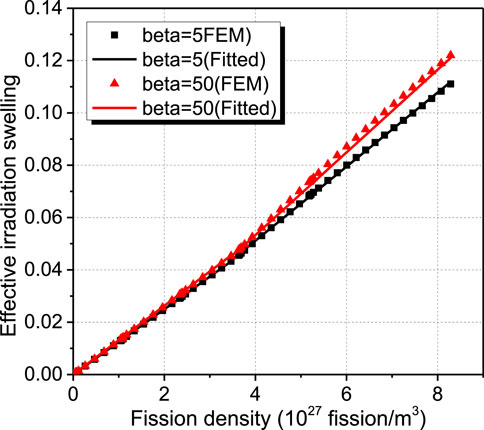
FIGURE 18. Verification of the fitted model for the effective irradiation swelling of U-10Mo/Zr dispersion fuels.

It should be mentioned that the homogenization pressures of dispersion fuel foil in the plate-type fuel elements are distributed heterogeneously and vary with the burnup levels and also depend on the matrix creep and the particle volume fractions. As a result, it will be possible for the homogenization pressures to differ greatly from the coolant pressure. Further research should be carried out to obtain a comprehensive mathematic model for usage in the numerical simulations of the irradiation-induced thermal-mechanical behaviors in dispersion fuel elements or assemblies.

Conclusion

In this study, a meso-mechanical model is established for the homogenized irradiation swelling of U-10Mo/Zr dispersion fuels. An equivalent sphere is chosen as the RVE, with an initial particle volume fraction of 30% and a temperature of 373 K. A newly developed fission gas swelling mechanistic model for U-10Mo is involved and validated with the experimental results in literatures. To investigate the effect of Zr matrix creep properties on effective irradiation swelling of U-10Mo/Zr dispersion fuels, different creep amplification factors are imposed on a typical creep model. Based on the developed method, the results of effective irradiation swelling for U-10Mo/Zr dispersion fuels are obtained and analyzed. The main conclusions are as follows:

1) The Zr matrix has the effects of restraining and compensating for the irradiation swelling of fuel particles. The effective irradiation swelling of U-10Mo/Zr dispersion fuels increases with the increase of the creep amplification factor of the Zr matrix due to the stress relaxation effect of matrix creep deformations. When the creep amplification factor increases from 0.01 to 100, the effective irradiation swelling at the fission density of 8.3 × 10²⁷ fission/m³ increases from 11 to 13%, with a relative increase of 18%.

2) Although the effective irradiation swelling increases with the increase of the creep amplification factor, the stresses in the matrix of U-10Mo/Zr dispersion fuels decrease to result in a reduction of the risk of radial crack initiation and propagation. So, the creep properties of the Zr matrix need to be optimized according to design requirements and service conditions.

3) When the creep amplification factor increases from 0.01 to 100, the maximum hydrostatic pressure of the fuel particle decreases from 299 to 24 MPa, with a reduction of 92%. The different fission gas swelling results for the varied cases of the creep amplification factor stems mainly from the discrepancy of inter-granular bubble size influenced by hydrostatic pressure.

4) Based on the results of finite element simulation, a mathematic model for the effective irradiation swelling of U-10Mo/Zr dispersion fuels is fitted and verified. The fitted model is acceptable under the adopted irradiation condition and the selected parameter ranges.

In reality, the initial particle volume fraction and the temperature could be different under different irradiation environments or in different positions. The mechanical interaction between particles and between fuel meat and cladding could also lead to the external equilibrium hydrostatic pressure. So, wide future research studies should be performed.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

YoL: Software, Validation, Formal analysis, Investigation, Data Curation, Writing, Original Draft, Visualization. JZ: Software, Validation, Formal analysis, Investigation, Review & Editing. XJ, FY: Software, Validation, Formal analysis. SD: Conceptualization, Methodology, Software, Resources, Writing, Review & Editing, Supervision, Project administration. YuL: Conceptualization, Supervision, Formal analysis.

Funding

The authors are very grateful for the support of the National Natural Science Foundation of China (No. 12132005, 12102094, and 12135008) and the support of the Foundation from Science and Technology on Reactor System Design Technology Laboratory. This study is also sponsored by Shanghai Sailing Program (21YF1402200).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Carmack, W. J., Todosow, M., Meyer, M. K., and Pasamehmetoglu, K. O. (2006). Inert Matrix Fuel Neutronic, Thermal-Hydraulic, and Transient Behavior in a Light Water Reactor. J. Nucl. Mater. 352, 276–284. doi:10.1016/j.jnucmat.2006.02.098

CrossRef Full Text | Google Scholar

Cox, B. (2005). Some Thoughts on the Mechanisms of In-Reactor Corrosion of Zirconium Alloys. J. Nucl. Mater. 336, 331–368. doi:10.1016/j.jnucmat.2004.09.029

CrossRef Full Text | Google Scholar

Cui, Y., Ding, S., Chen, Z., and Huo, Y. (2015). Modifications and Applications of the Mechanistic Gaseous Swelling Model for UMo Fuel. J. Nucl. Mater. 457, 157–164. doi:10.1016/j.jnucmat.2014.11.065

CrossRef Full Text | Google Scholar

Dai, X., Cao, X., Yu, S., and Zhu, C. (2014). Conceptual Core Design of an Innovative Small PWR Utilizing Fully Ceramic Microencapsulated Fuel. Prog. Nucl. Energ. 75, 63–71. doi:10.1016/j.pnucene.2014.04.010

CrossRef Full Text | Google Scholar

Ding, S. R., Gong, X., Zhao, Y. M., Huo, Y. Z., and Wei, H. Y. (2018). Key Mechanical Problems in Dispersion Nuclear Fuels during Their Burning Evolution Process. Chin. Q. Mech. 039 (001), 1–21. doi:10.15959/j.cnki.0254-0053.2018.01.001

CrossRef Full Text | Google Scholar

Duyn, L. (2003). Evaluation of the Mechanical Behavior of a Metal-Matrix Dispersion Fuel for Plutonium Burning. [master’s thesis]. Atlanta: Georgia Institute of Technology.

Google Scholar

Gong, X., Ding, S., Zhao, Y., Huo, Y., Zhang, L., and Li, Y. (2013). Effects of Irradiation Hardening and Creep on the Thermo-Mechanical Behaviors in Inert Matrix Fuel Elements. Mech. Mater. 65, 110–123. doi:10.1016/j.mechmat.2013.05.008

CrossRef Full Text | Google Scholar

Gonzalez, A. G., Muñoz, C. A., and Arnaldo, G. J. (2015). Metallographic Study on Alloy Zircaloy-4 of Nuclear Use. Proced. Mater. Sci. 8, 494–501. doi:10.1016/j.mspro.2015.04.101

CrossRef Full Text | Google Scholar

Hagrman, D. T., Allison, C. M., and Berna, G. A. (1995). SCDAP/RELAP5/MOD 3.1 Code Manual: MATPRO, A Library of Materials Properties for Light-Water-Reactor Accident Analysis. Off. scientific Tech. Inf. Tech. Rep. 4, 212–449. doi:10.2172/100327

CrossRef Full Text | Google Scholar

Hales, D. J., Williamson, R. L., Novascone, S. R., Pastore, G., Spencer, B. W., Stafford, D. S., et al. (2016). Bison Theory Manual the Equations behind Nuclear Fuel Analysis. Idaho Falls, Idaho National Laboratory. doi:10.2172/1374503

CrossRef Full Text | Google Scholar

Hayes, T. A., and Kassner, M. E. (2006). Creep of Zirconium and Zirconium Alloys. Metall. Mat Trans. A. 37 (8), 2389–2396. doi:10.1007/BF02586213

CrossRef Full Text | Google Scholar

Holden, A. N. (1967). Dispersion Fuel elements[M]. New York: Gordon and Breach Science Publishers Inc. doi:10.1016/0029-554X(68)90177-8

CrossRef Full Text | Google Scholar

Huber, T. K., Breitkreutz, H., Burkes, D. E., Casella, A. J., Casella, A. M., Elgeti, S., et al. (2018). Thermal Conductivity of Fresh and Irradiated U-Mo Fuels. J. Nucl. Mater. 503 (C), 304–313. doi:10.1016/j.jnucmat.2018.01.056

CrossRef Full Text | Google Scholar

Jeong, G. Y., Kim, Y. S., and Park, J. (2020). Analytical Local Stress Model for UMo/Al Dispersion Fuel. J. Nucl. Mater. 528, 151881. doi:10.1016/j.jnucmat.2019.151881

CrossRef Full Text | Google Scholar

Jian, X., Kong, X., and Ding, S. (2019a). A Mesoscale Stress Model for Irradiated U 10Mo Monolithic Fuels Based on Evolution of Volume Fraction/Radius/Internal Pressure of Bubbles. Nucl. Eng. Technol. 51 (6), 1575–1588. doi:10.1016/j.net.2019.04.011

CrossRef Full Text | Google Scholar

Jian, X., Yan, F., Kong, X., and Ding, S. (2019b). Effects of U-Mo Irradiation Creep Coefficient on the Mesoscale Mechanical Behavior in U-Mo/Al Monolithic Fuel Plates. Nucl. Mater. Energ. 21, 100706. doi:10.1016/j.nme.2019.100706

CrossRef Full Text | Google Scholar

Keiser, D. D., Jue, J.-F., Miller, B., Gan, J., Robinson, A., Medvedev, P., et al. (2015). Microstructural Characterization of the U-9.1Mo Fuel/AA6061 Cladding Interface in Friction-Bonded Monolithic Fuel Plates Irradiated in the RERTR-6 Experiment. Metallurgical Mater. Trans. E 2, 173–189. doi:10.1007/s40553-015-0055-8

CrossRef Full Text | Google Scholar

Keiser, D. D., Jue, J. F., Miller, B. D., Gan, J., Robinson, A. B., Medvedev, P., et al. (2014). Scanning Electron Microscopy Analysis of Fule/matirx Interaction Layers in Highly-Irradiation U-Mo Dispersion Fuel Plates with Al and Al-Si alloy Matrices. Nucl. Eng. Technol. 46 (2), 147–158. doi:10.5516/NET.07.2014.704

CrossRef Full Text | Google Scholar

Kim, D., Hong, J., Kim, H., Kim, J., and Kim, H. (2021). Study of the Mechanical Properties and Effects of Particles for Oxide Dispersion Strengthened Zircaloy-4 via a 3D Representative Volume Element Model. Nucl. Eng. Technol., 1–11. doi:10.1016/j.net.2021.10.044

CrossRef Full Text | Google Scholar

Kim, K., Park, J., Kim, C. L., Hofman, G., and Meyer, M. K. (2002). Irradiation Behavior of Atomized U-10wt.% Mo alloy Aluminum Matrix Dispersion Fuel Meat at Low Temperature. Nucl. Eng. Des. 211 (2-3), 229–235. doi:10.1016/S0029-5493(01)00459-9

CrossRef Full Text | Google Scholar

Kim, Y. S., Hofman, G. L., and Cheon, J. S. (2013). Recrystallization and Fission-Gas-Bubble Swelling of U-Mo Fuel. J. Nucl. Mater. 436, 14–22. doi:10.1016/j.jnucmat.2013.01.291

CrossRef Full Text | Google Scholar

Kim, Y. S., and Hofman, G. L. (2011). Fission Product Induced Swelling of U-Mo Alloy Fuel. J. Nucl. Mater. 419 (1), 291–301. doi:10.1016/j.jnucmat.2011.08.018

CrossRef Full Text | Google Scholar

Kim, Y. S., Jeong, G. Y., Park, J. M., and Robinson, A. B. (2015). Fission Induced Swelling of U-Mo/Al Dispersion Fuel. J. Nucl. Mater. 465, 142–152. doi:10.1016/j.jnucmat.2015.06.006

CrossRef Full Text | Google Scholar

Kong, X., Tian, X., Yan, F., Ding, S., Hu, S., and Burkes, D. E. (2018). Thermo-Mechanical Behavior Simulation Coupled with the Hydrostatic-Pressure-Dependent Grain-Scale Fission Gas Swelling Calculation for a Monolithic UMo Fuel Plate under Heterogeneous Neutron Irradiation. Open Eng. 8, 243–260. doi:10.1515/eng-2018-0029

CrossRef Full Text | Google Scholar

Krishnan, R., and Asundi, M. K. (1980). Zirconium Alloys in Nuclear Technology[J]. Proc. Indian Acad. Sci. 4, 41–56. doi:10.1007/BF02843474

CrossRef Full Text | Google Scholar

Lee, D. B., Kim, K. H., and Kim, C. K. (1997). Thermal Compatibility Studies of Unirradiated U-Mo Alloys Dispersed in Aluminum. J. Nucl. Mater. 250, 79–82. doi:10.1016/S0022-3115(97)00252-3

CrossRef Full Text | Google Scholar

Leenaers, A., Van den Berghe, S., and Detavernier, C. (2013). Surface Engineering of Low Enriched Uranium-Molybdenum. J. Nucl. Mater. 440, 220–228. doi:10.1016/j.jnucmat.2013.04.068

CrossRef Full Text | Google Scholar

Leenaers, A., Van den Berghe, S., Koonen, E., Jarousse, C., Huet, F., Trotabas, M., et al. (2004). Post-Irradiation Examination of Uranium–7wt% Molybdenum Atomized Dispersion Fuel. J. Nucl. Mater. 335 (1), 39–47. doi:10.1016/j.jnucmat.2004.07.004

CrossRef Full Text | Google Scholar

Leenaers, A., Van den Berghe, S., Koonen, E., Kuzminov, V., and Detavernier, C. (2015). Fuel Swelling and Interaction Layer Formation in the Selenium Si and ZrN Coated U(Mo) Dispersion Fuel Plates Irradiated at High Power in BR2. J. Nucl. Mater. 458, 380–393. doi:10.1016/j.jnucmat.2014.12.073

CrossRef Full Text | Google Scholar

Leenaers, A., Van den Berghe, S., Van Renterghem, W., Charollais, F., Lemoine, P., Jarousse, C., et al. (2011). Irradiation Behavior of Ground U(Mo) Fuel with and without Si Added to the Matrix. J. Nucl. Mater. 412 (1), 41–52. doi:10.1016/j.jnucmat.2011.02.002

CrossRef Full Text | Google Scholar

Liu, M., Lee, Y., and Rao, D. V. (2018). Development of Effective thermal Conductivity Model for Particle-Type Nuclear Fuels Randomly Distributed in a Matrix. J. Nucl. Mater. 508, 168–180. doi:10.1016/j.jnucmat.2018.05.044

CrossRef Full Text | Google Scholar

Liu, X., Lu, T. C., Xing, Z. H., and Qian, D. Z. (2011). Modeling the Swelling Performance of UMo Alloys for Al-Matrix Dispersion Fuel. J. Alloys Compd. 509, 6589–6594. doi:10.1016/j.jallcom.2011.03.099

CrossRef Full Text | Google Scholar

Lombardi, C., Luzzi, L., Padovani, E., and Vettraino, F. (2008). Thoria and Inert Matrix Fuels for a Sustainable Nuclear Power. Prog. Nucl. Energ. 50 (8), 944–953. doi:10.1016/j.pnucene.2008.03.006

CrossRef Full Text | Google Scholar

Lou, L., Chai, X. M., Yao, D., Wang, L. J., Li, M. C., Chen, L., et al. (2022). Theoretically Modified Optical Length Research on the Physical Boundary of the Double-Heterogeneous System. Front. Energ. Res. 9, 1–10. doi:10.3389/fenrg.2021.773067

CrossRef Full Text | Google Scholar

Macdonald, P. E., and Thompson, L. B. (1976). Matpro: A Handbook of Materials Properties for Use in the Analysis of Light Water Reactor Fuel Rod Behavior. Specif. Nucl. Reactors Associated Plants, 134–140. doi:10.2172/6442256

CrossRef Full Text | Google Scholar

Meyer, M. K., Hofman, G. L., Hayes, S. L., Clark, C. R., Wiencek, T. C., Snelgrove, J. L., et al. (2002). Low-Temperature Irradiation Behavior of Uranium-Molybdenum Alloy Dispersion Fuel. J. Nucl. Mater. 304 (2), 221–236. doi:10.1016/S0022-3115(02)00850-4

CrossRef Full Text | Google Scholar

Moorthy, K. B. (1969). Current Trends in the Use of Zirconium Alloys. Metallurgy, 181–187.

Google Scholar

Nakamura, S., Harada, H., Raman, S., and Koehler, P. E. (2007). Thermal Neutron Capture Cross Sections of Zirconium-91 and Zirconium-93 by Prompt γ-ray Spectroscopy. J. Nucl. Sci. Technol. 44 (1), 21–28. doi:10.1080/18811248.2007.9711252

CrossRef Full Text | Google Scholar

Neeft, E., Bakker, K., Belvroy, R. L., Tams, W. J., Schram, R. P. C., Conrad, R., et al. (2003b). Mechanical Behaviour of Macro-Dispersed Inert Matrix Fuels. J. Nucl. Mater. 317, 217–225. doi:10.1016/S0022-3115(03)00096-5

CrossRef Full Text | Google Scholar

Neeft, E., Bakker, K., Schram, R., Conrad, R., and Konings, R. (2003a). The EFTTRA-T3 Irradiation Experiment on Inert Matrix Fuels. J. Nucl. Mater. 320 (1), 106–116. doi:10.1016/S0022-3115(03)00176-4

CrossRef Full Text | Google Scholar

Oh, J.-Y., Kim, Y. S., Tahk, Y.-W., Kim, H.-J., Kong, E.-H., Yim, J.-S., et al. (2016). Modeling a Failure Criterion for U-Mo/Al Dispersion Fuel. J. Nucl. Mater. 473, 68–74. doi:10.1016/j.jnucmat.2016.02.015

CrossRef Full Text | Google Scholar

Pasqualini, E. E., Robinson, A. B., Porter, D. L., Wachs, D. M., and Finlay, M. R. (2016). Fabrication and Testing of U-7Mo Monolithic Plate Fuel with Zircaloy Cladding. J. Nucl. Mater. 479, 402–410. doi:10.1016/j.jnucmat.2016.07.034

CrossRef Full Text | Google Scholar

Perez, D. M., Lillo, M. A., Chang, G. S., Roth, G. A., Woolstenhulme, N. E., and Wachs, D. M. (2011). RERTR-9 Summary Report. Off. scientific Tech. Inf. Tech. Rep, 1–28. doi:10.2172/1023454

CrossRef Full Text | Google Scholar

Rest, J. (2010). An Analytical Study of Gas-Bubble Nucleation Mechanisms in Uranium-alloy Nuclear Fuel at High Temperature. J. Nucl. Mater. 402 (2-3), 179–185. doi:10.1016/j.jnucmat.2010.05.022

CrossRef Full Text | Google Scholar

Rest, J. (2005). A Model for the Effect of the Progression of Irradiation-Induced Recrystallization from Initiation to Completion on Swelling of UO2 and U-10Mo Nuclear Fuels. J. Nucl. Mater. 346 (2-3), 226–232. doi:10.1016/j.jnucmat.2005.06.012

CrossRef Full Text | Google Scholar

Rest, J., and Hofman, G. L. (1997). DART Model for Irradiation-Induced Swelling of Dispersion Fuel Elements Including Aluminum-Fuel Interaction. Trans. Am. Nucl. Soc. 77, 1–4.

Google Scholar

Salvato, D., Leenaers, A., Van den Berghe, S., and Detavernier, C. (2018). Pore Pressure Estimation in Irradiated UMo. J. Nucl. Mater. 510, 472–483. doi:10.1016/j.jnucmat.2018.08.039

CrossRef Full Text | Google Scholar

Saoudi, M., Barry, A., Lang, J., Boyer, C., Rogge, R. B., Corbett, S., et al. (2022). Post-irradiation Examination of U-7Mo/Mg and U-10Mo/Mg Dispersion Fuels Irradiated in the NRU Reactor. J. Nucl. Mater. 558, 153343. doi:10.1016/j.jnucmat.2021.153343

CrossRef Full Text | Google Scholar

Savchenko, A., Konovalov, I., Vatulin, A., Morozov, A., Orlov, V., Uferov, O., et al. (2007). Dispersion Type Zirconium Matrix Fuels Fabricated by Capillary Impregnation Method. J. Nucl. Mater. 362, 356–363. doi:10.1016/j.jnucmat.2007.01.211

CrossRef Full Text | Google Scholar

Savchenko, A., Vatulin, A., Morozov, A., Sirotin, V., Dobrikova, I., Kulakov, G., et al. (2006). Inert Matrix Fuel in Dispersion Type Fuel Elements. J. Nucl. Mater. 352 (1-3), 372–377. doi:10.1016/j.jnucmat.2006.03.003

CrossRef Full Text | Google Scholar

Savchenko, A., Vatulin, A., Konovalov, I., Morozov, A., Sorokin, V., and Maranchak, S. (2010). Fuel of Novel Generation for PWR and as Alternative to MOX Fuel. Energ. Convers. Manage. 51 (9), 1826–1833. doi:10.1016/j.enconman.2010.01.027

CrossRef Full Text | Google Scholar

Schappel, D., Terrani, K., Powers, J. J., Snead, L. L., and Wirth, B. D. (2018). Modeling the Performance of TRISO-Based Fully Ceramic Matrix (FCM) Fuel in an LWR Environment Using BISON. Nucl. Eng. Des. 335 (C), 116–127. doi:10.1016/j.nucengdes.2018.05.018

CrossRef Full Text | Google Scholar

Van den Berghe, S., and Lemoine, P. (2014). Review of 15 Years of High Density Low Enriched UMo Dispersion Fuel Development for Research Reactors in Europe. Nucl. Eng. Technol. 46, 125–146. doi:10.5516/NET.07.2014.703

CrossRef Full Text | Google Scholar

Van den Berghe, S., Parthoens, Y., Charollais, F., Kim, Y. S., Leenaers, A., Koonen, E., et al. (2012). Swelling of U(Mo)-Al(Si) Dispersion Fuel under Irradiation-Non-Destructive Analyses of the Leonidas E-Future Plates. J. Nucl. Mater. 430, 246–258. doi:10.1016/j.jnucmat.2012.06.045

CrossRef Full Text | Google Scholar

Van den Berghe, S., Van Renterghem, W., and Leenaers, A. (2008). Transmission Electron Microscopy Investigation of Irradiated U-7wt%Mo Dispersion Fuel. J. Nucl. Mater. 375 (3), 340–346. doi:10.1016/j.jnucmat.2007.12.006

CrossRef Full Text | Google Scholar

Wood, M. H., and Kear, K. L. (1983). On the In-Pile Nucleation and Growth of Grain-Boundary Bubbles. J. Nucl. Mater. 118, 320–324. doi:10.1016/0022-3115(83)90240-4

CrossRef Full Text | Google Scholar

Zhang, J., Wang, H., Wei, H., Zhang, J., Tang, C., Lu, C., et al. (2021). Modelling of Effective Irradiation Swelling for Inert Matrix Fuels. Nucl. Eng. Technol. 53, 2616–2628. doi:10.1016/j.net.2021.02.019

CrossRef Full Text | Google Scholar

Zhang, T., Yin, H., Li, X., She, D., Pan, Q., He, D., et al. (2021). Studies on Calculation Models of ASTRA Critical Facility Benchmark Using OpenMC. Ann. Nucl. Energ. 158, 108291. doi:10.1016/j.anucene.2021.108291

CrossRef Full Text | Google Scholar

Zhao, Y., Gong, X., Ding, S., and Huo, Y. (2014). A Numerical Method for Simulating the Non-homogeneous Irradiation Effects in Full-Sized Dispersion Nuclear Fuel Plates. Int. J. Mech. Sci. 81, 174–183. doi:10.1016/j.ijmecsci.2014.02.012

CrossRef Full Text | Google Scholar

Zhao, Y., Gong, X., and Ding, S. (2015). Simulation of the Irradiation-Induced Thermo-Mechanical Behaviors Evolution in Monolithic U-Mo/Zr Fuel Plates under a Heterogeneous Irradiation Condition. Nucl. Eng. Des. 285, 84–97. doi:10.1016/j.nucengdes.2014.12.030

CrossRef Full Text | Google Scholar

Appendix A.List of the Involved Acronyms and Symbols

RVE representative volume element

RERTR Reduced Enrichment for Research and Test Reactors

IL interaction layer

FE finite element

$F_d$ fission density

$C_b$ the defined grain-boundary bubble concentration of un-recrystallization region

$C_{bx}$ the defined grain-boundary bubble concentration of fine grain region

${\eta }_{F_d}$ the modified factor for the gas bubble number

$h_s$ the fitting parameter to make the Van der Waals equation equivalent to the hard-sphere equation of state

$b_v$ the Van der Waals gas constant of Xe

$P_h$ the external hydrostatic pressure

k the Boltzmann constant

$\overline{N}$ the average number of fission gas atoms in each inter-granular bubble

$\beta$ the creep amplification factor

${\dot{\epsilon }}_m^{cr}$ creep strain rate of Zr matrix

${\dot{\epsilon }}^{ss}$ thermal creep strain rate

${\dot{\epsilon }}^{ir}$ irradiation creep strain rate

Q the activation energy

$\varphi$ the fast neutron flux