- 1Engineering Technology Research Institute, Xinjiang Oilfield Company, PetroChina, Karamay, China
- 2College of Petroleum Engineering, China University of Petroleum, Beijing, China
- 3Baikouquan Oil Production Plant, Xinjiang Oilfield Company, PetroChina, Karamay, China
Re-fracturing treatments of horizontal wells are increasingly gaining popularity to address the issue of rapid production decline and low recovery ratio for the conglomerate reservoir of the Mahu Oilfield. How to effectively select the horizontal wells with potentiality for re-fracturing and conduct the re-fracturing operation to achieve the purpose is the key problem that needs to be investigated urgently. However, the conventional methods for vertical wells are not in our consideration, and some methods for horizontal wells have their limits for the Mahu reservoir. To cope with problems mentioned above, fourteen factors from geology parameters, engineering parameters, and production performance parameters are considered to establish a multi-level evaluation model to quantify the potentiality of each horizontal well for re-fracturing in the Mahu Oilfield. First, the analytic hierarchy process (AHP) is used to obtain the weights of various factors affecting the productivity of horizontal wells, and on this basis, the subordination degree and evaluation matrix are then calculated, and finally, the fuzzy synthetic determination is obtained to determine the candidate wells for re-fracturing. The results have shown that the weights corresponding to engineering parameters obtained by the AHP method are the largest, followed by geology parameters, and the weights of production performance parameters are the minimal relatively; the number of fractures and the sand quantity of single cluster are the main controlling factors in engineering factors, and the initial formation pressure is the main controlling factor in geological factors; there is obvious correlation between the cumulative oil production after 90 days of primary fracturing with final cumulative production. Wells M15, M13, and M7 rank top three among the candidate wells. Through re-fracturing treatment by temporary plugging, the daily oil production of well M15 has increased significantly and is even higher than that of the primary hydraulic fracturing stimulation, confirming the reliability of the proposed selection method.
Introduction
The conglomerate reservoir of the Mahu Oilfield located in Xinjiang, Northwest China, with low permeability, large two-dimensional stress difference, and strong pressure-sensitive effect, is the largest uncompartmentalized conglomerate reservoir around the world. The factors influencing productivity are complicated and, hence, make the development of the oilfield difficult. Due to the influence of sedimentation, diagenesis, and structure, the conglomerate reservoir in Mahu has the characteristics of small pore throat and extremely poor physical properties. Without hydraulic fracturing, natural industrial productivity cannot be achieved (Jia et al., 2012; Zhao et al., 2016; Zou et al., 2017). Although multi-fractured technology of horizontal wells has been gradually introduced since 2012 in the Mahu Oilfield to improve oil productivity, some severe problems, including rapid production decline and low recovery ratio, usually occur. On the basis of a previous study in the literature (Hu et al., 2004; Yang et al., 2016; Guang and Wang, 2019), re-fracturing is a good treatment to improve oil production and recovery ratio by enlarging the contact area between the wellbore and reservoir. The core problem becomes how to select the horizontal wells with the potentiality for re-fracturing.
Conventional well selection methods such as the empirical method (Gu et al., 2006; Roussel and Sharma, 2013), grey correlation method (Sun et al., 2012; Wen et al., 2015; Zhu et al., 2017; Hui, 2019), and multiple regression method (Liu et al., 2018) have their limitations. The conventional empirical method usually defines a set of criteria, and the well which meets one of them will be regarded as a good candidate well for re-fracturing. It is indeed a valuable tool for vertical wells which have only one hydraulic fracture. For example, Roussel proposed (Roussel and Sharma, 2013) that two groups of wells showed the most promise for re-fracturing: 1) ineffective initial completions with a small initial production decline and 2) long initial fractures in underdepleted reservoirs. Therefore, for horizontal wells with different length of multistage fractures, the empirical method is no longer applicable. As for grey correlation, it is a mathematical statistical method to determine the main controlling factors which will be used for selecting wells. For example, permeability is a controlling factor with the largest correlation degree for a well block, and when selecting candidates, priority is usually given to the wells with high permeability (Hui, 2019). The idea behind the multiple regression method is to regress the relationship between geology and engineering factors with production to predict the re-fracturing effect. The well that can improve productivity after re-fracturing predicted by the regression model will be the potential candidate. However, this method is usually used for vertical wells and also cannot consider the heterogeneity. For the Mahu Oilfield, the reservoir heterogeneity has to be considered, and the predictive production is less accurate than numerical simulation.
There are many factors influencing oil production of horizontal wells, among which the nonlinear relation is strong; however, the impact of various factors on production capacity is uncertain, which brings great difficulties to select re-fracturing wells. Existing selecting methods of horizontal wells for re-fracturing can be summarized as the fuzzy mathematics method (Tao et al., 2018; Guo et al., 2019), artificial intelligence method (Wu et al., 2001; Zeng et al., 2017), and coefficient introduction method (Lu, 2014; Cui et al., 2018), among which the fuzzy mathematics method is widely used. The fuzzy mathematics method includes fuzzy clustering and fuzzy evaluation.
As mentioned above, the nonlinear relation between influence factors and production is strong, and the artificial intelligence method can solve this problem by using nonlinear activation functions on an artificial intelligence network rather than the mathematical formula. However, a large number of wells are required to improve accuracy when using the artificial intelligence method, which limits its applicability. As for the coefficient introduction method, some evaluation coefficients are introduced by dimensionless treatment. Multiple basic factors are considered to establish a coefficient. For instance, the porous elastic stress steering coefficient (Cui et al., 2018) is introduced by considering the maximum horizontal principal stress, minimum horizontal principal stress, formation pressure, and bottom-hole flowing pressure. The wells with larger or smaller coefficient than the standard value will be eliminated, and the remaining will be proceeded to the screening of next coefficient. The number of candidate wells gradually decreases after layer-by-layer screening. The last remaining wells will be re-fractured. However, it could be possible that some wells eliminated by the first coefficient are suitable to be re-fractured for meeting the standard value of the subsequent coefficients.
The fuzzy clustering method quantifies the potentiality for re-fracturing by establishing an ideal well and then calculating the similarity between each horizontal well and the ideal well. Each parameter of the ideal horizontal well including geology and engineering parameters is taken from the optimal value of candidate well samples. For example, the larger the oil saturation is, the more potentiality the well has for re-fracturing, and the oil saturation of the ideal well will be the maximum value among the values of all candidate wells. On the contrary, the smaller the rate in primary fracturing is, the more potentiality the well has for re-fracturing because the scale of primary fractures is small. Then, the rate of the ideal well will be the minimum value among the values of all candidate wells. The ideal well will be the most suitable to be re-fractured under any condition. Also, the candidate well which is most similar to the ideal well will be the most suitable one. However, the fuzzy clustering method does not consider the weight of each main control factor, which will have a certain impact on the well selection results.
The fuzzy evaluation model considers the weights of control factors by multiplying the parameter matrix and weight matrix, and on this basis, the potentiality of each candidate well can be quantified.
The weight of each control factor is usually obtained by using the mathematical statistical method and analytic hierarchy process (AHP). The AHP is a method for determining weights and analyzing complex decisions. The basic principle of the AHP is to regard the complex problem as a large system and draw the ordering layers through the analysis of multiple factors. Then, experts are invited to make more objective judgments on the factors at each layer and give a quantitative expression of relative importance accordingly. A mathematical model is established to calculate the weights of factors at each layer and rank them. The AHP method is widely used to calculate weights. Yu et al. determined the main controlling factors using the AHP in a high-water cut oilfield (Yu et al., 2018). Zhang et al. selected wells for acidizing based on the weights obtained by the AHP method (Zhang et al., 2019). Li et al. integrated the AHP, grey correlation, and random forest to determine weights in a tight oil reservoir (Li et al., 2021). Besides, the AHP method is also used to evaluate reservoirs (Lu et al., 2021; Zhang et al., 2021).
The parameter matrix needs to be normalized due to the unit difference. The normalization method will be different based on the influence of parameters to production, such as maximization normalization and minimization normalization.
The fuzzy evaluation method has the advantages of strong systematicness, clear calculation results, and improved algorithm flexibility and intelligence (Wang et al., 2008; Xu, 2011; Hou et al., 2014).
However, the factors considered when using the fuzzy evaluation model generally only include geology and engineering parameters, and the number of sub-factors is small. In this article, the production performance data after primary fracturing including flowback rate and initial production are considered innovatively. For the Mahu conglomerate reservoir with strong heterogeneity, some parameters, e.g., wettability and capillary pressure, are difficult to obtain. The flowback rate after primary fracturing reflects these properties to some degree. Besides, for the multi-fracturing horizontal wells in a tight reservoir, the number of primary fracturing segments and clusters should also be considered when evaluating the potentiality for re-fracturing. To assess the re-fracturing potentiality quantitatively of candidate wells in Mahu block, by considering as many as 14 factors in three categories of geology, engineering, and production performance parameters, we propose a comprehensive fuzzy evaluation mathematical model, which provides an easy-to-use tool to select the re-fracturing wells.
Analytic Hierarchy Process
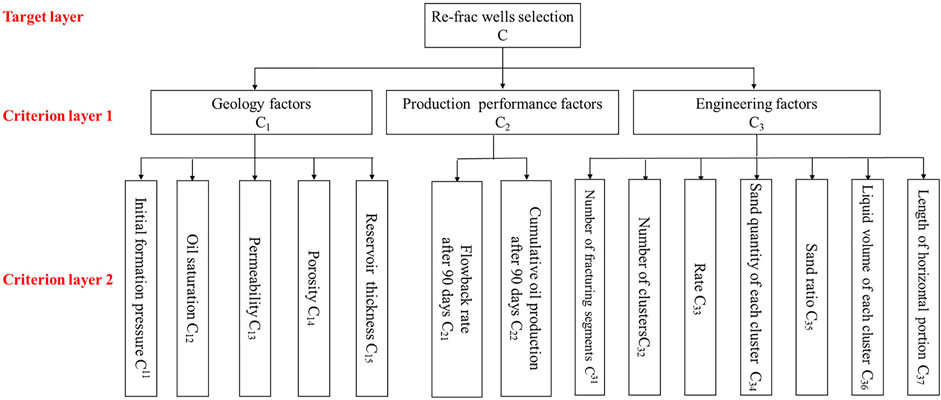
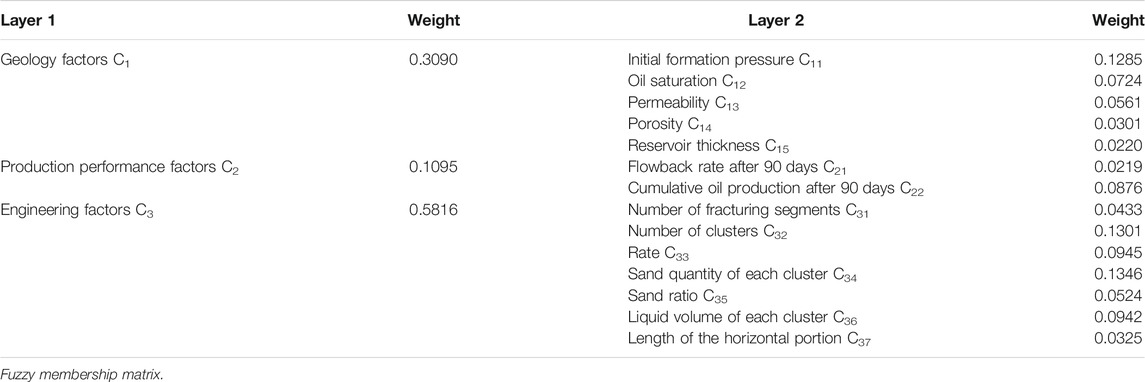
The analytic hierarchy process (AHP) is used to determine the weight of each factor. In this study, fourteen factors from geology, engineering, and production performance are considered. The geology factors include initial formation pressure, oil saturation, permeability, porosity, and reservoir thickness. Initial formation pressure represents the energy basis of the reservoir. Oil saturation is the ratio of oil volume to effective pore volume, expressed as a percentage. Permeability refers to the ability of rock that allows fluid to pass through under a certain pressure difference. It is a parameter characterizing the ability of rock to conduct liquid. Porosity is the ratio of the sum of all pore space volumes in rock to the volume of the rock, expressed as a percentage. It is worth noting that reservoir thickness is the horizontal thickness which is the same as the length of the horizontal well section drilled in the reservoir, not the vertical formation thickness. As for the production performance factors, flowback rate and cumulative oil production after 90 days of primary fracturing are considered. Flowback rate is the ratio of flowback fluid volume to the total pumped fluid volume. Cumulative oil production is the total oil production at some point in time. In this paper, the flowback rate and cumulative oil production after 90 days of primary fracturing are used to reflect some unknown properties which are difficult to obtain, such as wettability and capillary pressure. The engineering factors include the number of fracturing segments, the number of clusters, rate, sand quantity of each cluster, sand ratio, liquid volume of each cluster, and length of the horizontal portion. The number of fracturing segments is also described as the number of stages. The part between the two bridge plugs is one stage. The number of clusters can be explained as the number of fractures. Rate refers to the volume of liquid pumped per minute. Sand quantity of each cluster is the average proppant volume per fracture. Sand ratio is the average ratio of total sand to total fluid per stage. Liquid volume of each cluster is average fluid volume per fracture. Length of the horizontal portion is the total length of the horizontal well section which is different from reservoir thickness.
The hierarchical structure model is established including a target layer and two criterion layers. As shown in Figure 1, the target layer is well selection for re-fracturing, criterion layer 1 includes geology, production performance, and engineering set, and criterion layer 2 includes three sets of factors, reflecting their impacts on well selection for re-fracturing.
Judgment Matrix
The judgment matrix is obtained by comparing factors in pairs in one same layer including criterion layer 1 and 2. The element of judgment matrix is indicated as Pij, which means the importance comparison results of the i-th factor and the j-th factor in one same layer. The importance between two elements is determined by the nine-scale method (Ye, 2010) which is shown in Table 1. In addition, the judgment matrix has the following properties:
The maximum eigenvalue and weight matrix are calculated by the square root method. First, the product of each row element of the judgment matrix is calculated by
where
The n-th root of
The weight vector can be obtained by normalizing the n-th root.
Finally, the maximum eigenvalue is
The expert scoring method is used to judge the importance, and then, the reliability of score-giving will be verified by the consistency test. For the Mahu Oilfield, the experts think that the influence of geology factors is slightly more important than production performance, and the ratio of C1 to C2 is 3; in other words, the ratio of C2 to C1 is 1/3. Compared to the geology factors, the importance of engineering factors is the mid-value of “same important” and “slightly more important,” and the ratio of C1 to C3 is 0.5. The engineering factors are obviously more important than production performance, and the ratio of C3 to C2 is 5.
The judgment matrix of criterion layer 1 is
The weight matrix is
Similarly, for criterion layer 2, the judgment matrices of geology, production performance, and engineering factors, respectively, are
The weight matrices are
Consistency Test
The weight vector represents the relative importance of each element in its layer to an element of the previous level. Whether the single ranking can be confirmed needs to be verified by the consistency test. When the consistency ratio is smaller than 0.1, the judgment matrix meets the requirements. The consistency ratio can be calculated by the consistency test formula as follows:
where
Here, λmax is the maximum eigenvalue of the judgment matrix and n is the unique nonzero eigenvalues of n-order uniform matrices. RI is the random consistency index which can be obtained by looking up Table 2.
The total ranking weight vector of the multilevel model can be calculated by the following formula:
where ωi is the weight of each element.
If the consistency ratio of any layer fails to pass, it needs to be corrected again until the condition of CR < 0.10 is met. According to the results, the consistency ratio of criterion layer 1 is 0.0036, and consistency ratios of criterion layer 2 are 0.0792, 0, and 0.0036, respectively, which meet the requirements.
By multiplying the judgment matrices of the two criterion layers, the weights of the two layers are shown in Table 3.
Fuzzy Membership Matrix
The suitable membership functions including maximum optimal function and minimum optimal function are established to build the membership matrix.
In this study, 14 sub-factors including geological, engineering, and production performance factors are considered when using the fuzzy comprehensive evaluation model for well selection for re-fracturing. The subordination degree of each sub-factor is determined by maximum or minimum optimal type normalization, which depends on the influence of each factor on the potentiality for re-fracturing. For example, initial formation pressure has a positive influence on production after re-fracturing, the subordination degree of initial formation pressure can be obtained by the following equation:
where xij is the value of a sub-factor of a single horizontal well; xmax is the maximum value of the single factor; and xmin is the minimum value of the single factor.
Similarly, the subordination degree of other seven sub-factors including oil saturation, permeability, porosity, reservoir thickness, length of horizontal portion, flowback rate, and cumulative oil production after 90 days of primary fracturing can be obtained by Eq. 17.
On the contrary, the larger the number of fracturing segments is in the primary fracturing, the less the volume with high oil saturation can be re-fractured. The subordination degree of the number of fracturing segments can be obtained by the following equation:
where xij is the value of a sub-factor of a single horizontal well; xmax is the maximum value of the single factor; and xmin is the minimum value of the single factor.
Similar to the number of fracturing segments, the subordination degree of other five factors including number of clusters, rate, sand quantity of each cluster, sand ratio, and liquid volume of each cluster can be obtained by Eq. 18.
The membership matrix named as F is established as follows:
Assuming that ω is the weight set of factors, the comprehensive evaluation matrix is the combinatorial multiplication of the weight set with F, which can be written as follows:
where
Practical Application
In the development process of horizontal wells in the Mahu Oilfield, the production decreases rapidly and the stable production period is short. It is necessary to conduct a re-fracturing test to improve oil production. In this study, 15 horizontal wells are selected as samples, whose parameters are shown in Supplementary Appendix S1. The fuzzy comprehensive evaluation model is established to select the well with potentiality for re-fracturing.
The subordination degree of each sub-factor is calculated by Eqs 17, 18, and the results are shown in Supplementary Appendix S2. Based on Eq. 20, the comprehensive evaluation matrix is multiplied by the weight matrix and subordination degree matrix, as shown in Supplementary Appendix S3. The comprehensive evaluation results are shown in Table 4. Among the 15 wells, M15, M13, and M7 rank the top three, and well M15 has been conducted field re-fracturing tests.
Well M15 is a horizontal well with open-hole completion located at the Ma-x block of the Junggar Basin, with a completed vertical depth of 3,419.09 m and a completed measured depth of 4168 m. The length of horizontal section is 425 m located at the target interval of 3,676–4101 m. The reservoir permeability is 0.28–2.03 mD, the reservoir porosity is 7.51–14.74%, the initial formation pressure is 52.33 MPa, and the formation temperature is 84°C.
The primary fracturing consists of five stages with a total fluid volume of 1,678.5 m3, a total sand volume of 180.25 m3, an average fluid volume per stage of 335.7 m3, and an average sand volume per stage of 36.05 m3. The temporary plugging and diversion process are selected, and the old fractures and new fractures are re-stimulated at the same time. The re-fracturing consists of six stages in total. The microseismic monitoring results show that the microseismic event covers the whole horizontal section of well M15. As shown in Figure 2, compared with the microseismic monitoring of the primary fracturing, the purpose of uniform re-stimulation of the horizontal section has been achieved by re-fracturing.
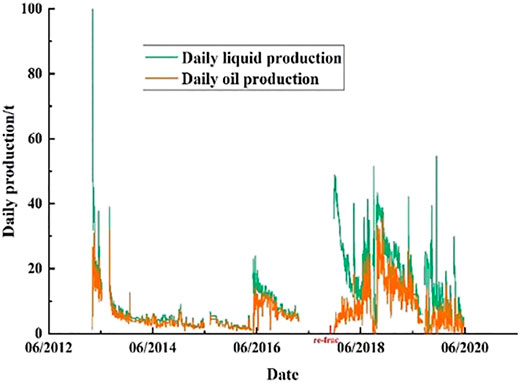
As shown in Figure 3, the daily oil production of well M15 after re-fracturing is greatly improved, and the peak daily oil production after re-fracturing reaches 35 t/d, which is higher than 30 t/d after primary fracturing. The cumulative oil production in 4 years before re-fracturing is 6,500 t, while the cumulative oil production within 2 years after re-fracturing is 7,500 t. The re-stimulation effect is very remarkable, indicating that the method of well selection is reliable.
Conclusion
1) Among the three categories of factors affecting the productivity of horizontal wells, the influences of engineering factors are the greatest, followed by the geological factors, and the production performance after the primary fracturing is minimal.
2) The number of fractures and the sand quantity of single cluster are the main controlling factors in engineering factors, and the initial formation pressure is the main controlling factor in geology factors; there is obvious correlation between the cumulative oil production after 90 days of primary fracturing with final cumulative production.
3) Among the well selection samples including the 15 wells, the potentiality for re-fracturing of well M15, M13, and M7 ranks the top three.
4) The stimulation effect of the M15 well after re-fracturing is remarkable, which verifies the reliability of the well selection method.
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
QX and XM: article ideas and research scheme. BW, GR, and JP: data collection and modeling. XY: result analysis. WD and YY: manuscript writing.
Funding
This work is supported by Foundation of Key Technologies of Mahu Conglomerate Reservoir (ZLZX2020-01-04).
Conflict of Interest
QX, BW, JP, WD, YY, and XY were employed by the Xinjiang Oilfield Company, PetroChina.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2022.851582/full#supplementary-material
References
Cui, J., Gao, D., Bi, W., and Liao, R. (2018). Refracturing Selection Evaluation Model for Shale Gas wells and its Application[J]. Lithologic Reservoirs 30 (6), 145–150. doi:10.12108/yxyqc.20180618
Gu, D., Wang, S., and Mu, L. (2006). Method of Selecting Refracturing wells by Production Data Analysis[J]. Nat. Gas Industry 26 (8), 102–106. doi:10.3321/j.issn:1000-0976.2006.08.032
Guang, X., and Wang, M. (2019). Re-fracturing Key Technologies of Shale Oil and Gas in North America and the Suggestions[J]. Oil Drilling Prod. Techn. 41 (2), 224–229. doi:10.13639/j.odpt.2019.02.016
Guo, J., Tao, L., and Zeng, F. (2019). Optimization of Refracturing Timing for Horizontal wells in Tight Oil Reservoirs: A Case Study of Cretaceous Qingshankou Formation, Songliao Basin, NE China[J]. Pet. Exploration Develop. 46 (1), 146–154. doi:10.1016/s1876-3804(19)30015-1
Hou, H., Shao, L., Tang, Y., Luo, X., Wang, X., and Liu, S. (2014). Criteria for Selected Areas Evaluation of Low Rank CBM Based on Multi-Layered Fuzzy Mathematics: A Case Study of Turpan-Hami Basin[J]. Geology. China 41 (3), 1002–1009. doi:10.3969/j.issn.1000-3657.2014.03.025
Hu, Y., Lin, H., Zhao, J., and Wang, S. (2004). Study on Rrepetitive Fracturing Technology[J]. Nat. Gas Industry 24 (03), 72–75+147. doi:10.3321/j.issn:1000-0976.2004.03.021
Hui, F. (2019). Application of Grey Correlation Method in Well Selection of Old Well by Repeated Fracturing[J]. China Pet. Chem. Stand. Qual. 39 (14), 115–116.
Jia, C., Zheng, M., and Zhang, Y. (2012). Unconventional Hydrocarbon Resources in China and the prospect of Exploration and Development[J]. Pet. Exploration Develop. 39 (2), 129–136. doi:10.1016/s1876-3804(12)60026-3
Li, X., Ma, X., Xiao, F., and Zhang, S. (2021). “Combined Method of the Candidate Fracturing Well in the Tight Oil Reservoirs Based on Fuzzy Comprehensive Evaluation[J],” in Petroleum Geology & Oilfield Development in Daqing. Daqing: Petroleum Geology & Oilfield Development in Daqing. doi:10.19597/J.ISSN.1000-3754.202008048
Liu, J., Yang, X., Yuan, X., Zhang, J., Wu, H., and Ding, L. (2018). Method of Re-stimulation Candidate Selection and Productivity Prediction for Silurian Reservoirs in Tazhong Area [J]. Well Test. 27 (1), 55–61.
Lu, M. (2014). Candidate Selection and Optimization for Refracturing in Low Permeability reservoir[D]. Qingdao, China: China University of Petroleum.
Lu, Y., Wang, J., and Cao, M. (2021). Evaluation Method of Shale Gas Development Area Selection Based on Improved Analytic Hierarchy Process[J]. Reservoir Eval. Develop. 11 (2), 70–77. doi:10.13809/j.cnki.cn32-1825/te.2021.02.009
Roussel, N., and Sharma, M. (2013). Selecting Candidate wells for Refracturing Using Production Data[J]. SPE Prod. Operations 28 (1), 36–45. doi:10.2118/146103-pa
Sun, J., Liu, D., Zhang, L., and Tang, J. (2012). Grey Correlation Analysis of the Influencing Factors on Production Decline in Low Permeability Reservoirs[J]. Spec. Oil Gas Reservoirs 19 (2), 90–93. doi:10.3969/j.issn.1006-6535.2012.02.023
Tao, L., Guo, J., Li, L., Li, H., and He, N. (2018). Multi-stage Well Selection for Refracturing Operations in Horizontal wells for Tight Oil Reservoir Development[J]. Spec. oil gas reservoir 25 (4), 67–71. doi:10.3969/j.issn.1006-6535.2018.04.013
Wang, X., Zhao, B., and Zhang, Q. (2008). Mining Method Choice Based on AHP and Fuzzy Mathematics[J]. J. Cent. South University(Science Technology) 39 (5), 875–880. doi:10.3969/j.issn.1673-1328.2013.12.067
Wen, H., Liu, Y., and Sun, N. (2015). Research on the Influencing Factors of Volume Fracturing of Horizontal Well in Gas Reservoir Based on Orthogonal Design and Grey Relation Analysis Theory[J]. Maths. Pract. Theor. 45 (7), 133–140.
Wu, Y., Li, X., Zhong, D., and Lin, T. (2001). Application of Artificial Neural Network in Fracturing Well Selection and Layer Selection[J]. J. China Univ. Petroleum(Edition Nat. Science) 25 (5), 42–44. doi:10.3321/j.issn:1000-5870.2001.05.012
Xu, X. (2011). Study and Application of Fuzzy Comprehensive Evaluation model[D]. Chengdu, China: Southwest Petroleum University.
Yang, G., Zhou, Q., and Li, Y. (2016). Technological Progress in Re-fracturing of US Shale Oil and Gas wells for Higher Production Factor[J]. Pet. Sci. Techn. Forum 35 (02), 46–51+65. doi:10.3969/j.issn.1002-302x.2016.02.009
Ye, Z. (2010). Study and Application of Fuzzy Comprehensive Evaluation Based on AHP[D]. Mianyang, China: South China University of Technology.
Yu, Q., Liu, Y., and Yu, Y. (2018). Research on Fuzzy Comprehensive Evaluation of fine Controlled Fracturing wells and Layers Based on Analytical Hierarchy Process[J]. Maths. Pract. Theor. 48 (03), 107–114.
Zeng, F., Cheng, X., Guo, J., Tao, L., and Chen, Z. (2017). Hybridising Human Judgment, AHP, Grey Theory, and Fuzzy Expert Systems for Candidate Well Selection in Fractured Reservoirs. Energies 10 (4), 447. doi:10.3390/en10040447
Zhang, H., Liu, H., Wang, P., Meng, X., Liu, J., and Zheng, J. (2019). Producer Acidization Candidate Screen Method Based on Fuzzy Comprehensive Evaluation[J]. Unconventional Oil & Gas. 6 (02), 97–101.
Zhang, R., Gao, L., Wang, Y., and Zhao, J. (2021). Application of Improved AHP in Comprehensive Reservoir Evaluation:a Case Study on the Upper Es4 Formation in W146 Area of Wangjiagang Oilfield, Dongying Depression[J]. China Sci. paper 16 (09), 943–947. doi:10.3969/j.issn.2095-2783.2021.09.004
Zhao, L., Mou, M., Luo, Z., Liu, P., and Zou, D. (2016). The Outlook for China’s Tight Oil Reservoir Stimulation Concept and Technology[J]. J. Southwest Pet. Univ. Sci. Techn. Edition) 38 (6), 111–118. doi:10.11885/j.issn.16745086.2015.03.25.21
Zhu, Z., Lin, C., Zhang, S., Ren, L., Zhao, J., Chen, S., et al. (2017). Application of Improved Fuzzy-Grey Comprehensive Evaluation Method to Quantitative Reservoir Evaluation: A Case Study of the Low-Permeability Gas Reservoirs of the Lower Part of 8th Member of the Shihezi Formation in Su X Block of Sulige Gasfield[J]. Oil Gas Geology. 38 (1), 197–208. doi:10.11743/ogg20170121
Keywords: conglomerate reservoir, well selection, re-fracturing, analytic hierarchy process, fuzzy comprehensive evaluation
Citation: Xiong Q, Ma X, Wu B, Ren G, Pan J, Yi X, Deng W and Yi Y (2022) Re-Fracturing Wells Selection by Fuzzy Comprehensive Evaluation Based on Analytic Hierarchy Process—Taking Mahu Oilfield as An Example. Front. Energy Res. 10:851582. doi: 10.3389/fenrg.2022.851582
Received: 10 January 2022; Accepted: 27 January 2022;
Published: 25 February 2022.
Edited by:
Xun Zhong, Yangtze University, ChinaCopyright © 2022 Xiong, Ma, Wu, Ren, Pan, Yi, Deng and Yi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xinfang Ma, bWF4aW5mYW5nQGN1cC5lZHUuY24=
 Qiyong Xiong1
Qiyong Xiong1 Guangcong Ren
Guangcong Ren