- School of Materials and Metallurgy, Guizhou University, Guiyang, China
Blockage of the U-type channel exacerbates the intermittency of production, and clarifying the channel heat transfer characteristics and pressure drop is an effective way to address this problem. The channel heat transfer and flow characteristics of the fluid in the channel are experimentally investigated in this study. According to the experiments, the heat transfer coefficient is between 59.95 and 200.29 W/m2⋅K and increases with the flow velocity and fluid temperature. Because the pressure drop is usually accompanied by a change in the energy loss of the fluid, the energy loss is evaluated experimentally. The results demonstrate that the friction loss in the straight tube section accounts for 80% of the energy loss. A bent tube of 90° is recommended instead of a right-angle tube to reduce the pressure drop. A dimensionless relation regarding the Nusselt number is presented to predict the heat transfer characteristics. We provided proposals to address the problem of blockage of the U-type channel, this is helpful to reduce production energy consumption and improve the quality of titanium sponge.
Introduction
The Kroll process is a unique existing industrial process for titanium sponge, the primary industrial choice in titanium chains, and this process has played a significant role in the titanium industry over the past decades (Nagesh et al., 2008; Zhang et al., 2011; Wang and Wu., 2021). The Kroll process is costly, energy-intensive, and intermittent (Wang et al., 2017; Takeda and Okabe, 2019). After the reduction process, the remaining magnesium and magnesium chloride were separated via vacuum distillation to obtain a titanium sponge (Nagesh et al., 2004; Cui et al., 2011). The fluid was distilled from the reduction reactor to the condenser, and the channel was easily blocked in the production process because of the unreasonable heating system of the heater and the energy loss of the fluid. This further exacerbated the intermittency of production, leading to a long production period. Titanium sponge pores were easy to sinter and other problems (Li et al., 2015; Liang et al., 2018) affected the distillation period, further increasing the energy consumption. However, this difficulty has not yet been effectively addressed. To address this blockage, it is necessary to clarify the channel heat transfer characteristics and pressure drop.
Currently, there is no research on the heat transfer characteristics and pressure drop of U-type channels in the vacuum distillation processes for titanium sponges. Therefore, this experiment referred to the literature on the heat transfer of fluids in a tube (Gorman et al., 2015; Moghadam et al., 2020; Qi et al., 2019; Baik et al., 2019). Hekmatipour et al. (2017) experimentally studied the convective heat transfer of nanofluids in a tube. In this study, we present a correlation relation for the nanofluid to predict the Nusselt number. Wen et al. (2019) experimentally investigated the air flowing through helical tube bundles and obtained the flow and convective heat transfer characteristics. We propose two empirical relations to describe the convective heat transfer coefficient and friction factor. Sarmadian et al. (2020) investigated the heat transfer characteristics in a heat exchanger and discussed the heat transfer improved by twisted tapes. The channel heat transfer performance and pressure drop improved with the installation of the twisted tapes. The friction and heat transfer characteristics of a fluid influenced by a circular ring turbulator in a tube were experimentally studied (Kongkaitpaiboon et al., 2010), and the heat transfer rates increased from approximately 57–195% when the CRTs were installed. Baba et al. (2018) studied the convective heat transfer of an Fe3O4-water nanofluid in a heat exchanger. The heat transfer and pressure drop of different heat exchangers are also discussed. We propose a correlation for the Nusselt number. Similarly, the aforementioned studies provide theoretical support for this experiment.
The heat transfer and flow characteristics of a mixed system of nitrogen, gaseous magnesium, and gaseous magnesium chloride in the channel were investigated experimentally. The Nusselt number dimensionless correlation relation was obtained based on experimental data.
Methods
Experimental Apparatus
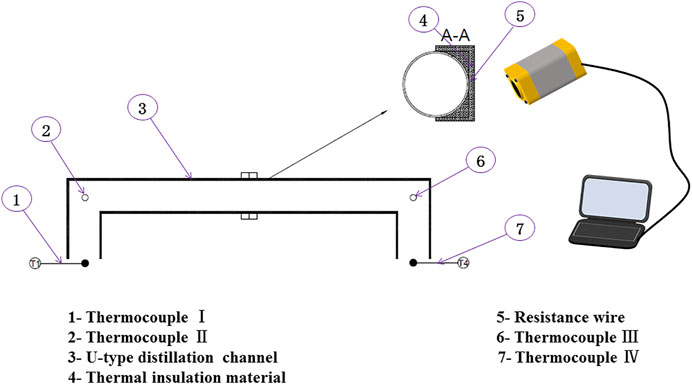
Figure 1 shows the apparatus used in this experiment. The distillation channel is 1Cr18Ni9Ti stainless steel tube, length of the horizontal section is 3.62 m, vertical section is 0.40 m, inner diameter is 0.129 m, and outer diameter is 0.159 m. A heater with constant power was used to heat the distillation tube to maintain the fluid temperature, and the parameters are listed in Table 1.
To measure the temperature of the outer wall of the heater, an RSE300 infrared thermal imager was used. Two K-type thermocouples were installed on the tube to obtain the temperature of its outer wall. In addition, the fluid temperature was measured using two other K-type thermocouples at the inlet and outlet. By pumping a vacuum with nitrogen, the pressure drop can be obtained based on the vacuum degree.
In this study, the fluid consisted of a mixed system of nitrogen, gaseous magnesium, and gaseous magnesium chloride (listed in Table 2). As the temperature increased from 913.00 to 1023.00 K.
Theoretical Background
Pressure Drop
Clearly, as the fluid is distilled from the reduction reactor to the condenser in the straight tube section, the energy loss is caused by the viscous force of the fluid. There was a local loss because the flow direction changed dramatically at the right angle of the channel.
Taking the horizontal line of the channel inlet and outlet as a benchmark, the inlet velocity was considered as zero. The Bernoulli equation of the fluid is as follows:
Furthermore, the energy loss of the fluid is as follows:
Clearly, the local loss coefficient is 1.97. The coefficient of frictional loss was calculated using formula (3) to (5) (Demirkir and Erturk, 2021) and verified according to the range of the Reynolds number.
Hence, the flow velocity can be solved by Eq. (1)–(5).
Heat Conduction
In the distillation process, the channel is isothermal, and the axial heat transfer can be ignored and regarded as a one-dimensional heat conduction with an internal heat source.
The resistance wire conducts heat through the channel and insulation layer, and the power is obtained as follows:
Mathematical formulation of heat conduction in thermal insulation layer is expressed as follows:
Heat transfer process with the channel is analyzed as follows:
The heat transfer coefficient is complex heat transfer coefficient, and the heat transfer coefficient is obtained as follows:
Furthermore, the Nusselt, Reynolds, and Prandtl numbers are obtained as follows, respectively:
Results and Discussions
Energy Loss
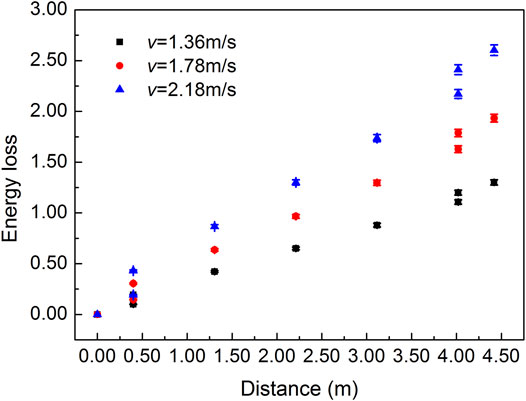
The pressure drop is usually accompanied with change in the energy loss of the fluid. Figure 2 shows the energy loss of the fluid inside the channel under various flow velocities. It is observed that the energy loss increases with distance and reaches a maximum as the fluid reaches the condenser. The energy loss doubled when the flow velocity increased from 1.36 to 2.18 m/s. Furthermore, the friction loss in the straight tube section accounted for 80% of the energy loss, which was proportional to the square of the flow velocity. Therefore, the pressure drop can be controlled at a reasonable level by pumping the vacuum in the production process to reduce energy loss.
As shown in Figure 2, the energy loss increases suddenly owing to the local loss at the right angle of the channel. As observed in the theoretical background sections, the pressure drop increases because of the increase in fluid energy loss to a great extent. Improving the channel structure to reduce the local loss coefficient may be an effective way to reduce pressure drop. The local loss coefficient of the bent tube with 90° was several times smaller than that of the right-angle tube, and under similar conditions, the fluid energy loss in the bent tube with 90° decreased by 13% compared with that in the right-angle tube. Therefore, a bent tube of 90° is recommended instead of a right-angle tube.
Heat Transfer Coefficient
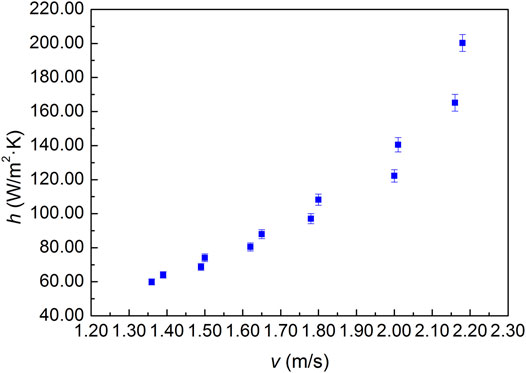
The heat transfer coefficient inside the whole channel is not constant, and the heat transfer coefficient in this study is mean heat transfer coefficient. Figure 3 shows the variation in the heat transfer coefficient with fluid velocity. The heat transfer coefficient increased as the Reynolds number increased because the flow velocity increased, resulting in an increase in the intensity of convective heat transfer. The extent of the increase in the heat-transfer coefficient also increased with a further increase in the flow velocity. Furthermore, as observed in Figure 3, the heat transfer coefficient is between 59.95 and 200.29 W/m2⋅K.
In addition, the effect of the fluid temperature on heat transfer was investigated. The temperature difference decreases as the fluid temperature increases. An increase in the fluid temperature increases the thermal conductivity and reduces the dynamic viscosity of the fluid. Therefore, the heat transfer coefficient increases and boosts the intensity of the convective heat transfer.
Heat Transfer Characteristics
The temperature ranges from 913.00 to 1023.00 K, fluid thermo-physical properties have no significant change, and the Prandtl number is between 0.0204 and 0.0208, which is approximately 0.0205 in this study. Therefore, the dimensionless relation is determined by the Nusselt and Reynolds numbers, as expressed in Eq. 16 as follows:
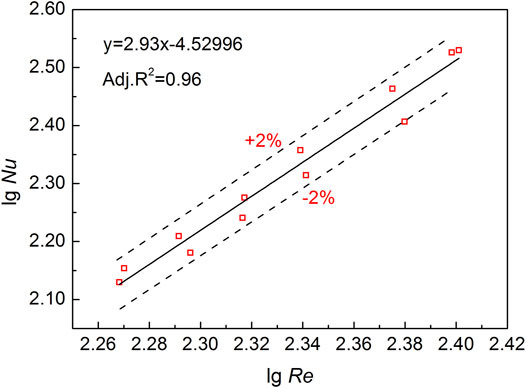
Constants C and n were determined from the experimental data. Figure 4 shows the Reynolds and Nusselt numbers logarithmic fitting relation, and the relational formula is expressed as follows:
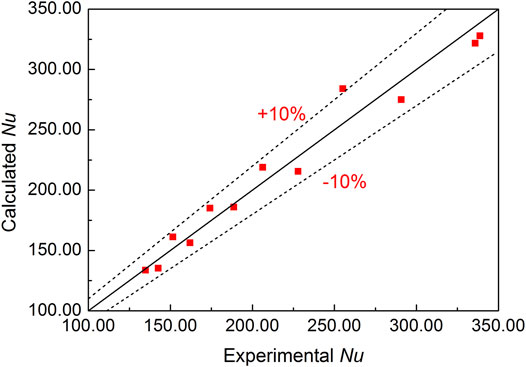
Furthermore, Figure 5 shows a comparison of the Nusselt numbers calculated from Eq. 17 using the experimental Nusselt number, that is, the convective heat transfer characteristics for 185.45 < Re < 250.18, Pr = 0.0205 could be predicted using Eq. 17 and with no significant errors.
Conclusion
The channel heat transfer and flow characteristics of the fluid in the channel were investigated experimentally. The energy loss of the fluid was also analyzed. The impact of the flow velocity and temperature on the heat transfer coefficient was discussed. The conclusions are as follows:
1) The pressure drop increased with the energy loss. The energy loss of the fluid in the channel consists of the friction loss in the straight tube section and local loss at the right angle of the channel. The friction loss in the straight-tube section accounted for 80% of the energy loss. A bent tube of 90° is recommended to minimize the local loss to lower the pressure drop.
2) The heat transfer coefficient is between 59.95 and 200.29 W/m2⋅K. Moreover, the heat transfer coefficient increases with fluid velocity and fluid temperature.
3) A dimensionless relation regarding the Nusselt number is presented to predict the heat transfer characteristics.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
KY, CZ, HY, and FW conceived and designed the study. KY, CZ, and HY were responsible for the experimental operation, and KY analyzed the experimental data. KY wrote the manuscript, and FW revised it.
Funding
The author acknowledges the financial support received from the National Natural Science Foundation of China (grant number 51874108), the Science and Technology Foundation of Guizhou Province (grant number QKHJC 2019-1406, and QKHJC-ZK 2021-YB261), and the Talent Projects of Guizhou University and the Education Department of Guizhou Province (grant number GDPY 2019-20, and QJHKYZ 2021-097).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors thank Qiang Liang and Lvguo Zhang of Zunyi Titanium Co., Ltd. for providing experimental batches in this work.
References
Baba, M. S., Raju, A. V. S. R., and Rao, M. B. (2018). Heat Transfer Enhancement and Pressure Drop of Fe3O4 -water Nanofluid in a Double Tube Counter Flow Heat Exchanger with Internal Longitudinal Fins. Case Stud. Therm. Eng. 12, 600–607. doi:10.1016/j.csite.2018.08.001
Baik, W., Lee, W., and Yun, R. (2019). Heat Transfer and Pressure Drop Characteristics of CO2 Mixtures in a Pipeline under the Seawater Condition. Int. J. Heat Mass Transfer 136, 627–634. doi:10.1016/j.ijheatmasstransfer.2019.03.026
Bera, T. K., Biswas, S. K., Rajan, K., and Nagaraju, J. (2014). Projection Error Propagation-Based Regularization (PEPR) Method for Resistivity Reconstruction in Electrical Impedance Tomography (EIT). Measurement 49, 329–350. doi:10.1016/j.measurement.2013.11.003
Cui, C., Hu, B., Zhao, L., and Liu, S. (2011). Titanium alloy Production Technology, Market Prospects and Industry Development. Mater. Des. 32, 1684–1691. doi:10.1016/j.matdes.2010.09.011
Demirkır, Ç., and Ertürk, H. (2021). Convective Heat Transfer and Pressure Drop Characteristics of Graphene-Water Nanofluids in Transitional Flow. Int. Commun. Heat Mass Transfer 121, 105092. doi:10.1016/j.icheatmasstransfer.2020.105092
Gorman, J. M., Carideo, M., Sparrow, E. M., and Abraham, J. P. (2015). Heat Transfer and Pressure Drop Comparison of Louver- and plain-finned Heat Exchangers where One Fluid Passes through Flattened Tubes. Case Stud. Therm. Eng. 5, 122–126. doi:10.1016/j.csite.2015.03.002
Hekmatipour, F., Akhavan-Behabadi, M. A., Sajadi, B., and Fakoor-Pakdaman, M. (2017). Mixed Convection Heat Transfer and Pressure Drop Characteristics of the Copper Oxide-Heat Transfer Oil (CuO-HTO) Nanofluid in Vertical Tube. Case Stud. Therm. Eng. 10, 532–540. doi:10.1016/j.csite.2017.09.009
Kongkaitpaiboon, V., Nanan, K., and Eiamsa-ard, S. (2010). Experimental Investigation of Convective Heat Transfer and Pressure Loss in a Round Tube Fitted with Circular-Ring Turbulators. Int. Commun. Heat Mass Transfer 37, 568–574. doi:10.1016/j.icheatmasstransfer.2009.12.016
Liang, L., Dachun, L., Heli, W., Kaihua, L., Juhai, D., and Wenlong, J. (2018). Removal of Chloride Impurities from Titanium Sponge by Vacuum Distillation. Vacuum 152, 166–172. doi:10.1016/j.vacuum.2018.02.030
Liang, L., Kaihua, L., Qingdong, M., and Cong, W. (2015). “Research on Quality Improvement of Titanium Sponge by Process Optimization,” in Rare Metal Technology 2015. Editors N. R. Neelameggham, S. Alam, H. Oosterhof, A. Jha, D. Dreisinger, and S. Wang (Switzerland, FL: Springer, Cham Press), 231–237. doi:10.1007/978-3-319-48188-3_26
Moghadam, M. T., Behabadi, M. A. A., Sajadi, B., Razi, P., and Zakaria, M. I. (2020). Experimental Study of Heat Transfer Coefficient, Pressure Drop and Flow Pattern of R1234yf Condensing Flow in Inclined plain Tubes. Int. J. Heat Mass Transfer 160, 120199. doi:10.1016/j.ijheatmasstransfer.2020.120199
Nagesh, C. R. V. S., Ramachandran, C. S., and Subramanyam, R. B. (2008). Methods of Titanium Sponge Production. Trans. Indian Inst. Met. 61, 341–348. doi:10.1007/s12666-008-0065-7
Nagesh, C. R. V. S., Rao, C. S., Ballal, N. B., and Rao, P. K. (2004). Mechanism of Titanium Sponge Formation in the Kroll Reduction Reactor. Metall. Materi Trans. B 35, 65–74. doi:10.1007/s11663-004-0097-2
Qi, C., Chen, X., Wang, W., Miao, J., and Zhang, H. (2019). Experimental Investigation on Flow Condensation Heat Transfer and Pressure Drop of Nitrogen in Horizontal Tubes. Int. J. Heat Mass Transfer 132, 985–996. doi:10.1016/j.ijheatmasstransfer.2018.11.092
Sarmadian, A., Moghaddam, H. A., Asnaashari, A., Joushani, H. A. N., Moosavi, M., Islam, M. S., et al. (2020). Flow Boiling Heat Transfer and Pressure Drop Characteristics of Isobutane in Horizontal Channels with Twisted tapes. Int. J. Heat Mass Transfer 162, 120345. doi:10.1016/j.ijheatmasstransfer.2020.120345
Takeda, O., and Okabe, T. H. (2019). Current Status of Titanium Recycling and Related Technologies. JOM 71, 1981–1990. doi:10.1007/s11837-018-3278-1
Wang, W., Wu, F., and Jin, H. (2017). Enhancement and Performance Evaluation for Heat Transfer of Air Cooling Zone for Reduction System of Sponge Titanium. Heat Mass. Transfer 53, 465–473. doi:10.1007/s00231-016-1836-z
Wang, W., and Wu, F. (2021). Quantifying Heat Transfer Characteristics of the Kroll Reactor in Titanium Sponge Production. Front. Energ. Res. 9, 759781. doi:10.3389/fenrg.2021.759781
Wen, J., Fu, Y., Bao, X., Liu, Y., and Xu, G. (2019). Flow Resistance and Convective Heat Transfer Performances of Airflow through Helical-Tube Bundles. Int. J. Heat Mass Transfer 130, 778–786. doi:10.1016/j.ijheatmasstransfer.2018.10.129
Zhang, W., Zhu, Z., and Cheng, C. Y. (2011). A Literature Review of Titanium Metallurgical Processes. Hydrometallurgy 108, 177–188. doi:10.1016/j.hydromet.2011.04.005
Nomenclature
cp Specific heat capacity of the fluid, J/mol⋅K
d Diameter, m
g Acceleration of gravity (9.81 m/s2)
h Heat transfer coefficient, W/m2⋅K
L Energy losses
l Tube length, m
M Relative molecular mass
Nu Nusselt number
Pr Prandtl number
P Power
Re Reynolds number
t Temperature , K
U Uncertainty
v Fluid velocity, m/s
▵p Pressure drop, kPa
α Kinetic energy correction factor
γ Frictional loss coefficient
δ Thickness, m
λ Thermal conductivity, W/m⋅K
ξ Local loss coefficient
ω Molar fraction
ρ Density, Kg/m3
μ Dynamic viscosity, Pa⋅s
Φ˙ Inner heat source, W/m3
Φ Heat flux, W
Subscripts
a Aluminum silicate fiber
ef Effective
h Outer wall of heater
lo Loss
i Inner
o Outer
t Tube
x Component
Keywords: convective heat transfer, energy loss, heat transfer coefficient, nusselt number, pressure drop
Citation: Yang K, Zhang C, Yuan H and Wu F (2022) Heat Transfer Characteristics and Pressure Drop of U-type Channel in Vacuum Distillation Process for Titanium Sponge. Front. Energy Res. 10:850431. doi: 10.3389/fenrg.2022.850431
Received: 07 January 2022; Accepted: 14 February 2022;
Published: 18 March 2022.
Edited by:
Zongliang Zuo, Qingdao University of Technology, ChinaReviewed by:
Kaijie Liu, Ganjiang Innovation Academy, (CAS), ChinaXianglong Li, Soochow University, China
Limin Hou, Inner Mongolia University of Science and Technology, China
Copyright © 2022 Yang, Zhang, Yuan and Wu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Fuzhong Wu, Z3V0d2Z6QDE2My5jb20=
 Kangquan Yang
Kangquan Yang Fuzhong Wu
Fuzhong Wu