Optimal Virtual Inertial-Based Power System Frequency Regulation Through Multi-Cluster Wind Turbines Using BWOA

Large-scale wind power connected to the grid efficiently reduces fossil fuel consumption, but extremely decreases grid inertial and increases frequency regulation pressure on the grid. Therefore, various wind farm-based frequency regulation technologies have been investigated in recent decades. Adaptive inertial droop control of wind turbines was considered as one of the most effective methods to enhance the inertia of the grid, because it can solve the decoupling problem between the power of wind farms and power system frequency. However, the present approaches mainly pay attention to the first frequency drop (FFD) or ignore the influence of control parameters. Hence, this paper proposes a black widow optimization algorithm (BWOA)-based step start-up adaptive inertial droop controller to smooth frequency fluctuation as well as alleviate FFD, the secondary frequency drop (SFD), and the third frequency drop (TFD). Besides, BWOA is employed to extract the best parameters of the designed controller under a 150-MW load increase. Then, the extracted parameters are used in three other load variation events to evaluate the performance of the proposed method in MATLAB/Simulink. Simulation results indicate that BWOA acquires satisfactory performances on various designed load variations. Compared with the trial-and-error method, FFD and TFD with BWOA under load increase are decreased by 10.9% and 12.8% at most, respectively.

Introduction

As the limited fossil energy is progressively exhausted after continuous development (Yang et al., 2019a; Xiong et al., 2020), the high-efficiency and high-quality exploitation and utilization of renewable energies are considered a promising solution for energy shortage and environmental degradation owing to their characteristics of sustainability (Zhang et al., 2015; Zhang et al., 2021) and low pollution (Yan et al., 2021), among which wind energy technology is relatively mature (Wang et al., 2015), highly marketized, and well-stocked (Chen et al., 2018; Pabitra and Abhik, 2020), and has been widely applied in areas where traditional power generation is insufficient (Huang et al., 2021).

However, currently extensively used wind turbines (WTs) are connected to the grid by direct current (DC) transmission (Yang et al., 2018a; AyyaraoTummala, 2020; Thakallapelli et al., 2020; Gu et al., 2021). The rotor speed of WTs is decoupled from the system frequency, which is tough to provide effective inertial support for the power grid and gravely threatens the safe and stable operation of the power system (Yang et al., 2018b). Besides, the doubly fed induction generator (DFIG) has become the most widely used wind generator because of its advantages of wide range of running speed, small size, and low cost. Unfortunately, DFIG cannot respond to the system frequency disturbance similar to traditional synchronous generators (SG) (Yang et al., 2016). In order to maximize the utilization of wind energy, WTs generally adopt maximum power point tracking control (Yang et al., 2018c), which lack the active-standby capacity traditional generators can provide. Moreover, if the additional standby capacity of electric active power brought by wind turbine grid connection is only provided by conventional units, the operating cost of the system will greatly increase and may result in the waste of fossil energy (Wei Yao et al., 2015; Zhou et al., 2020; Li et al., 2021). In summary, it is enormously significant to study the frequency characteristics and frequency regulation control of large-scale wind power grid connection (Yang et al., 2019b; Tan et al., 2021).

In recent years, multifarious frequency regulation control strategies through wind farms (WFs) have been developed, which can be mainly divided into energy storage control, de-loading control, rotor speed control, and droop control (Nguyen and Mitra, 2016; Yang et al., 2021). In particular, Wen et al. (2016), Gan et al. (2019), Jami et al. (2020), Kadri et al. (2020), and Zhang et al. (2020) achieved frequency regulation of alternative current (AC) side by releasing the energy of energy storage devices. However, introduced energy storage devices rapidly increased costs. Besides, Vidyanandan and Senroy (2013), Zhang et al. (2018), and Yao et al. (2019) adopted de-loading control to implement primary frequency regulation, which reserved backup power but seriously impeded the efficient engagement of wind energy. Similarly, rotor speed control (Boyle et al., 2021) was suggested to provide the same frequency support. Besides, the active power-frequency droop feature was introduced into the outer loop control in many studies (Arani and MohamedYasser Abdel-Rady, 2015; Van de Vyver et al., 2016; Vennelaganti and Chaudhuri, 2018; Sun et al., 2021). The droop control solves the coupling problem between the power of the flexible DC system and the frequency of the AC power grid. Unfortunately, the inverter still cannot provide inertia and achieve primary frequency regulation as well as resist load disturbance like the SG insufficient capacity (Haileselassie et al., 2011; Pipelzadeh et al., 2012). In view of the main problems existing in droop control, the virtual synchronous generator technology came into being (Morren et al., 2006). By simulating the characteristics of SG through mechanical and electromagnetic equations, the inverter performs inertia, damping characteristics, and primary frequency regulation capability in the literature (Lee et al., 2015). In Fu et al. (2017), the inertia control link was introduced into the virtual governor to provide inertia response and implement primary frequency regulation.

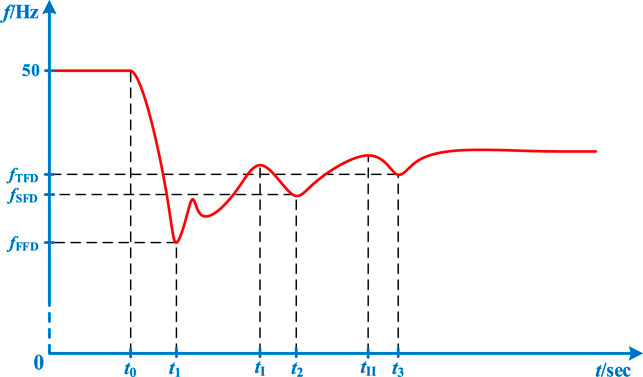
Nevertheless, the aforementioned studies only paid attention to suppressing the first frequency drop (FFD) of the power system. Actually, the secondary frequency drop (SFD) phenomenon is inevitable during the recovery process of wind turbine speed, which is even more grievous than FFD when the active power is seriously insufficient. Accordingly, Xiong et al. (2021) developed a two-level combined control strategy based on integrated offshore WFs to provide appropriate frequency support and alleviate SFD. However, the crucial parameters of the controller were determined via the trial-and-error method, which made it difficult to maintain high accuracy and reliable stability, and was also time-consuming.

For addressing these tricky obstacles, a black widow optimization algorithm (BWOA) (Hayyolalam and PourhajiKazem, 2020)-based parameter optimization method is developed to automatically extract the optimal parameters of step start-up adaptive inertial droop controller and reduce FFD, SFD, and even third frequency drop (TFD) in this paper. Furthermore, the main contributions of this paper can be summarized as follows:

• Each wind farm is classified into two clusters, i.e., cluster 1 and cluster 2, which are put into frequency regulation at the moments of load variation and rotor speed recovery, respectively, to accomplish step start-up;

• Adaptive inertial droop control scheme is designed to significantly enhance the system inertia and organically establish the relationships between the power of the flexible DC system and grid frequency;

• BWOA is applied to accurately and quickly identify eight optimal parameters of the designed controller, upon which five critical frequency characteristics are comprehensively considered as the fitness function, e.g., the integral of frequency deviation and frequency variation rate, FFD, SFD, as well as TFD;

• Two typical simulation tests under various load increases and decreases are set to evaluate the effectiveness and superiority of the proposed strategy.

The remainder of this paper is organized as follows. Modeling and Control Scheme chiefly introduces step start-up adaptive inertial droop control schemes. Then, Parameter Design of Step Start-up Adaptive Inertial Droop Controller via BWOA provides in detail the controller parameter optimization framework based on BWOA. Besides, the effectiveness of the proposed method is evaluated and validated in Case Studies. Finally, Conclusion thoughtfully summarizes conclusions and presents perspectives for future work.

Modeling and Control Scheme

Modeling of Wind Turbine

According to aerodynamic principles (Shkara et al., 2018), the power captured by WT can be expressed as

$P_{\text{in}}=\frac{1}{2}\rho S{v}^3=\frac{1}{2}\rho \pi R^2{v}^3(1)$

where $\rho$, $S$, and $v$ represent air density, the area swept by the blade of WT, and wind speed, respectively; $R$ is the radius of the blade of WT.

Furthermore, the output power of WT can be calculated as

$P_{\text{out}}=P_{\text{in}}\cdot C_{\text{p}}\left(\lambda , \theta \right)=\frac{1}{2}\rho \pi R^2{v}^3{C}_{\text{p}}\left(\lambda , \theta \right)(2)$

where $\lambda$ and $\theta$ denote tip speed ratio and the pitch angle of WT, respectively; $\lambda =\omega R/v$, $\omega$ stands for the rotational angular speed of WT in rad/s; $C_{\text{p}}\left(\lambda , \theta \right)$ is wind energy utilization coefficient (Slootweg et al., 2003), which satisfies the following expression:

$C_{\text{p}}\left(\lambda , \theta \right)=c_1\cdot \left(\frac{c_2}{{\lambda }_i}-\theta c_3-c_4\right)\cdot e^{\frac{c_5}{{\lambda }_i}}+c_6(3)$

$\frac{1}{{\lambda }_i}=\frac{1}{\lambda +0.08\beta }-\frac{0.035}{{\theta }^3+1}(4)$

where $c_1=0.5176$; $c_2=116$; $c_3=0.4$; $c_4=5$; $c_5=-21$; $c_6=0.0068$.

From Eqs. 3, 4, one can know that the wind energy utilization coefficient $C_{\text{p}}$ of WT is determined by $\lambda$ and $\theta$, and the relationships of $C_{\text{p}}$ between $\lambda$ and $\theta$ are illustrated in Figure 1. It can be seen from Figure 1 that the wind energy utilization coefficient increases and then decreases with the increase of tip speed ratio for a certain pitch angle. Besides, the maximum wind energy utilization coefficient decreases with the increase of pitch angle. Therefore, maximum power output can be achieved by controlling the angular speed of WT under different wind speeds. Furthermore, the pitch angle $\theta$ of WT remains as 0° for capturing maximum power output, and rated wind speed is settled as 12 m/s in this paper.

FIGURE 1

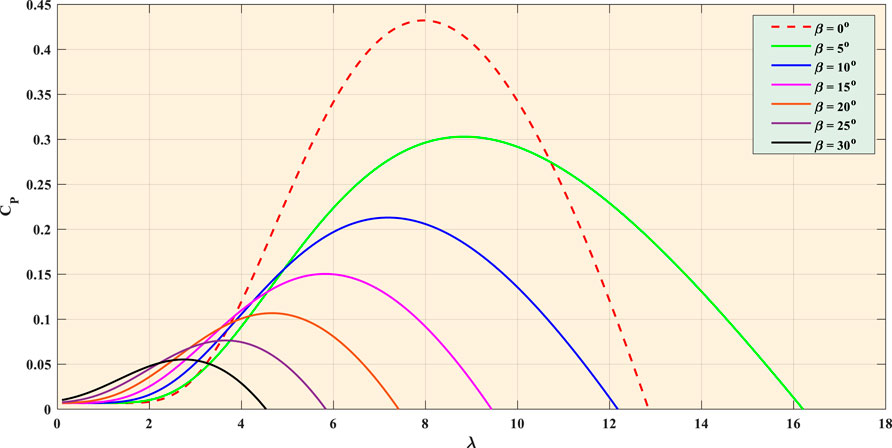
FIGURE 1. Relationships between wind energy utilization coefficient and tip speed ratio under various pitch angles.

Step Start-up Adaptive Virtual Inertial Droop Control Scheme

As shown in Figure 2, a three-area four-terminal voltage source converter-based multi-terminal high voltage direct current system (VSC-MT-HVDCs) combined with WFs and AC system is adopted as the test system, which consists of two WFs, a VSC-MT-HVDCS, and an AC system (Vennelaganti and Chaudhuri, 2018; Xiong et al., 2021), among which each WF includes five equivalent WTs that transmit electricity to the AC system together. In this paper, the rotor angular speeds of WT1–WT5 in WF1 are determined as 0.90 pu, 0.95 pu, 0.85 pu, 1.00 pu, and 1.05 pu, respectively. Besides, the rotor angular speeds of WT6–WT10 are also settled as 0.90 pu, 0.95 pu, 0.85 pu, 1.00 pu, and 1.05 pu, respectively. Note that only WTs of WF1 participate in frequency support through step start-up adaptive inertial droop control scheme after frequency events (e.g., load increase or decrease) while all WTs of WF2 merely operate in maximum power point (MPP) states. Meanwhile, WTs in the WF1 are categorized into different clusters in a certain ratio according to their rotor angular speeds. For instance, under load increase, WT2, WT4, and WT5 belong to cluster 1 while cluster 2 involves WT1 and WT3 if the cluster classification ratio is settled as 6:4. On the contrary, under load decrease, WT1–WT3 are classified as cluster 1 while WT4 and WT5 are cluster 2 if the classification ratio is also 6:4.

FIGURE 2

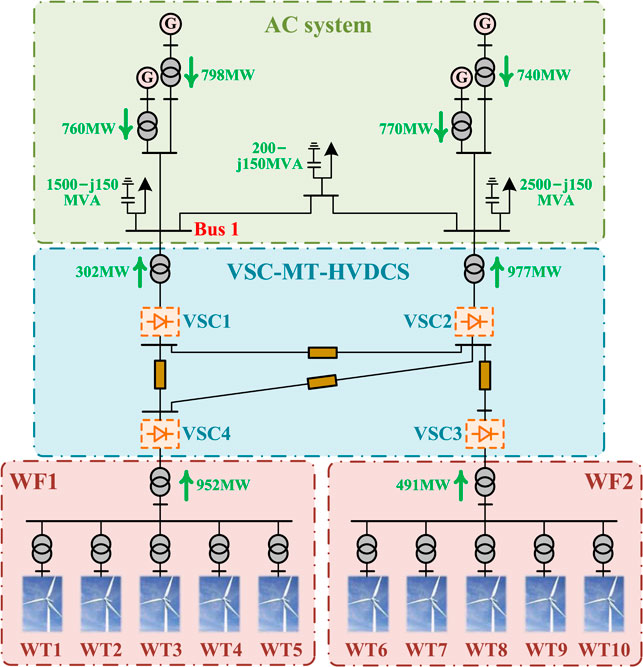
FIGURE 2. Schematic diagram of test system: A three-area four-terminal VSC-MT-HVDC-based WFs and AC system.

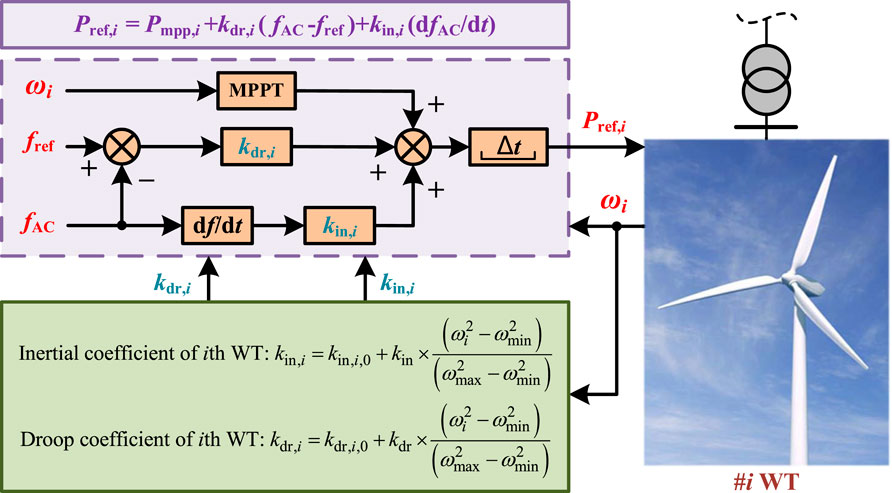
For the ith WT, furthermore, the step start-up adaptive inertial droop control scheme is demonstrated in Figure 3, among which the active power reference value $P_{\text{ref},i}$ of the ith WT mainly consists of three parts, i.e., MPP under real-time rotor angular speed ${\omega }_i$ of this WT, inertial control, and droop control, which is reacted after a certain time delay $\Delta t$ for matching with WTs of another cluster. In other words, cluster 1 and cluster 2 are utilized to respectively support system frequency in a certain order. Meanwhile, both coefficients of inertial control and droop control are adaptively varied with ${\omega }_i$, respectively. Besides, $f_{\text{AC}}$ stands for the frequency of the AC system, which is measured in VSC1 in this paper; $f_{\text{ref}}=50\text{Hz}$, ${\omega }_{\text{min}}=0.70\text{pu}$, and ${\omega }_{\text{max}}=1.20\text{pu}$.

FIGURE 3

FIGURE 3. Step start-up adaptive inertial droop control scheme for the ith WT.

Compared with the conventional droop control method that adopts constant coefficients, adaptive inertial droop control coefficients vary with real-time rotor angular speed ${\omega }_i$ of WT, which can not only guarantee rotor operating within a safe condition but also effectively utilize wind energy and timely adjust states (i.e., absorb or generate power) of WT, among which the variation rate of AC system frequency $f_{\text{AC}}$ is used as the input signal of inertial control while the input signal of droop control is the frequency deviation. Owing to the frequency deviation being small while frequency variation rate being large in the primary stage of frequency response, inertial control can rapidly provide frequency support (Kayikci and Milanovic, 2009). Besides, droop control is utilized to simulate the primary frequency regulation capability of SGs, which can improve steady-state frequency in the later stage after frequency events.

Additionally, more information about modeling parameters of the whole system and control strategy of VSC stations can be obtained from the literature (Xiong et al., 2021).

Parameter Design of Step Start-up Adaptive Inertial Droop Controller via BWOA

Mathematical Description of BWOA

Inspired by the courtship behaviors of spiders, Hayyolalam and PourhajiKazem (2020) proposed a novel meta-algorithm, namely, BWOA, which obtained satisfactory performance not only in test functions but also in engineering optimization applications (Adrián et al., 2020).

In order to ensure the global searching ability of BWOA, the population with N individuals is initialized as

$X=\left[\begin{array}{c}{x}_{\mathrm{1,1}}\\ x_{\mathrm{2,1}}\\ ⋮\\ x_{l,1}\\ ⋮\\ x_{N,1}\end{array}\begin{array}{c}{x}_{\mathrm{1,2}}\\ x_{\mathrm{2,2}}\\ \ddots \\ x_{l,2}\\ \ddots \\ x_{N,2}\end{array}\begin{array}{c}\begin{array}{cc}\cdots & x_{1,D}\end{array}\\ \begin{array}{cc}\cdots & x_{2,D}\end{array}\\ \begin{array}{cc}\ddots & ⋮\end{array}\\ \begin{array}{cc}\cdots & x_{l,D}\end{array}\\ \begin{array}{cc}\ddots & ⋮\end{array}\\ \begin{array}{cc}\cdots & x_{N,D}\end{array}\end{array}\right](1)$

where D represents the dimension of the problem to be solved; each row of candidate solution matrix $X$ determines a current location (corresponding to a solution) of a spider. Thus, the lth individual can be presented as

$\overrightarrow{X_l}=\left(U_{\text{B}}-L_{\text{B}}\right)\cdot rand+L_{\text{B}}=\left[x_{l,1},x_{l,2},\begin{array}{cc}\cdots & x_{l,D}\end{array}\right](2)$

where $U_{\text{B}}$ and $L_{\text{B}}$ denote the upper bound vector and the lower bound vector of optimized parameters; $rand$ is equal to a random number from 0 to 1.

Besides, the fundamental update rules of BWOA during iteration can be mathematically described as

$\{\begin{array}{c}\overrightarrow{X_l}\left(t+1\right)=\overrightarrow{X_{\text{b}}}\left(t\right)-m\cdot \overrightarrow{X_r}\left(t\right) if rand\left(\right)\le 0.3\\ \overrightarrow{X_l}\left(t+1\right)=\overrightarrow{X_{\text{b}}}\left(t\right)-\mathrm{c}\mathrm{o}\mathrm{s}\left(2\pi \beta \right)\cdot \overrightarrow{X_l}\left(t\right) \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{s}\end{array}(3)$

where $\overrightarrow{X_l}\left(t+1\right)$ and $\overrightarrow{X_l}\left(t\right)$ denote new solution and the old one for the lth individual in the $\left(t+1\right)$ th iteration, respectively; $\overrightarrow{X_{\text{b}}}\left(t\right)$ and $\overrightarrow{X_l}\left(t\right)$ stand for the best solution and a random solution in the previous iteration, respectively, with $r\ne l$; $m$ is defined as a random float number from 0.4 to 0.9 while $\beta$ is randomly generated in the interval of [−1.0,1.0].

Furthermore, pheromones of female spiders decide their mating rates with males, which can be calculated by

$ph\left(l\right)=\frac{Fitnes{s}_{\text{max}}-Fitness\left(l\right)}{Fitnes{s}_{\text{max}}-Fitnes{s}_{\text{min}}}(4)$

where $ph\left(l\right)$ represents the pheromone value of the lth female spider, which is a float number from 0 to 1; $Fitnes{s}_{\text{max}}$, $Fitnes{s}_{\text{min}}$, and $Fitness\left(l\right)$ denote fitness values of the worst, the best, and the lth females, respectively. For minimum optimization problems, female spiders [like $\overrightarrow{X_l}\left(t\right)$] with low pheromone [$ph\left(l\right)\le 0.3$] are difficult to mate with males, which will be replaced according to Eq. 5 to improve the quality of the population, as follows:

$\overrightarrow{X_l}\left(t+1\right)=\overrightarrow{X_{\text{b}}}\left(t\right)-\frac{1}{2}(\overrightarrow{X_{r_1}}\left(t\right)-{\left(-1\right)}^{\sigma }\cdot \overrightarrow{X_{r_2}}\left(t\right))(5)$

where $\overrightarrow{X_{r_1}}\left(t\right)$ and $\overrightarrow{X_{r_2}}\left(t\right)$ are two different search agents randomly selected in the current population; $\sigma$ stands for a random binary number, which is equal to either 0 or 1.

Parameter Extraction Process of the Controller via BWOA

In order to acquire the best performance of frequency regulation, an optimal parameter extraction process of step start-up adaptive inertial droop controller based on BWOA is proposed in this section. On the one hand, this paper primarily concentrates on dynamic response characteristics of system frequency $f_{\text{AC}}$ after an increase in load illustrated in Figure 4, i.e., FFD, SFD, and TFD, that reflect local details, among which $f_{\text{FFD}}$, $f_{\text{SFD}}$, and $f_{\text{TFD}}$ represent the nadirs of FFD, SFD, and TFD, respectively. Specifically, cluster 1 is immediately put into operation after frequency event at $t_0$ (i.e., $\Delta t$ equal to 0 for WTs of cluster 1) while cluster 2 is launched when the rotor angular speeds of cluster 1 start to recover at $t_I$, i.e., $\Delta t$ is 0 for WTs of cluster 2.

FIGURE 4

FIGURE 4. General dynamic characteristics of system frequency under load increase.

On the other hand, the integrals of frequency deviation and frequency variation rate ($S_{\text{IoFD}}$ and $S_{\text{IoFVR}}$, respectively) are also considered, which principally manifest global information of system frequency fluctuation, among which $S_{\text{IoFD}}$ and $S_{\text{IoFVR}}$ can be respectively expressed as

$S_{\mathrm{IoFD}}={\displaystyle \int \left|50-f_{AC}\right|}dt(6)$

$S_{\mathrm{IoFVR}}={\displaystyle \int \left|\frac{\mathrm{d}{\mathrm{f}}_{\mathit{AC}}}{\text{d}t}\right|}dt(7)$

As indicated in Eq. 8, each indicator is assigned a coefficient according to the relative significance, and they are added up as the fitness function.

$F_{\mathrm{fit}}\left(S_{\mathrm{IoFD}}, S_{\mathrm{IoFVR}}, f_{\mathrm{FFD}}, f_{\mathrm{SFD}}, f_{\text{TFD}}\right)=\min \left\{\left(10A_{\mathrm{IoFD}}+100A_{\mathrm{IoFVR}}+200f_{\mathrm{FFD}}+100f_{\mathrm{SFD}}+100f_{\mathrm{TFD}}\right)\cdot 50\right\}(8)$

Additionally, parameters of the controller for different WTs within the same cluster are identically designed for reducing the complexities of the problem and enhancing the search efficiency of BWOA. Therefore, optimized parameters can be further refined as $X=\left[k_{\text{dr},i,0}^1, k_{\text{in},i,0}^1, k_{\text{dr}}^1, k_{\text{in}}^1, k_{\text{dr},i,0}^2, k_{\text{in},i,0}^2, k_{\text{dr}}^2, k_{\text{in}}^2\right]$, in which the superscript 1 and 2 stand for cluster 1 and cluster 2, respectively. Besides, the lower and upper limits of optimized parameters are demonstrated in Table 1.

TABLE 1

TABLE 1. The range of optimized parameters.

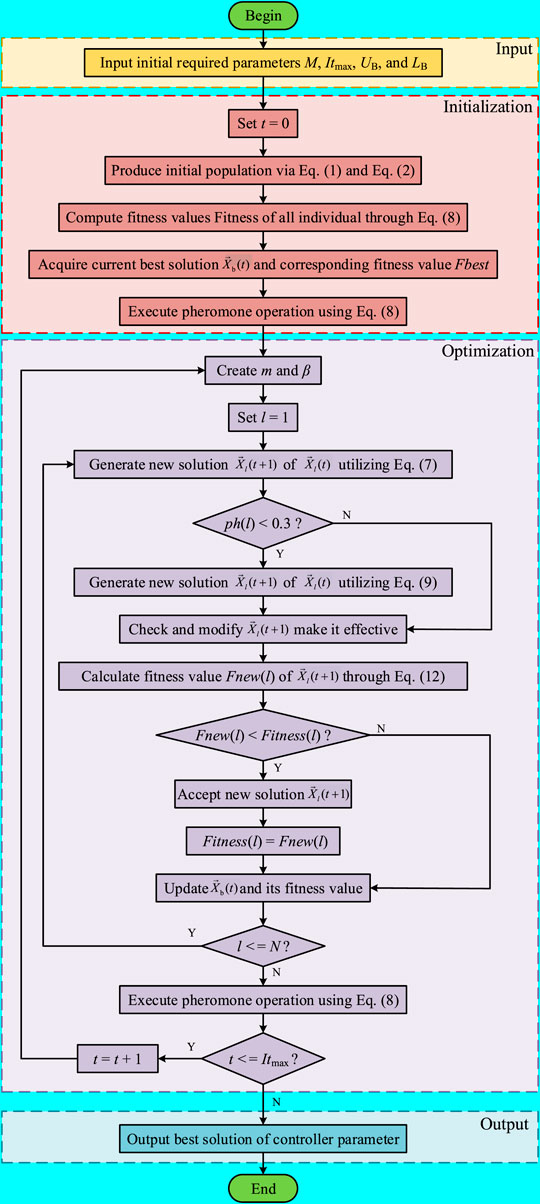
Finally, the parameter optimization pseudocode and flow chart of step start-up adaptive inertial droop controller with BWOA are explicitly exhibited in Table 2 and Figure 5, respectively, among which N and It_max denote the size of population and maximum iteration, respectively.

TABLE 2

TABLE 2. Parameter optimization pseudocode of controller based on BWOA.

FIGURE 5

FIGURE 5. Parameter optimization flow chart of controller based on BWOA.

Case Studies

In this section, parameters of step start-up adaptive inertial droop controller are carefully optimized via BWOA through 10 times independent running under load increase 150 MW. Additionally, two simulation tests (i.e., load increase and decrease) are designed to evaluate and validate the effectiveness of the optimized parameters. All case studies are carried out by MATLAB/Simulink environment with variable-step solver (e.g., DAESSC). Besides, the number of population N and the maximum iteration It_max are set as 5 and 8, respectively. Note that all load variation occurred at the fifth second. Meanwhile, wind turbine cluster 1 and cluster 2 are put into frequency regulation at the moments of load variation and rotor speed recovery, respectively, i.e., $\Delta t=0s$ for cluster 1 and $\Delta t=5s$ for cluster 2.

Table 3 provides optimal control parameters obtained by various approaches under a 150-MW load increase, i.e., without WFs participating in frequency regulation (without FSC), trial and error (Xiong et al.), and BWOA. Note that the symbol “/” stands for no value, which is also applicable for the rest of the tables of this paper.

TABLE 3

TABLE 3. Optimal control parameters obtained by different methods under load increase 250 MW.

Load Increase

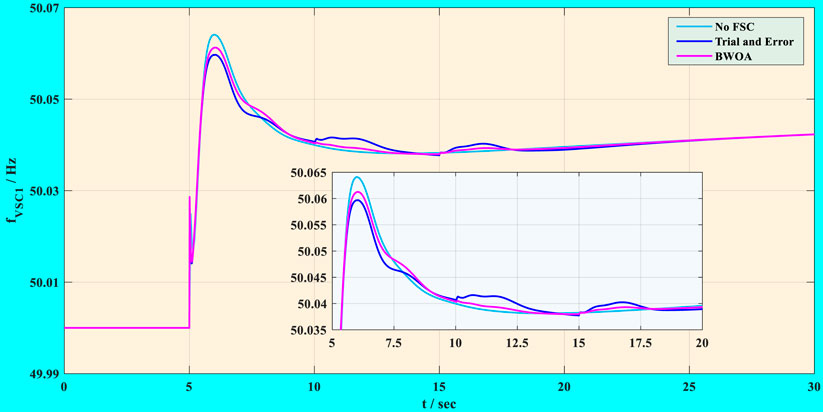
The dynamic frequency responses acquired by different methods under various load increase variations are elaborately depicted in Figure 6. One can easily observe that the system frequency based on BWOA optimization performs the least fluctuation in all load increase scenarios compared with those of other methods. Furthermore, BWOA-based parameter optimization method efficiently suppresses the FFD, SFD, and TFD of system frequency, which can dramatically ensure grid stability and reliability.

FIGURE 6

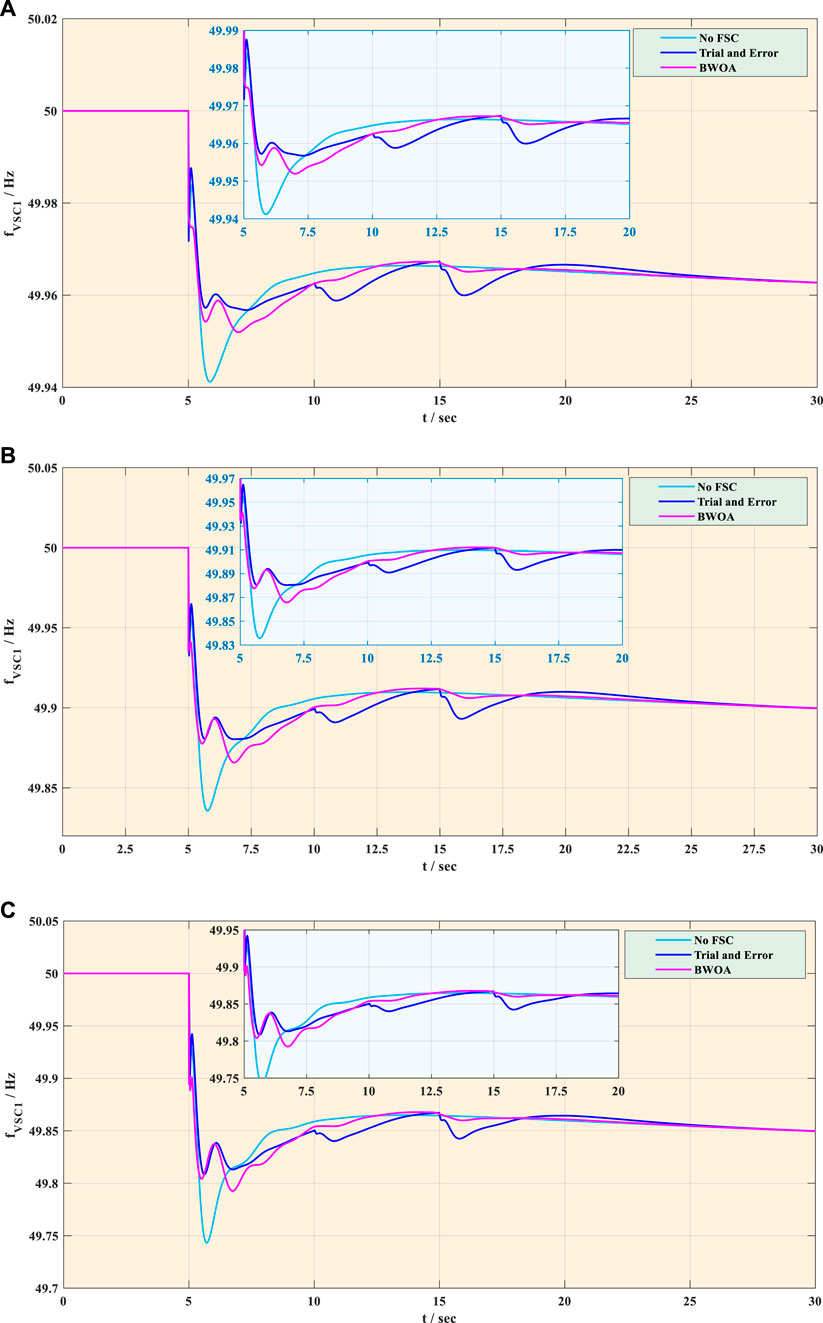
FIGURE 6. Frequency response acquired by different methods under various load increase variations: (A) 50 MW load increase; (B) 150 MW load increase; (C) 250 MW load increase.

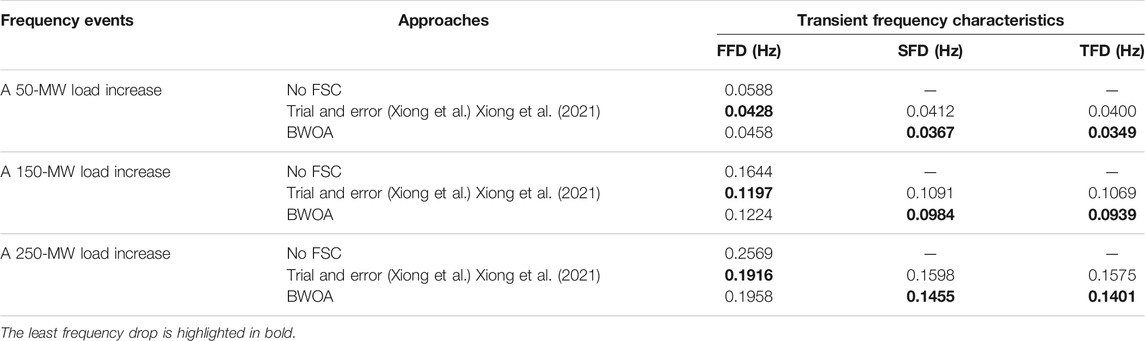
Furthermore, quantitative comparison results of frequency drop based on different strategies under three typical load increase situations are tabulated in Table 4, where the least frequency drop is highlighted in bold. In general, the trial-and-error method acquired the least FFD followed by BWOA and without FSC. However, the performances of the trial-and-error method on suppressing SFD and TFD were inferior to those of BWOA. In particular, compared with the trial-and-error method, the FFDs and TFDs obtained by BWOA are reduced by 10.9%, 9.8%, and 8.9%, as well as 12.8%, 12.2%, and 11% under 50 MW load increase, 150 MW load increase, and 250 MW load increase, respectively.

TABLE 4

TABLE 4. FFD, SFD, and TFD obtained by various methods.

Load Decrease

So as to confirm the effectiveness of control parameters acquired by BWOA in load decrease, Bus 1 of the test system experienced a 50-MW load decrease at 5 s, which was used as a simulation case. In this frequency event, cluster 1 (i.e., WT1, WT2, and WT2) is immediately started up at the fifth second while cluster 2 (i.e., WT4 and WT5) is launched at the 10th second. The simulation results are demonstrated in Figure 7 and Figure 8. It can be seen from Figure 7 that three control schemes caused 0.0641-, 0.0597-, and 0.0613-Hz frequency increases, respectively. Although frequency increase with the trial-and-error method is lower than that with BWOA at the sixth second, two obvious frequency fluctuations occur with the former one in the following procedures, which are caused by superabundant active power injection corresponding to Figure 8. Therefore, obtained optimal control parameters by BWOA are applicable to load decrease with low-frequency fluctuation.

FIGURE 7

FIGURE 7. Frequency response acquired by different methods under a 50-MW load decrease.

FIGURE 8

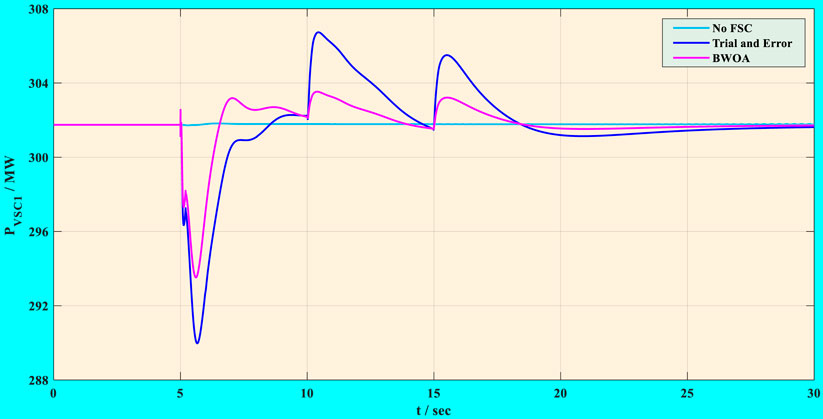
FIGURE 8. Transmitted active power of VSC1 acquired by different methods under a 50-MW load decrease.

Conclusion

Lastly, three main conclusions can be concluded in this paper, as follows:

• A step start-up adaptive inertial droop controller is carefully designed to support the frequency of the grid system based on two WFs including 5 WTs, respectively, upon which WTs in WF 1 are classified into two clusters according to their speeds, i.e., cluster 1 and cluster 2. For the sake of accomplishing step start-up, the former one immediately participates in frequency regulation when load variations occur while the latter operates at the moment of rotor speed recovery of the former;

• BWOA is successfully used to extract eight optimal parameters of the designed controller under 150 MW load increase with high accuracy, fast speed, and powerful stability, where five reasonable frequency factors are comprehensively considered to set up the fitness function, e.g., the integral of frequency deviation and frequency variation rate, FFD, SFD, as well as TFD;

• Simulation results indicate that the optimal control parameters are also applicable tests under various load increases and decreases. Compared with the trial-and-error method, FFD and TFD with BWOA under load increase are decreased by 10.9% and 12.8% at most, respectively, which significantly verify the effectiveness and superiority of the proposed method.

A BWOA-based parameter optimization strategy can significantly enhance the performance of the controller, then smooth frequency fluctuation and improve power quality under various load variations. Therefore, it may be efficient to optimize other controller parameters and may even be applied to other complex optimization issues.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

CL: Conceptualization, Writing—Reviewing and Editing; QL: Writing—Original draft preparation, Investigation; XT: Writing—Reviewing and Editing, Software; CL: Supervision.

Funding

This paper was supported in part by the National Natural Science Foundation of China (No. 52007174).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Abbreviations

AC, alternating current; BWOA, black widow optimization algorithm; DFIG, doubly fed induction generator; DC, direct current; FFD, first frequency drop; MPPT, maximum power point tracking; ${\mathit{k}}_{\mathbf{dr}}{\mathit{k}}_{\mathbf{in}}$, slopes of $k_{\text{dr},i}$ (MW/Hz) and $k_{\text{in},i}$ (MW∙s/Hz), respectively; M, number of population for BWOA; ${\mathit{P}}_{\mathbf{ref},\mathit{i}}$, output power reference value of the ith wind turbine in WF1; ${\mathit{P}}_{\mathbf{mpp},\mathit{i}}$, maximum power point of the ith wind turbine under rotor speed ${\omega }_i$; $\Delta \mathit{t}$, time delay of cluster 1 and cluster 2 participating frequency regulation (s); α, stochastic coefficient for imitating the movement constraints of solution; $\mathit{\beta }$, $\mathit{\gamma }$ random integer uniformly distributed in (); ${\mathit{\omega }}_{\mathit{i}}$, rotor speed of the ith wind turbine (rad/s); SFD, secondary frequency drop; TFD, tertiary frequency drop; MT-HVDCs, multi-terminal high voltage direct current system; WHE, water hammer effect; WFs, wind farms; FSC, WFs participating in frequency regulation; ${\mathit{S}}_{\mathbf{IoFD}}$, integral of frequency deviation (Hz∙s); ${\mathit{S}}_{\mathrm{IoFVR}}$, integral of frequency variation rate (Hz); ${\mathit{f}}_{\mathbf{AC}}$, frequency of AC system (Hz); ${\mathit{f}}_{\mathbf{ref}}$, reference value of system frequency (Hz); ${\mathit{f}}_{\mathbf{MFDP}}$, maximum frequency deviation point (Hz); It_max, maximum iteration; ${\mathit{k}}_{\mathbf{dr},\mathit{i}}$, coefficient of adaptive droop control (MW/Hz); ${\mathit{k}}_{\mathbf{in},\mathit{i}}$, virtual inertial control coefficient (MW∙s/Hz).

References

Adrián, F. P. D., Hernán, P. V., JuanAlmazán-Covarrubias, H., Cruz, N. T., and Ramirez-Arredondo, J. M. (2020). A Novel Bio-Inspired Algorithm Applied to Selective Harmonic Elimination in a Three-phase Eleven-Level Inverter. Math. Probl. Eng. 2020, 1. doi:10.1155/2020/8856040

CrossRef Full Text | Google Scholar

Arani, M. F. M., and MohamedYasser Abdel-Rady, Y. A.-R. I. (2015). Analysis and Impacts of Implementing Droop Control in DFIG-Based Wind Turbines on Microgrid/weak-Grid Stability. IEEE Trans. Power Syst. 30 (1), 385–396. doi:10.1109/tpwrs.2014.2321287

CrossRef Full Text | Google Scholar

AyyaraoTummala, S. L. V. (2020). A Robust Composite Wide Area Control of a DFIG Wind Energy System for Damping Inter-area Oscillations. Prot. Control. Mod. Power Syst. 5 (3), 79–88. doi:10.1186/s41601-020-00170-y

CrossRef Full Text | Google Scholar

Boyle, J., Littler, T., Muyeen, S. M., and Foley, A. M. (2021). An Alternative Frequency-Droop Scheme for Wind Turbines that Provide Primary Frequency Regulation via Rotor Speed Control. Int. J. Electr. Power Energ. Syst. 133, 107219. doi:10.1016/j.ijepes.2021.107219

CrossRef Full Text | Google Scholar

Chen, J., Yao, W., Zhang, C., Ren, Y., and Jiang, L. (2018). Design of Robust MPPT Controller for Grid-Connected PMSG-Based Wind Turbine via Perturbation Observation Based Nonlinear Adaptive Control. Renew. Energ. 101, 34. doi:10.1016/j.renene.2018.11.048

CrossRef Full Text | Google Scholar

Fu, Y., Wang, Y., and Zhang, X. (2017). Integrated Wind Turbine Controller with Virtual Inertia and Primary Frequency Responses for Grid Dynamic Frequency Support. IET Renew. Power Generation 11 (8), 1129–1137. doi:10.1049/iet-rpg.2016.0465

CrossRef Full Text | Google Scholar

Gan, W., Ai, X., Fang, J., Yan, M., Yao, W., Zuo, W., et al. (2019). Security Constrained Co-planning of Transmission Expansion and Energy Storage. Appl. Energ. 239, 383–394. doi:10.1016/j.apenergy.2019.01.192

CrossRef Full Text | Google Scholar

Gu, M., Meegahapola, L., and Wong, K. L. (2021). Coordinated Voltage and Frequency Control in Hybrid AC/MT-HVDC Power Grids for Stability Improvement. IEEE Trans. Power Syst. 36 (1), 635–647. doi:10.1109/tpwrs.2020.2983431

CrossRef Full Text | Google Scholar

Haileselassie, T. M., Torres-Olguin, R. E., Vrana, T. K., Uhlen, K., and Undeland, T. (2011). Main Grid Frequency Support Strategy for VSC-HVDC Connected Wind Farms with Variable Speed Wind Turbines. IEEE Trondheim PowerTech. Norway: IEEETrondheim, 1–6. doi:10.1109/ptc.2011.6019348

CrossRef Full Text | Google Scholar

Hayyolalam, V., and Pourhaji Kazem, A. A. (2020). Black Widow Optimization Algorithm: A Novel Meta-Heuristic Approach for Solving Engineering Optimization Problems. Eng. Appl. Artif. Intelligence 87, 103249. doi:10.1016/j.engappai.2019.103249

CrossRef Full Text | Google Scholar

Huang, S., Wu, Q., Liao, W., Wu, G., Li, X., and Wei, J. (2021). Adaptive Droop-Based Hierarchical Optimal Voltage Control Scheme for Vsc-Hvdc Connected Offshore Wind Farm. IEEE Trans. Ind. Inf. 17 (12), 8165–8176. doi:10.1109/tii.2021.3065375

CrossRef Full Text | Google Scholar

Jami, M., Shafiee, Q., Gholami, M., and Bevrani, H. (2020). Control of a Super-capacitor Energy Storage System to Mimic Inertia and Transient Response Improvement of a Direct Current Micro-grid. J. Energ. Storage 32, 101788. doi:10.1016/j.est.2020.101788

CrossRef Full Text | Google Scholar

Kadri, A., Marzougui, H., Aouiti, A., and Bacha, F. (2020). Energy Management and Control Strategy for a DFIG Wind Turbine/fuel Cell Hybrid System with Super Capacitor Storage System. Energy 192, 116518. doi:10.1016/j.energy.2019.116518

CrossRef Full Text | Google Scholar

Kayikci, M., and Milanovic, J. V. (2009). Dynamic Contribution of DFIG-Based Wind Plants to System Frequency Disturbances. IEEE Trans. Power Syst. 24 (2), 859–867. doi:10.1109/tpwrs.2009.2016062

CrossRef Full Text | Google Scholar

Lee, J., Muljadi, E., and Srensen, P. (2015). Releasable Kinetic Energy-Based Inertial Control of a DFIG Wind Power Plant. IEEE Trans. Sust. Energ. 7 (1), 279–288.

Google Scholar

Li, H., Qiao, Y., Lu, Z., Zhang, B., and Teng, F. (2021). Frequency-constrained Stochastic Planning towards a High Renewable Target Considering Frequency Response Support from Wind Power. IEEE Trans. Power Syst. 36 (5), 4632–4644. doi:10.1109/tpwrs.2021.3066991

CrossRef Full Text | Google Scholar

Morren, J., de Haan, S. W. H., Kling, W. L., and Ferreira, J. A. (2006). Wind Turbines Emulating Inertia and Supporting Primary Frequency Control. IEEE Trans. Power Syst. 21 (1), 433–434. doi:10.1109/tpwrs.2005.861956

CrossRef Full Text | Google Scholar

Nguyen, N., and Mitra, J. (2016). An Analysis of the Effects and Dependency of Wind Power Penetration on System Frequency Regulation. IEEE Trans. Sustain. Energ. 7 (1), 354–363. doi:10.1109/tste.2015.2496970

CrossRef Full Text | Google Scholar

Pabitra, K. G., and Abhik, B. (2020). Stability Enhancement of Wind Energy Integrated Hybrid System with the Help of Static Synchronous Compensator and Symbiosis Organisms Search Algorithm. Prot. Control. Mod. Power Syst. 5 (2), 43

Google Scholar

Pipelzadeh, Y., Chaudhuri, B., and Green, T. C. “Inertial Response from Remote Offshore Wind Farms Connected through VSC-HVDC Links: A Communication-Less Scheme,” in Power and Energy Society General Meeting (San Diego, CA, USA: IEEE 2012), 1–6.

Google Scholar

Shkara, Y., Schelenz, R., and Jacobs, G. (2018). The Effect of Blade-tower Interaction on the Structure Loading of Multi Megawatt Horizontal axis Wind Turbine. J. Phys. Conf. Ser. 1037 (7), 072033. doi:10.1088/1742-6596/1037/7/072033

CrossRef Full Text | Google Scholar

Slootweg, J. G., Polinder, H., and Kling, W. L. (2003). Representing Wind Turbine Electrical Generating Systems in Fundamental Frequency Simulations. IEEE Trans. Energ. Convers. 18 (4), 516–524. doi:10.1109/tec.2003.816593

CrossRef Full Text | Google Scholar

Sun, M., Min, Y., Chen, L., Hou, K., Xia, D., and Mao, H. (2021). Optimal Auxiliary Frequency Control of Wind Turbine Generators and Coordination with Synchronous Generators. CSEE J. Power Energ. Syst. 7 (1), 78. doi:10.17775/CSEEJPES.2020.00860

CrossRef Full Text | Google Scholar

Tan, J., Wu, Q., Zhang, M., Wei, W., Liu, F., and Pan, B. (2021). Chance-constrained Energy and Multi-type Reserves Scheduling Exploiting Flexibility from Combined Power and Heat Units and Heat Pumps. Energy 233, 121176. doi:10.1016/j.energy.2021.121176

CrossRef Full Text | Google Scholar

Thakallapelli, A., Nair, A. R., Biswas, B. D., and Kamalasadan, S. (2020). Frequency Regulation and Control of Grid-Connected Wind Farms Based on Online Reduced-Order Modeling and Adaptive Control. IEEE Trans. Ind. Applicat. 56 (2), 1980–1989. doi:10.1109/tia.2020.2965507

CrossRef Full Text | Google Scholar

Van de Vyver, J., De Kooning, J. D. M., Meersman, B., Vandevelde, L., and Vandoorn, T. L. (2016). Droop Control as an Alternative Inertial Response Strategy for the Synthetic Inertia on Wind Turbines. IEEE Trans. Power Syst. 31 (2), 1129–1138. doi:10.1109/tpwrs.2015.2417758

CrossRef Full Text | Google Scholar

Vennelaganti, S. G., and Chaudhuri, N. R. (2018). Selective Power Routing in MTDC Grids for Inertial and Primary Frequency Support. IEEE Trans. Power Syst. 33 (6), 7020–7030. doi:10.1109/tpwrs.2018.2854647

CrossRef Full Text | Google Scholar

Vidyanandan, K. V., and Senroy, N. (2013). Primary Frequency Regulation by Deloaded Wind Turbines Using Variable Droop. IEEE Trans. Power Syst. 28 (2), 837–846. doi:10.1109/tpwrs.2012.2208233

CrossRef Full Text | Google Scholar

Wang, X., Wei, X., and Meng, Y. (2015). Experiment on Grid-Connection Process of Wind Turbines in Fractional Frequency Wind Power System. IEEE Trans. Energ. Convers. 30 (1), 22–31. doi:10.1109/tec.2014.2358498

CrossRef Full Text | Google Scholar

Wei Yao, W., Lin Jiang, L., Jinyu Wen, J., Qinghua Wu, Q., and Shijie Cheng, S. (2015). Wide-area Damping Controller for Power System Interarea Oscillations: A Networked Predictive Control Approach. IEEE Trans. Contr. Syst. Technol. 23 (1), 27–36. doi:10.1109/tcst.2014.2311852

CrossRef Full Text | Google Scholar

Wen, J., Liu, J., Long, Y., and Yao, W. (2016). Solution to Short-Term Frequency Response of Wind Farms by Using Energy Storage Systems. IET Renew. Power Generation 10 (5), 669. doi:10.1049/iet-rpg.2015.0164

CrossRef Full Text | Google Scholar

Xiong, L. S., Liu, X. K., Liu, Y. H., and Zhuo, F. (2020). Modeling and Stability Issues of Voltage-Source Converter Dominated Power Systems: a Review. Csee Jpes. doi:10.17775/CSEEJPES.2020.03590

CrossRef Full Text | Google Scholar

Xiong, Y., Yao, W., Wen, J., Lin, S., Ai, X., Fang, J., et al. (2021). Two-level Combined Control Scheme of VSC-MTDC Integrated Offshore Wind Farms for Onshore System Frequency Support. IEEE Trans. Power Syst. 36 (1), 781–792. doi:10.1109/tpwrs.2020.2998579

CrossRef Full Text | Google Scholar

Yan, C., Tang, Y., Dai, J. F., Wang, C. G., and Wu, S. J. (2021). Uncertainty Modeling of Wind Power Frequency Regulation Potential Considering Distributed Characteristics of Forecast Errors. Prot. Control. Mod. Power Syst. 6 (3), 276–288. doi:10.1186/s41601-021-00200-3

CrossRef Full Text | Google Scholar

Yang, B., Jiang, L., Wang, L., Yao, W., and Wu, Q. H. (2016). Nonlinear Maximum Power point Tracking Control and Modal Analysis of DFIG Based Wind Turbine. Int. J. Electr. Power Energ. Syst. 74, 429–436. doi:10.1016/j.ijepes.2015.07.036

CrossRef Full Text | Google Scholar

Yang, B., Yu, T., Shu, H., Dong, J., and Jiang, L. (2018). Robust Sliding-Mode Control of Wind Energy Conversion Systems for Optimal Power Extraction via Nonlinear Perturbation Observers. Appl. Energ. 210, 711–723. doi:10.1016/j.apenergy.2017.08.027

CrossRef Full Text | Google Scholar

Yang, B., Yu, T., Shu, H., Zhang, X., Qu, K., and Jiang, L. (2018). Democratic Joint Operations Algorithm for Optimal Power Extraction of PMSG Based Wind Energy Conversion System. Energ. Convers. Manage. 159, 312–326. doi:10.1016/j.enconman.2017.12.090

CrossRef Full Text | Google Scholar

Yang, B., Yu, T., Shu, H., Zhang, Y., Chen, J., Sang, Y., et al. (2018). Passivity-based Sliding-Mode Control Design for Optimal Power Extraction of a PMSG Based Variable Speed Wind Turbine. Renew. Energ. 119, 577–589. doi:10.1016/j.renene.2017.12.047

CrossRef Full Text | Google Scholar

Yang, B., Yu, T., Zhang, X., Li, H., Shu, H., Sang, Y., et al. (2019). Dynamic Leader Based Collective Intelligence for Maximum Power point Tracking of PV Systems Affected by Partial Shading Condition. Energ. Convers. Manage. 179, 286–303. doi:10.1016/j.enconman.2018.10.074

CrossRef Full Text | Google Scholar

Yang, D., Jin, Z., Zheng, T., and Jin, E. (2021). An Adaptive Droop Control Strategy with Smooth Rotor Speed Recovery Capability for Type III Wind Turbine Generators. Int. J. Electr. Power Energ. Syst. 135, 107532. doi:10.1016/j.ijepes.2021.107532

CrossRef Full Text | Google Scholar

Yang, P., Dong, X., Li, Y., Kuang, L., Zhang, J., He, B., et al. (2019). Research on Primary Frequency Regulation Control Strategy of Wind-thermal Power Coordination. IEEE Access 7, 144766–144776. doi:10.1109/access.2019.2946192

CrossRef Full Text | Google Scholar

Yao, Q., Liu, J., and Hu, Y. (2019). Optimized Active Power Dispatching Strategy Considering Fatigue Load of Wind Turbines during De-loading Operation. IEEE Access 7, 17439–17449. doi:10.1109/access.2019.2893957

CrossRef Full Text | Google Scholar

Zhang, K., Zhou, B., Or, S. W., Li, C., Chung, C. Y., and Voropai, N. I. (2021). Optimal Coordinated Control of Multi-Renewable-To-Hydrogen Production System for Hydrogen Fueling Stations. IEEE Trans. Ind. Applicat. 1, 1. doi:10.1109/TIA.2021.3093841

CrossRef Full Text | Google Scholar

Zhang, X., Huang, W., Chen, S., Xie, D., Liu, D., and Ma, G. (2020). Grid-source Coordinated Dispatching Based on Heterogeneous Energy Hybrid Power Generation. Energy 205, 117908. doi:10.1016/j.energy.2020.117908

CrossRef Full Text | Google Scholar

Zhang, X., Yu, T., Yang, B., Zheng, L., and Huang, L. (2015). Approximate Ideal Multi-Objective Solution Q(λ) Learning for Optimal Carbon-Energy Combined-Flow in Multi-Energy Power Systems. Energ. Convers. Manage. 106, 543–556. doi:10.1016/j.enconman.2015.09.049

CrossRef Full Text | Google Scholar

Zhang, X., Zha, X., Yue, S., and Chen, Y. (2018). A Frequency Regulation Strategy for Wind Power Based on Limited Over-speed De-loading Curve Partitioning. IEEE Access 6, 22938–22951. doi:10.1109/access.2018.2825363

CrossRef Full Text | Google Scholar

Zhou, B., Fang, J., Ai, X., Yang, C., Yao, W., and Wen, J. (2020). Dynamic Var reserve-constrained Coordinated Scheduling of LCC-HVDC Receiving-End System Considering Contingencies and Wind Uncertainties. IEEE Trans. Sust. Energ. 12 (1), 469–481. doi:10.1109/TSTE.2020.3006984

CrossRef Full Text | Google Scholar