A GPU-Based Resilience Enhanced Voltage Optimization Model for Distribution Networks

Improving the survivability of critical loads after extreme events is essential to enhance the resilience of power systems, especially for distribution networks. A distribution network with various operational resources can be separated into several sub-distribution networks without electrical connections. Maintaining the power supply with acceptable power quality to critical loads in such separated distribution networks is a challenging task for the operators of power systems. In this paper, an optimization model is proposed to maximize the ability to supply power to critical loads in distribution networks. Moreover, a GPU was employed to accelerate the proposed model using genetic algorithm. With the acceleration of the GPU platform, the solving time was reduced and the population size can be enlarged to enhance the convergence rate and convergence quality of the algorithm. Finally, case studies were carried out in IEEE 33-bus and 118-bus systems, and the effectiveness of the method was validated by comparing the solution results on GPU and CPU platforms.

Introduction

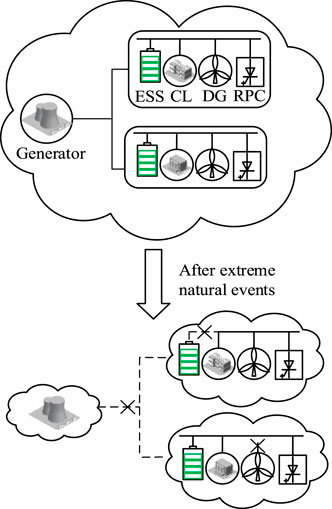
In recent years, a number of extreme natural events have brought huge economic losses to the society (Panteli and Mancarella, 2015a; Wang et al., 2016; Mohamed et al., 2019). Critical loads, such as government buildings, communication systems, transportation systems, and the sensors and controllers of power systems, are essential for the operation of power systems during extreme natural events, as well as the restoration of power systems after such extreme natural events. Improving the survivability of critical loads after these extreme natural events can enhance the resilience of the power system. Resilience is defined as the survivability and the ability to defend against extreme natural events. It is defined as the ability of the power system to survive, defend, and recover from extreme natural disasters (Panteli and Mancarella, 2015b; Gao et al., 2016). Nowadays, more and more distributed generation resources, such as photovoltaic (PV) systems, small scale wind turbines, and gas turbines are integrated into distribution networks. Moreover, most loads of power systems, especially critical loads, are supplied by distribution networks. The operation of distribution network during and after extreme natural events is essential to enhance the resilience of power systems.

A huge challenge for the distribution network operation during and after extreme natural events is the insufficiency of controllable operational resources. Conventional fossil fueled power generators with large capacities may not be able to connect to distribution networks because of the damaged transmission networks. In this case, all kinds of operational resources in distribution networks, such as distributed PV resources, distributed wind farms, small scale energy storage systems, diesel generators, demand response devices, and voltage support devices, should be well coordinated to provide sufficient operation resources.

Currently, a large number of distributed PV stations, other renewable resources, and energy storage systems with declining costs are connected to the distribution network (Mahmud et al., 2014). Comparing with traditional distribution networks, these distributed resources make the operating environment of the distribution network more complex and challenging (Wang et al., 2020). As indicated in (Wang et al., 2020), the PV systems could take effects on the voltage quality of distribution network in different locations. On the other hand, these resources can be survived after extreme natural events in most cases and bring more flexible resources to the distribution networks and provide new technical devices and methods to enhance power supply to critical loads. All types of flexible operational resources should be effectively involved in the operation of the distribution networks to ensure a stable power supply of critical loads and support restoration after extreme natural events (Utkarsh et al., 2021). An operation framework is proposed in (Utkarsh et al., 2021) to coordinate the demand response resources, such as the home energy systems.

Regulating bus voltages within acceptable area is an important operational target in distribution networks. Considering the critical loads are sensitive to the voltage quality, the voltage optimization model can improve the survival ability of critical loads. The distribution networks should dispatch various types of reactive power and voltage support devices, such as distribution static synchronous compensators (D-STATCOMs), capacitor banks, and line voltage regulators (LVRs). These devices have different operational characteristics. For instance, the capacitor banks (CBs) are ON/OFF-type devices and several discrete control states are available for LVRs. While D-STATCOMs can adjust its output power continuously. Thus, coordinate these devices with different types of mathematic models is a challenge for the operation of distribution networks. An optimal operational model is proposed in this paper to coordinate the operation of different types of devices with a multi objective optimization model. The proposed model is a mixed integer nonlinear programming (MINLP) model. These models can be solved by traditional solution methods and commercial software, such as the gradient based optimization algorithm (Nicholson and H. Sterling, 1973; Mamandur and Chenoweth, 1981; Grudinin, 1998), and decomposition approach (Deeb and Shahidehpour, 1990). However, the nonlinear characteristics and binary variables of the optimization model make the global optimization results can not be achieved guaranteed. The computing time is varied a lot depends on the proposed mathematic models. The Genetic algorithms (GAs) are metaheuristic algorithms and the first GA was proposed by Professor J Holland in 1975. GAs are widely used to solve the nonlinear programming (NLP) optimization models of power systems and can achieve better robustness for various kinds of mathematic models (Delfanti et al., 2000; Swarup and Yamashiro, 2002; Enacheanu et al., 2008; Queiroz and Lyra, 2009). However, in solving MINLP problems with strong nonlinear objective functions, the calculation time and convergence quality requires a large population number and a long solving time. In this way, the GA is not acceptable for practical applications.

Population size is an essential parameter for the performance of the GA. By choosing a large initial population size, the convergence rate and convergence quality of the algorithm can be enhanced to obtain better results (Harik et al., 1999). However, increasing the population size will greatly increase the computing time, which significantly reduces the value of the algorithm for practical projects. The genetic operation in the evolution process has strong independence, and there is no data dependence between individuals, so the algorithm can be computed parallelly (Xing Chen et al., 2005). Based on this feature, Xing Chen, F. Gonzalez Bulnes et al. used a distributed computing method to calculate the population size generated on multiple computers, and finally mixed the population to obtain the result (Gonzalez Bulnes et al., 2013; de la Calle et al., 2015). However, the distributed computing method needs to switch data results among multiple computers, which requires powerful communication capabilities and increase the total computing time. The cost of setting up powerful control and communication systems limits the application of distributed and parallel GAs.

In this study, the proposed optimization model was solved by GA and accelerated on a graphics processing unit (GPU) platform by implementing a parallel computing structure. With the rapid development and iteration of AI technologies, such as deep learning and reinforcement learning, the hardware performance of GPU platforms have increased rapidly. For instance, the GPU of Nvidia 2080TI has Turing TU102 architecture, 11 GB GDDR6 memory, and the single precision floating point computing performance can exceed 10 Tera floating-point operations per second (TFLOPS). The GPU can process large amounts of data in parallel in the form of single instruction multiple data (SIMD) through its unique hardware architecture, which greatly increases the computing speed of artificial intelligence algorithms. This increased computing speed, in turn, makes artificial intelligence algorithms widely used (Topa et al., 2011a; Topa et al., 2011b). Thanks to the powerful computing performance of GPU platform, a GPU and GA combined structure was applied to solve the GA in this paper. The GPU parallelization technology was used to improve the convergence rate and convergence quality of the algorithm while reducing the calculation time to ensure that the proposed method can potentially be applied to practical projects. Currently, there are some similar works about the parallelized GA algorithms on GPU platforms (Tsutsui and Fujimoto, 2009; Jaros, 2012; Luo et al., 2017). In (Tsutsui and Fujimoto, 2009), a standard quadratic assignment problem was solved by GA on a GPU platform parallelized. The results showed that the GPU can accelerate the quadratic assignment problem with GA effectively. Moreover, multiple GPUs are applied to improve the performance for Gas on a knapsack problem in (Jaros, 2012). In (Luo et al., 2017), the GPU accelerated GA/MLP algorithms are applied to extract and classify the features of electrical signals of neural systems. These indicates the voltage optimization problem is potential to be solved by the GA on GPU platform. In this paper, an improved GA was used to solve the proposed optimization model of the distribution network. This work is a try to apply the parallelized GPU solved GA algorithms for the voltage optimization problem in distribution network.

The major contributions of this paper are listed as follows:

1) An optimization model was proposed to coordinate the different types of operational resources to maximize the resilience of the distribution network. Power flow constraints were also considered in the proposed model.

2) A parallel GA was proposed to solve the proposed model on a GPU platform. The solving performance was improved by the proposed method and has the potential to be applied in practical projects.

3) The critical loads in the distribution network can be reliably supplied with power using the proposed model in this study. Multiple operational targets can be coordinated in the proposed model.

The remainder of this paper is organized as follows: Modeling Typical Reactive Power Compensation Devices presents the models for various kinds of resources. Voltage Optimization Model in Distribution Network presents an optimization model of the distribution network, and describes the large population genetic algorithm and the parallel computing architecture of the GPU in detail. Then, in Case Studies, IEEE 33-and 118-bus systems are tested, and the results demonstrate the effectiveness of the proposed methods. Finally, Conclusion draws the conclusions in this study.

Modeling Typical Reactive Power Compensation Devices

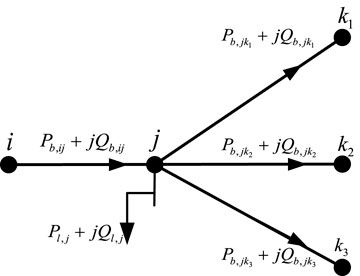
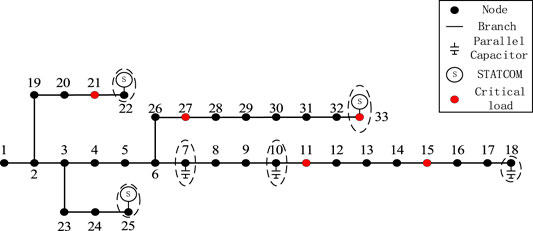
As shown in Figure 1, after extreme natural events, such as typhoons, snow disasters and storms, distribution networks may lose power supply from bulk power systems. Critical loads such as hospitals, government agencies, and automatic devices associated with the operation of power systems are directly connected to the distribution networks. Once the power supply to these critical loads is lost, the emergency repair and restoration speed of the power systems will be affected and reduced. Moreover, cascading failures may be occurred due to the lost of these critical loads. To ensure a stable power supply of critical loads after extreme natural events, it is necessary to dispatch all types of controllable operational resources in the distribution networks to regulate bus voltages and maintain the system frequency. Modeling these operational resources is an essential task for the proposed optimization model in this paper.

FIGURE 1

FIGURE 1. Condition of distribution network after extreme natural events.

Capacitor Banks

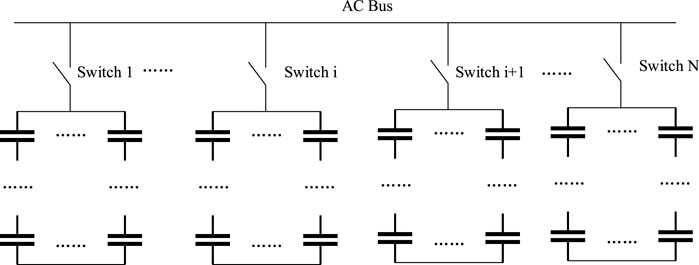
CBs are the cheapest reactive power compensation devices in power systems. The CB is consisted of several group of capacitors in both serial and parallel connection as shown in Figure 2.

FIGURE 2

FIGURE 2. Structure of the CBs.

Each group of capacitors can be connected and disconnected from the power systems by the status of the switch. In this way, the CB is a kind of ON/OFF controlled device and can be modeled as a 0/1 variable in mathematic models.

$Q_i^{C,out}=Q_C{\left(\frac{U_i}{U_N}\right)}^2{N}_C^i(1)$

$0\le N_C^i\le N_{C\max }^i,\forall i\in {\mathrm{\Omega }}_C(2)$

where $Q_i^{C,out}$ is the output reactive power of the CB at bus i. The $U_i$ represents the voltage at bus i and $U_N$ represents the nominal voltage. ${\Omega }_C$ is the set of nodes where the capacitor banks are arranged, $Q_C$ is the rated output reactive power of each group capacitors under the nominal voltage. $N_C^i$ is the number of switches to be closed to active the capacitors. $N_{C\max }^i$ is the upper limit of the number of closed switches and is determined by the group number of CBs.

Line Voltage Regulator

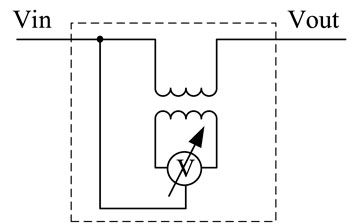
The LVR is consisted of a transformer and several solid-state switches as shown in Figure 3. The LVR could regulate the bus voltage to several setpoints with a fixed step, such as 2.5%, around the nominal voltage. It is achieved by changing the status of the solid-state switches to change the ratio of the transformer connected with the bus.

FIGURE 3

FIGURE 3. Structure of the LVR.

In this way, the voltage of the bus connected with LVR can be modeled as a positive discrete variable in mathematic models.

$U_i=U_0+N_{LVR}^i{U}_{St}^i(3)$

$-N_{LVR\max }^i\le N_{LVR}^i\le N_{LVR\max }^i,\forall i\in {\mathrm{\Omega }}_{LVR}(4)$

where ${\Omega }_{LVR}$ is the set of nodes where the LVR is arranged, $U_i$ represents the voltage of bus i, $U_0$ is the nominal bus voltage, $U_{St}^i$ is the voltage step for the LVR installed at bus i, $N_{LVR}^i$ is the setpoint for the LVR at bus i and is a discrete variable. $N_{LVR\max }^i$ is the limit for the setpoint of LVR.

D-STATCOM

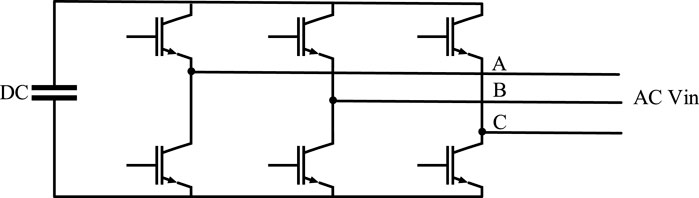
D-STATCOM could compensate the reactive power with fast response and high accuracy. It is consisted of a full bridge power converter and could adjust its output reactive power according to the operation commands as shown in Figure 4. Different from the CB and LVR, D-STATCOM can be modeled as a continuous variable in mathematic models.

$Q_i^{S,out}=Q_S^i(5)$

$P_i^{S,out}=0(6)$

Where $Q_i^{S,out}$ represents the output reactive power of D-STATCOM installed at node i. $Q_S^i$ represents the reactive output power of D-STATCOM for bus i. $P_i^{S,out}$ represents the output active power of D-STATCOM installed at node i.

FIGURE 4

FIGURE 4. Structure of the D-STATCOM.

All of these resources need to be coordinated to regulate the voltages of the distribution power systems.

Voltage Optimization Model in Distribution Network

Optimization Model

Determining the power flows in a distribution network is an important task for the optimization of distribution networks. The radial structure is the most common topology for practical distribution networks, as shown in Figure 5. The Distflow equation can be applied to determine the power flows in the radial distribution networks as follows (Baran and Wu, 1989),

$P_{l,j}=P_{b,ij}-{\displaystyle \sum _{k\in S\left(j\right)}(P_{b,jk}+\frac{P_{b,jk}^2+Q_{b,jk}^2}{U_k^2}{R}_{jk}),}(7)$

$Q_{l,j}=Q_{b,ij}-{\displaystyle \sum _{k\in S\left(j\right)}(Q_{b,jk}+\frac{P_{b,jk}^2+Q_{b,jk}^2}{U_k^2}{X}_{jk}),}(8)$

$U_j^2=U_i^2-2(P_{b,ij}{R}_{ij}+Q_{b,ij}{X}_{ij})+(R_{ij}^2+X_{ij}^2)\frac{P_{b,ij}^2+Q_{b,ij}^2}{U_i^2},(9)$

where $k\in S\left(j\right)$, the set S(j) refers to the set of child nodes of node j.

FIGURE 5

FIGURE 5. Radial network with active power flow.

The objectives of the proposed optimization model network are to minimize the active power loss, voltage deviations of buses, and operational costs by dispatching controllable voltage regulating devices. It includes three main objectives as follows,

1. Bus voltage: This is one of the most important targets for ensuring a stable power supply to critical loads. Due to the fluctuating output power of renewable resources, controllable devices need to respond to fluctuating output power in a short time to reduce voltage deviations.

2. Active power loss: The energy capacity of energy storage systems is limited, and the distributed power generation is random. To maintain power supply for as long as possible, it is necessary to reduce the active power loss of the distribution networks.

3. Cost of devices: Compared to D-STATCOM, capacitor banks have smaller operational costs. To reduce the total cost of the distribution network economy, capacitor banks will be dispatched preferentially.

The optimization model of the distribution network is proposed as follows,

$\underset{Q_S^1,\mathrm{...},Q_S^m,N_C^1,\mathrm{...},N_C^m}{\min }{\gamma }_v{C}^{VQ}+{\gamma }_p{C}^{ploss}+{\gamma }_c{C}^{\cos t}.(10)$

such that

$C^{ploss}={\displaystyle \sum _{(i,j)\in Nd}\frac{P_{b,ij}^2+Q_{b,ij}^2}{U_j^2}{R}_{ij}}(11)$

$C^{VQ}={\displaystyle \sum _{i\in M}{(U_i-U_{ref})}^2}(12)$

$C^{\cos t}={\lambda }_c{\displaystyle \sum _{i\in \mathrm{\Omega }\cap {\mathrm{\Omega }}_S}{\left(Q_S^2\right)}^2}(13)$

$P_{l,j}=P_{b,ij}-{\displaystyle \sum _{k\in S\left(j\right)}(P_{b,jk}+\frac{P_{b,jk}^2+Q_{b,jk}^2}{U_k^2}{R}_{jk})},\forall j\in Nd(14)$

$Q_{l,j}=Q_{b,ij}-{\displaystyle \sum _{k\in S\left(j\right)}(Q_{b,jk}+\frac{P_{b,jk}^2+Q_{b,jk}^2}{U_k^2}{X}_{jk})},\forall j\in Nd(15)$

$\begin{array}{l}{U}_j^2=U_i^2-2(P_{b,ij}{R}_{ij}+Q_{b,ij}{X}_{ij})+(R_{ij}^2+X_{ij}^2)\frac{P_{b,ij}^2+Q_{b,ij}^2}{U_i^2}\\ \forall (i,j)\in Nd\end{array}(16)$

$Q_{l,i}=Q_{l,i}^c-Q_{l,i}^{com},\forall i\in \mathrm{\Omega }(17)$

$Q_{l,i}^{com}=Q_S^i+Q_C{\left(\frac{U_i}{U_N}\right)}^2{N}_C^i,\forall i\in \mathrm{\Omega }(18)$

$U_{ref}-\xi \le U_i\le U_{ref}+\xi ,\forall i\in Nd(19)$

$-Q_{S\max }^i\le Q_S^i\le Q_{S\max }^i,\forall i\in {\mathrm{\Omega }}_S,(20)$

$0\le N_C^i\le N_{C\max }^i,\forall i\in {\mathrm{\Omega }}_C,(21)$

and the constrains as in (Eqs. 1–7).

Where N_d is the set of nodes of the distribution network, M is the set of critical nodes, $\Omega$ is the set of nodes where the voltage regulation devices are arranged, ${\Omega }_S$ is the set of nodes where the D-STATCOM is arranged, ${\Omega }_C$ is the set of nodes where the capacitor banks are arranged, $C^{ploss}$ is the active power loss of the distribution network, $C^{VQ}$ is the bus voltage offset of critical loads, $C^{\cos t}$ is the D-STATCOM and CBs operation cost, and ${\gamma }_p,{\gamma }_v,{\gamma }_c$ are the weight coefficients. The LVR is installed at the root node of the distribution network and the voltage of the root bus can be controlled to several discrete values as constrained by Eqs. 3, 4. Constraint (11) represents the active power loss of the distribution network, which is equal to the summation of the active power loss in all branches of the distribution network. Constraint (12) represents the bus voltage deviations of the critical loads, which represent the voltage quality of critical loads. The bus voltage deviations can be calculated based on the bus voltage and reference voltage. The reference voltage is related to the demands of critical loads and is set to 1 p.u. in most cases. Constraint (13) represents the operational costs associated with the operations of the D-STATCOMs, which are related to the reactive power output of the D-STATCOMs. Constraints (14–16) are the Distflow equations. Constraint (17) represents the actual reactive power load of the node $i$, which is related to the reactive power generated by the voltage regulation devices. Constraint (18) represents the reactive power generated by the voltage regulation devices. The reactive power output of the capacitor banks is related to the number of groups and the bus voltage of the corresponding node. Constraint (19) guarantees that the voltage of each node meets the operating standards of distribution networks, $U_{ref}$ represents the nominal voltage for all buses and $\xi$ is commonly set to 0.1 p.u. This constraint ensures the voltage deviations for all buses are within secured region. The voltage deviations on the critical loads can be minimized by the objective function described in Eq. 12. Constraint (20) represents the upper and lower limits of the reactive power output of the D-STATCOM at node i. Constraint (21) represents the upper and lower limits of the number of capacitor banks that can be switched at node i.

Improved Genetic Algorithm

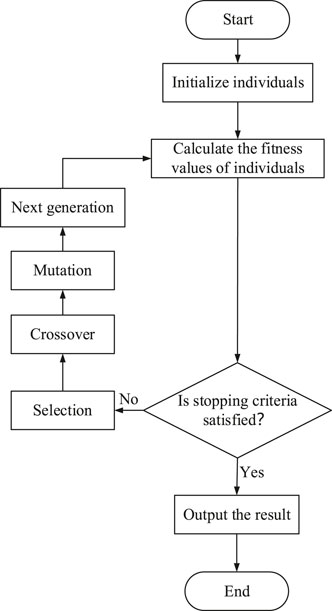
As shown in Figure 6, the standard GA consists of the following parts: population initialization, code, fitness function, selection operator, crossover operator, and mutation operator.

FIGURE 6

FIGURE 6. Calculation procedure of GA.

The current mainstream coding methods include binary coding and real number coding. Although binary encoding is simple to operate and can prove the convergence of GA through the mode theorem, The hamming cliff problem is still existed and the binary variable takes up a lot of storage. To avoid these problems, the real number encoding method was chosen in this study.

Population Initialization

Although the GA is widely used to solve various types of optimization model problems, the performance of the standard GA is not good enough to be applied in practical projects that have a large number of variables and strong nonlinear characteristics as an MINLP problem. The convergence quality of the standard GA is poor and it easily converges to local optimal solutions. Population size is the main factor that determines the convergence rate and convergence quality of the GA. When the population size is small, the diversity of individuals is insufficient, and the search space is small. In particular, for the optimization model with a large number of variables, the solution space of the initial individuals covered is limited. Once an individual obtains a local optimal solution, majority of individuals will converge to the solution after several iterations of evolution, and it will be difficult to jump out of the local optimal solution by the operation of the crossover or mutation operator, which results in the prematurity phenomenon. In addition, the penalty function leads to the degradation phenomenon in the early stage of the iteration, which significantly reduces the evolution speed.

Increasing the population size can increase the diversity of the individuals, making the initial solution cover a larger area. This initial solution not only restrains the degradation of the individuals in the early iteration, but also improves the convergence rate, and expands the solution space of the individuals covered. This, in turn, significantly improves the search ability of the GA. Consequently, there is a high probability of obtaining a global optimal solution.

Fitness Function

The fitness function is essential to the performance of the GA, which evaluates the excellence of an individual. The fitness function is closely related to the objective function of the optimization model, whereas the constraints in the optimization model cannot be neglected. Hence, the fitness function will be constituted by two parts: the first part is the objective function written in Eq. 10, and the other part is the penalty function established to satisfy the constraints. The fitness function can be described using the following equation.

$f=\frac{1}{{\gamma }_p{C}^{ploss}+{\gamma }_v{C}^{VQ}+{\gamma }_c{C}^{\cos t}+{\lambda }_u{\displaystyle \sum _{i\in Nd}\frac{\mathrm{\Delta }{U}_i^2}{{\left(U_{\max }-U_{\min }\right)}^2}}}(22)$

Where ${\lambda }_u$ is the coefficient of penalty function, is described as:

$\mathrm{\Delta }{U}_i=\{\begin{array}{l}{U}_{\max }-U_i,\hfill \\ 0,\hfill \\ U_{\min }-U_i,\hfill \end{array}\begin{array}{c}if\\ if\\ if\end{array}\begin{array}{c}\\ \\ \end{array}\begin{array}{l}{U}_i>U_{\max }\hfill \\ U_{\min }\le U_i\le U_{\max }\hfill \\ U_i<U_{\min }\hfill \end{array}(23)$

The most common selection operators are the roulette, tournament, and elite methods. In this study, the selection operator is composed of the tournament method combined with the elite method to ensure convergence of the algorithm. In addition to good time complexity, the tournament method has a greater probability of selecting better individuals than the roulette method.

Crossover and Mutation Operation

The crossover operation is a search process. Individuals can gradually approach the global optimal solution with the crossover operation. Because the coding method is based on real number coding, the simulated binary crossover (SBX) was selected as the crossover operator. This can be described by the following equations.

$c_1=0.5[(1+\beta )p_1+(1-\beta )p_2],(24)$

$c_2=0.5[(1-\beta )p_1+(1+\beta )p_2],(25)$

where is calculated as:

$\beta =\{\begin{array}{l}{\left(2u_c\right)}^{1/({\eta }_c+1)}{u}_c\le 0.5\\ {\left(\frac{1}{2(1-u_c)}\right)}^{1/({\eta }_c+1)}{u}_c>0.5,\end{array}(26)$

$p_1,p_2$ are the parents to be crossed; $c_1,c_2$ are the offspring generated by the cross operation; $\beta$ is the spread factor; $u_C$ is a random number between 0 and 1; ${\eta }_c$ is the cross-distribution index. From Eqs. 18–20, it can be seen that the difference between the values of the offspring and the parent is inversely proportional to ${\eta }_c$, which affects the convergence rate and the convergence precision of the GA. The standard GA is usually set ${\eta }_c=2$ to maintain the balance of the convergence precision and convergence rate. However, in the early stage of evolution, a smaller ${\eta }_c$ would lead to larger individual change steps to improve the convergence rate. In the later stage of evolution, when the population has gathered near the global optimal solution, more attention is paid to the convergence accuracy, and a larger ${\eta }_c$ can make the search more accurate. In addition, due to the differences in variable types, such as 0/1 variables and continuous variables, the value of the cross-distribution index needs to be set separately. Hence, the value of the cross-distribution index before $i_{iter}$ is ${\eta }_{c,0/1}$, ${\eta }_{c,conti}$, and the value of the cross-distribution index after $i_{iter}$ is ${\eta }_{c,0/1}^{\text{'}}$, ${\eta }_{c,conti}^{\text{'}}$.

The mutation operation aims to avoid premature convergence of solutions by expanding the existing search space. A polynomial mutation was selected as the mutation operator. This can be described by the following equation.

${\nu }_k^{\text{'}}={\nu }_k+\delta (u_k-l_k),(27)$

Where $\delta$ is calculated as

$\delta =\{\begin{array}{l}{[2u_m+(1-2u_m){(1-{\delta }_1)}^{{\eta }_m+1}]}^{1/({\eta }_m+1)}\text{,}{u}_m\le 0.5\\ 1-{[2(1-u_m)+2(u_m-0.5){(1-{\delta }_2)}^{{\eta }_m+1}]}^{1/({\eta }_m+1)}\text{,}{u}_m>0.5.\end{array}(28)$

The ${\delta }_1,{\delta }_2$ is described as:

${\delta }_1=({\nu }_k-l_k)/(u_k-l_k),(29)$

${\delta }_2=(u_k-{\nu }_k)/(u_k-l_k),(30)$

where ${\nu }_k^{\text{'}}$ is the offspring generated by the mutation operation, ${\nu }_k$ is the parent to be mutated, $u_k$ is the upper limit of the variable k, $l_k$ is the lower limit of the variable k, $\delta$ is the coefficient of variation, $u_m$ is a random number between 0 and 1, and ${\eta }_m$ is the variation distribution index. Similar to the crossover operation, the variation distribution index also needs to be set separately. Before $i_{iter}$, the value of the cross-distribution index is ${\eta }_{m,0/1}$, ${\eta }_{m,conti}$ and after i_iter, the value of the cross-distribution index is ${\eta }_{m,0/1}^{\text{'}}$, ${\eta }_{m,conti}^{\text{'}}$.

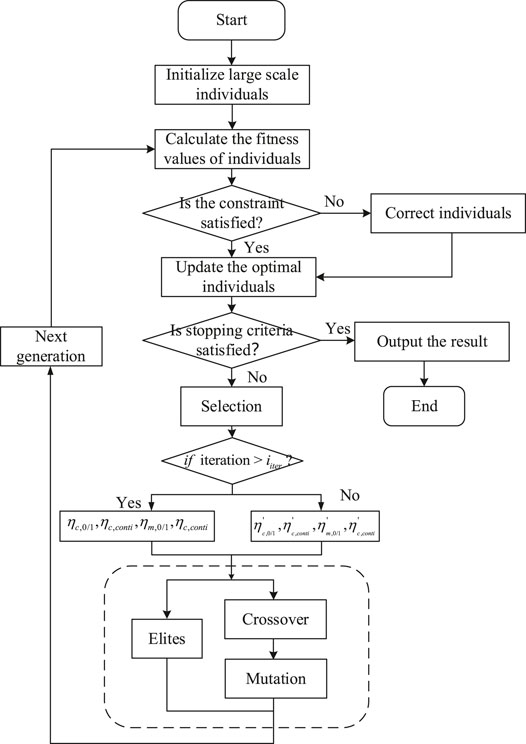
The calculation procedure for the improved GA is illustrated in Figure 7. Modifying the individuals that do not meet the constraints, preserving the optimal solution of each iteration and setting the distribution index by stages are added.

FIGURE 7

FIGURE 7. The calculation procedure of improved GA.

Parallel Computing Structure of GPU

Although increasing the population will effectively improve the performance of the algorithm, the population size is generally set from 50 to 100 due to the linear increase in computation time. The typical time intervals are several seconds or minutes depending on the control systems of the distribution networks, which require that the solving time of the optimization model for the distribution networks cannot be too long to update the operation commands. Considering that the calculation time of the fitness function takes up to 90% of the total calculation time for the GA algorithm, which is not a logical and temporal correlation between individuals, it is essential to reduce the calculation time of fitness functions in parallel computing to make the GA algorithm available for practical projects.

At present, artificial intelligence algorithms, such as deep learning and reinforcement learning, are widely used in various fields. To take advantage of AI algorithms, a large amount of data is required to train the model. Hence, new structures of computing systems, such as GPUs and field programmable gate arrays (FPGAs), that can quickly process massive data parallelly, have been developed in recent years.

The GPU has a unique hardware structure. Compared with the CPU, the GPU abandons a large number of storage and control units to configure additional computing units. Hence, compared to the CPU, which is good at processing complex logic operations, GPUs are better at processing large amounts of data with the same instructions. These computing units are called streaming processors (SPs). Multiple SPs form a streaming multiple processor (SM). Each SM has an independent share memory, and all SMs share the global memory and constant memory. Thus, the data in different SMs can be shared. When solving a GA on a GPU platform, each individual can be assigned to different computing cores for parallel computing, and the population size can be set to a larger value than a CPU platform. As a result, increasing the population size of the GA has less effect on the computing time than the CPU platform.

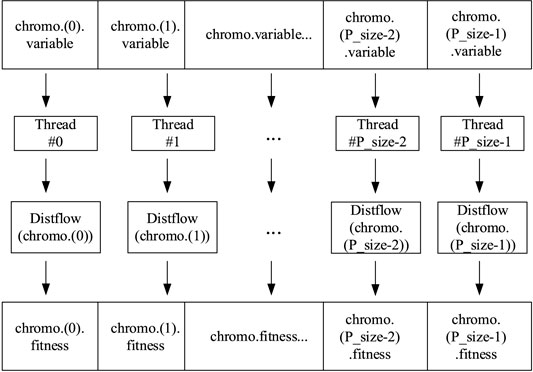
Figure 8 shows the process of using a GPU to accelerate the GA. The data of individuals are transmitted from the host (CPU side) to the device (GPU side), and then a large number of threads are opened on the device to be prepared for calculation. Each thread is responsible for calculating the fitness function of an individual. All the fitness functions of individuals are calculated in parallel mode on the GPU. Finally, the results were transmitted from the device back to the host.

FIGURE 8

FIGURE 8. Calculation procedure of fitness function on GPU platform.

Case Studies

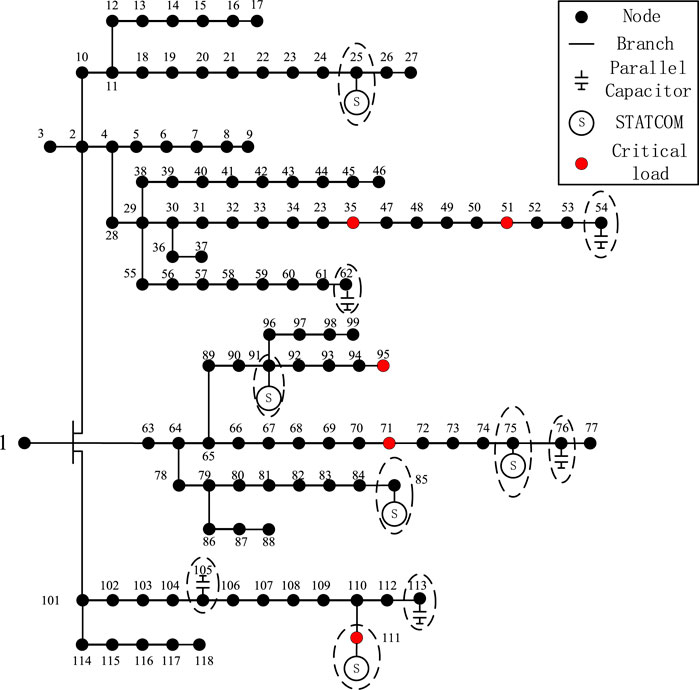
To verify the effectiveness of the proposed optimization model and solving method, two distribution network systems, IEEE 33-bus and IEEE 118-bus as shown in Figure 9 and 10 respectively, were selected for case studies. The computing system includes an Intel i9-9900K CPU, Nvidia 2080 Ti GPU, 32GB RAM, 12GB GPU RAM, and CUDA version 10.2.

FIGURE 9

FIGURE 9. IEEE 33-bus distributed network topology.

FIGURE 10

FIGURE 10. IEEE 118-bus distributed network topology.

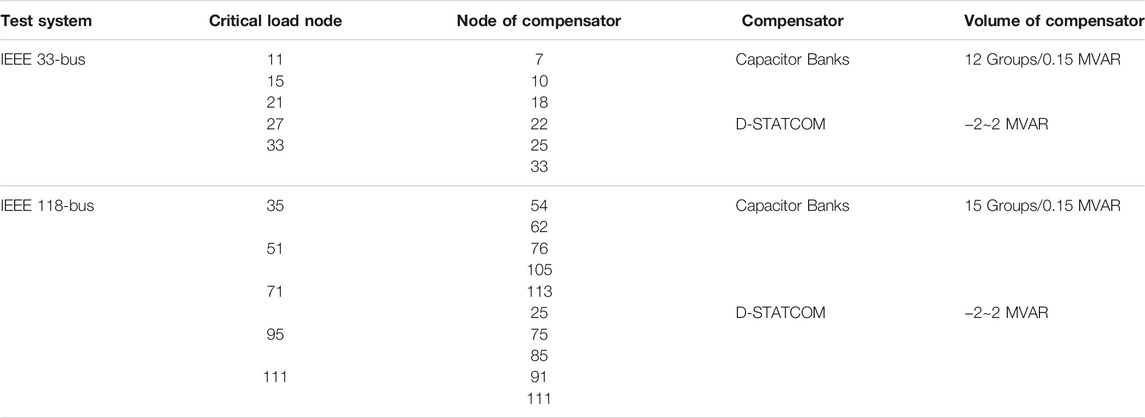
Table 1 shows the configuration of the test systems, including the nodes of the critical load and compensators, as well as the type and capacity of the compensators. The parameters of the GA are selected as follows: $n\_generation=500$, crossover probability $P_c=0.85$, mutation probability $P_m=0.1$, $i_{iter}=20$, ${\eta }_{c,0/1}=3$, ${\eta }_{c,conti}=6$, ${\eta }_{m,0/1}=1$, ${\eta }_{m,conti}=3$, ${\eta }_{c,0/1}^{\text{'}}=5$, ${\eta }_{c,conti}^{\text{'}}=9$, ${\eta }_{m,0/1}^{\text{'}}=2$, ${\eta }_{m,conti}^{\text{'}}=5$.

TABLE 1

TABLE 1. Configuration of test systems.

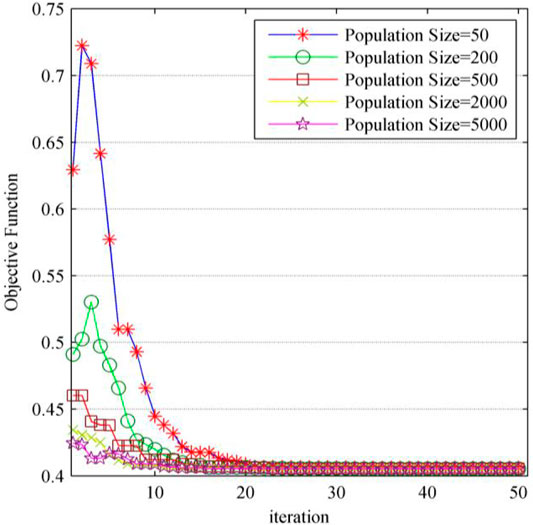
When the population size is 50, the solution results are poorly convergent and the maximum standard deviation of the variables is 0.4. Although the standard deviation of the objective function is 0.00064, the binary (discrete) type variables cannot converge to a unique solution. Then, the population size was increased from 50 to 5,000, while the other parameters remained the same. The optimization model is solved again, and new solution results are obtained with different population sizes.

Figure 11 shows a comparison of the convergence speed of the algorithm with different population sizes. This indicates that as the population size increases, the initial solution and convergence speed of the algorithm become better. When the population size is 5,000, the convergence of the solution is completed at the 18th generation, while the population size of 50 achieves convergence of the solution at the 35th generation. In addition, the values of the objective function will be smaller when the population size is larger. This means that better optimized results can be achieved. When the population size increases to 5,000, the convergence quality of the algorithm is improved. The binary (discrete) type variables can converge to a unique solution, while the maximum standard deviation of continuous variables is 0.00088, and the objective function can converge to the same value. The results of control variables of CBs installed at bus 7, 10, 18 are 5, 2, and 1, respectively. The output reactive power of D-STATCOMs installed at bus 22, 25 and 33 are 0.08MVar, 0.283MVar, and 0.543MVar, respectively.

FIGURE 11

FIGURE 11. Comparison of consequence speeds with different population size in IEEE 33-bus system.

However, increasing the population size will greatly increase the calculation time of the algorithm, as mentioned before. When the population size is increased from 50 to 5,000, the running time is also changed from 2.18 to 180.69 s, which is an increase of 90 times.

Table 2 shows the comparison of computing time on both the GPU and CPU platforms with different population sizes in the IEEE 33-bus and IEEE 118-bus system. The GA algorithm computed on the GPU platform has been revised to parallelized to enhance the computing performance. For the IEEE 33-bus system, on the GPU platform, the growth in the population size had almost no effect on the running time. Compared with the population size of 50 and the population size of 5,000, the difference in calculation time is only 1.15 s. This means that within a certain population size range, the larger the population size, the better the acceleration effect of the GPU. The algorithm is accelerated by parallel computing on the GPU platform, which greatly reduces the running time and effectively improves the practicality of the algorithm. In testing the IEEE 33-bus system, increasing the population size of the GA can effectively enhance the convergence ability of the algorithm. The long computing time caused by the large population size was effectively reduced through parallel computing on the GPU platform.

TABLE 2

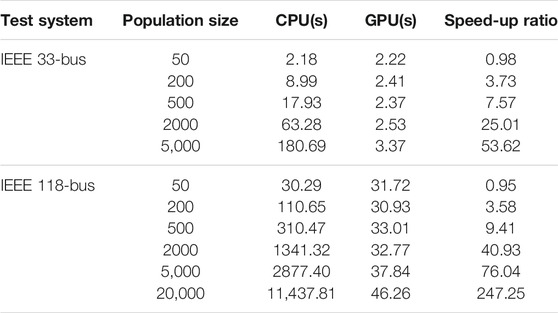
TABLE 2. Computing time of CPU platform and GPU platform with different populations (IEEE 33-bus system and IEEE-118-bus system).

Furthermore, the IEEE 118-bus system was emulated to test the effect of the method and the speedup effect of calculating on the GPU platform in solving the optimization model of the larger scale distribution network. As shown in Figure 12, in the optimization model of the larger scale distribution network, increasing the population size can also improve the convergence speed of the algorithm. Consider the IEEE 118-bus system contains more buses than the IEEE 33-bus system, the maximal size of population is set to 20,000 as shown in Figure 12 to improve the convergence performance. The results of the population size under 20,000 is marked as the line with rhombus. When the population size is 20,000, binary (discrete) type variables of the result can converge to a unique solution, and the maximum standard deviation of the continuous variables is only 0.011. When the population size is 50, the binary (discrete) type variables cannot complete convergence, and the maximum standard deviation of continuous variables is 0.137. The results of control variables of CBs installed at bus 54, 62, 76, 105, and 113 are 11, 13, 4, 10, and 10, respectively. The output reactive power of D-STATCOMs installed at bus 25, 75, 85, 91, and 111 are 0.32MVar, 0.23MVar, 0.17MVar, 0.36MVar 0.18MVar, and 0.44MVar, respectively. Table 2 also shows in the IEEE 118-bus system, the calculation time for different population sizes on the CPU and GPU platforms. It can be seen that in the IEEE 118-bus system, the speedup effect was further improved, and the speedup ratio reached 247 times when the population size was 20,000. The results show that the effect of speedup in solving the optimization model of a larger scale distribution network will be more powerful.

FIGURE 12

FIGURE 12. Comparison of consequence speeds with different population size in IEEE 118-bus system.

Finally, Table 3 shows the bus voltage comparison of the critical loads before and after optimization. By dispatching the voltage regulation devices, the voltages of the critical loads are increased, which guarantees the stable and secure operation of the critical loads. Meanwhile, the active power loss of the system was reduced. The active power loss of the IEEE 33-bus system was reduced from 0.2056 to 0.1353 MW, which is a decrease of 34.14%. The active power loss of the IEEE 118-bus system was reduced from 1.289 to 0.9236 MW, which is a decrease of 28.34%.

TABLE 3

TABLE 3. The voltage comparison of the critical loads before and after optimization.

Conclusion

This paper proposes an optimization model for distribution networks to dispatch controllable operational resources, which aim to improve the resilience of the distribution networks after extreme natural events. A GPU-based parallelized GA method was proposed to solve the proposed MINLP type model for the operations. A large population size of the GA, and setting the value of the distributed index by two stages can improve the convergence quality and consequence speed of the GA. Meanwhile, the GPU can also accelerate solving of the fitness function of the GA method with large populations, which effectively reduces the excessive calculation time. Finally, case studies with IEEE 33-bus and 118-bus were carried out to show that the proposed GA method can be solved effectively and accelerated to enhance the resilience of distribution networks. The GPU platform can improve the calculation performance and facilitate GA algorithms to be applied in practical projects. Further work will consider adding the electrical vehicles to the optimization model, whose limited energy needs to be allocated on multiple time scales to achieve the best optimization results.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

LL-Original paper draft, PI of the support funding CL-Case studies, GA implementation.

Funding

This research was funded by National Natural Science Foundation of China, grant number 52077045 and Open Fund of State Key Laboratory of Operation and Control of Renewable Energy and Storage Systems (China Electric Power Research Institute, DG80-20-001).

Conflict of Interest

Author CL was employed by the company Guangzhou Power Supply Bureau of Guangdong Power Grid Corporation.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

Thanks to the discussions with Dr. Xuewei Pan and his suggestions on this paper.

References

Baran, M., and Wu, F. F. (1989). Optimal Sizing of Capacitors Placed on a Radial Distribution System. IEEE Trans. Power Deliv. 4 (1), 735–743. doi:10.1109/61.19266

CrossRef Full Text | Google Scholar

de la Calle, F. J., Bulnes, F. G., Garcia, D. F., Usamentiaga, R., and Molleda, J. (2015). A Parallel Genetic Algorithm for Configuring Defect Detection Methods. IEEE Latin Am. Trans. 13 (5), 1462–1468. doi:10.1109/tla.2015.7112003

CrossRef Full Text | Google Scholar

Deeb, N., and Shahidehpour, S. M. (1990). Linear Reactive Power Optimization in a Large Power Network Using the Decomposition Approach. IEEE Trans. Power Syst. 5 (2), 428–438. doi:10.1109/59.54549

CrossRef Full Text | Google Scholar

Delfanti, M., Granelli, G. P., Marannino, P., and Montagna, M. (2000). Optimal Capacitor Placement Using Deterministic and Genetic Algorithms. IEEE Trans. Power Syst. 15 (3), 1041–1046. doi:10.1109/59.871731

CrossRef Full Text | Google Scholar

Enacheanu, B., Raison, B., Caire, R., Devaux, O., Bienia, W., and HadjSaid, N. (2008). Radial Network Reconfiguration Using Genetic Algorithm Based on the Matroid Theory. IEEE Trans. Power Syst. 23 (1), 186–195. doi:10.1109/TPWRS.2007.913303

CrossRef Full Text | Google Scholar

Gao, H., Chen, Y., Xu, Y., and Liu, C.-C. (2016). Resilience-Oriented Critical Load Restoration Using Microgrids in Distribution Systems. IEEE Trans. Smart Grid 7 (6), 2837–2848. doi:10.1109/TSG.2016.2550625

CrossRef Full Text | Google Scholar

Gonzalez Bulnes, F., Usamentiaga, R., Fernando Garcia, D., and Molleda, J. (2013). A Parallel Genetic Algorithm for Optimizing an Industrial Inspection System. IEEE Latin Am. Trans. 11 (6), 1338–1343. doi:10.1109/tla.2013.6710381

CrossRef Full Text | Google Scholar

Grudinin, N. (1998). Reactive Power Optimization Using Successive Quadratic Programming Method. IEEE Trans. Power Syst. 13 (4), 1219–1225. doi:10.1109/59.736232

CrossRef Full Text | Google Scholar

Harik, G., Cantú-Paz, E., Goldberg, D. E., and Miller, B. L. (1999). The Gambler's Ruin Problem, Genetic Algorithms, and the Sizing of Populations. Evol. Comput. 7 (3), 231–253. doi:10.1162/evco.1999.7.3.231

PubMed Abstract | CrossRef Full Text | Google Scholar

Jaros, J. (2012). Multi-GPU Island-Based Genetic Algorithm for Solving the Knapsack Problem. In 2012 IEEE Congress on Evolutionary Computation. IEEE, 1–8. doi:10.1109/cec.2012.6256131

CrossRef Full Text | Google Scholar

Luo, W., Zhang, Z., Wen, T., Li, C., and Luo, Z. (2017). Features Extraction and Multi-Classification of sEMG Using a GPU-Accelerated GA/MLP Hybrid Algorithm. Xst 25 (2), 273–286. doi:10.3233/xst-17259

PubMed Abstract | CrossRef Full Text | Google Scholar

Mahmud, M. A., Hossain, M. J., and Pota, H. R. (2014). Voltage Variation on Distribution Networks with Distributed Generation: Worst Case Scenario. IEEE Syst. J. 8 (4), 1096–1103. doi:10.1109/jsyst.2013.2265176

CrossRef Full Text | Google Scholar

Mamandur, K. R. C., and Chenoweth, R. D. (1981). Optimal Control of Reactive Power Flow for Improvements in Voltage Profiles and for Real Power Loss Minimization. IEEE Power Eng. Rev.PER- PER-1 (7), 29–30. doi:10.1109/mper.1981.5511679

CrossRef Full Text | Google Scholar

Mohamed, M. A., Chen, T., Su, W., and Jin, T. (2019). Proactive Resilience of Power Systems against Natural Disasters: A Literature Review. IEEE Access 7, 163778–163795. doi:10.1109/access.2019.2952362

CrossRef Full Text | Google Scholar

Nicholson, H., and H. Sterling, M. (1973). Optimum Dispatch of Active and Reactive Generation by Quadratic Programming. IEEE Trans. Power Apparatus Syst. PAS-92 (2), 644–654. doi:10.1109/tpas.1973.293768

CrossRef Full Text | Google Scholar

Panteli, M., and Mancarella, P. (2015). Influence of Extreme Weather and Climate Change on the Resilience of Power Systems: Impacts and Possible Mitigation Strategies. Electric Power Syst. Res. 127, 259–270. doi:10.1016/j.epsr.2015.06.012

CrossRef Full Text | Google Scholar

Panteli, M., and Mancarella, P. (2015). The Grid: Stronger, Bigger, Smarter?: Presenting a Conceptual Framework of Power System Resilience. IEEE Power Energ. Mag. 13 (3), 58–66. doi:10.1109/MPE.2015.2397334

CrossRef Full Text | Google Scholar

Queiroz, L. M. O., and Lyra, C. (2009). Adaptive Hybrid Genetic Algorithm for Technical Loss Reduction in Distribution Networks under Variable Demands. IEEE Trans. Power Syst. 24 (1), 445–453. doi:10.1109/TPWRS.2008.2009488

CrossRef Full Text | Google Scholar

Swarup, K. S., and Yamashiro, S. (2002). Unit Commitment Solution Methodology Using Genetic Algorithm. IEEE Trans. Power Syst. 17 (1), 87–91. doi:10.1109/59.982197

CrossRef Full Text | Google Scholar

Topa, T., Karwowski, A., and Noga, A. (2011). Using GPU with CUDA to Accelerate MoM-Based Electromagnetic Simulation of Wire-Grid Models. Antennas Wirel. Propag. Lett. 10, 342–345. doi:10.1109/LAWP.2011.2144557

CrossRef Full Text | Google Scholar

Topa, T., Noga, A., and Karwowski, A. (2011). Adapting MoM with RWG Basis Functions to GPU Technology Using CUDA. Antennas Wirel. Propag. Lett. 10, 480–483. doi:10.1109/LAWP.2011.2154373

CrossRef Full Text | Google Scholar

Tsutsui, S., and Fujimoto, N. (2009). Solving Quadratic Assignment Problems by Genetic Algorithms with GPU Computation: a Case Study. In Proceedings of the 11th Annual Conference Companion on Genetic and Evolutionary Computation Conference: Late Breaking Papers, 2523–2530.

Google Scholar

Utkarsh, K., Ding, F., Jin, X., Blonsky, M., Padullaparti, H., and Balamurugan, S. P. (2021). A Network-Aware Distributed Energy Resource Aggregation Framework for Flexible, Cost-Optimal, and Resilient Operation. IEEE Trans. Smart Grid, 1. (early acess).

Google Scholar

Wang, P., Liang, F., Song, J., Jiang, N., Zhang, X., Guo, L., et al. (2020). Impact of the PV Location in Distribution Networks on Network Power Losses and Voltage Swings with PSO Analysis. CSEE J. Power Energ. Syst., 1. (early acess).

Google Scholar

Wang, Y., Chen, C., Wang, J., and Baldick, R. (2016). Research on Resilience of Power Systems under Natural Disasters-A Review. IEEE Trans. Power Syst. 31 (2), 1604–1613. doi:10.1109/tpwrs.2015.2429656

CrossRef Full Text | Google Scholar

Xing Chen, Xing., Xiao-Bang Xu, Kama., and Xu, Xiao-Bang. (2005). Automated Design of a Three-Dimensional Fishbone Antenna Using Parallel Genetic Algorithm and NEC. Antennas Wirel. Propag. Lett. 4, 425–428. doi:10.1109/lawp.2005.859384

CrossRef Full Text | Google Scholar