Mass Transport Limitations and Kinetic Consequences of Corn Stover Deacetylation

Alkaline pretreatment of herbaceous feedstocks such as corn stover prior to mechanical refining and enzymatic saccharification improves downstream sugar yields by removing acetyl moieties from hemicellulose. However, the relationship between transport phenomena and deacetylation kinetics is virtually unknown for such feedstocks and this pretreatment process. Here, we report the development of an experimentally validated reaction–diffusion model for the deacetylation of corn stover. A tissue-specific transport model is used to estimate transport-independent kinetic rate constants for the reactive extraction of acetate, hemicellulose and lignin from corn stover under representative alkaline conditions (5–7 g L⁻¹ NaOH, 10 wt% solids loadings) and at low to mild temperatures (4–70°C) selected to attenuate individual component extraction rates under differential kinetic regimes. The underlying transport model is based on microstructural characteristics of corn stover derived from statistically meaningful geometric particle and pore measurements. These physical descriptors are incorporated into distinct particle models of the three major anatomical fractions (cobs, husks and stalks) alongside an unsorted, aggregate corn stover particle, capturing average Feret lengths of 917–1239 μm and length-to-width aspect ratios of 1.8–2.9 for this highly heterogeneous feedstock. Individual reaction–diffusion models and their resulting particle model ensembles are used to validate and predict anatomically-specific and bulk feedstock performance under kinetic-controlled vs. diffusion-controlled regimes. In general, deacetylation kinetics and mass transfer processes are predicted to compete on similar time and length scales, emphasizing the significance of intraparticle transport phenomena. Critically, we predict that typical corn stover particles as small as ∼2.3 mm in length are entirely diffusion-limited for acetate extraction, with experimental effectiveness factors calculated to be 0.50 for such processes. Debilitatingly low effectiveness factors of 0.021–0.054 are uncovered for cobs—implying that intraparticle mass transfer resistances may impair observable kinetic measurements of this anatomical fraction by up to 98%. These first-reported quantitative maps of reaction vs. diffusion control link fundamental insights into corn stover anatomy, biopolymer composition, practical size reduction thresholds and their kinetic consequences. These results offer a guidepost for industrial deacetylation reactor design, scale-up and feedstock selection, further establishing deacetylation as a viable biorefinery pretreatment for the conversion of lignocellulosics into value-added fuels and chemicals.

Introduction

Lignocellulosic biomass has long been investigated as a renewable feedstock for the production of biofuels and bio-based chemicals. Modern biorefinery strategies employ chemical pretreatment steps to alter feedstock structure and composition in order to enhance downstream bioproduct yields (Mosier et al., 2005; Rollin et al., 2011; Yang et al., 2017). One such pretreatment is deacetylation, or the selective, reactive removal of enzyme-inhibiting (Palmqvist and Hahn-Hägerdal, 2000; Mills et al., 2009) acetyl functionalities from the hemicellulose component of herbaceous feedstocks such as corn stover (Chen et al., 2012; Chen et al., 2016). Deacetylation features advantages of mild temperature and ambient pressure chemical processing and occurs prior to mechanical refining (a combination termed DMR) and enzymatic saccharification (Chen et al., 2019). Corn stover DMR enables high sugar monomer concentrations (≤230 g L⁻¹) and subsequent ethanol titers (≤86 g L⁻¹) at substantial projected cost savings (Tao et al., 2012; Chen et al., 2016). Basic environments enhance deacetylation rates in aqueous media, and the treatment introduces nanoscale porosity via mesoscale plant tissue-loosening for increased enzyme accessibility (Lima et al., 2018). Lignin and small amounts of hemicellulose are also co-extracted under these conditions. Separately, extracted DMR lignin is a promising access point for co-valorization and has received recent literature attention (Karp et al., 2014; Katahira et al., 2016; Kruger et al., 2016; Rodriguez et al., 2017; Xu et al., 2020).

Nonetheless, little is known about the coupled chemistry and physics of deacetylation processes, particularly at the biomass particle scale where such phenomena are known to compete in other biorefinery steps (Luterbacher et al., 2013; Thornburg et al., 2020; Ciesielski et al., 2021). While biomass transport phenomena are typically discussed qualitatively (Viamajala et al., 2010), studies on alkaline deacetylation often only quantitatively emphasize end-of-experiment performance metrics such as liquor yield, molecular weight (MW) distribution or residual solids compositional analysis (Karp et al., 2014; Lima et al., 2018), which do not account for transient behaviors, such as diffusion or heat transfer, that occur throughout the course of reaction. Others have reported alkaline decomposition kinetics of lignin model compounds (Gierer et al., 1977; Shimizu et al., 2012; Shimizu et al., 2013), although these insights are not readily extensible to real biomass, where cell wall biopolymer assemblies and tissue pore structures at the nanoscale and mesoscale, respectively, heavily influence experimental kinetic measurements (Min et al., 2014; Lima et al., 2018). Indeed, given the complexity surrounding experimental diffusion measurements (Jakes et al., 2020), few reports attempt to quantify the significant mass or heat transfer effects that accompany deacetylation of real biomass (Costanza and Costanza, 2002), especially as they apply to complicated continuous reactor configurations such as packed corn stover beds (Sahayaraj et al., 2021) or twin-screw extruders (Morales-Huerta et al., 2021). Lastly, the vast majority of these studies employ whole (unsorted) corn stover as the feedstock, despite the known structural and compositional differences among its major anatomical fractions (Min et al., 2014), which are expected to imbue unique kinetic and physical transport properties.

Ultimately, the untangling of chemical kinetics from mass and heat transfer and from plant anatomy is paramount to reconcile laboratory reactor data, practical feedstock comminution targets, and engineering scaling principles in overall biorefinery process development (Ciesielski et al., 2021). Some of us have recently utilized a generalizable mesoscale modeling framework to determine the transport-independent kinetics of condensed-phase biomass fractionation processes, first demonstrated for the methanolysis of poplar hardwood (Thornburg et al., 2020). These models leverage feedstock-specific measurements of particle geometries and tissue microstructures to inform assumptions of mass transport phenomena, while experimental reactor temperature profiles capture the non-isothermality of such dynamic pretreatment systems. Batch reactor experiment campaigns using known biomass particle size ranges then enable the mathematical regression of kinetic rate parameters within non-isothermal reaction–diffusion simulations evaluated for representative particle sizes and pretreatment conditions.

Here, we extend this two-dimensional (2D) mesoscale modeling approach to the sodium hydroxide-mediated deacetylation of corn stover. We develop first-principled reaction–diffusion models (i) to calculate transport-independent, anatomically-specific kinetic rate parameters describing corn stover deacetylation and (ii) to identify practical particle size thresholds for kinetic vs. mass transfer control. These actionable, quantitative relationships connect key insights of corn stover anatomy with biorefinery reactor performance, informing new best practices for feedstock preparation, experimentation and scaling.

Experimental and Computational Methods

While brief descriptions are provided below, full details of feedstock preparation, batch kinetics, liquor analysis, imaging and computational techniques are included in Supplementary Material (SM).

Materials Preparation and Characterization

Unsorted (whole, WH) corn stover received from Idaho National Laboratory (INL) was manually separated into cob (CB), husk (HS) and stalk (SK) anatomical fractions, and each of the four fractions was milled with a 2-mm screen in a laboratory-scale Wiley mill. Kramer corn stover (KR) was cultivated on Kramer farm in Wray, Colorado, and prior to experimental use at the National Renewable Energy Laboratory (NREL), KR was Wiley milled through a 2-mm screen without additional sorting. Compositional analysis was performed for each milled fraction following standard NREL Laboratory Analytical Protocols (Sluiter et al., 2005; Sluiter et al., 2008b). Particle size measurements were collected via external analysis performed by Microtrac, Inc. for each corn stover sample, while data distributions were analyzed in MATLAB R2021a. Select particles were imaged via X-ray computed tomography (XCT) in three vertical segments while rotating a complete 360° revolution; resultant radiographs were dimensionally reconstructed before data processing and visualization using the open-source NREL Microstructure Analysis Toolbox, MATBOX (Cooper et al., 2016; Arganda-Carreras et al., 2017; Usseglio-Viretta et al., 2020; Pettersen et al., 2021; Sun et al., 2021; Usseglio-Viretta et al., 2022). Segmentation and characterization methods leverage threshold selection and denoising methods developed by others (Otsu, 1979; Buades et al., 2005; Villanova et al., 2013; Tanaka, 2021). See Supplementary Table S1 and SM methods discussion for details.

Batch Kinetics and Product Characterization

Batch reactor experiments were conducted with a 10 wt% solids loading (500 ± 5 mg feedstock) in 10-ml glass reactor vials placed in the center wells of an aluminum block subjected to temperature-regulated heating (40°C, 70°C and higher-temperature experiments) or cooling in an ice-water bath (4°C experiments). Final sodium hydroxide (NaOH) concentrations in the 5.00 mL total reaction volume were either 5.00, 7.00 or 9.00 g L⁻¹ (preliminary screening only). While some experiments were subjected to periodic vortexing, typical batch experiments remained unagitated for a prescribed reaction duration (0, 2, 5, 10, 20, 60 min or longer) before being quenched via vacuum filtration.

Upon neutralization, filtrate liquors were analyzed for total sugars (via 4% sulfuric acid hydrolysis), acetate (via sulfuric acidification) and soluble lignin (via dilution in water) by high-performance liquid chromatography (HPLC) following standard NREL Laboratory Analytical Protocols (Sluiter et al., 2008a; Sluiter et al., 2008b).

Computational Modeling

2D axisymmetric corn stover models were constructed and tetrahedrally meshed directly in COMSOL Multiphysics 5.6 for finite-element computational fluid dynamics (CFD) simulations. Kinetic rate coefficients were regressed to experimental batch reactor data via the COMSOL–MATLAB R2021a API using an iterative generalized least-squares estimation procedure. Initial guesses for coefficients were randomly perturbed by ±20% via an exterior function, and parameters were iteratively re-fit to prevent convergence of the algorithm onto local minima. Classical molecular dynamics (MD) simulations were conducted using CHARMM program (MacKerell et al., 1998; Hynninen and Crowley, 2014) along with SHAKE and PME algorithms (Darden et al., 1993; Kräutler et al., 2001) to estimate diffusion coefficients (see Supplementary Equation S1) in NaOH solution (Jorgensen et al., 1983) at 4–90°C for solutes xylan (Guvench et al., 2008; Hatcher et al., 2009) [degree of polymerization (DP) 1–5, 10], lignin (Orella et al., 2019; Vermaas et al., 2019) [DP 1–5, 10; see Supplementary Table S2 for decamer linkage details (Min et al., 2014)], and acetate (Vanommeslaeghe et al., 2010) and hydroxide anions.

Results and Discussion

Deacetylation Activity Benchmarking and Experimental Design

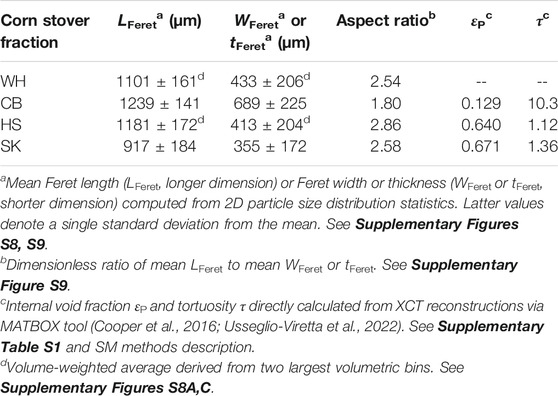
The first objective of this study is to determine suitable laboratory reaction conditions amenable to analytical measurements of individual corn stover components (i.e., acetate, xylan and lignin) within differential kinetic (i.e., <15 wt% extraction) regimes. Notably, the intended goal is not to maximize yield, but rather to identify reaction conditions that elucidate important kinetic and mass transport information. Key handles for such laboratory experiments include reactor volume, temperature, corn stover loading, NaOH concentration and agitation. A highly characterized NREL Kramer corn stover (KR) sample was selected for initial activity screening and selection of reaction conditions given its similarity in composition to whole (WH) corn stover received from INL and its anatomical fractions (CB, HS, SK) (Supplementary Table S3). As a preliminary trial set, KR deacetylation was examined at 10 wt% solids loading in 5–9 g L⁻¹ NaOH in 5 mL total reaction volume at 85–95°C for durations of up to 120 min (Chen et al., 2012; Tao et al., 2012; Chen et al., 2016; Katahira et al., 2016), with subsequent HPLC analysis conducted on soluble acetate, xylan and lignin products in the resultant vacuum-filtered liquor phase (Sluiter et al., 2008a); we note that structural glucan is not extractable for any corn stover feedstock under any condition reported here. Further, lignin extracted during the course of deacetylation is likely to be non-structural in nature, or possibly bound through lignin–carbohydrate complex ester linkages (akin to the ester cleavages required to remove acetate). However, alternate mechanisms such as de-etherification or de-esterification of structural lignin polymers are known to require significantly higher reaction temperatures (e.g., 270–300°C) than those studied here (Katahira et al., 2016). Results are summarized in Supplementary Figure S1. While NaOH concentration is monotonically related to overall component yield, each yield profile illustrates minimal time or temperature dependence, suggesting that deacetylation chemistries occur too rapidly at such conditions to allow for insightful kinetic measurements.

Hence, to slow observable reaction rates, KR was next screened at 4 and 20°C for 5–9 g L⁻¹ NaOH loadings with and without periodic vial vortexing (Supplementary Figure S2) to assess the impact of agitation on time-course yields for reaction times up to 30 min. Overall, yields of each acetate, xylan and lignin plateau around 20 min, with similar extents of extraction observed for 5 and 7 g L⁻¹ conditions and higher final yields for 9 g L⁻¹. Importantly, minimal differences are observed between vortexed and unagitated data sets (Supplementary Figure S2), implying that external (film) mass transfer at the exterior corn stover surface does not impact liquid-phase yield measurements at this reactor scale. This finding allows for important simplifications to particle-scale reaction–diffusion models developed and validated later in this study (vide infra).

From the initial KR trials, a final set of reaction conditions is selected for the primary study of WH corn stover deacetylation and that of its anatomical fractions, CB, HS and SK: each fraction is Wiley milled to <2 mm and evaluated at 500 mg loadings in 5 mL total reaction volume, without agitation, at initial NaOH concentrations (C_NaOH) of 5 and 7 g L⁻¹. Batch deacetylation is conducted at temperatures of 4, 40 and 70°C for batch reaction times of 0, 2, 5, 10, 20 and 60 min, after which the liquid phases are vacuum-filtered to quench the reaction. Initial feedstock compositions are determined using standard biomass compositional analysis protocols developed by NREL (Sluiter et al., 2005; Sluiter et al., 2008b), and maximum extractable components are gleaned from 60-min residence time experiments at each C_NaOH (Supplementary Table S3). Finally, anatomical fraction sorting data summarized in Supplementary Table S4 reveals the overall breakdown on a mass basis of the WH bulk feedstock as received.

Apparent Trends in Deacetylation Kinetics

Batch deacetylation was first evaluated for the WH feedstock at 4–70°C and 5–7 g L⁻¹ NaOH for residence times of 0–20 min. Individual component yields of acetate, xylan and lignin in the liquid phase are traced as a function of residence time and C_NaOH for a suite of reactions conducted at the 5-mL scale, and data are summarized in Figure 1 and Supplementary Figure S3. Additionally, given the rapid nature of deacetylation chemistries, apparent time-zero yields (i.e., upon instantaneous fluid–solid contact) are quantified for each C_NaOH and feedstock (Supplementary Table S5) to establish reactor “start-up” behavior, which practically manifests as the y-axis intercept on time-course yield plots (Figure 1, Supplementary Figure S3). These time-zero yields are also important for defining proper initial conditions for reaction–diffusion models developed later in this study (vide infra).

FIGURE 1

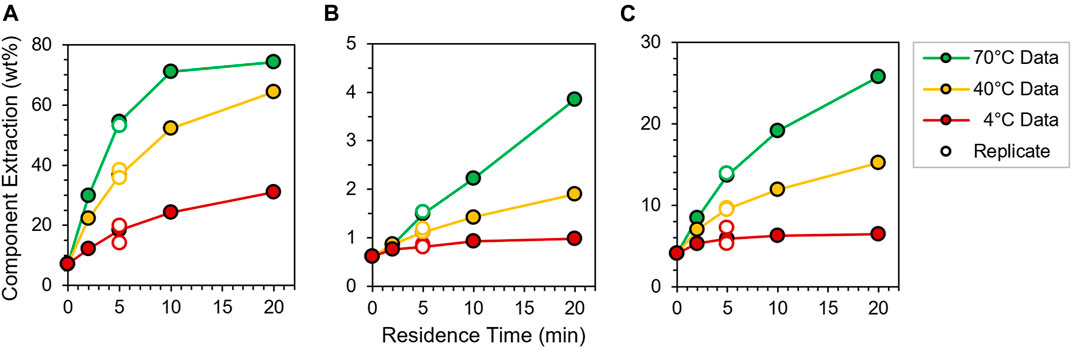
FIGURE 1. Time-course deacetylation profiles for (A) acetate, (B) xylan and (C) lignin extraction from WH corn stover at 4, 40 and 70°C and 5 g L⁻¹ NaOH concentration. Component extraction (wt%) determined from analyte yield of filtered liquor relative to fresh biomass composition (Supplementary Table S3). Connecting lines included for visual clarity.

Several readily observable kinetic trends arise. First, as expected, relative rates of component extraction rise with increasing C_NaOH, consistent with its role as a stoichiometric reagent for deacetylation. Second, xylan extraction proceeds at controllably slow rates across all conditions, while immobilized lignin converts to soluble products at sufficiently slow rates only at the two lower temperatures. In contrast, acetate production proceeds rapidly at all temperatures, but rates observed at the 4°C condition are manageably slow for the kinetic regression and modeling purposes of this study. To this end, kinetic fitting generally requires at least a subset of data to be collected under differential conditions, wherein total extents of component extraction (i.e., conversion) are kept at or below ∼15 wt%; conditions here were deliberately selected from screening experiments described in the previous section to enable differential kinetic measurements and subsequent model regression for acetate, xylan and lignin components (vide infra). Third, time-course component yields across all conditions are highly reproducible (±14% maximum relative error), as shown by the close agreement among open and closed circles plotted in Figure 1 and Supplementary Figure S3.

Next, CB, HS and SK were assessed at the same conditions as WH, and results are illustrated in Supplementary Figures S4–S6. Intriguingly, acetate extraction profiles observed for WH closely match that of SK (24 wt% of WH, Supplementary Table S4), suggesting this anatomical fraction’s deacetylation behavior is highly representative of the parent unsorted material. In contrast, HS (18 wt% of WH, Supplementary Table S4) exhibits slightly enhanced acetate removal profiles relative to the other fractions, while CB (8 wt% of WH, Supplementary Table S4) yield profiles for all components and conditions appear to lag across the entire feedstock series. Lastly, replicates performed for 5- and 20-min residence times once again illustrate high reproducibility of kinetic measurements taken at this millireactor scale.

Taken together, these data indicate that each aggregate feedstock and anatomically-specific kinetic parameters may be confidently determined using reaction–diffusion models and parameter regression methods. However, the experimental results also reveal several non-obvious complexities underlying batch deacetylation pretreatment:

1) Broad differences are observed in component extraction rates, temperature dependencies and feedstock anatomy, requiring a wide range of experimental conditions to access differential kinetic regimes (Figure 1, Supplementary Figures S3–S6).

2) Particle size effects are known to influence apparent yield for condensed-phase biomass pretreatment (Thornburg et al., 2020) and hence must also be quantified (vide infra).

3) Reactor heating (40°C, 70°C) and cooling (4°C) timescales are on the order of reaction–diffusion phenomena (Supplementary Figure S7, Supplementary Equations S2, S3), meaning observable kinetic measurements are non-isothermal—thus complicating the interpretation of temperature dependencies.

Therefore, conclusions may not be drawn simply from the suite of experimental data presented in this section. Particle-scale modeling emerges as a critical tool to account for the non-isothermality and transport phenomena that accompany experimental biomass extraction measurements, and reaction–diffusion models developed here enable the decoupling of these physics to determine the underlying chemical kinetic information.

Corn Stover Particle Model Construction

Milled biomass contains a heterogeneous mixture of different particle sizes and aspect ratios, which in turn plays an important role in the physical behavior of such particles when immersed in chemically reactive fluid environments. To understand these behaviors, we first examined statistically meaningful distributions of corn stover particle sizes and aspect ratios obtained from tens of thousands of individual 2D particle measurements via a commercial particle size analysis service. Data and statistics were analyzed using MATLAB R2021a. Mean values of Feret lengths, widths/thicknesses and aspect ratios resulting from volume-binning of each corn stover sample output are summarized in Table 1, while histograms and aspect ratio trends are illustrated in Supplementary Figures S8, S9, respectively.

TABLE 1

TABLE 1. Summary of mean particle size and porosity attributes.

Three conclusions are made from these analyses. First, WH and SK exhibit nearly identical aspect ratios, highlighting physical similarities between these samples that complement their closely related acetate extraction profiles (Figure 1, Supplementary Figures S3–S6). Second, CB once again emerges as an outlier among the set of feedstocks, further emphasizing the unique characteristics of this fraction. And third, the relatively small (11–20%) standard deviations observed per sample volume bin imply that the geometric descriptors reported in Table 1 are representative of a majority of each sample volume, and hence should adequately describe the typical length scales associated with their particle-scale physics.

Separately, we assessed the internal microstructures of each anatomical fraction using X-ray computed tomography. Cross-sectional images extracted from the 3D control volumes are shown in Figure 2 after contrast correction. The slice through the SK reconstruction (Figure 2A) reveals that both vascular bundles, comprised of thick, heavily lignified cell walls, and pith, which consists of thinner walls with lower lignin content, are present in the sample. The slice through the HS reconstruction (Figure 2B) reveals mostly leaf tissue, although some xylem and phloem domains are also observed. However, the microstructure revealed by the CB reconstruction (Figure 2C) is notably different than the other tissue types, exhibiting densely-packed cells that generally lack the elongated shape and regularly arrayed configuration characteristic to the vascular and leaf tissues. Post-processed 3D radiographs collected for each CB, HS and SK were analyzed using MATBOX, a custom image processing toolbox that enables direct calculation of particle-scale porosity features (Cooper et al., 2016; Usseglio-Viretta et al., 2020; Usseglio-Viretta et al., 2022). Specifically, we compute void fraction ε_P and tortuosity τ for each anatomical fraction, and calculated values are reported in Table 1. Values must be considered with caution, however, as segmentation was performed without prior knowledge of the true volume fractions (i.e., blind segmentation) and with limited XCT image resolution (see SM methods and Supplementary Table S1 for details); however, the selected fields of view capture spatially distributed patterns that appear periodically throughout the whole microstructure by visual inspection, providing some confidence in the calculated results. Accordingly, the pore descriptors of HS and SK share clear similarities. Void fractions of ∼0.65 have been assumed in other lignocellulosic biomass types (Thornburg et al., 2020), and τ values close to unity indicate straight pore channels easily traversed by diffusing solutes. However, CB is yet again remarkably distinct from the other anatomical fractions, and its low ε_P of 0.129 and extremely high τ of 10.3 suggest severe mass transport limitations through this tissue anatomy (Figure 2C). Finally, given the strong similarity between WH and SK, the calculated ε_P of 0.671 and τ of 1.36 for SK are also assumed for WH particle models.

FIGURE 2

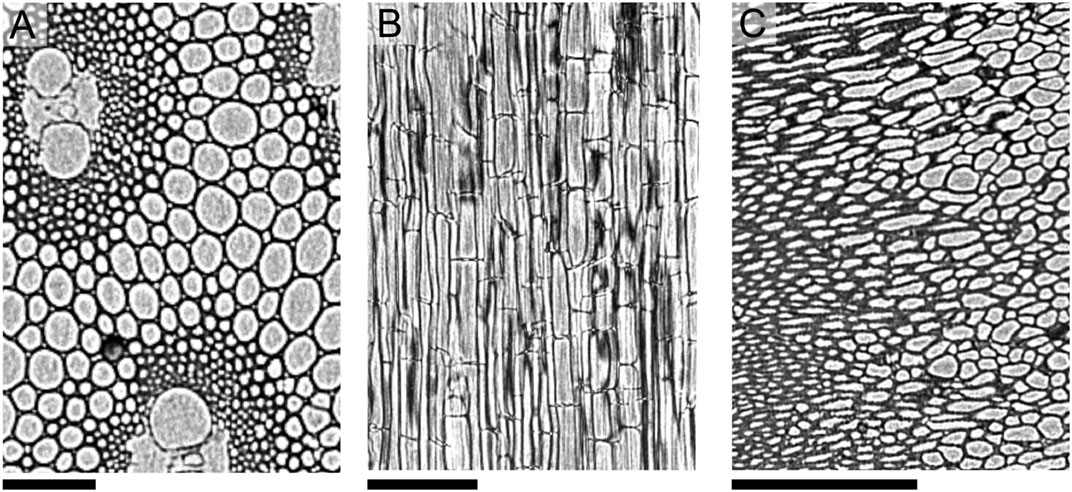
FIGURE 2. Select 2D slices through X-ray computed tomographic reconstructions taken after contrast correction of (A) SK, (B) HS and (C) CB corn stover tissues. All scale bars are 200 μm.

Armed with external and internal physical descriptors, we then construct model geometries for finite-element simulations. 2D axisymmetric models are selected here based on their advantages of mathematical simplicity and known agreement with more computationally intensive 3D microstructural models, as validated in prior biomass conversion modeling studies performed by some of us (Ciesielski et al., 2015; Pecha et al., 2018; Thornburg et al., 2020). Characteristic particle Feret lengths and widths/thicknesses (i.e., averaged to radii) are gleaned from Table 1; axisymmetry is enforced along the tall axis of the particle with a separate symmetry boundary condition along its short axis. Next, porosity metrics from Table 1 describe the porous portion of the particle domain. In addition, a 100-fold diffusion penalty is imposed in the radial direction to account for anisotropic biases of longitudinal diffusion, similar to other well-characterized feedstocks (Comstock, 1970). Specifically, 2D porous geometries are assumed to have uniformly distributed pores, and thus spatially uniform porosity along a given diffusion coordinate, as per Darcy’s law. Initial chemical compositions of extractable acetate, extractable xylan, extractable lignin and the balance of unextractable components are imported from compositional data in Supplementary Table S3. Furthermore, the particle domain is enveloped by an equidistantly spaced aqueous fluid domain that is prescribed the identical initial C_NaOH and solid:fluid volumetric ratios (0.169) as in batch deacetylation experiments, and a no-flux boundary condition at the exterior edges. As a final step, the final dual-domain geometries undergo finite-element meshing to prepare them for CFD simulation in COMSOL Multiphysics 5.6. An example of the meshed 2D WH particle is illustrated in Figure 3.

FIGURE 3

FIGURE 3. 2D axisymmetric meshed model geometry for WH particle (blue) and aqueous solution (grey) domains constructed in COMSOL Multiphysics 5.6. Inset text indicates scale bar and (axi)symmetry boundary conditions; no-flux boundary conditions are imposed at the unmarked grey solution domain edges.

Reaction–Diffusion Model Development

A primary objective of this study is to determine non-isothermal, transport-independent kinetic rate parameters for the reactive extraction of acetate, xylan and lignin from three major corn stover anatomical fractions (CB, HS, SK). Geometries and pore structure descriptors are now incorporated into 2D axisymmetric reaction–diffusion models to describe the chemistry and physics of mesoscale deacetylation processes. Mass transfer is described by various physical equations and assumptions described below, while the system’s heat transfer is handled explicitly by global, time-dependent temperature profiles characteristic of experimental reactor temperatures (Supplementary Figure S7, Supplementary Equations S2, S3). Treatment of temperature as a time-dependent function allows temperature-dependent rate constants and diffusion coefficients each to be implicit functions of residence time, further reducing complexity in the subsequent finite-element calculations.

First, the effective diffusivity D_eff,i of species i is defined by Eq. 1, where D_F,i is the fluid diffusion coefficient and i refers to reactant species acetate (act), xylan (xyl), lignin (lig) or hydroxide (OH⁻). Void fraction ε_P and tortuosity τ vary by anatomical fraction (Table 1) and are assumed to be constant throughout the reactive extraction process, whereas D_F,i is specific to each solute’s molecular diffusivity in aqueous alkaline solutions.

$D_{\text{eff},i}=\frac{{\epsilon }_{\text{P}}}{\tau }{D}_{\text{F},i}(1)$

Fluid diffusion coefficients D_F,i are estimated via classical MD simulations of the various solute species diffusing in 0.125 M (i.e., 5 g L⁻¹) and 0.175 M (i.e., 7 g L⁻¹) NaOH solutions for quasi-equilibrated system temperatures of 4–90°C. Acetate (Vanommeslaeghe et al., 2010) diffusion and hydroxide self-diffusion are readily calculated using straightforward anion assemblies (Jorgensen et al., 1983), while xylan and lignin oligomer structures (DP 1–5, 10) are constructed using internal coordinates of the appropriate xylose (Guvench et al., 2008; Hatcher et al., 2009) or lignin monomers and linkages (Min et al., 2014), with the latter assigned via the Lignin–KMC tool (Orella et al., 2019; Vermaas et al., 2019) (Supplementary Table S2). Estimates of D_F,i at the two C_NaOH are illustrated in Figure 4 and Supplementary Figure S10. Diffusion coefficients generally decrease with increasing solute MW and increase with increasing temperature, albeit varying within the same orders of magnitude. Temperature-dependent exponential functions are then determined from log-linear plots of ln(D_F,i) vs. 1/T (K⁻¹) (Supplementary Figures S11, S12) for incorporation into Eq. 1 and subsequent model physics. Similar to the authors’ prior study on lignin solvolysis (Thornburg et al., 2020), base-case models assume trimeric structures (DP 3) of each xylan and lignin as intermediate-MW reactive solutes. Sensitivity analyses are assessed following kinetic parameter determination in the next section to validate these speciation assignments (vide infra).

FIGURE 4

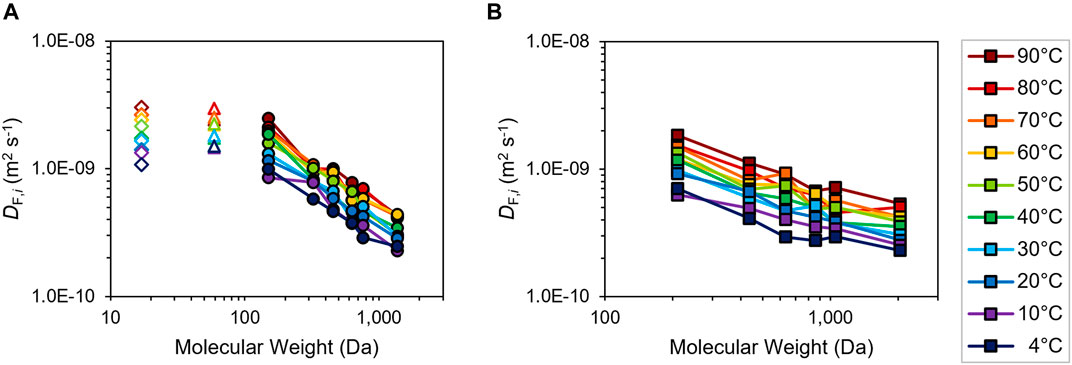
FIGURE 4. Logarithmic plots of fluid diffusion coefficients D_F,i from MD calculations vs. solute molecular weight of (A) hydroxide anion (open diamonds), acetate anion (open triangles) and xylan oligomers (filled circles; DP 1–5, 10) and of (B) lignin oligomers (filled squares; DP 1–5, 10) in 5 g L⁻¹ NaOH at temperatures of 4–90°C (inset color legend). Connecting lines drawn for visual clarity.

Second, simultaneous diffusion (Eq. 1) and chemical reaction (R_i) are described by mass continuity equations in porous media and in free solution. As noted above, Darcy’s law and Fick’s second law (Eq. 2) describe the reaction and diffusion of species i at local concentration C_i within uniformly distributed pores of the 2D particle domain (Figure 3, blue portion). Complementarily, mass continuity (Eq. 3) captures the equivalent competing phenomena occurring in aqueous solution (Figure 3, grey portion). The authors note the explicit residence time and implicit temperature dependencies of each expression’s reaction and diffusion terms, which are handled by finite-element calculations of material fluxes for each mesh element illustrated in Figure 3.

$\frac{\partial \left({\epsilon }_{\text{P}}{C}_i\right)}{\partial t}+\nabla \cdot \left(-D_{\text{eff},i}\nabla C_i\right)=R_i(2)$

$\frac{\partial C_i}{\partial t}+\nabla \cdot \left(-D_{\text{F},i}\nabla C_i\right)=R_i(3)$

Finally, reaction rate expressions are defined in Eq. 4 for the sodium hydroxide-mediated extraction of corn stover. Note that Eq. 4 describes rates of consumption of each biomass-derived species i in the particle domain P, thus assigning a negative sign convention (–R_i, mol m⁻³ s⁻¹) along with reactant concentrations specific to the solid corn stover phase (C_i,P). Pseudo-second order rate laws are prescribed following the assumption of pseudo-first order behavior in each reactant. Arrhenius-type rate constants k_i (m³ mol⁻¹ s⁻¹; Eq. 5) describe the temperature dependence of these parameters, where k_0,i (m³ mol⁻¹ s⁻¹) is the pre-exponential factor, E_a,i (kJ mol⁻¹) is the activation barrier, R is the universal gas constant and T is the absolute reaction temperature (K; Supplementary Equations S2, S3).

$-R_i= k_i{C}_{i,\text{P}}{C}_{\mathrm{NaOH}},\mathrm{where}(4)$

$k_i=k_{0,i}{e}^{-E_{a,i}/RT}(5)$

Each species’ maximum extent of extraction (i.e., conversion) is a function of feedstock identity and C_NaOH, and experimentally determined values reported in Supplementary Table S3 are used to normalize the individual component extraction profiles calculated from –R_i. The authors note that alternate rate expressions (e.g., reversible rate laws, non-integer reaction orders) were assessed early into our study, but none except Eq. 4 provided adequate representation of time-course extraction data (Figure 1, Supplementary Figures S4–S6). Although other rate expressions may be possible, the assigned rate form of Eq. 4 is phenomenologically relevant to deacetylation processes and is appropriately selected here.

Kinetic Rate Constant Determination

Upon defining model geometry (Table 1; Figure 3), physics (Eqs 1–3, Supplementary Equations S2, S3; Figure 4) and chemistry (Eqs. 4–5) of deacetylation, kinetic rate constants in Eqs 4, 5 may be regressed to experimental data illustrated in Figure 1 and Supplementary Figures S4–S6 using a COMSOL–MATLAB R2021a API. Specifically, pre-exponential factors k_0,i and activation barriers E_a,i of Eq. 5 were systematically fitted to time-course acetate, xylan and lignin extraction data measured at the 5 g L⁻¹ NaOH condition as a basis for parameter regression. In a typical fitting routine, an outer MATLAB function randomly perturbs a set of initial parameter guesses by ±20% of the base value before feeding the values to an inner fitting function. The inner function supplies the perturbed guesses as rate parameter inputs to the specified 2D COMSOL model (WH, CB, HS or SK), which calculates and returns to MATLAB the individual component extraction extents at simulated residence times of 0, 2, 5, 10 and 20 min. Model outputs are compared to experimental values for each species, and an iterative generalized least-squares regression routine modifies the rate parameters to minimize the residual objective function until an exit criterion is satisfied. The entire procedure is repeated an additional 9 times with uniquely perturbed initial parameters fed each round to assess the sensitivity of initial guesses (Thornburg et al., 2020). About 110–140 iterations were required to obtain satisfactory fits in a given round; full details are described in SM.

The resultant best-fit parameters averaged across ten independent fitting rounds are reported in Table 2. Several key observations are made across the parameter collection. First, WH, HS and SK yield statistically identical pre-exponential factors and activation barriers for all three reactants, further reinforcing the performance similarities of these three fractions; this observation is also consistent with HS and SK anatomies comprising the majority of WH on a weight basis (Supplementary Table S4). Second, while pre-exponential factors remain consistent for CB, this fraction’s activation barriers are notably lower for acetate and lignin while considerably higher for xylan. These differences may be attributed to the expectedly different types of lignin and hemicellulose—and thereby to the emergent differences in the cell wall nanoscale architecture—present in this portion of plant tissue (thus bearing different reactivities), and/or as a compensating consequence of the relatively severe mass transport limitations inherent to CB (Table 1; Figure 2C); nonetheless, we qualify Table 2 values for CB as approximate upper or lower boundaries rather than definitive coefficients. Third, among the three species studied, acetate and lignin share similar activation barriers across different tissue types, whereas k_0,act values are nearly an order of magnitude larger than k_0,lig in all cases. These results suggest that while the two species may share similar temperature dependencies, lignin extraction may suffer pronounced entropic penalties (e.g., strong surface adsorption of extracted products, inferior hydrogen bonding, unfavorable local solvation) that may ultimately belie the major differences in each reactant’s apparent extraction kinetics. Such kinetic considerations are worthy of further investigation and may help inform on suitable lignin extraction technique(s) for a given biorefinery strategy (Schutyser et al., 2018). Fourth, WH, HS and SK all feature standard deviations of <18% for each parameter, suggesting reasonably low initial guess sensitivity during fitting; CB fits are demonstrably worse (i.e., parameter standard deviations <27%), which may be a mathematical consequence of the severely counteractive transport resistances discussed later (vide infra). Lastly, the authors note that each reactive species’ rate coefficients are valid only when taken as a duet (i.e., k_0,i and E_a,i) and that other, mathematically equivalent local solution pairs likely exist.

TABLE 2

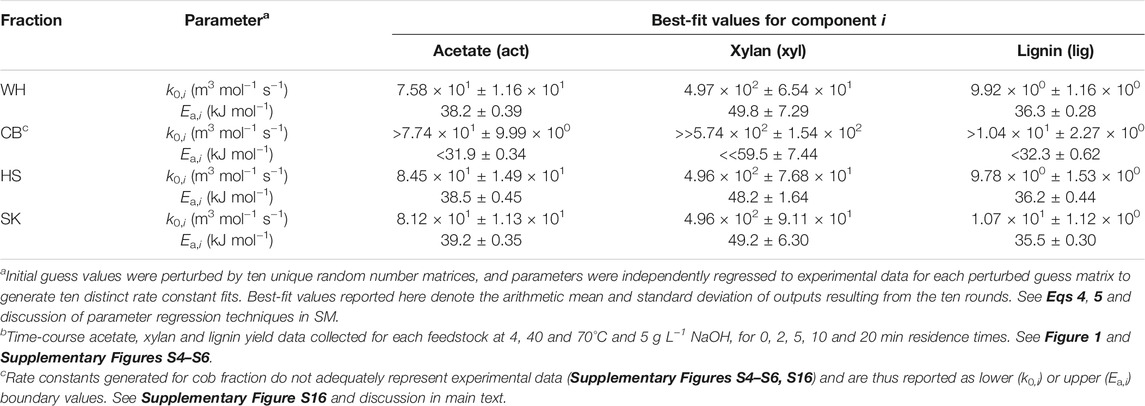
TABLE 2. Best-fit deacetylation kinetic rate constants (mean values and standard deviations) across ten independent regression rounds^a using individual particle models and data^b evaluated at 4–70°C and 5 g L⁻¹ NaOH.

Next, mean rate constants from Table 2 are incorporated directly into 2D reaction–diffusion models of each particle type to inspect the goodness of fit. Supplementary Figure S13 illustrates the resulting best-fit WH simulated extraction profiles and individual component parity plots at the three deacetylation temperatures, highlighting reasonably good fits for all three species. In general, simulated lignin and acetate profiles are slightly overpredictive at longer residence times, while the xylan model trace slightly underpredicts this component’s experimental trends. Similar patterns of strong model agreement are observed for HS (Supplementary Figure S14) and SK (Supplementary Figure S15). However, CB yet again emerges as an outlier feedstock fraction (Supplementary Figure S16). While reasonable fits are observed for lignin at 4 and 40°C, the best-fit curve for this species at 70°C falls significantly short, with concomitantly worse agreement among acetate and xylan data sets. Acetate and xylan traces effectively collapse to single profiles at all three temperatures, albeit for distinct reasons. Given the rapid kinetics anticipated by Table 2 parameters, supposedly fast rates of acetate extraction are likely to be severely outcompeted by mass transfer resistance, mathematically dampening any practical influence of reaction temperature on the simulated response. Conversely, CB xylan rate parameters predict considerably slower kinetics than other feedstocks, and the presence of strongly limiting transport effects leads to zero-rate model responses and thus considerable error in this component’s best fits (Table 2). The quantitative consequences of mass transfer resistance on apparent extraction kinetics are discussed at length in the final Results and Discussion subsection of this study (vide infra).

As a final validation exercise, myriad sensitivity analyses were carried out to evaluate the influence of various mass transport parameters, none of which appear to be highly sensitive to the resultant WH model outputs. Results are summarized in Supplementary Figures S17–S19 and further confirm the validity of transport assumptions incorporated into base-case reaction–diffusion models.

Anatomical Ensemble Calculations and Model Predictions

Upon fitting kinetic rate coefficients, we now seek to test the validity of our four individual particle models as aggregate ensembles and also under deacetylation conditions beyond the original regression data set. First, we create a simulated ensemble of the collective feedstock by weighting the responses of anatomical particle models by their mass fractions within the bulk corn stover feedstock (Supplementary Table S4); here, the balance of feedstock that is not cobs, husks or stalks is deemed to be “whole” material, and hence is used to weight the extraction response of the WH model. Figure 5 shows the aggregate ensemble model responses and experimental data comparison for acetate, xylan and lignin at 4–70°C and 5 g L⁻¹ NaOH. Excellent fits are seen for all species and conditions, as illustrated by each species’ parity plot in Figures 5D–F with no greater than 13% variance from any experimental batch reactor measurement. Thus, calculations of corn stover ensemble responses demonstrate the robustness and versatility of 2D axisymmetric models in capturing experimental deacetylation trends.

FIGURE 5

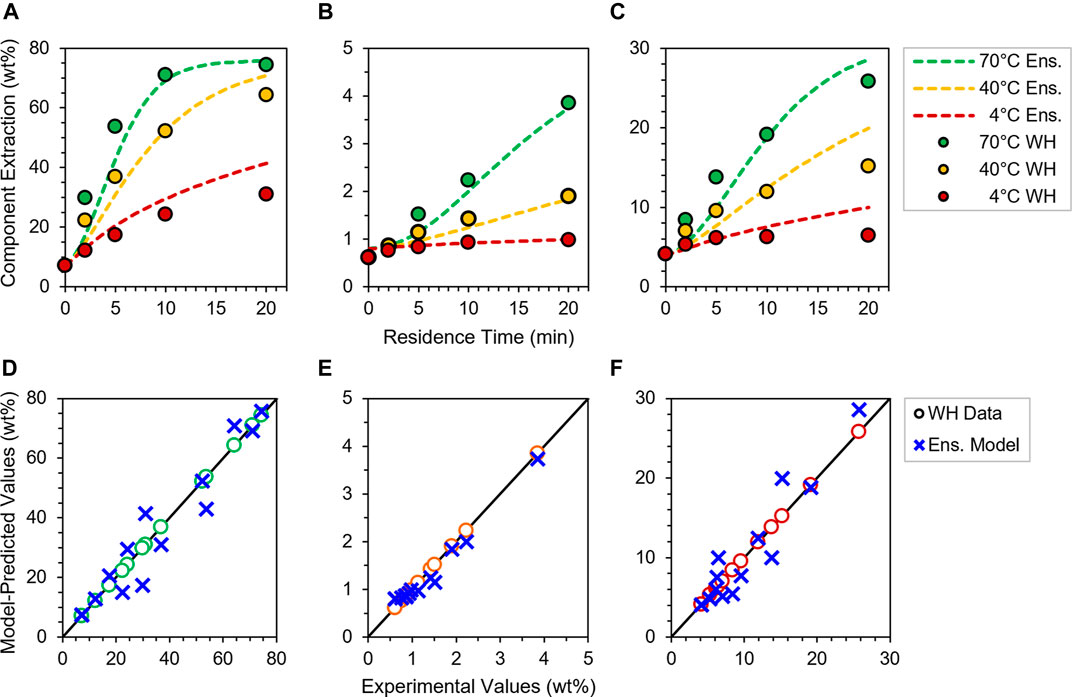
FIGURE 5. Ensemble model predictions (dashed lines) at 4–70°C and 5 g L⁻¹ NaOH of (A) acetate, (B) xylan and (C) lignin extraction profiles compared to experimental data collected for WH at the same deacetylation conditions (filled circles), and parity plots of (D) acetate, (E) xylan and (F) lignin model values (blue crosses), with individual species data from WH experiments (open circles) at all three temperatures plotted along a 45° parity line (black) for visual reference. See Figure 1 and Supplementary Table S4.

Next, models are extended beyond their original reaction condition to assess their predictive capability under different circumstances. While 5 g L⁻¹ NaOH data are used for kinetic rate parameter fitting, the 7 g L⁻¹ NaOH data sets of Supplementary Figures S3–S6 are now utilized to evaluate the four particle models’ predictivities. Select input parameters in WH, CB, HS and SK models are now adjusted for the 7 g L⁻¹ NaOH condition, including initial C_NaOH in the aqueous domain (Figure 3), apparent time-zero yields (Supplementary Table S5), mass fractions of extractable material (Supplementary Table S3), maximum extents of component extraction (Supplementary Table S3), diffusion coefficients (Supplementary Figure S10) and their temperature profiles (Supplementary Figure S12).

Figure 6 shows the predicted 7 g L⁻¹ acetate extraction profiles and corresponding parity plot for an anatomically weighted corn stover particle ensemble (Supplementary Table S4); analogous xylan and lignin model responses are included in Supplementary Figure S20. Importantly, model simulations at this deacetylation condition have not been regressed to experimental data, and time-course responses thus may be considered as blind predictions for validation purposes. Despite slight overprediction at late residence times, good agreement is observed for acetate and xylan extraction kinetics at this higher C_NaOH condition, with no greater than 21% variance from experiment—further implying high fidelity of these two component models under extrapolative deacetylation conditions. However, lignin profiles are significantly overpredictive in this case (Supplementary Figure S20B). This may be attributable to realistic lignin solubility limitations at higher alkalinity that are not captured in the idealized model physics, which would practically raise entropic barriers and thus uniquely reduce the value of k_0,lig at this condition. Future investigations at high C_NaOH may seek to incorporate solubility effects into mesoscale models to reconcile these apparent prediction gaps. Overall, however, 2D reaction–diffusion models and their aggregate ensembles appear to be valid and reasonably predictive of corn stover deacetylation behaviors at two process-relevant alkaline conditions.

FIGURE 6

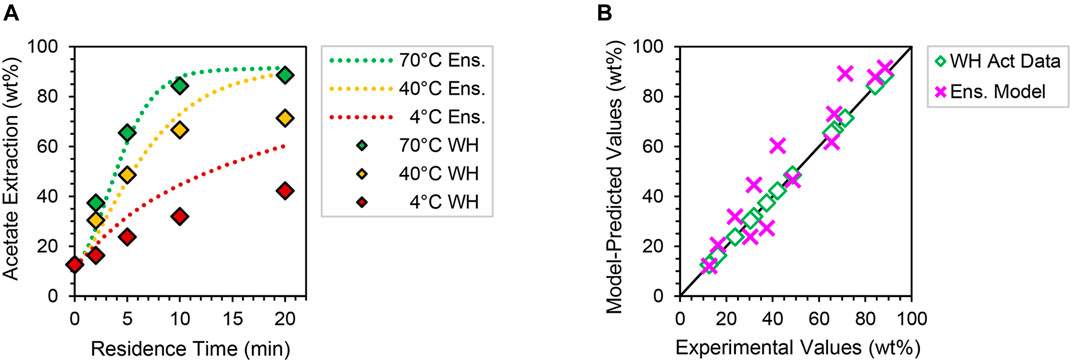
FIGURE 6. (A) Ensemble model predictions (dotted lines) at 4–70°C and 7 g L⁻¹ NaOH of acetate extraction in comparison to WH data collected at the same deacetylation conditions (filled diamonds). (B) Parity plot of the 7 g L⁻¹ NaOH acetate extraction model predictions (pink crosses) compared to WH acetate extraction data (open diamonds) at all three temperatures plotted along a 45° parity line (black) for visual reference. See Supplementary Figure S20 for analogous xylan and lignin trends.

Intraparticle Mass Transfer Resistance and Kinetic Consequences

Actionable insights into corn stover deacetylation may be gleaned from the foundational reaction–diffusion models developed in this report. Of particular value are questions of mass transfer rates and how they may (or may not) compete with the kinetic rates of deacetylation chemistry. An historical approach to achieve this rate comparison is to calculate the Thiele modulus for the case of a reactive solute undergoing simultaneous diffusion and chemical reaction (Thiele, 1939; Froment and Bischoff, 1990; Levenspiel, 1998). An adaptation of the intraparticle Thiele modulus φ_i for incompletely convertible chemical reactions is described by:

${\phi }_i=\sqrt{\frac{\text{reaction}\text{rate}}{\text{diffusion}\text{rate}}}=L\sqrt{\frac{k_i^{\prime }}{\left(D_{\text{eff},{\text{OH}}^{-}}\right)\left(Y_{\text{max},i}\right)}}(6)$

where L (m) is the characteristic path length, k_i' (s⁻¹) is the pseudo-first-order rate coefficient of species i extraction, D_eff,OH- (m² s⁻¹) is the effective diffusivity of the mobile OH⁻ reactant and Y_max,i is the maximum extractable yield of component i (non-dimensionalized and normalized to a value between 0 and 1) observed at long residence times (Supplementary Table S3); the latter term is included to account for incomplete extraction (i.e., incomplete conversion). Subscript i again refers to acetate, xylan or lignin, the immobile, corn stover-bound reactants, and k_i' is calculated by multiplying k_i (mol m⁻³ s⁻¹; Table 2) by the initial molar content of each solid-bound species (mol; see Supplementary Table S3 and MW values in Figure 4 and Supplementary Figure S17). Path length L of the diffusing reactant is defined as half the particle length; this characteristic length may be visualized as the long axis of the blue 2D WH particle illustrated in Figure 3. We note that φ_i is dimensionless, and calculated values indicate whether the deacetylation process is either effectively controlled (i.e., limited) by the reaction rate (φ_i < 0.4) or the diffusion rate (φ_i > 4.0), or instead governed by an intermediate regime (0.4 < φ_i < 4.0) where reaction kinetics and mass transfer compete along similar time and length scales (Levenspiel, 1998).

A related dimensionless expression that quantifies reaction vs. diffusion control is the effectiveness factor η_i, defined by Eq. 7 for arbitrary geometries (Aris, 1957; Levenspiel, 1998) applicable to biomass particles (Thornburg et al., 2020):

${\eta }_i=\frac{\tanh \left({\phi }_i\right)}{{\phi }_i}(7)$

Values of η_i are bounded by 0 and 1. Like φ_i, the magnitude of η_i indicates whether a process is kinetically limited (η_i > 0.95), mass transport-limited (η_i < 0.25) or in between; note that a low φ_i indicates a high η_i and vice versa. The effectiveness factor also bears tangible interpretations: for example, if η_i = 0.40, apparent kinetic measurements observed via experiment may actually be attenuated by up to 60% due to diffusion limitations.

The Thiele modulus φ_i and the related effectiveness factor η_i are therefore important descriptors of mass transport resistances in biomass pretreatment and conversion (Ciesielski et al., 2021), and here we use them to interpret the observable and predicted performance of corn stover deacetylation. Calculated values of φ_i and η_i are reported in Table 3 for each acetate, xylan and lignin extracted from WH with 5 g L⁻¹ NaOH and at temperatures of 4–70°C. In general, Thiele moduli increase with increasing temperature, indicating that diffusion limitations become more pronounced at high temperatures where kinetic rates expectedly become very rapid, and thus non-controlling. This is especially true for acetate extraction, which faces severe mass transfer resistances at 70°C (η_i = 0.50) while curiously approaching kinetic limitations at 4°C (η_i = 0.90). In contrast, effectiveness factors for lignin and xylan are generally high at all conditions, although mass transfer does appear to compete somewhat with extraction kinetics at the two elevated temperatures (η_i ∼ 0.84–0.92).

TABLE 3

TABLE 3. Thiele moduli and effectiveness factors for WH calculated at 4–70°C and 5 g L⁻¹ NaOH.

Next, we compare intraparticle reaction and diffusion rates across the family of anatomical fractions. Table 4 lists the computed φ_i and η_i values for each CB, HS and SK at 4 and 70°C for the three reactive components. Trends in reaction vs. diffusion resistance for HS and SK are remarkably similar to WH (Table 3), further reinforcing the similar performance attributes among these corn stover fractions. As expected, CB remains a significant outlier among the material set, and given the uncertainty in determining accurate kinetic parameters (vide supra), values reported in Table 4 for CB should be regarded as approximate boundaries rather than definitive metrics. Even so, debilitating mass transport resistances are identified for the extraction of lignin and especially acetate, with η_act as low as 0.021—suggesting laboratory deacetylation measurements may be impaired by nearly 98% due to mass transport phenomena! Remarkably, however, external (film) mass transfer resistances (Frössling, 1938; Levenspiel, 1998) at the exterior particle surface are negligible across all four corn stover samples, including CB (see Supplementary Table S6, Supplementary Equation S4 and surrounding SM discussion). Such alarming findings further edify the critical importance of mesoscale modeling in biomass pretreatment and conversion by illuminating these obscured, but crucial performance-limiting bottlenecks.

TABLE 4

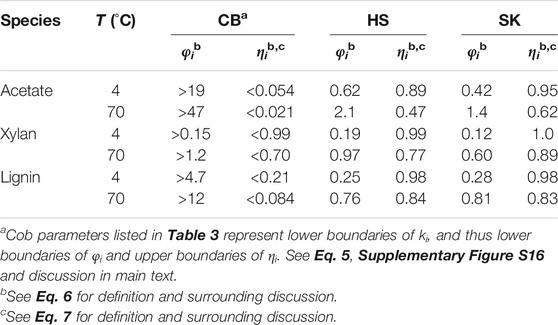
TABLE 4. Computed values of Thiele moduli and effectiveness factors for CB, HS and SK component extraction performed at 4 and 70°C and at 5 g L⁻¹ NaOH.

Processing conditions and feedstock anatomy clearly influence the phenomena that control alkaline deacetylation, as do the size of the feedstock particles. We now isotropically scale the WH model to simulate deacetylation across proportionally smaller and larger 2D particles; results for acetate extraction at 70°C and 5 g L⁻¹ are illustrated in Figure 7A, while Thiele moduli are plotted as a function of full particle length 2L in Figure 7B. Corn stover particle size indeed has a pronounced impact on acetate removal: precipitous drops in yield are predicted for particles larger than 2.2 mm, with the largest 22-mm particle achieving only 22% extraction after 20 min reaction time (Figure 7A). Size-dependent mass transport consequences are accordingly witnessed in Figure 7B by the span of φ_act from 0.19 to 38, the largest of which corresponds to an η_act of 0.026.

FIGURE 7

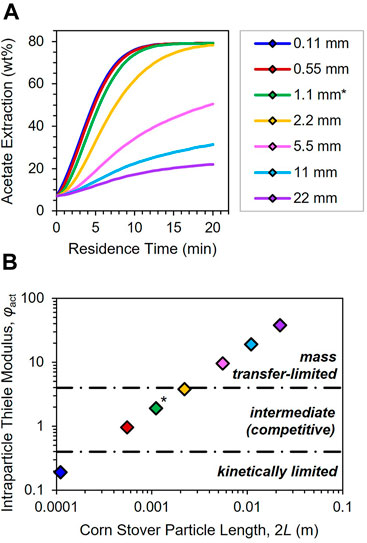
FIGURE 7. (A) Acetate extraction profiles and (B) intraparticle Thiele moduli φ_act (see Eq. 6) as a function of corn stover particle length. Isotropically scaled 2D WH particle models simulated at deacetylation conditions of 70°C and 5 g L⁻¹ NaOH. Asterisk (*) label in each denotes 1.1-mm-long WH base case particle (green; see Figure 3). Dot-dashed lines in (B) divide regimes by their controlling phenomena (inset italicized labels). See Eq. 6, Supplementary Table S7 and discussion in main text for regime definitions.

Finally, we propose actionable insights into feedstock size thresholds for corn stover deacetylation by back-calculating from critical values of φ_act (vide supra). Eq. 6 is rearranged to solve for L_crit at the two φ_crit,act boundaries to determine anatomically-specific particle size thresholds of mass transfer resistance at 4 and 70°C. Full particle lengths 2L_crit are reported in Supplementary Table S7 alongside physical interpretations. Crucially, unsorted corn stover particles as little as 2.3 mm in length are predicted to be entirely diffusion-limited for acetate extraction at the higher temperature—approximately the average Feret length of milled WH, HS and SK particles used in this study (Table 1), and nearly identical to hardwood size limits determined in the authors’ previous study on poplar methanolysis (Thornburg et al., 2020). Size thresholds for these three corn stover fractions are indeed similar, whereas CB particles will virtually always be subjected to mass transfer control despite any practical attempt at size reduction. Conversely, kinetic control may be achieved for WH, HS and SK if particle lengths are kept below 0.23 mm; in other words, finely milled corn stover is predicted to enable laboratory kinetic measurements of deacetylation chemistry devoid of transport limitations. However, milling feedstock to this size range is impractical for pilot- and industrial-scale applications, where mass transport is anticipated to play a dominant role in deacetylation process performance. Additional strategies such as air classification (Thompson et al., 2016) may enable the practically scalable removal of cob fractions to obviate their severe mass transfer penalties in processing contexts. Overall, the predictors proposed in Supplementary Table S7 will inform both biomass conversion researchers and biorefinery practitioners of practical feedstock size reduction targets to properly account for mesoscale mass transfer resistances in pretreatment systems that straddle myriad time and length scales.

Conclusion

Alkaline deacetylation prior to mechanical refining is an emerging biorefinery pretreatment strategy to improve enzymatic saccharification yields of herbaceous feedstocks such as corn stover. In this study, we develop first-principled reaction–diffusion models of three primary anatomical fractions of milled corn stover (cobs, husks and stalks) and of an aggregate particle representative of the unsorted (whole) feedstock to understand and corroborate how microscopic differences in biopolymer and tissue assemblies impact observable deacetylation performance at 4–70°C and 5–7 g L⁻¹ NaOH for residence times of 0–20 min. Anatomically-specific 2D models then incorporate key physical and chemical descriptors of corn stover particle microstructure, geometry and biopolymer composition.

With appropriate assumptions for particle-scale physics, such as condensed-phase mass transfer, kinetic rate constants for acetate, xylan and lignin extraction are regressed from experimental data sets at 5 g L⁻¹ NaOH and subsequently validated by 7 g L⁻¹ data and anatomically-weighted ensemble calculations. Individual and ensemble model responses provide excellent fits to experimental data and offer reasonably valid predictions of reaction–diffusion behavior at extrapolated conditions. Crucially, mass transfer resistances are predicted to dominate acetate extraction kinetics at moderate temperatures for all feedstock fractions, but especially so for cobs, which demonstrate vanishingly small effectiveness factors of 0.021 for deacetylation at 70°C. Indeed, unsorted corn stover particles as small as 2.3 mm in length are expected to be completely mass transfer-limited for deacetylation—therefore establishing critical particle size reduction guidelines for laboratory and industrial practitioners to heed when studying this important pretreatment process.

Mesoscale modeling is a vital tool to uncover performance-controlling phenomena and to decouple chemical kinetics from mass and heat transfer in multiphase systems. Historical reaction engineering theories such as the Thiele modulus and effectiveness factor offer a renewed perspective on modern approaches to biomass deconstruction. Transport phenomena indeed lie at the heart of most biomass conversion processes, and the unique model frameworks developed in this report provide both scale-unifying information and actionable guideposts for chemical reactor design, scale-up and deployment of future biorefineries.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding authors.

Author Contributions

NT conceived the study, designed kinetic experiments, executed all CFD simulations and MATLAB programs, and wrote the article. RN conducted all kinetic and analytical experiments and designed the experimental apparatuses under the advisement of EW, XC, DS and MR. MC and PC performed XCT experiments, post-processing and visualization while FU performed XCT data analysis in MATBOX. LB and VB executed MD simulations, and VB determined lignin decamer structures and MD coordinates. YL assisted with design of kinetic experiments and coordinated corn stover feedstock sorting, milling, storage, and material and data transfers. MR, XC and DS advised experimental campaigns, equipment resources and project timelines while EW oversaw analytical measurement needs and data quality assurance. MP assisted with reaction–diffusion model development and co-wrote and debugged algorithms. PC directed the scientific project, developed particle model frameworks, wrote data regression algorithms with NT and MP, and advised the overall scientific objectives of the study.

Funding

Funding provided by the U.S. Department of Energy Office of Energy Efficiency and Renewable Energy Bioenergy Technologies Office through the Feedstock-Conversion Interface Consortium. A portion of this research was performed using computational resources sponsored by the Department of Energy’s Office of Energy Efficiency and Renewable Energy and located at the National Renewable Energy Laboratory.

Author’s Disclaimer

The views expressed in the article do not necessarily represent the views of the DOE or the U.S. Government. The U.S. Government retains and the publisher, by accepting the article for publication, acknowledges that the U.S. Government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this work, or allow others to do so, for U.S. Government purposes.

Conflict of Interest

All authors were employed by the National Renewable Energy Laboratory, operated by Alliance for Sustainable Energy, LLC, for the U.S. Department of Energy (DOE) under Contract No. DE-AC36-08GO28308.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

NT and YL acknowledge corn stover hand fractionation activities and information provided by Amber Hoover, Neal Yancey and Allison Ray of Idaho National Laboratory. NT and RN further acknowledge Brittany Thornton, Darren Peterson and William Michener of NREL for their assistance with analytical characterization. VB and LB acknowledge Heather Mayes of NREL for her assistance with lignin MD structures.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2022.841169/full#supplementary-material

References

Arganda-Carreras, I., Kaynig, V., Rueden, C., Eliceiri, K. W., Schindelin, J., Cardona, A., et al. (2017). Trainable Weka Segmentation: a Machine Learning Tool for Microscopy Pixel Classification. Bioinformatics 33 (15), 2424–2426. doi:10.1093/bioinformatics/btx180

PubMed Abstract | CrossRef Full Text | Google Scholar

Aris, R. (1957). On Shape Factors for Irregular Particles-I. Chem. Eng. Sci. 6 (6), 262–268. doi:10.1016/0009-2509(57)85028-3

CrossRef Full Text | Google Scholar

Buades, A., Coll, B., and Morel, J. “(Year). "A Non-local Algorithm for Image Denoising,” in 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR'05)), 60–65.62

Google Scholar

Chen, J., Adjallé, K., Barnabé, S., Perrier, M., and Paris, J. (2019). Mechanical and Thermal Pretreatment Processes for Increasing Sugar Production from Woody Biomass via Enzymatic Hydrolysis. Waste Biomass Valor. 10 (7), 2057–2065. doi:10.1007/s12649-018-0217-x

CrossRef Full Text | Google Scholar

Chen, X., Kuhn, E., Jennings, E. W., Nelson, R., Tao, L., Zhang, M., et al. (2016). DMR (Deacetylation and Mechanical Refining) Processing of Corn stover Achieves High Monomeric Sugar Concentrations (230 G L−1) during Enzymatic Hydrolysis and High Ethanol Concentrations (>10% V/v) during Fermentation without Hydrolysate Purification or Concentration. Energy Environ. Sci. 9 (4), 1237–1245. doi:10.1039/C5EE03718B

CrossRef Full Text | Google Scholar

Chen, X., Tao, L., Shekiro, J., Mohaghaghi, A., Decker, S., Wang, W., et al. (2012). Improved Ethanol Yield and Reduced Minimum Ethanol Selling Price (MESP) by Modifying Low Severity Dilute Acid Pretreatment with Deacetylation and Mechanical Refining: 1) Experimental. Biotechnol. Biofuels 5 (1), 60. doi:10.1186/1754-6834-5-60

PubMed Abstract | CrossRef Full Text | Google Scholar

Ciesielski, P. N., Crowley, M. F., Nimlos, M. R., Sanders, A. W., Wiggins, G. M., Robichaud, D., et al. (2015). Biomass Particle Models with Realistic Morphology and Resolved Microstructure for Simulations of Intraparticle Transport Phenomena. Energy Fuels 29 (1), 242–254. doi:10.1021/ef502204v

CrossRef Full Text | Google Scholar

Ciesielski, P. N., Pecha, M. B., Thornburg, N. E., Crowley, M. F., Gao, X., Oyedeji, O., et al. (2021). Bridging Scales in Bioenergy and Catalysis: A Review of Mesoscale Modeling Applications, Methods, and Future Directions. Energy Fuels 35 (18), 14382–14400. doi:10.1021/acs.energyfuels.1c02163

CrossRef Full Text | Google Scholar

Comstock, G. L. (1970). Directional Permeability of Softwoods. Wood Fiber 1 (4), 283–289.

Google Scholar

Cooper, S. J., Bertei, A., Shearing, P. R., Kilner, J. A., and Brandon, N. P. (2016). TauFactor: An Open-Source Application for Calculating Tortuosity Factors from Tomographic Data. SoftwareX 5, 203–210. doi:10.1016/j.softx.2016.09.002

CrossRef Full Text | Google Scholar

Costanza, V., and Costanza, P. (2002). Estimating Pure Diffusion Contributions in Alkaline Pulping Processes. Lat. Am. Appl. Res. 32, 151–159.

Google Scholar

Darden, T., York, D., and Pedersen, L. (1993). Particle Mesh Ewald: AnN⋅Log(N) Method for Ewald Sums in Large Systems. J. Chem. Phys. 98 (12), 10089–10092. doi:10.1063/1.464397

CrossRef Full Text | Google Scholar

Froment, G. F., and Bischoff, K. B. (1990). Chemical Reactor Analysis and Design, Ch 3. New York, NY, U.S.A.: John Wiley & Sons.

Google Scholar

Frössling, N. (1938). Uber die Verdunstung Fallender Tropfen (The Evaporation of Falling Drops). Gerlands Beitr. Geophys. 52, 107–216.

Google Scholar

Gierer, J., Imsgard, F., Norén, I., Stilkerieg, B., Christensen, A., and Schroll, G. (1977). Studies on the Degradation of Phenolic Lignin Units of the Beta-Aryl Ether Type with Oxygen in Alkaline Media. Acta Chem. Scand. 31b, 561–572. doi:10.3891/acta.chem.scand.31b-0561

CrossRef Full Text | Google Scholar

Guvench, O., Greene, S. N., Kamath, G., Brady, J. W., Venable, R. M., Pastor, R. W., et al. (2008). Additive Empirical Force Field for Hexopyranose Monosaccharides. J. Comput. Chem. 29 (15), 2543–2564. doi:10.1002/jcc.21004

CrossRef Full Text | Google Scholar

Hatcher, E. R., Guvench, O., and MacKerell, A. D. (2009). CHARMM Additive All-Atom Force Field for Acyclic Polyalcohols, Acyclic Carbohydrates, and Inositol. J. Chem. Theor. Comput. 5 (5), 1315–1327. doi:10.1021/ct9000608

PubMed Abstract | CrossRef Full Text | Google Scholar

Hynninen, A. P., and Crowley, M. F. (2014). New Faster CHARMM Molecular Dynamics Engine. J. Comput. Chem. 35 (5), 406–413. doi:10.1002/jcc.23501

CrossRef Full Text | Google Scholar

Jakes, J. E., Zelinka, S. L., Hunt, C. G., Ciesielski, P., Frihart, C. R., Yelle, D., et al. (2020). Measurement of Moisture-dependent Ion Diffusion Constants in wood Cell wall Layers Using Time-Lapse Micro X-ray Fluorescence Microscopy. Sci. Rep. 10 (1), 9919. doi:10.1038/s41598-020-66916-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Jorgensen, W. L., Chandrasekhar, J., Madura, J. D., Impey, R. W., and Klein, M. L. (1983). Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 79 (2), 926–935. doi:10.1063/1.445869

CrossRef Full Text | Google Scholar

Karp, E. M., Donohoe, B. S., O’Brien, M. H., Ciesielski, P. N., Mittal, A., Biddy, M. J., et al. (2014). Alkaline Pretreatment of Corn Stover: Bench-Scale Fractionation and Stream Characterization. ACS Sust. Chem. Eng. 2 (6), 1481–1491. doi:10.1021/sc500126u

CrossRef Full Text | Google Scholar

Katahira, R., Mittal, A., McKinney, K., Chen, X., Tucker, M. P., Johnson, D. K., et al. (2016). Base-Catalyzed Depolymerization of Biorefinery Lignins. ACS Sust. Chem. Eng. 4 (3), 1474–1486. doi:10.1021/acssuschemeng.5b01451

CrossRef Full Text | Google Scholar

Kräutler, V., van Gunsteren, W. F., and Hünenberger, P. H. (2001). A Fast SHAKE Algorithm to Solve Distance Constraint Equations for Small Molecules in Molecular Dynamics Simulations. J. Comput. Chem. 22 (5), 501–508. doi:10.1002/1096-987X(20010415)22:5<501:AID-JCC1021>3.0.CO;2-V

CrossRef Full Text | Google Scholar

Kruger, J. S., Cleveland, N. S., Zhang, S., Katahira, R., Black, B. A., Chupka, G. M., et al. (2016). Lignin Depolymerization with Nitrate-Intercalated Hydrotalcite Catalysts. ACS Catal. 6 (2), 1316–1328. doi:10.1021/acscatal.5b02062

CrossRef Full Text | Google Scholar

Levenspiel, O. (1998). Chemical Reaction Engineering, Ch 18. New York, NY, U.S.A: John Wiley & Sons.

Google Scholar

Lima, C. S., Rabelo, S. C., Ciesielski, P. N., Roberto, I. C., Rocha, G. J. M., and Driemeier, C. (2018). Multiscale Alterations in Sugar Cane Bagasse and Straw Submitted to Alkaline Deacetylation. ACS Sust. Chem. Eng. 6 (3), 3796–3804. doi:10.1021/acssuschemeng.7b04158

CrossRef Full Text | Google Scholar

Luterbacher, J. S., Parlange, J.-Y., and Walker, L. P. (2013). A Pore-Hindered Diffusion and Reaction Model Can Help Explain the Importance of Pore Size Distribution in Enzymatic Hydrolysis of Biomass. Biotechnol. Bioeng. 110 (1), 127–136. doi:10.1002/bit.24614

PubMed Abstract | CrossRef Full Text | Google Scholar

MacKerell, A. D., Brooks, B., Brooks, C. L., Nilsson, L., Roux, B., Won, Y., et al. (1998). “CHARMM: The Energy Function and its Parameterization,” in Encyclopedia of Computational Chemistry.

Google Scholar

Mills, T. Y., Sandoval, N. R., and Gill, R. T. (2009). Cellulosic Hydrolysate Toxicity and Tolerance Mechanisms in Escherichia coli. Biotechnol. Biofuels 2 (1), 26. doi:10.1186/1754-6834-2-26

PubMed Abstract | CrossRef Full Text | Google Scholar

Min, D.-Y., Chang, H.-M., Jameel, H., Lucia, L., Wang, Z.-G., and Jin, Y.-C. (2014). The Structure of Lignin of Corn stover and its Changes Induced by Mild Sodium Hydroxide Treatment. BioResources 9 (2), 2405–2414. doi:10.15376/biores.9.2.2405-2414

CrossRef Full Text | Google Scholar

Morales-Huerta, J. C., Hernández-Meléndez, O., Hernández-Luna, M. G., Manero, O., Bárzana, E., and Vivaldo-Lima, E. (2021). An Experimental and Modeling Study on the Pretreatment and Alkaline Hydrolysis of Blue Agave Bagasse in Twin-Screw Extruders. Ind. Eng. Chem. Res. 60 (34), 12449–12460. doi:10.1021/acs.iecr.1c02175

CrossRef Full Text | Google Scholar

Mosier, N., Wyman, C., Dale, B., Elander, R., Lee, Y. Y., Holtzapple, M., et al. (2005). Features of Promising Technologies for Pretreatment of Lignocellulosic Biomass. Bioresour. Tech. 96 (6), 673–686. doi:10.1016/j.biortech.2004.06.025

PubMed Abstract | CrossRef Full Text | Google Scholar

Orella, M. J., Gani, T. Z. H., Vermaas, J. V., Stone, M. L., Anderson, E. M., Beckham, G. T., et al. (2019). Lignin-KMC: A Toolkit for Simulating Lignin Biosynthesis. ACS Sust. Chem. Eng. 7 (22), 18313–18322. doi:10.1021/acssuschemeng.9b03534

CrossRef Full Text | Google Scholar

Otsu, N. (1979). A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man. Cybern. 9 (1), 62–66. doi:10.1109/TSMC.1979.4310076

CrossRef Full Text | Google Scholar

Palmqvist, E., and Hahn-Hägerdal, B. (2000). Fermentation of Lignocellulosic Hydrolysates. II: Inhibitors and Mechanisms of Inhibition. Bioresour. Tech. 74 (1), 25–33. doi:10.1016/S0960-8524(99)00161-3

CrossRef Full Text | Google Scholar

Pecha, M. B., Ramirez, E., Wiggins, G. M., Carpenter, D., Kappes, B., Daw, S., et al. (2018). Integrated Particle- and Reactor-Scale Simulation of Pine Pyrolysis in a Fluidized Bed. Energy Fuels 32 (10), 10683–10694. doi:10.1021/acs.energyfuels.8b02309

CrossRef Full Text | Google Scholar

Pettersen, E. F., Goddard, T. D., Huang, C. C., Meng, E. C., Couch, G. S., Croll, T. I., et al. (2021). UCSF ChimeraX : Structure Visualization for Researchers, Educators, and Developers. Protein Sci. 30 (1), 70–82. doi:10.1002/pro.3943

PubMed Abstract | CrossRef Full Text | Google Scholar

Rodriguez, A., Salvachúa, D., Katahira, R., Black, B. A., Cleveland, N. S., Reed, M., et al. (2017). Base-Catalyzed Depolymerization of Solid Lignin-Rich Streams Enables Microbial Conversion. ACS Sust. Chem. Eng. 5 (9), 8171–8180. doi:10.1021/acssuschemeng.7b01818

CrossRef Full Text | Google Scholar

Rollin, J. A., Zhu, Z., Sathitsuksanoh, N., and Zhang, Y.-H. P. (2011). Increasing Cellulose Accessibility Is More Important Than Removing Lignin: A Comparison of Cellulose Solvent-Based Lignocellulose Fractionation and Soaking in Aqueous Ammonia. Biotechnol. Bioeng. 108 (1), 22–30. doi:10.1002/bit.22919

PubMed Abstract | CrossRef Full Text | Google Scholar

Schutyser, W., Renders, T., Van den Bosch, S., Koelewijn, S.-F., Beckham, G. T., and Sels, B. F. (2018). Chemicals from Lignin: an Interplay of Lignocellulose Fractionation, Depolymerisation, and Upgrading. Chem. Soc. Rev. 47 (3), 852–908. doi:10.1039/C7CS00566K

PubMed Abstract | CrossRef Full Text | Google Scholar

Shimizu, S., Posoknistakul, P., Yokoyama, T., and Matsumoto, Y. (2013). Quantitative Difference in the Rates of the β-O-4 Bond Cleavage between Lignin Model Compounds with and without γ-Hydroxymethyl Groups during the Alkaline Pulping Process. BioResources 8 (3), 11. doi:10.15376/biores.8.3.4312-4322

CrossRef Full Text | Google Scholar

Shimizu, S., Yokoyama, T., Akiyama, T., and Matsumoto, Y. (2012). Reactivity of Lignin with Different Composition of Aromatic Syringyl/Guaiacyl Structures and Erythro/Threo Side Chain Structures in β-O-4 Type during Alkaline Delignification: As a Basis for the Different Degradability of Hardwood and Softwood Lignin. J. Agric. Food Chem. 60 (26), 6471–6476. doi:10.1021/jf301329v

CrossRef Full Text | Google Scholar

Sluiter, A., Hames, B., Ruiz, R., Scarlata, C., Sluiter, J., and Templeton, D. (2008a). Determination of Sugars, Byproducts, and Degradation Products in Liquid Fraction Process Samples. Golden, CO: National Renewable Energy Laboratory. Technical Report NREL/TP-510-42623.

Google Scholar

Sluiter, A., Hames, B., Ruiz, R., Scarlata, C., Sluiter, J., Templeton, D., et al. (2008b). Determination of Structural Carbohydrates and Lignin in Biomass. Golden, CO: National Renewable Energy Laboratory. Technical Report NREL/TP-510-42618.

Google Scholar

Sluiter, A., Ruiz, R., Scarlata, C., Sluiter, J., and Templeton, D. (2005). Determination of Extractives in Biomass. Golden, CO: National Renewable Energy Laboratory. Technical Report NREL/TP-510-42619.

Google Scholar

Sun, Q., Xia, Y., Klinger, J., Seifert, R., Kane, J., Thompson, V., et al. (2021). X-ray Computed Tomography-Based Porosity Analysis: Algorithms and Application for Porous Woody Biomass. Powder Tech. 388, 496–504. doi:10.1016/j.powtec.2021.05.006

CrossRef Full Text | Google Scholar

Tanaka, M. (2021). Noise Level Estimation from a Single Image (Available at: https://www.mathworks.com/matlabcentral/fileexchange/36921-noise-level-estimation-from-a-single-image)[Online]. MATLAB Central File Exchange. [Accessed December 21, 2021].

Google Scholar

Tao, L., Chen, X., Aden, A., Kuhn, E., Himmel, M. E., Tucker, M., et al. (2012). Improved Ethanol Yield and Reduced Minimum Ethanol Selling price (MESP) by Modifying Low Severity Dilute Acid Pretreatment with Deacetylation and Mechanical Refining: 2) Techno-Economic Analysis. Biotechnol. Biofuels 5 (1), 69. doi:10.1186/1754-6834-5-69

PubMed Abstract | CrossRef Full Text | Google Scholar

Thiele, E. W. (1939). Relation between Catalytic Activity and Size of Particle. Ind. Eng. Chem. 31 (7), 916–920. doi:10.1021/ie50355a027

CrossRef Full Text | Google Scholar

Thompson, V. S., Lacey, J. A., Hartley, D., Jindra, M. A., Aston, J. E., and Thompson, D. N. (2016). Application of Air Classification and Formulation to Manage Feedstock Cost, Quality and Availability for Bioenergy. Fuel 180, 497–505. doi:10.1016/j.fuel.2016.04.040

CrossRef Full Text | Google Scholar

Thornburg, N. E., Pecha, M. B., Brandner, D. G., Reed, M. L., Vermaas, J. V., Michener, W. E., et al. (2020). Mesoscale Reaction-Diffusion Phenomena Governing Lignin‐First Biomass Fractionation. ChemSusChem 13 (17), 4495–4509. doi:10.1002/cssc.202000558

PubMed Abstract | CrossRef Full Text | Google Scholar

Usseglio-Viretta, F. L. E., Patel, P., Bernhardt, E., Mistry, A., Mukherjee, P. P., Allen, J., et al. (2020). MATBOX: An Open-Source Microstructure Analysis Toolbox for Microstructure Generation, Segmentation, Characterization, Visualization, Correlation, and Meshing Available at: (https://github.com/NREL/MATBOX_Microstructure_analysis_toolbox) [Online]. GitHub. [Accessed December 20, 2021].

Google Scholar

Usseglio-Viretta, F. L. E., Patel, P., Bernhardt, E., Mistry, A., Mukherjee, P. P., Allen, J., et al. (2022). MATBOX: An Open-Source Microstructure Analysis Toolbox for Microstructure Generation, Segmentation, Characterization, Visualization, Correlation, and Meshing. SoftwareX 17, 100915. doi:10.1016/j.softx.2021.100915

CrossRef Full Text | Google Scholar

Vanommeslaeghe, K., Hatcher, E., Acharya, C., Kundu, S., Zhong, S., Shim, J., et al. (2009). CHARMM General Force Field: A Force Field for Drug-like Molecules Compatible with the CHARMM All-Atom Additive Biological Force fields. J. Comput. Chem. 31 (4), NA. doi:10.1002/jcc.21367

CrossRef Full Text | Google Scholar

Vermaas, J. V., Petridis, L., Ralph, J., Crowley, M. F., and Beckham, G. T. (2019). Systematic Parameterization of Lignin for the CHARMM Force Field. Green. Chem. 21 (1), 109–122. doi:10.1039/C8GC03209B

CrossRef Full Text | Google Scholar

Viamajala, S., Donohoe, B. S., Decker, S. R., Vinzant, T. B., Selig, M. J., Himmel, M. E., et al. (2010). “Heat and Mass Transport in Processing of Lignocellulosic Biomass for Fuels and Chemicals,” in Sustainable Biotechnology: Sources of Renewable Energy. Editors O. V. Singh, and S. P. Harvey (Dordrecht: Springer Netherlands), 1–18. doi:10.1007/978-90-481-3295-9_1

CrossRef Full Text | Google Scholar

Villanova, J., Laurencin, J., Cloetens, P., Bleuet, P., Delette, G., Suhonen, H., et al. (2013). 3D Phase Mapping of Solid Oxide Fuel Cell YSZ/Ni Cermet at the Nanoscale by Holographic X-ray Nanotomography. J. Power Sourc. 243, 841–849. doi:10.1016/j.jpowsour.2013.06.069

CrossRef Full Text | Google Scholar

Vincent Sahayaraj, D., Lusi, A., Mitchell, E. M., Bai, X., and Tessonnier, J.-P. (2021). Comparative Study of the Solvolytic Deconstruction of Corn stover Lignin in Batch and Flow-Through Reactors. Green. Chem. 23 (19), 7731–7742. doi:10.1039/D1GC02420E

CrossRef Full Text | Google Scholar

Xu, L., Zhang, S.-J., Zhong, C., Li, B.-Z., and Yuan, Y.-J. (2020). Alkali-Based Pretreatment-Facilitated Lignin Valorization: A Review. Ind. Eng. Chem. Res. 59 (39), 16923–16938. doi:10.1021/acs.iecr.0c01456

CrossRef Full Text | Google Scholar

Yang, B., Tao, L., and Wyman, C. E. (2017). Strengths, Challenges, and Opportunities for Hydrothermal Pretreatment in Lignocellulosic Biorefineries. Biofuels, Bioproducts and Biorefining, n/a. doi:10.1002/bbb.1825

CrossRef Full Text | Google Scholar