- Nuclear Power Plant Institute, Harbin Engineering University, Harbin, China
The gravitational deposition and coagulation of aerosols were studied experimentally based on the COSTTHES (Containment Source-Term and Thermal Hydraulics Experiment System) facility and numerically investigated based on a continuous general dynamic equation; the experimental and the numerical results were in good agreement. In the present study, the applicability of the zero-dimensional model for deposition and coagulation of aerosols was verified. A considerable distortion can occur due to the coagulation of the aerosol, which significantly influenced the removal rate of the aerosol with a diameter greater than 0.76 µm, and the dynamic shape factor value of the aerosol used in the present experiment was obtained as 4. In the experimental and numerical studies, it was found that the combined effect of the gravitational deposition and coagulation of the aerosol can increase the number density of the aerosol with specific diameters, and the concentration-increment size would increase as settling continued.
Introduction
Aerosol is one of the matter of concerns in the area of nuclear safety. During the course of a severe accident of a Pressurized Water Reactor (PWR), aerosols might be released from the ruptures of the coolant loop or generated from the Molten Core—Concrete Interaction (MCCI) (Sevón, 2005), and water vapor can be generated in the containment building, which causes the increase in pressure and temperature. Once the containment is breached, the radioactive aerosol will be released, which leads to a severe threat to the environment and the public. The radioactivity and the health hazard of the potential leakage are related to the concentration and size of the aerosol, and the time evolution of the aerosol concentration and the size distribution is influenced by various mechanisms. It is therefore of great importance to investigate the time evolution of the aerosol concentration and the size distribution of the aerosol.
The natural removal mechanisms (gravitational deposition, Brownian diffusion, thermophoresis settling, and diffusiophoresis settling) dominate aerosol size distribution and aerosol concentration in the absence of a spray system (Powers et al., 1996). In addition to the aforementioned settling mechanisms, coagulation affects the behavior of aerosol as well (Kwon and Lee, 2002). Though the coagulation does not result in the change in the mass of the aerosol in the containment, it influences the Particle Size Distribution (PSD) of the aerosol and then influences the overall removal efficiency of the aerosol (Schnell et al., 2006). The zero-dimensional Continuous General Dynamic Equation (Continuous GDE) is the commonly used numerical model to describe the settling and coagulation behavior of the aerosol (Friendlander, 2000). Many methods were developed to solve the GDE: the moment method (Zurita-Gotor and Rosner, 2004; Xie, 2014; Yu et al., 2015), the direct simulation Monte Carlo (DSMC) method (Sheng and Shen, 2006; Sheng and Shen, 2007), the and sectional treatment method (Hounslow et al., 1988; Lister et al., 1995; Kumar and Ramkrishna, 1996; Geng et al., 2013). The moment method suffers from the shortcoming that a priori knowledge of the mathematical form of the size distribution of the aerosol is required; however, the experimental data provided by the instrument usually deviate more or less from the perfect mathematical form. As to the DSMC, its computation is expensive if the number of aerosol particles is large. In the settling process, the continuous decay of the particle number leads to a decrease in the simulation accuracy of the DSMC (Sheng and Shen, 2006).
Numerical studies related to the gravitational deposition and coagulation of the aerosol were conducted to analyze the behavior of the aerosol settling and coagulation. Lindauer and Castleman (1970) numerically studied the relative importance of Brownian and gravitational coagulation on the transient behavior of aerosol undergoing coagulation and gravitational settling. In his study, the homogeneous dispersed aerosol particles were assumed to be spherical. Powers et al. (1996) established a numerical model in which the settling mechanisms and coagulation mechanisms of aerosol were considered. In their study, it was indicated that the coagulation of the aerosol particles could lead to fantastic distortion from spherical, and the distortion of the aerosol agglomerate was considered by employing the dynamic shape factor. Garcia-Nieto (2006) numerically studied the scavenging efficiencies of aerosol emissions from coal-fired power plants; in the model, the coagulation and settling of aerosol were considered and the aerosol was considered as spherical particles, and it was found that the respirable dust has the lowest scavenging efficiency. Ghosh et al. (2017) developed a numerical model based on a semi-implicit solved GDE method, and it was revealed that the charge could significantly enhance the coagulation process of the aerosol. The model was validated against the results obtained by the experiment which was conducted in a
Kwon and Lee (2002) investigated separately the gravitational deposition and coagulation of aerosol using a horizontal cylinder and vertical cylinder; the experimental facility structure and its scale ensured the homogeneous distribution of the aerosol, that is, the potential stratification of the aerosol concentration was eliminated. The discussion of effective time in this study implied that the stratification of the aerosol concentration could occur under a static condition. The characteristics of the size evolution and the deposition velocity of the aerosol were studied experimentally by Kumar et al. (2015) (Subramanian et al., 2011; Misra et al., 2013; Kumar et al., 2015), and the experiments were conducted based on the ATF facility which had a closed chamber of
In the present work, the combined effect of aerosol coagulation and gravitational deposition was studied experimentally based on the COSTTHES (Containment Source-Term and Thermal Hydraulics Experiment System) facility. The multisampling configuration (three sampling elevations) and the dimensions of the COSTTHES facility (a vessel with a height of
Experimental Facility and Method
Experimental Facility
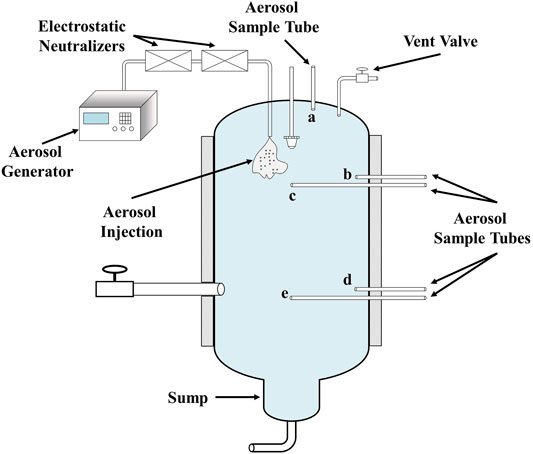
The experimental study in the present work was conducted based on the COSTTHES facility. The facility and schematic of COSTTHES are shown in Figure 1 and Figure 2
The COSTTHES facility is composed of a closed cylindrical vessel (
Experimental Procedure
In the experiment, as dried and filtered air was blown into the vessel to remove the water vapor and environmental aerosols, the humidity in the vessel was close to zero. While the air was transmitted, the vessel permitted the gas discharge to remain at atmospheric pressure; therefore, the pressure in the vessel was
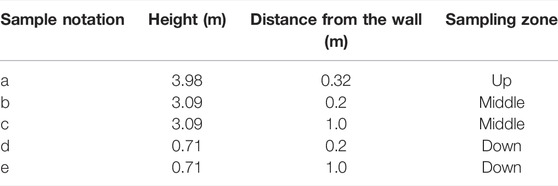
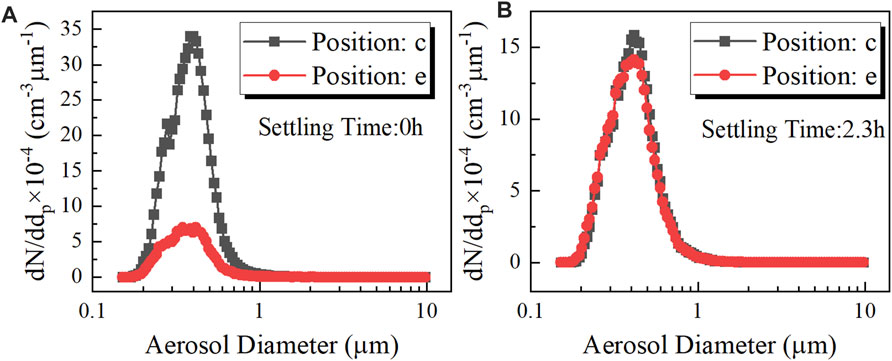
An experiment was conducted to investigate the radial distribution of aerosol and the results are presented in Figure 3; it can be noted that the size spectra at the same height were adequately close to each before the aerosol was homogenous. Therefore, the experimental data acquired at the sampling positions c and e were employed to represent the size spectra at the corresponding heights. Because the aerosol was injected from the dome of the vessel, when the aerosol injection was just complete the number density at the higher position was much higher than that at the lower position, as shown in Figure 4. After 2.3 h of settling and mixing, the aerosol became almost homogeneous in the vessel and the aerosol state at this moment and thereafter was used in the analysis.
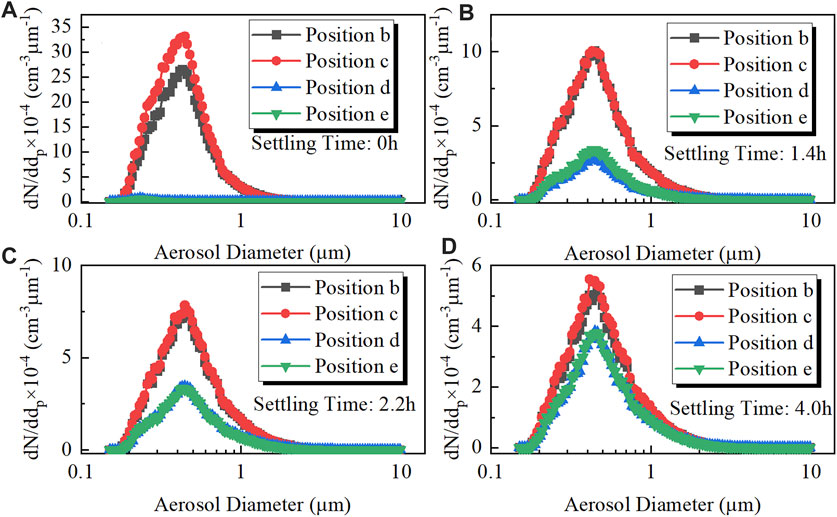
FIGURE 3. Radial distribution of aerosol: (A) 0 h settling, (B) 1.4 h settling, (A) 2.2 h settling and (D) 4.0 h settling.
Computation Model
General Dynamic Equation
In the present model, the aerosol spatial distribution was assumed to be homogeneous and the gravitational coagulation, Brownian coagulation, and gravitational deposition were considered the influencing mechanisms. Hence, the Continuous General Dynamic Equation (Continuous GDE) that governs the aerosol kinetic behavior can be written in the following form (García-Nieto, 2001; García-Nieto, 2006; Kwon and Lee, 2002):
where
The first term on the right-hand side (RHS) of Eq. 1 represents the rate of formation of particles between volumes
where
where
where
where
Discretization of the General Dynamic Equation
The form of the nonlinear integro-partial-differential equation of the GDE makes the analytical solution rarely tractable. The widely used moment method can be used to determine the solution of the GDE with a low computation time; nevertheless, it does not permit variation in the resolution of the size distribution due to the fixed number of parameters (Lister et al., 1995). Moreover, in the moment method, one needs to assume the form of the initial size distribution of the particle, such as log-normal distribution for aerosols. However, the size distribution of the aerosol obtained with an instrument (e.g., a particle size spectrometer) usually does not perfectly fit the ideal log-normal distribution. Hence, the sectional treatment of the aerosol size distribution introduced by Lister et al. (1995) was used in the present model. In Lister’s discretization scheme, the size distribution of the aerosol is divided into a finite number of sections (groups) and the ratio of volumes of two adjacent sections is
where
According to Lister’s discretization scheme, Eq. 1 can be transformed into
where
where
The accuracy and the resolution of the discretized size distribution of the aerosol increase with the increasing value of
Experimental Results and Analysis
Dynamic Shape Factor
The sedimentation velocity of the aerosol particle is related to the dynamic shape factor of the aerosol, the diameter of the aerosol, the viscosity of air, and the density of the aerosol. The dynamic shape factor
The removal constant defined by Eq. 9 was usually used to evaluate the settling process of the aerosol. However, when the deposition is combined with coagulation of the aerosol, the removal constant might not be a constant throughout the settling process. Hence, in the present study, the relative removal rate was defined by Eq. 10 and employed to analyze the settling process of the aerosol.
where
The comparison between the relative removal rate of the experimental result and that of the numerical result is shown in Figure 6. It can be noticed that the numerical relative removal rate was approaching the experimental one for the aerosol with a diameter greater than 0.76 µm as the dynamic shape factor of the aerosol increased. According to Eq. 8, the gravitational deposition velocity of the aerosol particle decreases with increasing dynamic shape factor. Therefore, the gravitational deposition dominates the removal rate of
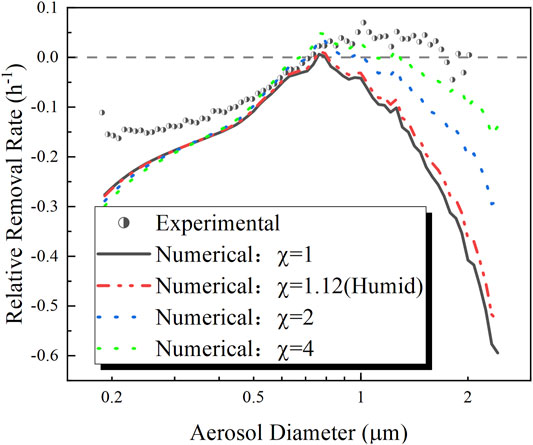
FIGURE 6. Distributions of the relative removal rate of the experimental result and the numerical result.
The max discrepancies between the experimental distribution of the relative removal rate and the numerical ones with different dynamic shape factors are shown in Figure 7 which indicates that the value of the dynamic shape factor is 4 in the present experiment.
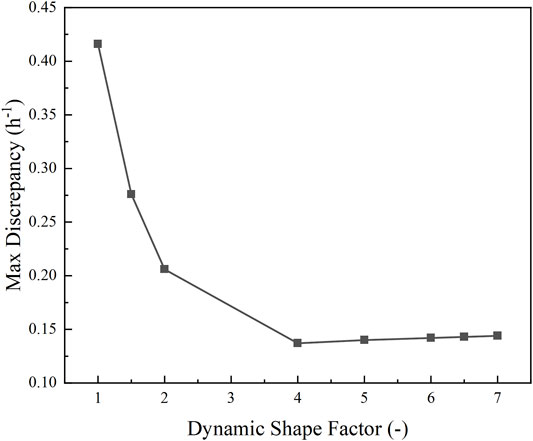
FIGURE 7. Max discrepancy between the relative removal rate of the experimental result and the numerical result.
Stratification of Aerosol Concentration
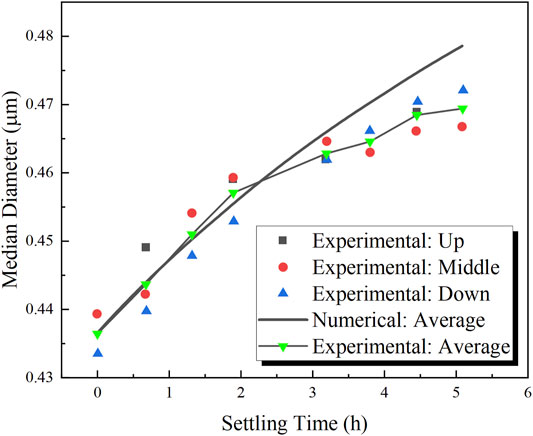
In the light of the above analysis, the dynamic shape factor in the present numerical study was set to 4, and the size distribution of the aerosol of the experimental result and that of the numerical result are compared in Figure 8. The comparison indicated that the experimental result and the numerical prediction were in good agreement.
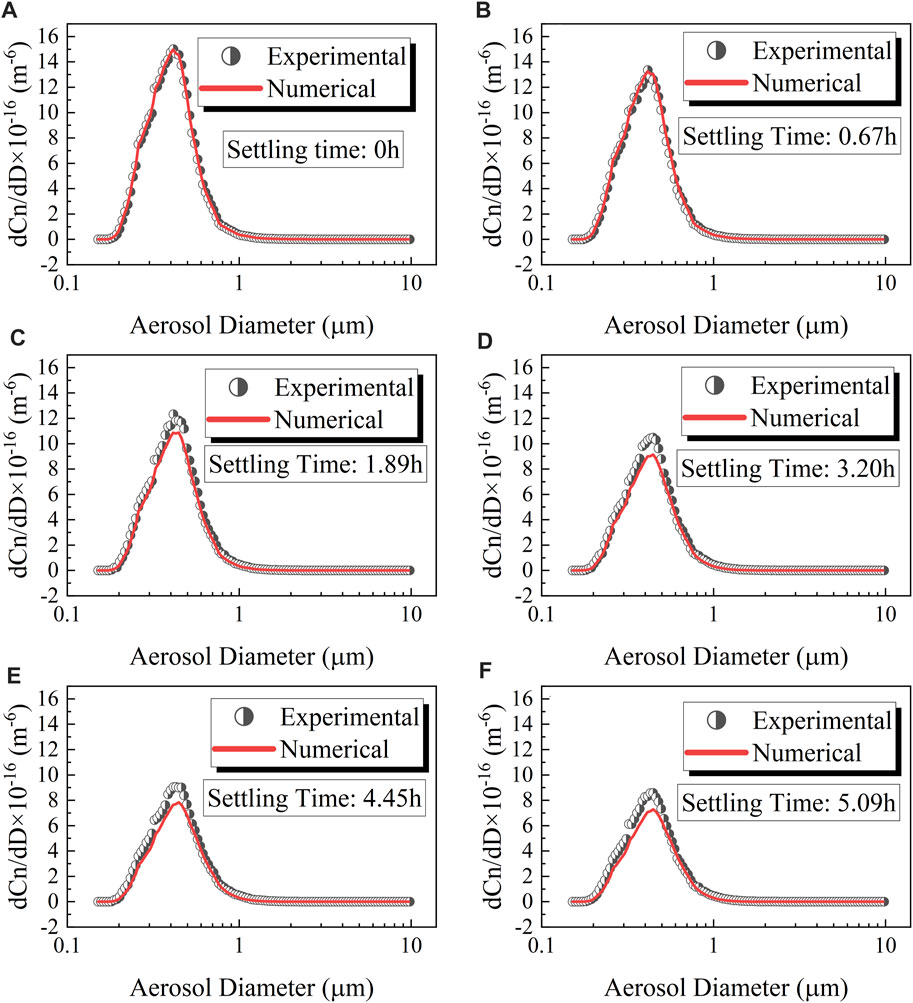
FIGURE 8. Comparison of the experimental and numerical size distribution of the aerosol at different time, the dynamic shape factor x = 4: (A) 0 h, (B) 0.67 h, (C) 1.89 h, (D) 3.20 h, (E) 4.45 h and (F) 5.09 h.
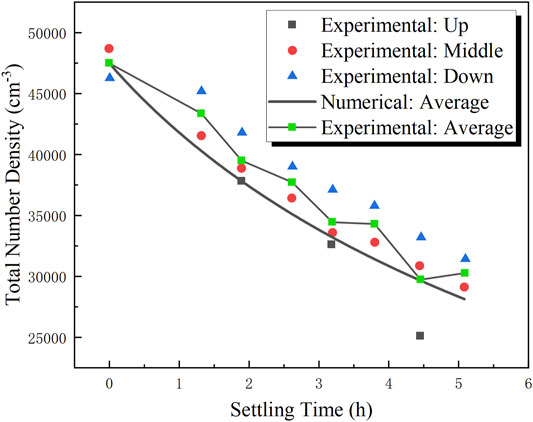
Under the action of the gravitational deposition, the number density of the aerosol continuously decreased, as shown in Figure 9 and Figure 10. As shown in Figure 10, the total number density of the aerosol increased with decreasing height; in other words, the stratification of the aerosol concentration could be observed. However, in Figure 9, the median diameter of the aerosol did not appear stratified like the number density. As shown in Figure 10, the largest difference in the total number density of the aerosol in the Up Zone and the Down Zone was observed to be 9.5% at 3.2 h, and the largest prediction error with respect to the average total number density of the aerosol was 8.4% at 3.8 h. Hence, in 5.1 h of aerosol settling the stratification did not significantly affect the applicability of the zero-dimensional numerical model (GDE).
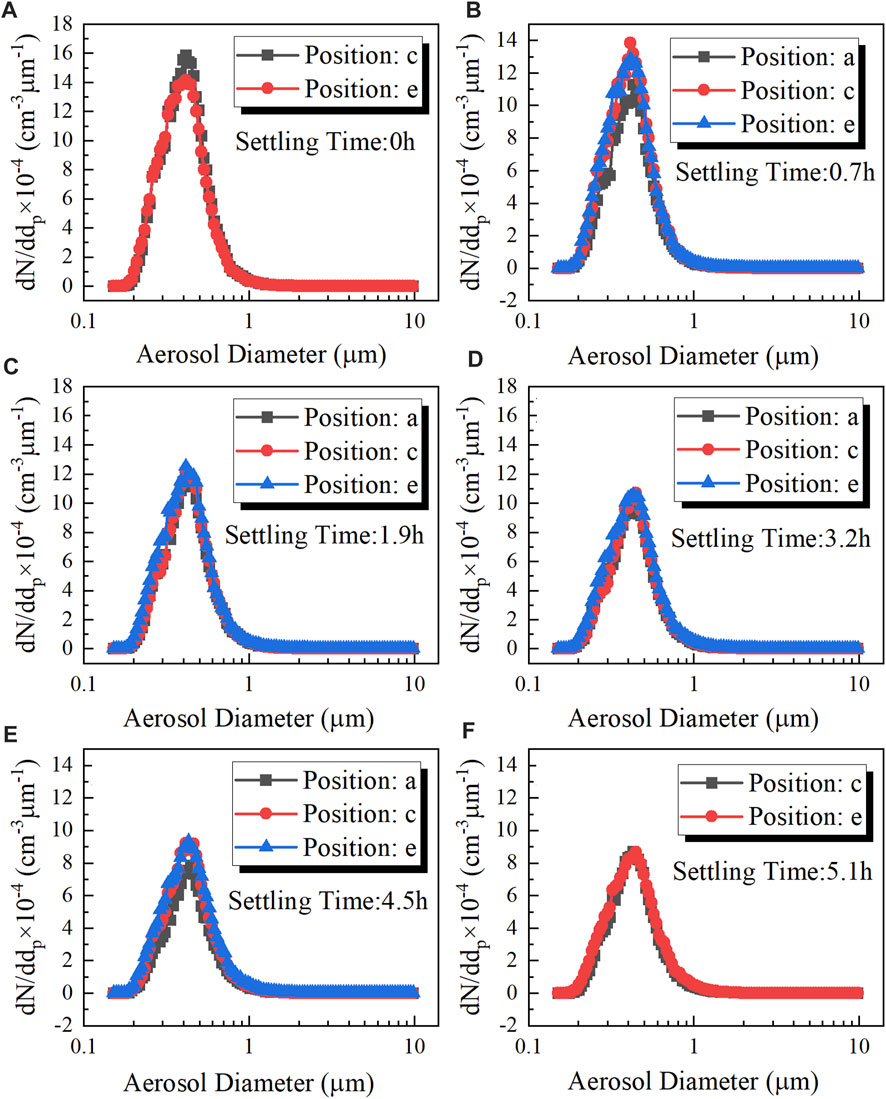
FIGURE 9. Evolution of the size distribution of the aerosol at different elevations: (A) 0 h, (B) 0.7 h, (C) 1.9 h, (D) 3.2 h, (E) 4.5 h, and (F) 5.1 h.
In the coagulation process, small particles aggregate into larger particles, which leads to an increase in the number density of the large particles. Nevertheless, the deposition of the large particle is much stronger than that of the small particles, which, on the contrary, results in a decrease in the number density of the large particles. In the present experiment, the median diameter of the aerosol particles increased throughout the duration of aerosol settling, as shown in Figure 11, which indicated that the coagulation mechanism is stronger than the deposition mechanism in the total number density range of the present experiment (
Concentration-Increment Size
In order to analyze separately the influences of different mechanisms considered in the numerical model, the relative removal rate due to coagulation and gravitational deposition was calculated and is shown in Figure 12. According to Eq. 7, Eq. 8, and Eq. 10, the gravitational deposition is not affected by the number density of the aerosol, and the relative removal rate due to gravitational deposition did not vary with the settling time. However, the absolute value of the relative removal rate due to coagulation of the aerosol decreased with settling time, which is attributed to the decreasing collision frequency due to the decreasing number density of the aerosol.
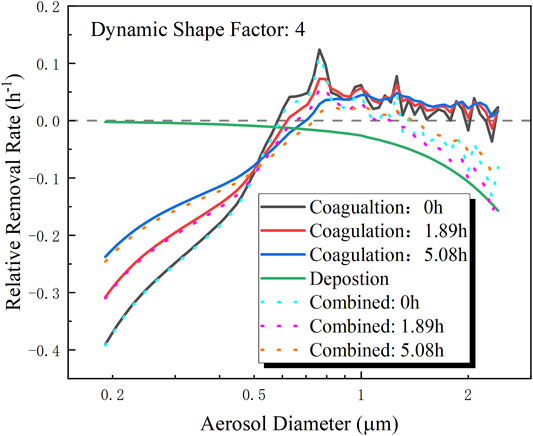
FIGURE 12. Size distribution of the relative removal rate due to gravitational deposition and coagulation.
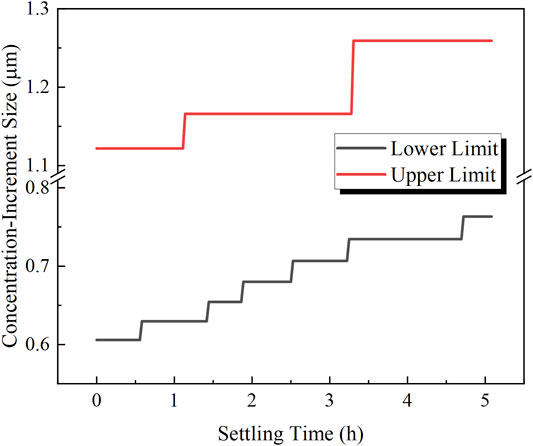
In the experimental result (Figure 6) and numerical result (Figure 12), a concentration increment phenomenon was observed. For the tiny aerosol (diameter below 0.6 µm), the relative removal rate was negative because of the predominant coagulation mechanism. For the large aerosol (diameter above 1.1 µm), the relative removal rate was negative as well because of the predominant gravitational deposition mechanism. However, the two aforementioned mechanisms were both weak for the medium size aerosol (diameter between 0.6 and 1.1 µm), which led to a positive relative removal rate (that is, the number density increased in a period). The time evolution of the concentration-increment size range is shown in Figure 13, within 5.1 h of settling; the lower limit of the concentration-increment size range was increased from 0.61 to 0.76 µm and the upper limit increased from 1.12 to 1.26 µm. Hence, as the gravitational deposition and coagulation continued, the concentration-increment size increased.
Conclusion
The gravitational deposition and coagulation are significant phenomena for the aerosol in the severe reactor accident. In this study, the gravitational deposition and coagulation were studied experimentally based on the COSTTHES facility and numerically with the population balance method. According to the present experimental and numerical studies, we draw the following conclusions: 1) The comparison between the experimental results and the numerical results showed that the present numerical model could predict the deposition and coagulation behavior of the aerosol with a satisfying agreement. 2) The experimental results and the numerical predictions showed that the behavior of the aerosol with a diameter greater than 0.76 µm was dominated by the gravitational deposition mechanism, which was influenced significantly by the dynamic shape factor, and, in the present experiment, the dynamic shape factor was inferred to be 4. 3) The stratification of aerosol concentration was observed in the experiment; the largest difference in the total number density of the aerosol at different elevations was observed to be 9.5%, and the largest prediction error was 8.4%. Hence, the zero-dimensional numerical model was still applicable within 5.1 h of settling though the aerosol concentration stratification existed. 4) In the present experiment, the median diameter of the aerosol kept growing within 5.1 h of settling, which indicated that gravitational deposition was the predominant mechanism compared with coagulation. The slowing down growth trend of the median diameter of the aerosol indicated the weakening coagulation mechanism due to the decreasing number density of the aerosol. 5) A concentration increment phenomenon was observed in the experiment and predicted by the numerical model during aerosol settling, and it was found that as the gravitational deposition and coagulation continued the concentration increment size increased.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author Contributions
YH contributed to the conception and design and data analysis of the study. GH, SZ, and ZY provided guidance and suggestions for the study. CJ and LY assisted in the experiment.
Funding
This work was supported by the National Key R&D Program of China under Grant (number 2020YFB1901401).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
REFERENCES
Friendlander, S. K. (2000). Smoke, Dust and Haze: Fundamentals of Aerosol Dynamics. New York, USA: Oxford University Press. 38-2208-38-2208. doi:10.5860/choice.38-2208
Freitag, M., Gupta, S., Beck, S., and Sonnenkalb, M. (2018). Experimental and Analytical Investigations of Aerosol Processes—Wash-Out and Wash-Down. Nucl. Sci. Eng. 193, 198–210. doi:10.1080/00295639.2018.1479091
García-Nieto, P. J. (2001). Parametric Study of Selective Removal of Atmospheric Aerosol by Coagulation, Condensation and Gravitational Settling. Int. J. Environ. Health Res. 11, 149–160. doi:10.1080/09603120020047528
García-Nieto, P. J. (2006). Study of the Evolution of Aerosol Emissions from Coal-Fired Power Plants Due to Coagulation, Condensation, and Gravitational Settling and Health Impact. J. Environ. Manag. 79, 372–382. doi:10.1016/j.jenvman.2005.08.006
Geng, J., Park, H., and Sajo, E. (2013). Simulation of Aerosol Coagulation and Deposition under Multiple Flow Regimes with Arbitrary Computational Precision. Aerosol Sci. Technol. 47, 530–542. doi:10.1080/02786826.2013.770126
Ghosh, K., Tripathi, S. N., Joshi, M., Mayya, Y. S., Khan, A., and Sapra, B. K. (2017). Modeling Studies on Coagulation of Charged Particles and Comparison with Experiments. J. Aerosol Sci. 105, 35–47. doi:10.1016/j.jaerosci.2016.11.019
Hounslow, M. J., Ryall, R. L., and Marshall, V. R. (1988). A Discretized Population Balance for Nucleation, Growth, and Aggregation. AIChE J. 34, 1821–1832. doi:10.1002/aic.690341108
Hussein, T., Hruška, A., Dohányosová, P., Džumbová, L., Hemerka, J., Kulmala, M., et al. (2009). Deposition Rates on Smooth Surfaces and Coagulation of Aerosol Particles inside a Test Chamber. Atmos. Environ. 43, 905–914. doi:10.1016/j.atmosenv.2008.10.059
Kumar, A., Subramanian, V., Baskaran, R., and Venkatraman, B. (2015). Size Evolution of Sodium Combustion Aerosol with Various Rh. Aerosol Air Qual. Res. 15, 2270–2276. doi:10.4209/aaqr.2015.03.0150
Kumar, S., and Ramkrishna, D. (1996). On the Solution of Population Balance Equations by Discretization-I. A Fixed Pivot Technique. Chem. Eng. Sci. 51, 1311–1332. doi:10.1016/0009-2509(96)88489-2
Kwon, S. B., and Lee, K. W. (2002). Experimental and Numerical Study of Aerosol Coagulation by Gravitation. Part. Part. Syst. Charact. 19, 103–110. doi:10.1002/1521-4117(200205)19:2<103::AID-PPSC103>3.0.CO;2-I
Lau, R., and Chuah, H. K. L. (2013). Dynamic Shape Factor for Particles of Various Shapes in the Intermediate Settling Regime. Adv. Powder Technol. 24, 306–310. doi:10.1016/j.apt.2012.08.001
Lindauer, G. C., and Castleman, A. W. (1970). The Importance of Gravitational Coagulation on the Settling of High-Mass Density Aerosols. Nucl. Sci. Eng. 42, 58–63. doi:10.13182/nse70-a19327
Lister, J. D., Smit, D. J., and Hounslow, M. J. (1995). Adjustable Discretized Population Balance for Growth and Aggregation. AIChE J. 41, 591–603. doi:10.1002/aic.690410317
Liu, L., Zhang, Z., Wu, Y., Yang, W., Wu, S., and Zhang, L. (2017). Decay of High-Concentration Aerosol in a Chamber. Aerosol Sci. Eng. 1, 155–159. doi:10.1007/s41810-017-0015-z
Misra, J., Subramanian, V., Kumar, A., Baskaran, R., and Venkatraman, B. (2013). Investigation of Aerosol Mass and Number Deposition Velocity in a Closed Chamber. Aerosol Air Qual. Res. 13, 680–688. doi:10.4209/aaqr.2012.06.0159
Narayanam, S. P., Kumar, A., Pujala, U., Subramanian, V., Srinivas, C. V., Venkatesan, R., et al. (2021). Theoretical Simulation on Evolution of Suspended Sodium Combustion Aerosols Characteristics in a Closed Chamber. Nucl. Eng. Technol. 0–6. doi:10.1016/j.net.2021.12.029
Powers, D. A., Washington, K. E., Burson, S. B., and Sprung, J. L. (1996). A Simplified Model of Aerosol Removal by Natural Processes in Reactor Containment. U.S. Nucl. Regul. Comm. Albuquerque USA: (NRC), NUREG-CR-6173.
Schnell, M., Cheung, C. S., and Leung, C. W. (2006). Investigation on the Coagulation and Deposition of Combustion Particles in an Enclosed Chamber with and without Stirring. J. Aerosol Sci. 37, 1581–1595. doi:10.1016/j.jaerosci.2006.06.001
Sevón, T. (2005). Molten Core-Concrete Interactions in Nuclear Accidents: Theory and Design of an Experimental Facility. Helsinki, Finland: VTT Technical Research Centre of Finland.
Sheng, C., and Shen, X. (2006). Modelling of Acoustic Agglomeration Processes Using the Direct Simulation Monte Carlo Method. J. Aerosol Sci. 37, 16–36. doi:10.1016/j.jaerosci.2005.03.004
Sheng, C., and Shen, X. (2007). Simulation of Acoustic Agglomeration Processes of Poly-Disperse Solid Particles. Aerosol Sci. Technol. 41, 1–13. doi:10.1080/02786820601009704
Subramanian, V., Baskaran, R., Misra, J., and Indira, R. (2011). Experimental Study on the Behavior of Suspended Aerosols of Sodium and Nonradioactive Fission Products (SrO2and CeO2) in a Closed Vessel. Nucl. Technol. 176, 83–92. doi:10.13182/NT11-A12544
Tian, L. T., Gu, H., Yu, H., and Chen, J. (2020). Experimental Study on the Natural Deposition Characteristics of Erosols in Containment. Front. Energy Res. 8, 345. doi:10.3389/fenrg.2020.527598
Xie, M.-L. (2014). Asymptotic Behavior of TEMOM Model for Particle Population Balance Equation over the Entire Particle Size Regimes. J. Aerosol Sci. 67, 157–165. doi:10.1016/j.jaerosci.2013.10.001
Yu, M., Koivisto, A. J., Hämeri, K., Seipenbusch, M., and Hämeri, K. (2013). Size Dependence of the Ratio of Aerosol Coagulation to Deposition Rates for Indoor Aerosols. Aerosol Sci. Technol. 47, 427–434. doi:10.1080/02786826.2012.759640
Yu, M., Liu, Y., Lin, J., and Seipenbusch, M. (2015). Generalized TEMOM Scheme for Solving the Population Balance Equation. Aerosol Sci. Technol. 49, 1021–1036. doi:10.1080/02786826.2015.1093598
Keywords: gravitational deposition, coagulation, COSTTHES, GDE, aerosol
Citation: Yu H, Gu H, Sun Z, Zhou Y, Chen J and Li Y (2022) Experimental and Numerical Study on the Gravitational Deposition and Coagulation of Aerosols. Front. Energy Res. 10:840503. doi: 10.3389/fenrg.2022.840503
Received: 21 December 2021; Accepted: 20 April 2022;
Published: 20 May 2022.
Edited by:
Jun Wang, University of Wisconsin-Madison, United StatesReviewed by:
Longchao Yao, Zhejiang University, ChinaGuangzong Zheng, China Institute of Atomic Energy, China
Copyright © 2022 Yu, Gu, Sun, Zhou, Chen and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Haifeng Gu, Z3VoYWlmZW5nQGhyYmV1LmVkdS5jbg==
 Huiyu Yu
Huiyu Yu Haifeng Gu
Haifeng Gu Zhongning Sun
Zhongning Sun Yanmin Zhou
Yanmin Zhou Yingzhi Li
Yingzhi Li