Application of the Material Balance Equation Based on the BET Multimolecular Fractal Theory in a Shale Gas Reservoir

Qiu, Tingting; Hu, Shuyong; Zhang, Jiayi

doi:10.3389/fenrg.2022.829800

METHODS article

Front. Energy Res., 26 April 2022

Sec. Advanced Clean Fuel Technologies

Volume 10 - 2022 | https://doi.org/10.3389/fenrg.2022.829800

This article is part of the Research Topic Cleaner Treatment Technologies and Productions in The Energy Industry View all 24 articles

Application of the Material Balance Equation Based on the BET Multimolecular Fractal Theory in a Shale Gas Reservoir

Tingting Qiu

Shuyong Hu

Jiayi Zhang*

State Key Laboratory of Oil and Gas Reservoir Geology and Development Engineering, Southwest Petroleum University, Chengdu, China

During shale gas reservoir development, obtaining actual formation pressure is challenging; therefore, it is challenging to obtain a single well production allocation using the current formation pressure based on a productivity equation. Different shale gas reservoirs with different rock adsorption properties and the traditional Langmuir isotherm adsorption equations are not accurate in describing the adsorption properties of shale gas reservoirs, causing significant errors. BET multimolecular adsorption, considering the shale gas surface fractal dimension theory to describe the adsorption properties, can describe the adsorption surface as a multimolecular layer and regard adsorption using a fractal dimension, describing the adsorption property of shale gas more accurately. According to the core adsorption test data and theory, the actual BET multimolecular adsorption is established by considering the shale gas surface fractal dimension. Therefore, the actual material balance equation was obtained using the theory, establishing the relationship between the formation pressure and cumulative shale gas production. A time-independent distribution and cumulative gas production chart were formed using the productivity equation. Consequently, the material balance equation, which takes advantage of the BET multimolecular fractal theory, was conducted. This allocation production method obtained from the material balance equation has significant importance in shale gas development.

Introduction

Shale gas reserves comprised free, adsorbed, and dissolved gases, of which free and adsorbed gases are the main parts (Taghavinejad et al., 2020); (Mengal and Wattenbarger, 2011); (Huang and Zhao, 2017); (Boadu, 2000); (Sanyal et al., 2006); (Curtis, 2002); (Jenkins and Boyer, 2008). In this regard, the study of shale gas adsorption behavior is significant to reservoir volume calculation and development (Huang and Zhao, 2017); (Shao et al., 2017); (Wu et al., 2015). Currently, the Langmuir isotherm, BET equations, and other modified Langmuir and BET equations predominantly describe the adsorption behavior (Li et al., 2020); (Jaroniec et al., 1989); (Zhang et al., 2015). The classic Langmuir equation assumes that methane is monolayer-adsorbed, and the surface of the adsorbent is homogeneous with constant adsorption heat (Langmuir, 1918); (Langmuir, 2015). The adsorption behavior of shale gas is complex, and Langmuir’s isotherm adsorption equation is too ideal and cannot describe it accurately. The BET adsorption theory considers the adsorption surface as a multilayer, and the adsorption capacity of every layer is the same (Myers, 1968); (Brunauer et al., 1940); (Zhou et al., 2019); (Myers and Prausnitz, 1965); (Ritter and Yang, 1987); (Dang et al., 2020). To simulate the enrichment and production of methane in shale gas reservoirs, an accurate gas adsorption model is critically required (Chareonsuppanimit et al., 2012), (Clarkson and Haghshenas, 2013), (Huang et al., 2018a). Fortunately, the BET multi-molecular fractal theory, considering the surface fractal dimension of shale gas, can describe adsorption more accurately by considering the multilayer and fractal dimension of shale gas adsorption (Brunauer et al., 1938), (Wang et al., 2022), (Chai et al., 2019), (Zheng et al., 2019), (Wang et al., 2016), (Fan and Liu, 2021). Therefore, the material balance equation can enhance the accuracy of future reservoir prediction about reserves and formation pressure based on the adsorption theory (Zhang et al., 2017), (Canel and Rosbaco, 2006), (Fianu et al., 2019).

Ambrose et al., (2012), (Xiong et al., 2021), and (Memon et al., 2020) combined the Langmuir adsorption isotherm with the volume for free gas and formulated a new gas-in-place equation accounting for the pore space occupied by the adsorbed phase; however, the adsorption surface layer and fractal dimension were not considered (Pang et al., 2019). The material balance equation proposed by Daniel et al. (Orozco and Aguilera, 2015) simultaneously considered stress-dependent porosity and permeability, free gas, adsorbed gas, and dissolved gas but also excluded the adsorption surface layer and fractal dimension. Usually, the material balance equation combined with the shale gas productivity equation is used to calculate the reservoir reserves and conduct the relevant model for predicting the production rate and formation pressure versus time (Sun et al., 2019), (Gu et al., 2014), (Hu et al., 2019). The shale gas well allocation is usually based on this method to carry out well productivity tests (Deng et al., 2014), (Wheaton, 2019). According to the test, the shale gas well binomial productivity formula is determined. If the present reservoir pressure is calculated by the material balance equation, then the actual open flow capacity of a single well can be calculated. The reasonable gas well allocation is also determined. Nevertheless, practical reservoir production requires convenient and efficient allocation progress. The aforementioned method aims at a certain moment, is complex, and cannot satisfy the practical production needs. Therefore, finding an efficient and convenient shale gas allocation method for the whole well life is necessary.

Huang et al. (2018b) proposed a new method. Shale reservoirs were depicted by the De Swaan dual porosity model, where the secondary and hydraulic fractures were characterized by discrete units to conduct the shale gas well productivity equation. This method can calculate more efficiently than the Eclipse simulator. Furthermore, it can describe the complex fracture network more correctly even though the calculating process and single shale gas well allocation of every production moment are complex. Sang et al. (2014) used a numerical model considering desorption and adsorption processes to establish and solve, under polar coordinates and Laplace space, respectively, predicting the productivity of volume-fractured horizontal wells in shale gas reservoirs. This model can predict the production rate versus time, but the allocation production of the single well cannot be obtained. At present, the existing allocation methods combining the material balance equation with productivity formula cannot offer well the allocation of well life and satisfy the convenience of practical allocation apart from numeric simulation, decline analysis, and so on (Huang et al., 2018b); (Arps, 1945). As for the adsorption of shale gas reservoirs, we adopted the BET multi-molecular fractal theory. Creatively, we developed a material balance equation based on the BET multi-molecular fractal theory, considering the dissolved gas of the formation water. Furthermore, we combined this new material balance equation with the productivity equation to obtain single well allocation production versus cumulative gas production for the well life cycle. As a result, we can offer the shale gas development worker an allocation plate, and there is no need for paying attention to complex equations about the well and gas reservoir properties. In a word, this method can not only calculate the adsorption gas volume but also propose a convenient and fast life cycle allocation method for shale gas reservoirs.

Material Balance Equation of a Shale Gas Well Based on the BET Multi-Molecular Fractal Theory

The material balance equation of the confining shale gas reservoir was established by considering the reservoir as a fracture-matrix dual system and the dissolved gas in the formation water to obtain the chart of shale gas dynamic allocation production. Furthermore, the BET multimolecular and fractal adsorption theory described the gas adsorption behavior.

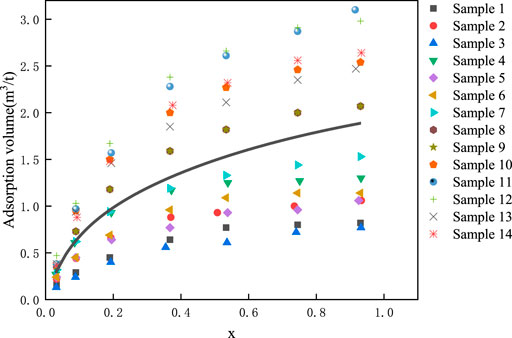
The Actual Isotherm Adsorption Curve of Shale Gas Block XX

Brunauer et al. (1940) proposed the BET multimolecular adsorption theory in 1940, and it was an addition to the Langmuir monolayer molecular adsorption equation. The assumption of the BET multimolecular adsorption theory is as follows:

1) The gas adsorption is multimolecular, and it does not have to cover the first layer completely and then the second.

2) The heat of adsorption (E₁) of the first layer is a certain value; the other is the liquefaction heat (E_L) of the adsorbate.

3) The adsorption and desorption of the adsorbate are exposed on the surface of the gas phase directly.

Consequently, the BET multimolecular adsorption expression is described in Eq. 1.

\frac{V}{V_{m}} = \frac{C x [1 - (n + 1) x^{n} + n x^{n + 1}}{(1 - x) [1 + (C - x) - C x^{n + 1}]} . (1)

In the equation, $x$ is the relative pressure $\frac{p}{p_{0}}$ , $p_{0}$ is the saturated vapor pressure, $n$ is the adsorption layer of the gas surface, and $C$ is the constant related to the energy of adsorption and liquefaction.

Eq. 2 shows the relationship of the adsorption capacity between layers $i$ and One proposed by Fripiat et al., (1986) and (Zhou et al., 2019) based on numeric simulation.

f_{i} = \frac{N_{i}}{N_{1}} = i^{- (D_{s} - 2)} . (2)

In Eq. 2, $D_{s}$ is the fractal dimension of the adsorption surface, $N_{1}$ is the adsorption capacity of layer One, and $N_{i}$ is the adsorption capacity of layer $i$ . Therefore, the BET multimolecular adsorption, considering the fractal dimension of the adsorption surface expression, was obtained as Eq. 3.

V = \frac{V_{m} C \overset{n}{\sum_{i = 1}} i^{2 - D_{s}} \overset{n}{\sum_{j = i}} x^{j}}{1 + C \overset{n}{\sum_{i = 1}} x^{i}} . (3)

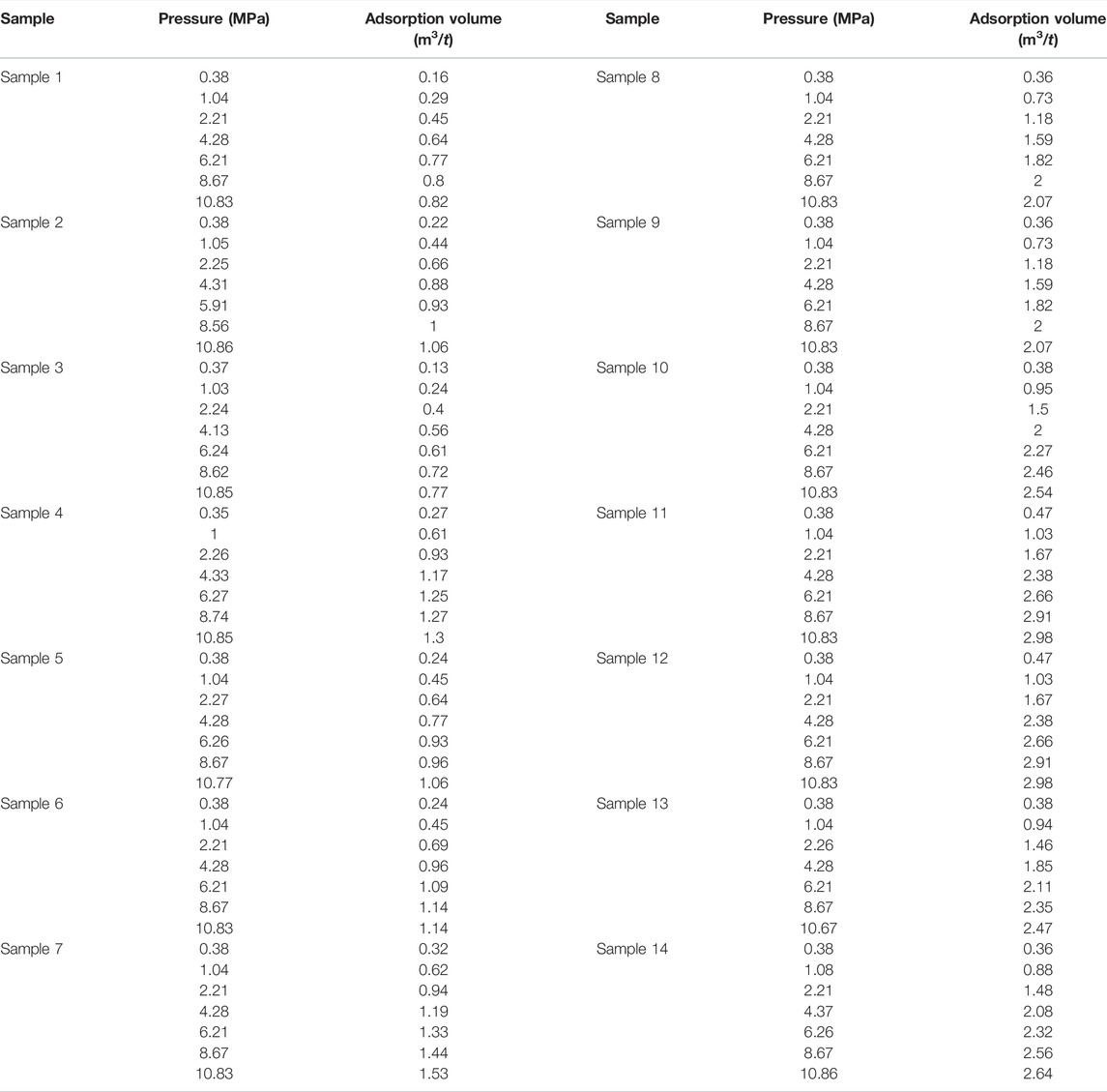
According to Eq. 3, the actual isotherm adsorption curve of shale gas Block XX can be obtained by regression, as shown in Eq. 4, and Figure 1 shows the curve. The gas adsorption test data is showed in Table 1. According to the regression results, we obtained the following conclusions. The adsorption volume of shale gas Block XX was 1.19924 m³/t, and the constant related to the energy of adsorption and liquefaction was 9.86193, based on the fractal dimension 2.5 and the layer of surface molecular adsorption 3 (Figure 1).

V = 1.19924 \frac{9.86193 \times [\begin{array}{l} \frac{P}{P_{0}} + {(\frac{P}{P_{0}})}^{2} + {(\frac{P}{P_{0}})}^{3} + \\ 2^{2 - 2.5} ({(\frac{P}{P_{0}})}^{2} + {(\frac{P}{P_{0}})}^{3}) + 3^{2 - 2.5} {(\frac{P}{P_{0}})}^{3} \end{array}]}{1 + 9.86193 \times [(\frac{P}{P_{0}}) + {(\frac{P}{P_{0}})}^{2} + (\frac{P}{P_{0}})]} . (4)

FIGURE 1

FIGURE 1. Actual isotherm adsorption curve of shale gas Block XX.

TABLE 1

TABLE 1. Test data of shale gas Block XX.

Material Balance Equation of Shale Gas Block XX

The assumption of the material balance equation of shale gas Block XX is as follows:

1) The shale gas reservoir is an isotherm system; in other words, the reservoir temperature is unchanged during exploitation.

2) The water saturation of the matrix and fracture system is different.

3) There is no formation of water to be produced.

According to the principle of the material balance equation, the underground volume of the produced shale gas comprised underground expansion, including free gas, formation water, rock, dissolved gas of formation water underground volume variation of the matrix, and fracture system. For the shale gas reservoir, it included the underground adsorption gas volume variation of the matrix system. When the shale gas reservoir proceeded to desorption, the material balance equation was as shown in Eq. 5.

\begin{array}{l} G_{p g} B_{g} = G_{m} (B_{g} - B_{g i}) + G_{m} B_{g i} \frac{C_{w} S_{m w i}}{1 - S_{m w i}} (P_{i} - P) + \\ G_{m} B_{g i} \frac{C_{m}}{1 - S_{m w i}} (P_{i} - P) + \frac{G_{m} B_{g i}}{(1 - S_{m w i}) B_{w}} S_{m w i} (R_{s i} - R_{s}) B_{g} + \\ G_{f} (B_{g} - B_{g i}) + G_{f} B_{g i} \frac{C_{w} S_{f w i}}{1 - S_{f w i}} (P_{i} - P) + \\ G_{f} B_{g i} \frac{C_{f}}{1 - S_{f w i}} (P_{i} - P) + \frac{G_{f} B_{g i}}{(1 - S_{f w i}) B_{w}} S_{f w i} (R_{s i} - R_{s}) B_{g} \\ + ρ_{s} V_{S} {\begin{cases} V_{m} \frac{C [\begin{array}{l} \frac{P_{c d}}{P_{0}} + {(\frac{P_{c d}}{P_{0}})}^{2} + {(\frac{P_{c d}}{P_{0}})}^{3} + 2^{2 - D_{s}} ({(\frac{P_{c d}}{P_{0}})}^{2} + {(\frac{P_{c d}}{P_{0}})}^{3}) \\ + 3^{2 - D_{s}} {(\frac{P_{c d}}{P_{0}})}^{3} \end{array}]}{1 + C [\frac{P}{P_{0}} + {(\frac{P}{P_{0}})}^{2} + {(\frac{P}{P_{0}})}^{3}]} \\ - \frac{C [\begin{array}{l} \frac{P}{P_{0}} + {(\frac{P}{P_{0}})}^{2} + {(\frac{P}{P_{0}})}^{3} + 2^{2 - D_{s}} ({(\frac{P}{P_{0}})}^{2} + {(\frac{P}{P_{0}})}^{3}) \\ + 3^{2 - D_{s}} {(\frac{P}{P_{0}})}^{3} \end{array}]}{1 + C [\frac{P}{P_{0}} + {(\frac{P}{P_{0}})}^{2} + {(\frac{P}{P_{0}})}^{3}]} \end{cases}} . \end{array} (5)

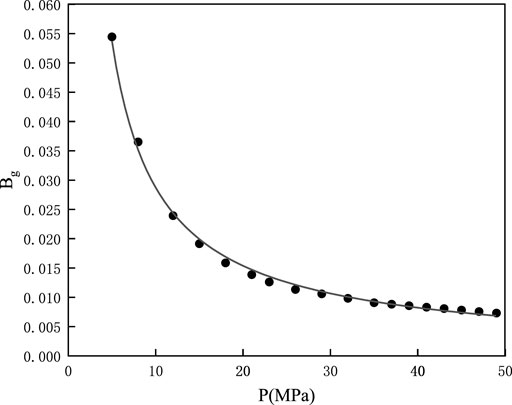
The high-pressure fluid parameter testing of shale gas Block XX regressed the relationship between the gas volume factor and formation pressure. Eq. 6 shows the function, and Figure 2 shows the curve of the gas volume factor versus the formation pressure.

B_{g} = 0.22919 P^{- 0.902} . (6)

FIGURE 2

FIGURE 2. Curve of the gas volume factor versus formation pressure of shale gas Block XX.

The empirical formula of the formation water property is as suggested by Yuanqian (Chen, 1990) and (Myers and Prausnitz, 1965), as shown in Eq. 7.

\begin{array}{l} R_{s} = (T, M, P) = - 3.1670 \times 10^{- 10} T^{2} \times M + 1.997 \times 10^{- 8} T \times M \\ + 1.0635 \times 10^{- 10} P_{S}^{2} \times M - 9.7764 \times 10^{- 8} P_{S} \times M + 2.9745 \times 10^{- 10} T \times P_{S} \times M \\ + 1.6230 \times 10^{- 4} T^{2} - 2.7879 \times 10^{- 2} T - 2.0587 \times 10^{- 5} P_{S}^{2} \\ + 1.7323 \times 10^{- 2} P_{S} + 9.5233 \times 10^{- 6} T \times P_{S} + 1.1937. \end{array} (7)

In the equation, $R_{s}$ is the natural gas solubility in the formation water ( $m^{3} / m^{3}$ ). $T$ is the temperature (°C). $P_{S}$ is the pressure ( $M P a \times 10$ ), and $M$ is the salinity of formation water ( $m g / L$ ).

Practical Material Balance Equation of Shale Gas Block XX

Based on the BET multimolecular adsorption theory equation (Eq. 4) of shale gas Block XX, the practical material balance equation of the shale gas Block XX can be established by considering the dissolved gas of formation water and adsorption of shale gas. The practical material balance equation of Well #1 Block XX was obtained from Eq. 8 by substituting Eqs 6 and 7 into Eq. 5.

\begin{array}{l} G_{p g} \times 0.22919 P^{- 0.902} = G_{m} (0.22919 P^{- 0.902} - B_{g i}) + \\ G_{m} B_{g i} \frac{C_{w} S_{m w i}}{1 - S_{m w i}} (P_{i} - P) + G_{m} B_{g i} \frac{C_{m}}{1 - S_{m w i}} (P_{i} - P) + \\ \frac{G_{m} B_{g i}}{(1 - S_{m w i}) B_{w}} S_{m w i} (R_{s i} - (\begin{array}{l} 3.1670 \times 10^{- 10} T^{2} \times M + 1.997 \times 10^{- 8} T \times M + \\ 1.0635 \times 10^{- 10} P_{S}^{2} \times M - 9.7764 \times 10^{- 8} P_{S} \times M + \\ 2.9745 \times 10^{- 10} T \times P_{S} \times M + 1.6230 \times 10^{- 4} T^{2} - \\ 2.7879 \times 10^{- 2} T - 2.0587 \times 10^{- 5} P_{S}^{2} + \\ 1.7323 \times 10^{- 2} P_{S} + 9.5233 \times 10^{- 6} T \times P_{S} + 1.1937 \end{array})) \\ 0.22919 P^{- 0.902} + G_{f} (0.22919 P^{- 0.902} - B_{g i}) + G_{f} B_{g i} \frac{C_{w} S_{f w i}}{1 - S_{f w i}} (P_{i} - P) + \\ G_{f} B_{g i} \frac{C_{f}}{1 - S_{f w i}} (P_{i} - P) + \frac{G_{f} B_{g i}}{(1 - S_{f w i}) B_{w}} S_{f w i} \\ (R_{s i} - (\begin{array}{l} 3.1670 \times 10^{- 10} T^{2} \times M + 1.997 \times 10^{- 8} T \times M + \\ 1.0635 \times 10^{- 10} P_{S}^{2} \times M - 9.7764 \times 10^{- 8} P_{S} \times M + \\ 2.9745 \times 10^{- 10} T \times P_{S} \times M + 1.6230 \times 10^{- 4} T^{2} - \\ 2.7879 \times 10^{- 2} T - 2.0587 \times 10^{- 5} P_{S}^{2} + \\ 1.7323 \times 10^{- 2} P_{S} + 9.5233 \times 10^{- 6} T \times P_{S} + 1.1937 \end{array})) \times \\ 0.22919 P^{- 0.902} + ρ_{s} V_{S} {\begin{cases} V_{m} \frac{C [\begin{array}{l} \frac{P_{c d}}{P_{0}} + {(\frac{P_{c d}}{P_{0}})}^{2} + {(\frac{P_{c d}}{P_{0}})}^{3} + \\ 2^{2 - D_{s}} ({(\frac{P_{c d}}{P_{0}})}^{2} + {(\frac{P_{c d}}{P_{0}})}^{3}) + \\ 3^{2 - D_{s}} {(\frac{P_{c d}}{P_{0}})}^{3} \end{array}]}{1 + C [\frac{P}{P_{0}} + {(\frac{P}{P_{0}})}^{2} + {(\frac{P}{P_{0}})}^{3}]} \\ - \frac{C [\begin{array}{l} \frac{P}{P_{0}} + {(\frac{P}{P_{0}})}^{2} + {(\frac{P}{P_{0}})}^{3} + \\ 2^{2 - D_{s}} ({(\frac{P}{P_{0}})}^{2} + {(\frac{P}{P_{0}})}^{3}) + \\ 3^{2 - D_{s}} {(\frac{P}{P_{0}})}^{3} \end{array}]}{1 + C [\frac{P}{P_{0}} + {(\frac{P}{P_{0}})}^{2} + {(\frac{P}{P_{0}})}^{3}]} \end{cases}} . \end{array} (8)

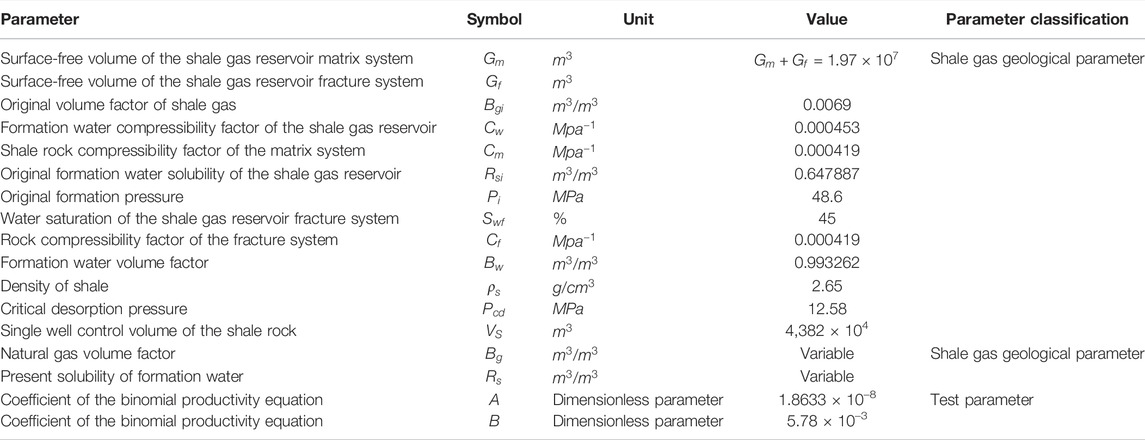
According to the formation of physics and fluid properties (Table 2), the practical material balance equation can be established, and a double logarithm chart (allocation versus cumulative gas production) can be obtained. Therefore, the allocation of a single shale gas well can be calculated according to the cumulative gas production using the chart in the progress of shale gas exploitation.

TABLE 2

TABLE 2. Formation physics and fluid property of Well #1 shale gas Block XX.

From the productivity test data, the gas well productivity equation was as in Eq. 9.

P^{2} - P_{w f}^{2} = A q^{2} + B q . (9)

The 1/5 times of the gas well open flow was often used as the allocation in situ production; therefore, the production allocation formula was as in Eq. 10.

q = \frac{1}{5} \cdot (\frac{- B + \sqrt{B^{2} + 4 A (P^{2} - {0.1}^{2})}}{2 A}) . (10)

Case Study

As the description of the practical material balance equation of shale gas Block XX, at first, the shale gas material balance equation is conducted, considering multimolecular fractal adsorption about the single shale gas well. Second, the binomial productivity equation is obtained by regressing the productivity test data. Third, cumulative gas productivity is substituted into the first step regarding the material balance equation in order to obtain the present reservoir pressure. Fourth, the pressure is substituted into the second step productivity equation, and the single well allocation can be calculated. Finally, the abovementioned steps are repeated, and then, the allocation plate allocation production versus cumulative gas production double logarithm is drawn. According to the plate, the practical allocation process is guided quickly. The specific procedures are as follows.

Figures 3, 4 and Table 3 show the cumulative gas production chart versus formation pressure and single well production allocation chart taking advantage of Eqs 8–10.

FIGURE 3

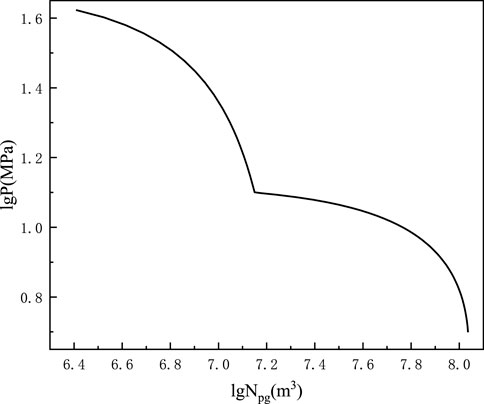
FIGURE 3. Formation pressure versus the cumulative gas production double logarithm chart of Well #1 shale gas Block XX.

FIGURE 4

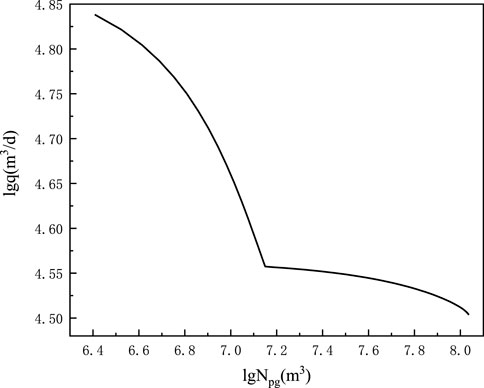
FIGURE 4. Allocation production versus the cumulative gas production double logarithm chart of Well #1 shale gas Block XX.

TABLE 3

TABLE 3. Cumulative gas production versus the formation pressure and single well allocation production.

By viewing the cumulative gas production in Figure 4, the allocation production can be obtained. Through analysis, in Figure 3, the decrease in the formation pressure on the cumulative gas production was gentle, and the allocation on cumulative gas production decreased similar to that in Figure 4 when the shale gas reservoir entered desorption. Thus, the formation pressure can keep well after desorption, and shale gas had a long dependable crop time.

Conclusion

Based on the practical BET multimolecular adsorption, considering the fractal dimension of the adsorption surface, a production allocation chart about Well #1 shale gas Block XX can be established using the material balance equation. The conclusions are as follows:

1) The adsorption volume of the shale gas Block XX was 1.19924 m³/t, and the constant related to the energy of adsorption and liquefaction was 9.86193, based on the fractal dimension 2.5 and the layer of surface molecular adsorption 3.

2) According to the production allocation chart of Well #1 shale gas Block XX, before the shale gas reservoir entered the desorption, the desorption pressure decreased faster, and the cumulative gas production increased slowly. However, when the reservoir entered the desorption stage, the decrease in the formation pressure was gentle, despite the low formation pressure. Furthermore, the shale gas production allocation can maintain a certain time, indicating that most shale gas of the production well was exploited during the desorption stage.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

TQ: responsible for the main writing of the thesis and the derivation of the formula. SH: responsible for guiding the author’s research and revision of the manuscript. JZ: responsible for the provision of experimental data and email communication.

Funding

This work was supported by the National Science and Technology Major Project “Zhaotong Shale Gas Exploration and Development Demonstration Project-Comprehensive Mountain Shale Gas Well Productivity Evaluation and Production System Optimization and Application” (Grant No. 2017ZX05063005-019) and The National Natural Science Fund (No. 51574199) administered by the National Natural Science Foundation of China.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Abbreviations

$A$ and $B$ , coefficient of binomial productivity equation and dimensionless parameter; $B_{g}$ , natural gas volume factor, $m^{3} / m^{3}$ ; $B_{g i}$ , original volume factor of shale gas, $m^{3} / m^{3}$ ; $B_{w}$ , formation water volume factor, $m^{3} / m^{3}$ ; $C$ , constant related to the energy of adsorption and liquefaction; $C_{m}$ , shale rock compressibility factor of the matrix system; $M p a^{- 1}$ ; $C_{f}$ , rock compressibility factor of the fracture system, $M p a^{- 1}$ ; $C_{w}$ , formation water compressibility factor of the shale gas reservoir, $M p a^{- 1}$ ; $D_{s}$ , —fractal dimension of the adsorption surface; $G_{f}$ , surface free volume of the shale gas reservoir fracture system, $m^{3}$ ; $G_{m}$ , surface free volume of the shale gas reservoir matrix system, $m^{3}$ ; $M$ , —salinity of formation water, $m g / L$ ; $n$ , adsorption layer of the gas surface; $N_{1}$ , adsorption capacity of layer One; $N_{i}$ , adsorption capacity of layer $i$ ; $p_{0}$ , saturated vapor pressure, $M P a$ ; $P_{c d}$ , critical desorption pressure, $M P a$ ; $P_{i}$ , original formation pressure, $M P a$ ; $P_{S}$ , pressure, $M P a \times 10$ ; $R_{s}$ , natural gas solubility in the formation water, m3/m3Rsi, original formation water solubility of the shale gas reservoir, $m^{3} / m^{3}$ ; $S_{w f}$ , water saturation of the shale gas reservoir fracture system, $%$ ; $T$ , temperature, °C; $V_{S}$ , single well control volume of the shale rock, $m^{3}$ ; $x$ , relative pressure $\frac{p}{p_{0}}$ , $M P a / M P a$ ; $ρ_{s}$ , density of shale, $g / c m^{3}$ .

References

Ambrose, R. J., Hartman, R. C., Diaz-Campos, M., Akkutlu, I. Y., and Sondergeld, C. H. (2012). Shale Gas-In-Place Calculations Part I: New Pore-Scale Considerations. SPE J. 17, 219–229. doi:10.2118/131772-PA