- 1Department of Electrical and Computer Engineering, Faculty of Engineering, King Abdulaziz University, Jeddah, Saudi Arabia
- 2Center of Research Excellence in Renewable Energy and Power Systems, King Abdulaziz University, Jeddah, Saudi Arabia
- 3Department of Electrical Engineering, University of Hafr Al Batin, Hafr Al Batin, Saudi Arabia
The output voltage of a photovoltaic (PV) system relies on temperature and solar irradiance; therefore, the PV system and a load cannot be connected directly. To control the output voltage, a DC-DC boost converter is required. However, regulating this converter is a very complicated problem due to its non-linear time-variant and non-minimum phase circuit. Furthermore, the problem becomes more challenging due to uncertainty about the output voltage of the PV system and variation in the load, which is a non-linear disturbance. In this study, an observer-based backstepping sliding mode control (OBSMC) is proposed to regulate the output voltage of a DC-DC boost converter. The input voltage of the converter can be a DC energy source such as PV-based microgrid systems. An adaptive scheme and sliding mode controller constructed from a dynamic model of the converter is used to design an observer. This observer estimates unmeasured system states such as inductor current, capacitor voltage, uncertainty output voltages of the PV cell, and variation of loads such that the system does not need any sensors. In addition, the backstepping technique has been combined with the SMC to make the controller more stable and robust. In addition, the Lyapunov direct method is employed to ensure the stability of the proposed method. By employing the proposed configuration, the control performance was improved. To verify the effectiveness of the proposed controller, a numerical simulation was conducted. The simulation results show that the proposed method is always able to accurately follow the desired voltage with more robustness, fewer steady-state errors, smaller overshoot, faster recovery time, and faster transient response time. In addition, the proposed method consistently produces the least value of integral absolute error.
Introduction
The development of small renewable energy sources (RES) integrated into the power system has significantly increased since the last decade as an effort to boost global penetration of such energy sources. As alternative energy sources, RES are implemented within localized grids, which are called microgrids, that can be disconnected from the main grid whenever needed. These microgrids can be implemented in the form of AC and DC microgrid coupled with power converter. The intensive use of DC-based renewable energy and electronic DC loads (e.g., electric vehicle and data center) have made DC microgrids option more efficient (Mahajan and Potdar, 2020). The DC microgrid has several benefits such as improved reliability, high efficiency with less energy conversion, high controllability without synchronization problem, and economics (Saveen et al., 2018). Moreover, DC microgrids can avoid problems in AC microgrids such as power quality issues, reactive power flow, and frequency synchronization (Abhinav et al., 2019). In the DC microgrid, the DC energy source such as PV, fuel cell, and battery is connected to the DC bus through a DC-DC boost converter (Balog et al., 2012). Nowadays, DC-DC converters are developing quickly and widely being applied in renewable energy sources, power grids, DC motor drives, uninterruptible power supply, computers, data communications, and other fields (Toumi et al., 2021; Vazquez et al., 2017). This motivates to improve converters to be more reliable (Yu et al., 2012), high quality (Alsolami 2021), efficient (Eguchi et al., 2020), and well controlled (Li et al., 2021). There are several DC-DC converter topologies, such as the boost type (Chen et al., 2020), buck type (Basharat et al., 2021), buck-boost type (Yang et al., 2020), Cuk type (Ramos-Paja, et al., 2020), and zeta type converter (Arun and Manigandan, 2021). Among these topologies, the boost type is widely used in many industrial applications (Amirabadi 2016). Generally, a DC-DC boost converter is utilized to convert the DC voltage to a higher DC voltage (Premkumar et al., 2019).
The DC-DC boost converter is well known as a variable structure in a non-linear (Cajamarca et al., 2019), non-minimum phase (Tahri et al., 2019) and time-varying system (Zhang et al., 2017). Disturbance from load variation, input voltage uncertainty, and interference of electromagnetism created by the switching action of the semiconductor make the problem of the converter more challenging (Liu et al., 2018). Moreover, regulating the output voltage cannot be carried out directly without involving the inductor current (Bouchekara et al., 2021). Thus, the system requires a sensor to continuously measure the current (Shen et al., 2021); however, installing the sensor can make the system quite vulnerable to disturbance and raise construction costs (Abdelmalek et al., 2020). Therefore, to reach a suitable control performance for the system, a high-performance control is needed to have good disturbance rejection, less steady-state error, small overshoot, a fast recovery time, and fast transient response time (Mehdi et al., 2020; Mobayen and Tchier, 2018). In addition, the observer method is proposed for induction current estimation, meaning no sensor is needed for real-time measurement (Mehreganfar et al., 2019).
In the literature, many different control techniques have been introduced to control the output voltage of boost converters such as proportional-integral (PI) and proportional-integral-derivative (PID). In Guo et al. (2011), linear PID and PI controllers are used to control the boost converter with a DSP-based digital controller. The results of this study indicate that the PID and PI controllers are slow to achieve transient response with a big overshoot during startup, being less stable, and less robust against operating point changes. Kobaku et al. (2021a) investigated the problem of disturbance rejection for a non-minimum phase DC-DC boost converter employing a novel robust PID. The equivalent feedforward technique of the modified direct synthesis is used to build the controller. The results indicated that the proposed technique has robust performance and provides a fast recovery to the reference in the presence of disturbances. Another study (Cisneros et al., 2015) evaluated a linear time-varying PI controller for an interleaved boost and multilevel converter, while Ahmed et al. conducted a design of fractional order PI for the PV system with a DC-DC boost converter (Mohamed et al., 2021). In other studies, robust control was proposed to regulate boost converter (Mushi et al., 2017; Villegas-Ruvalcaba et al., 2021). Research results indicate that the proposed method shows good performance under different operating conditions. Moreover, Seo and Choi (2019) implemented a fractional order PID to regulate the DC-DC boost converter. In this research, input inductance and output capacitance values are used to characterize gains of integer order PID that will create a transfer function of the closed system equal to the first-order system. The results showed that the proposed technique is better than a conventional integer-order PID. Furthermore, the adaptive control technique was presented for controlling the boost converter, concluding that the driving voltage of the boost converter is controlled automatically (Alawieh et al., 2011; Johnson, et al., 2021). A quantitative feedback theory adapted to build a robust PID controller was proposed to address the problem of instability in voltage control of DC-DC boost converter. The results revealed that the proposed method is better than the conventional PID for various disturbances (Kobaku et al., 2021b). Moreover, Van et al. (2021) proposed phase shift full bridge to improve the output of DC-DC converter. The controller used in this study is PI controller. The results indicated that the phase shift full bridge converter has a better performance compared with other converters.
The aforementioned methods have a disadvantage. To obtain a control parameter, the controller needs a linearization in a certain operating point. Hence, the boost converter cannot achieve all conditions and operating range. To solve this problem, a non-linear controller using intelligent control techniques has been proposed. Nizami and Chakravarty (2020) presented an output voltage control problem for a DC-DC boost converter using a neural network integrated with an adaptive backstepping framework. The results obtained revealed the method is faster at estimating the unknown parameter and has satisfactory tracking of the output voltage. Wai et al. (2012) proposed an adaptive fuzzy neural network to control the voltage of a conventional boost converter. The results indicated that the proposed method is more suitable to control the voltage tracking of the boost converter. Moreover, in Guo and Abdul (2021), a fuzzy adaptive PSO controller was investigated to control maximum power point tracking (MPPT). The results revealed that the developed control method can enhance the global search process and raise the speed of convergence. A robust pulse width modulation-based type 2 fuzzy control to control DC-DC boost converter for improving the stability of converter is presented in Farsizadeh et al. (2020). However, the controller stability of intelligent control techniques cannot be investigated.
Another approach is employing the SMC method. Yuan et al. (2015) proposed the passive sliding mode to regulate the boost converter. The simulation results showed that the proposed method has good dynamic, static performance and robustness against disturbance. Martínez-Treviño et al. (2017) presented an SMC of a boost converter to supply a constant power load and concluded that the technique has proven to be an effective solution to control the converter. Moreover, a new non-linear sliding surface form with optimal parameter to regulate DC-DC boost converter was presented by Yosra Massaoudi et al. (2013). It is concluded that the proposed method is more effective to eliminate chattering and has fast response. In other studies, an adaptive SMC for a load frequency control system based on disturbance observer was proposed (Wei et al., 2021), while Cucuzzella et al. (2018) conducted SMC to regulate the boost converter in a DC microgrid. Different from other methods, this can ensure the stability of the system design. In previous works, SMC was constructed based on observer design to consider disturbances from load variation and input voltage uncertainty (Oucheriah and Guo, 2013; Pandey et al., 2018), whereas in Pandey et al. (2020), the authors proposed two methods for estimating uncertainties of input voltage and load variation, namely, state observer–based adaptive law and sliding mode control, to regulate output voltage of the converter. The results indicate that the steady state and transient performance of the converter using the proposed method is satisfactory. Furthermore, Talbi et al. (2020) presented adaptive sliding mode observer for regulating boost converter using model predictive control and concluded that the proposed method can accurately estimate the output voltage of the converter. However, the recovery time due to the disturbance tends to slow the system and must be improved. To make the system more robust, backstepping SMC techniques are proposed in Xu et al. (2019). This technique is combined with a command filter to adjust the DC-link voltage. The simulation results show that the developed strategy can precisely regulate the grid-connected inverter. An adaptive backstepping sliding mode control method to enhance DC bus voltage stability is presented by Wu and Lu (2019). The results showed that the proposed control method has better performance and is more robust. In other studies, backstepping SMC was presented for maximum power point tracking in a solar cell (Bjaoui et al., 2019; Dahech et al., 2017) and concluded that the proposed technique has a good transient response, small tracking error, and very fast reaction against variations of solar irradiation. However, disturbance from load variation and input voltage uncertainty was not considered. Furthermore, observer design to estimate inductor current is not included in the SMC design. To the best of the authors’ knowledge, no study has been conducted to design controller using a combination of observer-based backstepping technique and sliding mode control. In addition, to evaluate the performance of the proposed controller, most literature do not employ dynamic system testing for input voltage uncertainty and load variation.
In this paper, to improve the controller performance, observer-based backstepping sliding mode control (OBSMC) for regulating output voltage of DC-DC boost converter is proposed. The proposed controller will make the system performance more robust with less steady-state error, small overshoot, fast recovery time, and fast transient response time. The disturbance from load variation, input voltage uncertainty, and the estimation of the inductor current is considered in the design. The contributions of this paper are summarized as follows:
1. Combining the observer-based backstepping technique and sliding mode control and the mathematical model of DC-DC boost converter, a novel sliding surface is constructed. Then, using the Lyapunov method, the stability of the design is verified.
2. A novel controller formula is designed based on the novel sliding surface to regulate a DC-DC boost converter considering load variation and input voltage uncertainty.
3. The dynamic system testing for input voltage uncertainty and the load variation is applied to evaluate the performance of the controller.
The rest of this work is structured as follows. The mathematical modeling of the DC-DC boost converter is explained in Section 2. Section 3 defines the OBSMC. In Section 4, the simulation results and analyses are discussed. Finally, conclusions are presented at the end of the study in Section 5.
Mathematical Modeling of A DC-DC Boost Converter
To connect and regulate the output voltage of the PV system and a load, a DC-DC boost converter is required because the output voltage of a PV system relies on temperature and solar irradiance, as shown in Figure 1. Furthermore, due to the presence of an uncertain output voltage of the solar cell and variation of load, which is a non-linear disturbance, the controller technique is required to provide the gating signal pulse for regulating the DC-DC boost converter. To obtain the controller, the mathematical modeling of the converter is considered.
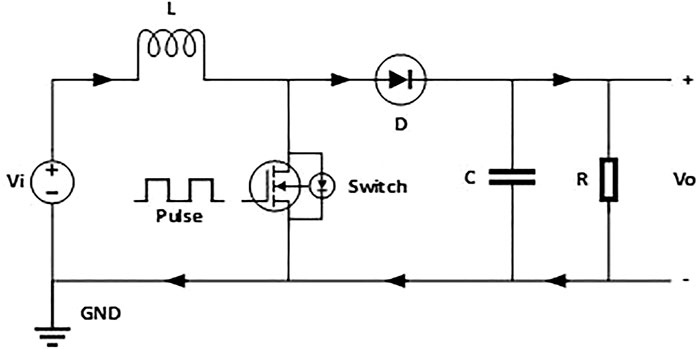
The circuit of a DC-DC boost converter, as presented in Figure 2, is a power electronic circuit comprising an inductor and a capacitor as energy storage to change one voltage level to another voltage level using a switching method, where the parameters of
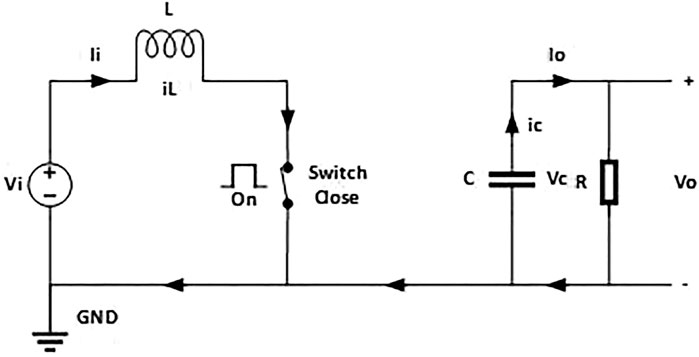
When the switch is closed, as shown in Figure 3, the inductor
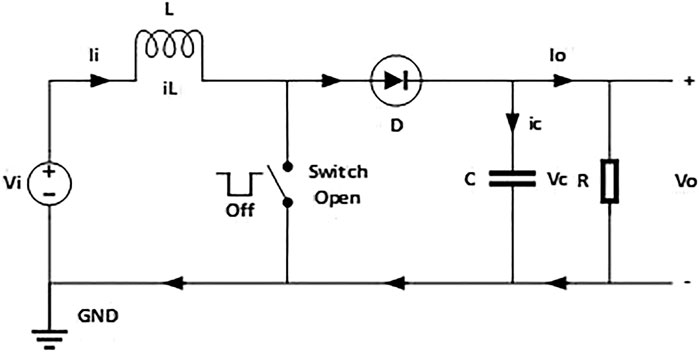
For the open switch, as seen in Figure 4, the inductor
By taking the state variable of the current inductor
Observer-Based Backstepping Sliding Mode Control
In the application, we have to note that the value of the input voltage,
To obtain the adaptation laws, the quadratic Lyapunov function is considered.
The gains of adaptation are represented by
For stabilization of the observer design, (9) should be negative definite; hence, the terms in the bracket must be cancelled to obtain the adaptation laws in Eqs 10, 11.
Because the DC-DC boost converter has non-minimum phase characteristics, an indirect control method must be used. For this condition, the voltage of the system output should be regulated using its inductor current. The reference of the inductor current
where
where
To provide robustness and to ensure the stability of the system, the backstepping method is added into the observer-based SMC. The main idea of the backstepping method is that a complex non-linear system is divided into two subsystems. Consequently, the medial fictitious control and Lyapunov function are constructed, respectively, and the main system is gained through backstepping. The design procedure of the basic OBSMC can be defined as follows:
There are two steps to designing the OBSMC. The first step is to select the Lyapunov function as
Accordingly,
In the second step, the Lyapunov function is selected as
The time derivative of Eq. 16 will get
Substituting (13), the derivative of Eqs 13, 15 into Eq. 17 gives
To meet
The block diagram of the proposed system using signal control Eq. 19 is presented in Figure 5A. The proposed system does not need an inductor current sensor. To replace the sensor and to obtain the estimation value of inductor current accurately, the input and output voltage are fed to the observer gained as in Eq. 6. The estimated values of the inductor current and the output voltage are used to design the purposed controller. The control signal in (19), which is a gating signal to drive the MOSFET, is generated by the purposed controller such that the output voltage can reach the reference voltage as close as possible although disturbance appears in the system.
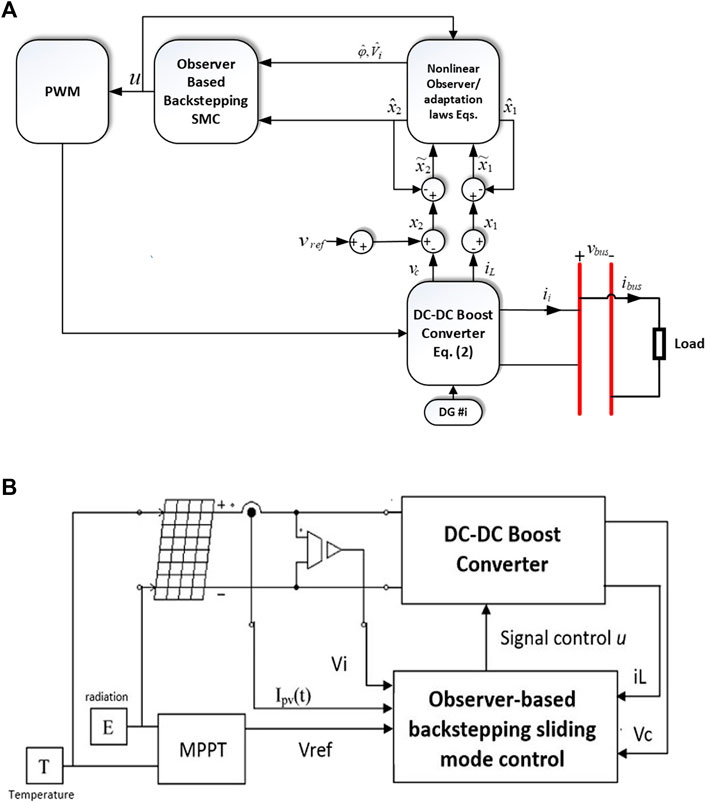
FIGURE 5. Block diagram of the proposed system (A) implemented for DC microgrid; (B) implemented for PV system with MPPT.
Simulation Result and Discussion
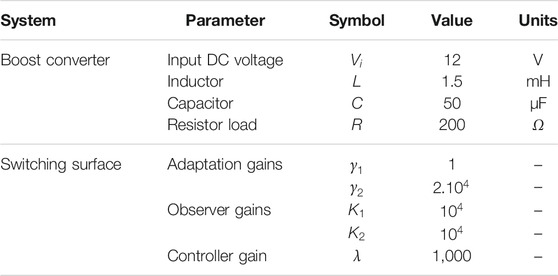
To verify the performance of the proposed controller, a numerical simulation has been performed using MATLAB Simulink. The DC-DC boost converter and switching surface parameters utilized in this paper are provided in Table 1. For the initial system simulation,
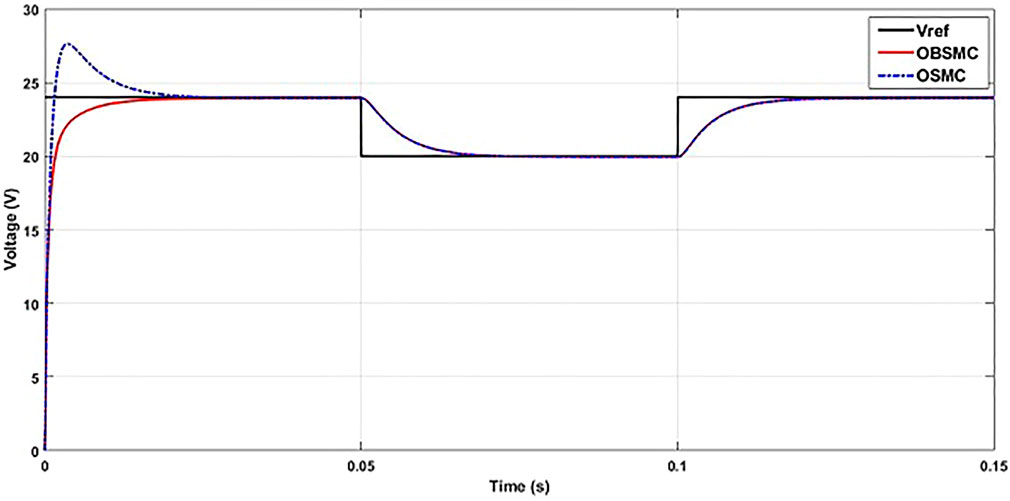
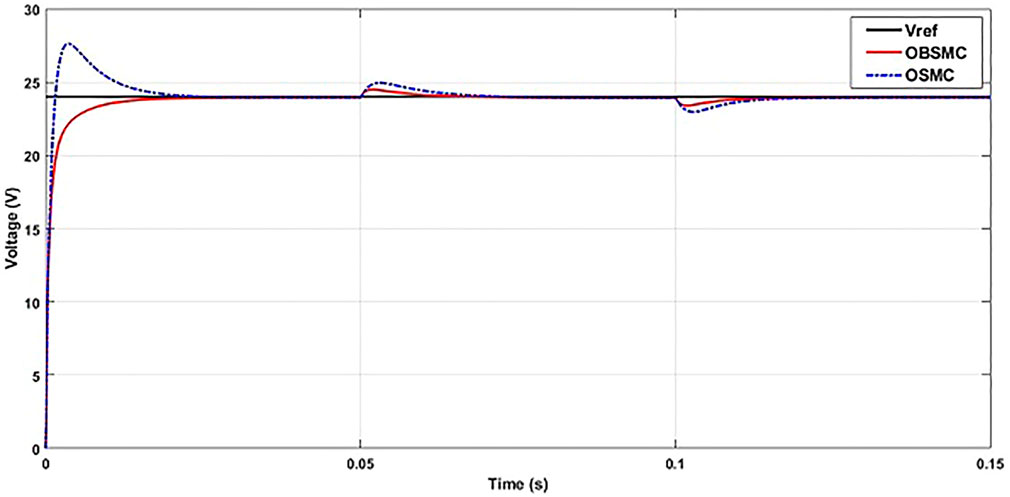
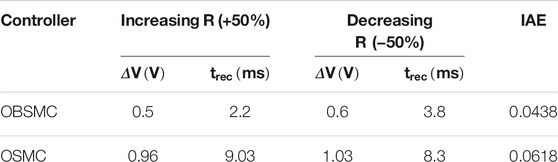
In this paper, the proposed controller, OBSMC, is compared with observer-based SMC (OSMC) in Pandey et al. (2018). Three types of system testing are employed in this paper. The first system testing is reference voltage changing. The simulation time is set to be 0.15 s. In addition, to evaluate the performance quality of the controller, integral absolute error (IAE) is utilized. IAE is the sum of the areas below and above the reference signal and process value. At the beginning of the simulation, reference voltage,
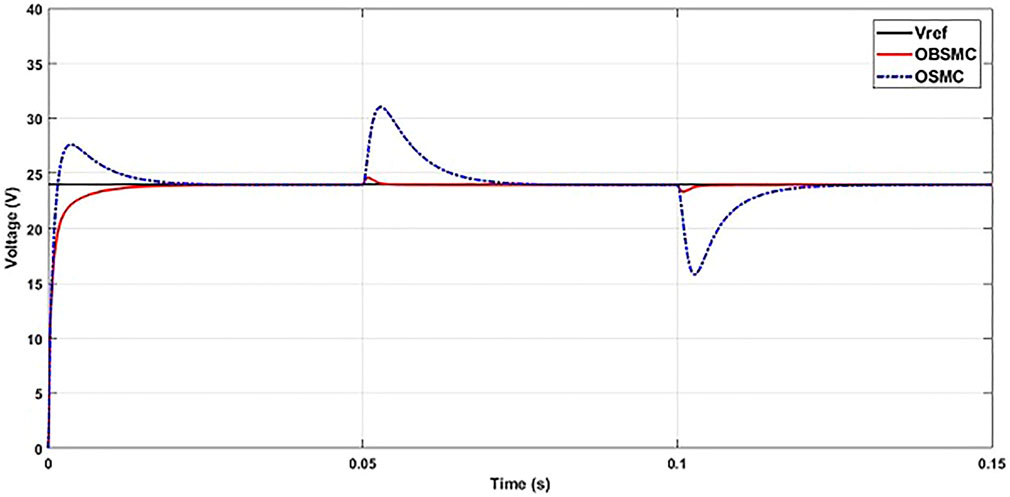
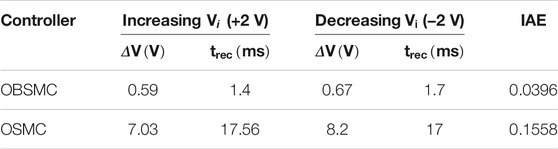
The next system testing is the input voltage variation
The last system testing is the load resistance variation. The simulation time is set to be
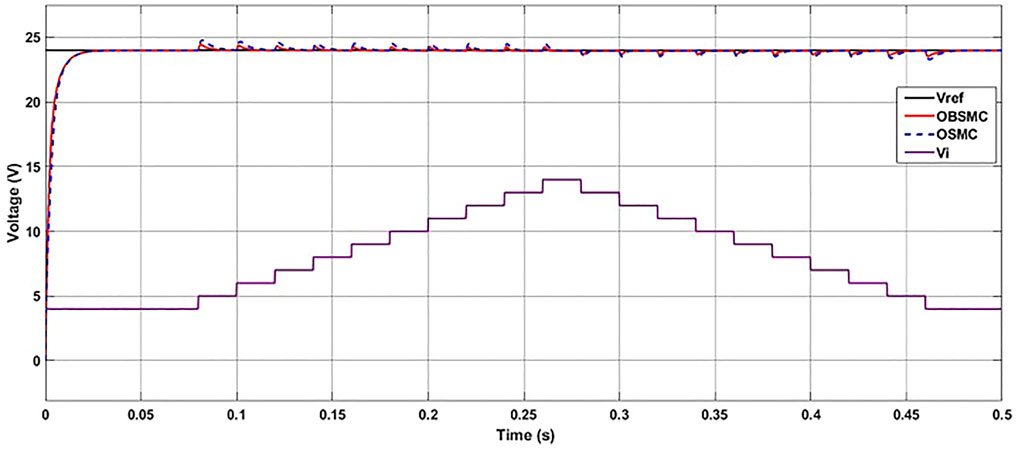
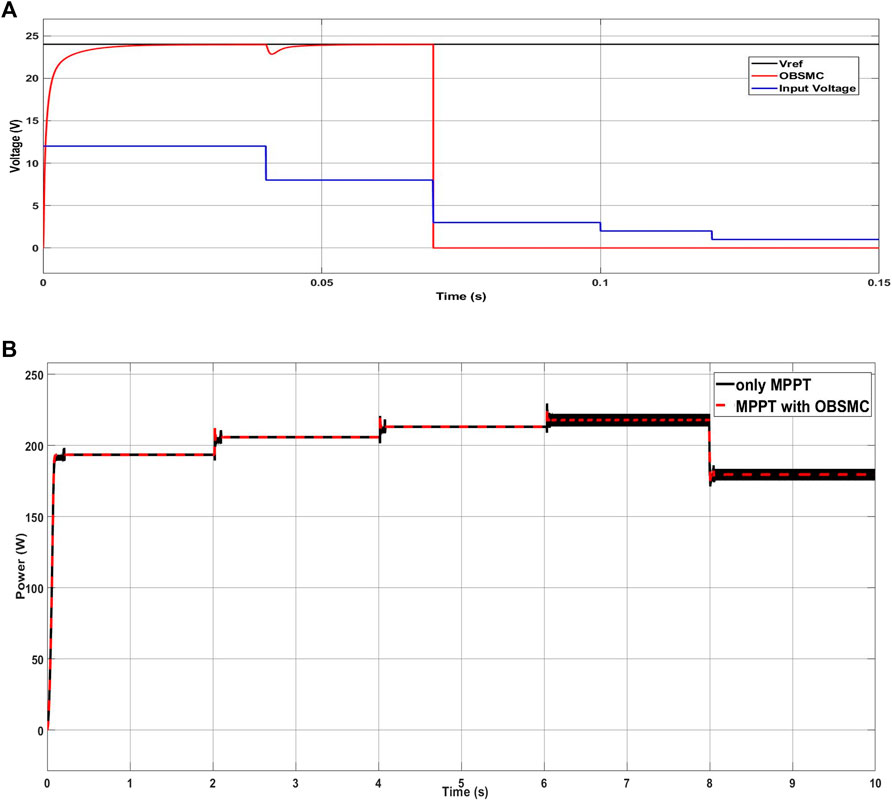
To avoid low efficient operations, the proposed controller has been evaluated with minimum input voltage of the DC-DC boost converter. We assume that if PV is considered as DC source of the system, the minimum solar irradiation will produce minimum output voltage of PV, which is 3 V. Therefore, if the input of the converter
Another implementation of the proposed controller is to control the optimal output of the PV system. Due to variation of solar irradiation and temperature, a MPPT is required to run the PV system at maximum power point (MPP) (Nguyen et al., 2020). The MPPT algorithm employed in this study is based on perturb and observe (P&O) method. As proposed by Dahech et al. (2017), in this study, the output of the MPPT system is used as a voltage reference to the proposed controller, that is, OBSMC. The signal control of OBSMC is then utilized to regulate the switching device. Figure 5B shows the structure of the MPPT system and the proposed controller applied in the PV system. The output power of DC-DC boost converter with MPPT and the proposed controller is presented in Figure 11B. In this implementation, the performance of the MPPT system with OBSMC and without OBSMC is compared. In the beginning, solar irradiation is 200 W/m2 and the temperature value is 25°C. At
Conclusion
This paper presents observer-based backstepping SMC considering load variation and input voltage uncertainty to regulate a DC-DC boost converter. The backstepping technique has been combined with the SMC to make the controller more robust and have a less steady-state error, small overshoot, a fast recovery time, and fast transient response time. Moreover, the Lyapunov direct method was employed to ensure the stability of the proposed method. To verify the performance of the proposed controller, the numerical simulation is performed using MATLAB Simulink. There were three types of system testing employed in this paper, namely, the reference voltage
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
The main idea, simulation, analysis, and writing of this work was provided by RM. MS and FB carried out a literature review, overall layout formatting, and proof-reading while MAR and HB provided substantial and intellectual contribution. Revision of the article was carried out by RM, AM, and MR. All authors listed have approved the submitted version of the article.
Funding
The authors extend their appreciation to the Deputyship for Research and Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number IFPRC-190-135-2020 and King Abdulaziz University, DSR, Jeddah, Saudi Arabia.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abdelmalek, S., Dali, A., Bakdi, A., and Bettayeb, M. (2020). Design and Experimental Implementation of a New Robust Observer-Based Nonlinear Controller for DC-DC Buck Converters. Energy 213, 118816. doi:10.1016/j.energy.2020.118816
Abhinav, S., Modares, H., Lewis, F. L., and Davoudi, A. (2019). Resilient Cooperative Control of DC Microgrids. IEEE Trans. Smart Grid 10 (1), 1083–1085. doi:10.1109/tsg.2018.2872252
Alawieh, A., Ortega, R., Pillai, H., Astolfi, A., and Berthelot, E. (2011). “Adaptive Control of the Boost Converter in Discontinuous Conduction Mode,” in IFAC Proceedings Volumes (IFAC-PapersOnline), Milano, Italy, January 2011. doi:10.3182/20110828-6-it-1002.03558
Alsolami, M. (2021). A Multi-Input, Multi-Stage Step-Up DC-DC Converter for PV Applications. Alexandria Eng. J. 60 (2), 2315–2324. doi:10.1016/j.aej.2020.12.030
Amirabadi, M. (2016). “Ćuk-Based Universal Converters in Discontinuous Conduction Mode of Operation,” in ECCE 2016 - IEEE Energy Conversion Congress and Exposition, Milwaukee, WI, USA, 18-22 Sept. 2016. doi:10.1109/ecce.2016.7854978
Arun, S., and Manigandan, T. (2021). Design of ACO Based PID Controller for Zeta Converter Using Reduced Order Methodology. Microprocessors and Microsystems 81, 103629. doi:10.1016/j.micpro.2020.103629
Balog, R. S., Weaver, W. W., and Krein, P. T. (2012). The Load as an Energy Asset in a Distributed DC Smartgrid Architecture. IEEE Trans. Smart Grid 3 (1), 253–260. doi:10.1109/tsg.2011.2167722
Basharat, S., Awan, S. E., Akhtar, R., Hussain, A., Iqbal, S., Shah, S. A., et al. (2021). A Duty Cycle Controlled ZVS Buck Converter with Voltage Doubler Type Auxiliary Circuit. Front. Energ. Res. 9. doi:10.3389/fenrg.2021.550115
Bjaoui, M., Khiari, B., Benadli, R., Memni, M., and Sellami, A. (2019). Practical Implementation of the Backstepping Sliding Mode Controller MPPT for a PV-Storage Application. Energies 12 (18), 3539. doi:10.3390/en12183539
Bouchekara, H. R. E-H., Javaid, M. S., Shaaban, Y. A., Shahriar, M. S., Ramli, M. A. M., and Latreche, Y. (2021). Decomposition Based Multiobjective Evolutionary Algorithm for PV/Wind/Diesel Hybrid Microgrid System Design Considering Load Uncertainty. Energ. Rep. 7, 52–69. doi:10.1016/j.egyr.2020.11.102
Cajamarca, B., Quintero, Ó. C., Chávez, D., Leica, P., and Pozo, M. (2019). Sliding Mode Control Based on Internal Model for a Non-minimum Phase Buck and Boost Converter. Enfoque UTE 10 (1), 41–53. doi:10.29019/enfoqueute.v10n1.442
Chen, D., Lin, Y., and Xiao, L. (2020). An EMI Filter Design Method Based on Improved Foster Network Model for Boost PFC Converter. Energ. Rep. 6, 1268–1275. doi:10.1016/j.egyr.2020.11.044
Cisneros, R., Pirro, M., Bergna, G., Ortega, R., Ippoliti, G., and Molinas, M. (2015). Global Tracking Passivity-Based PI Control of Bilinear Systems: Application to the Interleaved Boost and Modular Multilevel Converters. Control. Eng. Pract. 43, 109–119. doi:10.1016/j.conengprac.2015.07.002
Cucuzzella, M., Lazzari, R., Trip, S., Rosti, S., Sandroni, C., and Ferrara, A. (2018). Sliding Mode Voltage Control of Boost Converters in DC Microgrids. Control. Eng. Pract. 73, 161–170. doi:10.1016/j.conengprac.2018.01.009
Dahech, K., Allouche, M., Damak, T., and Tadeo, F. (2017). Backstepping Sliding Mode Control for Maximum Power Point Tracking of a Photovoltaic System. Electric Power Syst. Res. 143, 182. doi:10.1016/j.epsr.2016.10.043
Eguchi, K., Shibata, A., and Harada, Y. (2020). A Direct High Step-Down DC/DC Converter Using Cascade Ring-type Converters. Energ. Rep. 6, 119–124. doi:10.1016/j.egyr.2019.11.051
Farsizadeh, H., Gheisarnejad, M., Mosayebi, M., Rafiei, M., and Khooban, M. H. (2020). An Intelligent and Fast Controller for DC/DC Converter Feeding CPL in a DC Microgrid. IEEE Trans. Circuits Syst. Express Briefs 67 (6), 1104–1108. doi:10.1109/tcsii.2019.2928814
Guo, L., and Abdul, N. M. M. (2021). Design and Evaluation of Fuzzy Adaptive Particle Swarm Optimization Based Maximum Power Point Tracking on Photovoltaic System under Partial Shading Conditions. Front. Energ. Res. 9. doi:10.3389/fenrg.2021.712175
Guo, L., Hung, J. Y., and Nelms, R. M. (2011). Comparative Evaluation of Sliding Mode Fuzzy Controller and PID Controller for a Boost Converter. Electric Power Syst. Res. 81 (1), 99–106. doi:10.1016/j.epsr.2010.07.018
Johnson, R. S., Altin, B., and Sanfelice, R. G. (2021). Hybrid Adaptive Control for the DC-DC Boost Converter. IFAC-PapersOnLine 54 (5), 73–78. doi:10.1016/j.ifacol.2021.08.477
Joseph, X. F., and Kumar, S. P. (2012). Design and Simulation of a Soft Switched Dc Boost Converter for Switched Reluctance Motor. Am. J. Appl. Sci. 9 (3), 440–445.
Kaddoura, T. O., Ramli, M. A. M., and Al-Turki, Y. A. (2016). On the Estimation of the Optimum Tilt Angle of PV Panel in Saudi Arabia. Renew. Sust. Energ. Rev. 65, 626–634. doi:10.1016/j.rser.2016.07.032
Kobaku, T., Jeyasenthil, R., Sahoo, S., and Dragicevic, T. (2021a). Experimental Verification of Robust PID Controller under Feedforward Framework for a Nonminimum Phase DC-DC Boost Converter. IEEE J. Emerging Selected Top. Power Elect. 9 (3), 3373–3383. doi:10.1109/jestpe.2020.2999649
Kobaku, T., Jeyasenthil, R., Sahoo, S., Ramchand, R., and Dragicevic, T. (2021b). Quantitative Feedback Design-Based Robust PID Control of Voltage Mode Controlled DC-DC Boost Converter. IEEE Trans. Circuits Syst. Express Briefs 68 (1), 286–290. doi:10.1109/tcsii.2020.2988319
Li, G., Huang, H., Song, S., and Liu, B. (2021). A Nonlinear Control Scheme Based on Input–Output Linearized Method Achieving PFC and Robust Constant Voltage Output for Boost Converters. Energ. Rep. 7, 5386–5393. doi:10.1016/j.egyr.2021.08.169
Liu, L., Zhao, Y., Chang, D., Xie, J., Ma, Z., Sun, Q., et al. (2018). Prediction of Short-Term PV Power Output and Uncertainty Analysis. Appl. Energ. 228, 700–711. doi:10.1016/j.apenergy.2018.06.112
Mahajan, T., and Potdar, M. S. (2020). “An Improved Strategy for Distributed Generation Control and Power Sharing in Islanded Microgrid,” in 2nd International Conference on Innovative Mechanisms for Industry Applications, ICIMIA 2020, Bangalore, India, 5-7 March 2020, 133–136.
Martínez-Treviño, B. A., Jammes, R., El Aroudi, A., and Martínez-Salamero, L. (2017). Sliding-Mode Control of a Boost Converter Supplying a Constant Power Load. IFAC-PapersOnLine 50 (1), 7807–7812. doi:10.1016/j.ifacol.2017.08.1055
Mehdi, M., Kim, C.-H., and Saad, M. (2020). Robust Centralized Control for DC Islanded Microgrid Considering Communication Network Delay. IEEE Access 8, 77765–77778. doi:10.1109/access.2020.2989777
Mehreganfar, M., Saeedinia, M. H., Davari, S. A., Garcia, C., and Rodriguez, J. (2019). Sensorless Predictive Control of Afe Rectifier with Robust Adaptive Inductance Estimation. IEEE Trans. Ind. Inf. 15 (6), 3420–3431. doi:10.1109/tii.2018.2879060
Mobayen, S., and Tchier, F. (2018). Robust Global Second-Order Sliding Mode Control with Adaptive Parameter-Tuning Law for Perturbed Dynamical Systems. Trans. Inst. Meas. Control. 40 (9), 2855–2867. doi:10.1177/0142331217708832
Mohamed, A. T., Mahmoud, M. F., Swief, R. A., Said, L. A., and Radwan, A. G. (2021). Optimal Fractional-Order PI with DC-DC Converter and PV System. Ain Shams Eng. J. 12 (2), 1895. doi:10.1016/j.asej.2021.01.005
Mushi, A., Nagai, S., Obara, H., and Kawamura, A. (2017). Fast and Robust Nonlinear Deadbeat Current Control for Boost Converter. IEEJ J. Industry Appl. 6 (5), 311–319. doi:10.1541/ieejjia.6.311
Nguyen, B. N., Nguyen, V. T., Duong, M. Q., Le, K. H., Nguyen, H. H., and Doan, A. T. (2020). Propose a MPPT Algorithm Based on Thevenin Equivalent Circuit for Improving Photovoltaic System Operation. Front. Energ. Res. 8. doi:10.3389/fenrg.2020.00014
Nizami, T. K., and Chakravarty, A. (2020). Neural Network Integrated Adaptive Backstepping Control of DC-DC Boost Converter. IFAC-PapersOnLine 53 (1), 549–554. doi:10.1016/j.ifacol.2020.06.092
Oucheriah, S., and Guo, L. (2013). PWM-based Adaptive Sliding-Mode Control for Boost DC-DC Converters. IEEE Trans. Ind. Elect. 60 (8), 3291–3294. doi:10.1109/tie.2012.2203769
Pandey, S. K., Patil, S. L., and Phadke, S. B. (2018). Comment on PWM-Based Adaptive Sliding-Mode Control for Boost DC-DC Converters. IEEE Trans. Ind. Elect. 65 (6), 5078–5080. doi:10.1109/tie.2017.2764872
Pandey, S. K., Veeranna, K., Patil, S. L., and Phadke, S. B. (2020). Uncertainty Estimator Based Sliding Mode Control Schemes for Multimode Noninverting Buck-Boost DC-DC Converter. IFAC-PapersOnLine 53 (1), 555–560. doi:10.1016/j.ifacol.2020.06.093
Premkumar, M., Kumar, C., and Sowmya, R. (2019). Analysis and Implementation of High-Performance DC-DC Step-Up Converter for Multilevel Boost Structure. Front. Energ. Res. 7. doi:10.3389/fenrg.2019.00149
Ramos-Paja, C. A., Montoya, D. G., and Bastidas-Rodríguez, J. D. (2020). Sliding-Mode Control of a CuK Converter for Voltage Regulation of a Dc-Bus. Sustainable Energ. Tech. Assessments 42, 100807. doi:10.1016/j.seta.2020.100807
Saveen, G., Raju, P. P., Manikanta, D. V., and Praveen, M. S. (20182018). Design and Implementation of Energy Management System with Fuzzy Control for Multiple Microgrid. Proc. 2nd Int. Conf. Inventive Syst. Control ICISC 28 (4), 1239–1244. doi:10.1109/icisc.2018.8399003
Shen, H., Tao, P., Lyu, R., Ren, P., Ge, X., and Wang, F. (2021). Risk-Constrained Optimal Bidding and Scheduling for Load Aggregators Jointly Considering Customer Responsiveness and PV Output Uncertainty. Energ. Rep. 7, 4722–4732. doi:10.1016/j.egyr.2021.07.021
Tahri, A., El Fadil, H., Rachid, A., Eric, M., and Giri, F. (2019). A Nonlinear Controller Based on a High Gain Observer for a Cascade Boost Converter in a Fuel Cell Distributed Power Supply System. IFAC-PapersOnLine 52 (29), 91–96. doi:10.1016/j.ifacol.2019.12.627
Tan, R. H. G., and Hoo, L. Y. H. (2015). “DC-DC Converter Modeling and Simulation Using State Space Approach,” in 2015 IEEE Conference on Energy Conversion, CENCON, Johor Bahru, Malaysia, 19-20 Oct. 2015.
Toumi, D., Benattous, D., Ibrahim, A., Abdul-Ghaffar, H. I., Obukhov, S., Aboelsaud, R., et al. (2021). Optimal Design and Analysis of DC–DC Converter with Maximum Power Controller for Stand-Alone PV System. Energ. Rep. 7, 4951–4960. doi:10.1016/j.egyr.2021.07.040
Van, T. H., et al. (2021). Improving the Output of DC-DC Converter by Phase Shift Full Bridge Applied to Renewable Energy. Rev. Roum. Si. Techn.-Electrotechn. Energ 66 (3).
Vazquez, S., Rodriguez, J., Rivera, M., Franquelo, L. G., and Norambuena, M. (2017). Model Predictive Control for Power Converters and Drives: Advances and Trends. IEEE Trans. Ind. Elect. 64 (2), 935–947. doi:10.1109/tie.2016.2625238
Villegas-Ruvalcaba, M., Gurubel-Tun, K. J., and Coronado-Mendoza, A. (2021). Robust Inverse Optimal Control for a Boost Converter. Energies 14 (9), 2507. doi:10.3390/en14092507
Wei, M., Lin, S., Zhao, Y., Wang, H., and Liu, Q. (2021). An Adaptive Sliding Mode Control Based on Disturbance Observer for LFC. Front. Energ. Res. 9. doi:10.3389/fenrg.2021.733910
Wu, J., and Lu, Y. (2019). Adaptive Backstepping Sliding Mode Control for Boost Converter with Constant Power Load. IEEE Access 7, 50797–50807. doi:10.1109/access.2019.2910936
Xu, D., Wang, G., Yan, W., and Yan, X. (2019). A Novel Adaptive Command-Filtered Backstepping Sliding Mode Control for PV Grid-Connected System with Energy Storage. Solar Energy 178, 222–230. doi:10.1016/j.solener.2018.12.033
Yang, M., Wang, J., and An, J. (2020). Day-Ahead Optimization Scheduling for Islanded Microgrid Considering Units Frequency Regulation Characteristics and Demand Response. IEEE Access 8, 7093–7102. doi:10.1109/access.2019.2963335
Yu, D., Iu, H. H. C., Chen, H., Rodriguez, E., Alarcón, E., and El Aroudi, A. (2012). Instabilities in Digitally Controlled Voltage-Mode Synchronous Buck Converter. Int. J. Bifurcation Chaos 22 (1), 1250012. doi:10.1142/s0218127412500125
Yuan, X., Cheng, L., and Wei, X. (2015). Control Strategy for Boost Converter Based on Passive Sliding Control Mode. IFAC-PapersOnLine 48 (28), 134–137. doi:10.1016/j.ifacol.2015.12.113
Keywords: observer design, backstepping, sliding mode control, DC-DC boost converter, DC microgrid
Citation: Muktiadji RF, Ramli MAM, Bouchekara HREH, Milyani AH, Rawa M, Seedahmed MMA and Budiman FN (2022) Control of Boost Converter Using Observer-Based Backstepping Sliding Mode Control for DC Microgrid. Front. Energy Res. 10:828978. doi: 10.3389/fenrg.2022.828978
Received: 04 December 2021; Accepted: 31 January 2022;
Published: 18 March 2022.
Edited by:
Sudhakar Babu Thanikanti, Chaitanya Bharathi Institute of Technology, IndiaReviewed by:
Minh Quan Duong, University of Science and Technology, VietnamKarthik Balasubramanian, McMaster University, Canada
Copyright © 2022 Muktiadji, Ramli, Bouchekara, Milyani, Rawa, Seedahmed and Budiman. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Rifqi Firmansyah Muktiadji, cmlmcWlmaXJtYW5zeWFoQHVuZXNhLmFjLmlk
 Rifqi Firmansyah Muktiadji
Rifqi Firmansyah Muktiadji Makbul A. M. Ramli
Makbul A. M. Ramli Houssem R. E. H. Bouchekara
Houssem R. E. H. Bouchekara Ahmad H. Milyani1
Ahmad H. Milyani1 Mustafa M. A. Seedahmed
Mustafa M. A. Seedahmed Firmansyah Nur Budiman
Firmansyah Nur Budiman