Controller Design for Distributed Secondary Voltage Restoration in the Islanded Microgrid

The extensive usage of the cyber communication system in multiple distributed secondary controls of islanded microgrids (MGs) suggests that the effects of the communication network and security concerns on system stability cannot be negligible. This study proposes a distributed fault-tolerant secondary voltage recovery method for multiple distributed generators (DGs) in the MGs of islanded mode based on a sliding mode surface. Compared to the traditional asymptotically convergent distributed control method, the proposed controller quickly eliminates the voltage deviation caused by the primary control and provides power sharing in the presence of external disturbance and actuator fault, which can regulate the average voltage magnitude of all the DGs to an expected value. The effectiveness of the proposed strategy is verified by the simulation studies conducted in the MATLAB/Simulink platform.

Introduction

As a scale-down power system, the MG, which is a cluster of distributed energy resources (DERs), energy storage modules, and local loads, operates in either the grid-connected or islanded mode, providing improved monitoring, control, and advanced service technologies to consumers depending on the information transmission capacity (Farrokhabadi et al., 2020; Sedhom et al., 2020). Several cyber communication-based system control schemes are exploited to regulate the MG under the autonomous mode, which can provide proper power distribution, high power quality, and quick cooperative response capability (Hossain et al., 2017). However, the presence of the communication network brought some problems of stability and security, such as communication delay, data packet loss, module failure, disturbance, etc., which is worthy of further research (Ding et al., 2019).

The hierarchical control is typically divided into three layers (Dehkordi et al., 2017) (Yamashita et al., 2020). The primary control posesses the responsibility for stabilizing the voltage and frequency and keeping them within rational ranges by using a local controller. The secondary control is usually introduced to compensate the voltage derivation that resulted from the primary control. At this stage, the reference value and node information are transmitted through the communication network between different DG units. In addition, the third level is in charge of issues such as economic dispatch and power flow between the main grid and the MG. A different scheme developed in the study by Dehkordi et al., (2019) studied the secondary voltage and frequency control with random noise in the communication channel. This method shows robust performance in the presence of network topology change and the uncertainty. A secondary control method based on the consensus algorithm is proposed in the study by Alhasnawi et al., (2021) to solve the system voltage and frequency deviation under the short-circuit current fault and can carry out reasonable power distribution among the DGs. A distributed secondary control architecture is designed in the study by Shotorbani et al., (2017) to balance the energy storage state and adjust the system frequency at the same time. The terminal sliding mode controller is used to improve the transient response and convergence speed, reducing the overshot. However, there is less consideration of the charging/discharging efficiency of the energy storage system in the absence of the situation of module faults. A secondary control based on a dynamic algorithm is proposed in the study by Yoo et al., (2020) for the AC/DC hybrid MG that designs an improved normalized droop strategy for power sharing and the AC frequency and DC voltage to restore to their nominal values. The majority of existing methods researched on voltage restoration based on the ideal conditions without module faults and disturbance. As one of the most severest threats, module faults can degrade the performance of the system and even bring some destructive consequences (Zhu et al., 2021), which can be categorized as the actuator fault, sensor fault, communication network fault, plant fault, and short-circuit fault (Shahab et al., 2020). Therefore, research on the fault-tolerant control (FTC) is an essential subject. The H_∞ observer is employed in the study by Huang et al., (2021) to estimate the voltage and current of the DC MG with sensor faults and external disturbances, which are provided to the state feedback controller to achieve the desired voltage tracking performance. The proposed method can tolerate sensor faults and realize current sharing among DGs under the DC MG. Aiming at the sensor faults and network attacks in the DC MG, a diagnosis and mitigation strategy is proposed in the study by Saha et al., (2018). The theory of fault diagnosis based on the sliding mode observer has been used in the proposed strategy to estimate the error in the sensor measurement due to any sensor failure or network attack in the DC MG, ensuring the resilient operation of faults and network attacks. The problem of potential heterogenous faults of the actuator and power sharing under the system with DGs and energy storage is addressed in the study by Afshari et al., (2020), but the communication of information and data is limited to local neighbors. An original strategy based on fault detection and FTC is proposed in the work by Sardashti and Ramezani., (2021); the advantage is it does not depend on neither the system model nor the controller type using the black-box approach for sensor or communication link faults. The aforementioned literature studies relax the intermittent constraint of distributed generation units, that is, each DG is treated as a voltage source and can work approximately stably. The conflict between the economics and the environment of the MG is not taken into account. This problem is addressed in the study by Liu and Yang., (2021), which used the distributed algorithm to achieve reasonable optimal scheduling of operating costs and gas emissions, which has more practical significance for stable and efficient operation of MGs. The fixed step size is used to solve the problem of slow convergence speed and is easier to implement in practice. The problem of distributed energy management is addressed in the study by Li et al., (2020) by using the idea of the event-triggered communication strategy, which proposes a dynamic event-triggered algorithm to solve energy management problems in the islanded mode and grid-connected mode. The physical constraints of the electricity–heat–gas network and the coordinated control of the system will be further considered, and the constraints will be relaxed to expand the application of this method.

In this study, a novel method is used to design the controller based on the nonlinear terminal sliding mode surface, which solves the problem of MG voltage restoration in the presence of actuator failure, improving the transient response capability and convergence speed of the system. The sliding mode control (SMC) is an effective way to solve uncertainties and nonlinear characteristics due to complete robustness of the sliding mode surface. The proposed control scheme realizes the communication between distributed units through a simple communication network, effectively reducing the dependency on the MG central controller (MGCC) and the complexity of the communication network, and brought down the incidence of system faults fundamentally. This study is organized as follows. In Section 2, the islanded MG is modeled, and the problem is formulated. The architecture of the multiple DGs is discussed. In Section 3, we proposed a distributed secondary voltage restoration controller design based on the sliding mode surface considering actuator faults and disturbance. In Section 4, the derived controller is verified experimentally by the simulation studies conducted in the MATLAB/Simulink platform. Finally, the conclusions are summarized in Section 5.

Problem Formulation and Preliminaries

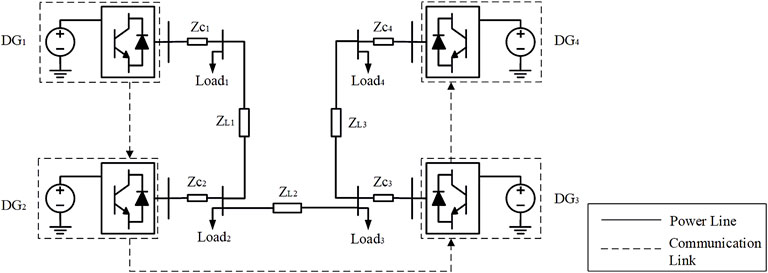
As shown in Figure 1, this connection method of DGs of an islanded MG is employed to avoid the presence of MGCC and achieve distributed control based on the information transmitted by adjacent DGs. Z_ci and Z_Li are output impedance and line impedance, respectively. The DGs are connected by power lines for power sharing.

FIGURE 1

FIGURE 1. Diagram of islanded MGs considering communication topology.

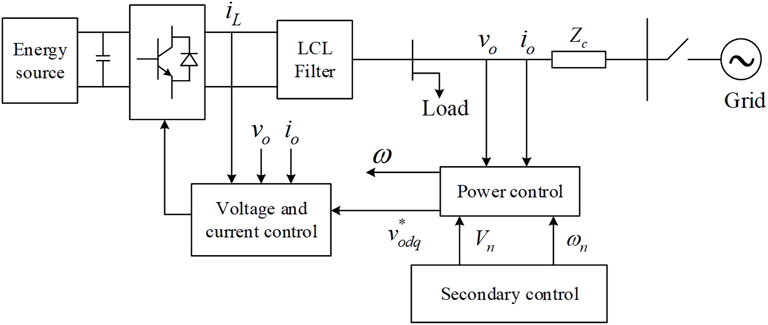
Figure 2 presents an inverter-based DG and control block. The primary control, as a local controller, supports stability of voltage and frequency of the MG so that these values remain in a predesignated range avoiding system instability. The secondary control is accomplished by communication and cooperation among DGs.

FIGURE 2

FIGURE 2. Block diagram of an inverter-based DG and control.

The instantaneous active power and reactive power can be obtained according to load voltage v_o and current i_o (Pogaku et al., 2007).

$\{\begin{array}{l}\tilde{p}=v_d{i}_d+v_q{i}_q\\ \tilde{q}=v_d{i}_q-v_q{i}_d\end{array},(1)$

where the subscript “d, q” is the representation of v_o and i_o in the dq frame, respectively.

In order to eliminate the high-frequency components of the converter output power, the output P and Q of the low-pass filter are usually conveyed as the input of the primary control, and the expression is

$\{\begin{array}{l}P=\frac{{\omega }_c}{s+{\omega }_c}\tilde{p}\\ Q=\frac{{\omega }_c}{s+{\omega }_c}\tilde{q}\end{array},(2)$

where ω_c is the cut-off frequency of the low-pass filter.

The primary control requires the distributed unit to automatically distribute the active and reactive loads using local information, while keeping the voltage and frequency in a stable range. According to Bidram and Davoudi., (2012), we assumed the line impedance is purely inductive and takes advantage of the droop technique to describe the relationship between frequency and active power, voltage amplitude, and reactive power as

$\omega ={\omega }_n-mP,(3)$

$v_m=V_n-nQ,(4)$

where ω is the angular frequency, and $v_m$ is the amplitude of the output voltage. ${\omega }_n$ and $V_n$ represent corresponding desired values to be the input for droop characteristics. m and n are droop coefficients adjusted by the control algorithm. P and Q represent real and reactive power, respectively.

According to the dq transformation, the magnitude of the DG output voltage is

$v_m=\sqrt{v_d^2+v_q^2}.(5)$

Because of v_q = 0, the purpose of $v_m\to V_n$ is equal to $v_d\to V_n$.Therefore, the nonlinear state space model (Bidram et al., 2013), according to Figure 2 based on the i^th DG, is

$\{\begin{array}{l}{\dot{x}}_i=f_i\left(x\right)+g_i\left(x\right)u_i+d_i\left(t\right)\\ y_i=v_{di}\end{array},(6)$

where i = 1, 2, …, N represents the number of DG. x_i, f_i(x) and g_i(x) are described in detail in the study by Bidram et al., (2013). u_i = V_ni is the control signal to be designed. d_i(t) is external disturbances and uncertainties of the i^th DG. We established the nonlinear equation corresponding to voltage control,

$\{\begin{array}{l}{\dot{y}}_{i1}=y_{i2}\\ {\dot{y}}_{i2}=v_i+d_i\left(t\right),i=\mathrm{1,2},\cdots ,N\end{array}(7)$

where ${\left[\begin{array}{cc}{y}_{i1}& y_{i2}\end{array}\right]}^{\mathrm{T}}={\left[\begin{array}{cc}{v}_{di}& {\dot{v}}_{di}\end{array}\right]}^{\mathrm{T}}$ and $v_i=f_i\left(x\right)+g_i\left(x\right)V_{ni}$ is the virtual input.

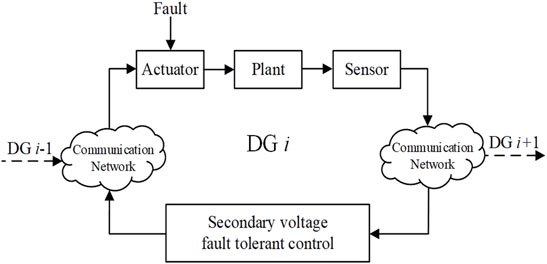
In this study, we considered the biased fault and partial failure of the actuator, as shown in Figure 3. Then, the actual output of the actuator is

${\tilde{v}}_i=\left(1-{\phi }_i\right)v_i+{\psi }_i,(8)$

where φ_i and ψ_i are the severity of the partial loss fault and the biased fault of the i^th DG, respectively. Combining Eqs 7 and 8, the dynamic model with disturbance and actuator faults can be represented as follows:

$\{\begin{array}{l}{\dot{y}}_{i1}=y_{i2}\\ {\dot{y}}_{i2}=(1-{\phi }_i)v_i+{\psi }_i+d_i\left(t\right)\end{array}.(9)$

FIGURE 3

FIGURE 3. Structure of i^th MG with the actuator fault.

Assumption 1:. The severity of the partial loss fault and the biased fault of the i^th DG are time-varying and bounded. i.e., there exist constants $\overline{\phi }$ and $\overline{\psi }$ such that ‖φ_i‖≤ $\overline{\phi }$,‖ψ_i‖≤ $\overline{\psi }$. 0<φ_i(t)< $\overline{\phi }$ <1.

Assumption 2:. The external disturbances are time-varying and bounded, i.e., there exists constant $\overline{d}$ such that ‖d_i(t)‖≤ $\overline{d}$.In practical application, the denotation of these assumptions is that the disturbances and faults that occur are within a certain range.In the leader-followers’ multi-agent system, the leader node must be appointed, and only a few nodes receive the information from the leader node. In this study, we assigned the communication network shown in Figure 4. The remaining nodes are synchronized to the reference value according to the communication with neighbors to ensure the voltage quality of the local load. This can effectively enhance the reliability of the system and improve the scalability of DGs.Therefore, the state space expression of the leader is

${\dot{\mathit{y}}}_{\mathit{0}}=\mathbf{C}{\mathit{y}}_{\mathit{0}},(10)$

where ${\mathit{y}}_0={\left[\begin{array}{cc}{y}_{01}& y_{02}\end{array}\right]}^{\mathrm{T}}=\left[\begin{array}{cc}{v}_{ref}& {\dot{v}}_{ref}\end{array}\right]$ and C = $\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right]$.

FIGURE 4

FIGURE 4. Communication-directed graph.

Distributed Secondary Voltage Control

However, the primary control may not be able to make the MG run in an optimal state. In this section, we designed the secondary voltage control based on the nonlinear sliding mode surface to eliminate the deviation of voltage. The communication network between multi-DGs can be modeled by a digraph, and DGs are considered as the nodes in the digraph. The edges of the digraph represent the communication links of the network. A digraph is usually expressed as G= (γ, ξ, Α) with a non-empty finite set of N nodes γ = {v₁, v₂, …, v_N}, a set of edges or arcs ξ⊂γ×γ, and the associated adjacency matrix А = [a_ij]∈ ${\mathrm{ℝ}}^{N\times N}$. a_ij is the weight of edge from node j to node i. The set of neighbors of node i is denoted as N_i = {j∣(v_j,v_i)∈ξ}. If node j receives the information from node i, a_ij = 1; otherwise, a_ij = 0. The in-degree matrix is defined as D = diag{d_i}∈ ${\mathrm{ℝ}}^{N\times N}$, and d_i is the number of nodes which send message to i^th DG. The Laplacian matrix is defined as L = D-А. L and has all row sums equal to zero.

Therefore, we define the local neighborhood’s voltage deviation as

$e_i={\displaystyle {\sum }_{j=1}^N{a}_{ij}\left(y_{i1}-y_{j1}\right)+b_i\left(y_{i1}-y_{01}\right)},(11)$

${\dot{e}}_i={\displaystyle {\sum }_{j=1}^N{a}_{ij}(y_{i2}-y_{j2})+b_i(y_{i2}-y_{02})}.(12)$

The pining gain b_i is the weight of the edge which i^th DG is connected to the reference. If the i^th DG is connected to the leader, b_i = 1, otherwise, b_i = 0.

Let $e=[e_1,e_2,\cdots ,e_{\mathrm{N}}]$ and $\dot{e}$ = $[{\dot{e}}_1,{\dot{e}}_2,\cdots ,{\dot{e}}_{\mathrm{N}}]$, the compacted form of the global error vector e and $\dot{e}$ is

$\mathbf{e}=(\mathbf{L}+\mathbf{B}){\mathbf{\text{Δ}}}_1(13)$

$\dot{\mathbf{e}}=(\mathbf{L}+\mathbf{B}){\mathbf{\text{Δ}}}_2(14)$

where B = diag [b_i] is the pining gain matrix. ${\mathbf{\Delta }}_1={\left[y_{11}-y_{01},\cdots ,y_{\mathrm{N}1}-y_{01}\right]}^{\mathrm{T}}$ and ${\mathbf{\Delta }}_2={\left[y_{12}-y_{02},\cdots ,y_{\mathrm{N}2}-y_{02}\right]}^{\mathrm{T}}$.

Therefore, the global tracking errors’ dynamics can be written as

$\ddot{\mathbf{e}}=\left(\mathbf{L}+\mathbf{B}\right)\left(\left({\mathbf{I}}_{\mathbf{N}}-\mathit{\varphi }\right)\mathbf{v}+\mathit{\psi }+\mathbf{d}\right),(15)$

where I_N is the N×N diagonal matrix, and the diagonal element is 1. $\mathit{\phi }=\mathrm{diag}\left[{\phi }_i\right]$, $\mathit{v}={[v_1,\cdots ,v_N]}^{\mathrm{T}}$, $\mathit{\psi }={[{\psi }_1,\cdots ,{\psi }_{\mathrm{N}}]}^{\mathrm{T}}$, $\mathrm{d}={[d_1,\cdots ,d_{\mathrm{N}}]}^{\mathrm{T}}$,and i = 1, …, N.

Therefore, the voltage restoration problem of the secondary control is transformed into the problem of error elimination. We define the matrix ρ=(L + B)φ(L + B)⁻¹. λ_i is the eigenvalue of matrix ρ. Because L + B is the invertible matrix, 0<λ_i < 1. λ_m = max{λ₁, λ₂, … , λ_n}.Then, we designed the sliding surface as

$s=\left(1-{\lambda }_m\right)e+\frac{1}{\beta }{\dot{e}}^{p/q},(16)$

where β is the positive constant, and p and q are positive odd constants. 1 < p/q < 2. $s={[s_1^{\mathrm{T}},\cdots ,s_{\mathrm{N}}^{\mathrm{T}}]}^{\mathrm{T}}$.

Theorem 1:. Suppose that Assumptions 1 and 2 are valid with a known partial loss, biased fault and disturbance bounds. It is assumed that the function nonzero vector sig(s)^α is not identically equal to zero, and there exist proper positive constants α and β (0<α < 1) and positive odd integers p and q (1 < p/q < 2). Therefore, the DG output voltage in system Eq. 9 can synchronize with the reference value in the presence of the actuator fault and external disturbance under the FTC:

$V_{ni}=\frac{1}{g_i}(v_i-f_i\left(x\right)),i=\mathrm{1,2},\cdots ,N(17)$

$v_i={(l_{ii}+b_i)}^{-1}(-\frac{\beta q}{p}{\dot{e}}_i^{2-p/q})+{\displaystyle \sum _{i\ne j}{l}_{ij}(-\frac{\beta q}{p}{\dot{e}}_j^{2-p/q})}+\mathrm{sig}{\left(s_i\right)}^{\alpha }(18)$

$v={(\mathbf{L}+\mathbf{B})}^{-1}(-\frac{\beta q}{p}{\dot{e}}^{2-p/q}-(\mathbf{L}+\mathbf{B})\mathrm{sig}{\left(s\right)}^{\alpha }),(19)$

where v = [v₁, v₂, …, v_N]^T, sig(s)^α = |s|^αsign(s) = [|s₁|^αsign (s₁), |s₂|^αsign (s₂),…, |s_N|^αsign (s_N)]^T, and sign (•) is sign function.

Proof:. The Lyapunov function is constructed as follows.

$V=\frac{1}{2}{s}^{\text{T}}s.(20)$

The time derivative of Eq. 20 is $\dot{V}=s^T\dot{s}$. Then, we make the following derivation.

$\begin{array}{c}\dot{s}=(1-{\lambda }_m)\dot{e}+\frac{p}{\beta q}{\dot{e}}^{\frac{p}{q}-1}\circ \ddot{e}\\ =(1-{\lambda }_m)\dot{e}+\frac{p}{\beta q}{\dot{e}}^{\frac{p}{q}-1}\circ \left[(\mathbf{L}+\mathbf{B})(({\mathbf{I}}_{\mathbf{N}}-\varphi )v+\psi +d)\right]\\ =(1-{\lambda }_m)\dot{e}+\frac{p}{\beta q}{\dot{e}}^{\frac{p}{q}-1}\circ \left[(\mathbf{L}+\mathbf{B})(({\mathbf{I}}_{\mathbf{N}}-\mathbf{\varphi }){(\mathbf{L}+\mathbf{B})}^{-1}(-\frac{\beta q}{p}{\dot{e}}^{2-p/q}-(\mathbf{L}+\mathbf{B})\mathrm{sig}{\left(s\right)}^{\alpha })+\psi +d)\right]\\ =(1-{\lambda }_m)\dot{e}+\frac{p}{\beta q}{\dot{e}}^{\frac{p}{q}-1}\circ -\frac{\beta q}{p}{\dot{e}}^{2-p/q}-(\mathbf{L}+\mathbf{B})\mathrm{sig}{\left(s\right)}^{\alpha }-(\mathbf{L}+\mathbf{B})\varphi {(\mathbf{L}+\mathbf{B})}^{-1}(-\frac{\beta q}{p}{\dot{e}}^{2-p/q}-(\mathbf{L}+\mathbf{B})\mathrm{sig}{\left(s\right)}^{\alpha })+\mathbf{L}+\mathbf{B}\psi +d)\\ =-{\lambda }_m\dot{e}-\frac{p}{\beta q}{\dot{e}}^{\frac{p}{q}-1}\circ (\mathbf{L}+\mathbf{B})\mathrm{sig}{\left(s\right)}^{\alpha }-\frac{p}{\beta q}{\dot{e}}^{\frac{p}{q}-1}\circ \mathit{\rho }(-\frac{\beta q}{p}{\dot{e}}^{2-p/q}-(\mathbf{L}+\mathbf{B})\mathrm{sig}{\left(s\right)}^{\alpha })+\frac{p}{\beta q}{\dot{e}}^{\frac{p}{q}-1}\circ (\mathbf{L}+\mathbf{B})(\psi +d)\\ =-{\lambda }_m\dot{e}-\frac{p}{\beta q}{\dot{e}}^{\frac{p}{q}-1}\circ (\mathbf{L}+\mathbf{B})\mathrm{sig}{\left(s\right)}^{\alpha }+\frac{p}{\beta q}{\dot{e}}^{\frac{p}{q}-1}\circ \rho \frac{\beta q}{p}{\dot{e}}^{2-p/q}+\frac{p}{\beta q}{\dot{e}}^{\frac{p}{q}-1}\circ (\mathbf{L}+\mathbf{B})\mathbf{\varphi }\mathrm{sig}{\left(s\right)}^{\alpha }+\frac{p}{\beta q}{\dot{e}}^{\frac{p}{q}-1}\circ (\mathbf{L}+\mathbf{B})(\psi +d),\end{array}(21)$

where “$\circ$” is the Hadamard product.Assuming there exists a nonzero vector x, the following function hold

$\mathit{\rho }x={\lambda }_{i}x.(22)$

We select λ_i = λ_m. Defining τ_i is the eigenvalue of matrix L + B, which are also positive real numbers. τ_m = max{τ₁, τ₂, … , τ_N }. Then,

$\begin{array}{c}\dot{s}=-{\lambda }_m\dot{e}-\frac{p}{\beta q}{\dot{e}}^{\frac{p}{q}-1}\circ \tau \mathrm{sig}{\left(s\right)}^{\alpha }+\frac{p}{\beta q}{\dot{e}}^{\frac{p}{q}-1}\circ {\lambda }_m\frac{\beta q}{p}{\dot{e}}^{2-p/q}+\frac{p}{\beta q}{\dot{e}}^{\frac{p}{q}-1}\circ \tau \mathit{\varphi }\mathrm{sig}{\left(s\right)}^{\alpha }+\frac{p}{\beta q}{\dot{e}}^{\frac{p}{q}-1}\circ \tau (\psi +d)\\ =-\frac{p}{\beta q}{\dot{e}}^{\frac{p}{q}-1}\circ \tau {\left|s\right|}^{\alpha }\mathrm{sign}\left(s\right)+\frac{p}{\beta q}{\dot{e}}^{\frac{p}{q}-1}\circ \tau \mathit{\varphi }{\left|s\right|}^{\alpha }\mathrm{sign}\left(s\right)+\frac{p}{\beta q}{\dot{e}}^{\frac{p}{q}-1}\circ \tau (\psi +d).\end{array}(23)$

If every item $s_i{\dot{s}}_i$ is less than zero, the sum must be less than zero, i.e.,

$s_i{\dot{s}}_i<0\Rightarrow \dot{V}=s^{\text{T}}\dot{s}=s_1{\dot{s}}_1+s_2{\dot{s}}_2+\cdots +s_N{\dot{s}}_N<0,i=\mathrm{1,2},\cdots N.(24)$

The following function hold

$\begin{array}{c}{s}_i{\dot{s}}_i=-\frac{p}{\beta q}{{\dot{e}}_i}^{\frac{p}{q}-1}{\tau }_m{\left|s_i\right|}^{\alpha }{s}_i\mathrm{sign}\left(s_i\right)+\frac{p}{\beta q}{{\dot{e}}_i}^{\frac{p}{q}-1}{\tau }_m{\phi }_i{\left|s_i\right|}^{\alpha }{s}_i\mathrm{sign}\left(s_i\right)+\frac{p}{\beta q}{{\dot{e}}_i}^{\frac{p}{q}-1}{\tau }_m({\psi }_i+d_i)\left|s_i\right|\mathrm{sign}(s_i))\\ =-\frac{p}{\beta q}{\dot{e}}_i\frac{p}{q}-1{\tau }_m\left|s_i\right|({\left|s_i\right|}^{\alpha }-{\phi }_i{\left|s_i\right|}^{\alpha }-({\psi }_i+d_i)\mathrm{sign}\left(s_i\right))\\ <-\frac{p}{\beta q}{{\dot{e}}_i}^{\frac{p}{q}-1}{\tau }_m\left|s_i\right|{\left|s_i\right|}^{\alpha }-{\phi }_i{\left|s_i\right|}^{\alpha }-\overline{\psi }+\overline{d}\mathrm{sign}{s}_i.\end{array}(25)$

Then, we can infer that

$s_i{\dot{s}}_i<0\iff {\left|s_i\right|}^{\alpha }-{\phi }_i{\left|s_i\right|}^{\alpha }-(\overline{\psi }+\overline{d})\mathrm{sign}\left(s_i\right)>0,(26)$

$\iff \left|s_i\right|>{\left(\frac{\overline{\psi }+\overline{d}}{1-{\phi }_i}\right)}^{\frac{1}{\alpha }}.(27)$

The boundary Ω is

$\text{Ω}={\left(\frac{\overline{\psi }+\overline{d}}{1-{\phi }_i}\right)}^{\frac{1}{\alpha }}.(28)$

According to the Lyapunov theory, the fault-tolerant system is Lyapunov-stable outside the boundary (28). Therefore, the sliding manifold converge to and remain inside the boundary at the steady state. The error tracking also converges along with the sliding mode surface.

Remark 1:. The biased fault and partial loss of the actuator have a great impact on the stability and quality of the MG, even secure operation. It is worth mentioning that in order to ensure the realizability of the controller and reduce communication lines, the controller (18) is suitable for only one DG node connected to the reference node, and the data flow direction is monodirectional, but it may also limit the application of this method.

Remark 2:. SMC possesses inherent robustness against faults and disturbances. The proposed controller design method achieves consensus-based voltage recovery using the information of local and adjacent nodes through a simple communication network. In addition, this method provides the capability of plug and play of DGs because of relative independence, which enhances the flexibility of the system and the utilization of DGs. The designed controller based on the nonlinear sliding mode surface can stabilize the system in a finite time and make the error approach the zero point infinitely. At the same time, it intelligently avoids the singularity problem caused by the terminal SMC.

An Illustrative Example

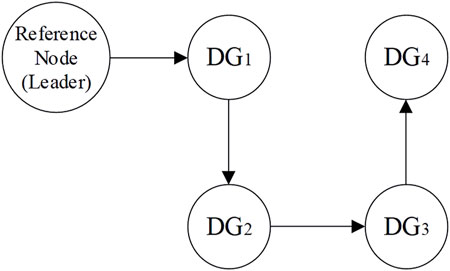
In this section, we verified the feasibility and effectiveness of the proposed method based on the islanded MG test system illustrated in Figure 4. The system frequency is 50Hz, and detailed parameters are shown in Table.1; Table.2. Due to the insensitivity of the proposed sliding mode controller to parameters and uncertainties, the simulation is carried out in a 100% uncertain environment. According to the graph theory, the adjacency matrix, in-degree matrix, and pining gain matrix of the communication network based on Figure 4 are shown as follows, respectively. Only the first DG is connected to the reference. $\mathbf{A}=\left[\begin{array}{cccc}0& 0& 0& 0\\ 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\end{array}\right]$, $\mathbf{D}=\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$, and $\mathbf{B}=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right]$

TABLE 1

TABLE 1. Structural parameters of DGs.

TABLE 2

TABLE 2. Load parameters of DGs.

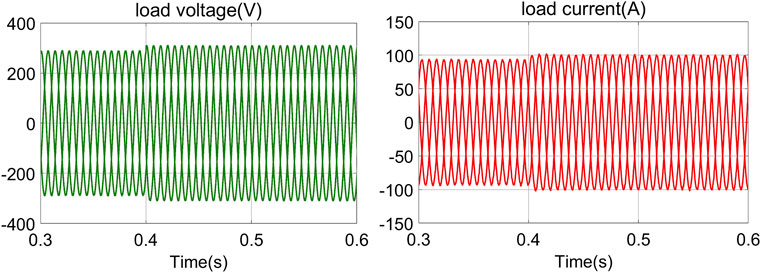
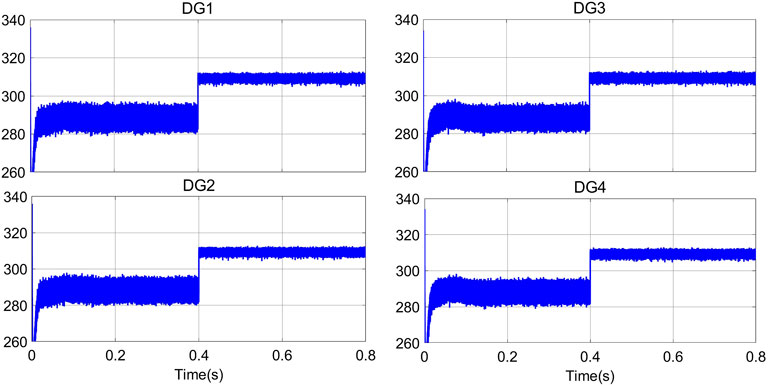
It is worth mentioning that before designing the secondary voltage control, we ensured that the MG system under the primary voltage control is stable. The purpose of designing the recovery layer is to improve the resilience and reliability of the MG. At the beginning, in order to test the stability of the system under primary control, we intentionally disabled the secondary control. The secondary voltage recovery layer is introduced at 0.4 s to highlight the functions and advantages of the secondary voltage regulation in the control system, as shown in Figure 5, Figure 6 and Figure 7. The simulation results of 0–0.4 s show that the main controller can be activated quickly when the system starts up, and four DGs supply power to the load, noting that the voltage can be quickly restored to the nominal value after the addition of secondary voltage regulation at 0.4 s. Compared to the study by Shahab et al., (2020), voltage restores to the nominal reference value more quickly and with less fluctuation. Moreover, the voltage chattering decreases significantly with the addition of SMC, as shown in Figure 7. We can conclude that the proposed method makes the system respond quickly and is able to achieve consistency tracking.

FIGURE 5

FIGURE 5. Load voltage and current.

FIGURE 6

FIGURE 6. d-component of load voltage.

FIGURE 7

FIGURE 7. power sharing of DGs.

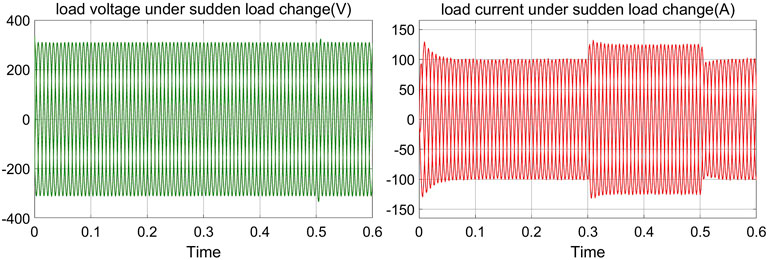
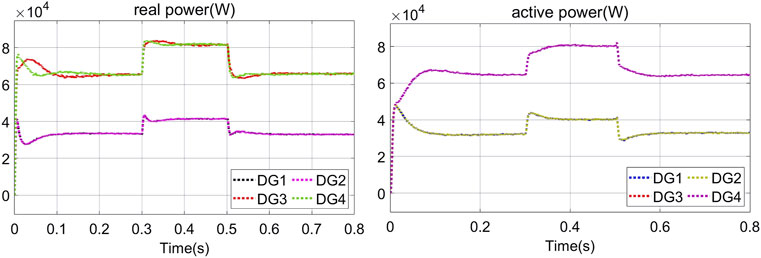
In order to test the system’s ability to cope with load mutation, the 20kW/20kVar mutation load was added on DG1 and DG2, and the 40 kW/40 kVar mutation load was added on DG3 and DG4 at 0.3–0.5 s under the secondary voltage control. According to Figure 8, the bus voltage can be stable when the load changes, maintaining the stability of the system and ensuring the quality of power supply.

FIGURE 8

FIGURE 8. Load voltage and current under load mutation.

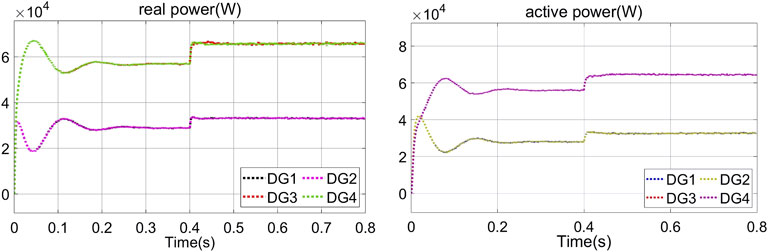
As can be seen from Figures 9, 10, the proposed strategy can keep the output voltage of each DG as the rated value, and the output power of the system has good response characteristics under the load fluctuates.

FIGURE 9

FIGURE 9. Load voltage of DGs.

FIGURE 10

FIGURE 10. Power sharing under load mutation.

Conclusion

With the integration of the network communication system and physical components, the emergence of huge advantages came along with security and reliability issues. This study addressed the problem of the secondary voltage regulation of the network communication-based MG system with actuator-biased faults and partial failure faults. By constructing a controller based on a nonlinear sliding mode surface, the voltage error variable is approached to the sliding mode surface in a finite time. To eliminate the adverse effects of disturbances and faults, we made use of insensitivity to disturbance of SMC to design the fault-tolerant controller. The average voltage magnitude of each DG is synchronized with the leader node by a simple communication network which effectively reduces a series of problems caused by frequent communication. The stability of the system is proved by the Lyapunov method, and the feasibility is verified by MATLAB/Simulink. The simulation results show that the proposed method can effectively deal with load mutation and has good dynamic characteristics. However, there are still some problems to be solved. The applicability of this method is not wide enough, which limits the promotion of this method.

In the future work, it is necessary to establish a more practical global closed-loop system model and take into account the possible delay and packet loss in the communication process. At the same time, the demand for power electronic converters and energy storage technologies is growing as renewable energy penetration increases. Converters must be designed to meet future-ride-through (FRT) requirements and can be protected with special energy storage devices such as supercapacitors to control voltage rise during faults (Badal et al., 2019).

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

YF and JM have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This research was funded in part by the Key Science and Technology Program of Gansu Province, China (grant number 20YF8NA059), and in part by the National Natural Science Foundation of China (grant number 62141304).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Afshari, A., Karrari, M., Baghaee, H. R., Gharehpetian, G. B., and Karrari, S. (2020). Cooperative Fault-Tolerant Control of Microgrids under Switching Communication Topology. IEEE Trans. Smart Grid 11 (3), 1866–1879. doi:10.1109/tsg.2019.2944768

CrossRef Full Text | Google Scholar

Alhasnawi, B. N., Jasim, B. H., and Sedhom, B. E. (2021). Distributed Secondary Consensus Fault Tolerant Control Method for Voltage and Frequency Restoration and Power Sharing Control in Multi-Agent Microgrid. Int. J. Electr. Power Energ. Syst. 133, 107251. doi:10.1016/j.ijepes.2021.107251

CrossRef Full Text | Google Scholar

Badal, F. R., Das, P., Sarker, S. K., and Das, S. K. (2019). A Survey on Control Issues in Renewable Energy Integration and Microgrid. Prot. Control. Mod. Power Syst. 4. doi:10.1186/s41601-019-0122-8

CrossRef Full Text | Google Scholar

Bidram, A., and Davoudi, A. (2012). Hierarchical Structure of Microgrids Control System. IEEE Trans. Smart Grid 3 (4), 1963–1976. doi:10.1109/tsg.2012.2197425

CrossRef Full Text | Google Scholar

Bidram, A., Davoudi, A., Lewis, F. L., and Guerrero, J. M. (2013). Distributed Cooperative Secondary Control of Microgrids Using Feedback Linearization. IEEE Trans. Power Syst. 28 (3), 3462–3470. doi:10.1109/tpwrs.2013.2247071

CrossRef Full Text | Google Scholar

Dehkordi, N. M., Baghaee, H. R., Sadati, N., and Guerrero, J. M. (2019). Distributed Noise-Resilient Secondary Voltage and Frequency Control for Islanded Microgrids. IEEE Trans. Smart Grid 10 (4), 3780–3790. doi:10.1109/tsg.2018.2834951

CrossRef Full Text | Google Scholar

Dehkordi, N. M., Sadati, N., and Hamzeh, M. (2017). Distributed Robust Finite-Time Secondary Voltage and Frequency Control of Islanded Microgrids. IEEE Trans. Power Syst. 32 (5), 3648–3659. doi:10.1109/tpwrs.2016.2634085

CrossRef Full Text | Google Scholar

Ding, D., Han, Q.-L., Wang, Z., and Ge, X. (2019). A Survey on Model-Based Distributed Control and Filtering for Industrial Cyber-Physical Systems. IEEE Trans. Ind. Inf. 15 (5), 2483–2499. doi:10.1109/tii.2019.2905295

CrossRef Full Text | Google Scholar

Farrokhabadi, M., Canizares, C. A., Simpson-Porco, J. W., Nasr, E., Fan, L., Mendoza-Araya, P. A., et al. (2020). Microgrid Stability Definitions, Analysis, and Examples. IEEE Trans. Power Syst. 35 (1), 13–29. doi:10.1109/tpwrs.2019.2925703

CrossRef Full Text | Google Scholar

Hossain, M., Pota, H., Issa, W., and Hossain, M. (2017). Overview of AC Microgrid Controls with Inverter-Interfaced Generations. Energies 10 (9), 1300. doi:10.3390/en10091300

CrossRef Full Text | Google Scholar

Huang, M., Ding, L., Li, W., Chen, C.-Y., and Liu, Z. (2021). Distributed Observer-Based H ∞ Fault-Tolerant Control for DC Microgrids with Sensor Fault. IEEE Trans. Circuits Syst. 68 (4), 1659–1670. doi:10.1109/tcsi.2020.3048971

CrossRef Full Text | Google Scholar

Li, Y., Gao, D. W., Gao, W., Zhang, H., and Zhou, J. (2020). Double-Mode Energy Management for Multi-Energy System via Distributed Dynamic Event-Triggered Newton-Raphson Algorithm. IEEE Trans. Smart Grid 11 (6), 5339–5356. doi:10.1109/tsg.2020.3005179

CrossRef Full Text | Google Scholar

Liu, L.-N., and Yang, G.-H. (2021). Distributed Optimal Economic Environmental Dispatch for Microgrids over Time-Varying Directed Communication Graph. IEEE Trans. Netw. Sci. Eng. 8 (2), 1913–1924. doi:10.1109/tnse.2021.3076526

CrossRef Full Text | Google Scholar

Pogaku, N., Prodanovic, M., and Green, T. C. (2007). Modeling, Analysis and Testing of Autonomous Operation of an Inverter-Based Microgrid. IEEE Trans. Power Electron. 22 (2), 613–625. doi:10.1109/tpel.2006.890003

CrossRef Full Text | Google Scholar

Saha, S., Roy, T. K., Mahmud, M. A., Haque, M. E., and Islam, S. N. (2018). Sensor Fault and Cyber Attack Resilient Operation of DC Microgrids. Int. J. Electr. Power Energ. Syst. 99, 540–554. doi:10.1016/j.ijepes.2018.01.007

CrossRef Full Text | Google Scholar

Sardashti, A., and Ramezani, A. (2021). Fault Tolerant Control of Islanded AC Microgrids under Sensor and Communication Link Faults Using Online Recursive Reduced-Order Estimation. Int. J. Electr. Power Energ. Syst. 126, 106578. doi:10.1016/j.ijepes.2020.106578

CrossRef Full Text | Google Scholar

Sedhom, B. E., El-Saadawi, M. M., Hatata, A. Y., and Alsayyari, A. S. (2020). Hierarchical Control Technique-Based Harmony Search Optimization Algorithm versus Model Predictive Control for Autonomous Smart Microgrids. Int. J. Electr. Power Energ. Syst. 115, 105511. doi:10.1016/j.ijepes.2019.105511

CrossRef Full Text | Google Scholar

Shahab, M. A., Mozafari, B., Soleymani, S., Dehkordi, N. M., Shourkaei, H. M., and Guerrero, J. M. (2020). Distributed Consensus-Based Fault Tolerant Control of Islanded Microgrids. IEEE Trans. Smart Grid 11 (1), 37–47. doi:10.1109/tsg.2019.2916727

CrossRef Full Text | Google Scholar

Shotorbani, A. M., Ghassem-Zadeh, S., Mohammadi-Ivatloo, B., and Hosseini, S. H. (2017). A Distributed Secondary Scheme with Terminal Sliding Mode Controller for Energy Storages in an Islanded Microgrid. Int. J. Electr. Power Energ. Syst. 93, 352–364. doi:10.1016/j.ijepes.2017.06.013

CrossRef Full Text | Google Scholar

Yamashita, D. Y., Vechiu, I., and Gaubert, J.-P. (2020). A Review of Hierarchical Control for Building Microgrids. Renew. Sustain. Energ. Rev. 118, 109523. doi:10.1016/j.rser.2019.109523

CrossRef Full Text | Google Scholar

Yoo, H.-J., Nguyen, T.-T., and Kim, H.-M. (2020). Consensus-Based Distributed Coordination Control of Hybrid AC/DC Microgrids. IEEE Trans. Sustain. Energ. 11 (2), 629–639. doi:10.1109/tste.2019.2899119

CrossRef Full Text | Google Scholar

Zhu, B., Wang, Y., Zhang, H., and Xie, X. (2021). Distributed Finite-Time Fault Estimation and Fault-Tolerant Control for Cyber-Physical Systems with Matched Uncertainties. Appl. Maths. Comput. 403, 126195. doi:10.1016/j.amc.2021.126195

CrossRef Full Text | Google Scholar