
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Energy Res. , 07 April 2022
Sec. Process and Energy Systems Engineering
Volume 10 - 2022 | https://doi.org/10.3389/fenrg.2022.822776
This article is part of the Research Topic Enhancing Heat Transfer by Using Nanofluid to Improve the Efficiency of Thermal Systems View all 7 articles
Addition of nanoparticles into a fluid can improve the heat transfer performance of the base fluid in heat exchangers. In this work, the preparation method and process of nanofluids are introduced, and thermal properties of nanofluids, such as thermal conductivity and viscosity, are discussed deeply. This paper summarizes various theoretical models of thermal conductivity and viscosity of nanofluids. A comprehensive literature survey on applications and limitations of nanofluids has been compiled. This paper also aims to review the natural and forced convective heat transfer characteristics of nanofluids with and without magnetic fields. The discussion for the natural convective heat transfer of nanofluids focuses on the heat transfer performance of non-conventional enclosures and electric heaters. The effects on heat transfer due to variations of heated walls are also investigated. Specific applications of nanofluids in a tube with trapezoidal ribs, double-tube heat exchangers, and plate heat exchangers have been reviewed and presented in a discussion about forced convective heat transfer. The previous results show that the inlet temperature of nanofluids obviously affects the heat transfer characteristics of double-tube heat exchangers, whereas a multi-walled carbon nanotube–water nanofluid shows significant advantages in plate heat exchangers. Finally, this paper studies natural convective heat transfer of magnetic fluids in a square cavity and forced convection heat transfer in a straight tube and a corrugated structure under the action of magnetic fields. It is found that the heat transfer performance of an Fe3O4–water nanofluid is enhanced when a magnetic field is applied to the corrugated plate heat exchangers, and the pressure drop can be reduced by around 10%. It is recommended that natural convection of magnetic fluids needs to be investigated experimentally in a real cavity and a corrugated channel under the influence of a magnetic field. In addition, studies of alternating magnetic field are recommended to reveal any improvements of thermal performance of magnetic fluids in heat exchange devices. This review puts forward an effective solution for improvement of the thermal performance of heat transfer equipment and serves as a basic reference for applications of nanofluids in heat transfer fields.
With the increased requirements of heat transfer enhancement in industrial applications, various heat transfer technologies have been developed rapidly. Due to excellent thermal performance, uniformity, and stability of dispersion, nanofluids are used as efficient working media in heat pipes (Sun et al., 2018), heat exchangers, automobile radiators (Hussein et al., 2014; Selvam et al., 2017), solar energy systems (Chen et al., 2019; Amirahmad et al., 2021), and electronic chips. The concept of nanofluid was first proposed by Choi (Carmichael et al., 1963). Nanofluids are stable colloidal suspensions prepared by dispersing nanoparticles in water, oil, ethylene glycol, and other base fluids.
Nanoparticles significantly affect thermal properties of base fluids, such as thermal conductivity and viscosity. Theoretical models of thermal conductivity of nanofluids were summarized by Yang et al. (2021), Kumar et al. (2015a), and Sarviya and Fuskele (2017). These researchers found that concentration, temperature, nanoparticle diameter, and particle shape were main factors affecting the thermal conductivity of nanofluids. When the temperature range was from 25 to 100°C, the thermal conductivity of magnesia–ethylene glycol nanofluid increases with the increase of concentration. Kumar et al. (2016) showed that the thermal conductivity of 1.25 vol% multi-walled carbon nanotube nanofluids at 35°C was 122.67% higher than that of water.
Usually, nanofluids have higher viscosity than base fluids. Wang et al. (2021a) found that the viscosity of Fe3O4–CNT magnetic fluids at 0.5 and 1% concentrations was 144.2 and 149.9% compared to that of deionized water. In the study of Arya et al. (2019), the viscosity of 0.3 wt% MgO–ethylene glycol nanofluids at 25°C increased by 13.8%. Kumar et al. (2016) found that the viscosities of TiO2, Al2O3, ZnO, and CeO2 nanofluids were higher than that of the base fluid, and the viscosity of Al2O3 nanofluids with 0.5% volume fraction increased by 10% compared to that of water.
The heat transfer performance of nanofluids can be enhanced by different heat transfer mechanisms, especially for conductive and convective heat transfer (natural convection and forced convection) (Vajjha and Das, 2012; Leela Vinodhan et al., 2016; Yang et al., 2021). Natural convection caused by temperature differences in a cavity is widely used in electronic device cooling, solar energy harvesting, energy conversion, food processing, and petrochemical engineering. Hdhiri et al. (2019) investigated natural convection of an electrically conductive fluid in a rectangular cavity with porous medium. They considered that the Prandtl number was an important factor affecting the average Nusselt number. Souayeh et al. (2020) carried out a three-dimensional numerical study of the natural convection heat transfer between the square cavity and the inner sphere with air. The results showed that the heat transfer performance for the spherical interior was better than that for the cylindrical interior. Many researchers have studied natural convection of nanofluids from different aspects. Rostami et al. (2020) introduced natural convection with various nanofluids in a cavity. It was found that types and concentrations of nanofluids, shapes of cavities, and Rayleigh number showed important effects on heat transfer characteristics. They concluded that the heat transfer characteristics in the cavity were weakened due to the increase in fluid viscosity caused by nanoparticles. Locations of heat sources also had a significant impact on fluid flow and heat transfer of nanofluids inside the cavity (Öztop et al., 2015). They concluded that there is little generalized relation between heat transfer characteristics and heating conditions of the nanofluids in the cavity. Electric heating is a practical application of natural convective heat transfer in industrial production and daily life. Electric heaters are indoor heating equipment, which have advantages of flexible heating and low costs. The base fluid used in the electric heaters is generally water or heat transfer oil.
Compared with improving the structure of the heat exchanger to enhance the heat transfer, the application of nanofluids with better thermophysical properties is a good choice. Double-tube heat exchangers and plate heat exchangers are two widely used energy conversion devices. A double-tube heat exchanger consists of two tubes with different diameters. Heat transfer is achieved between fluids in a small diameter tube and in an annulus region. When the nanofluids are used in the double-tube heat exchanger, the heat transfer performance is significantly enhanced (Darzi et al., 2013; Moradi et al., 2019). Moradi et al. (2019) found that the heat transfer coefficient increased by 35% for 4 wt% multi-walled carbon nanotube nanofluid in a double-tube heat exchanger with porous media. Darzi et al. (2013) studied heat transfer and pressure drop of Al2O3 nanofluids in a double-tube heat exchanger. They found that high Reynolds number resulted in high heat transfer coefficient. Onyiriuka et al. (2019) used new biological nanofluid–water-based mango bark nanofluid in a double-tube heat exchanger. They found that the heat transfer coefficient of the nanofluid was higher than that of the base fluid, and when the Reynolds number was 5,000, the Nusselt number increased by 68%.
Plate heat exchangers are widely used in heating and refrigeration in various fields due to their high heat transfer efficiency and flexible application. The plate heat exchanger is made of a series of metal plates, and hot and cold fluids flow on both sides of the metal plates to achieve high-efficiency heat transfer (Galeazzo et al., 2006). Kumar et al. (2015b) reviewed several references on heat transfer characteristics of nanofluids in plate heat exchangers. They pointed out that most of the research results showed that the improvement of heat transfer performance was attributed to enhancements of thermophysical properties of fluids by nanoparticles, and the increase of the concentration of nanofluids resulted in the increase in heat transfer coefficient. However, some studies showed that the heat transfer coefficient further increased with the reduction of nanofluid concentration. Moreover, the heat transfer performance of nanofluids was also related to the flow pattern. Therefore, applications of nanofluids in plate heat exchangers needed further studies.
Nanofluids also have shown great potentials in thermal performance when magnetic fields are applied. The magnetic fluid as a functional nanofluid shows both flow characteristics and magnetic properties. Magnetic fluids are made by adding magnetic particles (such as iron, nickel, cobalt, and their oxides) to a base fluid with no magnetism. Sundar et al. (2013) experimentally studied thermal conductivity and viscosity of Fe3O4–water nanofluids. It was found that the thermal conductivity of Fe3O4–water nanofluids was affected by particle size, concentration, and temperature. At the same conditions, the increase in viscosity was higher than that in thermal conductivity compared to the base fluid. The intensity and direction of magnetic fields played vital roles in heat transfer of magnetic fluids. Giwa et al. (2021) found that researchers conducted many numerical simulations concerning heat transfer of magnetic fluids in a square cavity, but few experiments are available. They concluded that, for magnetic fluids, the heat transfer enhancement deteriorated because of the magnetic field, and only a few works indicated that a magnetic field enhanced heat transfer.
The magnetic field is another important research aspect in the studies on forced convection of magnetic fluid in tubes. Hariri et al. (2017) numerically simulated the heat transfer performance of Fe3O4 nanofluids in tubes under non-uniform magnetic fields. The existence of the magnetic field increased the Nusselt number of the magnetic fluid by more than 300% in the tube. Gorjaei et al. (2020) showed that the flow velocity of the magnetic fluid in the center of the tube decreased when the velocity near the wall increased due to the non-uniform magnetic field. However, limited research studies on magnetic fluids have been conducted for different structured tubes, such as corrugated tubes.
The purpose of this research is to summarize heat transfer characteristics of natural convection and forced convection of nanofluids in various heat exchange devices. In this paper, the preparation methods of nanofluids are introduced, and various physical properties of nanofluids, such as stability and thermophysical properties (thermal conductivity and viscosity), are discussed in detail. In applications of nanofluids, effects of location of the heat sources on natural convective heat transfer of nanofluids are analyzed in different cavity structures, such as the T-shaped cavity, C-shaped cavity, Γ-shaped cavity, and H-shaped cavity. This paper also summarizes the heat transfer performance of various nanofluids in different heat transfer devices, including electric heaters, plate heat exchangers, straight tubes, and double-tube heat exchangers. For magnetic fluids, this paper reviews findings about effects of magnetic field factors such as the magnetic field direction, magnetic field magnitude, and magnetic field gradient on the heat transfer performance of magnetic fluids in square cavities, straight tubes, and electric heaters. Effective solutions are put forward for improving the thermal performance of heat transfer equipment to provide a basic reference for applications of nanofluids.
As working media with high thermal efficiency, nanofluids have played a very important role in heat transfer enhancement. Preparation methods of nanofluids directly affect their stability and thermophysical properties. This part mainly investigates preparation methods and thermophysical properties of nanofluids.
The ideal nanofluid is nanoparticle suspension with uniform dispersion and high stability. However, due to a large specific surface area and high surface energy of nanoparticles, these can easily agglomerate and precipitate in the base liquid, which affects heat transfer characteristics of nanofluids (Chakraborty, 2019). It is particularly important to obtain nanofluids with good suspension stability. The stability of nanofluids depends on preparation methods, i.e., one-step method (Zhu et al., 2004; Kumar et al., 2009) or two-step method (Wang et al., 2019; Zheng et al., 2020a; Zheng et al., 2020b; Chen et al., 2020; Wang et al., 2020; Wang et al., 2021a; Zheng et al., 2021). In the one-step method, nanoparticles are directly dispersed into the base solution during the preparation process, and preparations of nanoparticles and nanofluids are completed simultaneously (Hiroshi et al., 1978). In the two-step method, nanoparticles are directly added into the base solution, and then ultrasonic dispersion is used to interrupt hard agglomeration of nanoparticles. A stable nanofluid is obtained by adding the dispersant and adjusting the pH value. Compared with the two-step method, the one-step method prepares nanofluids with uniform dispersion performance and long-term stability. However, the one-step method is not suitable for large-scale production due to the complicated preparation process and expensive processing equipment.
In the past decades, nanofluids are mainly prepared by the two-step method as shown in Figure 1.
The morphology of various nanoparticles and nanoparticle suspensions is often characterized using scanning electron microscopy (SEM) and transmission electron microscopy (TEM). A set of special coils is used to scan samples in a raster pattern and collect scattered electrons. Variations of particle structure and shape are analyzed using SEM, and the fine structure inside the objects is observed using TEM. SEM images in Figure 2 show distributions and shapes of nanoparticles Al2O3 (Zheng et al., 2020b), SiC (Zheng et al., 2020b), CuO (Zheng et al., 2020b), and carbon nanotubes (CNTs) (Wang et al., 2021a). The nanoparticles have spherical or elliptical shapes. It is observed that these particles exist in the form of aggregates. The uniform suspensions ZnO (Zheng et al., 2020a) and Fe3O4 (Wang et al., 2019) were observed by TEM images. Physical appearance, size, and shape of various nanoparticles in suspensions are characterized.

FIGURE 2. SEM images of nanoparticles (A) Al2O3 (Zheng et al., 2020b), (B) SiC (Zheng et al., 2020b), (C) CuO (Zheng et al., 2020b), and (D) CNTs (Wang et al., 2021a) and TEM images of (E) ZnO (Zheng et al., 2020a) and (F) Fe3O4 (Wang et al., 2019).
Nanoparticles in fluids have complex stress conditions and high surface activity, and they are prone to self-polymerization in base fluids. When the size of aggregation reaches a certain level, sedimentation of nanoparticles occurs, which results in an uneven distribution of nanoparticles. The nanofluid shows strong instability in a macroscopic view, which affects flow characteristics and heat transfer performance of the nanofluid. The polymerized nanoparticles are precipitated from the base fluid after resting for a long time. Suspension stability of nanofluids is solved by using dispersion technologies, such as using an appropriate electrolyte as the dispersant, addition of surfactant, and ultrasonic vibration during dispersion. In a sedimentation technique, stability of colloidal suspension is evaluated by taking sedimentation photos of suspension in a tube with a camera. The settlement process has strong visibility, but ultrasonic oscillation destroys interaction between nanoparticles. Addition of dispersant provides a strong repulsive force between nanoparticles, weakening agglomeration and sedimentation of particle swarms (Wang et al., 2020).
The aggregation behavior of nanoparticles has been widely concerned. Sun et al. clarified the unique aggregation mechanism of nanoparticles with smaller particle size, which provided reference for predicting the migration of nanoparticles (Sun et al., 2021). Particle migration can lead to non-uniformity in the concentration distribution in flowing nanofluids. According to the existing thermophysical properties of nanofluids, a theoretical model for predicting the agglomeration and migration of nanoparticles in pipelines has been established. The effects of Brownian motion, shear rate, and viscosity gradient on particle diffusion should be considered (Ding and Wen, 2005; Bahiraei, 2015). In the study by Ding and Wen (2005), the agglomeration of nanoparticles mainly occurred in the center of the pipeline, and the pressure drop had a minor effect on the improvement of thermal conductivity of nanofluids.
Ultrasonic oscillation due to ultrasonic cavitation is an effective method to reduce agglomeration of nanoparticles. The mechanism reveals that ultrasonic cavitation causes micro flow in the nanofluid, which decomposes the agglomerated nanoclusters into scattered nanoparticles, so that the stability of the nanofluid is improved. The interaction between nanoparticles is destroyed by local high temperature, high pressure, or strong shock wave generated by cavitation (Wang et al., 2019; Zheng et al., 2020a; Zheng et al., 2020b; Chen et al., 2020; Wang et al., 2020; Wang et al., 2021a; Zheng et al., 2021). However, ultrasonic oscillation time has important effect on the stability of nanofluids. It is concluded that a long ultrasonic oscillation time does not mean good stability of nanofluids (Zheng et al., 2020b). The optimal ultrasonic oscillation time results in the highest thermal conductivity. Ultrasonic treatment has a direct impact on the stability of nanofluids, but the effect of surfactants cannot be ignored.
Surfactants are classified into anionic surface dispersants, cationic surface dispersants, non-ionic surface dispersants, and polymeric surface dispersants. Dispersant adsorbs more liquid molecules on the particle surface. By increasing attraction between solid and liquid, agglomeration is avoided. Many surfactants have been commonly used in nanofluid research, such as sodium hexametaphosphate (SHMP) (Zheng et al., 2020a), cetyltrimethylammonium bromide (CTMAB) (Zheng et al., 2020a), trisodium citrate dehydrate (TSC) (Wang et al., 2019), and sodium dodecyl sulfate (SDS) (Wang et al., 2021a). Wang et al. (2021a) found that surfactants Acacia senegal (GA), trisodium citrate dehydrate (TSC), and sodium laurylsulfonate (SLS) had different effects on delaying sedimentation of nanoparticles. Figure 3A shows the prepared Fe3O4–CNT–water nanofluids after standing for 5 min and 2 weeks. Zheng et al. (2020a) studied effects of dispersant and ultrasonic vibration on distributions of six nanoparticles as shown in Figure 3B. SHMP and CTMAB were added, and the mixed fluid was ultrasonically vibrated. After 10 days, the nanoparticles obtained good dispersibility and low agglomeration.

FIGURE 3. Samples of various nanofluids. (A) Fe3O4–CNT–water nanofluid 5 h after preparation (left) and Fe3O4–CNT–water nanofluid after 2 weeks (right) (Wang et al., 2021a). (B) Water-based nanofluids with nanoparticles Al2O3, CuO, Fe3O4, ZnO, SiC, and SiO2 [29].
The stability of nanofluids also depends on their size-dependent characteristics and dispersion conditions. van der Waals gravitational force and electric double-layer repulsion are related to particle size. A large particle size results in large attractive potential energy between particles, which causes agglomeration easily. If no sedimentation appears during a certain time, it is considered that the nanofluids achieve stabilities of dynamics and aggregation. The stability of nanofluids is analyzed and characterized using TEM, SEM, zeta potential testing, and static sedimentation. As a standard test, a zeta potential analyzer is used to evaluate dispersion stability of particles in water. The absolute value of the zeta potential is positively related to the stability of the dispersion system (Chakraborty and Panigrahi, 2020). For a stable nanofluid, nanoparticles in liquid contain numerous positive and negative charges. Their repulsion leads to a high zeta potential. Generally, the zeta potential of a particle surface in a stable dispersion system is above 30 mV, which is used to judge the stability of nanofluids. Figure 4 shows zeta potential distributions of 1.2 wt% Fe3O4–water (Wang et al., 2021a), 1.32 wt% Fe3O4–CNT–water (Wang et al., 2021a), 1.0 wt% Al2O3–water (Zheng et al., 2020b), and 1.0 wt% CuO–water (Zheng et al., 2020b). The results show that the prepared nanofluids have good dispersion stability.
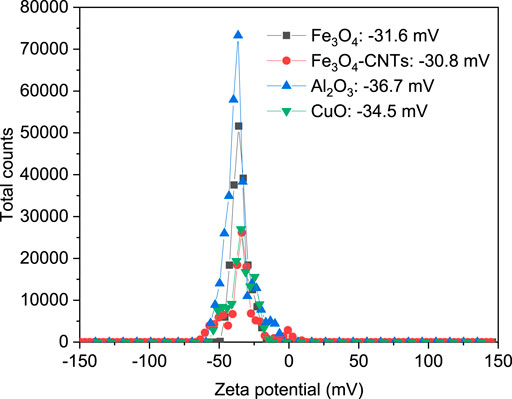
FIGURE 4. Zeta potential distributions of 1.2 wt% Fe3O4 (Wang et al., 2021a), 1.32 wt% Fe3O4–CNT (Wang et al., 2021a), 1.0 wt% Al2O3 (Zheng et al., 2020b), and 1.0 wt% CuO (Zheng et al., 2020b) water-based nanofluids.
The base fluid influences the stability of nanofluids as well. The repulsive force between nanoparticles mainly depends on the dielectric of base fluid when the particle concentration and particle size remain unchanged. Generally, the repulsive force between particles is positively correlated with the dielectric constant of the base fluid. The purpose of slowing down the sedimentation of nanoparticles and improving the stability of nanofluids is achieved by increasing the dielectric constant of the base fluid (Chakraborty and Panigrahi, 2020). The most common base fluids are water, ethylene glycol, and oil.
Dispersion of nanoparticles in a base fluid directly affects thermophysical properties of nanofluids, including thermal conductivity, viscosity, density, and specific heat. The thermophysical properties of various nanofluids are briefly discussed in this section.
Improvement of thermal conductivity of nanofluids has great influence in enhancing their convective heat transfer characteristics. Thermal conductivities of nanofluids are affected by many factors such as nanoparticle materials (Zheng et al., 2020a; Zheng et al., 2020b; Wang et al., 2021a), base fluid materials (Zheng et al., 2020b), nanoparticle shapes, nanoparticle sizes (Wang et al., 2021a), nanoparticle concentrations (Zheng et al., 2020a), and temperature conditions (Zheng et al., 2021). The thermal boundary layer is destroyed due to irregular movement of nanoparticles, enhancing the heat transfer between water and nanofluids (Zheng et al., 2020a; Wang et al., 2021b). For example, addition of copper nanoparticles into ethylene glycol–water (EGW) intensifies Brownian motion of the nanoparticles. The thermophysical properties of fluids were improved due to intensified movement of nanomaterials in the fluid (Chen et al., 2020). The intensified Brownian motion also caused the reduction of nanoparticle size and in turn improved the thermal conductivities of the nanofluids. (Mahbubul et al., 2013). By changing the shape of nanoparticles, the heat conduction area is increased, and accordingly, the thermal conductivity of nanoparticles is improved. Zheng et al. (2020b) studied effects of nanoparticle materials, base fluid materials, and nanoparticle concentration on convective heat transfer. They found that Fe3O4–water and CuO–water nanofluids showed the best and the worst thermal performance, respectively, among four nanofluids with nanoparticles Al2O3, SiC, CuO, and Fe3O4. This was because the supply of nanoparticles improved the thermal conductivity of the base fluid. Thermal conductivities of nanofluids increased with the increment of nanoparticle concentration. Thermal conductivity had a minor increase with the increase of nanoparticle concentration ratio. If the concentration ratio is large enough, particle agglomeration will occur. It is very important to find the best concentration ratio as shown in the studies by Zheng et al. (2020a) and Zheng et al. (2021) The surfactant is one of the factors affecting the thermal conductivity of nanofluids (Zheng et al., 2020a; Wang et al., 2021a). Under the action of nanoparticles and surfactants, the thermal conductivity of the fluid was somewhat improved in the study by Wang et al. (2021a). In the study by Wang et al. (2021a), the surfactant SDS improved the thermal conductivity of CNT–water nanofluid, while the thermal conductivity of Fe3O4–CNT–water nanofluid was improved by adding the surfactant SLS.
Viscosity of nanofluids increased with the increase of nanoparticles as shown in studies by Zheng et al. (2020a), Zheng et al. (2020b), and Zheng et al. (2021). This was due to increases in friction resistances between nanoparticles and adjacent layers of the base fluid, as well as the formation of intermolecular layers between the nanoparticles themselves. Temperature is also an important factor affecting the viscosity of nanofluids as shown by Ahmadi Nadooshan et al. (2018) and Zheng et al. (2021). Flow characteristics of the fluid change with temperature, and viscosity decreases with the increase of temperature (Ahmadi Nadooshan et al., 2018). High temperature of fluids causes the molecules to move at a faster rate. The increase in molecular motion decreases the fluid viscosity. Under high Reynolds number, the average Nusselt number was more sensitive to viscosity than to heat conduction (Abu-Nada et al., 2010). Other than temperature, viscosities of nanofluids are mainly affected by volume fraction, size, surface property of nanoparticles, ionic strength of the base fluid, and pH value. The viscosities of nanofluids increase with the increase in the amount of surfactants (Wang et al., 2019; Wang et al., 2021a).
The density of nanofluids also shows direct effects on the Nusselt number and Reynolds number, pressure loss, and friction coefficients. Generally, when nanoparticles are added to the base fluid, the specific heat of the nanofluids decreases and density increases. Table 1 summarizes the thermophysical properties of several nanoparticles.
In the previous studies, many methods have been used to analyze thermal conductivities of nanofluids. Numerous studies have emphasized that thermal conductivity increases with a growth of concentration ratio of nanoparticles. Maxwell (2011) investigated transmission characteristics of a heterogeneous system. He put forward a pioneering thermal conductivity model for non-contact spherical particle suspension, which was applied to analyze the thermal conductivity of the mixture of solid nanoparticles and base fluid. Many researchers developed novel models based on Maxwell’s model. For example, the Bruggeman equation was derived from the Maxwell model by differential re-integration, which was used to analyze interaction between random fillers (Bruggeman, 1935). The Hamilton–Crosser model studied effects of particle shapes, compositions, and pure component conductivities on thermal conductivities of a heterogeneous two-component mixture composed of a continuous phase and a discontinuous phase (Hamilton and Crosser, 1962). This model modified the Maxwell equation by adding a shape factor, and the empirical shape factor n depended on the thermal conductivity and shape of particles. Because abnormal enhancements of thermal conductivity in nanoparticle liquid suspension are inconsistent, many studies have shifted to efforts in theoretical research. Yu and Choi (2003) extended the Hamilton–Crosser model of non-spherical particle suspension using a generalized empirical shape factor to correctly predict thermal conductivities of nanotubes in petroleum nanofluids. Kumar et al. (2004) indicated that thermal conductivities of nanofluids increased linearly with temperature at low concentration. It depended on the intensity of the Brownian motion of the particles. They also found that an increase in the size of nanoparticles reduced thermal conductivities of nanofluids, which was determined by a large specific surface area of nanoparticles. Timofeeva et al. (2008) put forward an operative medium theory to calculate the thermal conductivity of TiO2 nanofluids. Moghaddam et al. (2021) presented a model of thermal conductivity based on regression analysis of data. Table 2 shows present calculation models of thermal conductivity.
Various models have been introduced to calculate the viscosity of nanofluids. Table 3 summarizes the classical formulas for viscosity calculation. Einstein (1906) put forward a viscosity model of liquid–solid two-phase mixture media at concentrations below 0.02 vol%. Based on the Einstein viscosity model (Einstein, 1906), Brinkman (1952) proposed a viscosity formula with a wider application range and volume concentration up to 0.04 vol%. With the further studies on nanofluids, researchers had gradually realized important influence of the Brownian motion of nanoparticles on the suspension stability of nanofluids. Considering influence of the Brownian motion of nanoparticles, many researchers modified Einstein’s model (Einstein, 1906). Batchelor (1977) analyzed the influence of the Brownian motion of particles on the stress of nearly isotropic suspension of rigid and spherical particles and proposed a high-order Einstein viscometer formula. Wang et al. (1999) realized that the Brownian motion of nanoparticles had important influence on suspension stability and rheological characteristics of a two-phase mixture system of nanofluids, and they proposed a new formula for calculating the viscosity of nanofluids. The above studies show that the factors affecting the viscosity of nanofluids are very complex. The existing viscosity models consider the volume fraction of nanoparticles, without considering effects of nanoparticles’ size (Moghaddam et al., 2021), temperature (Renner et al., 2000; Moghaddam et al., 2021), shear rate (Phuoc and Massoudi, 2009), and magnetic field (Syam Sundar et al., 2013). Moghaddam et al. (2021) considered comprehensive influence of volume fraction, particle size, and temperature of nanoparticles. They expanded the correlation based on linear regression. It is found that no comprehensive review considering various factors in theoretical models of the nanofluid viscosity exists. Nevertheless, it is an important problem to consider in future research on nanofluid viscosity.
According to the existing thermal conductivity and viscosity models, it is obvious no existing theoretical analysis of thermophysical models can accurately predict the results under certain conditions. Numerical simulation results are limited and have weak relevance for a certain nanofluid in an experiment. Theoretical thermophysical property models need to quantify the influencing factors more accurately, so that the prediction range becomes smaller and more accurate, and thus, a general thermophysical property model of nanofluids can be obtained.
The concentration of nanoparticles and the Rayleigh number (Ra) are the common factors affecting heat transfer of nanofluids in cavities. The structures of the cavity and the variations of heat sources also play a significant role. A few research works on nanofluids in electric heaters as a special cavity have been presented.
Figure 5 illustrates the variation of the average Nusselt number (Num) of various nanofluids in a square cavity with the Reynolds number. The average Nusselt number is determined by the integral of the local Nusselt number on the heat source. The average Nusselt numbers of CuO (Aminossadati and Ghasemi, 2011), TiO2 (Aminossadati and Ghasemi, 2009), Ag (Aminossadati and Ghasemi, 2009), Al2O3 (Sert and Ti̇muralp, 2015), and Cu (Sert and Ti̇muralp, 2015) nanofluids increase slowly with the increasing Rayleigh number for Rayleigh numbers in the range of 1,000 to 10,000. The heat transfer mechanism of nanofluids is mainly heat conduction at low Rayleigh number. The flow boundary layer and thermal boundary layer do not change with a modest increase of Rayleigh number. The heat transfer on the heat source surface does not change obviously. The average Nusselt numbers also have a minor variation. When the Rayleigh number is in the range of 10,000 to 1,000,000, the average Nusselt numbers of those nanofluids increase rapidly. Due to the high Rayleigh number, the buoyancy force is the main factor to enhance the flow intensity. The heat transfer in a square cavity is affected by convection. With the increase of Rayleigh number, the thermal boundary layer on the heat source surface becomes thinner. The heat transfer intensity in the cavity is enhanced accordingly in this case. When the results in the cavity are used to enhance heat transfer of nanofluids in actual applications, it is recommended to increase the Rayleigh number of nanofluids in the cavity. This strengthens the influence of buoyancy and causes an increase in the intensity of the flow. According to Figure 5, the convective heat transfer is dominant when the Rayleigh number is in the range of 10,000 to 1,000,000.
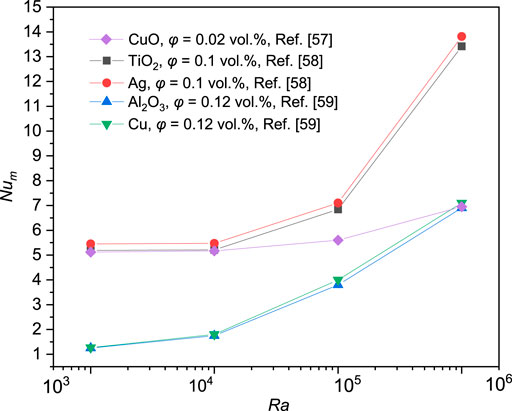
FIGURE 5. Variations of average Nusselt numbers of water-based nanofluids with various Rayleigh numbers in a square cavity.
Table 4 shows the information of water-based nanofluids inside cavities with arrangements of the heating sources. The location of the heat source changes the flow field and temperature field in a square cavity. To enhance the heat transfer, it is recommended to disturb the nanofluid flow in the square cavity. When multiple cold and hot sources exist in the square cavity, the alternating arrangement of the hot and cold sources is a good choice. When alternating cold and hot sources were arranged, the average Nusselt number of 4 vol% CuO nanofluid was 19.3% higher than that of non-alternating arrangement of cold and hot sources (Aminossadati and Ghasemi, 2011). Streamlines and isotherms of nanofluids for alternating heat sources show better heat transfer. The alternating cold and hot sources form smaller flow vortices in the square cavity, which strengthens the flow intensity of the nanofluid.
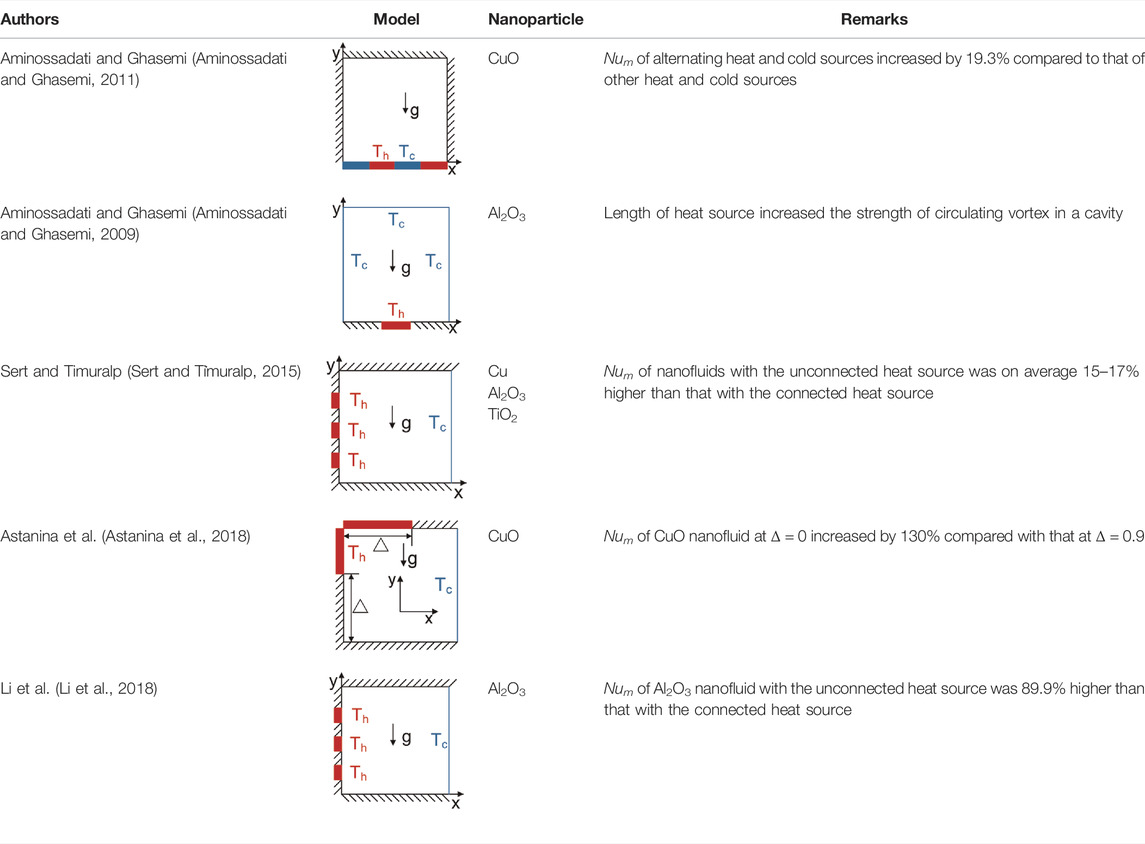
TABLE 4. Information of water-based nanofluids inside enclosures with arrangements of heating walls.
When choosing the arrangement of heat sources, the range of fluid flows in the square cavity should be expanded to avoid the occurrence of flow dead zone as much as possible. The length of the heat source is an influencing factor. Aminossadati and Ghasemi (2009) found that the effect of using a long heat source to increase the flow range in the cavity was better than that of a short heat source. This was because the size of the circulating eddy current in the cavity increases with the extension of the heat source. The extended heat source increases the heat yield and enhances the buoyancy. However, the increase in heat yield is not conducive to heat transfer. To obtain the best results, it is necessary to find a balance between flow intensity and heat flux with an increase of the length of the heat source.
Although the heat transfer rate is faster when the hot source is in contact with the cold source (Aminossadati and Ghasemi, 2011), the relative arrangement of the hot source and the cold source in the square cavity forms a larger vortex and aggravates the flow. Astanina et al. (2018) found that the average Nusselt number of the relative arrangement of hot and cold sources was 1.3 times higher than that of the vertical arrangement of hot and cold sources. It is inferred that the effect is optimal when the hot source and the cold source are arranged relatively close to each other. This is a traditional hot source arrangement (Lai and Yang, 2011). While Aminossadati and Ghasemi (2009) moved the hot source from near the cold source to the middle, a larger vortex existed in the square cavity. This increased convective heat transfer of the nanofluid. But heat conduction of nanofluid between the hot source and the cold source of the square cavity was reduced, so that the overall heat transfer efficiency of nanofluid became low. Therefore, the influence of heat transfer state of nanofluid in a square cavity should be considered when a hot source is arranged.
Finally, to intensify flow turbulence, especially near the hot source, using an unconnected hot source instead of a connected hot source is a significant method when the length of the hot source is fixed. Sert and Ti̇muralp (2015) concluded that the heat transfer performance of Cu, Al2O3, and TiO2 nanofluids with the unconnected hot source was improved by an average of 15 and 17% compared with that with the connected hot source. Li et al. (2018) also found that the heat transfer performance of 1 vol% Al2O3–water nanofluids was improved by 89.9% when the hot source was replaced by unconnected sources. The thermal boundary layer and the flow boundary layer near the hot source are destroyed more seriously when the hot source is changed from connected to unconnected. The flow and heat transfer are strengthened. Therefore, it is necessary to consider changing the connected hot source into an unconnected hot source to enhance the heat transfer.
Heat transfer of nanofluids in a closed cavity is affected by the structure of cavities, such as a traditional square cavity (Lai and Yang, 2011), T-shaped cavity (Esfe et al., 2017), Γ-shaped cavity (Mohebbi et al., 2019), C-shaped cavity (Izadi et al., 2018; Abedini et al., 2019), and H-shaped cavity (Keramat et al., 2020; Rahimi et al., 2018; A. S. Raizah and M. Aly, 2021). Table 5 shows some information about water-based nanofluids inside non-conventional cavities. The aspect ratio (AR = L/H) of these cavities affects the heat transfer performance of nanofluids. When the Rayleigh number in a T-shaped cavity was between 1,000 and 10,000 for multi-walled carbon nanotube (MWCNT)–water nanofluids, the average Nusselt number of the heat source decreased with an increase of aspect ratio (Esfe et al., 2017). In this case, heat transfer performance was mainly determined by thermal conductivity. It is concluded that, with an increase of aspect ratio, the distance between hot and cold walls increases and heat transfer efficiency decreases. Mohebbi et al. (2019) found that heat transfer characteristics of Al2O3–water nanofluid in a Γ-shaped cavity with an aspect ratio of 0.2 (smaller cavity) were better than those with aspect ratios of 0.4 and 0.6. Izadi et al. (2018) have drawn the same conclusion for the C-shaped cavity as shown by Mohebbi et al. (2019). For a small cavity, the distance between the hot source and the cold source decreases. In this case, heat conduction of the fluid is dominant, and streamlines and temperature gradients of the fluid are closer to those of the hot source and cold source (Esfe et al., 2017; Izadi et al., 2018; Mohebbi et al., 2019; Keramat et al., 2020). The fluid has difficulty to flow in a small cavity, and convective heat transfer is weak in the cavity. A large cavity leads to a large distance between the hot source and the cold source, which weakens nanofluid heat conduction. The convective heat transfer of the nanofluid is dominant at a large space. When the Rayleigh number is between 105 and 106, the average Nusselt number increases with an increase in aspect ratio. The main heat transfer was convection. The increase in aspect ratio resulted in a large flow space, which improved heat transfer efficiency (Esfe et al., 2017). The heat transfer enhancement effect due to the aspect ratio on natural convective heat transfer of nanofluids in a cavity is mainly affected by the heat transfer state (heat conduction and convection). To achieve the optimal heat transfer performance, it is necessary to choose an appropriate aspect ratio by analyzing the flow regime and heat transfer of nanofluids.
Heat transfer of nanofluids is also affected by structures within the cavities. Keramat et al. (2020) installed baffles on top and bottom ribs in H-shaped cavities. With the installation of the baffles at the bottom, the average Nusselt number on the bottom wall increased by 3%, whereas the average Nusselt number of the bottom wall was reduced by 2% for the baffle at the top. Armaghani et al. (2018) found that the average Nusselt number on a hot source was 25% higher than that without baffle, when the length of the cold source baffle was 60% length of a T-shaped cavity. The baffle also enhanced heat transfer of Fe3O4 nanofluid in a C-cavity (Abedini et al., 2019). The baffle of the cold source narrows the distance between the cold and hot sources, enhancing heat transfer characteristics of nanofluids in the cavity (Armaghani et al., 2018; Abedini et al., 2019). However, a flow vortex in the fluid occurs in a limited space due to the presence of baffles, and a small vortex showed a negative effect on heat convection. When the baffle is adiabatic, convective heat transfer of nanofluids in cavities is significantly weakened (Armaghani et al., 2018; Abedini et al., 2019). Therefore, it is necessary to in detail discuss about effects of adiabatic baffles on heat transfer enhancement of nanofluids in the cavity.
Figure 6 shows increases in the average Nusselt number (ηNum) on a hot source under the optimal and the worst aspect ratios in various cavities. The Rayleigh number of all nanofluids in cavities is 1,000,000 with a volume concentration of 1%. In the study by Abbood et al. (2018), when the surface radius (ξ) changes from 1/8 height of the cavity (1/8H) to 3/8 height of the cavity (3/8H), the average Nusselt number of TiO2 and Cu nanofluids increases by 144.4 and 147.5%, respectively. Thermal conductivities of TiO2 and Cu nanoparticles are 8.6 W/m K and 400 W/m K (Abbood et al., 2018), convective heat transfer of nanofluids in the cavity is the main factor affecting heat transfer, and the type of nanofluid (TiO2 and Cu) has a minor effect on heat transfer enhancement. When the aspect ratio increases from 0.2 to 0.8 in a T-shaped cavity, the increment of the average Nusselt number of MWCNT nanofluids is 9.2% (Esfe et al., 2017). The change of aspect ratio has no significant effect on heat transfer of MWCNT nanofluids because the heat transfer in the cavity is dominated by heat conduction. Effects of aspect ratios of cavities on heat transfer of Al2O3 nanofluids are studied by Mohebbi et al. (2019) and Keramat et al. (2020). It is interesting to note that the increase of the average Nusselt number is not sensitive to changes of aspect ratio in an H-shaped cavity (an increase of 26.2%) compared to that in the Γ-shaped cavity (an increase of 114.4%).
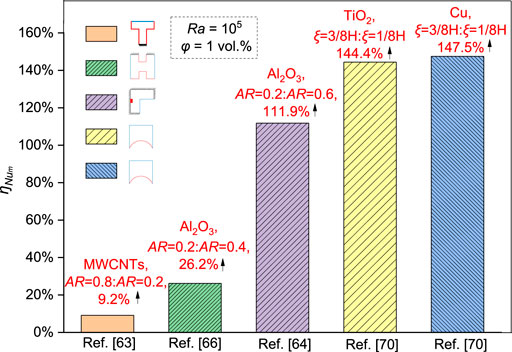
FIGURE 6. Increments of average Nusselt numbers of nanofluids in various cavities with the optimal and the worst aspect ratios.
There are very few experimental studies on the natural convection of nanofluids in electric heaters by previous researchers. Table 6 shows the experimental studies of nanofluids with different base fluids in electric heaters. The electric heater used by Chen et al. (2020) consists of two horizontal tubes (the diameter of 30 mm and the length of 660 mm) and vertical finned tubes (the diameter of 20 mm and the length of 450 mm). Nanofluids account for 85% of the volume of the electric heater because nanofluids expand due to heating (Chen et al., 2020). The fluid in the electric heater performs natural convection better due to the existence of the bottom heating rod. To obtain accurate experimental results, the electric heater is located in an insulated square cavity, and the heat loss at the outlet of the electric heater is generated from the bottom of the square cavity. The arrangement of thermocouples for measuring the temperature on the electric heater (red dot) is shown in Table 6. The maximum temperature of the heating fluid is generally below 100°C (Chen et al., 2020; Wang et al., 2020; Sahin and Namli, 2021).
The base fluid of nanofluid applied in the electric heater is also different. Wang et al. (2020) applied the commonly used deionized water as the base fluid, while Chen et al. (2020) chose the base fluid as a mixture of ethylene glycol and deionized water with a mass ratio of 4:6. Sahin and Namli (2021) used heat transfer oil. The thermal conductivities of deionized water, ethylene glycol, and heat transfer oil are 0.6 W/m·K (Azizian et al., 2014), 0.224 W/m·K (Chen et al., 2020), and 0.128 W/m·K (Sahin and Namli, 2021), respectively. It is obvious that the thermal conductivity of deionized water is significantly higher than that of ethylene glycol and heat transfer oil. As discussed previously, the thermophysical property of a nanofluid is determined by base fluids and nanoparticles. Therefore, it is recommended to use deionized water as a base fluid in electric heaters in normal circumstances. However, in a low-temperature environment (when the temperature is less than 0°C), the deionized water is not suitable to be used as a base fluid. The mixed base solution of ethylene glycol and deionized water is a good choice because it is still liquid when the temperature is below 0°C. The mixed liquid in this case has a better operating performance at low temperature (Chen et al., 2020). This mixed liquid makes the electric heater to have certain anti-freezing characteristics, which is helpful for applications of electric heaters in cold regions.
Al2O3 (Chen et al., 2020; Wang et al., 2020) nanoparticles are dispersed into different base fluids to form nanofluids. This is because Al2O3 nanoparticles have good thermophysical properties and low cost. The thermal conductivity of Al2O3 nanoparticles with an average particle size of 30 nm is 28.3 times higher than that of ionic water because Al2O3 nanoparticles have a thermal conductivity of 35 W/m·K and the deionized water has a thermal conductivity of 0.6 W/m·K (Wang et al., 2020). Wang et al. (2020) found that, among Al2O3–water nanofluids with five concentrations (0.1 wt%, 0.5 wt%, 1.0 wt%, 1.5 wt%, and 2.0 wt%), 1.0% Al2O3–water nanofluids had an optimal heat transfer effect. Filled in the electric heater, the equilibrium temperature of 1.0% Al2O3–water nanofluid is 10.3% higher than that of the base fluid. This illustrates that those thermal conductivities and viscosities of nanofluids increase with an increase in the mass fraction of nanofluids. The reason is that a balance was observed between thermal conductivity and viscosity at high concentration. An increase in thermal conductivity is beneficial to heat transfer enhancement of nanofluids. However, the increase in viscosity aggravates the agglomeration of nanoparticles and deteriorates the heat transfer. Therefore, an optimal concentration is needed to consider a balance between thermal conductivity and viscosity. The optimal concentration of nanofluids in the electric heater should be selected considering the balance between cost and the heat transfer performance.
The nanoparticle material is an important factor for heat transfer performance. Based on findings from Chen et al. (2020), under the same heating conditions, the equilibrium temperature values of Cu–EGW, Fe3O4–EGW, and Al2O3–EGW were higher than that of the base fluid. The equilibrium temperature of Cu–EGW nanofluid was the highest, and the heating time to the equilibrium temperature was the shortest. Cu–EGW nanofluid showed higher heat transfer performance than Fe3O4–EGW and Al2O3–EGW nanofluids. This is caused by the increase of thermal conductivity of nanofluid due to the addition of nanoparticles. It is concluded that the heating time and heat transfer performance of nanofluids have more advantages than those of the base fluid. Sahin and Namli (2021) considered that the thermal characteristic of Al2O3–oil nanofluids was better than that of TiO2–oil nanofluids. The interaction of particle size and thermal conductivity of nanoparticles plays a major part in the heat transfer performance of nanofluids. The optimal properties of nanoparticles would be small sizes and high thermal conductivity. The thermal conductivity of Al2O3 (40 W/m·K (Sahin and Namli, 2021)) is higher than that of TiO2 (11.7 W/m·K (Sahin and Namli, 2021)), and the particle size of Al2O3 (20–30 nm) is smaller than that of TiO2 (30–40 nm) (Sahin and Namli, 2021). However, the thermal conductivity of Cu nanoparticles is much higher than that of Fe3O4, Al2O3, and TiO2 (Chen et al., 2020; Sahin and Namli, 2021). In this case, because there is almost no difference of nanoparticle size, the effect of particle diameter on heat transfer is not significant. Therefore, Cu of the four selected nanomaterials is recommended for electric heaters.
This part briefly introduces forced convective heat transfer of nanofluids in various heat transfer equipment. Nanofluids improve heat transfer characteristics in ribbed tubes, double-tube heat exchangers, and plate heat exchangers. Figure 7 shows experimental systems of nanofluids in a straight tube (Li et al., 2021), a double-tube heat exchanger (Zheng et al., 2020a), and a plate heat exchanger (Zheng et al., 2020b; Zheng et al., 2021). These experimental devices mainly consist of two parts: fluid circulation system and test section. A straight tube system includes a nanofluid circulation and a straight tube (test section). For a two-circulation system, the cold fluid side and hot fluid side are typically composed of power plants (pump), flow-measuring device (flowmeter), valve, thermostat water bath, test section, and storage tank. In double-tube heat exchangers (Zheng et al., 2020a) and plate heat exchangers (Zheng et al., 2020b; Zheng et al., 2021), the nanofluid and water are used for a cold fluid and hot fluid, respectively. The stability of nanofluids decreases with an increase in nanofluid temperature, leading to agglomeration deposition of nanoparticles in the test section and reduction of thermal efficiency. Nanofluids are widely used to cool straight tubes which are heated by thermostatic heat flow. Li et al. (2021) used a direct current power supply of 0–150 W to provide a required heat flux.
Temperature values for the hot fluid and cold fluid in the test section are kept constant in experiments. The flow rate is determined by adjusting control valves. The pressure drop of nanofluids is obtained by connecting the pressure gauge at the inlet and outlet of the test section. Thermocouples are used to measure the temperature of the fluid. The measured data are input into a computer through a data acquisition device.
Thermal efficiency in ribbed tubes is enhanced by adding nanoparticles (metals and metal oxides). Metal oxides (such as Al2O3 (Mohebbi et al., 2015; Habibi and Salimpour, 2019; Salman, 2019; Kaood and Hassan, 2020), CuO (Salman, 2019; Wang et al., 2021b), and ZnO (Salman, 2019)) have low cost and good stability. On the contrary, coarsened surfaces are obtained by changing geometry structures with ribs, grooves, lines, or spiral bellows. The ribbed tube structures have been commonly used, such as rectangular ribs (Mohebbi et al., 2015; Salman, 2019; Kaood and Hassan, 2020), triangular ribs (Salman, 2019; Kaood and Hassan, 2020), semicircular ribs (Mohebbi et al., 2015), and trapezoidal ribs (Mohebbi et al., 2015; Salman, 2019; Kaood and Hassan, 2020). Compared with only using nanofluids or ribs, nanofluids in different ribbed tubes further improve the heat transfer performance.
Table 7 shows information of nanofluids in some tubes with various ribbed structures. Some scholars have explored heat transfer characteristics of nanofluids in ribbed tubes after adding nanoparticles. It was found that the heat transfer performance of prepared nanofluids by adding nanoparticles was better than that of the base fluid (Mohebbi et al., 2015; Habibi and Salimpour, 2019; Salman, 2019; Kaood and Hassan, 2020; Wang et al., 2021b). Compared with those in smooth tubes, convective heat transfer coefficients of Al2O3–water nanofluids in trapezoidal ribbed tubes, semicircular ribbed tubes, rectangular ribbed tubes, and sinusoidal tubes increased by 66% (Mohebbi et al., 2015), 65% (Mohebbi et al., 2015), 58% (Mohebbi et al., 2015), and 42.1% (Habibi and Salimpour, 2019). Compared with those in the rectangular ribbed structure, the streamlines and isotherms of Al2O3–water nanofluids are denser in the ribbed structures of trapezoidal and semicircular ribbed tubes (Mohebbi et al., 2015). This is because various ribbed tube structures have different curvature parameters and disturbances of nanofluids in the boundary layer are significantly different. Al2O3–water nanofluids in trapezoidal ribbed tubes show a significant heat transfer enhancement. Due to increases in heat transfer area, more mixing surfaces and sweeping surfaces are observed in trapezoidal ribbed tubes compared to those in other ribbed tubes. Researchers also studied effects of different nanoparticles on heat transfer enhancement in the same tube structure. Based on a comparison of nanoparticles Al2O3, CuO, SiO2, and ZnO, SiO2 nanoparticles showed the highest Nusselt numbers (Salman, 2019). Compared with other fluids, the SiO2 nanofluid has the minimum density and the maximum average flow velocity, which plays an important role in forced convection heat transfer (Salman, 2019). Triangular ribs have a higher surface friction coefficient and significantly enhanced heat transfer, compared to trapezoidal ribs and rectangular ribs. The main reason is that the increased concentration of the phase with higher thermal conductivity results in an increase in the thermal conductivity of the fluid. From the above, it is recommended to obtain a good heat transfer enhancement by using 4% Al2O3–water nanofluid in a triangular tube.
This part mainly introduces heat transfer characteristics of nanofluids in double-tube heat exchangers as shown in Table 8. The inlet temperature (Tin) of nanofluids shows an important effect on heat transfer characteristics. Zheng et al. (2020c) observed that 0.25 vol% and 0.5 vol% Al2O3–water nanofluids at an inlet temperature of 40°C had 8.27 and 4.84% higher Nusselt numbers than those at an inlet temperature of 50°C. The Nusselt numbers for 0.15 vol% Al2O3–water nanofluids at 65 and 55°C were 17.7 and 10.2% higher than that at 45°C. For 0.05% Al2O3–water nanofluids, the increases in the Nusselt numbers were 18.2 and 13.6% (Raei et al., 2017). The effects of inlet temperature on the thermal conductivity and viscosity of Al2O3–water nanofluids were like that of mass fraction. The increase in the viscosity of Al2O3–water nanofluid had a higher adverse effect on heat transfer than the increase of thermal conductivity in the study by Zheng et al. (2020c). The increase in the viscosity of Al2O3–water nanofluid had a lower adverse effect on heat transfer than the increase of thermal conductivity in the study by Raei et al. (2017). In addition, the particle sizes of Al2O3 nanoparticles used by Zheng et al. (2020c) and Raei et al. (2017) are 50 and 20 nm. The nanoparticles of small size are more easily affected by temperature than the nanoparticles of large size, and the Brownian motion of nanoparticles of small size is more intense with the increase of temperature. Al2O3+TiO2–water nanofluid is made with Al2O3 nanofluid by adding TiO2 nanoparticles at a mass ratio of 1:1 (Singh and Sarkar, 2021). When the inlet temperature was 50°C, the Nusselt number of Al2O3+TiO2–water nanofluid was 38.5% higher than that at 70°C (Singh and Sarkar, 2021). Singh and Sarkar (2021) explained that this phenomenon was caused by the alteration of nanofluid density, viscosity, and thermal diffusivity with temperature. When studying individual TiO2 nanofluids, it was also found that when the inlet temperature was 15, 20, and 25°C, the heat transfer coefficient of 0.2% TiO2–water nanofluid was the highest at 15°C (Duangthongsuk and Wongwises, 2009). The heat transfer coefficient of TiO2 nanofluids at low temperature was higher than that at high temperature (Duangthongsuk and Wongwises, 2009). The Nusselt number of CNT nanofluids at the inlet temperature of 70°C was higher than that at 50°C (Sarafraz et al., 2016). This is because with the increase of temperature, thermal properties of CNT nanofluids are slightly improved, and the Brownian motion and thermal diffusion ability of nanofluids are enhanced (Sarafraz et al., 2016). When the inlet temperature was 60°C, 0.3 wt% MgO–EG nanofluid was 9% higher than that at 25°C (Arya et al., 2019). Arya et al. (2019) detected the alteration of thermal conductivity, specific heat, and viscosity of MgO–EG nanofluid in the temperature range of 25–100°C. The thermal conductivity of MgO–EG nanofluids increased with the increase of temperature, while the viscosity decreased with the increase of temperature. This is the reason why MgO–EG nanofluid has good heat transfer effect at higher temperatures. It also shows that an increase in inlet temperature improves overall heat transfer performance for fluids with MgO and CNTs, whereas TiO2 nanofluid has better heat transfer performance at lower inlet temperatures than other fluids. This result requires further investigation of the effects of thermal conductivity and viscosity of fluids.
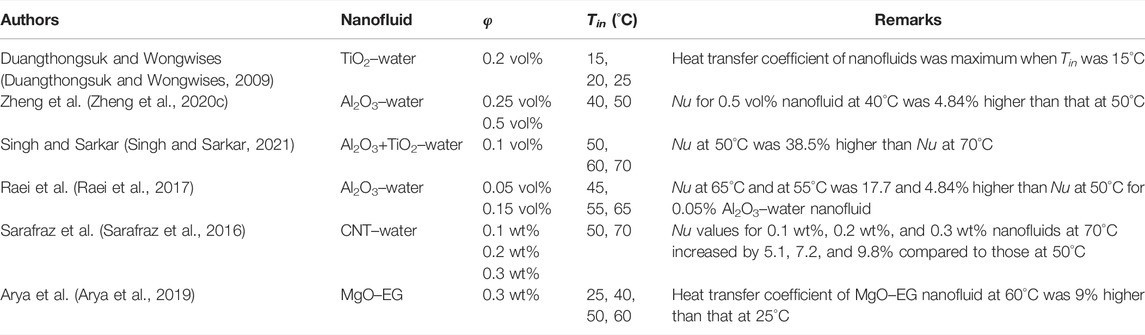
TABLE 8. Effects of inlet temperature on heat transfer characteristics of nanofluids in double-tube heat exchangers.
The performance evaluation criterion (PEC) (Kongkaitpaiboon et al., 2010) is the ratio of the heat transfer coefficient of nanofluids to that of base fluids at the same pumping power. Figure 8 shows variations of the performance evaluation criterion of TiO2 (Subramanian et al., 2020), Al2O3 (Zheng et al., 2020a), ZnO (Zheng et al., 2020a), and CuO (Zheng et al., 2020a) nanofluids in a double-tube heat exchanger with Reynolds numbers. The PEC is calculated by (Kongkaitpaiboon et al., 2010)
where Nunf and Nuf are Nusselt numbers of the nanofluid and the base fluid and fnf and ff are friction factors of the nanofluid and the base fluid.
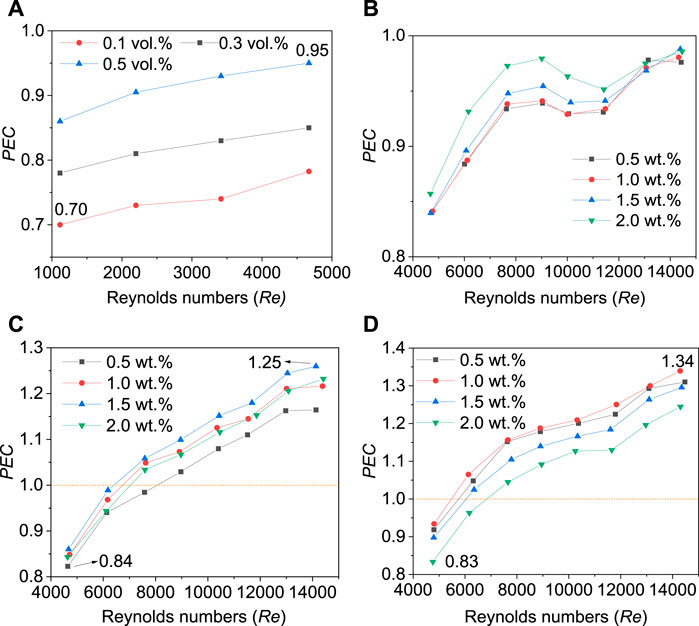
FIGURE 8. Variations of performance evaluation criteria of water-based nanofluids with various Reynolds numbers. (A) TiO2 nanofluids [71]. (B) Al2O3 nanofluids [29]. (C) ZnO nanofluids [29]. (D) CuO nanofluids [29].
Figure 8 shows that performance evaluation criteria of TiO2 (Subramanian et al., 2020), ZnO (Zheng et al., 2020a), and CuO (Zheng et al., 2020a) nanofluids in their respective concentration ranges mainly increase with the increase of Reynolds number. The flow intensity effect of Al2O3 nanofluids on the performance evaluation criterion is not monotonously increasing. It is also found that the performance evaluation criteria of TiO2 (Subramanian et al., 2020) and Al2O3 (Zheng et al., 2020a) nanofluids are less than 1 (base fluid) in the studied range of Reynolds numbers. The maximum performance evaluation criterion of TiO2 (Subramanian et al., 2020) nanofluid is 0.95, and the maximum performance evaluation criterion of Al2O3 (Zheng et al., 2020a) is 0.98. It shows that, under the experimental conditions, the performance of TiO2 (Subramanian et al., 2020) and Al2O3 (Zheng et al., 2020a) is not as good as for the base fluid. The reason why the performance evaluation criterion of TiO2 is less than 1 might be due to its insufficient flow intensity (the Reynolds number in the experimental range is below 5,000). Applications of TiO2 and Al2O3 nanofluids in double-tube heat exchangers should be carefully considered. When the Reynolds number increases to a certain extent, the performance evaluation criteria of ZnO and CuO nanofluids are greater than 1. The maximum performance evaluation criterion of ZnO is 1.25, and the maximum performance evaluation criterion of CuO is 1.34 (Zheng et al., 2020a). This shows that only when the flow of the nanofluid in the casing reaches a certain strength, the performance of the nanofluid is better than that of the base fluid. CuO nanofluids show the optimal performance among four nanofluids.
The concentration of nanofluids affects the performance evaluation criterion. The performance evaluation criterion of TiO2 (Subramanian et al., 2020) nanofluids increases with the increase of volume fraction. Among the four mass fractions (0.5, 1.0, 1.5, and 2.0%), the average performance evaluation criteria for Al2O3, ZnO, and CuO nanofluids are obtained at 2.0, 1.5, and 1.0%, respectively (Zheng et al., 2020a). This result is because of the effect of the increase of concentration on the thermal conductivity and viscosity of nanofluids. The optimal concentration should be selected based on their largest performance evaluation criterion (PEC). Therefore, it is not recommended to use high-concentration ZnO and CuO nanofluids in double-tube heat exchangers for the consideration of economy and thermal performance.
Table 9 shows the maximum heat transfer enhancement (MHTE) of several nanofluids in plate heat exchangers. With the addition of nanoparticles, the heat transfer intensity of the fluid is improved in varying degrees. MWCNT–water nanofluids showed the optimal performance, and the maximum heat transfer enhancement was up by 52.86% (Kumar et al., 2016) compared with that of the base fluid. However, the heat transfer effect of some nanofluids was minor, and the minimum enhancement effect was only 4% of that of graphene (GnP)–EGW (Wang et al., 2018). The heat transfer performance of graphene nanofluids was also tested in the study of Kumar et al. (2016), and the maximum heat transfer enhancement was 45.45%. This might be due to the difference of base fluid choices. The thermal conductivity of water (0.6 W/m·K (Azizian et al., 2014)) is significantly higher than that of ethylene glycol (0.224 W/m·K (Zheng et al., 2021)). In these studies, most of the nanofluids used are oxide nanofluids, such as Al2O3 (Tiwari et al., 2013; Kumar et al., 2016; Bhattad and Sarkar, 2020; Zheng et al., 2020b), TiO2 (Tiwari et al., 2013; Kumar et al., 2016), CeO2 (Tiwari et al., 2013; Kumar et al., 2016), Fe3O4 (Zheng et al., 2020b), and ZnO (Tiwari et al., 2013). As the stability and cost of oxide nanofluids are lower than those of other nanofluids, Al2O3 nanofluids are widely used in plate heat exchangers. The enhancement effect of Al2O3 nanofluids on heat transfer is also obvious, and the maximum heat transfer enhancement was 19.8% (Zheng et al., 2020b), 16.81% (Kumar et al., 2016), 26.3% (Tiwari et al., 2013), and 17.1% (Bhattad and Sarkar, 2020), respectively. This is mainly because of the difference in thermal conductivity of the Al2O3 nanofluids from different references (thermal conductivity of 0.659 W/m·K in the study by Tiwari et al. (2013) and thermal conductivity of 0.6004 W/m·K in the study by Bhattad and Sarkar (2020)). However, the heat transfer enhancement of a single nanofluid is limited, so a variety of nanoparticles are hybridized and mixed with the base fluid to form hybrid nanofluids. “Hybrid” nanofluid means two or more nanoparticles are hybridized and mixed with the base fluid to form a functionally thermal fluid. Compared with single component nanofluids, hybrid nanofluids have better rheological properties and chemical stability (Farbod and Ahangarpour, 2016). It was found that compared with that of Al2O3–water nanofluid, the maximum heat transfer performance of Cu + Al2O3–water nanofluid was improved by 17.38% (Tiwari et al., 2013). Similarly, the heat transfer enhancement effect of adding MWCNTs to Al2O3–water nanofluid was also obvious, up to 7% (Tiwari et al., 2013). This is because Cu nanoparticles and MWCNT materials have better thermophysical properties than Al2O3 nanoparticles. Therefore, hybrid nanofluids have a good application prospect. Zheng et al. (2020b) found that Fe3O4 nanofluids showed the optimal thermal properties compared with the other three nanofluids. Fe3O4 nanofluids show more unique properties under the action of magnetic field, which will be described in detail in the following section.
Figure 9 illustrates the enhancement of the overall heat transfer coefficient (U) of nanofluids at the optimal concentration when the flow rate is 3 lpm compared with the base fluid. The optimal concentration of all nanofluids observed by Kumar et al. (Tiwari et al., 2013) is 0.75 vol%. From the experiments of Kumar et al. (2016) and Zheng et al. (2020b), it is concluded that each nanofluid had its own optimal concentration. The optimal concentrations of SiC, Fe3O4, and Al2O3 nanofluids obtained by Zheng et al. (2020b) are 1.0 wt% (the concentration range is 0.05 wt%–1.0 wt%). The optimal concentration examined might be lower than the real optimal concentration. As mentioned earlier, the increase of nanofluid concentration affects its viscosity and thermal conductivity.
FIGURE 9. Overall heat transfer coefficient enhancements of various nanofluids with the optimum concentration at a flow rate of 3 lpm.
As shown in Figure 9, compared with other nanofluids, MWCNT and GnP nanofluids (Kumar et al., 2016) have more obvious improvement in the overall heat transfer coefficient, reaching 48 and 41%, respectively. These two kinds of nanofluids have more advantages in heat transfer enhancement. The reason is that these two kinds of carbon-based nanofluids have better thermophysical properties than other nanofluids. In contrast, the overall heat transfer coefficient of CuO (Zheng et al., 2020b), TiO2 (Kumar et al., 2016), and SiO2 (Tiwari et al., 2013) with less heat transfer enhancement only increased by 6.1, 9.3, and 10.0%. Therefore, as mentioned above, the application of carbon-based nanofluids in plate heat exchangers has great advantages.
Compared with common nanofluids, magnetic fluids have unique magnetic properties and can be controlled by magnetic fields. The application of magnetic field in the natural convection of magnetic fluids provides additional constraints or disturbances for the movement of magnetic fluids, which in turn affects the flow and heat transfer performance. A square cavity structure is widely used in various fields for studying purpose and provides more convenient magnetic field layout conditions. Many researchers have numerically studied the natural convection of magnetic fluid in a square cavity (Ghaffarpasand, 2016; Sajjadi et al., 2019; Abdi et al., 2021). The heat transfer performance of the magnetic fluid is enhanced by the existence of magnetic field (Abdi et al., 2021). However, it can adversely affect the heat transfer (Ghaffarpasand, 2016; Sajjadi et al., 2019). Usually, the heat transfer performance of magnetic fluid is enhanced by applying a magnetic field. However, an excessive magnetic field intensity results in aggregation of nanoparticles, which weakens the heat transfer enhancement by applying a magnetic field. The experimental studies are relatively few. This part mainly reviews the experimental studies of natural convection in a square cavity. Magnetic particles used in natural convection include Fe (with a particle size of 80–100 nm) (Dixit and Pattamatta, 2020), Fe3O4 (with a particle size of 60–80 nm) (Dixit and Pattamatta, 2020), Mn–Zn ferrite–alkyl–naphthalene (Yamaguchi et al., 2009), Fe2O3 (with a particle size of 15–20 nm) (Joubert et al., 2017), and Fe3O4–CNTs (Shi et al., 2019). It is found that most of the magnetic particles applied are iron oxides and composites of iron oxides with other materials. Pure iron nanoparticles are rarely used alone. This is due to the stable magnetic properties of iron oxides and simple processes that rarely require pretreatment.
In these studies, the generation of the magnetic field mainly depended on electromagnets (Helmholtz coil (Yamaguchi et al., 2009; Shi et al., 2019; Dixit and Pattamatta, 2020)) and bar magnets (Joubert et al., 2017). The electromagnet is mainly composed of electrified coils. The advantage of electromagnets is that the presence or absence of the magnetic field can be controlled anytime and the intensity of the magnetic field is produced by controlling the current passing through the coil. It is noteworthy that electromagnets can also produce alternating magnetic fields. The magnetic field produced by a bar magnet is a permanent magnetic field, and the intensity of the magnetic field can be realized by the superposition of magnets. The bar magnet is commonly used to study the influence of the arrangement of magnetic field on the convective heat transfer of magnetic fluid in the cavity.
Those studies proved that the presence of a magnetic field aggravates the Brownian motion of magnetic particles and enhances the heat transfer (Yamaguchi et al., 2009; Joubert et al., 2017; Shi et al., 2019). Dixit et al. (Dixit and Pattamatta, 2020; Jiao et al., 2021) concluded that the magnetic field made the nanoparticles form a chain structure in the square cavity, forming a heat transfer channel and strengthening the heat transfer. The intensity and position of magnetic field are two important factors in heat transfer of the magnetic fluid. In most cases, if the direction of magnetic field and temperature gradient are the same, it leads to an increase in heat transfer performance (Yamaguchi et al., 2009; Joubert et al., 2017). A study found that the maximum heat transfer enhancement of Fe2O3–water nanofluids was 2.81% (Joubert et al., 2017). The heat transfer performance of Fe3O4–CNT–water nanofluid was increased by 24%. The heat transfer of Fe3O4–water nanofluid was increased by 28%. The enhancement effect of other magnetic field arrangements is not very obvious and even leads to the deterioration of heat transfer effect (Joubert et al., 2017; Dixit and Pattamatta, 2020).
In addition, the increase of magnetic field intensity also leads to the increase of heat transfer efficiency, but an excessively large magnetic field jeopardizes heat transfer enhancement (Joubert et al., 2017; Shi et al., 2019). Due to an increase in the motion of particles with a large specific surface area, resistance to water increases (Ben-Nakhi and Chamkha, 2007; Sheikholeslami and Gorji-Bandpy, 2014), and nanoparticles aggregate with a high magnetic field (Joubert et al., 2017). The present experimental research mainly focuses on the permanent magnetic field and single direction magnetic field. The research on the alternating magnetic field is scarce. Thus, the influence of an alternating magnetic field on the heat transfer performance needs to be further explored.
This part briefly introduces the heat transfer characteristics of magnetic fluid in straight tubes and corrugated channels.
Table 10 shows the information of magnetic fluid in straight tubes under the action of magnetic field. It is reflected from Table 10 that the current experimental research on forced convection heat transfer of magnetic fluids under the magnetic field is mainly focused on straight tubes (Azizian et al., 2014; Ahangar Zonouzi et al., 2018; Sun et al., 2020) and round tube structures (Wang et al., 2019; Li et al., 2021). The adopted heat transfer working medium is mainly Fe3O4–water magnetic nanofluid. By comparing the heat transfer coefficients of magnetic fluids with and without applied magnetic field, it is found that applying the magnetic field can significantly affect the convective heat transfer characteristics of magnetic fluids. At present, there are some doubts about the enhancement effect of magnetic field on the heat transfer of magnetic fluids (Tekir et al., 2020), but most studies have proved the enhancement effect of magnetic field on the heat transfer of magnetic fluids (Azizian et al., 2014; Ahangar Zonouzi et al., 2018; Mei et al., 2019; Wang et al., 2019; Sun et al., 2020; Tekir et al., 2020; Li et al., 2021). To gain more insights into the effect of magnetic field on convective heat transfer of magnetic fluids, the magnetic flux density, magnetic field intensity, and magnetic field gradient are studied experimentally. The data show that the local heat transfer coefficient is greatly improved by increasing the magnetic field density (Azizian et al., 2014; Wang et al., 2019), magnetic field intensity (Azizian et al., 2014; Mei et al., 2019; Wang et al., 2019; Sun et al., 2020; Li et al., 2021), and magnetic field gradient (Azizian et al., 2014; Sun et al., 2020).
Compared with a uniform magnetic field, gradient magnetic fields have more obvious heat transfer enhancement effect on magnetic nanofluids (Sun et al., 2020). This is because magnetic particles gather nearer to the tube wall under the action of gradient magnetic field force. This activity enhances the disturbance of the thermal boundary layer, which further enhances convective heat transfer (Sun et al., 2020). Different magnetic field distributions have different effects on heat transfer enhancement of magnetic fluids. The heat transfer enhancement of alternating magnetic field is better than that of constant magnetic field (Sun et al., 2020; Tekir et al., 2020). When the magnetic field direction is staggered, the convective heat transfer performance is enhanced. This is due to the strong disturbance of magnetic particles in the tube caused by the abrupt change of magnetic field direction. However, Tekir et al. (2020) found an interesting phenomenon that the heat transfer effect of magnetic fluid did not increase with the increase of alternating magnetic field frequency. For alternating magnetic fields with square and triangle waves, the frequency of external magnetic field is inversely proportional to the enhancement effect of convective heat transfer. This means the enhancement effect of heat transfer increases with the decrease of external magnetic field frequency (Tekir et al., 2020). Mei et al. (2019) also reached a similar conclusion, and compared with that of the single-sided electromagnet, the Nusselt number of the double-sided interlaced electromagnet nanofluid was increased by 2.0% at most. Many researchers have studied the optimal magnetic field position for heat transfer enhancement. Different magnetic field positions have different effects on heat transfer enhancement of magnetic nanofluids. It is pointed out that the enhancement of local heat transfer coefficient starts from the starting point of the applied magnetic field, then increases gradually, and reaches the maximum value at the end point of the applied magnetic field (Ahangar Zonouzi et al., 2018).
By comparing the maximum heat transfer enhancement of magnetic fluids in different structures in Table 10, it is found that the circular tube magnetic field is superior to the straight tube magnetic field. Accordingly, when the Reynolds number was 966, the heat transfer of Fe3O4–CNT–water nanofluid was enhanced by 61.54% (Li et al., 2021). According to the research of Wang et al. (2019) and Li et al. (2021), the local heat transfer of Fe3O4–CNT–water hybrid nanofluid was higher than that of Fe3O4–water nanofluid under the action of horizontal circular tube magnetic field. This is because CNTs have higher thermal conductivity, and the aggregation of CNTs and Fe3O4 under the action of magnetic field will aggravate the disturbance and destruction of the thermal boundary layer. Based on the above conclusions, it is indicated that the optimal heat transfer enhancement is obtained by using Fe3O4–CNT–water hybrid nanofluid as a heat transfer working medium in horizontal circular tubes under a magnetic field.
The coupling of magnetic field and flow field increases the pressure drop. Sun et al. (2020) found that the friction factor of Fe3O4 magnetic fluid increased by 6.72% with an applied magnetic field. The alternating magnetic field resulted in a higher pressure drop, and the average Darcy friction factor increased with the increase of frequency (Tekir et al., 2020). Under the magnetic field condition, Zonouzi et al. (2018) found that a relative increase of pressure drop was less than 1%. This result indicates that flow losses are in an acceptable range compared to benefits from the heat transfer enhancement applying a magnetic field.
This part mainly discusses the heat transfer characteristics of magnetic fluids in various corrugated structures including wavy channels (Heidary et al., 2017; Mousavi et al., 2020), triangular corrugated channels (Aminfar et al., 2014), and corrugated plates (Zheng et al., 2021). These structures are shown in Figures 10A–C. When the magnetic fluid in a corrugated channel is in the state of laminar flow, the heat transfer of the magnetic fluid can be enhanced by applying a vertical uniform magnetic field (B) (Heidary et al., 2017) or a vertical magnetic field with gradient (G) (Aminfar et al., 2014; Mousavi et al., 2020). However, the strengthening effect is limited. When the Hartmann number was 60, the average Nusselt number near the wall of the non-corrugated channel (smooth channel) and the corrugated channel increases by 150 and 5% (Heidary et al., 2017). In this case, the strengthening effect of the magnetic field on the magnetic fluid in the non-corrugated channel is more significant. When the magnetic field is not present, vortices are produced in corrugation troughs (triangular corrugated channel (Aminfar et al., 2014) and wavy corrugated channels (Heidary et al., 2017; Mousavi et al., 2020)), which intensifies the fluid disturbance. Therefore, the flow boundary layer and thermal boundary layer near the wall are destroyed by the corrugated structure, and the heat transfer is enhanced. When the magnetic field exists, whether in the non-corrugated channel or in the corrugated channel, the magnetic field “pulls” the streamline of the magnetic fluid onto the wall, and the streamline near the wall is denser. For a non-corrugated channel, this reduces the thickness of the flow boundary layer and enhances the heat transfer. However, when the channel is a corrugated channel, the existence of the magnetic field reduces the vortex intensity in the corrugation troughs of the corrugated channel and even makes the vortices disappear. This reduces the flow intensity in the channel and worsens the heat transfer. It is worth noting that the flow states studied in these studies are laminar flow (Reynolds numbers are 25 and 250 (Heidary et al., 2017), Reynolds number is 100 (Aminfar et al., 2014), and Reynolds numbers range from 100 to 700 (Mousavi et al., 2020)). However, the flow intensity of magnetic fluid in the turbulent state is more intense than that in the laminar flow state, and its application range is wider. It is unknown whether the effects of corrugated structure and vertical magnetic field on the heat transfer of magnetic fluid in turbulence are the same as those in the laminar flow. The effect of magnetic field on heat transfer enhancement of a magnetic fluid in a corrugated channel needs to be further studied under a turbulence flow.
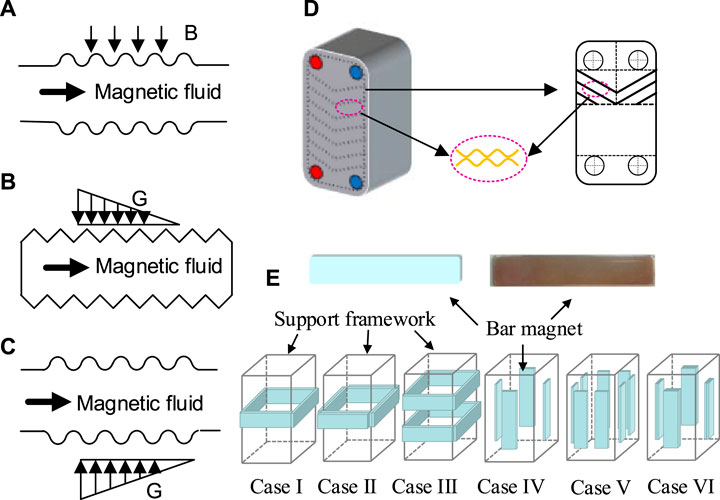
FIGURE 10. (A) A wavy channel with a magnetic field (Heidary et al., 2017), (B) a triangular corrugated channel and arrangements of magnetic field gradients (Aminfar et al., 2014), (C) a wavy channel with a gradient magnetic field (Mousavi et al., 2020), (D) schematic diagram of a heat exchanger with corrugated plates (Zheng et al., 2020b), and (E) schematic diagram of six arrangements of magnets (Zheng et al., 2020b).
Fan et al. (2020) experimentally studied the effect of horizontal magnetic field parallel to a corrugated tube on the heat transfer characteristics of Fe3O4–H2O nanofluids. When the magnetic field intensity was 6, 12, and 18 mT, the Nusselt numbers decreased by 2.8, 5.7, and 9.0%, respectively. When a horizontal magnetic field parallel to the tube is applied, the Fe3O4 particles gather in the center of the pipe and become arranged in a chain. This led to the decrease of the concentration of particles around the boundary layer. The damage of nanoparticles to the boundary layer is weakened. The horizontal magnetic field weakens the heat transfer in the corrugated channel. This shows that the position of magnetic field and flow field has a great influence on the heat transfer performance of magnetic fluid. Unfortunately, Fan et al. (2020) did not analyze the heat transfer performance of the magnetic fluid in the bellows by the magnetic field perpendicular to the flow field. Zheng et al. (2021) studied the heat transfer performance of magnetic fluid in a corrugated plate heat exchanger (Figure 10D) under different magnetic field arrangements and intensities. They arranged the magnetic field under six cases (Figure 10E) around the plate heat exchanger. Compared with no magnetic field, the heat transfer enhancement of 0.1 vol% magnetic fluid in six cases of magnetic field arrangements was 21.8, 23.8, 20.4, 20.4, 21.2, and 21.8%, respectively. However, their study did not examine the influence of the horizontal magnetic field (the magnetic field is arranged above and below the plate heat exchanger). They also made an interesting finding: when the magnetic field was arranged in the case of VI, the average pressure drop decreased by 10%. Overall, when the heat transfer of Fe3O4 nanofluid in a plate heat exchanger is enhanced, the average pressure drop increases (Zheng et al., 2020b). Due to the complexity of the corrugated channel in the plate heat exchanger, the effect of the magnetic field on the magnetic fluid is also complex. The relationship between heat transfer of magnetic fluids and pressure drop under the magnetic field should be studied more. Another suitable research direction would be experimental studies on the alternating magnetic field for the magnetic field in the corrugated structures.
This paper briefly reviewed effects of nanofluids on natural and forced convection with and without magnetic fields in heat exchange devices. Challenges and prospects in applications of nanofluids are summarized as follows:
1) Nanofluids are prepared in a variety of methods to improve dispersion stability. As an important issue, long-term stability of nanofluids should be solved for practical applications. Base fluids mainly consist of water, ethylene glycol, and oil. More varieties of base fluids with higher thermal conductivity should be studied in future research.
2) This paper reviews existing findings about thermophysical properties, especially the viscosity and thermal conductivity of nanofluids. Most researchers applied theoretical models instead of experimental correlations to obtain thermophysical properties of nanofluids for numerical simulations. There are large differences between thermophysical properties predicted by theoretical models and measured by experimental studies. Accuracies of theoretical models should be improved by considering empirical formulas involved with temperature-dependent and base-fluid–dependent thermophysical properties.
3) In studies on natural convection of nanofluids in cavities, researchers are recommended to pay attention to the effects of positions of heat sources in a square cavity. The experimental study on nanofluids in electric heaters should also be further studied. Most of studies on natural convective heat transfer of nanofluids without a magnetic field were carried out numerically. However, few studies are carried out experimentally to complete model validation with a magnetic field, which is necessary to be investigated soon.
4) The heat transfer performance of nanofluids is improved by using various ribbed structures. The temperature of nanofluids at the inlet of a heat exchanger is also an important parameter affecting the performance of the heat exchanger. The nanoparticle material is an important factor that affects the heat transfer performance of nanofluids. Considering that CNTs have good thermophysical properties, hybrid nanofluids are good options to improve the thermal performance of the base liquid significantly. The optimal concentrations of nanofluids should be properly selected to obtain a balance between heat transfer enhancement and flow resistance, but cost-savings are also under consideration. An idea for heat transfer enhancement is to apply a magnetic field due to the field synergy.
5) Under natural convection and forced convection heat transfer, the presence of magnetic fields enhances or deteriorates heat transfer characteristics of magnetic fluids. This paper reviews the heat transfer performance of magnetic fluid in the square cavity, straight tube, and corrugated structure under magnetic fields. These results depend on the magnetic field intensity, arrangement of magnetic field, flow distribution, and temperature distribution. In addition, the experimental study of magnetic fluid in a square cavity and the study of corrugated structure need to be strengthened. A constant magnetic field was applied in most studies, and few researchers have conducted effects of alternating magnetic fields. This is expected to be a research direction for applications of magnetic fluids.
JW and BS conceptualized the research idea and supervised the project. JW, JY, XY, HC, and BS wrote the manuscript. JY, XY, and HC were involved in literature survey and data evaluation. BS edited the manuscript. JW led the project and revised the manuscript.
This work was supported by the National Natural Science Foundation of China (Grant No. 52176067), the Natural Science Foundation of Hebei Province of China (Grant No. E2021202163), the Special Project of Science and Technology Winter Olympics in the Hebei Technology Innovation Guidance Plan (Grant No. 21474501D), and the Project of Innovation Ability Training for Postgraduate Students of Education Department of Hebei Province (Grant No. CXZZSS2021046). The support from the Swedish Research Council (VR) is also acknowledged (2017-04724).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abbood, S. A., Wang, J., Wu, Z., and Sunden, B. (2018). Analysis of Natural Convection of Cu and TiO2 Nanofluids inside Nonconventional Enclosures. J. Enh Heat Transf 25, 315–332. doi:10.1615/JEnhHeatTransf.2018021861
Abdi, H., Motlagh, S. Y., and Soltanipour, H. (2021). Numerical Study of Two-phase Flow in a Square Cavity under Magnetic Field of Parallel Wires. Meccanica 56, 2005–2020. doi:10.1007/s11012-021-01347-x
Abedini, A., Armaghani, T., and Chamkha, A. J. (2019). MHD Free Convection Heat Transfer of a Water-Fe3O4 Nanofluid in a Baffled C-Shaped Enclosure. J. Therm. Anal. Calorim. 135, 685–695. doi:10.1007/s10973-018-7225-8
Abu-Nada, E., Masoud, Z., Oztop, H. F., and Campo, A. (2010). Effect of Nanofluid Variable Properties on Natural Convection in Enclosures. Int. J. Therm. Sci. 49, 479–491. doi:10.1016/j.ijthermalsci.2009.09.002
Ahangar Zonouzi, S., Khodabandeh, R., Safarzadeh, H., Aminfar, H., Trushkina, Y., Mohammadpourfard, M., et al. (2018). Experimental Investigation of the Flow and Heat Transfer of Magnetic Nanofluid in a Vertical Tube in the Presence of Magnetic Quadrupole Field. Exp. Therm. Fluid Sci. 91, 155–165. doi:10.1016/j.expthermflusci.2017.10.013
Ahmadi Nadooshan, A., Eshgarf, H., and Afrand, M. (2018). Measuring the Viscosity of Fe3O4-MWCNTs/EG Hybrid Nanofluid for Evaluation of thermal Efficiency: Newtonian and Non-newtonian Behavior. J. Mol. Liquids 253, 169–177. doi:10.1016/j.molliq.2018.01.012
Aminfar, H., Mohammadpourfard, M., and Ahangar Zonouzi, S. (2014). Hydrothermal Behavior of a Ferrofluid in a Corrugated Channel in the Presence of a Magnetic Field. Heat Trans. Asian Res. 43, 80–92. doi:10.1002/htj.21060
Aminossadati, S. M., and Ghasemi, B. (2009). Natural Convection Cooling of a Localised Heat Source at the Bottom of a Nanofluid-Filled Enclosure. Eur. J. Mech. - B/Fluids 28, 630–640. doi:10.1016/j.euromechflu.2009.05.006
Aminossadati, S. M., and Ghasemi, B. (2011). Natural Convection of Water-CuO Nanofluid in a Cavity with Two Pairs of Heat Source-Sink. Int. Commun. Heat Mass Transfer 38, 672–678. doi:10.1016/j.icheatmasstransfer.2011.03.013
Amirahmad, A., Maglad, A. M., Mustafa, J., and Cheraghian, G. (2021). Loading PCM into Buildings Envelope to Decrease Heat Gain-Performing Transient thermal Analysis on Nanofluid Filled Solar System. Front. Energ. Res. 9, 727011. doi:10.3389/fenrg.2021.727011
Armaghani, T., Kasaeipoor, A., Izadi, M., and Pop, I. (2018). MHD Natural Convection and Entropy Analysis of a Nanofluid inside T-Shaped Baffled Enclosure. Hff 28, 2916–2941. doi:10.1108/HFF-02-2018-0041
Arya, H., Sarafraz, M. M., Pourmehran, O., and Arjomandi, M. (2019). Heat Transfer and Pressure Drop Characteristics of MgO Nanofluid in a Double Pipe Heat Exchanger. Heat Mass. Transfer 55, 1769–1781. doi:10.1007/s00231-018-02554-1
A. S. Raizah, Z., and M. Aly, A. (2021). Natural Convection in an H-Shaped Porous Enclosure Filled with a Nanofluid. Comput. Mater. Continua 66, 3233–3251. doi:10.32604/cmc.2021.012402
Astanina, M. S., Abu-Nada, E., and Sheremet, M. A. (2018). Combined Effects of Thermophoresis, Brownian Motion, and Nanofluid Variable Properties on CuO-Water Nanofluid Natural Convection in a Partially Heated Square Cavity. J. Heat Transfer 140, 082401. doi:10.1115/1.4039217
Azizian, R., Doroodchi, E., McKrell, T., Buongiorno, J., Hu, L. W., and Moghtaderi, B. (2014). Effect of Magnetic Field on Laminar Convective Heat Transfer of Magnetite Nanofluids. Int. J. Heat Mass Transfer 68, 94–109. doi:10.1016/j.ijheatmasstransfer.2013.09.011
Bahiraei, M. (2015). Effect of Particle Migration on Flow and Heat Transfer Characteristics of Magnetic Nanoparticle Suspensions. J. Mol. Liquids 209, 531–538. doi:10.1016/j.molliq.2015.06.030
Batchelor, G. K. (1977). The Effect of Brownian Motion on the Bulk Stress in a Suspension of Spherical Particles. J. Fluid Mech. 83, 97–117. doi:10.1017/S0022112077001062
Ben-Nakhi, A., and Chamkha, A. J. (2007). Conjugate Natural Convection Around a Finned Pipe in a Square Enclosure with Internal Heat Generation. Int. J. Heat Mass Transfer 50, 2260–2271. doi:10.1016/j.ijheatmasstransfer.2006.10.036
Bhattad, A., and Sarkar, J. (2020). Hydrothermal Performance of Plate Heat Exchanger with an Alumina-Graphene Hybrid Nanofluid: Experimental Study. J. Braz. Soc. Mech. Sci. Eng. 42, 1–10. doi:10.1007/s40430-020-02459-3
Brinkman, H. C. (1952). The Viscosity of Concentrated Suspensions and Solutions. J. Chem. Phys. 20, 571. doi:10.1063/1.1700493
Bruggeman, D. A. G. (1935). Berechnung verschiedener physikalischer Konstanten von heterogenen Substanzen. I. Dielektrizitätskonstanten und Leitfähigkeiten der Mischkörper aus isotropen Substanzen. Ann. Phys. 416, 636–664. doi:10.1002/andp.19354160705
Carmichael, L. T., Berry, V., and Sage, B. H. (1963). Thermal Conductivity of Fluids. Ethane. J. Chem. Eng. Data 8, 281–285. doi:10.1021/je60018a001
Chakraborty, S. (2019). An Investigation on the Long-Term Stability of TiO2 Nanofluid. Mater. Today Proc. 11, 714–718. doi:10.1016/j.matpr.2019.03.032
Chakraborty, S., and Panigrahi, P. K. (2020). Stability of Nanofluid: A Review, 174, 115259. doi:10.1016/j.applthermaleng.2020.115259Stability of Nanofluid: A ReviewAppl. Therm. Eng.
Chen, W., Zou, C., and Li, X. (2019). Application of Large-Scale Prepared MWCNTs Nanofluids in Solar Energy System as Volumetric Solar Absorber. Solar Energ. Mater. Solar Cell 200, 109931. doi:10.1016/j.solmat.2019.109931
Chen, Z., Zheng, D., Wang, J., Chen, L., and Sundén, B. (2020). Experimental Investigation on Heat Transfer Characteristics of Various Nanofluids in an Indoor Electric Heater. Renew. Energ. 147, 1011–1018. doi:10.1016/j.renene.2019.09.036
Darzi, A. A. R., Farhadi, M., and Sedighi, K. (2013). Heat Transfer and Flow Characteristics of AL2O3-water Nanofluid in a Double Tube Heat Exchanger. Int. Commun. Heat Mass Transfer 47, 105–112. doi:10.1016/j.icheatmasstransfer.2013.06.003
Ding, Y., and Wen, D. (2005). Particle Migration in a Flow of Nanoparticle Suspensions. Powder Technology 149, 84–92. doi:10.1016/j.powtec.2004.11.012
Dixit, D. D., and Pattamatta, A. (2020). Effect of Uniform External Magnetic-Field on Natural Convection Heat Transfer in a Cubical Cavity Filled with Magnetic Nano-Dispersion. Int. J. Heat Mass Transfer 146, 118828. doi:10.1016/j.ijheatmasstransfer.2019.118828
Duangthongsuk, W., and Wongwises, S. (2009). Heat Transfer Enhancement and Pressure Drop Characteristics of TiO2-Water Nanofluid in a Double-Tube Counter Flow Heat Exchanger. Int. J. Heat Mass Transfer 52, 2059–2067. doi:10.1016/j.ijheatmasstransfer.2008.10.023
Einstein, A. (1906). Eine neue Bestimmung der Moleküldimensionen. Ann. Phys. 324, 289–306. doi:10.1002/andp.19063240204
Esfe, M. H., Arani, A. A. A., Yan, W.-M., and Aghaei, A. (2017). Natural Convection in T-Shaped Cavities Filled with Water-Based Suspensions of COOH-Functionalized Multi Walled Carbon Nanotubes. Int. J. Mech. Sci. 121, 21–32. doi:10.1016/j.ijmecsci.2016.12.011
Fan, F., Qi, C., Tang, J., and Liu, Q. (2020). Thermal and Exergy Efficiency of Magnetohydrodynamic Fe 3 O 4 ‐H 2 O Nanofluids Flowing through a Built‐in Twisted Turbulator Corrugated Tube under Magnetic Field. Asia‐pac J. Chem. Eng. 15, e2500. doi:10.1002/apj.2500
Farbod, M., and Ahangarpour, A. (2016). Improved thermal Conductivity of Ag Decorated Carbon Nanotubes Water Based Nanofluids. Phys. Lett. A 380, 4044–4048. doi:10.1016/j.physleta.2016.10.014
Galeazzo, F. C. C., Miura, R. Y., Gut, J. A. W., and Tadini, C. C. (2006). Experimental and Numerical Heat Transfer in a Plate Heat Exchanger. Chem. Eng. Sci. 61, 7133–7138. doi:10.1016/j.ces.2006.07.029
Ghaffarpasand, O. (2016). Numerical Study of MHD Natural Convection inside a Sinusoidally Heated Lid-Driven Cavity Filled with Fe3O4-Water Nanofluid in the Presence of Joule Heating. Appl. Math. Model. 40, 9165–9182. doi:10.1016/j.apm.2016.05.038
Giwa, S. O., Sharifpur, M., Ahmadi, M. H., and Meyer, J. P. (2021). A Review of Magnetic Field Influence on Natural Convection Heat Transfer Performance of Nanofluids in Square Cavities. J. Therm. Anal. Calorim. 145, 2581–2623. doi:10.1007/s10973-020-09832-3
Habibi, M. R., and Salimpour, M. R. (2019). Numerical Study of Nanofluid Convective Heat Transfer in Sinusoidal Tubes. Heat Transfer Eng. 40, 1259–1267. doi:10.1080/01457632.2018.1460927
Hamilton, R. L., and Crosser, O. K. (1962). Thermal Conductivity of Heterogeneous Two-Component Systems. Ind. Eng. Chem. Fund. 1, 187–191. doi:10.1021/i160003a005
Hariri, S., Mokhtari, M., Gerdroodbary, M. B., and Fallah, K. (2017). Numerical Investigation of the Heat Transfer of a Ferrofluid inside a Tube in the Presence of a Non-uniform Magnetic Field. Eur. Phys. J. Plus 132, 1–14. doi:10.1140/epjp/i2017-11324-1
Hdhiri, N., Souayeh, B., Alfannakh, H., and Beya, B. B. (2019). Natural Convection Study with Internal Heat Generation on Heat Transfer and Fluid Flow within a Differentially Heated Square Cavity Filled with Different Working Fluids and Porous Media. BioNanoSci. 9, 702–722. doi:10.1007/s12668-019-00626-y
Heidary, H., Kermani, M., and Dabir, B. (2017). Magnetic Field Effect on Convective Heat Transfer in Corrugated Flow Channel. Therm. Sci. 21, 2105–2115. doi:10.2298/tsci140610002h
Hiroshi, A., Tsukasaki, Y., Yatsuya, S., and Tasaki, A. (1978). Magnetic Properties of Ferromagnetic Ultrafine Particles Prepared by Vacuum. J. Cryst. Growth 45, 495–500. doi:10.1016/0022-0248(78)90482-7
Hussein, A. M., Bakar, R. A., and Kadirgama, K. (2014). Study of Forced Convection Nanofluid Heat Transfer in the Automotive Cooling System. Case Stud. Therm. Eng. 2, 50–61. doi:10.1016/j.csite.2013.12.001
Izadi, M., Mohebbi, R., Chamkha, A., and Pop, I. (2018). Effects of Cavity and Heat Source Aspect Ratios on Natural Convection of a Nanofluid in a C-Shaped Cavity Using Lattice Boltzmann Method. Hff 28, 1930–1955. doi:10.1108/HFF-03-2018-0110
Jiao, F., Li, Q., Jiao, Y., and He, Y. (2021). Heat Transfer of Ferrofluids with Magnetoviscous Effects. J. Mol. Liquids 328, 115404. doi:10.1016/j.molliq.2021.115404
Joubert, J. C., Sharifpur, M., Solomon, A. B., and Meyer, J. P. (2017). Enhancement in Heat Transfer of a Ferrofluid in a Differentially Heated Square Cavity through the Use of Permanent Magnets. J. Magnetism Magn. Mater. 443, 149–158. doi:10.1016/j.jmmm.2017.07.062
Kaood, A., and Hassan, M. A. (2020). Thermo-hydraulic Performance of Nanofluids Flow in Various Internally Corrugated Tubes. Chem. Eng. Process. - Process Intensification 154, 108043. doi:10.1016/j.cep.2020.108043
Keramat, F., Dehghan, P., Mofarahi, M., and Lee, C.-H. (2020). Numerical Analysis of Natural Convection of Alumina-Water Nanofluid in H-Shaped Enclosure with a V-Shaped Baffle. J. Taiwan Inst. Chem. Eng. 111, 63–72. doi:10.1016/j.jtice.2020.04.006
Kongkaitpaiboon, V., Nanan, K., and Eiamsa-ard, S. (2010). Experimental Investigation of Heat Transfer and Turbulent Flow Friction in a Tube Fitted with Perforated Conical-Rings. Int. Commun. Heat Mass Transfer 37, 560–567. doi:10.1016/j.icheatmasstransfer.2009.12.015
Kumar, D. H., Patel, H. E., Kumar, V. R. R., Sundararajan, T., Pradeep, T., and Das, S. K. (2004). Model for Heat Conduction in Nanofluids. Phys. Rev. Lett. 93, 144301. doi:10.1103/physrevlett.93.144301
Kumar, P. M., Kumar, J., Tamilarasan, R., Sendhilnathan, S., and Suresh, S. (2015). Review on Nanofluids Theoretical thermal Conductivity Models. Ej 19, 67–83. doi:10.4186/ej.2015.19.1.67
Kumar, S. A., Meenakshi, K. S., Narashimhan, B. R. V., Srikanth, S., and Arthanareeswaran, G. (2009). Synthesis and Characterization of Copper Nanofluid by a Novel One-step Method. Mater. Chem. Phys. 113, 57–62. doi:10.1016/j.matchemphys.2008.07.027
Kumar, V., Tiwari, A. K., and Ghosh, S. K. (2015). Application of Nanofluids in Plate Heat Exchanger: A Review. Energ. Convers. Management 105, 1017–1036. doi:10.1016/j.enconman.2015.08.053
Kumar, V., Tiwari, A. K., and Ghosh, S. K. (2016). Effect of Variable Spacing on Performance of Plate Heat Exchanger Using Nanofluids. Energy 114, 1107–1119. doi:10.1016/j.energy.2016.08.091
Lai, F.-H., and Yang, Y.-T. (2011). Lattice Boltzmann Simulation of Natural Convection Heat Transfer of Al2O3/water Nanofluids in a Square Enclosure. Int. J. Therm. Sci. 50, 1930–1941. doi:10.1016/j.ijthermalsci.2011.04.015
Leela Vinodhan, V., Suganthi, K. S., and Rajan, K. S. (2016). Convective Heat Transfer Performance of CuO-Water Nanofluids in U-Shaped Minitube: Potential for Improved Energy Recovery. Energ. Convers. Management 118, 415–425. doi:10.1016/j.enconman.2016.04.017
Li, G., Wang, J., Zheng, H., Xie, G., and Sundén, B. (2021). Improvement of Cooling Performance of Hybrid Nanofluids in a Heated Pipe Applying Annular Magnets. J. Therm. Anal. Calorim. 147, 4731–4749. doi:10.1007/s10973-021-10848-6
Li, Q., Wang, J., Wang, J., Baleta, J., Min, C., and Sundén, B. (2018). Effects of Gravity and Variable thermal Properties on Nanofluid Convective Heat Transfer Using Connected and Unconnected walls. Energ. Convers. Management 171, 1440–1448. doi:10.1016/j.enconman.2018.06.097
Mahbubul, I. M., Saidur, R., and Amalina, M. A. (2013). Thermal Conductivity, Viscosity and Density of R141b Refrigerant Based Nanofluid. Proced. Eng. 56, 310–315. doi:10.1016/j.proeng.2013.03.124
Maxwell, J. (2011). A Treatise on Electricity and Magnetism. Nature 7, 478–480. doi:10.1017/CBO9780511709333
Mei, S., Qi, C., Luo, T., Zhai, X., and Yan, Y. (2019). Effects of Magnetic Field on Thermo-Hydraulic Performance of Fe3O4-Water Nanofluids in a Corrugated Tube. Int. J. Heat Mass Transfer 128, 24–45. doi:10.1016/j.ijheatmasstransfer.2018.08.071
Moghaddam, H. A., Ghafouri, A., and Faridi Khouzestani, R. (2021). Viscosity and thermal Conductivity Correlations for Various Nanofluids Based on Different Temperature and Nanoparticle Diameter. J. Braz. Soc. Mech. Sci. Eng. 43, 1–9. doi:10.1007/s40430-021-03017-1
Mohebbi, K., Rafee, R., and Farhad, T. (2015). Effects of Rib Shapes on Heat Transfer Characteristics of Turbulent Flow of Al2O3-Water Nanofluid inside Ribbed Tubes. Iranian J. Chem. Chem. Eng. 34, 61–77.
Mohebbi, R., Izadi, M., Sajjadi, H., Delouei, A. A., and Sheremet, M. A. (2019). Examining of Nanofluid Natural Convection Heat Transfer in a Γ-shaped Enclosure Including a Rectangular Hot Obstacle Using the Lattice Boltzmann Method. Physica A: Stat. Mech. its Appl. 526, 120831. doi:10.1016/j.physa.2019.04.067
Moradi, A., Toghraie, D., Isfahani, A. H. M., and Hosseinian, A. (2019). An Experimental Study on MWCNT-Water Nanofluids Flow and Heat Transfer in Double-Pipe Heat Exchanger Using Porous media. J. Therm. Anal. Calorim. 137, 1797–1807. doi:10.1007/s10973-019-08076-0
Mousavi, S. M., Biglarian, M., Darzi, A. A. R., Farhadi, M., Afrouzi, H. H., and Toghraie, D. (2020). Heat Transfer Enhancement of Ferrofluid Flow within a Wavy Channel by Applying a Non-uniform Magnetic Field. J. Therm. Anal. Calorim. 139, 3331–3343. doi:10.1007/s10973-019-08650-6
Onyiriuka, E. J., Ighodaro, O. O., Adelaja, A. O., Ewim, D. R. E., and Bhattacharyya, S. (2019). A Numerical Investigation of the Heat Transfer Characteristics of Water-Based Mango Bark Nanofluid Flowing in a Double-Pipe Heat Exchanger. Heliyon 5, e02416. doi:10.1016/j.heliyon.2019.e02416
Öztop, H. F., Estellé, P., Yan, W.-M., Al-Salem, K., Orfi, J., and Mahian, O. (2015). A Brief Review of Natural Convection in Enclosures under Localized Heating with and without Nanofluids. Int. Commun. Heat Mass Transfer 60, 37–44. doi:10.1016/j.icheatmasstransfer.2014.11.001
Phuoc, T. X., and Massoudi, M. (2009). Experimental Observations of the Effects of Shear Rates and Particle Concentration on the Viscosity of Fe2O3-Deionized Water Nanofluids. Int. J. Therm. Sci. 48, 1294–1301. doi:10.1016/j.ijthermalsci.2008.11.015
Raei, B., Shahraki, F., Jamialahmadi, M., and Peyghambarzadeh, S. M. (2017). Experimental Study on the Heat Transfer and Flow Properties of γ-Al2O3/water Nanofluid in a Double-Tube Heat Exchanger. J. Therm. Anal. Calorim. 127, 2561–2575. doi:10.1007/s10973-016-5868-x
Rahimi, A., Sepehr, M., Lariche, M. J., Mesbah, M., Kasaeipoor, A., and Malekshah, E. H. (2018). Analysis of Natural Convection in Nanofluid-Filled H-Shaped Cavity by Entropy Generation and Heatline Visualization Using Lattice Boltzmann Method. Physica E: Low-Dimensional Syst. Nanostructures 97, 347–362. doi:10.1016/j.physe.2017.12.003
Renner, J., Evans, B., and Hirth, G. (2000). On the Rheologically Critical Melt Fraction. Earth Planet. Sci. Lett. 181, 585–594. doi:10.1016/S0012-821X(00)00222-3
Rezaei Gorjaei, A., Joda, F., and Haghighi Khoshkhoo, R. (2020). Heat Transfer and Entropy Generation of Water-Fe3O4 Nanofluid under Magnetic Field by Euler-Lagrange Method. J. Therm. Anal. Calorim. 139, 2023–2034. doi:10.1007/s10973-019-08627-5
Rostami, S., Aghakhani, S., Hajatzadeh Pordanjani, A., Afrand, M., Cheraghian, G., Oztop, H. F., et al. (2020). A Review on the Control Parameters of Natural Convection in Different Shaped Cavities with and without Nanofluid. Processes 8, 1011. doi:10.3390/pr8091011
Sahin, F., and Namli, L. (2021). Thermal Performances and Stabilities of Nanofluids in an Electrical Oil Heater. J. Therm. Anal. Calorim. 145, 3195–3206. doi:10.1007/s10973-020-09826-1
Sajjadi, H., Amiri Delouei, A., Izadi, M., and Mohebbi, R. (2019). Investigation of MHD Natural Convection in a Porous media by Double MRT Lattice Boltzmann Method Utilizing MWCNT-Fe3O4/water Hybrid Nanofluid. Int. J. Heat Mass Transfer 132, 1087–1104. doi:10.1016/j.ijheatmasstransfer.2018.12.060
Salman, S. D. (2019). Comparative Study on Heat Transfer Enhancement of Nanofluids Flow in Ribs Tube Using CFD Simulation. Heat Transfer-asian Res. 48, 148–163. doi:10.1002/htj.21376
Sarafraz, M. M., Hormozi, F., and Nikkhah, V. (2016). Thermal Performance of a Counter-current Double Pipe Heat Exchanger Working with COOH-CNT/water Nanofluids. Exp. Therm. Fluid Sci. 78, 41–49. doi:10.1016/j.expthermflusci.2016.05.014
Sarviya, R. M., and Fuskele, V. (2017). Review on thermal Conductivity of Nanofluids. Mater. Today Proc. 4, 4022–4031. doi:10.1016/j.matpr.2017.02.304
Selvam, C., Mohan Lal, D., and Harish, S. (2017). Enhanced Heat Transfer Performance of an Automobile Radiator with Graphene Based Suspensions. Appl. Therm. Eng. 123, 50–60. doi:10.1016/j.applthermaleng.2017.05.076
Sert, Z., and Ti̇muralp, Ç. (2015). Laminar Natural Convection Heat Transfer of Water-Based Nanofluids in Square Enclosure Containing Heater. Aku-j. Sci. Eng. 15, 1–12. doi:10.5578/fmbd.9381
Sheikholeslami, M., and Gorji-Bandpy, M. (2014). Free Convection of Ferrofluid in a Cavity Heated from below in the Presence of an External Magnetic Field. Powder Technology 256, 490–498. doi:10.1016/j.powtec.2014.01.079
Shi, L., He, Y., Hu, Y., and Wang, X. (2019). Controllable Natural Convection in a Rectangular Enclosure Filled with Fe3O4@CNT Nanofluids. Int. J. Heat Mass Transfer 140, 399–409. doi:10.1016/j.ijheatmasstransfer.2019.05.104
Singh, S. K., and Sarkar, J. (2021). Improving Hydrothermal Performance of Double-Tube Heat Exchanger with Modified Twisted Tape Inserts Using Hybrid Nanofluid. J. Therm. Anal. Calorim. 143, 4287–4298. doi:10.1007/s10973-020-09380-w
Souayeh, B., Hdhiri, N., Alam, M. W., Hammami, F., and Alfannakh, H. (2020). Convective Heat Transfer and Entropy Generation Around a Sphere within Cuboidal Enclosure. J. Thermophys. Heat Transfer 34, 605–625. doi:10.2514/1.T5960
Subramanian, R., Senthil Kumar, A., Vinayagar, K., and Muthusamy, C. (2020). Experimental Analyses on Heat Transfer Performance of TiO2-Water Nanofluid in Double-Pipe Counter-flow Heat Exchanger for Various Flow Regimes. J. Therm. Anal. Calorim. 140, 603–612. doi:10.1007/s10973-019-08887-1
Sun, B., Guo, Y., Yang, D., and Li, H. (2020). The Effect of Constant Magnetic Field on Convective Heat Transfer of Fe3O4/water Magnetic Nanofluid in Horizontal Circular Tubes. Appl. Therm. Eng. 171, 114920. doi:10.1016/j.applthermaleng.2020.114920
Sun, B., Peng, C., Yang, D., and Li, H. (2018). Effect of the Wick and the Working Medium on the Thermal Resistance of FPHP. Front. Energ. Res. 6, 37. doi:10.3389/fenrg.2018.00037
Sun, H., Jiao, R., An, G., Xu, H., Wang, D., and Lee, D. J. (2021). Influence of Particle Size on the Aggregation Behavior of Nanoparticles: Role of Structural Hydration Layer. J. Environ. Sci. 103, 33–42. doi:10.1016/j.jes.2020.10.007
Syam Sundar, L., Singh, M. K., and Sousa, A. C. M. (2013). Investigation of thermal Conductivity and Viscosity of Fe3O4 Nanofluid for Heat Transfer Applications. Int. Commun. Heat Mass Transfer 44, 7–14. doi:10.1016/j.icheatmasstransfer.2013.02.014
Tekir, M., Taskesen, E., Aksu, B., Gedik, E., and Arslan, K. (2020). Comparison of Bi-directional Multi-Wave Alternating Magnetic Field Effect on Ferromagnetic Nanofluid Flow in a Circular Pipe under Laminar Flow Conditions. Appl. Therm. Eng. 179, 115624. doi:10.1016/j.applthermaleng.2020.115624
Timofeeva, E. V., Gavrilov, A. N., Mccloskey, J. M., Tolmachev, Y. V., Sprunt, S., Lopatina, L. M., et al. (2008). Thermal Conductivity and Particle Agglomeration in Alumina Nanofluids: Experiment and Theory. Phys. Rev. E 76, 061203. doi:10.1103/PhysRevE.76.061203
Tiwari, A. K., Ghosh, P., and Sarkar, J. (2013). Performance Comparison of the Plate Heat Exchanger Using Different Nanofluids. Exp. Therm. Fluid Sci. 49, 141–151. doi:10.1016/j.expthermflusci.2013.04.012
Vajjha, R. S., and Das, D. K. (2012). A Review and Analysis on Influence of Temperature and Concentration of Nanofluids on Thermophysical Properties, Heat Transfer and Pumping Power. Int. J. Heat Mass Transfer 55, 4063–4078. doi:10.1016/j.ijheatmasstransfer.2012.03.048
Wang, J., Li, G., Li, T., Zeng, M., and Sundén, B. (2021). Effect of Various Surfactants on Stability and Thermophysical Properties of Nanofluids. J. Therm. Anal. Calorim. 143, 4057–4070. doi:10.1007/s10973-020-09381-9
Wang, J., Li, G., Zhu, H., Luo, J., and Sundén, B. (2019). Experimental Investigation on Convective Heat Transfer of Ferrofluids inside a Pipe under Various Magnet Orientations. Int. J. Heat Mass Transfer 132, 407–419. doi:10.1016/j.ijheatmasstransfer.2018.12.023
Wang, J., Zhai, Z., Zheng, D., Yang, L., and Sundén, B. (2020). Investigation of Heat Transfer Characteristics of Al2O3-Water Nanofluids in an Electric Heater. Heat Transfer Eng. 42, 1765–1774. doi:10.1080/01457632.2020.1818427
Wang, W., Zhang, B., Cui, L., Zheng, H., Klemeš, J. J., and Wang, J. (2021). Numerical Study on Heat Transfer and Flow Characteristics of Nanofluids in a Circular Tube with Trapezoid Ribs. Open Phys. 19, 224–233. doi:10.1515/phys-2021-0022
Wang, X., Xu, X., and Choi, S. U. S. (1999). Thermal Conductivity of Nanoparticle - Fluid Mixture. J. Thermophys. Heat Transfer 13, 474–480. doi:10.2514/2.6486
Wang, Z., Wu, Z., Han, F., Wadsö, L., and Sundén, B. (2018). Experimental Comparative Evaluation of a Graphene Nanofluid Coolant in Miniature Plate Heat Exchanger. Int. J. Therm. Sci. 130, 148–156. doi:10.1016/j.ijthermalsci.2018.04.021
Yamaguchi, H., Niu, X.-D., Zhang, X.-R., and Yoshikawa, K. (2009). Experimental and Numerical Investigation of Natural Convection of Magnetic Fluids in a Cubic Cavity. J. Magnetism Magn. Mater. 321, 3665–3670. doi:10.1016/j.jmmm.2009.07.013
Yang, T., Zhao, P., Li, Q., Zhao, Y., and Yu, T. (2021). Study on Thermophysical Properties of a lead-bismuth-based Graphene Nanofluid. Front. Energ. Res. 9, 727447. doi:10.3389/fenrg.2021.727447
Yu, W., and Choi, S. U. S. (2003). The Role of Interfacial Layers in the Enhanced Thermal Conductivity of Nanofluids: A Renovated Maxwell Model. J. Nanoparticle Res. 5, 167–171. doi:10.1007/s11051-004-2601-710.1023/a:1024438603801
Zheng, D., Wang, J., Chen, Z., Baleta, J., and Sundén, B. (2020). Performance Analysis of a Plate Heat Exchanger Using Various Nanofluids. Int. J. Heat Mass Transfer 158, 119993. doi:10.1016/j.ijheatmasstransfer.2020.119993
Zheng, D., Wang, J., Pang, Y., Chen, Z., and Sunden, B. (2020). Heat Transfer Performance and Friction Factor of Various Nanofluids in a Double-Tube Counter Flow Heat Exchanger. Therm. Sci. 24, 3601–3612. doi:10.2298/TSCI200323280Z
Zheng, D., Yang, J., Wang, J., Kabelac, S., and Sundén, B. (2021). Analyses of thermal Performance and Pressure Drop in a Plate Heat Exchanger Filled with Ferrofluids under a Magnetic Field. Fuel 293, 120432–120525. doi:10.1016/j.fuel.2021.120432
Zheng, M., Han, D., Asif, F., and Si, Z. (2020). Effect of Al2O3/water Nanofluid on Heat Transfer of Turbulent Flow in the Inner Pipe of a Double-Pipe Heat Exchanger. Heat Mass. Transfer 56, 1127–1140. doi:10.1007/s00231-019-02774-z
Zhu, H.-t., Lin, Y.-s., and Yin, Y.-s. (2004). A Novel One-step Chemical Method for Preparation of Copper Nanofluids. J. Colloid Interf. Sci. 277, 100–103. doi:10.1016/j.jcis.2004.04.026
Symbols
AR Aspect ratio
B Magnetic field induction, T
c Constant
dp Nanoparticle diameter, nm
f Friction factor Base fluid
G Magnetic field gradient, A/m2
k Thermal conductivity W/mK
MHTE Maximum heat transfer enhancement
n Empirical shape factor
Nu Nusselt number
Num Average Nusselt number
PEC Performance evaluation criterion
rp Radius of suspended particles, nm
Ra Rayleigh number
Re Reynolds number
T Temperature, °C
Tin Inlet temperature, °C
U Overall heat transfer coefficient, W/m2·K
Greek symbols
β Ratio of the thickness of solid–liquid interface layer to the particle size of nanoparticles
γ Shear rate, s−1
ηU Overall heat transfer coefficient enhancement
ηNum Increase in average Nusselt number
μ Viscosity, m2/s
Subscripts
f Friction factor Base fluid
nf Nanofluid
Keywords: heat transfer enhancement, heat exchanger, magnetic field, magnetic fluid, nanofluid
Citation: Yang J, Yang X, Wang J, Chin HH and Sundén B (2022) Review on Thermal Performance of Nanofluids With and Without Magnetic Fields in Heat Exchange Devices. Front. Energy Res. 10:822776. doi: 10.3389/fenrg.2022.822776
Received: 26 November 2021; Accepted: 02 March 2022;
Published: 07 April 2022.
Edited by:
Mohsen Sharifpur, University of Pretoria, South AfricaReviewed by:
Matteo Fasano, Polytechnic University of Turin, ItalyCopyright © 2022 Yang, Yang, Wang, Chin and Sundén. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jin Wang, d2p3Y24wMEAxNjMuY29t; Bengt Sundén, YmVuZ3Quc3VuZGVuQGVuZXJneS5sdGguc2U=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.