Nonlinear Seepage Mathematical Model of Fractured Tight Stress Sensitive Reservoir and Its Application

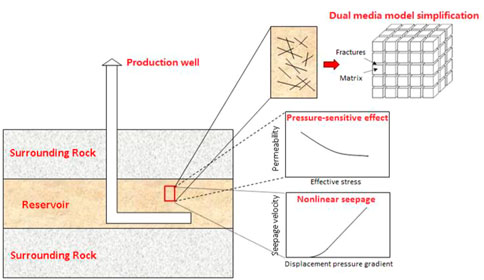
A tight reservoir can only have industrial production value after fracturing. After volume fracturing, there are artificial fracturing zones and fracturing unmodified zones composed of a matrix, microfractures, and main fractures. There are also pressure-sensitive effects and nonlinear seepage in the matrix. There is an unsteady channeling flow between the matrix and microfractures and main fractures and a threshold pressure gradient in the matrix. The fluid flow between the three media and the transfer flow between the media are very complex. Aiming at the problem of poor simulation accuracy because the above characteristics of tight reservoir fracturing development are not considered in the current commercial numerical simulation software Eclipse, CMG, and VIP, the triple medium coupling nonlinear mathematical model of tight reservoir fracturing development matrix/microfractures/main fractures was established in this study, and the discrete mathematical model was constructed using the full implicit numerical solution method. The model considered the effects of threshold fracturing gradient and nonlinear seepage on the reverse side of seepage. In terms of pressure-sensitive effect, the latest generalized pressure-sensitive effect calculation model, considering rock physical parameters established by authors, was adopted. In terms of matrix/fracture transfer flow, the nonlinear matrix/fracture transfer flow model considering threshold pressure gradient and pressure-sensitive effect established by authors was adopted. Finally, a tight reservoir numerical simulation software was developed based on a triple medium coupling nonlinear model. The software was used to simulate the development effect of turbidite tight reservoir in Wang 587 Block of Jiyang depression, Shengli Oilfield. The results showed that the fitting accuracy of the new model was 13.3% higher than that of Eclipse, and the calculation results were more in line with the production practice of tight reservoirs. The new model established an important theoretical basis for scientifically and effectively guiding the development of tight reservoirs.

Introduction

Reservoir numerical simulation technology is an effective means to guide development scheme design, development adjustment, and scheme prediction and provide a theoretical basis for oilfield development scheme preparation and policy-making (Chengzao et al., 2012a; Caineng et al., 2012). A tight reservoir is usually defined as a reservoir with gas-measured permeability less than 1.0 × 10^–3 μm². It has also been suggested that this limit is not very strict because a tight reservoir is defined as a reservoir with gas-measured permeability less than 2.0 × 10^–3 μm² based on the description of the National Energy Administration of China (Caineng et al., 2013; Fuxi et al., 2014). Taking the Jiyang Depression of Shengli Oilfield studied in this article as an example, the field classifies glutenite, turbidite, and beach bar sand reservoirs with gas-measured permeability less than 3.0 × 10⁻³μm² as tight reservoirs for development (Chengzao et al., 2012b; Zhenglian et al., 2012). Due to the differences in reservoir genesis of the three types of tight reservoirs, different types of tight reservoirs are developed in different ways. At present, effective development technology of three-dimensional injection and production of sand gravel “multi-storey” multistage fracturing horizontal wells, effective development technology of segmented fracturing fracture network adaptation of turbidite vertical wells, and long fracture fracturing development technology of beach bar sand vertical wells have been developed. However, due to the lack of special numerical simulation software for tight reservoirs, the development plan lacks a theoretical basis, and individual production blocks have problems such as large well spacing, low formation pressure level, and slow oil production rate. Special tight reservoir numerical simulation software is required for development simulation (Clarkson et al., 2013; Zhongxiang et al., 2016). In order to introduce the development characteristics of tight reservoir artificial fracturing zones, this study investigated the research status of pressure-sensitive effect, nonlinear seepage, nonlinear transfer flow, and tight reservoir numerical simulation.

Pressure-Sensitive Effect

In the study of pressure-sensitive effects in tight reservoirs, scholars currently mainly use experimental data fitting methods when studying pressure-sensitive effects. For experimental research methods, Holt et al. and Tian et al. experimentally studied the stress sensitivity of matrix cores and fractured natural cores and gave an exponential empirical model (Holt, 2005). Nie et al. investigated the effect of time effect on the stress sensitivity of tight gas reservoirs and established an empirical model of stress sensitivity considering the time factor (Xiangrong et al., 2018). Yang et al. combined CT structural scanning experiments to quantitatively evaluate the variation of pore and throat radii with surrounding pressure (Yang et al., 2017). Gu et al. experimentally analyzed the main controlling factors of stress sensitivity in tight sandstone in terms of material composition, fracture development, and pore structure. However, they did not give a quantitative model (Yang et al., 2018). Liu et al., based on experimental results, considered the relationship between effective stress sensitivity coefficient and Young’s modulus and established an exponential stress sensitivity model (Liu et al., 2018). Yang et al. analyzed the variation of pore structure parameters with effective stress from the microscopic scale by combining CT structural scanning techniques and gave empirical equations for the stress sensitivity of porosity and permeability (Yongfei et al., 2016). Tian et al. quantified the relationship between strain and effective stress based on experimental results and considering the effects of boundary layer and critical throat radii (Tian et al., 2015). Lei et al. applied an exponential-type function to quantify the stress sensitivity of shale reservoirs considering the effect of the initial permeability value (Hao et al., 2019). Shangxian Yin and Jones et al. proposed empirical models of permeability and effective stress in different functional forms. However, various empirical regression models were only applicable to a single sedimentary rock type and cannot be extended to different sedimentary rock reservoirs (Jones, 1975; David et al., 1994; Dong et al., 2010).

In the study of the pressure-sensitive effect of microfractures in tight reservoirs, Yanlong Zhao, Zijun Zheng, and others carried out a fracture permeability stress sensitivity experiment and analyzed the fracture structure characteristics by scanning electron microscope technology. They proposed that fracture permeability and effective stress show a negative exponential relationship (Zijun and Cheng, 2018; Yanlong et al., 2019). Lanqing Fu and others studied the stress sensitivity characteristics of tight cores with fractures under the experimental conditions of constant displacement pressure difference and constant confining pressure, respectively. They proposed that there was an inflection point in the fracture stress sensitivity curve, which was before the effective stress reached the inflection point, the permeability decreased sharply, the effective stress exceeded the inflection point, and the decline range of permeability tended to be gentle (Lanqing, 2016). Pingliang Fang studied the permeability loss of micro and nano fractures under variable pore pressure and variable confining pressure. The permeability loss rate exceeded 70%, and the damage degree of stress sensitivity was “strong” (Jianwei et al., 2019). Jianwei Feng and others proposed that, with the increase in effective stress, the fracture permeability gradually decreased and there was an “inflection point.” The reason was that brittle fracture occurred after the volume expansion of brittle minerals underground conditions, the connecting dominant channel was damaged, and the fracture system was complex. Then, the mechanical relationship model between crack opening and effective stress was deduced by the mathematical method. It was clear that the fracture opening conformed to the nonlinear variation law with confining pressure and effective stress (Wei et al., 2017). Wei Tian et al. studied the stress sensitivity of the reticulated fracture core using a fully digital servo controller, obtained the conclusion that the shape of the stress sensitivity curve presents an “L" shape, and divided the curve into two stages. The first stage was pseudoplastic deformation, and the permeability decreased greatly. The second stage was dominated by elastic deformation. As the rock became an isobaric body, the decline range of permeability became smaller (Pingliang et al., 2017a). Fraser Harris et al. studied the effect of fracture radial displacement and shear displacement on microfracture permeability by changing the size and direction of the radial stress field (Fraser Harris et al., 2020). Liang et al. established exponential microfracture pressure-sensitive model and cubic polynomial variation law of main fracture conductivity through microfracture and main fracture stress sensitivity experiments. They proposed that the influence of the microfracture pressure-sensitive effect on fluid flow was greater than that of the main fracture conductivity loss (Bin et al., 2016). He et al. studied the pressure-sensitive effect of microfractures through experiments and divided its stress sensitivity into medium to strong according to permeability loss. Combined with CT scanning imaging experiments, they studied the influence of the fracture surface on the pressure-sensitive effect of microfractures (Jingang et al., 2013). Haiyong Zhang et al. prepared the thermal stress microfracture dense core by heating in a microwave oven to approximately simulate the microfracture formed in the actual diagenesis and sedimentation process. Through the indoor experiment of stress sensitivity of the microfracture core, the stress sensitivity was evaluated as medium to strong, but the pressure-sensitive model was not given (Hai Yong et al., 2015).

Nonlinear Seepage

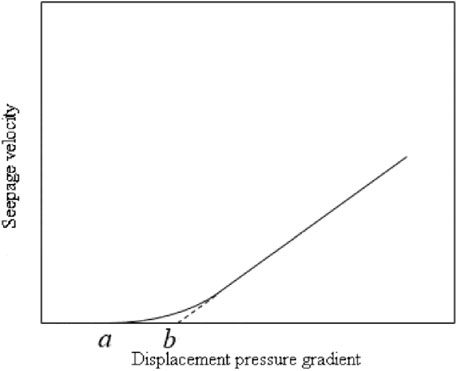
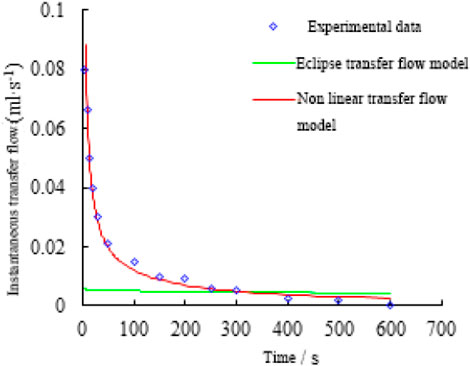
In the study of nonlinear seepage equations in tight reservoirs, Yanzhang Huang proposed a boundary layer theory that when the fluid flowed in micro- and nano-pore throats, there existed both bulk phase layers and boundary layers. When the driving pressure difference was low, the fluid in the boundary layer did not flow. With the gradual increase in pressure difference, the thickness of the boundary layer gradually decreased, which was characterized by nonlinear seepage under small pressure difference and linear seepage characteristics under large differential pressure (Shiming, 2019), as shown in Figure 1. In addition, scholars have verified this theory by conducting physical simulation experiments. Through core displacement experiments, Changjun Zhu et al. verified that the smaller the permeability, the greater the proportion of nano-throats in the total pore volume because with the decrease of permeability, the starting pressure gradient increased, the surface tension increased, and the nonlinear seepage became more obvious (Changjun, 2002). Pu Zhang et al. applied experimental methods to study the boundary layer on the seepage pattern and concluded that the smaller the radii of the throats, the greater the influence of the boundary layer on nonlinear seepage (Pu et al., 2008). However, in practical applications, it was difficult to accurately measure the boundary layer thickness by experimental means. Therefore, the seepage equations based on the boundary layer theory were limited in numerical simulation applications. At present, formula $v=-\frac{K}{\mu }\left(\nabla P-D_P\right)$ with pseudo threshold pressure gradient (D_P) is widely used to describe non-Darcy seepage in tight reservoirs. This formula has two problems: the experimentally determined proposed threshold pressure gradient is significantly high and it cannot describe the nonlinear section of low-velocity seepage.

FIGURE 1

FIGURE 1. Relation curve between seepage velocity and displacement pressure gradient.

Nonlinear Transfer Flow

In studying the matrix/fracture transfer flow laws, the most commonly used are Warren and Root and Kazemi formulations. Warren and Root proposed a constant shape factor formulation $\alpha =\frac{4n\left(n+2\right)}{L^2}$. In 1976, Kazemi (Kazemi et al., 1976) applied a finite difference equation to obtain a shape factor expression for each homogeneity in three dimensions $\alpha =4\left(\frac{1}{L_x^2}+\frac{1}{L_y^2}+\frac{1}{L_z^2}\right)$, the transfer flow equation $q=\alpha \left(p_m-p_f\right)$, which was the most commonly used dual-medium transfer flow equation for commercial numerical simulation software.

The matrix/fracture transfer flow laws of tight reservoirs differed from those of conventional sandstone reservoirs. The pressure changes of the matrix/fracture system were unsteady and affected by the pressure-sensitive effect, as shown in Figure 2.

FIGURE 2

FIGURE 2. The matrix/fracture transfer flow in the fracturing zone of tight reservoirs.

The pressure-sensitive effect on the transfer flow was mainly reflected in the following two aspects: first, the pore pressure change and permeability loss caused by the production pressure difference change during the development of tight reservoirs affected the matrix/fracture transfer flow. Second, in the process of transfer flow, the average matrix pressure gradually decreased, and the decrease in pore pressure caused permeability loss, thus affecting the instantaneous transfer flow.

Relatively few studies on non-steady-state transfer flow in tight reservoirs were conducted at home and abroad, and the related studies were mainly adopted theoretical studies, lacking experimental verification. In 2007, Yongming He derived the matrix/fracture transfer flow shape factors for one-dimensional, two-dimensional, and three-dimensional cases, considering the effect of the threshold pressure gradient (Yongming et al., 2017), as shown in Eq. 1. However, when establishing the pressure diffusion equation, the seepage equation was quasilinear, which cannot well describe the low-speed non-Darcy seepage stage of tight reservoirs:

$\alpha =\frac{{\pi }^2}{L^2},\alpha =\frac{5.78\pi }{L^2},\alpha =\frac{2.6{\pi }^2}{L^2}.(1)$

In 2014, Weibing Shu et al. developed a matrix/fracture transfer flow model by fitting experimental data on seepage in extra-low-permeability cores and solved for the transfer flow shape factor (Weibing et al., 2014), as shown in Eq. 2. However, they did not consider the initiating fracture gradients and pressure-sensitive effects:

${\alpha }_{xyzt}=\frac{4}{\left(a\nabla p+b+\frac{c}{\nabla p}\right)\left(1-\overline{p_m}\right)}\left(\frac{1}{H_{mx}^2}+\frac{1}{H_{my}^2}+\frac{1}{H_{mz}^2}\right)\frac{\partial \overline{p_m}}{\partial T}.(2)$

In 2018, Shenglai Yang established the matrix pressure diffusion equation considering the pressure-sensitive effect in tight reservoirs and applied the Boltzmann transformation to solve the transfer flow shape factor (Kazemi and Gilman, 1993), as follows:

$\alpha =\frac{L^2{\varphi }_{\text{m}}^2{\mu }^2{c}_{\text{t}}^2}{18a{k}_m^2\left({\overline{p}}_{\text{m}}-p_{\text{f}}\right)}\frac{1}{t^2}.(3)$

However, there were still some limitations in its conditions of use. First, a simple exponential pressure-sensitive model was used, which cannot be extended to different types of tight reservoirs. Second, a linear seepage equation was used to establish the matrix pressure diffusion equation, which cannot characterize the non-steady-state pressure diffusion characteristics in the fracturing process and the influence of the threshold pressure gradient.

Through the above research, different scholars have studied the dual medium matrix/fracture transfer flow law and influencing factors from multiple perspectives. However, most of the research results were only applicable to conventional sandstone reservoirs, while not to tight reservoirs with nonlinear seepage characteristics and pressure-sensitive effects.

Numerical Simulation of Tight Reservoirs

In the theoretical research of tight reservoir numerical simulation, Pingliang Fang et al. considered the evolution laws of matrix elastic shrinkage, fracture initiation and closure, and fracture and extension in the fracturing process and production process and established the multi-media dynamic change mechanical mechanism and fluid-solid coupling mathematical model of tight sandstone reservoirs (Pingliang et al., 2017b). Aiming at the problem of repeated fracturing in tight reservoirs, Kang Ma et al. established a two-dimensional two-phase nonlinear seepage mathematical model using the discrete main fracture treatment method (Kang et al., 2015). Dongling Yang established a three-dimensional three-phase seepage mathematical model of fractured reservoirs and developed a numerical simulator using the full implicit solution method. Both the seepage equation and matrix/fracture seepage equation are linear (Dongling, 2014). Based on the nonlinear seepage theory, Lu Li established the nonlinear mathematical model of tight reservoirs by considering the end effect of capillary force, steady matrix/fracture transfer flow, and tight reservoir imbibition (Lu, 2020). Considering the start-up pressure gradient, pressure-sensitive effect, and imbibition of tight reservoirs, Hong Li established a linear seepage model and developed a tight reservoir numerical simulator (Hong, 2015). Based on the experimental data, Rongze Yu and Huaqiang Zhang established the nonlinear seepage equation and the three-dimensional three-phase nonlinear seepage mathematical model of ultra-low permeability reservoirs (Rongze et al., 2012). Yueli Feng considered the pressure-sensitive equation of fracture directionality, established the mathematical model of oil, gas, and water three-phase seepage, considering the pressure-sensitive effect of fractures in different directions, and studied the influence of fracture angle and pressure-sensitive effect on development effect through numerical simulation (Yueli, 2019). Using the analytical solution method and effective numerical calculation method for solving the moving boundary problem in heat transfer, Wenchao Liu conducted accurate numerical simulation research on single-phase or oil, gas, and water three-phase nonlinear seepage in low permeability reservoirs based on the quasilinear motion equation and nonlinear motion equation (Wenchao, 2013). However, the above model had no substantive breakthrough in considering the pressure-sensitive effect, nonlinear seepage, and unsteady matrix/fracture transfer flow.

Based on the above investigation, the commercial numerical simulation software had some defects in simulating tight reservoirs. First, the mathematical model was generally derived based on the Darcy seepage equation, which cannot characterize the nonlinear seepage characteristics of a tight reservoir matrix. Second, the pressure-sensitive model was only a simple exponential function that could not be applied to different types of tight reservoirs. Thirdly, the dual medium steady-state transfer flow model proposed by Warren and Root could not characterize the unsteady transfer flow law of matrix/fracture in tight reservoirs. Therefore, the matrix/microfracture/main fracture triple medium mathematical model of tight reservoir fracturing development considering the pressure-sensitive effect, nonlinear seepage, and nonlinear channeling flow was established. Herein, the discrete mathematical model based on the full implicit solution method was constructed, and the special numerical simulation software suitable for tight reservoirs was developed. This laid a foundation for guiding the large-scale and efficient development of tight reservoirs.

Establishment of Mathematical Model

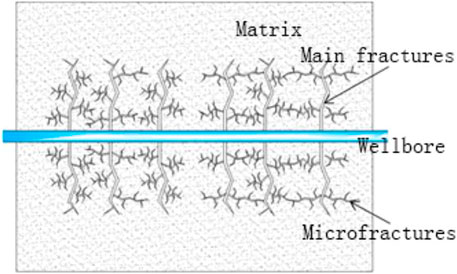
In the field of numerical simulation theory of tight reservoirs, scholars generally believe that there are three media of matrix, microfractures, and main fractures in tight reservoirs, as shown in Figure 3. Considering the influence of the pressure-sensitive effect on the seepage characteristics of different media and the nonlinear characteristics of matrix seepage and matrix/fracture transfer flow, a triple media coupling mathematical model was established in this study.

FIGURE 3

FIGURE 3. The schematic diagram of multi-media in the artificial fracturing zone.

Characterization of Pressure-Sensitive Effect

In 2020, Kai Liu and Dayin Yin et al. established a theoretical model of the pressure-sensitive effect applicable to different tight reservoirs through theoretical analysis based on experimental data (Kai et al., 2020a), as shown in Eq. 6. The specific idea is to determine the relationship between permeability and pore structure parameters (pore radii and throat radii) based on the Kozeny–Carman equation. Based on the Hertz contact deformation theory, the relationship between pore radii and effective stress was determined. Combined with microscopic experiments, the relationship between throat radii and effective stress was determined. Substituting the relationship between pore radii and throat radii into the permeability expression, the calculation formula of matrix pressure-sensitive effect was obtained:

$k=\{\begin{array}{c}\frac{n\pi r_p^4{\delta }^4{\left\{\frac{4b^2\sin \left[\frac{\pi }{2}-\frac{\pi }{6}\ln \left(\frac{\sigma }{{\sigma }_0}\right)\right]-\left(\pi -4\arctan \frac{a}{b}\right)R^2-4ab}{4R^2-\pi R^2}\right\}}^2\cdot r_t^4{\sigma }^{4\left[-0.8324\ln \left(E\right)+4.9381\right]}}{4\tau \left\{r_p^4{\delta }^4{\left\{\frac{4b^2\sin \left[\frac{\pi }{2}-\frac{\pi }{6}\ln \left(\frac{\sigma }{{\sigma }_0}\right)\right]-\left(\pi -4\arctan \frac{a}{b}\right)R^2-4ab}{4R^2-\pi R^2}\right\}}^2+r_t^4{\sigma }^{4\left[-0.8324\ln \left(E\right)+4.9381\right]}\right\}},{\sigma }_0<\sigma <1.92{\sigma }_0\\ \frac{n\pi r_p^4{\delta }^4{\left[\frac{2\sqrt{3}{b}^2-\left(\pi -6\arctan \frac{a}{b}\right)R^2-6ab}{4R^2-\pi R^2}\right]}^2\cdot r_t^4{\sigma }^{4\left[-0.8324\ln \left(E\right)+4.9381\right]}}{4\tau \left\{r_p^4{\delta }^4{\left[\frac{2\sqrt{3}{b}^2-\left(\pi -6\arctan \frac{a}{b}\right)R^2-6ab}{4R^2-\pi R^2}\right]}^2+r_t^4{\sigma }^{4\left[-0.8324\ln \left(E\right)+4.9381\right]}\right\}},\sigma \ge 1.92{\sigma }_0\end{array}(4)$

After simplifying the experimental data of rock physical properties of tight reservoirs in Jiyang depression, the formula can be written as

$k=k_{\text{m0}}{e}^{-\left[0.6535{\alpha }_{k_{\text{m0}}}+0.3465{\alpha }_{\text{E}}\right]\left(p_{\text{m}}^n-p_{\text{m0}}\right)}.(5)$

${\xi }_{\text{m}}\left(p_{\text{m}}\right)$ could be calculated as the following equation:

${\xi }_{\text{m}}\left(p_{\text{m}}\right)=\frac{k}{k_{\text{m0}}}=e^{-\left[0.6535{\alpha }_{k_{\text{m0}}}+0.3465{\alpha }_{\text{E}}\right]\left(p_{\text{m}}^n-p_{\text{m0}}\right)}.(6)$

In 2020, Kai Liu, Daiyin Yin, and others established an empirical model for calculating the pressure-sensitive effect of microfractures based on the pressure-sensitive experiment of microfractures as follows:

$k_{\text{f}}=k_{\text{f0}}{\left(\sigma -{\sigma }_0\right)}^{0.5898-0.1419\ln \left(k_{\text{f0}}+161.35\right)}.(7)$

Nonlinear Seepage Characteristics

In 2019, Fuquan Song deduced the nonlinear seepage equation of the tight reservoirs based on the experimental results of nanotube microseepage and the boundary layer theory:

$\overrightarrow{v}=\frac{K_0{\left(1-e^{-c_{\varphi }\left|\nabla p\right|}\right)}^4}{\mu }\nabla p.(8)$

After Taylor expansion, the higher-order term was ignored, and the pressure-sensitive calculation model Eq. 6 was introduced. Under the pressure-sensitive condition of the tight reservoirs, the nonlinear seepage equation was

$v_{\text{m}}=-\frac{{\xi }_{\text{m}}\left(p_{\text{m}}\right)k_{\text{m0}}}{\mu }\frac{\left(\nabla p_{\text{m}}-G_{\text{R}}\right)}{G_{\text{T}}}\nabla p_{\text{m}}.(9)$

Based on the relative permeability curves, the single-phase seepage equation was extended to three-phase flow, and the general equation of seepage for oil, water, and gas can be written as

$v_{\text{mp}}=-\frac{{\xi }_{\text{m}}\left(p_{\text{mp}}\right)k_{\text{m}}{k}_{\text{mrp}}}{{\mu }_{\text{mp}}}\frac{\left(\nabla p_{\text{m}}-G_{\text{R}}\right)}{G_{\text{T}}}\nabla p_{\text{m}},$(10-a)

${\xi }_{\text{m}}\left(p_{\text{m\_p}}\right)=e^{-\left[0.6535{\alpha }_{k_{\text{m0}}}+0.3465{\alpha }_{\text{E}}\right]\left(p_{\text{m\_p}}^n-p_{\text{m0}}\right)},$(10-b)

Where $p$ is the oil, water, and gas phases and $k_{rp}$ is the relative permeability of the oil, water, and gas phases.

Characterization of Nonlinear Transfer Flow

Kai Liu and Dayin Yin et al. established a single-phase flow matrix/microfracture unsteady transfer flow calculation model by theoretical derivation (Kai et al., 2020b), as shown in Eq. 11. The comparison results of instantaneous transfer flow between the new core transfer flow model and the traditional model are shown in Figure 4.

$q=\{\begin{array}{c}\frac{8\omega mn{\left(18\omega mnT\right)}^{-\frac{4}{3}}}{e^{-\left[0.6535{\alpha }_{k_{\text{m0}}}+0.3465{\alpha }_{\text{E}}\right]\left(S-p\right)}}\frac{K}{\mu }\left(\frac{1}{L_{\text{x}}^2}+\frac{1}{L_{\text{y}}^2}+\frac{1}{L_{\text{z}}^2}\right)\left({\overline{p}}_{\text{m}}-p_{\text{f}}-\frac{G_{\text{R}}L}{2}\right),T<{\left(18\omega mn\right)}^{-1}\\ \frac{8n^2\left(m-n\right)e^{3nT-\frac{1}{6\omega m}}{\left(m-n-m{e}^{3nT-\frac{1}{6\omega m}}\right)}^{-2}}{e^{-\left[0.6535{\alpha }_{k_{\text{m0}}}+0.3465{\alpha }_{\text{E}}\right]\left(S-p\right)}}\frac{K}{\mu }\left(\frac{1}{L_{\text{x}}^2}+\frac{1}{L_{\text{y}}^2}+\frac{1}{L_{\text{z}}^2}\right)\left({\overline{p}}_{\text{m}}-p_{\text{f}}-\frac{G_{\text{R}}L}{2}\right),T\ge {\left(18\omega mn\right)}^{-1}\end{array}.(11)$

FIGURE 4

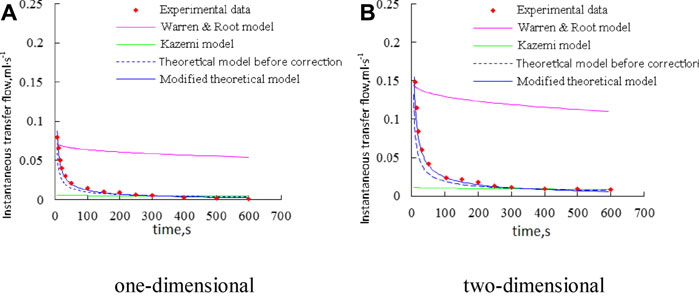
FIGURE 4. Comparison of the results of the new model of transfer flow with the conventional model of instantaneous transfer flow in #5–12 core.

The results of the comparison between the new transfer flow model and the conventional model showed the following: 1) the average error of the 1D and 2D instantaneous transfer flow calculation of the modified transfer flow theory model was 6.6 and 7.8%, which was more than double the accuracy of the classical Warren and Root model and 26.5% higher than that of the Kazemi model. 2) The transfer flow calculation results of the conventional Warren and Root model were always large. The reason for this was that, on the one hand, the transfer flow equation was based on the Darcy seepage, which did not consider the influence of the threshold pressure of the tight reservoirs, and the pressure difference was large. On the other hand, the derivation of this model was mainly used in well-testing theory, and the stage of the well-testing interpretation was usually the stage of pressure recovery instability, so the given empirical equation of the transfer flow equation exaggerates the elastic energy. 3) The transfer flow calculation result of the Kazemi model was low in the early stage and high in the late stage, which was because the transfer flow equation was based on the stable seepage theory, the effects of the tight reservoirs threshold pressure and elastic energy were not considered.

The new transfer flow model was derived based on the nonlinear seepage equation, which considered the threshold pressure and pressure-sensitive effects on the tight reservoirs and was applicable to the study of matrix/fracture transfer flow in the tight reservoirs. In contrast, the conventional Warren and Root model and Kazemi model were derived based on the steady seepage theory and applied to conventional sandstone reservoirs while the application to the tight reservoirs had some limitations.

Mass Conservation Equation

Herein, three-dimensional three-phase mass conservation equations of matrix, microfractures, and main fractures were established by considering the matrix pressure-sensitive effect, microfracture pressure-sensitive effect, matrix nonlinear seepage characteristics, and matrix/fracture nonlinear transfer flow in fracturing development of tight reservoirs.

The matrix mass conservation equation are as follows:

Oil phase:

$\frac{\partial }{\partial t}{\left(\frac{\varphi {\rho }_{\text{o}}{S}_{\text{m\_o}}}{B_{\text{o}}}\right)}_{\text{m}}=\nabla \cdot v_{\text{mo}}-q_{\text{mf\_o}}.$(12-a)

Water phase:

$\frac{\partial }{\partial t}{\left(\frac{\varphi {\rho }_{\text{o}}{S}_{\text{m\_w}}}{B_{\text{w}}}\right)}_{\text{m}}=\nabla \cdot v_{\text{mo}}-q_{\text{mf\_w}}.$(12-b)

Gas phase:

$\frac{\partial }{\partial \text{t}}{\left(\frac{\varphi {\rho }_{\text{g}}{S}_{\text{m\_g}}}{B_{\text{g}}}\right)}_{\text{m}}+R_s\cdot \frac{\partial }{\partial \text{t}}{\left(\frac{\varphi {\rho }_{\text{o}}{S}_{\text{m\_o}}}{B_{\text{o}}}\right)}_{\text{m}}=\nabla \cdot v_{\text{mo}}+R_s\cdot \nabla \cdot v_{\text{mo}}-q_{\text{mf\_g}}-R_{\text{s}}\cdot q_{\text{mf\_o}}.$(12-c)

${\varphi }_m$ is matrix porosity; ${\gamma }_o$, ${\gamma }_w$, ${\gamma }_g$ are the gravity coefficients of the oil, water, and gas phases; D is the depth calculated from a datum, downward is positive, m; $S_{m\_o}$, $S_{m\_w}$, $S_{m\_g}$ are the saturation of the oil, water, and gas phases in a matrix; $T_{m\_o}$, $T_{m\_w}$, $T_{m\_g}$ are the conductivities of the oil, water, and gas phases flowing from reservoir grid i to adjacent reservoir grid i + 1; and R_s is dissolved gas–oil ratio.

The conservation equation of microfractures mass is as follows:

Oil phase:

$\frac{\partial }{\partial t}{\left(\frac{\varphi {\rho }_{\text{o}}{S}_{\text{f\_o}}}{B_{\text{f\_o}}}\right)}_{\text{f}}=\nabla \cdot v_{\text{fo}}+q_{\text{mf\_o}}-q_{\text{fF\_o}}.$(13-a)

Water phase:

$\frac{\partial }{\partial t}{\left(\frac{\varphi {\rho }_{\text{w}}{S}_{\text{f\_w}}}{B_{\text{f\_w}}}\right)}_{\text{f}}=\nabla \cdot v_{\text{fw}}+q_{\text{mf\_w}}-q_{\text{fF\_w}}.$(13-b)

Gas phase:

$\begin{array}{l}\frac{\partial }{\partial \text{t}}{\left(\frac{\varphi {\rho }_{\text{g}}{\text{S}}_{\text{f\_g}}}{{\text{B}}_{\text{f\_g}}}\right)}_{\text{f}}+R_s\cdot \frac{\partial }{\partial \text{t}}{\left(\frac{{\varphi }_{\text{f}}{\rho }_{\text{o}}{\text{S}}_{\text{f\_o}}}{{\text{B}}_{\text{f\_o}}}\right)}_{\text{f}}=\nabla \cdot v_{\text{fg}}+\\ R_{\text{s}}\cdot \nabla \cdot v_{\text{fo}}+q_{\text{mf\_g}}-q_{\text{fF\_g}}+R_s\cdot q_{\text{mf\_o}}-R_s\cdot q_{\text{fF\_o}}\end{array}.$(13-c)

${\varphi }_f$ is the microfracture porosity; $q_{fF\_o}$, $q_{fF\_w}$, $q_{fF\_g}$ are volume transfer flows of the oil, water, and gas phases between microfractures and main fractures, m³/s; $S_{f\_o},S_{f\_w},S_{f\_g}$ are the saturation of the oil, water, and gas phases in microfractures; $T_{f\_o},T_{f\_w},T_{f\_g}$ are the conductivities of the oil, water, and gas phases flowing from microfracture grid i to adjacent grid i + 1 in the microfracture.

The mass conservation equation of main fractures are as follows:

Oil phase:

$\frac{\partial }{\partial t}{\left(\frac{\varphi {\rho }_{\text{o}}{S}_{\text{F\_o}}}{B_{\text{F\_o}}}\right)}_{\text{F}}=\nabla \cdot v_{\text{Fo}}+q_{\text{fF\_o}}-q_{\text{FW\_o}}.$(14-a)

Water phase:

$\frac{\partial }{\partial t}{\left(\frac{\varphi {\rho }_{\text{w}}{S}_{\text{F\_w}}}{B_{\text{F\_w}}}\right)}_{\text{F}}=\nabla {\cdot }_{\text{Fw}}+q_{\text{fF\_w}}-q_{\text{FW\_w}}.$(14-b)

Gas phase:

$\begin{array}{l}\frac{\partial }{\partial t}{\left(\frac{\varphi {\rho }_{\text{g}}{S}_{\text{F\_g}}}{B_{\text{F\_g}}}\right)}_{\text{F}}+R_s\cdot \frac{\partial }{\partial t}{\left(\frac{\varphi {\rho }_{\text{o}}{S}_{\text{F\_o}}}{B_{\text{F\_o}}}\right)}_{\text{F}}=\nabla \cdot v_{\text{Fg}}\\ +R_{\text{s}}\cdot \nabla \cdot v_{\text{Fo}}+q_{\text{fF\_g}}-{\tau }_{\text{Fw\_g}}+R_{\text{s}}\cdot {\tau }_{\text{fF\_o}}-R_{\text{s}}\cdot q_{\text{Fw\_o}}\end{array}.$(14-c)

${\varphi }_F$ is main fracture porosity; $S_{F\_o},S_{F\_w},S_{F\_g}$ are the saturation of the oil, water, and gas phases in the main fractures; $q_{\text{FW}\_o},q_{\text{FW}\_w},q_{\text{FW}\_g}$ are volume flows of the water, oil, and gas phases from the main fractures to horizontal wellbores per unit time, m³/s; $T_{F\_o},T_{F\_w},T_{F\_g}$ are the conductivities of the oil, water, and gas phases flowing from fracture grid i to adjacent fracture grid i + 1 in the main fracture. All fracture grids have flow exchange with adjacent microfracture grids on both sides, and only the main fracture grid passing through the horizontal wellbore has a flow term of$q_{\text{FW}\_o},q_{\text{FW}\_w},q_{\text{FW}\_g}$ , and the transfer flow terms of other fracture grids are zero.

Mathematical Model Solution

There are two kinds of numerical methods for solving multiphase seepage problems: one is the implicit pressure explicit saturation method (IMPES method) and the other is the simultaneous method; that is, by solving simultaneous equations, each independent variable is solved at the same time. When using the IMPES method, the calculation is small and the form is simple. However, for the multi-media numerical simulation of tight reservoirs, the variable permeability coefficient, and pressure are coupled in the seepage equation, and the convergence of the model is poor. The fully implicit simultaneous solution method with high stability and better convergence is adopted in this study.

Fully Implicit Simultaneous Solution Method

The fully implicit simultaneous solution method requires multiple iterations at each time step to solve the multiple coefficient matrix. Through the implicit difference of the mathematical model, the nonlinear difference equations of matrix, microfractures main fractures, and horizontal wellbores were established. After linearization by the fully implicit method, the general expression of the coefficient matrix of each iterative step in each time step was obtained, and the discretization of the multi-media mathematical model was completed:

Oil phase:

$\frac{V_{ijk}}{\Delta t}\left[{\left({\varphi }_{\text{m}}{\rho }_{\text{o}}{S}_{\text{m\_o}}\right)}^{n+1}-{\left({\varphi }_{\text{m}}{\rho }_{\text{o}}{S}_{\text{m\_o}}\right)}^n\right]=\Delta T_{\text{m\_o}}^{n+1}\Delta p_{\text{m\_o}}^{n+1}-\Delta T_{\text{m\_o}}^{n+1}{\gamma }_{\text{og}}\Delta D-\left(\Delta T_{\text{mf\_o}}^{n+1}\Delta p_{\text{m\_o}}^{n+1}-\Delta T_{\text{mf\_o}}^{n+1}{p}_{\text{f\_o}}^{n+1}\right).$(15-a)

Water phase:

$\begin{array}{l}\frac{V_{ijk}}{\Delta t}\left[{\left({\varphi }_{\text{m}}{\rho }_{\text{w}}{S}_{\text{m\_w}}\right)}^{n+1}-{\left({\varphi }_{\text{m}}{\rho }_{\text{w}}{S}_{\text{m\_w}}\right)}^n\right]=\Delta T_{\text{m\_w}}^{n+1}\left(\Delta p_{\text{m\_o}}^{n+1}-\Delta p_{\text{m\_cow}}^{n+1}\right)-\Delta T_{\text{m\_w}}^{n+1}{\gamma }_{\text{w}}\Delta D\\ -\left[\Delta T_{\text{mf\_w}}^{n+1}\left(\Delta p_{\text{m\_o}}^{n+1}-\Delta p_{\text{m\_cow}}^{n+1}\right)-\Delta T_{\text{mf\_w}}^{n+1}\left(\Delta p_{\text{f\_o}}^{n+1}-\Delta p_{\text{f\_cow}}^{n+1}\right)\right]\end{array}.$(15-b)

Gas phase:

$\begin{array}{l}\frac{V_{ijk}}{\Delta t}\left\{\left[{\left({\varphi }_{\text{m}}{\rho }_{\text{g}}{S}_{\text{m\_g}}\right)}^{n+1}-{\left({\varphi }_{\text{m}}{\rho }_{\text{g}}{S}_{\text{m\_g}}\right)}^n\right]+R_{\text{s}}\left[{\left({\varphi }_{\text{m}}{\rho }_{\text{o}}{S}_{\text{m\_o}}\right)}^{n+1}-{\left({\varphi }_{\text{m}}{\rho }_{\text{o}}{S}_{\text{m\_o}}\right)}^n\right]\right\}=\\ \Delta T_{\text{m\_g}}^{n+1}\left(\Delta p_{\text{m\_cgo}}^{n+1}-\Delta p_{\text{m\_o}}^{n+1}\right)-\Delta T_{\text{m\_g}}^{n+1}{\gamma }_{\text{g}}\Delta D+R_{\text{s}}\left(\Delta T_{\text{m\_o}}^{n+1}\Delta p_{\text{m\_o}}^{n+1}-\Delta T_{\text{m\_o}}^{n+1}{\gamma }_{\text{og}}\Delta D\right)\\ -\left[\Delta T_{\text{mf\_g}}^{n+1}\left(\Delta p_{\text{m\_cgo}}^{n+1}-\Delta p_{\text{m\_o}}^{n+1}\right)-\Delta T_{\text{mf\_g}}^{n+1}{p}_{\text{f\_g}}^{n+1}\right]-R_{\text{s}}\left(\Delta T_{\text{mf\_o}}^{n+1}\Delta p_{\text{m\_o}}^{n+1}-\Delta T_{\text{mf\_o}}^{n+1}{p}_{\text{f\_o}}^{n+1}\right)\end{array}.$(15-c)

In the formula, both the change of conductivity $\Delta T^{n+1}$ and the change of pressure $\Delta p^{n+1}$ are the solution variables at n + 1 time. There are two terms of product at the left end of the equation, which is nonlinear. In order to realize the solvability of the equation, the equation needs to be linearized and expanded. When the fully implicit method is used to solve the equations, each time step needs to go through a series of iterations.

Quick Solution Method

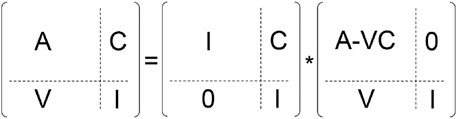
At present, the calculation method embedded in three-dimensional three-phase numerical simulation software is usually the ESPIDO algorithm. When dealing with the edge matrix, this method adopts the method of matrix conversion of the edge matrix and eliminates the edge elements to solve the problems of solving the edge matrix. The specific matrix elimination method is shown in Figure 5.

FIGURE 5

FIGURE 5. The schematic diagram of the ESPIDO algorithm for dealing with the bordered problem.

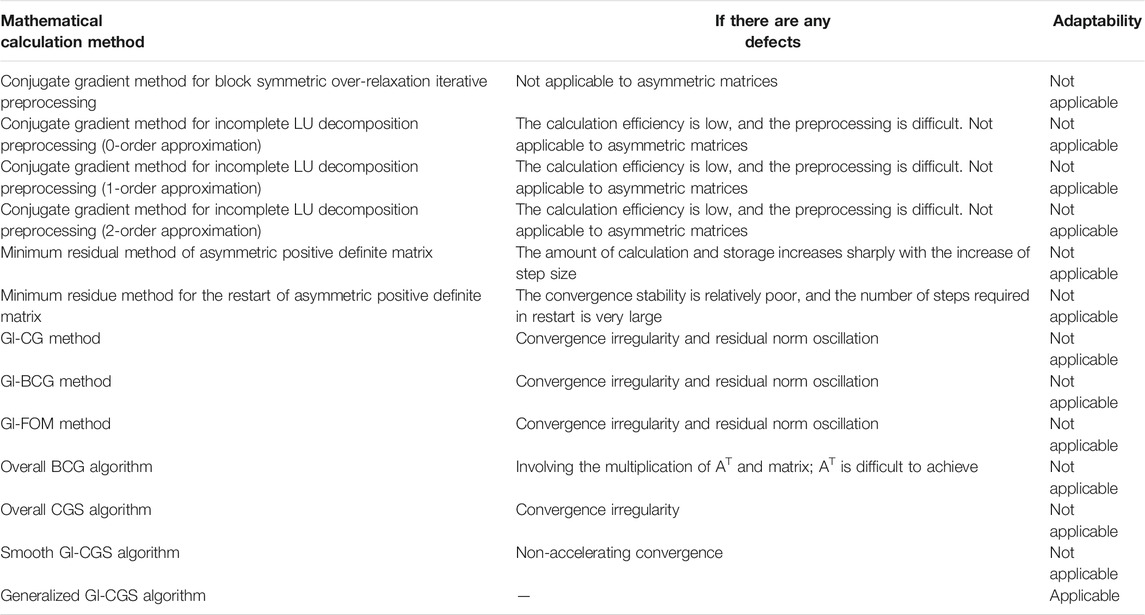
It can be seen from Figure 5 that this method of dealing with the edge matrix largely depends on whether the matrix in the lower right corner can be converted into a unit matrix. This transformation form will not bring much trouble when dealing with the traditional edging problems (such as implicit bottom hole pressure problem and double hole single permeability problem). However, it is prone to the problem of non-convergence or small convergence radius when facing the problem of multiple medium coupling. By investigating the commonly used large sparse matrix solution methods (Jianhua, 2007; Jianhua and Hua, 2008), the advantages and disadvantages of different algorithms were determined, and the adaptability of different algorithms to the solution of multi-media coupling model of tight reservoirs was evaluated, as shown in Table 1.

TABLE 1

TABLE 1. The adaptability analysis of the different matrix solving methods.

Considering the calculation workload, convergence stability, residual norm, and convergence speed, the generalized Gl-CGS algorithm with strong applicability was the generalized global conjugate gradient square algorithm (Zhongxiao, 1998).

Application of the Mathematical Model

Herein, new numerical simulation software for tight reservoirs was applied to study the tight reservoirs in Wang 587 Block of NiuZhuang oilfield in Jiyang Depression of Bohai Bay Basin. Firstly, the calculation accuracies of the development index of the new software and the commercial Eclipse software were compared. Then, the reasonable development policy was optimized for the problems of low liquid production and poor reservoir production effect in the Wang 587 block, which provided a theoretical basis and scheme guidance for the development scheme design of tight reservoirs in turbidites in other blocks.

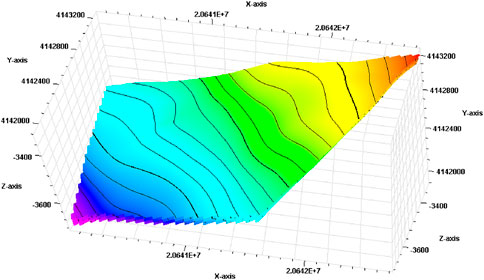
Based on the seismic data, logging data, and laying data of Wang 587 Block, fine geological modeling was carried out, including the structural model, sedimentary facies model, and property model. The top structure diagram of the No. 3 sand formation, member 4 of Shahejie Formation in Wang 587 Block, is shown in Figure 6.

FIGURE 6

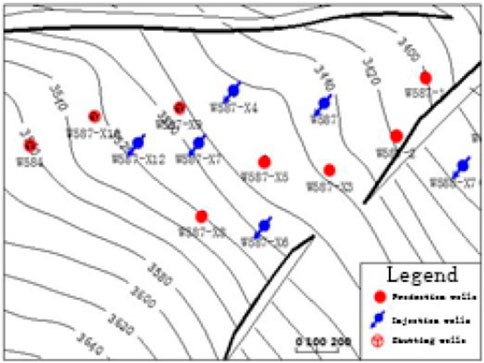
FIGURE 6. The top structure diagram of the No. 3 sand formation, member 4 of Shahejie Formation in the Wang 587 Block.

The structural model: the maximum principal stress direction in this block is NE72°. In order to facilitate the design of compression crack and avoid grid effects, the grid was divided along the principal stress direction with a plane grid step of 20 × 20 m. Vertically, taking the single sand body as the unit, the internal subdivision grid step of the single sand body was 0.2 m, the longitudinal heterogeneity was simulated, and the structure model was established by well control thickness modeling, as shown in Figure 7.

FIGURE 7

FIGURE 7. The structural model of the Wang 587 Block.

The sedimentary facies model: the sedimentary phase can truly reflect the river dynamics and the sedimentary rhythm. Its spreading mode has an important connection with the property distribution, which is an important means to accurately control the non-homogeneous characteristics of various sand bodies. The sedimentary facies model is the basis for establishing the facies-controlled property model. After importing the discrete sedimentary facies data, the sedimentary facies points were processed into sedimentary facies surfaces, and the sedimentary facies surfaces were integrated to establish the sedimentary facies model, as shown in Figure 8.

FIGURE 8

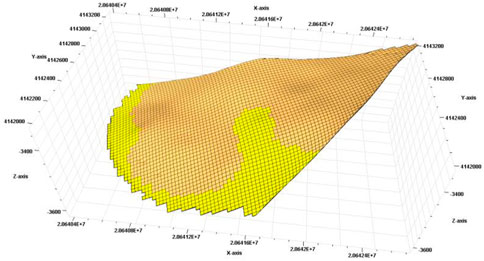
FIGURE 8. The sedimentary facies model of the No. 3 sand formation, No. 3 sublayer, member 4 of Shahejie Formation in the Wang 587 Block.

Facies controlled property model: Wang 587 Block has dense well points and complete logging and layering data, suitable for the deterministic modeling method. The property model of Wang 587 Block was established by using the facies-controlled property modeling method, including the permeability model and oil saturation model, as shown in Figure 9. The property model was calculated based on interpolation of the same sedimentary facies type, considering the superior and inferior characteristics of the sedimentary facies and randomly interpolating within a reasonable range, which preserved the randomness and ensured the reasonableness of the properties.

FIGURE 9

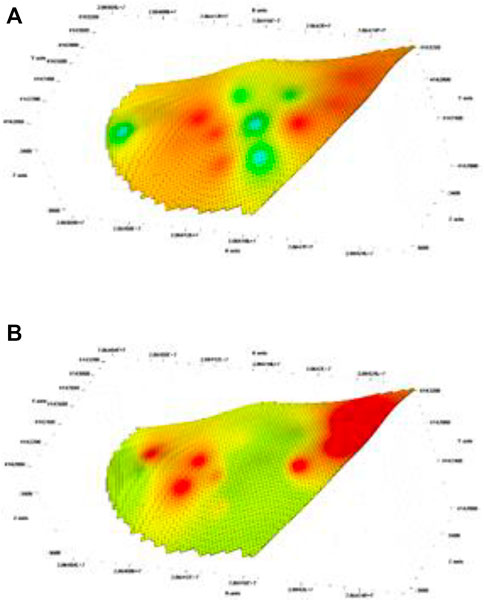
FIGURE 9. The property models of the No. 3 sand formation, No. 3 sublayer, member 4 of Shahejie Formation in the Wang 587 Block [(A) permeability; (B) oil saturation].

Compared with the Eclipse model, the applicability of the nonlinear seepage coupling model to tight reservoirs was mainly reflected in the calculation accuracy of oil production in the initial stage of development. Herein, the Wang 587 Block numerical simulation model was established using different software. Based on the actual development data of the single well, the accuracy of the calculation results of the new model and Eclipse numerical simulation was verified. The reasons for the difference in calculation results were analyzed.

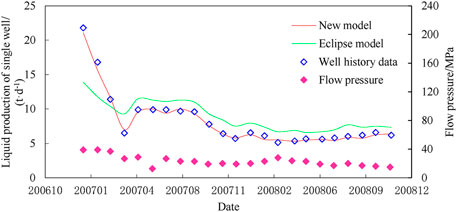
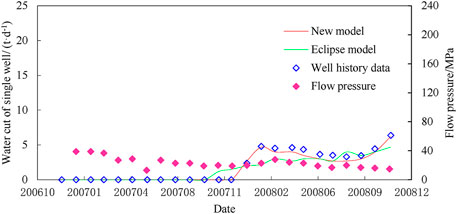
The Petrel property model was coarsened and imported into the structural module of the numerical simulation. The numerical simulation model of Wang 587 Block was established using the new numerical simulation software and commercial software Eclipse. Two working systems were mainly used for numerical simulation: constant liquid production and constant pressure production. During constant liquid production, if the liquid production was lower than the set liquid production, the bottom hole flowing pressure in the software would automatically decrease until the standard atmospheric pressure was 0.1 MPa. Thus, there would be the phenomenon that the calculated liquid production was consistent with the actual flow pressure, but the bottom hole flowing pressure was lower than the actual flow pressure. Moreover, there would be the phenomenon that the calculated liquid production was lower than the actual liquid production, and the bottom hole flowing pressure was reduced to 0.1 MPa. The accuracy of bottom hole flowing pressure can be ensured during the production of constant bottom hole flowing pressure. On this basis, the calculated and actual liquid production can be compared to achieve the purpose of controlling variables. Therefore, the working system of constant bottom hole flowing pressure in this article was adopted to predict the development indicators. Taking the actual initial development data of well W587-X3 as an example, the calculation effects of liquid production, water cut, and oil production were compared, as shown in Figures 10–12.

FIGURE 10

FIGURE 10. The liquid production comparison results of the well W587-X3.

FIGURE 11

FIGURE 11. The water cut comparison results of the well W587-X3.

FIGURE 12

FIGURE 12. The oil production comparison results of the well W587-X3.

The oil production validation results of different models showed that ① the calculation accuracy of the nonlinear seepage coupling model was 95.6%, which was in high agreement with the reality. While the average fitting rate of the Eclipse model was only 82.3%, especially in the early elastic development stage, the calculation error was as high as 34.1%. ② The low initial fluid production results and high late fluid production results calculated in the Eclipse software were because oil production from fracturing development in tight reservoirs was mainly influenced by the matrix/microfracture transfer flow, as shown in Figure 13. The transfer flow quantity of the transfer flow model used in the nonlinear seepage coupling was large at the initial stage but decreased rapidly. After entering the pseudo-steady flowing period, the transfer flow was small, which was highly consistent with the actual transfer flow. The calculation results of the steady-state transfer flow model used in Eclipse were lower in the early stage and higher in the late stage because the influence of elasticity was not considered in the early stage and the liquid production was low. The influence of threshold pressure gradient was not considered in the late stage, which exaggerated the production pressure difference and high liquid production. Generally speaking, the Eclipse model cannot simulate the phenomenon of large production decline in the early stage of tight reservoir development, and the calculation error of liquid production was large after entering the quasi-stable period.

FIGURE 13

FIGURE 13. The validation results of different transfer flow models.

The validation results of different models for fluid production and water cut showed that the nonlinear seepage coupling was consistent with the actual tight reservoir development state due to the consideration of the threshold pressure gradient, pressure-sensitive effect, and matrix/microfracture unsteady transfer flow. Moreover, the application of nonlinear seepage coupling numerical simulation software to optimize the development scheme was highly credible.

Conclusion

(1) The multi-media coupling seepage mathematical model of matrix/microfracture/main fracture for fracturing development of tight reservoirs was established. The effects of nonlinear seepage, threshold pressure gradient, pressure-sensitive effect, and matrix/fracture nonlinear transfer flow were considered, which can fully reflect the fracturing development characteristics of tight reservoirs.

(2) Based on the fully implicit simultaneous solution, the multi-media coupling discrete mathematical model was constructed, and the fast solution algorithm of the generalized global conjugate gradient was optimized, which provided theoretical support for the development of tight reservoir numerical simulation software.

(3) The model application effect of tight reservoirs in Block Wang 587 showed that the fitting accuracy of the new tight reservoir numerical simulation software was as high as 95.6%, which was 13.3% higher than that of Eclipse software, and the reliability of using the new numerical simulation software to optimize the tight reservoir development scheme was higher.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author Contributions

DY: conceptualization and methodology. CL: writing, review, and editing. SS: data curation and original draft preparation. KL: visualization and investigation.

Funding

This work was funded by the Ministry of Science and Technology of the People’s Republic of China, and the name of the project is “Demonstration Project for the Development of Dense Oil in Jiyang Depression, Bohai Bay Basin (2017ZX05072)”, of which National Science and Technology are major special projects.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

Thanks to the contributions of colleagues and institutions who assisted in this work.

References

Bin, L., Hanqiao, J., Junjian, L., Changcheng, G., Ruyi, J., and Yanli, P. (2016). Flow in Multi-Scale Discrete Fracture Networks with Stress Sensitivity. J. Nat. Gas Sci. Eng. 35, 851–859. doi:10.1016/j.jngse.2016.09.025

CrossRef Full Text | Google Scholar

Caineng, Z., Rukai, Z., Songtao, W., Zhi, Y., Shizhen, T., Xuanjun, Y., et al. (2012). Types, Characteristics, Mechanism and Prospect of Conventional and Unconventional Oil and Gas Accumulation -- Taking Tight Oil and Tight Gas in China as an Example. Acta Petrol. Sin. 33 (02), 173–187.

Google Scholar

Caineng, Z., Guosheng, Z., Zhi, Y., Shizhen, T., Lianhua, H., Rukai, Z., et al. (2013). Concept, Characteristics, Potential and Technology of Unconventional Oil and Gas -- Also on Unconventional Oil and Gas Geology. Pet. Explor. Develop. 40 (04), 385–399+454.

Google Scholar

Changjun, Z. (2002). Experimental Study and Mathematical Description of Non-darcy Seepage. Langfang City, China: Graduate School of Chinese Academy of Sciences Institute of seepage hydrodynamics.

Google Scholar

Chengzao, J., Min, z., and Yongfeng, Z. (2012). Unconventional Oil and Gas Resources and Exploration and Development Prospects in China. Pet. Exploration Develop. 39 (02), 129–136. doi:10.1016/s1876-3804(12)60026-3

CrossRef Full Text | Google Scholar

Chengzao, J., Caineng, Z., Jianzhong, L., Denghua, L., and Min, Z. (2012). Evaluation Criteria, Main Types, Basic Characteristics and Resource Prospects of Tight Oil in China. Acta Petrolei Sinica 33 (03), 343–350.

Google Scholar

Clarkson, C., Solano, N., Bustin, R. M., Bustin, A. M. M., Chalmers, G. R. L., He, L., et al. (2013). Pore Structure Characterization of North American Shale Gas Reservoirs Using USANS/SANS, Gas Adsorption, and Mercury Intrusion. Fuel 103, 606–616. doi:10.1016/j.fuel.2012.06.119

CrossRef Full Text | Google Scholar

David, C., Wong, T, F., Zhu, W., and Zhang, J. (1994). Laboratory Measurement of Compaction-Induced Permeability Change in Porous Rocks: Implications for the Generation and Maintenance of Pore Pressure Excess in the Crust. Pure Appl. Geophys. 143 (1), 425–456. doi:10.1007/bf00874337

CrossRef Full Text | Google Scholar

Dong, J.-J., Hsu, J.-Y., Wu, W.-J., Shimamoto, T., Hung, J.-H., Yeh, E.-C., et al. (2010). Stress-dependence of the Permeability and Porosity of sandstone and Shale from TCDP Hole-A. Int. J. Rock Mech. Mining Sci. 47 (7), 1141–1157. doi:10.1016/j.ijrmms.2010.06.019

CrossRef Full Text | Google Scholar

Dongling, Y. (2014). Study on Three-Dimensional Three-phase Numerical Simulation of Natural Fractured Reservoir. Chengdu City, China: Southwest Petroleum University.

Google Scholar

Fraser-Harris, A. P., McDermott, C. I., Couples, G. D., Edlmann, K., Lightbody, A., Cartwright‐Taylor, A., et al. (2020). Experimental Investigation of Hydraulic Fracturing and Stress Sensitivity of Fracture Permeability under Changing Polyaxial Stress Conditions. J. Geophys. Res. Solid Earth 125 (13), 1–30. doi:10.1029/2020jb020044

CrossRef Full Text | Google Scholar

Fuxi, H., Tao, Y., Weipeng, Y., Bincheng, G., Hui, T., Xin, L., et al. (2014). Analysis on Main Controlling Factors of Tight Oil Reservoir Performance in China. J. Chengdu Univ. Techn. (Nat. Sci. Ed.) 41 (05), 538–547. doi:10.3969/j.issn.1671-9727.2014.05.02

CrossRef Full Text | Google Scholar

Hai Yong, Z., Shunli, H., Guohua, L., Chengquan, M., Shaoyuan, M., and Hao, L. (2015). Experimental Study on Stress Sensitivity of Micro Fractured Ultra-low Permeability Reservoir. J. Xi'an Pet. Univ. (Nat. Sci. Ed.) 30 (01), 30–33+37+5. doi:10.3969/j.issn.1673-064X.2015.01.005

CrossRef Full Text | Google Scholar

Hao, L., Liu, H., Ruishan, L., Zhenguo, Hu., and Jianhua, He. (2019). Effects of Boundary Layer and Stress Sensitivity on the Performance of Low-Velocity and One-phase Flow in a Shale Oil Reservoir: Experimental and Numerical Modeling Approaches. J. Pet. Sci. Eng. 180, 186–196. doi:10.1016/j.petrol.2019.05.025

CrossRef Full Text | Google Scholar

Holt, R. M. (2005). Stress Sensitivity of Wave Velocities in Shale. SEG Tech. Program Expanded Abstr. 24 (1), 1593–1596. doi:10.1190/1.2147998

CrossRef Full Text | Google Scholar

Hong, L. (2015). Study on Numerical Simulation Method of Tight Reservoir. Beijing: China University of Geosciences.

Google Scholar

Jianhua, Z., and Hua, D. (2008). Global CGS Algorithm for Solving Linear Equations with Multiple Right End Terms. Numer. Maths. A J. Chin. Univ. 30 (04), 390–399. doi:10.3969/j.issn.1000-081X.2008.04.009

CrossRef Full Text | Google Scholar

Jianhua, Z. (2007). A Class of Matrix Krylov Subspace Methods for Solving Large Sparse Linear Systems. Nanjing City, China: Nanjing University of Aeronautics and Astronautics.

Google Scholar

Jianwei, F., Zhixue, S., Yandong, W., and Jiaofeng, S. (2019). Study on Stress Sensitivity of Ordovician Fractures in Hotianhe Gas Field, Tarim Basin. Geol. J. China Univ. 25 (02), 276–286. doi:10.16108/j.issn1006-7493.2018059

CrossRef Full Text | Google Scholar

Jingang, H., Kaoping, S., Jing, Y., Song, H., Liyan, S., Di, H., et al. (2013). The Effect of the Fracture Surface for Stress Sensitivity in Shale Reservoir. Adv. Mater. Res. 779-780, 1427–1430. doi:10.4028/www.scientific.net/amr.779-780.1427

CrossRef Full Text | Google Scholar

Jones, F. O. (1975). A Laboratory Study of the Effects of Confining Pressure on Fracture Flow and Storage Capacity in Carbonate Rocks. J. Pet. Techn. 27, 21–27. doi:10.2118/4569-pa

CrossRef Full Text | Google Scholar

Kai, L., Daiyin, Y., and Yeheng, S. (2020). The Mathematical Model of Stress Sensitivities on Tight Reservoirs of Different Sedimentary Rocks and its Application. J. Pet. Sci. Eng. 193, 107372. doi:10.1016/j.petrol.2020.107372

CrossRef Full Text | Google Scholar

Kai, L., Daiyin, Y., and Yeheng, S. (2020). Analytical and Experimental Study of Stress Sensitivity Effect on Matrix/fracture Transfer in Fractured Tight Reservoir. J. Pet. Sci. Eng. 195, 107958. doi:10.1016/j.petrol.2020.107958

CrossRef Full Text | Google Scholar

Kang, M., Hanqiao, J., Wenchao, F., Lin, Z., Zhentao, Z., Liang, G., et al. (2015). A Numerical Simulation Model for Multi-Scale Flow in Tight Oil Reservoirs. Pet. Exploration Develop. 29 (04), 128–130+133. doi:10.3969/j.issn.1673-8217.2015.04.039

CrossRef Full Text | Google Scholar

Kazemi, H., and Gilman, J. R. (1993). Multiphase Flow in Fractured Petroleum Reservoirs. Flow and Contaminant Transport in Fractured Rock. Littleton, Colorado, United States: Flow and Contaminant Transport in Fractured Rock, 267–323. doi:10.1016/b978-0-12-083980-3.50010-3

CrossRef Full Text | Google Scholar

Kazemi, H., Merrill, L. S., Porterfield, K. L., and Zeman, P. R. (1976). Numerical Simulation of Water-Oil Flow in Naturally Fractured Reservoirs. Soc. Pet. Eng. J. 16 (06), 317–326. doi:10.2118/5719-pa

CrossRef Full Text | Google Scholar

Lanqing, F. (2016). Influence of Fractures on Stress Sensitivity and Seepage Characteristics of Tight sandstone Reservoir. J. Yangtze Univ. (Nat. Sci. Ed.) 13 (20), 14–18+34. doi:10.16772/j.cnki.1673-1409.2016.20.003

CrossRef Full Text | Google Scholar

Liu, H. H., Chen, H., Han, Y., Eichmann, S. L., and Gupta, A. (2018). On the Relationship between Effective Permeability and Stress for Unconventional Rocks: Analytical Estimates from Laboratory Measurements[J]. J. Nat. Gas Sci. Eng. 56, 408–413. doi:10.1016/j.jngse.2018.06.026

CrossRef Full Text | Google Scholar

Lu, L. (2020). Study on Numerical Simulation Algorithm of Multiphase Flow in Tight Reservoir.Hefei City, China: University of science and technology of China.

Google Scholar

Pingliang, F., Qiquan, R., Binshan, J., Liming, S., and Jie, C. (2017). Fluid Solid Coupling Numerical Simulation of Injection Production Development in Tight sandstone Reservoir. Spec. Oil Gas Reservoirs 24 (03), 76–80. doi:10.3969/j.issn.1006-6535.2017.03.014

CrossRef Full Text | Google Scholar

Pingliang, F., Qiquan, R., and Binshan, J. (2017). Fluid Solid Coupling Numerical Simulation of Fracturing Development in Tight Reservoir. China Mining Mag. 26 (04), 140–145. doi:10.3969/j.issn.1004-4051.2017.04.028

CrossRef Full Text | Google Scholar

Pu, Z., Lianzhong, Z., Wenyao, L., and Yunfeng, W. (2008). Experimental Study on the Influence of Boundary Layer on Low Permeability Non-darcy Seepage Law. J. Hebei Univ. Eng. (Nat. Sci. Ed.) 25 (3), 1–3. doi:10.3969/j.issn.1673-9469.2008.03.020

CrossRef Full Text | Google Scholar

Rongze, Y., Yanan, B., Yang, L., Xiaowei, Z., Jun, Y., Hongchao, W., et al. (2012). Non-Darcy Flow Numerical Simulation of XPJ Low Permeability Reservoir. J. Pet. Sci. Eng. 92-93, 40–47. doi:10.1016/j.petrol.2012.06.006

CrossRef Full Text | Google Scholar

Shiming, Z. (2019). A New Nonlinear Seepage Model of Low Permeability Reservoir Based on Boundary Layer Theory. Pet. Geol. Recovery Effic. 26 (06), 100–106. doi:10.13673/j.cnki.cn37-1359/te.2019.06.013

CrossRef Full Text | Google Scholar

Tian, X., Cheng, L., Cao, R., Wang, Y., Zhao, W., Yan, Y., et al. (2015). A New Approach to Calculate Permeability Stress Sensitivity in Tight sandstone Oil Reservoirs Considering Micro-pore-throat Structure. J. Pet. Sci. Eng. 133, 576–588. doi:10.1016/j.petrol.2015.05.026

CrossRef Full Text | Google Scholar

Wei, T., Ruijian, D., Weiyao, Z., Dianbin, G., Zhongchao, L., Yunqian, L., et al. (2017). Stress Sensitivity of Shale Pressure Fracture Network Reservoir and its Influence on Productivity. Reservoir Eval. Dev. 7 (06), 71–77. doi:10.13809/j.cnki.cn32-1825/te.2017.06.013

CrossRef Full Text | Google Scholar

Weibing, S., Hehua, X., Tangwei, L., and Juying, W. (2014). Study on Unsteady Channeling Factors of Low Permeability Fractured Reservoirs. Chin. J. Theor. Appl. Mech. 46 (01), 70–77. doi:10.6052/0459-1879-13-154

CrossRef Full Text | Google Scholar

Wenchao, L. (2013). Numerical Simulation of Nonlinear Seepage in Low Permeability Reservoir Considering Moving Boundary. East China: China University of Petroleum.

Google Scholar

Xiangrong, N., Junbin, C., and Shaomin, Y. (2018). Experimental Study on Stress Sensitivity Considering Time Effect for Tight Gas Reservoirs. Mechanics 24 (6), 784–789. doi:10.5755/j01.mech.24.6.22462

CrossRef Full Text | Google Scholar

Yang, Y., Liu, Z., Sun, Z., An, S., Zhang, W., Liu, P., et al. (2017). Research on Stress Sensitivity of Fractured Carbonate Reservoirs Based on CT Technology. Energies 10 (11), 1833. doi:10.3390/en10111833

CrossRef Full Text | Google Scholar

Yang, G., Wenlong, D., Min, Y., Jingshou, L., Zikang, X., Baocheng, J., et al. (2018). Study on Pressure Sensitivity of Tight sandstone and its Influence on Reservoir Characteristics. Energy Sourc. A: Recovery, Util. Environ. Effects 40, 2671–2677. doi:10.1080/15567036.2018.1503753

CrossRef Full Text | Google Scholar

Yanlong, Z., Xiaolin, X., and Zhiming, W. (2019). Experimental Study on Stress Sensitivity of Coal Rock Fracture Permeability in Eastern Yunnan and Western Guizhou. Coal Sci. Technol. 47 (08), 213–218. doi:10.13199/j.cnki.cst.2019.08.030

CrossRef Full Text | Google Scholar

Yongfei, Y., Wenjie, Z., Ying, G., Yujin, W., Yunhe, S., Senyou, A., et al. (2016). Influence of Stress Sensitivity on Microscopic Pore Structure and Fluid Flow in Porous media. J. Nat. Gas Sci. Eng. 36, 20–31. doi:10.1016/j.jngse.2016.09.061

CrossRef Full Text | Google Scholar

Yongming, H., Xianchao, C., Yue, Z., and Wei, Y. (2017). Modeling Interporosity Flow Functions and Shape Factors in Low-Permeability Naturally Fractured Reservoir. J. Pet. Sci. Eng. 156, 110–117. doi:10.1016/j.petrol.2017.05.006

CrossRef Full Text | Google Scholar

Yueli, F. (2019). Study on Percolation Mechanism and Development Method of Ultra-low Permeability Fractured Pressure-Sensitive Reservoir. Beijing: China University of Petroleum.

Google Scholar

Zhenglian, P., Caineng, Z., Shizhen, T., Shizhen, T., Zhi, Y., and Songtao, W. (2012). Formation, Distribution and Resource Potential Evaluation of Tight Oil in China. Eng. Sci. 14 (07), 60–67. doi:10.3969/j.issn.1672-7703.2016.03.002

CrossRef Full Text | Google Scholar

Zhongxiang, C., Yu, Z., Pan, C., Youqiang, L., Jianlei, L., and Yuechang, D. (2016). New Achievements and Enlightenment of fine Exploration in Jiyang Depression. China Pet. Explor. 21 (03), 14–23.

Google Scholar

Zhongxiao, J. (1998). Incomplete Generalized Minimum Residue Method for Solving Asymmetric Linear Equations. Chin. Sci. (A) 1998 (08), 694–702.

Google Scholar

Zijun, Z., and Cheng, Y. (2018). Productivity Prediction Model Considering Stress Sensitivity of Matrix and Acid Fracturing. Spec. Oil Gas Reservoirs 25 (04), 76–81. doi:10.3969/j.issn.1006-6535.2018.04.015

CrossRef Full Text | Google Scholar