A Novel Method for Conventional Logging Prediction of Brittleness Index: A Case of Tight Sandstone in Western Ordos Basin

Brittleness index is an important parameter for the exploration and development of tight sandstone reservoir. In this paper, a new method for calculating brittleness index using conventional logging data was established to find the high-quality exploration and development target area of tight sandstone reservoir in He8 Member of Permian in the western margin of the Ordos Basin. Firstly, the mineral composition and content of rock samples in the study area were analyzed by rock mineral X-ray diffraction, and the brittleness index was calculated according to the mineral content with the average of 70.85%. Then, three kinds of brittleness index logging prediction models were obtained by conventional logging curves such as natural gamma and compressional wave interval transit time. Each prediction model was corrected by the brittleness index calculated according to the X-ray diffraction experiment, and the correlation coefficients were 0.83, 0.58, and 0.71, respectively. Finally, through multiple regression, the comprehensive equation for brittleness index prediction was established by combining these three kinds of models. According to the example of the specific well in the study area, the brittleness index predicted by conventional logging is highly matched with the interpretation results of array acoustic logging with the correlation coefficient of 0.90, which means the accuracy of the comprehensive equation has been verified. The new method can evaluate reservoir brittleness by conventional logging data in the absence of rock sample test data and popularize the application of brittleness index in oil and gas field exploration and development.

Introduction

With the development of the global energy industry, unconventional hydrocarbon resources, such as tight sandstone oil and gas, have become an important object of exploration and development. Tight sandstone oil and gas refer to sandstone oil and gas reservoirs with in situ permeability less than 0.1 mD (Rezaee et al., 2012). It is usually necessary to obtain industrial oil and gas production through technical measures such as fracturing (Zou et al., 2015). During formation fracturing analysis, brittleness is an important parameter for optimization of production stimulation interval and process (Lai et al., 2015; Yin et al., 2016).

At present, there is no unified definition of rock brittleness. It is generally accepted that rock brittleness refers to the mechanical characteristics of rock fracture with little deformation under external force (Meng et al., 2021). Brittleness index has been widely used as the parameter to quantitatively characterize rock brittleness. For hydrocarbon exploration and development, rock brittleness index is often related to the difficulty and effect of reservoir fracturing. When the brittleness index is greater than 60%, it is easy to form a large-scale fracture network system in the process of reservoir fracturing, so as to provide a favorable channel for the seepage of hydrocarbon in a tight sandstone reservoir (Kahraman and Altindag, 2004; Rickman et al., 2008; Guo et al., 2015). On the contrary, when the brittleness index is less than 40%, it is difficult to form a complex fracture network in the process of fracturing, which is not conducive to the efficient exploration and development (Kahraman and Altindag, 2004; Rickman et al., 2008; Guo et al., 2015).

There are various quantitative calculation methods of rock brittleness index (Meng et al., 2021). According to the different emphases, the calculation methods of brittleness index can be mainly summarized into three categories based on rock mechanical parameters, stress–strain characteristics, and mineral composition.

The calculation method of brittleness index based on rock mechanical parameters is the most commonly used quantitative evaluation method of rock brittleness. Through uniaxial and triaxial mechanical tests, rock mechanical parameters such as compressive and tensile strength can be obtained, and then the brittleness index of rock can be calculated (Hucka and Das, 1974; Altindag, 2002; Li et al., 2021). Under a continuous external load, rock will deform and destroy, and the stress–strain curve records the process from initial deformation to final failure. Through the stress–strain curve, the parameters used to calculate the rock brittleness index can be obtained, such as peak stress and residual stress (Bishop, 1967; Hucka and Das, 1974; Altindag, 2002; Hajiabdolmajid et al., 2002). A reservoir is composed of a variety of minerals, in which the content of brittle minerals directly affects brittleness. The brittleness evaluation method based on mineral composition is to characterize the brittleness index by calculating the content of brittle minerals in the reservoir (Jarvie et al., 2007; Rickman et al., 2008; Wang and Gale, 2009; Slatt, 2011; Jin et al., 2014; Chen et al., 2021).

Although there are many calculation methods of brittleness index, sufficient core sample test and special logging data are necessary in the calculation process. However, not every oil and gas field has the conditions to fully obtain these data in the production practice. For example, these data are not common in the Ordos Basin. Therefore, it is necessary to calculate the brittleness index by excavating information from conventional logging data to promote the evaluation of reservoir petrophysical properties.

In this paper, taking He8 Member of Lower Shihezi Formation of Permian in the western Ordos Basin as an example, research on the conventional logging prediction method of brittleness index was conducted. Based on conventional logging, a comprehensive mathematical model for predicting the brittleness index of tight sandstone reservoir was established. The new method for brittleness index prediction can enrich the technical means for the evaluation of tight sandstone gas reservoirs in the study area. In addition, the correlated workflow may popularize the application of brittleness index in oil and gas field exploration and development.

Geological Settings

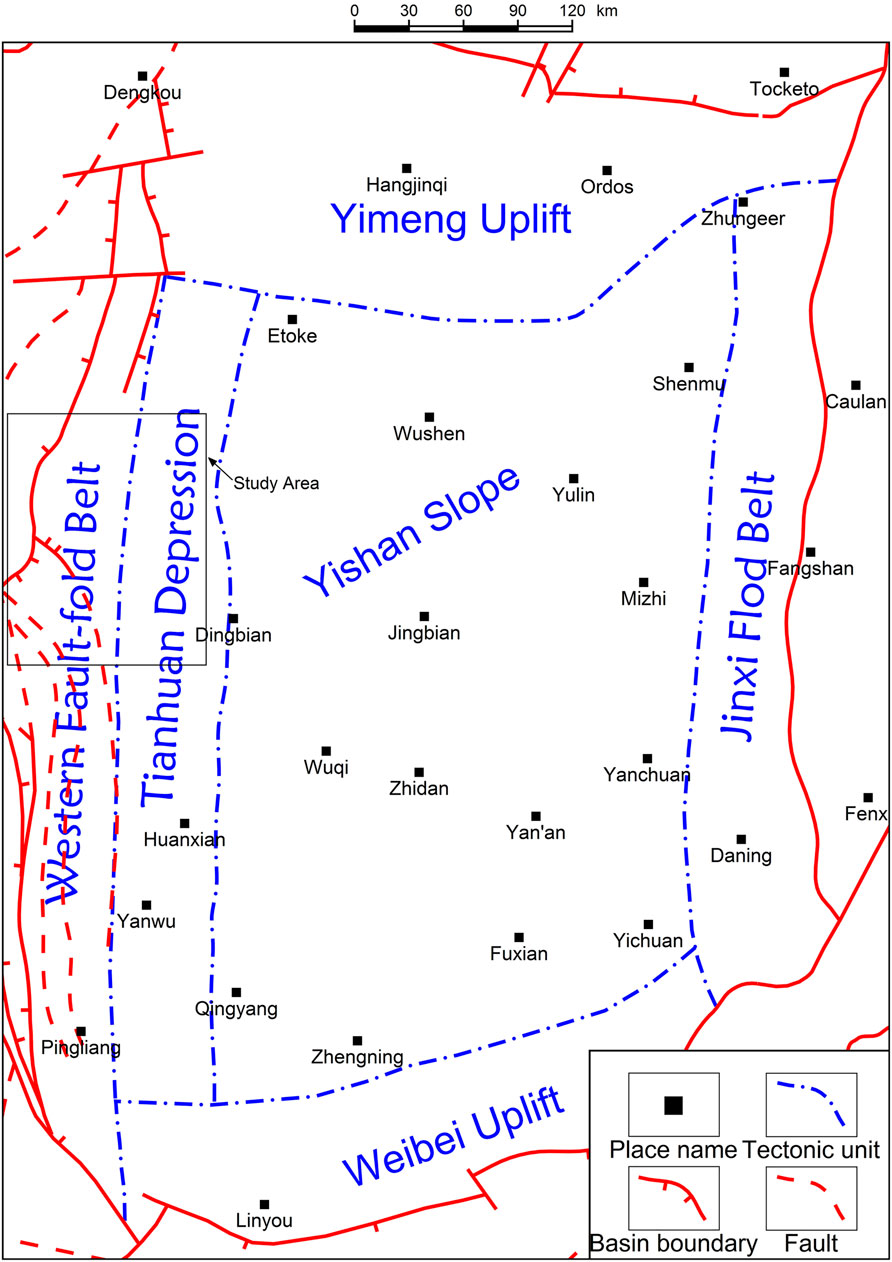
The study area is located in the north section of the western margin of the Ordos Basin, spanning two structural units: Tianhuan Depression and Western Fault-fold Belt (Figure 1). It is an oil and gas enrichment area with multiple strata superimposed. Mesozoic oil reservoirs are developed continuously in the southeast of the study area, and Paleozoic large-scale tight sandstone gas reservoirs are developed in the northeast (Zhang et al., 2018; Ouyang et al., 2021). With the continuous extraction, the proved reserves of hydrocarbon resources in this area have been almost exhausted. In recent years, the natural gas resource has been explored in the southeast and west of the study area to increase resource reserves. According to practice progress, the results are remarkable and the prospects are broad.

FIGURE 1

FIGURE 1. Tectonic unit and location of the study area in the Ordos Basin.

The Lower Shihezi Formation in the north section of the western margin of the Ordos Basin can be divided into four sections: He8 to He5. According to well logging and gas testing data, natural gas bearing and production intervals are mainly concentrated in He8 Member. The lithology of He8 Member is mainly gray mudstone and gray and gray white sandstone. The average thickness of sandstone in He8 Member is 15.1 m. The pore types are mainly dissolved pores and intergranular pores, with an average porosity of 6.37% and permeability of 0.265 mD.

Materials and Methods

As mentioned above, based on rock mechanical parameters, stress–strain characteristics, and mineral composition, methods for calculating the brittleness index can be divided into three types. In this study, three equations were selected for each kind of quantitative evaluation method to calculate the brittleness index of tight sandstone reservoir of He8 Member in the study area.

Method Based on Rock Mechanical Properties

Young’s modulus and Poisson’s ratio are two important rock mechanics parameters, which can be obtained from rock mechanics experiments. Young’s modulus can be used to characterize the ability of rock to resist deformation, while Poisson’s ratio can be used to characterize the ability of rock to deform along the cross section (Yin et al., 2016; Yang et al., 2021). Therefore, Young’s modulus is positively correlated with the brittleness index; on the contrary, Poisson’s ratio is negatively correlated with the brittleness index (Yin et al., 2016). The method of calculating the brittleness index by Young’s modulus and Poisson’s ratio is widely used in oil and gas industry.

The simple method is to calculate the relative values of Young’s modulus and Poisson’s ratio. Through the normalization of Young’s modulus and Poisson’s ratio, two values ranging from 0 to 100 were obtained, which can be regarded as brittleness indexes (Jarvie et al., 2007; Rickman et al., 2008; Wang and Gale, 2009; Slatt, 2011; Jin et al., 2014; Li et al., 2020):

$B{I}_E=\frac{E-E_{\min }}{E_{\max }-E_{\min }}\times 100,(1)$

where BI_E is the brittleness index calculated by Young’s modulus (%), E is Young’s modulus (GPa), and E_max and E_min are the maximum and minimum of Young’s modulus (GPa), which are usually taken as regional empirical values, and

$B{I}_{\nu }=\frac{\nu -{\nu }_{\min }}{{\nu }_{\max }-{\nu }_{\min }}\times 100,(2)$

where BI_ν is the brittleness index calculated by Poisson’s ratio (%), ν is Poisson’s ratio (decimal), and ν_max and ν_min are the maximum and minimum of Poisson’s ratio (decimal), which are usually taken as regional empirical values.

Through Eqs 1 and 2, the rock brittleness index can be calculated according to Young’s modulus and Poisson’s ratio. In scientific research studies and production practices of oil and gas fields, the two values calculated in Eqs 1 and 2 are usually averaged, and the calculated results are finally regarded as the rock brittleness index (Jarvie et al., 2007; Rickman et al., 2008; Wang and Gale, 2009; Slatt, 2011; Jin et al., 2014):

$B{I}_1=\frac{B{I}_E-B{I}_{\nu }}{2},(3)$

where BI₁ is the brittleness index calculated by Young’s modulus and Poisson’s ratio (%).

When core samples are absent, Young’s modulus and dynamic Poisson’s ratio of rock can also be calculated from array acoustic logging or dipole acoustic logging data. Shear wave interval transit time can be obtained through array acoustic logging or dipole acoustic logging (Lai et al., 2015; Yin et al., 2016). Using the logging data of bulk density and compressional and shear wave interval transit time, Young’s modulus and Poisson’s ratio can be calculated through the following equations:

$E=\frac{{\rho }_b}{\mathrm{\Delta }{t}_s^2}\times \frac{3\mathrm{\Delta }{t}_s^2-4\mathrm{\Delta }{t}_c^2}{\mathrm{\Delta }{t}_s^2-\Delta t_c^2}\times {10}^6,(4)$

$\nu =\frac{\mathrm{\Delta }{t}_s^2-2\mathrm{\Delta }{t}_c^2}{2\left(\mathrm{\Delta }{t}_s^2-\mathrm{\Delta }{t}_c^2\right)},(5)$

where ρ_b is the bulk density (g/cm³), Δt_s is the shear wave interval transit time (μs/m), and Δt_c is the compressional wave interval transit time (μs/m).

Substituting Eqs 4 and 5 into Eqs 1 and 2, respectively, Young’s modulus and Poisson’s ratio of rock can be calculated from logging data. Then, through Eq. 3, the value of BI₁ can be obtained.

Method Based on Stress–Strain Characteristics

The internal friction angle is the critical self-stable angle of rock under external load, which affects the fracture surface of rock failure (Sun et al., 2015; Zhao et al., 2021). The internal friction angle can reflect the frictional force between rock clastic grains and can be characterized by the relationship between normal stress and shear stress in any azimuth plane of rock (Deere and Miller, 1966). The rock brittleness index can be expressed as sine of its internal friction angle (Deere and Miller, 1966; Sun et al., 2015; Meng et al., 2021; Zhao et al., 2021). The larger the internal friction angle is, the higher the rock brittleness index is:

$B{I}_2=\sin \phi \times 100,(6)$

where BI₂ is the brittleness index calculated by the internal friction angle (%) and φ is the internal friction angle (°).

There is a negative correlation between rock internal friction angle and Poisson’s ratio, and the equation can be expressed as (Deere and Miller, 1966; Sun et al., 2015; Meng et al., 2021)

$\phi =\frac{\pi }{12}\left[2\left(1-\frac{\nu }{1-\nu }\right)+1\right].(7)$

Substituting Eq. 7 into Eq. 6, BI₂ can be obtained.

Method Based on Rock Mineral Composition

Rock is composed of various minerals, and the content of brittle minerals directly affects its brittleness index (Jarvie et al., 2007; Rickman et al., 2008; Wang and Gale, 2009; Slatt, 2011; Jin et al., 2014; Zhang et al., 2020). Reservoirs rich in brittle minerals can achieve good fracturing effect and improve well productivity. Each mineral has a specific X-ray diffraction pattern, and the characteristic peak intensity in the pattern is positively correlated with the content of the mineral in the sample (Lai et al., 2015). In the X-ray diffraction experiment, the rock samples were crushed and ground into powder, and the mineral composition and content were obtained. The experimental standards are those implemented by SY/T 5163-2018.

It is worth noting that the physical properties of minerals are different under different burial depth, pressure, temperature, sedimentary model, and diagenetic evolution (Wang et al., 2015; Hernandez-Uribe et al., 2017). In different areas, the definition of brittle minerals is often various for diverse types of reservoirs. Based on previous studies on brittleness evaluation of tight sandstone reservoirs in the Ordos Basin, quartz and carbonate are regarded as brittle minerals (Lai et al., 2015; Wang et al., 2015). Therefore, the brittleness index calculation equation based on the rock mineral composition can be expressed as

$B{I}_3=\frac{W_{qz}+W_{car}}{W_{qz}+W_{fels}+W_{car}+W_{clay}}\times 100,(8)$

where BI₃ is the brittleness index calculated by rock mineral composition (%), W_qz is the quartz content (%), W_car is the carbonate mineral content (%), W_fels is the feldspar content (%), and W_clay is the clay mineral content (%).

Results and Discussions

Through different methods stated in Section 3, the values of BI₁, BI₂, and BI₃ were calculated for typical well examples. On the basis of extracting the corresponding conventional logging parameters, the conventional logging prediction model of rock brittleness index was finally established through regression analysis.

Comparison and Analysis of Brittleness Index

Well #1 that implements array acoustic logging was selected. Using the data of shear wave interval transit time (DTS), compressional wave interval transit time (DTC), and bulk density (DEN), through Eqs 4 and 5, Young’s modulus and Poisson’s ratio were calculated. The values of Young’s modulus of Well #1 in He8 Member range from 17.47 to 63.65 GPa, with an average of 37.47 GPa. The average Poisson’s ratio is 0.28, with the values in the range of 0.09–0.38. Through Young’s modulus and Poisson’s ratio calculation results, BI₁ and BI₂ can be obtained from Eqs 1–3, 6, and 7. The value ranges of BI₁ and BI₂ are from 16.90 to 74.12% and from 44.39 to 66.96%, with an average of 43.41 and 54.20, respectively.

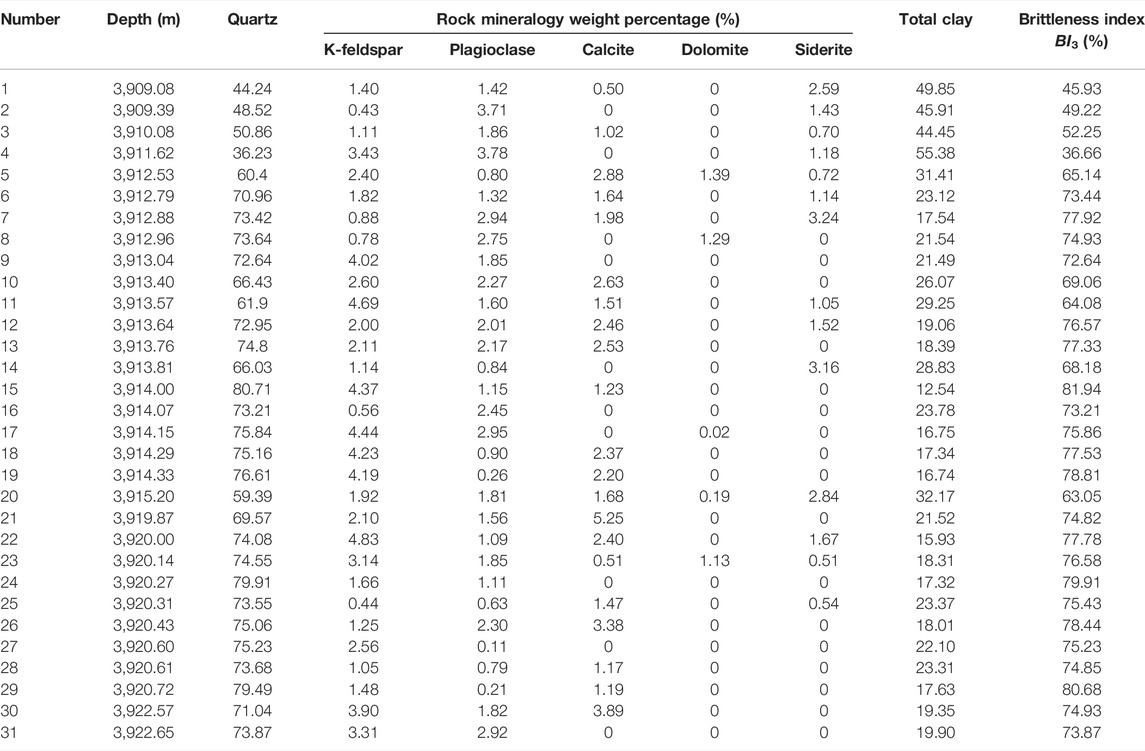
Through the rock mineral X-ray diffraction experiment, the mineral composition and content of the samples of Well #1 were tested and analyzed quantitatively (Table 1). Among the 31 samples, the maximum value of quartz content is 80.71%, the minimum value is 36.23%, and the average value is 68.84%; the maximum value of clay minerals is 55.38%, the minimum value is 12.54%, and the average value is 24.79%; the maximum value of carbonate minerals is 5.25%, the minimum value is 0.02%, and the average value is 2.08%. BI₃ of the 31 experimental samples was calculated by Eq. 8. The values range from 36.66 to 81.94%, with an average of 70.85% (Table 1).

TABLE 1

TABLE 1. Quantitative analysis of whole rock minerals by X-ray diffraction and brittleness index.

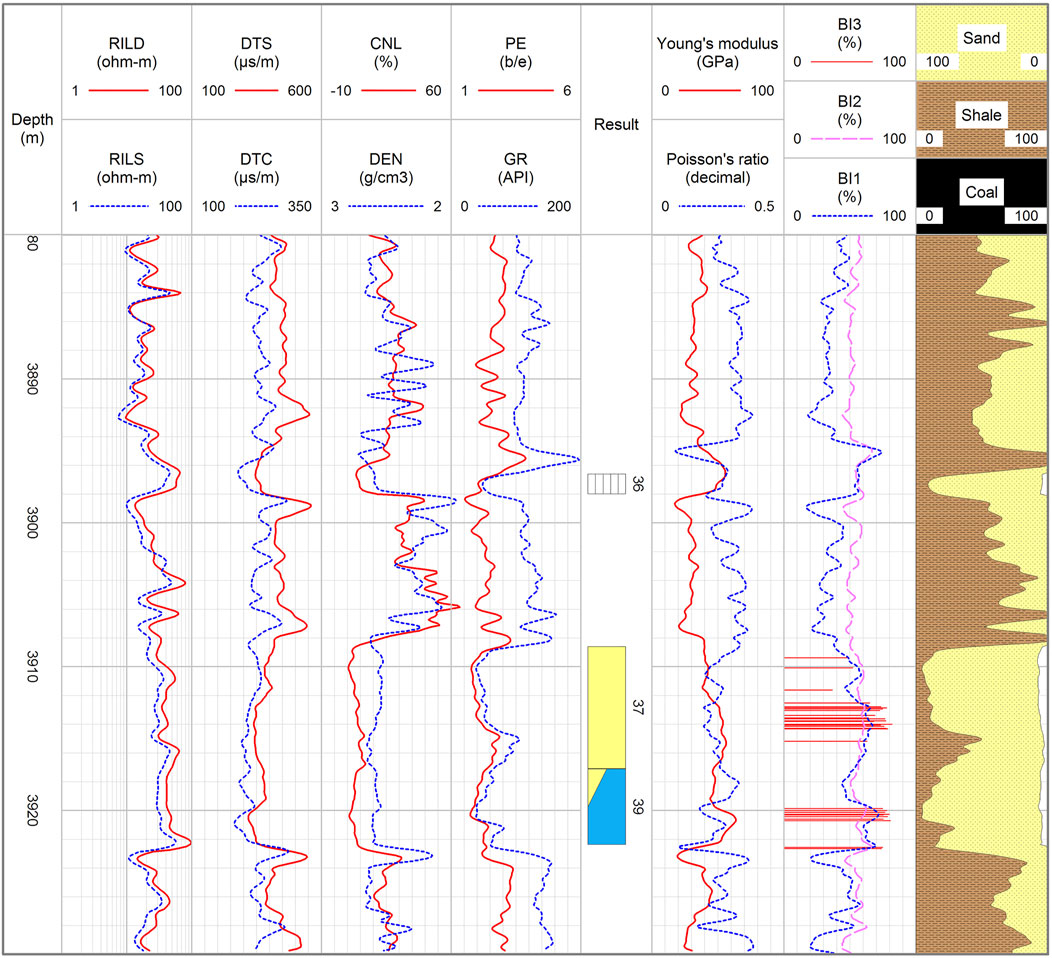
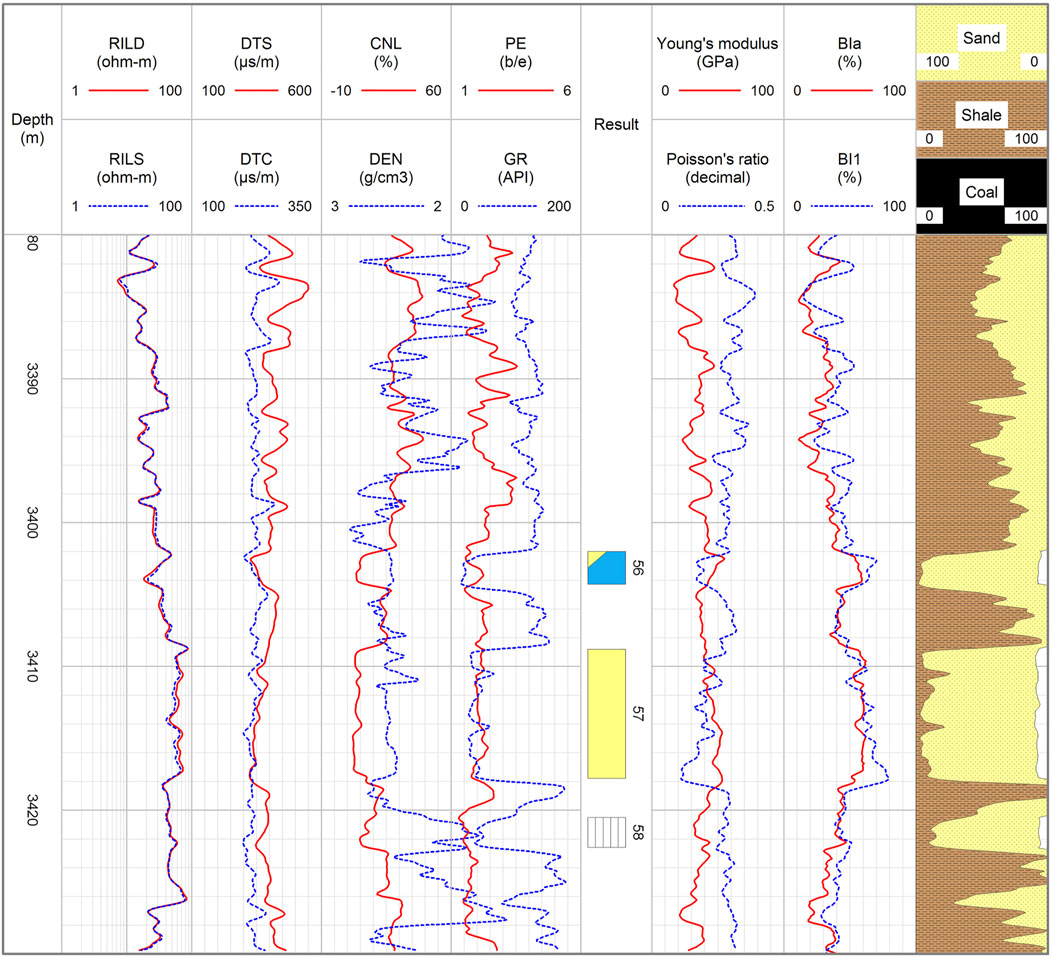
The curves of Young’s modulus and Poisson’s ratio were calculated and drawn in the seventh track in the log interpretation diagram of Well #1 (Figure 2). These two curves show an opposite change trend. In Figure 2, BI₁ and BI₂ are shown in the eighth track. The data range of BI₁ is wider, and the average value of BI₂ is higher. The discrete data values of BI₃ are also shown in the eighth track. The change trends of BI₁ and BI₂ are consistent with that of BI₃, which means the brittleness index calculation results by array acoustic logging are correct. Furthermore, it can be seen that the values of BI₁ and BI₃ are closer. For BI₃, the average value of the tested rock samples is 70.85%. Corresponding to the depth of the tested sample, the average values of BI₁ and BI₂ are 63.75 and 59.82%. Therefore, when using array acoustic logging or dipole acoustic logging data to evaluate rock brittleness, it is recommended to use the relevant method of calculating BI₁.

FIGURE 2

FIGURE 2. Well #1 logging interpretation results of He8 Member.

Brittleness Index Prediction by Fitting DTS

The data of DTC and DEN can be obtained from conventional logging data. Due to the limiting factors such as operation cost, only a few wells implement array acoustic logging or dipole acoustic logging (Li et al., 2014; Lai et al., 2015; Sun et al., 2015; Yin et al., 2016). Therefore, DTS logging data are often absent. To calculate the rock brittleness index, it is necessary to fit the calculation equation of DTS through the existing DTS data and conventional logging data.

In fact, there is a relatively strong correlation between each porosity logging curve. In Figure 2, curves of DTS and DTC are shown in the third track and those of DEN and compensated neutron logging (CNL) are drawn in the fourth track. It can be seen that there is high consistency among the curves of DTS, DTC, DEN, and CNL. The values of DTS are positively correlated with those of DTC and CNL while negatively correlated with those of DEN. Quantitative correlation analysis of DTS with DTC, DEN, and CNL shows that the correlation coefficients are 0.69, -0.58, and 0.72, respectively.

Due to high correlation, multiple regression was conducted, and the equation of calculating DTS by DTC, DEN, and CNL was obtained:

$\mathrm{\Delta }{t}_s=1.12\mathrm{\Delta }{t}_c-6.64{\rho }_b+2.10{\mathrm{\Phi }}_N+133.55,(9)$

where Φ_N is the compensated neutron logging value.

Substituting Eq. 9 into Eqs 4 and 5, Young’s modulus and Poisson’s ratio can be calculated in the absence of DTS logging. Using the calculation results, the apparent brittleness indexes BI_1a and BI_2a can be obtained from Eqs 1–3,6 and 7.

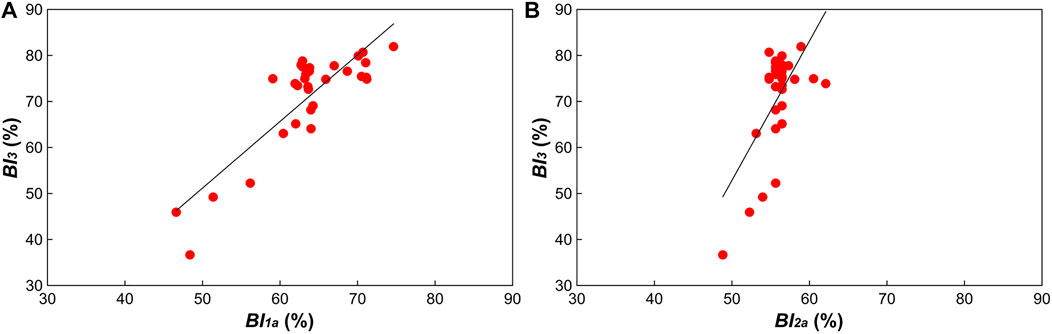
The cross plots of BI_1a and BI_2a versus BI₃ were established, respectively, to verify the logging prediction results (Figure 3). It can be seen that the data distribution range of BI_1a is wider than that of BI_2a, which is similar to the data distribution law of BI₁ and BI₂. According to the correlation between data points, the correlation coefficient between BI_1a and BI₃ is 0.83, while that between BI_2a and BI₃ is 0.58. Obviously, there is a stronger correlation between BI_1a and BI₃. Therefore, the method of calculating BI_1a is more suitable for the quantitative evaluation of rock brittleness. For BI_2a, although the absolute accuracy of the calculation results does not meet the requirements of quantitative evaluation of rock brittleness, the relative relationship between the calculated values is still maintained. In some cases of focusing on the relative relationship, such as the selection of stimulation interval in a specific well, the calculation method of BI_2a is more rapid and efficient because fewer parameters are involved.

FIGURE 3

FIGURE 3. Cross plots of BI₃ versus (A) BI_1a and (B) BI_2a.

Brittleness Index Multiple Parameter Fitting

According to Figure 2, it can be seen that the brittleness index is correlated with many logging parameters such as DTC, gamma ray (GR), and deep resistivity (RILD). In fact, there is a clear corresponding relationship between rock brittleness, lithology, and physical properties (Li et al., 2014; Lai et al., 2015; Sun et al., 2015; Liu et al., 2020).

Taking GR as an example, it is a method of radioactive logging, and the GR curve can indicate reservoir lithology. Clay rocks contain highly radioactive elements, and clay minerals have a strong adsorption capacity for cations, which can adsorb surrounding radioactive substances (Lai et al., 2015). Therefore, when the clay content of reservoir is high, it shows obvious characteristics of high GR. On the contrary, when the reservoir contains a large amount of non-radioactive substances such as quartz and carbonate, the GR curve shows the characteristics of low value (Lai et al., 2015). Meanwhile, according to the calculation method of brittleness index based on rock mineral composition, high content of clay minerals can cause low brittleness index, while high content of quartz and carbonate minerals can lead to high brittleness index. As a result, high value of GR corresponds to low brittleness index, while low value of GR corresponds to high brittleness index.

The correlation between brittleness index and conventional logging parameters was analyzed. There is high correlation between brittleness index and conventional logging parameters of GR, DTC, RT, and PE (Table 2). After calculating the reciprocal of the parameters negatively correlated with the brittleness index, it is multiplied by the parameters positively correlated with the brittleness index. The final calculated product is defined as the brittleness index sensitive parameter, which is represented by

$Ps={\displaystyle \prod P{s}_{pos}}\times \frac{1}{{\displaystyle \prod P{s}_{neg}}},(10)$

where Ps_pos is the conventional logging parameter positively correlated with the brittleness index and Ps_neg is the conventional logging parameter negatively correlated with the brittleness index.

TABLE 2

TABLE 2. Correlation coefficient between brittleness index and logging parameters.

Compared with the correlation coefficient between single conventional logging parameters, the correlation between Ps and BI₃ is significantly improved, with the correlation coefficient of 0.71. The cross plots of GR and Ps versus BI₃ were established, respectively (Figure 4). In the cross plot of GR versus BI₃ (Figure 4A), there is an obvious negative correlation between BI₃ and GR. However, the distribution of data points is relatively discrete, which means that there will be large errors in the calculation results if only GR is used to establish the regression formula of brittleness index. After the abscissa of the cross plot is optimized to Ps (Figure 4B), the distribution of data points obviously becomes centralized and convergent.

FIGURE 4

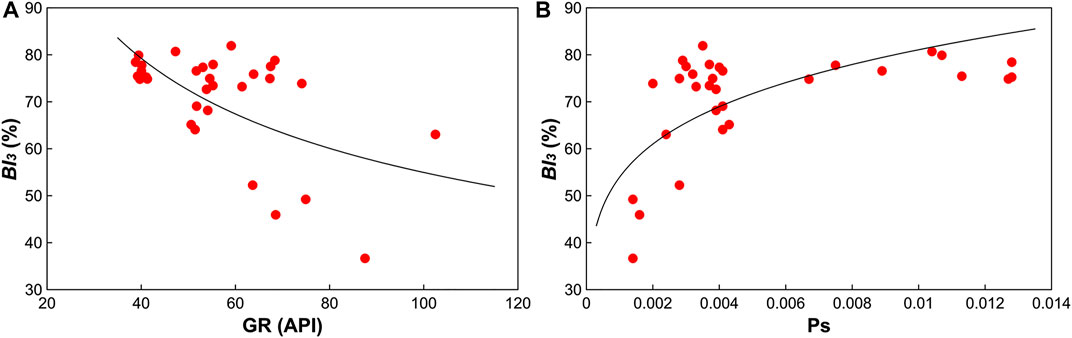
FIGURE 4. Cross plots of BI₃ versus (A) gamma ray logging values and (B) brittleness index sensitive parameter.

According to the cross plot of Ps versus BI₃, the mathematical relationship between the two parameters was fitted, and the obtained mathematical relation expression can be regarded as an equation for predicting the rock brittleness index using conventional logging data. The apparent brittleness index predicted by this method is represented by

$B{I}_{3a}=183.02\times P{s}^{0.1768}.(11)$

Brittleness Index Comprehensive Prediction Model

According to different emphases of rock brittleness index evaluation, the brittleness index prediction methods based on rock mechanical properties, stress–strain characteristics, and rock mineral composition using conventional logging data were established. Through multiple regression, BI_1a, BI_2a, and BI_3a can be corrected and calibrated by the experimental test data, and the corresponding multivariate function relationship can be obtained as the comprehensive prediction mathematical model of brittleness index of He8 Member in the study area:

$B{I}_a=1.33B{I}_{1a}+1.57B{I}_{2a}+0.08B{I}_{3a}-92.79,(12)$

where BI_a is the brittleness index predicted by the multiple regression comprehensive model (%).

Case Study

In previous studies, scholars have also used the regression relationship between conventional logging parameters and brittleness index to establish formulas (Li et al., 2014; Lai et al., 2015). However, it must be admitted that due to the difference of geological conditions, the fitting formula has limitations. In some tight sandstone reservoirs with laminated shale development, an accurate brittleness index prediction model can be obtained only using GR or PE (Lai et al., 2015). However, for the tight reservoir in the late diagenetic stage such as He8 Member in the study area, more parameters need to be introduced to improve the prediction accuracy of brittleness index.

Compared with the past, the innovation of this study is to calculate the brittleness index of tight sandstone in a specific area by introducing more conventional logging parameters and fully combining the three main kinds of methods of quantitative determination of brittleness index. In Eqs 9 and 11, many conventional logging parameters such as DTC, DEN, and GR were introduced to calculate the brittleness index of He8 Member in the study area. In Eq. 12, the three main kinds of methods of quantitative determination of brittleness index (based on rock mechanical parameters, stress–strain characteristics, and mineral composition) were combined.

Using Eq. 12, the rock brittleness index of He8 Member was calculated for the wells in the study area. Taking a well with array acoustic logging as an example, the established comprehensive prediction model of brittleness index has high calculation accuracy (Figure 5).

FIGURE 5

FIGURE 5. Well #2 logging interpretation results of He8 Member.

In the example (Well #2), through array acoustic logging, the calculated Young’s modulus and Poisson’s ratio are shown in the seventh track, and the brittleness index (BI₁) calculated by rock mechanical properties is shown in the eighth track. The brittleness index predicted by the multiple regression comprehensive model (BI_a) is also shown in the eighth track. It can be seen that the curves of BI₁ and BI_a have the same change trend. Through correlation analysis, the correlation coefficient between BI_a and BI₁ is 0.90. According to the result, the brittle index prediction value with high accuracy can be obtained by the model proposed in this paper. In addition, even in other regions, the fitting formulas proposed in this paper cannot be directly applied, but the corresponding workflow still has reference significance.

The interval is 3,408.5–3,417.7 m, RILD is 63.62 Ω-m, and DTC is 229.36 μm/s. The porosity of core test is 6.30%, and the permeability is 0.269 mD. The peak value of gas logging is 7.98%, and the base value is 0.21%. According to the logging interpretation conclusion, this interval is a gas layer. After gas test verification, the daily gas production of this interval was 4.55 m³. On the contrary, for the low brittleness index interval (3,420.5–3,422.6 m), there was no natural gas produced. The difference of gas test conclusions between the two intervals can also indirectly verify the accuracy of brittleness index prediction results.

Conclusion

1) Based on rock mechanical properties, stress–strain characteristics, and brittle mineral composition, the quantitative evaluation methods of rock brittleness can be summarized into three categories. The brittleness of a typical well in the study area was calculated by different methods. For the corresponding depth of the tested sample, the average values of BI₁, BI₂, and BI₃ are 63.75, 59.82, and 70.85%. According to the change trend of BI₁ and BI₂ versus BI₃, it is recommended to use the relevant method of calculating BI₁ when the data of array acoustic logging or dipole acoustic logging are provided.

2) Using conventional logging data, DTS can be fitted. The conventional logging prediction of brittleness index based on rock mechanical properties can be realized by using the fitted DTS. BI_1a and BI_2a were calculated by this method, and the correlation coefficients with the rock samples’ testing result were 0.83 and 0.58. There is a certain degree of correlation between brittleness index and many conventional logging parameters. Through correlation analysis, the sensitive parameter of brittleness index was proposed, and then the equation for calculating the brittleness index using this parameter was fitted. BI_3a was calculated by this method, and the correlation coefficient with the testing result was 0.71.

3) The results of brittleness index calculated by different conventional logging prediction methods were regressed with the result obtained by X-ray diffraction, and the brittleness index comprehensive prediction mathematical model by conventional logging was established. According to the wells in the study area, the rock brittleness index was predicted. The example shows that the predicted value coincides with the interpretation results of array acoustic logging, with the correlation coefficient of 0.90. The applicability of the model in the study area has been verified through the example.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding authors.

Author Contributions

JF and JG contributed to the methodology. JF supervised the work. JG wrote the original draft. LC conceptualized the research idea. LC and YL obtained the resources. QL contributed to data validation and funding acquisition. SW curated the data and reviewed and edited the paper. YL contributed to data investigation. All authors agreed to be accountable for the content of the work.

Funding

This work was financially supported by the National Natural Science Foundation of China (No. 42102170).

Conflict of Interest

The authors JF, LC, and YL were employed by Changqing Oil Field Company Ltd. (CNPC).

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Altindag, R. (2002). The Evaluation of Rock Brittleness Concept on Rotary Blast Hole Drills. J. South Afr. Inst. Min. Metallurgy 102 (1), 61–66. doi:10.1007/BF02822606

CrossRef Full Text | Google Scholar

Bishop, A. W. (1967). “Progressive Failure with Special Referenceto the Mechanism Causing it,” in Oslor Proceedings of the Geotechnical Conference, Oslo, April 12th, 142–150.

Google Scholar

Chen, G. B., Li, T., Yang, L., Zhang, G. H., Li, J. W., and Dong, H. J. (2021). Mechanical Properties and Failure Mechanism of Combined Bodies with Different Coal-Rock Ratios and Combinations. J. Min. Strata Control Eng. 3 (2), 84–94. doi:10.13532/j.jmsce.cn10-1638/td.20210108.001

CrossRef Full Text | Google Scholar

Deere, D. U., and Miller, R. P. (1966). “Engineering Classification and Index Properties for Intact Rock,” in Air Force Weapons Laboratory, 327. Technical Report. AFWL-TR-65-116. Kirtland: Air Force Weapons Laboratory. doi:10.21236/ad0646610

CrossRef Full Text | Google Scholar

Guo, T., Zhang, S., Ge, H., Wang, X., Lei, X., and Xiao, B. (2015). A New Method for Evaluation of Fracture Network Formation Capacity of Rock. Fuel 140, 778–787. doi:10.1016/j.fuel.2014.10.017

CrossRef Full Text | Google Scholar

Hajiabdolmajid, V., Kaiser, P. K., and Martin, C. D. (2002). Modelling Brittle Failure of Rock. Int. J. Rock Mech. Min. Sci. 39 (6), 731–741. doi:10.1016/s1365-1609(02)00051-5

CrossRef Full Text | Google Scholar

Hernandez-Uribe, L. A., Aman, M., and Espinoza, D. N. (2017). Assessment of Mudrock Brittleness with Micro-scratch Testing. Rock Mech. Rock Eng. 50 (11), 1–12. doi:10.1007/s00603-017-1279-y

CrossRef Full Text | Google Scholar

Hucka, V., and Das, B. (1974). Brittleness Determination of Rocks by Different Methods. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 11 (10), 389–392. doi:10.1016/0148-9062(74)91109-7

CrossRef Full Text | Google Scholar

Jarvie, D. M., Hill, R. J., Ruble, T. E., and Pollastro, R. M. (2007). Unconventional Shale-Gas Systems: The Mississippian Barnett Shale of North-Central Texas as One Model for Thermogenic Shale-Gas Assessment. AAPG Bull. 91 (4), 475–499. doi:10.1306/12190606068

CrossRef Full Text | Google Scholar

Jin, X., Shah, S., Truax, J., and Roegiers, J.-C. (2014). “A Practical Petrophysical Approach for Brittleness Prediction from Porosity and Sonic Logging in Shale Reservoirs,” in SPE Annual Technical Conference and Exhibition, Amsterdam, October 27th. doi:10.2118/170972-MS

CrossRef Full Text | Google Scholar

Kahraman, S., and Altindag, R. (2004). A Brittleness Index to Estimate Fracture Toughness. Int. J. Rock Mech. Min. Sci. 41 (2), 343–348. doi:10.1016/j.ijrmms.2003.07.010

CrossRef Full Text | Google Scholar

Lai, J., Wang, G., Huang, L., Li, W., Ran, Y., Wang, D., et al. (2015). Brittleness Index Estimation in a Tight Shaly Sandstone Reservoir Using Well Logs. J. Nat. Gas Sci. Eng. 27 (P3), 1536–1545. doi:10.1016/j.jngse.2015.10.020

CrossRef Full Text | Google Scholar

Li, H. Y., Zhou, C. C., Li, C. X., Li, C. L., Shi, Y. J., and Wang, C. S. (2014). Logging Evaluation and Application of Brittleness Index in Tight Sandstone Reservoir: A Case Study of Chang 7 Tight Sandstone Reservoir in Longdong Area of Ordos Basin. Xinjiang Pet. Geol. 35 (05), 593–597. doi:10.7657/XJPG201405022

CrossRef Full Text | Google Scholar

Li, L. F., Zhang, X. H., Deng, H. L., and Han, L. P. (2020). Mechanical Properties and Energy Evolution of Sandstone Subjected to Uniaxial Compression with Different Loading Rates. J. Min. Strata Control Eng. 2 (4), 83–89. doi:10.13532/j.jmsce.cn10-1638/td.20200407.001

CrossRef Full Text | Google Scholar

Li, S. L., Liu, G. J., Jia, R. F., Xue, F., and Wang, K. Y. (2021). Study on Friction Effect and Damage Evolution of End Face in Uniaxial Compression Test. J. Min. Strata Control Eng. 3 (3), 99–108. doi:10.13532/j.jmsce.cn10-1638/td.20210325.001

CrossRef Full Text | Google Scholar

Liu, Y. X., Gao, M. S., Zhao, H. S., He, S. L., Li, Z. G., and Zhang, Z. C. (2020). Detection of Overlying Rock Structure and Identification of Key Stratum by Drilling and Logging Technology. J. Min. Strata Control Eng. 2 (2), 85–93. doi:10.13532/j.jmsce.cn10-1638/td.202000929.001

CrossRef Full Text | Google Scholar

Meng, F., Wong, L., and Zhou, H. (2021). Rock Brittleness Indices and Their Applications to Different Fields of Rock Engineering: A Review. J. Rock Mech. Geotechnical Eng. 13 (1), 27. doi:10.1016/j.jrmge.2020.06.008

CrossRef Full Text | Google Scholar

Ouyang, Z., Feng, J., Gong, H., Ma, Y., Gao, M., and Li, Y. (2021). Structural Characteristics and Oil and Gas Exploration Target Optimization of Hengshanbu Area in the North of Western Margin of Ordos Basin. Chin. J. Geol. 56 (01), 19–27. doi:10.12017/dzkx.2021.002

CrossRef Full Text | Google Scholar

Rezaee, R., Saeedi, A., and Clennell, B. (2012). Tight Gas Sands Permeability Estimation from Mercury Injection Capillary Pressure and Nuclear Magnetic Resonance Data. J. Petroleum Sci. Eng. 88-89, 92–99. doi:10.1016/j.petrol.2011.12.014

CrossRef Full Text | Google Scholar

Rickman, R., Mullen, M., Petre, E., Grieser, B., and Kundert, D. (2008). “A Practical Use of Shale Petrophysics for Stimulation Design Optimization: All Shale Plays Are Not Clones of the Barnett Shale,” in SPE Annual Technical Conference and Exhibition, Collordo, September 21st, 2, 840–850. doi:10.2118/115258-ms

CrossRef Full Text | Google Scholar

Slatt, R. M. (2011). Important Geological Properties of Unconventional Resource Shales. Central Eur. J. Geosciences 3 (4), 435–448. doi:10.2478/s13533-011-0042-2

CrossRef Full Text | Google Scholar

Sun, J., Han, Z., Qin, R., and Zhang, J. (2015). Log Evaluation Method of Fracturing Performance in Tight Gas Reservoir. Shiyou Xuebao/Acta Pet. Sin. 36 (1), 74–80. doi:10.7623/syxb201501009

CrossRef Full Text | Google Scholar

Wang, F., and Gale, J. F. (2009). Screening Criteria for Shale-Gas Systems. Trans. Gulf Coast Assoc. Geol. Soc. 59, 779–793.

Google Scholar

Wang, M., Wilkins, R. W. T., Song, G., Zhang, L., Xu, X., Li, Z., et al. (2015). Geochemical and Geological Characteristics of the Es3L Lacustrine Shale in the Bonan Sag, Bohai Bay Basin, China. Int. J. Coal Geol. 138, 16–29. doi:10.1016/j.coal.2014.12.007

CrossRef Full Text | Google Scholar

Yang, J. X., Luo, M. K., Zhang, X. W., Huang, N., and Hou, S. J. (2021). Mechanical Properties and Fatigue Damage Evolution of Granite under Cyclic Loading and Unloading Conditions. J. Min. Strata Control Eng. 3 (3), 91–98. doi:10.13532/j.jmsce.cn10-1638/td.20210510.001

CrossRef Full Text | Google Scholar

Yin, S., Ding, W., Shan, Y., Zhou, W., Wang, R., Zhou, X., et al. (2016). A New Method for Assessing Young's Modulus and Poisson's Ratio in Tight Interbedded Clastic Reservoirs without a Shear Wave Time Difference. J. Nat. Gas Sci. Eng. 36, 267–279. doi:10.1016/j.jngse.2016.10.033

CrossRef Full Text | Google Scholar

Zhang, B. L., Shen, B. T., Zhang, J. H., and Zhang, X. G. (2020). Experimental Study of Edge-Opened Cracks Propagation in Rock-like Materials. J. Min. Strata Control Eng. 2 (3), 63–72. doi:10.13532/j.jmsce.cn10-1638/td.20200313.001

CrossRef Full Text | Google Scholar

Zhang, L., Feng, H., Chen, G., Du, J., and Huang, Z. (2018). Characteristics of Fault and Accumulation Models in Hengshanbu Block on the West Edge of Ordos Basin. Mar. Orig. Pet. Geol. 23 (02), 77–82. doi:10.3969/j.issn.1672-9854.2018.02.010

CrossRef Full Text | Google Scholar

Zhao, K. K., Jiang, P. F., Feng, Y. J., Sun, X. D., Cheng, L. X., and Zheng, J. W. (2021). Investigation of the Characteristics of Hydraulic Fracture Initiation by Using Maximum Tangential Stress Criterion. J. Min. Strata Control Eng. 3 (2), 14–22. doi:10.13532/j.jmsce.cn10-1638/td.20201217.001

CrossRef Full Text | Google Scholar

Zou, C., Zhi, Y., Rukai, Z., Guosheng, Z., Lianhua, H., Wu, S., et al. (2015). Progress in China's Unconventional Oil & Gas Exploration and Development and Theoretical Technologies. Acta Geol. Sin. (English Edition) 89 (06), 979–1007. doi:10.1111/1755-6724.12491

CrossRef Full Text | Google Scholar