Lithium Ion Battery Health Prediction via Variable Mode Decomposition and Deep Learning Network With Self-Attention Mechanism

Battery health prediction is very important for the safety of lithium batteries. Due to the factors such as capacity regeneration and random fluctuation in the use of lithium ion battery, the accuracy and generalization ability are poor when using a single scale feature to predict the health state of lithium ion battery. To solve these problems, we propose a comprehensive prediction method based on variational mode decomposition, integrated particle filter, and long short-term memory network with self-attention mechanism. Firstly, the capacity data of lithium ion battery is decomposed by variational mode decomposition to obtain the residual component which can reflect the global degradation trend of lithium ion battery and intrinsic mode functions component that can reflect the local random fluctuation. Then, the particle filter algorithm is employed to predict the residual component, and the long short-term memory network with self-attention mechanism is proposed to predict the intrinsic mode functions component. Finally, the prediction results of each subcomponent are reconstructed to obtain the final prediction value of lithium ion battery health state. The experimental results show that the prediction method proposed in this article has good prediction accuracy and stability.

Introduction

Lithium ion battery is widely used in automobile, aerospace, electric energy storage, military equipment, and other fields due to its advantages of stable voltage, high energy, and low price. With the increase of charge and discharge cycles, the activity of lithium-ion decreases, the battery capacity and power decline, and the remaining useful life (RUL) gradually shortens, which has an impact on the operation reliability of the whole equipment. Therefore, an accurate prediction of lithium ion battery health status is of great significance to ensure the reliability of equipment operation and reduce maintenance cost.

The data-driven method is a popular method for predicting the health state of lithium ion battery. It does not need to establish an accurate physical and chemical model of battery failure. The rule of lithium ion battery performance degradation is directly mined from the data of lithium ion battery voltage, current, temperature, and capacity, and the nonlinear quantitative model of degradation rule or battery health state is automatically established, which has strong applicability. Common data-driven methods include support vector machine (SVM) (Li et al., 2020), particle filter (PF) (Lyu et al., 2021b), deep learning network (Kaur et al., 2021; Sun et al., 2021), extreme learning machine (Xu et al., 2021), K-nearest neighbor regression (Zhou et al., 2020), etc. A battery capacity estimation method is proposed based on dynamic time warping algorithm in the study by Liu et al. (2019), which can quickly estimate the capacity of each battery in the battery pack by using the previous charging curve and current charging data of one battery in the battery pack. A random forest regression prediction method is proposed to evaluate the health status of different batteries under different cycle conditions in the study by Li et al. (2018), which can extract the features from the charging voltage and capacity measurement. A capacity estimation method of lithium-ion battery based on one-dimensional convolutional neural network (CNN) is proposed in the study by Qian et al. (2021), which takes the random segment of charging curve as the input to estimate the capacity. A deep learning method for lithium-ion battery capacity prediction based on long short-term memory (LSTM) recurrent neural network is studied in the study by Chen et al. (2020), which is used to capture the potential long-term correlation of capacity degradation. A multi-timescale extended Kalman filter (EKF) algorithm is proposed in the study by Yang et al. (2020) to estimate the state of charge and capacity of each battery in the battery pack. A linear aging model based on the capacity data in the sliding window is used to predict the RUL of the battery by combining Monte Carlo simulation to generate the prediction uncertainty (Xiong et al., 2019).

Because the PF algorithm is not constrained by the linear and Gaussian assumptions of the model and has good tracking effect, it is widely used in the research of battery health state prediction. According to the capacity attenuation curve obtained from the battery charge and discharge experimental data, the RUL of the battery is predicted by PF in the studies by Pan et al. (2021) and Gao et al. (2020). Considering the chemical mechanism of battery, a PF prediction framework based on the electrochemical model is proposed for the RUL prediction of lithium ion battery (Liu et al., 2020). Aiming at the particle degradation problem of the PF algorithm, many studies have also proposed many improved algorithms. An improved untracked PF method is proposed to predict the RUL of batteries (Li et al., 2015). Duan et al. (2020) analyzed the problems existing in standard PF and proposd a new extended Kalman PF, which uses the EKF as sampling density function to optimize the PF algorithm. An improved PF algorithm, untracked PF, is introduced into the prediction of battery RUL in the study by Miao et al. (2013). The PF algorithm is used as the main method; double exponential model is used as the equation of state; and artificial neural network is used for resampling to reduce the particle degradation problem in the study by Qin et al. (2020). Jiao et al. (2020) propose a PF framework based on conditional variational automatic encoder and resampling strategy to predict the RUL of battery. In the study by Sun et al. (2018), with the help of β distribution function, combined with capacitance, resistance, and constant current charging time, a comprehensive health indicator is developed to predict the RUL. A third-order polynomial model is used to fit the battery health degradation process; the PF algorithm is used to predict the RUL of the battery. It should be noted that to ensure that the PF algorithm has a good prediction effect, it is very key to establish an appropriate state equation, which has a great impact on the prediction results.

With its powerful self-adaptive feature learning ability, the deep learning model has been applied in many fields and has also been introduced into battery state of health (SOH) prediction by many scholars. Considering uncertainty measurement, feature dimensionality reduction, and various related tasks, an end-to-end deep learning framework is proposed to quickly predict the RUL of lithium-ion batteries in the study by Hong et al. (2020). Ma et al. (2019) proposed a hybrid neural network combined with pseudo nearest neighbor method, combined with the advantages of CNN and LSTM neural network, and designed a hybrid neural network for model training and prediction. An integrated deep learning method is proposed for RUL prediction of lithium-ion battery integrating automatic encoder and deep neural network (Ren et al., 2018). In the study by Wang et al. (2018), aiming at the practical and accurate prediction of RUL of satellite lithium-ion battery, an indirect prediction method is proposed based on dynamic LSTM neural network. Chinomona et al. (2020) proposed a feature selection technique to select the best statistical feature subset and use partial charge and discharge data to determine the RUL of battery via recursive neural network (RNN) and LSTM. In the study by Su et al. (2021), a generalized regression neural network is proposed to estimate the residual capacity of batteries based on several health indicators obtained from the historical operating data of batteries, and a nonlinear autoregression method is applied to predict the RUL of batteries based on the estimated capacity.

Although the deep learning model can adaptively learn high-level degradation features from battery capacity data, it has strong applicability. However, facing the complex degradation trend of lithium ion battery, it still exposes the shortcomings of poor generalization ability and poor robustness due to adopting a single scale. Therefore, many scholars propose some comprehensive methods to predict the SOH of batteries. In the study by Pan et al. (2019), a hybrid method is proposed, including PF, exponential smoothing, and capacity degradation model. An interactive multimodel framework based on PF and SVM is proposed to realize the multistep advance estimation of battery capacity and RUL in the study by Li et al. (2021). Lyu et al. (2021a) combined metabolic gray model and multi-output Gaussian process regression to establish a dynamic data-driven battery degradation model. PF is used to track battery capacity degradation for SOH estimation and extrapolate degradation trajectory for RUL prediction. Che et al. (2021) proposed an RUL prediction method based on optimized health indicators and transfer learning online model modification. On this basis, a method combining transfer learning and gated recurrent neural network is designed to predict the RUL directly according to the optimized health indicators, to promote online application. A generative adversarial network based on ternary network is proposed to solve the problem of leak detection when sensor data is incomplete (Hu et al., 2021a; Hu et al., 2021b).

As a matter of fact, there are some factors such as capacity regeneration and random interference in the use of lithium ion battery, which lead to the problem of insufficient prediction accuracy and generalization ability of single model or comprehensive method using single scale feature. The data-driven methods mentioned above take the battery capacity data as a single variable, so the predicted results of battery life are not sensitive to capacity regeneration, random interference, and other factors, leading to a large error between the prediction results and the actual values. Decomposing the battery capacity data into multiple variables of different scales can preserve some details of the data, then select the appropriate prediction method according to the characteristics of variables of different scales, and finally reconstruct the prediction results of different scales, which will be an effective way to improve the prediction accuracy. Variable mode decomposition (VMD) is an adaptive and completely non recursive method of modal variation and signal processing. This technology overcomes the problems of endpoint effect and modal component aliasing in empirical mode decomposition (EMD) method, and has a more solid mathematical theoretical basis. It can reduce the non-stationarity of time series with high complexity and strong nonlinearity. The relatively stable subsequences with different frequency scales obtained by decomposition are suitable for non-stationary sequences. LSTM is very suitable for dealing with prediction problems highly related to time series. Self-attention mechanism can help the model give different weights to the input features, extract more critical and important information, and make the model make more accurate judgments without bringing greater overhead to the calculation and storage of the model. Therefore, in this article we propose a hybrid prediction method for the SOH of lithium batteries based on variational mode decomposition and LSTM with self-attention mechanism (SA-LSTM) model, which makes up for the shortcomings of the degradation characteristics of battery performance that cannot be fully covered by a single scale input, low prediction accuracy, and poor generalization performance of a single model.

Methodology

Prediction Process and Steps of Battery State of Health

Lithium ion battery capacity is easy to collect and can reflect the performance degradation trend of the battery. It is often used as an indicator to evaluate the SOH of the battery. In IEEE standard 1188-1996, battery failure is defined as when the capacity of the battery degrades to 80% of the rated capacity. Therefore, the RUL of the battery is defined as the cycles of charge and discharge when the battery capacity decays to 80% of the rated capacity.

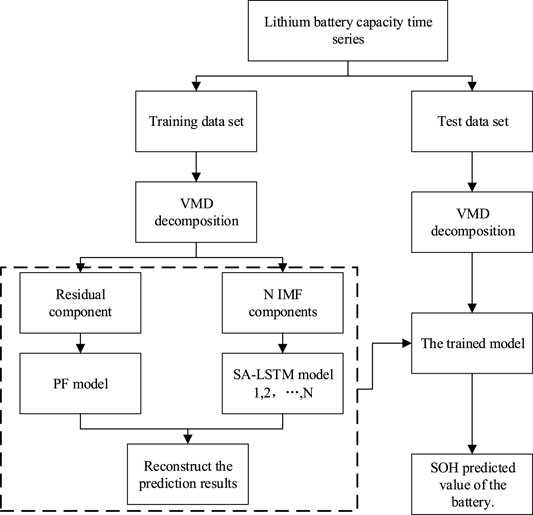
A method for predicting the SOH of lithium ion battery is proposed in this article by comprehensively using VMD, PF, and SA-LSTM. Firstly, VMD is used to decompose the intrinsic mode function (IMF) components with different scales and residual component from the lithium ion battery capacity time series. Then, each IMF component from the training data set is input into the SA-LSTM for training, and the residual component is input into the PF for training. Finally, the test data component is input into the trained model for the next cycle of value prediction, and the prediction results of each component are summed to obtain the predicted value of battery capacity. The overall prediction process is shown in Figure 1.

FIGURE 1

FIGURE 1. Overall process of battery capacity prediction.

The specific steps of the battery SOH prediction method proposed in this article are as follows:

1) Obtain lithium ion battery capacity degradation data. Divide the lithium ion battery capacity degradation data at time $1,\cdots ,t$ as the training set, and the data after time $t+1$ as the test set.

2) Variational modal decomposition. The capacity degradation data of lithium ion battery is decomposed by VMD to obtain multiple IMF components and residual components. The residual component can reflect the overall degradation trend of lithium ion battery capacity, and the IMF components can reflect the battery capacity regeneration and random fluctuation.

3) Use PF to predict the residual component. The residual component can reflect the overall degradation trend of battery capacity and has monotonicity and stability. The PF method has good advantages for the prediction of this time series data.

4) Construct SA-LSTM network to predict the IMF components. The IMF components reflect the lithium ion battery capacity regeneration and random fluctuation, which show a certain periodicity. Therefore, the LSTM network is selected as the prediction method. In order to improve the invalid information in the filtering deep features of the LSTM network and enhance the weight of the effective features, the self-attention mechanism is introduced to improve the prediction accuracy of the LSTM network. Each IMF component is input into the SA-LSTM network with the same structure for independent training and prediction.

5) Reconstruct predicted capacity of battery. The predicted value of battery capacity can be obtained by summing the prediction results of each IMF component and residual component according to Eq. 1.

${\widehat{C}}_{t+1}={\displaystyle \sum }_{k=1}^K{I}_k\left(t+1\right)+R\left(t+1\right),(1)$

where ${\widehat{C}}_{t+1}$ is the predicted value of battery capacity, $I_k\left(t+1\right)$ is the predicted value of the $k$th IMF component, K is the number of decomposed subsequences, and $R\left(t+1\right)$ is the predicted value of residual component predicted by PF.

Signal Multiscale Decomposition Based on Variational Mode Decomposition

VMD is developed from EMD. EMD has the disadvantages of mode aliasing, and it is difficult to determine endpoint effects and stop conditions. Compared with the recursive decomposition mode of EMD, VMD transforms the signal decomposition into a variational decomposition mode. In essence, it uses multiple adaptive Wiener filter banks to realize the adaptive segmentation of each component of the signal in the frequency domain. VMD can effectively overcome the mode aliasing phenomenon in EMD decomposition, has stronger noise robustness and weaker endpoint effect than EMD, and improves the decomposition component stationarity of nonlinear time series. The battery capacity degradation data of lithium ion battery not only contains the overall degradation trend information but also has the random fluctuation caused by factors such as battery capacity regeneration. Therefore, VMD can be used for multiscale decomposition to extract the features of battery capacity degradation at different scales. The essence of VMD is to construct and solve variational problems. For a signal $f\left(t\right)$, the corresponding constrained variational model is shown Eq. 2.

${\min }_{\left\{u_k\right\},\left\{w_k\right\}}\left\{{\displaystyle \sum }_{k=1}^K\Vert {\partial }_t\left[\left(\delta \left(t\right)+\frac{j}{\pi }\right)\ast u_k\left(t\right)\right]\ast {e^{-j{w}_{k}t}\Vert }_2^2\right\},(2)$

$s.t. {\displaystyle \sum }_{k=1}^K{u}_k\left(t\right)=f\left(t\right),(3)$

where $\left\{u_k\right\}$ is the $k$ decomposed IMF components, i.e., $\left\{u_k\right\}=\left\{u_1,\cdots ,u_k\right\}$, $\left\{w_k\right\}$ is the central frequency of each IMF, i.e., $\left\{w_k\right\}=\left\{w_1,\cdots ,w_k\right\},$ * represents convolution operation, ${\partial }_t$ means partial derivative, and $\delta \left(t\right)$ is Dirac function.

The constrained variational problem is changed into an unconstrained variational problem as Eq. 4, by introducing Lagrange operator $\lambda$ and quadratic penalty factor $\alpha$ into Eq. 2.

$\text{Γ}\left(\left\{u_k\right\},\left\{w_k\right\},\lambda \right)=\alpha {\displaystyle \sum }_{k=1}^K\Vert {\partial }_t\left[\left(\delta \left(t\right)+\frac{j}{\pi }\right)\ast u_k\left(t\right)\right]\ast {e^{-j{w}_{k}t}\Vert }_2^2+||f\left(t\right)-{\displaystyle \sum }_{k=1}^K{u}_k{\left(t\right)}_2^2-<\lambda \left(t\right),f\left(t\right)-{\displaystyle \sum }_{k=1}^K{u}_k\left(t\right)>.(4)$

The alternating direction method of multipliers is adopted to update $w_k^{n+1}$, $u_k^{n+1}$, and $\lambda$ in Eq. 4. The calculation is iterated repeatedly until the convergence condition Eq. 5 is satisfied.

${\displaystyle \sum }_k\frac{\Vert u_k^{n+1}-{u_k^n\Vert }_2^2}{{\Vert u_k^n\Vert }_2^2}<\epsilon \text{and}\mathit{n<N},(5)$

where $\epsilon$ is the termination iteration threshold, and $N$ is the maximum number of iterations. The capacity degradation data of lithium ion battery is decomposed into the multiscale expression of capacity data, including IMF components and residual component by VMD.

Particle Filter Algorithm

PF is widely used in the field of visual tracking, signal processing, robotics, image processing, financial economy, target positioning, navigation, and tracking. In this article, the PF model is applied to predict the SOH of lithium ion battery. Assume that the state equation of the system is as Eq. 6.

${\text{X}}_k=f\left(X_{k-1},W_k\right),(6)$

where ${\text{X}}_k$ is the state of the system at time $\text{k}$, $\text{f}(\cdot )$ represents the mapping function, $W_k$ represents the system process noise, if suppose $W_k$ follows the Gaussian distribution with a mean value of 0 and variance of $\text{Q}$, i.e., $W_k˜N\left(0,Q\right)$.

Let the state observation equation of the system be as Eq. 7.

${\text{Z}}_k=h\left(X_k,V_k\right),(7)$

where ${\text{Z}}_k$ is the measurement result of system state characteristics at time $\text{k}$, $\text{h}(\cdot )$ represents the mapping function, and $V_k$ is the measurement noise.

The specific steps of the PF algorithm are as follows:

1) Initialization. When $\text{k}=0$, the particle set $\left\{x_0^i,{\omega }_0^i\right\}˜p_0\left(x_0\right)$ is randomly generated according to the initial distribution, ${\omega }_0^i=\frac{1}{N}, i=\mathrm{1,2},\cdots ,\text{N}$。.

2) Importance sampling. When $\text{k}>0$, from importance function ${\text{x}}_k^i˜q\left(x_k{|x}_{k-1}^i,z_{1:k}\right)$, randomly extract $\text{N}$ particles, $i=\mathrm{1,2},\cdots ,N$.

3) Update weight. At time $k$, the weight of the sampled particles ${\text{ω}}_k^i$ is calculated as follows:

${\text{ω}}_k^i={\text{ω}}_{k-1}^i\frac{p\left(z_k\text{|}{\widehat{x}}_k^i\right)p\left({\widehat{x}}_k^i\text{|}{\widehat{x}}_{k-1}^i\right)}{p\left({\widehat{x}}_k^i\text{|}{x}_{k-1}^i,z_{1:k}\right)}.(8)$

4) Normalized weight.

${\widetilde{\text{ω}}}_k^i={\text{ω}}_k^i/{\displaystyle \sum }_{i=1}^N{\text{ω}}_k^i.(9)$

5) Resampling. New particles are obtained by resampling according to the importance weight, and the average weight is $1/N$. Particle degradation is an inevitable phenomenon in the PF algorithm. Resampling can reduce particle degradation.

6) State estimation. The estimated state is obtained by weighted summation of the extracted particles.

${\widehat{x}}_k={\displaystyle \sum }_{i=1}^N{\widetilde{\text{ω}}}_k^i{\widehat{x}}_k^i.(10)$

In this article, the double exponential empirical model (Jiao et al., 2020) is selected as the battery capacity degradation model, as shown in Eq. 11.

$\text{C}=\text{a∗exp}\left(b\ast n\right)+c\ast \text{exp}\left(d\ast n\right).(11)$

where $n$ is the number of cycles, $C, a, b,c, d$ contain Gaussian white noise, the mean value is 0, and the variance is unknown. The state of the prediction model can be denoted as Eq. 12.

$\text{X}\left(n\right)={\left[a\left(n\right),b\left(n\right),c\left(n\right),d\left(n\right)\right]}^T.(12)$

where the initial values of $a, b,c\text{ and} d$ can be obtained by using the least square method according to the training data.

The state update equation of the four parameters can be expressed as Eq. 13.

$\{\begin{array}{c}a\left(n+1\right)=a\left(n\right)+w_a\left(n\right), w_a˜N\left(0,{\sigma }_a\right)\\ b\left(n+1\right)=b\left(n\right)+w_b\left(n\right), w_b˜N\left(0,{\sigma }_b\right)\\ c\left(n+1\right)=c\left(n\right)+w_c\left(n\right), w_c˜N\left(0,{\sigma }_c\right)\\ d\left(n+1\right)=d\left(n\right)+w_d\left(n\right), w_d˜N\left(0,{\sigma }_d\right)\end{array}.(13)$

Therefore, the observation equation of battery capacity can be expressed as Eq. 14.

$C\left(n\right)=\text{a}\left(n\right)\text{∗exp}\left(b\left(n\right)\ast n\right)+c\left(n\right)\ast exp\left(d\left(n\right)\ast n\right)+v\left(n\right),(14)$

where $v\left(n\right)$ represents the measurement noise, and it is a Gaussian white noise when mean value is 0 and variance ${\text{σ}}_v$, i.e., $v\left(n\right)˜N\left(0,{\sigma }_v\right)$.

Long Short-Term Memory Model

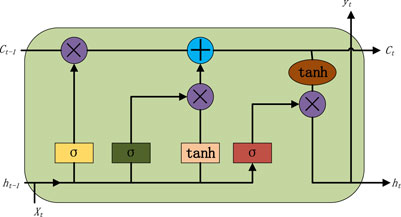
LSTM is a variant of RNN, which can reduce the problem of gradient disappearance or gradient explosion of RNN. Its structure is shown in Figure 2.

FIGURE 2

FIGURE 2. The structure of LSTM.

At time t, the network output value $y_t$ can be expressed as Eq. 15.

$y_t=\sigma \left(W_{xc}{x}_t+W_{hc}{c}_{t-1}+b_c\right),(15)$

where $W_{xc}$ is the weight matrix from input layer to hidden layer, $c_{t-1}$ is the output value of the hidden layer at time $t-1$, $W_{hc}$ is the weight matrix from the memory cell to the previous hidden layer, $b_c$ is the offset of the hidden layer, and $\text{σ}$ is the sigmoid nonlinear activation function.

The update status of the network during training is as follows:

1) Temporary memory status information ${\widehat{c}}_t$: before updating memory unit $c_t$, a temporary memory unit ${\widehat{c}}_t$ is generated, which can be calculated from the input $x_t$ of current time and the hidden state value $h_{t-1}$ of the previous time, and the calculation formula is as in Eq. 16:

${\widehat{c}}_t=tanh\left(W_{xc}{x}_t+W_{hc}{h}_{t-1}+b_c\right).(16)$

2) Calculate input gate value $i_t$: for input data, $i_t$ stores critical information to this unit with a limited extent, and the calculation formula is as in Eq. 17:

$i_t=\sigma \left(W_{xi}{x}_t+W_{hi}{h}_{t-1}+b_i\right).(17)$

3) Calculate the forgetting gate value f_t: the calculation formula is as in Eq. 18:

$f_t=\sigma \left(W_{xf}{x}_t+W_{hf}{h}_{t-1}+b_f\right).(18)$

4) Calculate the current memory unit status value $c_t$: the calculation formula is as in Eq. 19:

$c_t=f_t\ast c_{t-1}+i_t\ast {\widehat{c}}_t,(19)$

where * represents convolution.

5) Calculation output gate $o_t$: the prediction result currently is as in Eq. 20:

$o_t=\sigma \left(W_{xo}{x}_t+W_{ho}{h}_{t-1}+b_o\right).(20)$

6) Unit memory output: the calculation formula is as in Eq. 21:

$h_t=o_{t}tanh\left(c_t\right).(21)$

In the above formula, $W$ is the weight coefficient matrix, and $b$ is the offset vector.

To make the prediction result fully close to the real value, the direction propagation algorithm is used to adjust the weight matrix $W$ and offset vector $b$ in LSTM. In the process, we adopt the minimization loss function as in Eq. 22.

$Loss=\frac{1}{2}{\displaystyle \sum }_{k=1}^N{\left(y-\widehat{y}\right)}^2(22)$

where $y$ is the true value, and $\widehat{y}$ is the predicted value.

At last, the training data of battery capacity IMF components decomposed by VMD are input into LSTM network for training, and then the test data are input into the trained LSTM to get the prediction result of the next time.

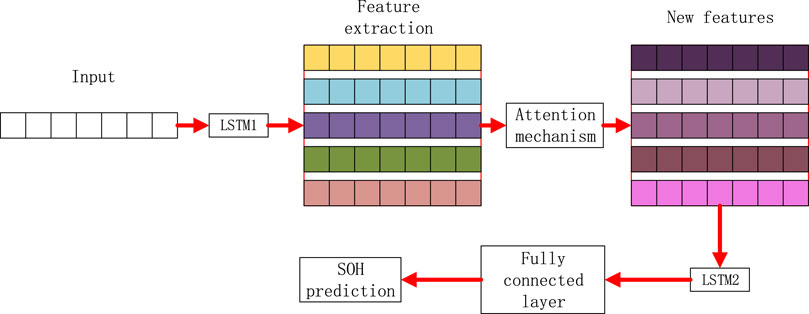
Self-Attention Mechanism

Self-attention mechanism can filter some irrelevant information in feature data, which adopts the query–key–value model. Suppose $X=\left[x_1,\cdots ,x_N\right]$ is the input sequence, and $H=\left[h_1,\cdots ,h_N\right]$ is the output sequence. In the calculation process of self-attention model, each input $x_i$ is mapped to three different spaces linearly to calculate the query vector $Q_i$, key vector $K_i$, and value vector $V_i$. They can be formulated as in Eqs 23–25:

$Q=W_{q}X(23)$

$K=W_{k}X,(24)$

$V=W_{v}X,(25)$

where $W_q$, $W_k$, and $W_v$ are linear mapping parameter matrix of three spaces, respectively. The output vector $H$ can be calculated by Eq. 26.

$H=Attention\left(Q,K,V\right)=softmax\left(\frac{Q{K}^T}{\sqrt{d_k}}\right),(26)$

where $d_k$ is the dimension of $K$. In this work, self-attention mechanism is employed to predict the battery SOH, which is mixed with multilayer LSTM. The specific process is as shown in Figure 3.

FIGURE 3

FIGURE 3. Battery SOH prediction process using SA-LSTM.

Experimental Verification

Introduction of Experimental Data

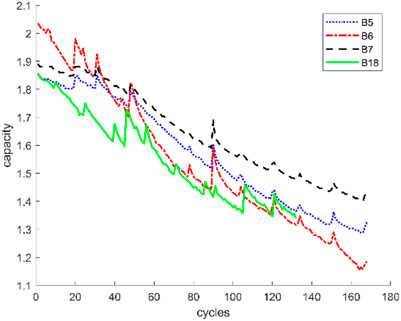
The lithium ion battery data used in this article are from the Idaho National Laboratory of NASA PCoE research center. In this experiment, there are four groups: 18650s batteries with a rated capacity of 2 Ah, which are numbered B5, B6, B7, and B18, respectively, and the ambient temperature is set to 24°C. The charging and discharging process of the battery is specified as follows. The maximum cut-off voltage of charging is set to 4.2 V. The battery is charged at a constant current of 1.5 A at the beginning. When the voltage reaches the maximum cut-off voltage, it will be charged at a constant voltage. When the charging current drops to 20 mA, the charging ends. When the battery is discharged, it is discharged at a constant current of 2 A to a capacity of 2.7 V. A battery cycle includes completing a charge and a discharge. We extract the battery capacity change data from the experimental data. The capacity data of the four batteries are all one-dimensional time series. The data length of B5, B6, and B7 is 167, and the data length of B18 is 132.

Variational Mode Decomposition of Battery Capacity Data

As described above, Figure 4 shows the capacity degradation of the four lithium batteries after multiple cycles. It can be seen that the battery capacity not only has an obvious downward trend but also has random fluctuations caused by factors such as battery capacity regeneration.

FIGURE 4

FIGURE 4. Capacity degradation curve of four batteries.

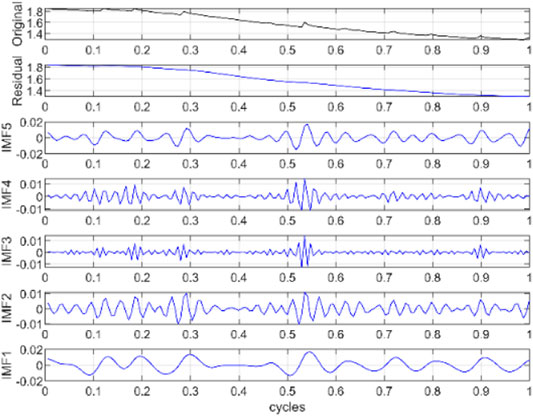
VMD is performed on the obtained lithium ion battery capacity data. Figure 5 shows the original capacity curve and components decomposed by VMD of B5 battery. In the VMD, the sequence number K is set to 6, and the relevant parameter alpha is set to 20. It can be seen that the residual component can show the global degradation trend of lithium ion battery performance, and the IMF components (IMF1–IMF5) can effectively reflect the local regeneration and the random fluctuation characteristics in the degradation of battery capacity.

FIGURE 5

FIGURE 5. VMD results of B5 battery capacity data.

Battery Capacity Degradation Prediction

After VMD, the residual component is trained and predicted by the PF method, and IMF components are input into the SA-LSTM for training and predicting. Taking B5 battery as an example, there are 168 sets of data. In this article, the first 67% sets are used as the training set and the rest as the test set, that is, 112 sets of training data and 56 sets of test data. In our experiment, the capacity data of the previous three consecutive cycles is used to predict the capacity of the next cycle. Firstly, the residual component is input into the PF algorithm, the first 10 sets of data are used to calculate the initial values of $a,b,c$, and $d$ via the least square method. The particles number is set to 300, and the variances are set as follows: ${\sigma }_a=1e-8, {\sigma }_b=1e-6$, ${\sigma }_c=1e-5$, and ${\sigma }_d=1e-7$. The prediction results are shown in Figure 6. The PF algorithm maintains high accuracy in all prediction groups. This also indicates that the PF algorithm has a good accuracy in the prediction of degradation time series with obvious function type curves.

FIGURE 6

FIGURE 6. PF prediction results of battery B5 residual component.

Following the same training sets and test sets ratio, the five IMF components decomposed by VMD are input into the SA-LSTM network for training and predicting. The specific structure and parameters of the SA-LSTM network are shown in Table 1. In this work, the training iterations is set to 200, the batch is set to 10, and the initial learning rate is set to 0.005.

TABLE 1

TABLE 1. Network structure of SA-LSTM.

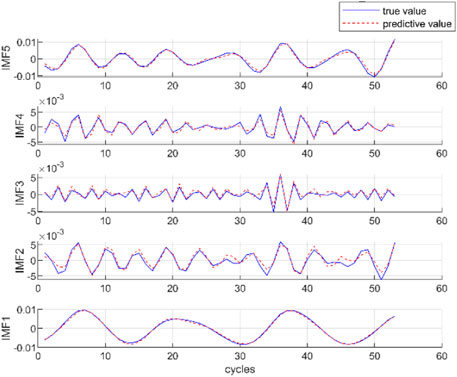
Figure 7 shows the prediction results of IMF components, each component is trained and predicted separately. It can be seen that the prediction results of the proposed SA-LSTM prediction network fit well with the real values, which also shows that the SA-LSTM model has advantages in nonlinear time series prediction.

FIGURE 7

FIGURE 7. Prediction result of IMF components.

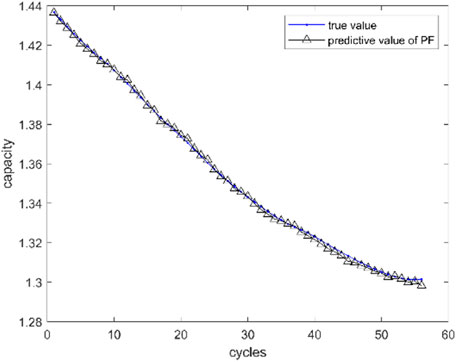
At last, the prediction results of the residual component and IMF components are reconstructed by Eq. 1, and we can obtain the predicted results of lithium ion battery capacity, which is shown in Figure 8. The prediction result is highly consistent with the measured values of battery capacity. It can not only predict the degradation trend of battery capacity but also adapt to the random fluctuation of battery capacity regeneration.

FIGURE 8

FIGURE 8. Capacity prediction results of B5 battery.

Evaluation Index

To evaluate the performance of the proposed prediction method and other methods, three common indexes are used to measure the prediction effect, including the mean absolute percentage error (MAPE), root mean square error (RMSE), and mean absolute error (MAE) (Pan et al., 2019).

The calculation formulas of the three indexes are as follows:

$MAPE=\frac{1}{N}{\displaystyle \sum }_{i=1}^N\frac{\left|\widehat{C}\left(i\right)-C\left(i\right)\right|}{C\left(i\right)}\times 100\%,(27)$

$RMSE=\sqrt{\frac{1}{N}{\displaystyle \sum }_{i=1}^N{\left|\widehat{C}\left(i\right)-C\left(i\right)\right|}^2},(28)$

$MAE=\frac{1}{N}{\displaystyle \sum }_{i=1}^N\left|\widehat{C}\left(i\right)-C\left(i\right)\right|,(29)$

where $\widehat{C}\left(i\right)$ is the predicted value of battery capacity, $C\left(i\right)$ is the true measurement value of the battery, and $N$ is the cycle number of prediction.

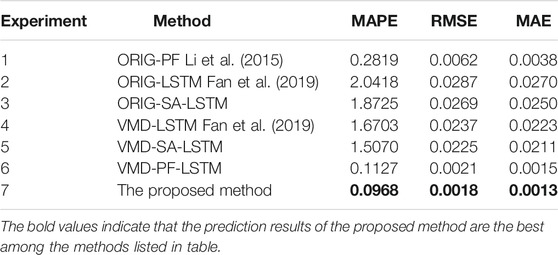
Comparison of Prediction Results

To verify the superiority of the prediction method proposed in this article, it is compared with some commonly used methods, including the following methods:

1) The original data of battery capacity measurement is directly used for SOH prediction by PF algorithm (ORIG-PF).

2) The original data of battery capacity measurement value is directly used for SOH prediction by LSTM network (ORIG-LSTM).

3) The original data of battery capacity measurement value is directly used for SOH prediction by SA-LSTM network (ORIG-SA-LSTM).

4) Firstly, the battery capacity measurement data is decomposed by VMD, then LSTM is used for the prediction of all components, and finally, the predicted value of capacity is reconstructed using Eq. 1 (VMD-LSTM).

5) Firstly, the battery capacity measurement data is decomposed by VMD, then SA-LSTM is used for the prediction of all components, and finally, the predicted value of capacity is reconstructed using Eq. 1 (VMD-SA-LSTM).

6) Firstly, the battery capacity measurement data is decomposed by VMD, then PF is used for the prediction of residual component and LSTM is used for the prediction of IMF components, and finally, the predicted value of capacity is reconstructed using Eq. 1 (VMD-PF-LSTM).

7) The proposed method. Firstly, the battery capacity measurement data is decomposed by VMD, then PF is used for the prediction of residual component and SA-LSTM is used for the prediction of IMF components, and finally, the predicted value of capacity is reconstructed using Eq. 1 (VMD-PF-LSTM).

The B5 battery capacity degradation data is taken as experimental data, and the above seven methods are used for experiments. The final prediction results are shown in Table 2. To avoid accidental errors, each experiment is repeated 20 times, and the average value of the prediction results is taken as the final prediction results.

TABLE 2

TABLE 2. Comparison of prediction results.

It should be noted that the LSTM structure in the above methods is the same as that shown in Table 1, and only the “SeqSelfAttention” layer is removed. For the seven experiments listed in Table 2, only one prediction method is used in experiments 1–3, and more than two comprehensive prediction methods are used in experiments 4–7. It can be seen from the evaluation indexes:

1) The method proposed in this article has the highest prediction accuracy.

2) In the prediction experiments using a single method, the PF method has the best prediction effect, which also shows that the PF algorithm has good advantages in lithium ion battery capacity prediction, so many studies on lithium ion battery capacity prediction adopt the PF method or its improved method.

3) Comparing experiment 2 with experiment 3, experiment 4 with experiment 5, and experiment 6 with experiment 7, it can be seen from the evaluation indexes that the prediction effect of SA-LSTM is better than that of LSTM. This illustrates that self-attention mechanism can further reduce noise and improve the prediction accuracy of deep network.

4) Comparing experiment 2 with experiment 4 and experiment 3 with experiment 5, it can be seen that VMD can greatly improve the prediction effect. It shows that VMD multiscale decomposition can effectively reduce the influence of capacity degradation data non-stationarity on prediction.

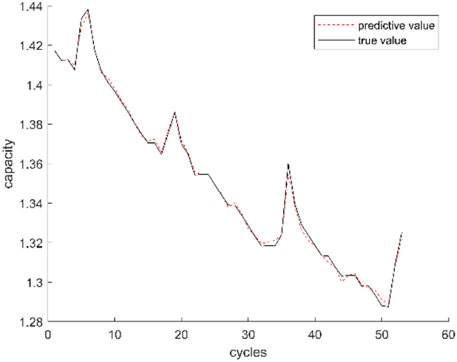
Finally, to further verify the generalization performance of the proposed method, comparative experiments were carried out using the battery capacity data of B6, B7, and B18. The results are shown in Figure 9. As can be seen from Figure 9, the prediction method proposed in this article has the best evaluation indexes for different battery capacity prediction, which shows that the method not only has good prediction accuracy but also has good generalization ability, and the prediction results for different batteries are relatively stable.

FIGURE 9

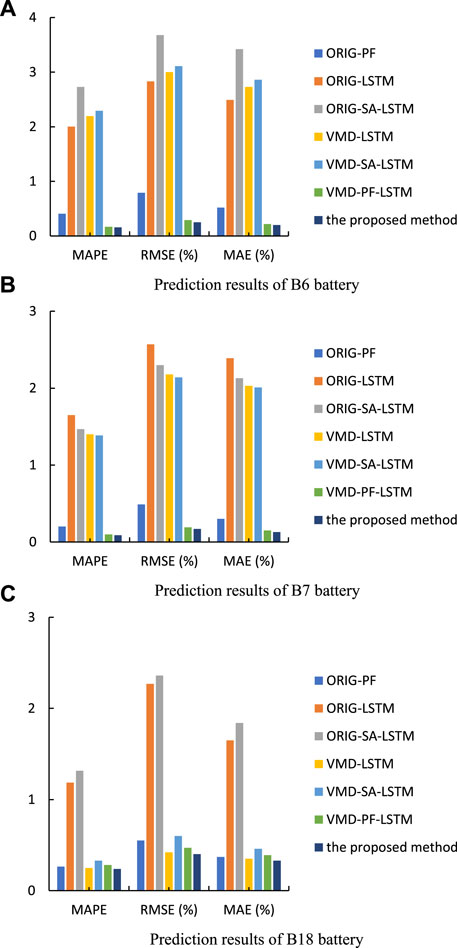
FIGURE 9. Prediction results of B6, B7, and B18 batteries. (A) Prediction results of B6 battery. (B) Prediction results of B7 battery. (C) Prediction results of B18 battery.

Conclusion

In this article, we proposed a comprehensive method for lithium ion battery SOH prediction based on VMD, PF, and LSTM with self-attention mechanism. VMD can decompose the lithium ion battery capacity data into components with a different scale, which can effectively reduce the influence of data instability caused by capacity regeneration on the prediction accuracy. According to the characteristics of the residual component and IMF components decomposed by VMD, the PF and SA-LSTM algorithms were used to predict the battery capacity, which solves the problems of low accuracy and poor generalization ability of single model prediction. NASA lithium ion battery data experiments showed that the prediction method proposed in this article had higher prediction accuracy and stronger stability than the common prediction method.

In future research, we will focus on the following issues: 1) research on battery health prediction methods under different working conditions, 2) automatic optimization of relevant parameters in data-driven methods, 3) prediction models based on multiple feature types, and 4) battery capacity prediction under zero sample conditions.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding author.

Author Contributions

YG performed the data analyses and wrote the manuscript. FZ helped perform the analysis with constructive discussions. YR performed the experiment. All authors listed have approved the work for publication.

Funding

This work was supported by the Suzhou Science and Technology Foundation of China under Grant SYG202021, and partly by the higher education colleges in Jiangsu province (No. 20KJA460011), and partly by the higher education colleges in Jiangsu province (No. 21KJA510003).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Che, Y., Deng, Z., Lin, X., Hu, L., and Hu, X. (2021). Predictive Battery Health Management with Transfer Learning and Online Model Correction. IEEE Trans. Veh. Technol. 70, 1269–1277. doi:10.1109/tvt.2021.3055811

CrossRef Full Text | Google Scholar

Chen, Z., Xue, Q., Wu, Y., Shen, S., Zhang, Y., and Shen, J. (2020). Capacity Prediction and Validation of Lithium-Ion Batteries Based on Long Short-Term Memory Recurrent Neural Network. Ieee Access 8, 172783–172798. doi:10.1109/access.2020.3025766

CrossRef Full Text | Google Scholar

Chinomona, B., Chung, C., Chang, L.-K., Su, W.-C., and Tsai, M.-C. (2020). Long Short-Term Memory Approach to Estimate Battery Remaining Useful Life Using Partial Data. Ieee Access 8, 165419–165431. doi:10.1109/access.2020.3022505

CrossRef Full Text | Google Scholar

Duan, B., Zhang, Q., Geng, F., and Zhang, C. (2020). Remaining Useful Life Prediction of Lithium‐ion Battery Based on Extended Kalman Particle Filter. Int. J. Energ. Res 44, 1724–1734. doi:10.1002/er.5002

CrossRef Full Text | Google Scholar

Fan, J., Fan, J., Liu, F., Qu, J., and Li, R. (2019). A Novel Machine Learning Method Based Approach for Li-Ion Battery Prognostic and Health Management. Ieee Access 7, 160043–160061. doi:10.1109/access.2019.2947843

CrossRef Full Text | Google Scholar

Gao, D., Zhou, Y., Wang, T., and Wang, Y. (2020). A Method for Predicting the Remaining Useful Life of Lithium-Ion Batteries Based on Particle Filter Using Kendall Rank Correlation Coefficient. Energies 13, 4183. doi:10.3390/en13164183

CrossRef Full Text | Google Scholar

Hong, J., Lee, D., Jeong, E.-R., and Yi, Y. (2020). Towards the Swift Prediction of the Remaining Useful Life of Lithium-Ion Batteries with End-To-End Deep Learning. Appl. Energ. 278, 115646. doi:10.1016/j.apenergy.2020.115646

CrossRef Full Text | Google Scholar

Hu, X., Zhang, H., Ma, D., and Wang, R. (2021a). Hierarchical Pressure Data Recovery for Pipeline Network via Generative Adversarial Networks. IEEE Trans. Automat. Sci. Eng., 1–11. doi:10.1109/TASE.2021.3069003

CrossRef Full Text | Google Scholar

Hu, X., Zhang, H., Ma, D., and Wang, R. (2021b). A tnGAN-Based Leak Detection Method for Pipeline Network Considering Incomplete Sensor Data. IEEE Trans. Instrum. Meas. 70, 1–10. doi:10.1109/tim.2020.3045843

CrossRef Full Text | Google Scholar

Jiao, R., Peng, K., and Dong, J. (2020). Remaining Useful Life Prediction of Lithium-Ion Batteries Based on Conditional Variational Autoencoders-Particle Filter. IEEE Trans. Instrum. Meas. 69, 8831–8843. doi:10.1109/tim.2020.2996004

CrossRef Full Text | Google Scholar

Kaur, K., Garg, A., Cui, X., Singh, S., and Panigrahi, B. K. (2021). Deep Learning Networks for Capacity Estimation for Monitoring SOH of Li‐Ion Batteries for Electric Vehicles. Int. J. Energ. Res 45, 3113–3128. doi:10.1002/er.6005

CrossRef Full Text | Google Scholar

Li, L., Wang, Z., and Jiang, H. (2015). Storage Battery Remaining Useful Life Prognosis Using Improved Unscented Particle Filter. Proc. Inst. Mech. Eng. O: J. Risk Reliability 229, 52–61. doi:10.1177/1748006x14550662

CrossRef Full Text | Google Scholar

Li, Y., Zou, C., Berecibar, M., Nanini-Maury, E., Chan, J. C.-W., Van Den Bossche, P., et al. (2018). Random forest Regression for Online Capacity Estimation of Lithium-Ion Batteries. Appl. Energ. 232, 197–210. doi:10.1016/j.apenergy.2018.09.182

CrossRef Full Text | Google Scholar

Li, X., Yuan, C., and Wang, Z. (2020). State of Health Estimation for Li-Ion Battery via Partial Incremental Capacity Analysis Based on Support Vector Regression. Energy 203, 117852. doi:10.1016/j.energy.2020.117852

CrossRef Full Text | Google Scholar

Li, S., Fang, H., and Shi, B. (2021). Remaining Useful Life Estimation of Lithium-Ion Battery Based on Interacting Multiple Model Particle Filter and Support Vector Regression. Reliability Eng. Syst. Saf. 210, 107542. doi:10.1016/j.ress.2021.107542

CrossRef Full Text | Google Scholar

Liu, Y., Zhang, C., Jiang, J., Jiang, Y., Zhang, L., and Zhang, W. (2019). Capacity Estimation of Serial Lithium-Ion Battery Pack Using Dynamic Time Warping Algorithm. Ieee Access 7, 174687–174698. doi:10.1109/access.2019.2956326

CrossRef Full Text | Google Scholar

Liu, Q., Zhang, J., Li, K., and Lv, C. (2020). The Remaining Useful Life Prediction by Using Electrochemical Model in the Particle Filter Framework for Lithium-Ion Batteries. Ieee Access 8, 126661–126670. doi:10.1109/access.2020.3006157

CrossRef Full Text | Google Scholar

Lyu, Z., Gao, R., and Chen, L. (2021a). Li-Ion Battery State of Health Estimation and Remaining Useful Life Prediction through a Model-Data-Fusion Method. IEEE Trans. Power Electron. 36, 6228–6240. doi:10.1109/tpel.2020.3033297

CrossRef Full Text | Google Scholar

Lyu, Z., Gao, R., and Li, X. (2021b). A Partial Charging Curve-Based Data-Fusion-Model Method for Capacity Estimation of Li-Ion Battery. J. Power Sourc. 483, 229131. doi:10.1016/j.jpowsour.2020.229131

CrossRef Full Text | Google Scholar

Ma, G., Zhang, Y., Cheng, C., Zhou, B., Hu, P., and Yuan, Y. (2019). Remaining Useful Life Prediction of Lithium-Ion Batteries Based on False Nearest Neighbors and a Hybrid Neural Network. Appl. Energ. 253, 113626. doi:10.1016/j.apenergy.2019.113626

CrossRef Full Text | Google Scholar

Miao, Q., Xie, L., Cui, H., Liang, W., and Pecht, M. (2013). Remaining Useful Life Prediction of Lithium-Ion Battery with Unscented Particle Filter Technique. Microelectronics Reliability 53, 805–810. doi:10.1016/j.microrel.2012.12.004

CrossRef Full Text | Google Scholar

Pan, C., Chen, Y., Wang, L. M., and He, Z. G. (2019). Lithium-Ion Battery Remaining Useful Life Prediction Based on Exponential Smoothing and Particle Filter. Int. J. Electrochem. Sci. 14, 9537–9551. doi:10.20964/2019.10.15

CrossRef Full Text | Google Scholar

Pan, C., Huang, A., He, Z., Lin, C., Sun, Y., Zhao, S., et al. (2021). Prediction of Remaining Useful Life for Lithium‐Ion Battery Based on Particle Filter with Residual Resampling. Energy Sci Eng 9, 1115–1133. doi:10.1002/ese3.877

CrossRef Full Text | Google Scholar

Qian, C., Xu, B., Chang, L., Sun, B., Feng, Q., Yang, D., et al. (2021). Convolutional Neural Network Based Capacity Estimation Using Random Segments of the Charging Curves for Lithium-Ion Batteries. Energy 227, 120333. doi:10.1016/j.energy.2021.120333

CrossRef Full Text | Google Scholar

Qin, W., Lv, H., Liu, C., Nirmalya, D., and Jahanshahi, P. (2020). Remaining Useful Life Prediction for Lithium-Ion Batteries Using Particle Filter and Artificial Neural Network. Ind. Manage. Data Syst. 120, 312–328. doi:10.1108/imds-03-2019-0195

CrossRef Full Text | Google Scholar

Ren, L., Zhao, L., Hong, S., Zhao, S., Wang, H., and Zhang, L. (2018). Remaining Useful Life Prediction for Lithium-Ion Battery: A Deep Learning Approach. Ieee Access 6, 50587–50598. doi:10.1109/access.2018.2858856

CrossRef Full Text | Google Scholar

Su, C., Chen, H., and Wen, Z. (2021). Prediction of Remaining Useful Life for Lithium-Ion Battery with Multiple Health Indicators. Eksploatacja I Niezawodnosc-Maintenance and Reliability 23, 176–183. doi:10.17531/ein.2021.1.18

CrossRef Full Text | Google Scholar

Sun, Y., Hao, X., Pecht, M., and Zhou, Y. (2018). Remaining Useful Life Prediction for Lithium-Ion Batteries Based on an Integrated Health Indicator. Microelectronics Reliability 88-90, 1189–1194. doi:10.1016/j.microrel.2018.07.047

CrossRef Full Text | Google Scholar

Sun, Y., Zhang, J., Zhang, K., Qi, H., and Zhang, C. (2021). Battery State of Health Estimation Method Based on Sparse Auto‐Encoder and Backward Propagation Fading Diversity Among Battery Cells. Int. J. Energ. Res 45, 7651–7662. doi:10.1002/er.6346

CrossRef Full Text | Google Scholar

Wang, C., Lu, N., Wang, S., Cheng, Y., and Jiang, B. (2018). Dynamic Long Short-Term Memory Neural-Network- Based Indirect Remaining-Useful-Life Prognosis for Satellite Lithium-Ion Battery. Appl. Sci. 8, 2078. doi:10.3390/app8112078

CrossRef Full Text | Google Scholar

Xiong, R., Zhang, Y., Wang, J., He, H., Peng, S., and Pecht, M. (2019). Lithium-Ion Battery Health Prognosis Based on a Real Battery Management System Used in Electric Vehicles. IEEE Trans. Veh. Technol. 68, 4110–4121. doi:10.1109/tvt.2018.2864688

CrossRef Full Text | Google Scholar

Xu, T., Peng, Z., and Wu, L. (2021). A Novel Data-Driven Method for Predicting the Circulating Capacity of Lithium-Ion Battery under Random Variable Current. Energy 218, 119530. doi:10.1016/j.energy.2020.119530

CrossRef Full Text | Google Scholar

Yang, C., Wang, X., Fang, Q., Dai, H., Cao, Y., and Wei, X. (2020). An Online SOC and Capacity Estimation Method for Aged Lithium-Ion Battery Pack Considering Cell Inconsistency. J. Energ. Storage 29, 101250. doi:10.1016/j.est.2020.101250

CrossRef Full Text | Google Scholar

Zhou, Y., Huang, M., and Pecht, M. (2020). Remaining Useful Life Estimation of Lithium-Ion Cells Based on K-Nearest Neighbor Regression with Differential Evolution Optimization. J. Clean. Prod. 249, 119409. doi:10.1016/j.jclepro.2019.119409

CrossRef Full Text | Google Scholar