Parameters Identification of Battery Model Using a Novel Differential Evolution Algorithm Variant

In order to deal with the fluctuation and intermittency of photovoltaic (PV) cells, the battery energy storage system (BESS) as a supplementary power source has been widely concerned. In BESS, the unknown parameters of the battery can affect its output, and its structure determines these parameters. Therefore, it is essential to establish the battery model and extract the parameters accurately, and the existing methods cannot effectively solve this problem. This study proposes an adaptive differential evolution algorithm with the dynamic opposite learning strategy (DOLADE) to deal with the issue. In DOLADE, the number of elite particles and particles with poor performance is expanded, the population’s search area is increased, and the population’s exploration capability is improved. The particles’ search area is dynamically changed to ensure the population has a good exploitation capability. The dynamic opposite learning (DOL) strategy increases the population’s diversity and improves the probability of obtaining the global optimum with a considerable convergence rate. The various discharging experiments are performed, the battery model parameters are identified, and the results are compared with the existing well-established algorithms. The comprehensive results indicate that DOLADE has excellent performance and could deal with similar problems.

1 Introduction

Nowadays, energy has become a vital driving force in social development and progress, and fossil fuels could bring greenhouse effects and environmental pollution, so the application of renewable energy is becoming more and more widespread (Bullich-Massagué et al., 2020; Maghyereh and Abdoh, 2021). Globally, solar energy is the third largest clean resource in addition to wind energy and tidal energy, whose volatility and intermittent nature will limit its further development (Siecker et al., 2017; Zhou et al., 2021a). The battery energy storage system (BESS) can be used as a supplementary power source to alleviate the volatility and intermittency of photovoltaic (PV) cells, providing a new possibility to make the system stable (Farhadi et al., 2019). The complementary working mode of PV cells and BESS can improve the solar utilization efficiency (Cheng et al., 2021) to deal with the imbalance of power output in different environments such as thewide range of light intensity change and the large temperature difference between day and night. The application of the system accelerates the pace of clean energy replacing traditional energy and can effectively alleviate the energy crisis (Xia and Xiang, 2020).

Lithium-ion batteries are the best devices for supplementing the power supply due to their sufficient life span and power/energy density (Li et al., 2021). In recent years, with the deepening of the research, in order to make the output power of PV cells stable at the maximum power point, BESS requires frequent charging and discharging to the PV cell system according to the actual situation. Accurate monitoring of BESS’s working state is significant, reducing the fault tolerance of the system and improving work efficiency. A critical factor reflecting the working condition of BESS is the battery output, which can be determined by the battery’s internal parameters, so obtaining the battery’s internal parameters is of decisive significance for detecting the working state of BESS. Extracting the battery parameters in BESS effectively and accurately is an urgent problem, which will help analyze the system and construct the open circuit voltage (OCV) state of charge (SOC) curve (Yang et al., 2020). The practical application is mainly divided into the deterministic and metaheuristic algorithms, which make the identified parameters different in accuracy, computational efficiency, and resource utilization (Alam et al., 2015). Looking for a more balanced method to solve parameter identification has attracted more and more research and attention in recent years and has become a hot topic.

Through the deterministic algorithm calculated by mathematical regulations, the choice of initial value has remarkable individual aspiration, directly affecting the efficiency of solving problems and the persuasion of results (Chen et al., 2018). Metaheuristic algorithms do not rely on specific mathematical rules but usually combine with defined rules and randomness (Ikeda and Ooka, 2019), which have been employed and utilized to tackle many complex issues as effective solvers due to their simplicity and easy implementation process (Heidari et al., 2019). In recent years, metaheuristic algorithms have been applied to solve parameter identification problems, promoting their development. Tan et al. (2021) pointed out that the real-time SOC of the battery is very important in practice as the indexes ensure the battery’s stable operation. The OCV–SOC relationship was conducted on different time scales based on the second-order RC equivalent circuit model. A dynamic identification algorithm was studied, which got more accurate results and stronger robustness than other algorithms. Zhou et al. (2021b) pointed out that a realistic model and precise model parameters are significant for the safety of electric vehicles and the efficiency of batteries. The traditional solution method has a problem of the limited number of search solutions, leading to insufficient accuracy. Therefore, a coupled hybrid adaptive particle swarm optimization–hybrid simulated annealing (HA-PSO) algorithm was adopted, and further exploration was made. The results concluded that the method could be used as one of the tools to solve the parameter identification of the battery model. In El-Sehiemy et al. (2020), a new model identification method was presented: using the state–space equation of the battery in the equivalent circuit. Then, the parameter identification process was transformed into a nonlinear problem for optimization. A new enhanced sunflower optimization algorithm (ESFOA) has an outstanding performance. Choi et al. (2020) established a subset to store the model parameters to be identified, and a steady-state model was established. The genetic algorithm was applied to the parameter estimation of the model. The parameters determined by the information matrix-based method were compared with the experimental results under different conditions, and the average relative error between them is less than 1.9%.

In addition to identifying the battery parameters in BESS, many existing methods have been designed to extract PV cells’ parameters and have achieved excellent results (Qais et al., 2019). In Zhang et al. (2020), the differential vectors are added to the intelligent algorithm to form a new backtracking search algorithm (BSARDV), which has attracted attention due to its low requirements for initial parameters. In Liang et al. (2020), a multi-structure optimization algorithm (SGEMTO) was proposed to improve the acquisition of useful information in the population. By enhancing the information exchange among the populations, the information transfer between different tasks was realized, so the quality and efficiency of the solution were improved. Lin and Wu (2020) explained that it has great practical significance to determine the parameters of the PV model, especially in predicting the output of the PV array and tracking the maximum power point. They also proposed a niche-based particle swarm optimization in parallel computing architecture (NPSOPC) algorithm to identify the parameters of the PV models.

Although the aforementioned methods have achieved good results, these methods often need to introduce more computing resources to maintain the accuracy of the products and are sensitive to the changes of the specific parameters, which lead to some methods not being popular. The common shortcoming of most metaheuristic algorithms is that if some parameters are set improperly, the desired results will not be obtained. Another disadvantage is that the metaheuristic algorithm may not always converge to the global optimum. If the parameters are adjusted improperly, it is easy for the particles to reach a local optimum, or the particle ability is insufficient. Hence, in order to solve these shortcomings of metaheuristic algorithms, in addition to the extensive research on the efficiency, performance, and results of the traditional algorithm, in recent years, new optimizers with excellent characteristics and new strategies with balanced performance in many aspects have emerged, providing many possibilities for resolving all kinds of complex problems in a variety of different fields.

In this study, a dynamic opposite learning (DOL) strategy is presented and applied to the differential evolution (DE) (Storn and Price, 1997) algorithm to improve DE’s performance in terms of convergence speed and optimization to obtain faster convergence speed and avoid falling into local optimum (Jiang et al., 2013). An adaptive differential evolution algorithm with a dynamic opposite learning strategy (DOLADE) was proposed, which can be used as a potential optimizer for extracting the battery model parameters efficiently and accurately in BESS. In DOLADE, a dynamic opposite learning process is carried out for the particles in the population to increase the population’s diversity and overcome the trap of falling into local optimum and premature convergence. The new population comprises the successfully selected individuals and poorly performing individuals, which is produced by merging two of them into a new set (population). Endowing particles with opposite learning behavior aims to enhance their own exploration (diversification) ability to find those areas with optimal solutions in the early phase and reduce the resource consumption of the particles in the later exploitation phase. By dynamically changing the area to be explored by particles, the particle’s exploitation (intensification) ability can be enhanced, and the exploitation can be carried out in the area of the early potential optimal solution to obtain the global optimum quickly. The DOL strategy balances the individuals’ exploration capability and exploitation capability in the DE algorithm well, which makes the DE algorithm not only obtain the global optimum but also have a fast convergence speed, improving the disadvantages. The performance of DOLADE and the effect of the DOL strategy have been tested in the parameter identification of BESS, and excellent results have been obtained.

The main contributions of this article are as follows:

1) An adaptive differential evolution algorithm with a dynamic opposite learning strategy is proposed. To the best of our knowledge, the DOL strategy is the first attempt to identify the parameters of the battery model in BESS.

2) The particles’ exploration and exploitation capabilities are significantly improved, leading to the speed of acquiring the global optimum considerably, preventing individuals from converging to the local optimal value.

3) According to the large amount of data obtained in the experiment, the parameter identification of the battery model is researched and demonstrated.

4) In order to highlight the effectiveness and competitiveness of DOLADE, the results are compared with several well-established algorithms.

The organization of the rest of this article is arranged as follows: In Section 2, the battery mathematical model in BESS is introduced to determine the objective function and extract the parameters. Section 3 generally presents the basic concepts of an adaptive DE algorithm. In Section 4, the DOLADE algorithm is proposed in detail. The experimental results are analyzed and compared with some algorithms in Section 5. Finally, Section 6 is a summary based on the whole article.

2 Model and Problem Description

A suitable model can accurately simulate the operational characteristics of the battery. The battery model is essential for the SOC estimation and the collaborative work with PV cells (Wang et al., 2017). The primary purpose of building the battery model is to obtain the mathematical relationship between the internal parameters of the battery and the external characteristics and then establish an effective equation to estimate the output voltage of BESS.

2.1 Battery Model in BESS

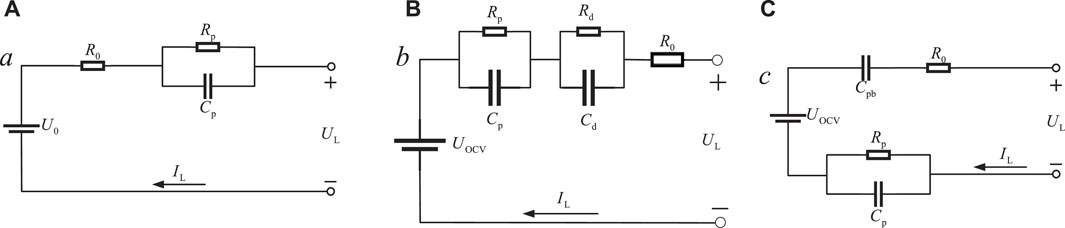
Accurate SOC estimation requires a precise battery model (Liu and Zhang, 2021). There are mainly three types of battery models: the electrochemical model, the mathematical model, and the equivalent circuit model. Among them, the electrochemical model has high accuracy, but the model is complex. The mathematical model is not affected by the external volt–ampere characteristics of the battery, and the model is uncertain due to significant errors. The equivalent circuit model can better simulate the external characteristics of the battery. The equivalent circuit model is mainly divided into the Thevenin model, the second-order RC equivalent circuit model (SECM), and the PNGV model (Bruch et al., 2021). They are shown in Figure 1. For PNGV: In September 1993, USCAR announced the Partnership for a New Generation of Vehicles (PNGVs). The PNGV standard equivalent circuit model was proposed in the PNGV Battery Test Manual published in 2001. A standard method for parameter identification of the model was proposed in the FreedomCAR Battery Test Manual published in 2003. In this research, SECM is employed, which could be used to simulate the external characteristics of the battery. Two RC networks are used to simulate the two dynamic processes of the battery’s electrochemical polarization characteristics and concentration polarization characteristics. While considering the influence of internal ohmic resistance, the internal ohmic resistance is connected in series in the circuit. The electromotive force adopts a controlled voltage source, and the electromotive force and SOC maintain a relatively stable monotonic relationship under a specific condition; the electromotive force can be controlled by SOC (Wang et al., 2020).

FIGURE 1

FIGURE 1. Battery model. (A) Thevenin model. (B) SECM. (C) PNGV.

For the SECM, according to Kirchhoff’s law of voltage and current, the equation could be known as Eq. 1 (Xiong et al., 2012; Bruen and Marco, 2016).

$\left\{\begin{array}{c}{U}_{\mathrm{L}}=U_{\mathrm{O}\mathrm{C}\mathrm{V}}-U_0-U_{\mathrm{P}}-U_{\mathrm{d}}\hfill \\ I_{\mathrm{L}}=\frac{U_{\mathrm{p}}}{R_{\mathrm{p}}}+C_{\mathrm{p}}*\frac{d{U}_{\mathrm{p}}}{dt}\hfill \\ I_{\mathrm{L}}=\frac{U_{\mathrm{d}}}{R_{\mathrm{d}}}+C_{\mathrm{d}}*\frac{d{U}_{\mathrm{d}}}{dt}\hfill \\ I_{\mathrm{L}}=\frac{U_0}{R_0}\hfill \end{array}\right.(1)$

where U_L is the terminal voltage of the BESS output; U_OCV is the open circuit voltage; U₀ is R₀’s voltage; U_p and U_d express the terminal voltages of the two RC networks, respectively; R_p represents the resistance of electrochemical polarization; C_p denotes the capacitance of electrochemical polarization; R_d and C_d are the resistance and the capacitance of concentration polarization, respectively; R_p, C_p, R_d, and C_d constitute two RC parallel loops used to simulate polarization effects; R₀ is the internal resistance; and I_L is the load current. There are five unknown parameters (R_p, C_p, R_d, C_d, and R₀) that could be calculated to observe the actual behavior of BESS.

2.2 Relation Curve Between OCV and SOC

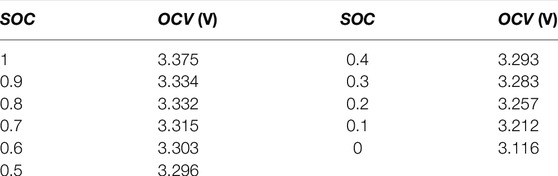
The parameter identification of resistance and capacitance in the battery model requires the value of open circuit voltage (OCV), so OCV is measured first. The identification of OCV is actually carried out to calibrate the relationship curve between OCV and SOC (Wang et al., 2018). The experimental data can depict the OCV–SOC curve, and the functional relationship between them can be obtained (Kang et al., 2012). According to the experimental principle, the practical steps of the static experiment are as follows: first, use the standard charging method to charge the battery fully, let it stand for 1 h, and measure the OCV at SOC = 1. Then, discharge the battery with 6A current for 20 min each time. Finally, let the battery stand for 1 h, and approximate the sampled voltage obtained at this time as the OCV value. There will be a specific difference in the final curve after the still standing time is different. The discharge data of SOC and OCV measured by the experiment are shown in Table 1. Data fitting is performed on the aforementioned experimental data to obtain the functional relationship between OCV and SOC. Considering the two factors of accuracy and computational complexity, a fourth-order polynomial function is selected to fit the experimental data. The fitting result is shown in Eq. 2.

$\begin{array}{c}{U}_{\mathrm{O}\mathrm{C}\mathrm{V}}=-0.925263*SO{C}^4+2.671602*SO{C}^3-\hfill \\ 2.614026*SO{C}^2+1.118892*SOC+3.118363\hfill \end{array}(2)$

TABLE 1

TABLE 1. OCV−SOC experimental data.

2.3 Objective Function

After determining the structure of the battery model, it is necessary to extract the unknown parameters of the battery. The experimental data will be compared with the extracted data. Therefore, choosing an appropriate objective function could minimize the error between the OCV and SOC. A continuous discharging experiment is used for the battery, and the sampling time T = 1s. According to Eq. 1, the differential equation of the battery model can be calculated by Eq. 3. Since sampling of battery discharge data in the experiment is not continuous but at a fixed time interval, the differential equation of Eq. 3 can be rewritten as a discrete differential equation, as shown in Eq. 4, where U_p(k) and U_d(k) represent the kth discrete voltage value of the two RC networks, respectively, U_L(k) denotes the kth discrete output voltage value of the battery, and τ₁ and τ₂ are the time constants of the two RC networks, respectively.

In the calculation process of the metaheuristic algorithm, the particles are saved according to their own objective function value, so the choice of the objective function is crucial. For the battery model parameter identification in BESS, the current data are obtained through the identified parameters, that is, the error between the calculated data and the experimental data is as small as possible. Eq. 5 is used to express the error function between the experimental and measured data for the SECM (Tong et al., 2018), where T is the sampling time; here, T = 1.

$\left\{\begin{array}{c}{U}_{\mathrm{O}\mathrm{C}\mathrm{V}}=f\left(SOC\right)\hfill \\ {\stackrel{•}{U}}_{\mathrm{p}}=\frac{d{U}_{\mathrm{p}}}{dt}\hfill \\ =-\frac{1}{R_{\mathrm{p}}*C_{\mathrm{p}}}*U_{\mathrm{p}}+\frac{1}{C_{\mathrm{p}}}*I_{\mathrm{L}}\hfill \\ {\stackrel{•}{U}}_{\mathrm{d}}=\frac{d{U}_{\mathrm{d}}}{dt}\hfill \\ =-\frac{1}{R_{\mathrm{d}}*C_{\mathrm{d}}}*U_{\mathrm{d}}+\frac{1}{C_{\mathrm{d}}}*I_{\mathrm{L}}\hfill \\ U_{\mathrm{L}}=U_{\mathrm{O}\mathrm{C}\mathrm{V}}-U_{\mathrm{p}}-U_{\mathrm{d}}-R_0*I_{\mathrm{L}}\hfill \end{array}\right.(3)$

$\left\{\begin{array}{c}\hfill U_{\mathrm{p}}\left(k\right)=\exp \left(-\frac{T}{{\tau }_1}\right)*U_{\mathrm{p}}\left(k-1\right)-\left[1-\exp \left(-\frac{T}{{\tau }_1}\right)\right]\hfill \\ \hfill *R_{\mathrm{p}}*I_{\mathrm{L}}\left(k-1\right)\hfill \\ \hfill U_{\mathrm{d}}\left(k\right)=\exp \left(-\frac{T}{{\tau }_2}\right)*U_{\mathrm{d}}\left(k-1\right)-\left[1-\exp \left(-\frac{T}{{\tau }_2}\right)\right]\hfill \\ \hfill *R_{\mathrm{d}}*I_{\mathrm{L}}\left(k-1\right)\hfill \\ \hfill U_{\mathrm{L}}\left(k\right)=U_{\mathrm{O}\mathrm{C}\mathrm{V}}\left(SOC\left(k\right)\right)-U_{\mathrm{p}}\left(k\right)-U_{\mathrm{d}}\left(k\right)\hfill \\ \hfill -R_0*I_{\mathrm{L}}\left(k-1\right)\hfill \\ \hfill \begin{array}{c}\hfill {\tau }_1=R_{\mathrm{p}}*C_{\mathrm{p}}\hfill \\ \hfill {\tau }_2=R_{\mathrm{d}}*C_{\mathrm{d}}\hfill \end{array}\hfill \end{array}\right.(4)$

$\left\{\begin{array}{c}\begin{array}{c}{f}_{\mathrm{k}}\left(U_{\mathrm{L}},I_{\mathrm{L}},SOC,X\right)=U_{\mathrm{O}\mathrm{C}\mathrm{V}}\left(SOC\left(k\right)\right)-\hfill \\ \exp \left(-\frac{T}{R_{\mathrm{p}}*C_{\mathrm{p}}}\right)*U_{\mathrm{p}}\left(k-1\right)-\hfill \\ \left[1-\exp \left(-\frac{T}{R_{\mathrm{p}}*C_{\mathrm{p}}}\right)\right]*R_{\mathrm{p}}*I_{\mathrm{L}}\left(k-1\right)-\hfill \\ \exp \left(-\frac{T}{R_{\mathrm{d}}*C_{\mathrm{d}}}\right)*U_{\mathrm{d}}\left(k-1\right)-\hfill \\ \left[1-\exp \left(-\frac{T}{R_{\mathrm{d}}*C_{\mathrm{d}}}\right)\right]*R_{\mathrm{d}}*I_{\mathrm{L}}\left(k-1\right)-\hfill \\ R_0*I_{\mathrm{L}}\left(k-1\right)-U_{\mathrm{L}}\hfill \end{array}\hfill \\ X=\left\{R_{\mathrm{p}},C_{\mathrm{p}},R_{\mathrm{d}},C_{\mathrm{d}},R_0\right\}\hfill \end{array}\right.(5)$

In this research, the root mean square error (RMSE) represents the overall difference between the experimental and estimated data. RMSE is defined by Eq. 6.

$\begin{array}{c}RMSE\left(X\right)=\sqrt{\frac{1}{N}\sum _{k=1}^N{f}_k{\left(U_{\mathrm{L}},I_{\mathrm{L}},X\right)}^2}\hfill \end{array},(6)$

where X represents the solution vector consisting of unknown parameters, N denotes the number of experimental data, and k = 1, …., N.

3 JADE Algorithm

Differential evolution (DE) algorithm is an efficient intelligent optimization algorithm. It is a metaheuristic search algorithm based on a group, and each individual in the group corresponds to a solution vector (Brest et al., 2020). The evolution process of DE is very similar to the genetic algorithm, but the specific definition of these operations is different from the genetic algorithm (Gao et al., 2021). The three stages of mutation, crossover, and selection are the basic phases of DE. The parameters about these stages need to be set before the start of each phase, and they have the same fixed value during the whole evolutionary process. Adaptive differential evolution with an optional external archive algorithm (JADE) is based on the DE algorithm (Zhang and Sanderson, 2009). JADE adopts a new mutation strategy: “DE/current-to-pbest/1” (with archive A), as shown in Eq. 7 (Peng et al., 2009). The greedy strategy ensures better performance of the particles.

$\begin{array}{c}{v}_{i,g}=x_{i,g}+F_i*\left(x_{best,g}^p-x_{i,g}\right)+F_i*\left(x_{r1,g}-{\tilde{x}}_{r2,g}\right)\hfill \end{array}(7)$

$\begin{array}{c}{F}_i=rand{c}_i\left(\mu F,0.1\right)\hfill \end{array}(8)$

where x_i,g and x_r1,g are acquired from Np, $x_{best,g}^p$ randomly chosen from the top 100p % ($p\in \left(\mathrm{0,1}\right]$). The mutation factor F_i is determined by x_i, and F_i is updated in the process by introducing Eq. 8. ${\tilde{x}}_{r2,g}$ is the individual randomly chosen from P ∪ A. Here, P represents the current population which saves individuals close to the optimal value, and the external archive A converses poor performance individuals.

The parameter adaption strategy is used for the mutation probability F_i. F_i is independently generated according to the Cauchy distribution with a location parameter μF = 0.5, and the scale parameter is 0.1. If F_i ≥ 1, it truncates to be 1; if F_i ≤ 0, it regenerated 1. S_F is the set that saves every successful mutation probability in each iteration. μF is initialized to be 0.5 and then updated in Eq. 9.

$\begin{array}{c}\mu F=\mu F*\left(1-c\right)+mean\left(S_F\right)*c\hfill \end{array}(9)$

where Eq. 10 can calculate mean (S_F).

$\begin{array}{c}mean\left(S_F\right)=\frac{{\sum }_{F\in S_F}{F}^2}{{\sum }_{F\in S_F}F}\hfill \end{array}(10)$

The parameter adaption strategy is not only used for the mutation probability F_i but also for the crossover factor CR_i. Each individual x_i’s crossover factor CR_i is independently generated according to the normal distribution. μCR is the mean value, and the standard deviation is 0.1, as shown in Eq. 11.

$\begin{array}{c}C{R}_i=rand{n}_i\left(\mu CR,0.1\right)\hfill \end{array}(11)$

The range of CR_i is limited to [0, 1]. The S_CR is a set of CR_i with a good performance. The initial value of μCR is 0.5, which is then regenerated using Eq. 12 (Peng et al., 2009).

$\begin{array}{c}\mu CR=\mu CR*\left(1-c\right)+mean\left(S_{CR}\right)*c\hfill \end{array}(12)$

where c is a constant in the range of [0,1], and mean(S_CR) is the average value.

4 A Novel DE Algorithm—DOLADE

4.1 Dynamic Opposite Learning

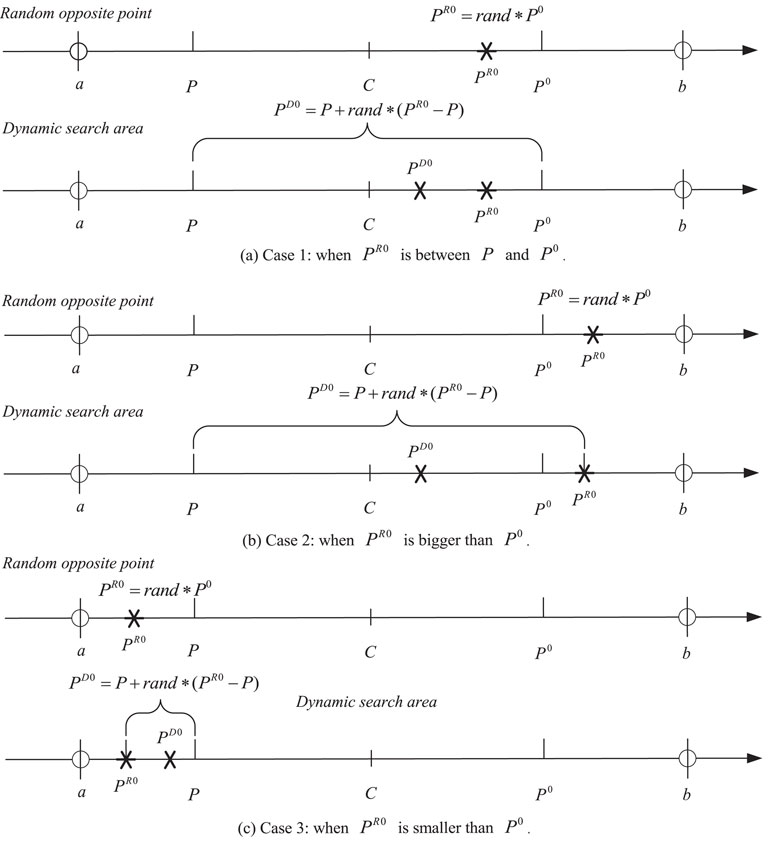
There are many successful learning strategies in the algorithm field, and these strategies have provided a significant contribution to the progress of algorithms. The opposition-based learning strategy has a considerable influence on enhancing the searchability of the algorithm itself (Tizhoosh, 2005), but these strategies also have some shortcomings. For example, the QOBL (Rahnamayan et al., 2007) and QRBL (Laquai et al., 2011) approaches are based on deterministic strategies for potential relative points, making the exploitation ability of particles lacking. In the DOL strategy, the current particle works in the new search area. The area is dynamically extended from the current to the opposite, which is explained in Figure 2. P is the current point, P⁰ denotes the opposite point, P^s represents the existing point in the new area, and a and b are the boundaries of the area. The individuals can obtain a larger area for movement to increase the probability of being close to the optimal value and enhance their exploration capability. However, the search area of individuals inevitably converges to the local optimum so that the particle’s exploitation capability is insufficient.

FIGURE 2

FIGURE 2. Symmetric area between the current point and the opposite point.

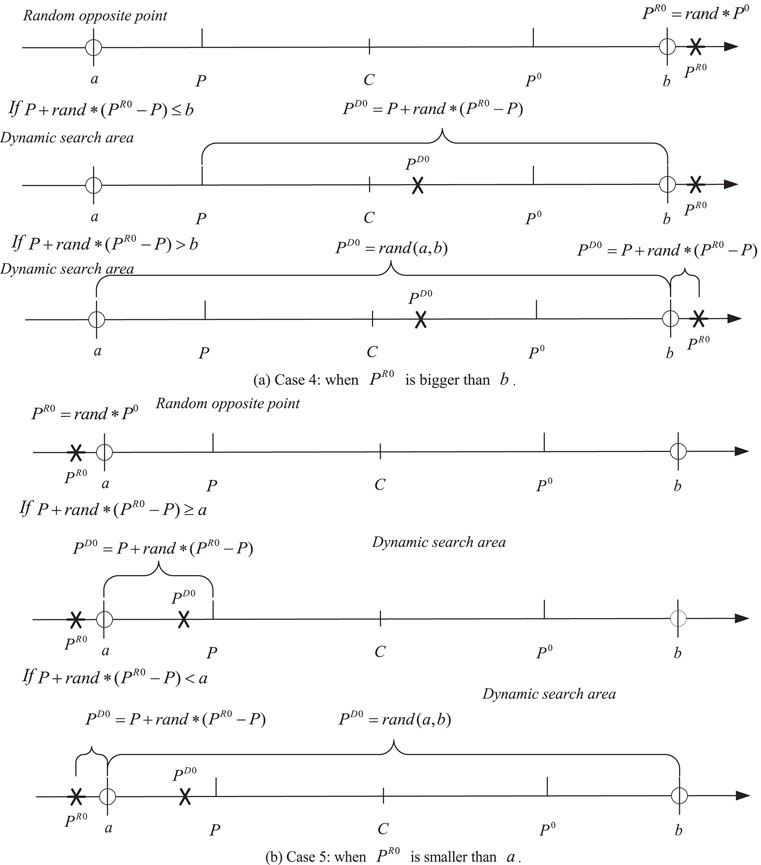
A random opposite point (P^R0) is introduced to avoid the solution falling into the local optimum, improving the particle’s capability; P^R0 = rand*P⁰, rand ∈ [0,1]. When P^R0 replaces P⁰, the symmetric search area in Figure 2 can be transformed into asymmetric search areas, which have a characteristic of dynamic adjusting along with P^R0. In Figures 3, 4, the novel search areas are demonstrated. According to the relative position of P^R0 to P and P⁰, three categories of the asymmetric search areas are formed in Figure 3 when P^R0 ∈ [a, b]. Case 1 is the scenario of the search area when P^R0 is between P and P⁰, case 2 illustrates the project of the search area when P⁰ is smaller than P^R0, and when P is larger than P^R0, the search area is represented in case 3. The strategy can be formulated by randomly generating a DOL point P^D0 from P to P^R0 and P^D0 = P + rand(P^R0 − P). In addition, the condition that P^R0 is out of the area boundaries [a,b] cannot be ignored, such as case 4 and case 5, which is depicted in Figure 4. The boundaries need to be limited: if P^D0 = P + rand(P^R0 − P) ∈ [a, b], and P^D0 is equal to P^D0 = P + rand(P^R0 − P). Otherwise, P^D0 should be regenerated as a random number between a and b.

FIGURE 3

FIGURE 3. DOL asymmetric dynamic search area when P^R0 ∈ (a, b).

FIGURE 4

FIGURE 4. DOL asymmetric dynamic search area when P^R0∉(a, b).

Although P^R0 can diversify the search area, the search area may shrink as the iteration progresses so that the particles’ exploration and exploitation capabilities cannot be fully utilized to the maximum. In order to prevent particles from being too large or too weak to be unbalanced in their exploration and exploitation capabilities, a weighting factor (ω) is used to improve this problem, which could help the particle arrive at the best region. Therefore, the DOL strategy is redefined as P^DOL = P + ω*(P^R0−P), where ω is a constant and ω > 0. Finally, DOL can be calculated by the formula with these foundations. The search area is expanded to a symmetric region so that the probability that is closer to the best solution is enhanced. The dynamic characteristics of the search area make the population become diverse and enhance the particle’s exploration and exploitation capabilities.

4.2 Mathematical Expression of DOL

In this subsection, the DOL strategy will be described by mathematical formulas.

• Dynamic opposite point. P (P ∈ [a, b]) is defined as a point. The dynamic opposite point P^D0 is defined in Eq. 13, where a is the lower boundary, b is the upper boundary, and rand ∈ (0,1) is a random number. Moreover, Eq. 13 applied the weighting factor ω (ω > 0) into DOL. P⁰ is the opposite number, as shown by Eq. 14.

• DOL-based optimization. Assume P = (P₁, P₂, … , P_D) in the D − dimensional area. P_j,…, P_D ∈ [a_j, b_j], where a_j and b_j are boundaries of the current searching area. $P_j^0$ is the opposite point defined in Eq. 15. $P_j^{D0}=(P_1^{D0},P_2^{D0},\dots ,P_D^{D0})$ is the dynamic opposite point, updated by P_j according to Eq. 16. $P_j^{D0}$ will replace P_j when the fitness value of $P_j^{D0}$ is better than P_j; otherwise, $P_j^{D0}$ will not be saved. Note that $P_j^{D0},\dots ,P_D^{D0}$ is limited within [a_j, b_j]. If $P_j^{D0}\notin [a_j,b_j]$, $P_j^{D0}$ should be redefined as a random in [a_j, b_j].

$\begin{array}{c}{P}^{D0}=P+\omega *rand*\left(rand*P^0-P\right)\hfill \end{array}(13)$

$\begin{array}{c}{P}^0=a+b-P\hfill \end{array}(14)$

$\begin{array}{c}{P}_j^0=a_j+b_j-P_j,j=1:D\hfill \end{array}(15)$

$\begin{array}{c}{P}_j^{D0}=P_j+\omega *rand*\left(rand*P_j^0-P_j\right),j=1:D\hfill \end{array}(16)$

4.3 DOLADE Algorithm Steps

4.3.1 Population Initialization

oP^D0 is randomly generated by the initial DOL strategy, which may obtain better knowledge than the original individual to a certain extent. At the beginning of generation, the population size is set as Np (for any individual i, i = 1, 2, … , Np), and D represents dimension of problems (for any problem j, j = 1, 2, … , D). Eq. 17 can calculate the initialization process.

$\begin{array}{c}o{P}_{i,j}^{D0}=o{P}_{i,j}+r{1}_i*\left(r{2}_i*\left(a_j+b_j-o{P}_{i,j}\right)-o{P}_{i,j}\right)\hfill \end{array}(17)$

Boundaries should be checked according to Eq. 18, which could improve the DOL effectiveness.

$\begin{array}{c}o{P}_{i,j}^{D0}=rand\left(a_j,b_j\right),if:o{P}_{i,j}^{D0}<a_j\Vert o{P}_{i,j}^{D0}>b_j\hfill \end{array}(18)$

where [a_j, b_j] is the range of the search area, r1_i and r2_i are random values among (0,1), and the weight factor ω is set as constant: 10. Then, fittest individuals Np are selected from {oP ∪ oP^D0}.

4.3.2 DOL Generation Jumping

The jumping rate Jr is introduced to control DOL to update the population. If rand < Jr, the DOL jumping process would be performed by Eq. 19.

$\begin{array}{c}{P}_{i,j}^{D0}=P_{i,j}+\omega *r{3}_i*\left(r{4}_i*\left(a_j+b_j-P_{i,j}\right)-P_{i,j}\right)\hfill \end{array}(19)$

Meanwhile, the boundaries should be checked by Eq. 18. Remarkably, the new candidates are locked within a shrunken search area by dynamically updating the interval boundaries [a_j, b_j] as follows (Wang et al., 2011):

$\begin{array}{c}\begin{array}{c}{a}_j=\min \left(P_{i,j}\right)\hfill \\ b_j=\max \left(P_{i,j}\right)\hfill \end{array}\hfill \end{array}(20)$

When the DOL jumping step is finished, the best individual Np is selected from {oP ∪ oP^D0}.

4.3.3 DOLADE Algorithm Steps

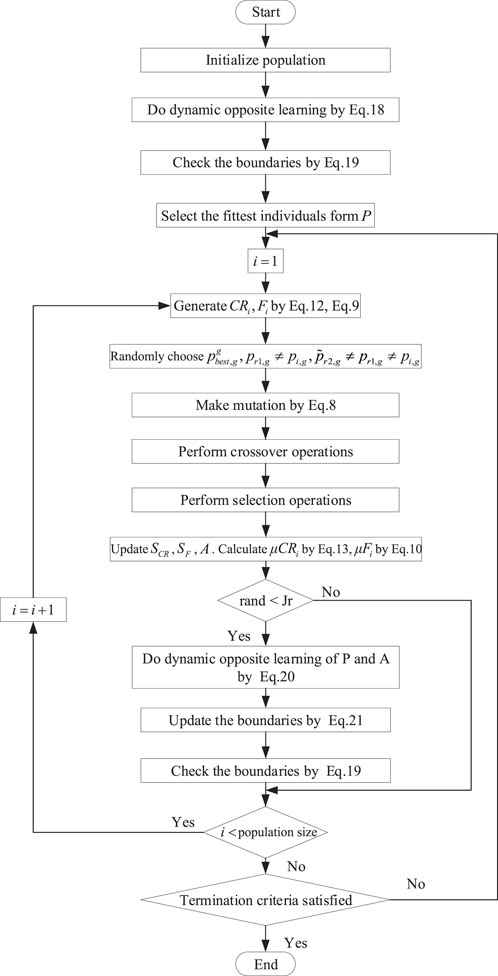
By employing the DOL strategy to JADE, an adaptive differential evolution algorithm with a dynamic opposite learning strategy is generated, namely, DOLADE. In order to make DOLADE convenient and simple to deal with problems, the pseudo-code is described in Algorithm 1, and the flowchart of DOLADE is exhibited in Figure 5.

FIGURE 5

FIGURE 5. Flowchart of DOLADE.

Algorithm 1. Pseudo-code of DOLADE.

5 Experimental Results and Analysis

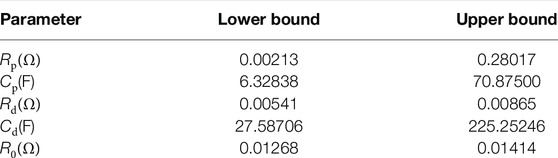
In this section, through the various data of the battery measured experimentally, the DOLADE algorithm is used to carry out the parameter identification experiment of the battery model. The efficiency and performance of the DOLADE algorithm are evaluated in solving such problems through various performance indicators. Continuous current discharging experiments under different current are implemented, the battery’s internal parameters are identified and verified using measured experimental data, and the parameter values identified under different conditions are displayed in table. Therefore, all these data are obtained under the same experimental conditions. Among them, the unknown model parameters R_p, C_p, R_d, C_d, and R₀ are shown in Table 2, which lists the lower and upper values of these parameters.

TABLE 2

TABLE 2. Parameter range of the SECM.

Some well-established algorithms, including JAYA (Venkata Rao, 2016), GWO (Mirjalili et al., 2014), MFO (Mirjalili, 2015), ETLBO (Rao and Patel, 2012), and cfPSO (Pathak and Singh, 2017) are compared to prove the effectiveness of the DOLADE algorithm. All of the data are obtained and compared under the same experimental conditions: the maximum number of function evaluations (MaxFEs) is 50 in each operation under different currents, and each algorithm runs 30 times independently to minimize statistical errors. The optimal values are taken out and listed in table, and the OCV and SOC are calculated according to the optimal value. The comparison result of each algorithm is to take the optimal value under the aforementioned operating conditions. Table 3 lists some specific parameter configurations that need to be prepared in advance for each algorithm adopted.

TABLE 3

TABLE 3. Parameters of the involved algorithms.

5.1 SECM Model Identification Results

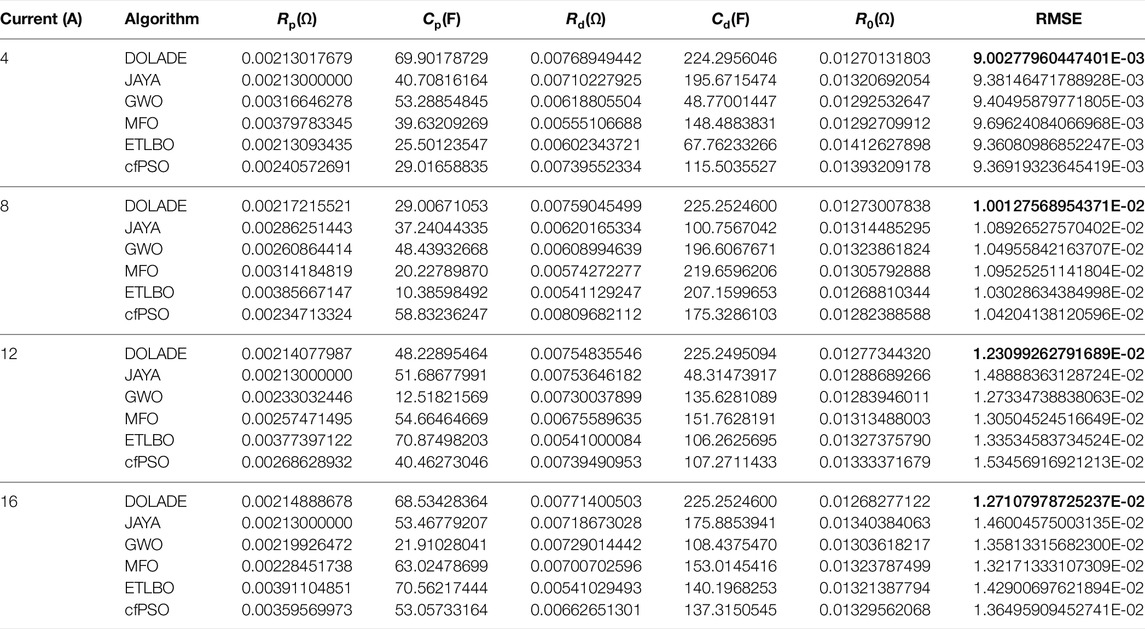
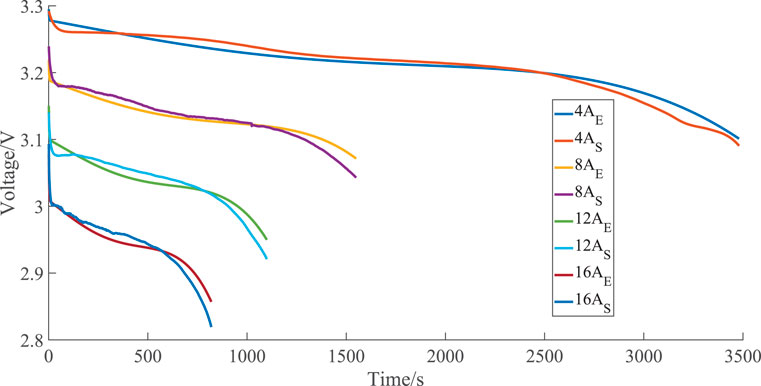
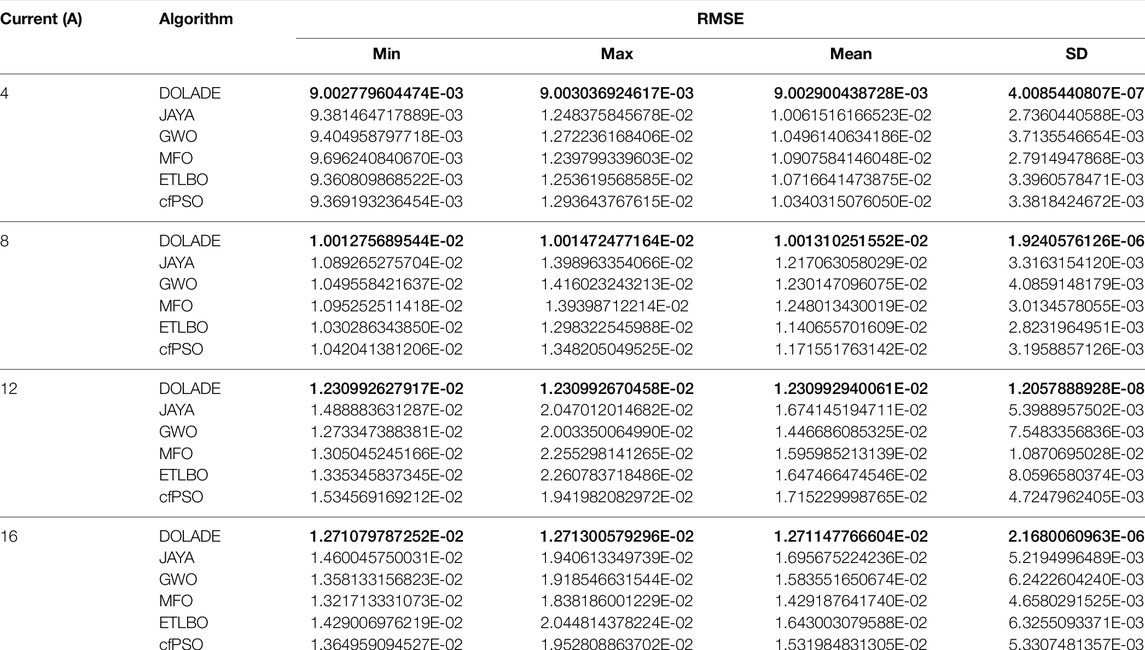
Table 4 lists the values of R_p, C_p, R_d, C_d, and R₀ extracted by the six algorithms under various currents. The RMSE value is also listed in the table, and the best value is highlighted in bold. RMSE represents the difference between the parameters extracted by the algorithm and the experimental data and represents the accuracy of the result. The smaller the value, the more accurate the result. It can be concluded that when the DOLADE algorithm is used, the result is the best, and the RMSE value is the smallest. The parameter values of the battery model identified by the DOLADE, JAYA, GWO, MFO, ETLBO, and cfPSO algorithms are different, and even the parameter values extracted by these algorithms under the same current are also different. This indicates that the internal parameter values of the battery are not constant in actual operation, but changes as a dynamic process in changing, and there must be an optimal value among these values. The evaluation standard of this optimal value is determined by the value of RMSE. The algorithm that affects the best in terms of extracted parameters is DOLADE. The parameter values extracted by DOLADE are substituted into the equation to calculate the OCV value. The experimentally measured voltage value and the calculated voltage value curve are shown in Figure 6. Here, A_E represents the experiment current, and A_S represents the calculated current. The estimated OCV curves coincide well with the experimental OCV curves. Whether it is a high-current discharging experiment or a low-current discharging experiment, the relationship between the two is in line with expectations, and the error of OCV in the figure is within a tiny field, which could satisfy the practical needs.

TABLE 4

TABLE 4. Comparison among six algorithms on the SECM under different currents.

FIGURE 6

FIGURE 6. Experimental and estimated OCV data comparison under different currents.

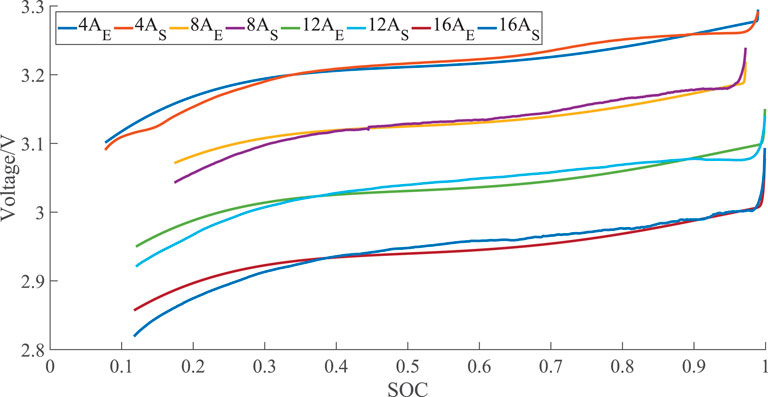
Furthermore, the relationship of OCV–SOC is depicted in Figure 7. The figure shows that the estimated OCV can replace the experimentally measured OCV to calculate SOC. In the range of SOC from 0 to 1, the computed value always maintains a reasonable range with the actual value and the changes of the two are consistent. The output voltage calculated using the identified parameters is the same as the actual voltage, which can correspond to the battery’s SOC. In other words, the voltage value obtained from the parameters identified by DOLADE could be used to calculate the value of SOC.

FIGURE 7

FIGURE 7. OCV–SOC curve diagram.

5.2 Statistical and Convergence Results

In the section 5.1, the parameters were extracted and RMSE values by the DOLADE algorithm are demonstrated, and these results are compared with the results of other algorithms. Then, the estimated OCV and the OCV–SOC relationship curves are described. This subsection clearly compares the statistical values of the DOLADE algorithm operation results with the other algorithms. Comparisons in many aspects verify the effectiveness of the DOL strategy, and it reflects the convergence speed and stability of the DOLADE algorithm. The comprehensive results of all algorithms after 30 independent runs are listed in Table 5. In addition to the minimum error, the table also lists the maximum error, the average value of the error, and the standard deviation reflecting the error distribution. For each current, the overall best results among the six algorithms are highlighted in bold.

TABLE 5

TABLE 5. Statistical results of RMSE for six algorithms under different currents.

Among the statistical results listed in Table 5, the six algorithms under different conditions and the performance indicators of the DOLADE algorithm all show strong competitiveness. In all the statistical results, the difference between the maximum and minimum values of the DOLADE algorithm is also the smallest, which indicates that the DOLADE algorithm perfectly performs the particles’ exploration and exploration capabilities through the DOL strategy when solving problems. On the average of all results, the average value of the DOLADE algorithm is close to the global optimal value, which shows the reliability and stability of the DOLADE algorithm in solving problems without excessive waste of resources. Finally, the standard deviation further verifies the aforementioned findings from this side, providing strong evidence for the DOLADE algorithm to be more convincing.

In Figure 8, the boxplot shows the distribution of the results of the aforementioned six different algorithms under 30 independent executions, demonstrating the dispersion of the statistical results of all algorithms under different currents. As can be seen from the boxplot, the DOLADE algorithm results are stable and have a superior performance by comparing with the other five algorithms, and the advantages are very obvious. It is verified once again that the DOLADE algorithm is superior to other algorithms in terms of accuracy and reliability, has an outstanding performance in enhancing particle capabilities, and can be trusted as an optimizer.

FIGURE 8

FIGURE 8. Best RMSE boxplot in 30 runs of six algorithms under different currents.

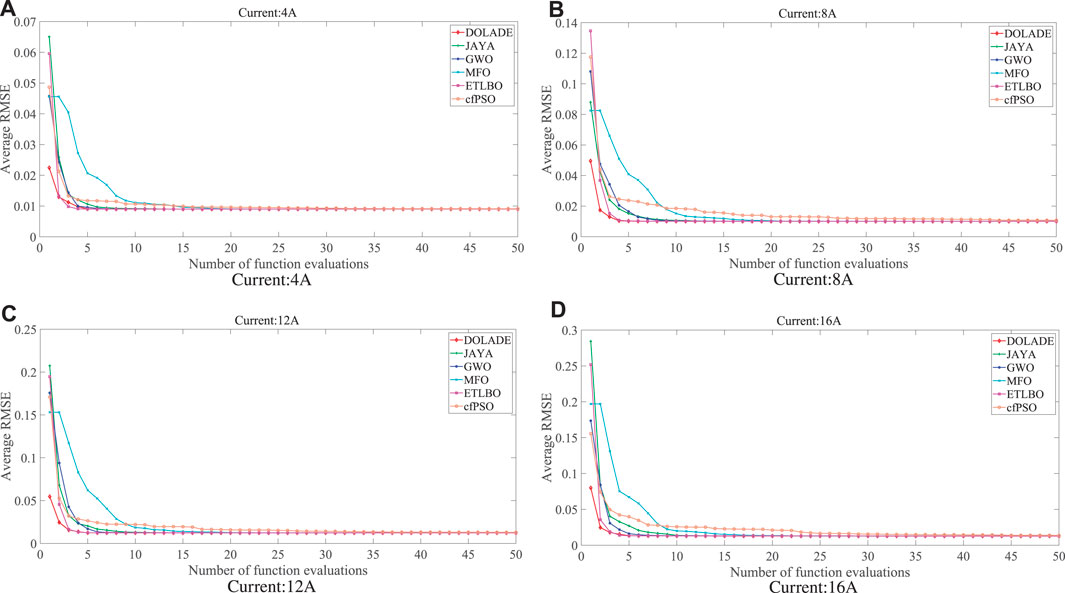
Figure 9 demonstrates the convergence curves of the six algorithms under different discharging currents in the SECM. The figures depict the convergence graph when different algorithms run independently 30 times, where the number of runs of each algorithm is 50. It is not difficult to obtain from the figure that the speed of converging to the optimal value using the DOLADE algorithm is very considerable. Compared with the other five algorithms, DOLADE has a wonderful optimization process, fewer times of iteration when the algorithm converges to the optimal value, and the initial value of the optimization is closest to the global optimum, which is highly competitive. Therefore, it could be concluded that DOLADE has an excellent performance in solving the parameter identification of the battery model in BESS, which provides a new choice for solving this kind of problem.

FIGURE 9

FIGURE 9. Convergence curves of six algorithms under different currents.

5.3 Effectiveness Evaluation in Different Sets

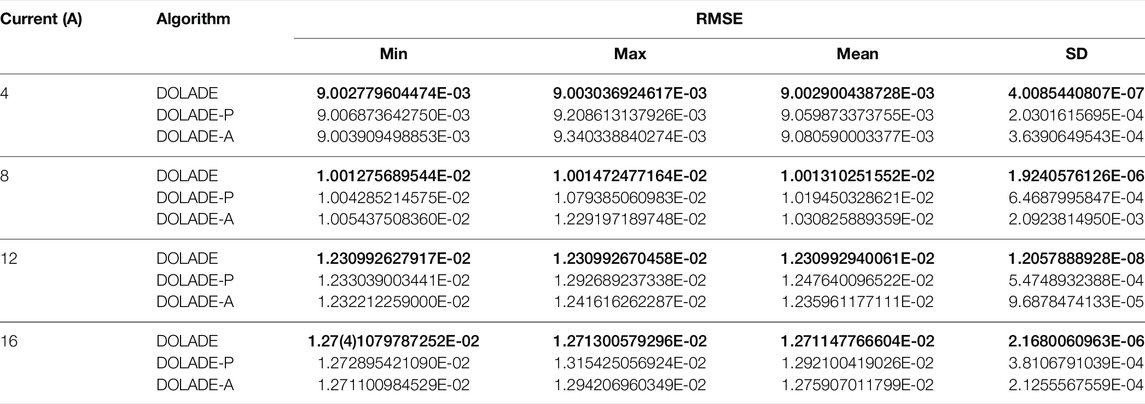
The DOL strategy is applied to the population P (elite individuals) that the individuals’ performance well and the external archive A (general individuals) that conserves the eliminated individuals, respectively. The excellent performance of DOL strategy in DE algorithm is verified by experimental results. The elite dynamic opposite learning for the elite particles in the population and the general dynamic opposite learning for the ordinary particles are used, and then the results are compared with the existing results of the combination of the two, that is, elite dynamic opposite learning and general dynamic opposite learning. The comparison results are shown in Table 6, and the best results are highlighted in bold. As can be seen from the data in the table, when the elite or general individuals in the population perform the dynamic opposite learning, the effect is not as good as when both the elite and general individuals are allowed to conduct dynamic opposite learning at the same time. These can be reflected from the data in the table, including minimum, maximum, mean, and standard deviation. Therefore, removing the DOL strategy from any set will not yield the best results. Only when the strategy is applied to both elite and general individuals, the following optimization process can satisfy the need of generating global optimal solutions.

TABLE 6

TABLE 6. Statistical results of RMSE for different sets under different currents.

6 Conclusion

In this study, a new method to solve the problem of identifying battery model parameters in BESS is proposed. This method can accurately obtain the internal parameters of the battery model, which is of great significance for the coordination work of PV-BESS. As a variant of the DE algorithm, the DOLADE algorithm introduces the DOL strategy to expand the number of particles in the population and improve the exploration and exploitation capability, achieving a faster convergence rate, accurately obtaining the global optimum and avoiding falling into the local optimum. First, based on the battery equivalent circuit model in BESS, the relationship between OCV and SOC is studied, and the parameters that need to be identified, the objective function, and the evaluation function are determined. Then, the parameters under various discharging currents are extracted, and the battery’s OCV is estimated according to the identified parameters. Finally, the estimated OCV is compared with the experimental OCV, and the experimental voltage-estimated voltage curve and the OCV–SOC curve are plotted. It can be known from the aforementioned figures that all the parameters and indicators are in line with the expected values and within a reasonable and acceptable range, which further verifies the effectiveness and accuracy of the DOLADE algorithm. Furthermore, compared with the well-established algorithm, the boxplot and the convergence curves of the algorithms are plotted, which shows that the advantages of the DOLADE algorithm are available. In general, the DOL strategy can significantly improve the diversity of the population and enhance the search efficiency of particles by endowing new searching abilities to individuals in the population. Therefore, DOLADE is one of the ideal methods to identify unknown parameters of the battery model. In future plans, research to address this type of problem will continue, and improvements will be made to the DOLADE algorithm to explore its potential for solving more complex problems.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

JZ: conceptualization, methodology, software, formal analysis, data curation, validation, and writing—original draft. YuZ: investigation and formal analysis. YG: formal analysis and validation. MM: resources and writing—review and editing. WF: funding acquisition. YaZ: writing—review and editing, supervision, project administration, and funding acquisition.

Funding

The authors are grateful for the financial support from the Shenzhen science and technology project (No. JCYJ20210324115606017), the Science and Technology Innovation Commission of Shenzhen (No. ZDSYS20190902093209795), the National Natural Science Foundation of China (No. U1813222), Guangdong Frontier and Key Technological Innovation (No. 2017B090910013), and the Science and Technology Innovation Commission of Shenzhen (Nos. JCYJ20180507182239617 and JCYJ2018050718 223961).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alam, D. F., Yousri, D. A., and Eteiba, M. B. (2015). Flower Pollination Algorithm Based Solar Pv Parameter Estimation. Energ. Convers. Manage. 101, 410–422. doi:10.1016/j.enconman.2015.05.074

CrossRef Full Text | Google Scholar

Brest, J., Maučec, M. S., and Bošković, B. (2020). “Differential Evolution Algorithm for Single Objective Bound-Constrained Optimization: Algorithm J2020,” in 2020 IEEE Congress on Evolutionary Computation (CEC) (Glasgow, UK: IEEE), 1–8. doi:10.1109/cec48606.2020.9185551

CrossRef Full Text | Google Scholar

Bruch, M., Millet, L., Kowal, J., and Vetter, M. (2021). Novel Method for the Parameterization of a Reliable Equivalent Circuit Model for the Precise Simulation of a Battery Cell's Electric Behavior. J. Power Sourc. 490, 229513. doi:10.1016/j.jpowsour.2021.229513

CrossRef Full Text | Google Scholar

Bruen, T., and Marco, J. (2016). Modelling and Experimental Evaluation of Parallel Connected Lithium Ion Cells for an Electric Vehicle Battery System. J. Power Sourc. 310, 91–101. doi:10.1016/j.jpowsour.2016.01.001

CrossRef Full Text | Google Scholar

Bullich-Massagué, E., Cifuentes-García, F.-J., Glenny-Crende, I., Cheah-Mañé, M., Aragüés-Peñalba, M., Díaz-González, F., et al. (2020). A Review of Energy Storage Technologies for Large Scale Photovoltaic Power Plants. Appl. Energ. 274, 115213. doi:10.1016/j.apenergy.2020.115213

CrossRef Full Text | Google Scholar

Chen, X., Xu, B., Mei, C., Ding, Y., and Li, K. (2018). Teaching-learning-based Artificial Bee colony for Solar Photovoltaic Parameter Estimation. Appl. Energ. 212, 1578–1588. doi:10.1016/j.apenergy.2017.12.115

CrossRef Full Text | Google Scholar

Cheng, S., Zhao, G., Gao, M., Shi, Y., Huang, M., and Marefati, M. (2021). A New Hybrid Solar Photovoltaic/phosphoric Acid Fuel Cell and Energy Storage System; Energy and Exergy Performance. Int. J. Hydrogen Energ. 46, 8048. doi:10.1016/j.ijhydene.2020.11.282

CrossRef Full Text | Google Scholar

Choi, Y. Y., Kim, S., Kim, S., and Choi, J.-I. (2020). Multiple Parameter Identification Using Genetic Algorithm in Vanadium Redox Flow Batteries. J. Power Sourc. 450, 227684. doi:10.1016/j.jpowsour.2019.227684

CrossRef Full Text | Google Scholar

El-Sehiemy, R. A., Hamida, M. A., and Mesbahi, T. (2020). Parameter Identification and State-Of-Charge Estimation for Lithium-Polymer Battery Cells Using Enhanced sunflower Optimization Algorithm. Int. J. Hydrogen Energ. 45 (15), 8833–8842. doi:10.1016/j.ijhydene.2020.01.067

CrossRef Full Text | Google Scholar

Farhadi, B., Marriam, I., Yang, S., Zhang, H., Tebyetekerwa, M., Zhu, M., et al. (2019). Highly Efficient Photovoltaic Energy Storage Hybrid System Based on Ultrathin Carbon Electrodes Designed for a Portable and Flexible Power Source. J. Power Sourc. 422, 196–207. doi:10.1016/j.jpowsour.2019.02.091

CrossRef Full Text | Google Scholar

Gao, S., Wang, K., Tao, S., Jin, T., Dai, H., and Cheng, J. (2021). A State-Of-The-Art Differential Evolution Algorithm for Parameter Estimation of Solar Photovoltaic Models. Energ. Convers. Manage. 230, 113784. doi:10.1016/j.enconman.2020.113784

CrossRef Full Text | Google Scholar

Heidari, A. A., Mirjalili, S., Faris, H., Aljarah, I., Mafarja, M., and Chen, H. (2019). Harris Hawks Optimization: Algorithm and Applications. Future generation Comput. Syst. 97, 849–872. doi:10.1016/j.future.2019.02.028

CrossRef Full Text | Google Scholar

Ikeda, S., and Ooka, R. (2019). Application of Differential Evolution-Based Constrained Optimization Methods to District Energy Optimization and Comparison with Dynamic Programming. Appl. Energ. 254, 113670. doi:10.1016/j.apenergy.2019.113670

CrossRef Full Text | Google Scholar

Jiang, L. L., MaskellMaskell, D. L., and Patra, J. C. (2013). Parameter Estimation of Solar Cells and Modules Using an Improved Adaptive Differential Evolution Algorithm. Appl. Energ. 112, 185–193. doi:10.1016/j.apenergy.2013.06.004

CrossRef Full Text | Google Scholar

Kang, J., Yan, F., Zhang, P., and Du, C. (2012). A Novel Way to Calculate Energy Efficiency for Rechargeable Batteries. J. Power Sourc. 206, 310–314. doi:10.1016/j.jpowsour.2012.01.105

CrossRef Full Text | Google Scholar

Laquai, F., Chowanetz, F., and Rigoll, G. (2011). “A Large-Scale Led Array to Support Anticipatory Driving,” in 2011 IEEE International Conference on Systems, Man, and Cybernetics (Anchorage, AK, USA: IEEE), 2087–2092. doi:10.1109/icsmc.2011.6083980

CrossRef Full Text | Google Scholar

Li, R., Li, W., Zhang, H., Zhou, Y., and Tian, W. (2021). On-line Estimation Method of Lithium-Ion Battery Health Status Based on Pso-Svm. Front. Energ. Res. 401, 693249. doi:10.3389/fenrg.2021.693249

CrossRef Full Text | Google Scholar

Liang, J., Qiao, K., Yuan, M., Yu, K., Qu, B., Ge, S., et al. (2020). Evolutionary Multi-Task Optimization for Parameters Extraction of Photovoltaic Models. Energ. Convers. Manage. 207, 112509. doi:10.1016/j.enconman.2020.112509

CrossRef Full Text | Google Scholar

Lin, X., and Wu, Y. (2020). Parameters Identification of Photovoltaic Models Using Niche-Based Particle Swarm Optimization in Parallel Computing Architecture. Energy 196, 117054. doi:10.1016/j.energy.2020.117054

CrossRef Full Text | Google Scholar

Liu, R., and Zhang, C. (2021). An Active Balancing Method Based on Soc and Capacitance for Lithium-Ion Batteries in Electric Vehicles. Front. Energ. Res. 9, 773838. doi:10.3389/fenrg.2021.773838

CrossRef Full Text | Google Scholar

Maghyereh, A., and Abdoh, H. (2021). The Impact of Extreme Structural Oil-price Shocks on Clean Energy and Oil Stocks. Energy 225, 120209. doi:10.1016/j.energy.2021.120209

CrossRef Full Text | Google Scholar

Mirjalili, S., Mirjalili, S. M., and Lewis, A. (2014). Grey Wolf Optimizer. Adv. Eng. Softw. 69, 46–61. doi:10.1016/j.advengsoft.2013.12.007

CrossRef Full Text | Google Scholar

Mirjalili, S. (2015). Moth-flame Optimization Algorithm: A Novel Nature-Inspired Heuristic Paradigm. Knowledge-based Syst. 89, 228–249. doi:10.1016/j.knosys.2015.07.006

CrossRef Full Text | Google Scholar

Pathak, V. K., and Singh, A. K. (2017). Form Error Evaluation of Noncontact Scan Data Using Constriction Factor Particle Swarm Optimization. J. Adv. Manuf. Syst. 16 (03), 205–226. doi:10.1142/s0219686717500135

CrossRef Full Text | Google Scholar

Peng, F., Tang, K., Chen, G., and Yao, X. (2009). “Multi-start Jade with Knowledge Transfer for Numerical Optimization,” in 2009 IEEE Congress on Evolutionary Computation (Trondheim: IEEE), 1889–1895. doi:10.1109/cec.2009.4983171

CrossRef Full Text | Google Scholar

Qais, M. H., Hasanien, H. M., and Alghuwainem, S. (2019). Identification of Electrical Parameters for Three-Diode Photovoltaic Model Using Analytical and sunflower Optimization Algorithm. Appl. Energ. 250, 109–117. doi:10.1016/j.apenergy.2019.05.013

CrossRef Full Text | Google Scholar

Rahnamayan, S., Tizhoosh, H. R., and Salama, M. M. A. (2007). “Quasi-oppositional Differential Evolution,” in 2007 IEEE congress on evolutionary computation (Singapore: IEEE), 2229–2236. doi:10.1109/cec.2007.4424748

CrossRef Full Text | Google Scholar

Rao, R. V., and Patel, V. (2012). An Elitist Teaching-Learning-Based Optimization Algorithm for Solving Complex Constrained Optimization Problems. Int. J. Ind. Eng. Computations 3 (4), 535–560. doi:10.5267/j.ijiec.2012.03.007

CrossRef Full Text | Google Scholar

Siecker, J., Kusakana, K., and Numbi, B. P. (2017). A Review of Solar Photovoltaic Systems Cooling Technologies. Renew. Sustain. Energ. Rev. 79, 192–203. doi:10.1016/j.rser.2017.05.053

CrossRef Full Text | Google Scholar

Storn, R., and Price, K. (1997). Differential Evolution–A Simple and Efficient Heuristic for Global Optimization over Continuous Spaces. J. Glob. optimization 11 (4), 341–359. doi:10.1023/a:1008202821328

CrossRef Full Text | Google Scholar

Tan, X., Zhan, D., Lyu, P., Rao, J., and Fan, Y. (2021). Online State-Of-Health Estimation of Lithium-Ion Battery Based on Dynamic Parameter Identification at Multi Timescale and Support Vector Regression. J. Power Sourc. 484, 229233. doi:10.1016/j.jpowsour.2020.229233

CrossRef Full Text | Google Scholar

Tizhoosh, H. R. (2005). “Opposition-based Learning: a New Scheme for Machine Intelligence,” in International conference on computational intelligence for modelling, control and automation and international conference on intelligent agents, web technologies and internet commerce (CIMCA-IAWTIC’06), volume 1 (Vienna, Austria: IEEE), 695–701.

Google Scholar

Tong, K., Yao, J., Jin, M., Yang, S., and Duong, T. (2018). A Novel Improved Cuckoo Search Algorithm for Parameter Estimation of Photovoltaic (Pv) Models. Energies 11 (5), 1060.

Google Scholar

Venkata Rao, R. (2016). Jaya: A Simple and New Optimization Algorithm for Solving Constrained and Unconstrained Optimization Problems. Int. J. Ind. Eng. Computations 7 (1), 19–34. doi:10.5267/j.ijiec.2015.8.004

CrossRef Full Text | Google Scholar

Wang, H., Wu, Z., Rahnamayan, S., Liu, Y., and Ventresca, M. (2011). Enhancing Particle Swarm Optimization Using Generalized Opposition-Based Learning. Inf. Sci. 181 (20), 4699–4714. doi:10.1016/j.ins.2011.03.016

CrossRef Full Text | Google Scholar

Wang, Q., Kang, J., Tan, Z., and Luo, M. (2018). An Online Method to Simultaneously Identify the Parameters and Estimate States for Lithium Ion Batteries. Electrochimica Acta 289, 376–388. doi:10.1016/j.electacta.2018.08.076

CrossRef Full Text | Google Scholar

Wang, Q., Wang, J., Zhao, P., Kang, J., Yan, F., and Du, C. (2017). Correlation between the Model Accuracy and Model-Based Soc Estimation. Electrochimica Acta 228, 146–159. doi:10.1016/j.electacta.2017.01.057

CrossRef Full Text | Google Scholar

Wang, S., Liu, S., Yang, F., Bai, X., Wang, S., and Yue, C. (2020). Novel Power Allocation Approach in a Battery Storage Power Station for Aging Minimization. Front. Energ. Res. 7, 166. doi:10.3389/fenrg.2019.00166

CrossRef Full Text | Google Scholar

Xia, Z., and Xiang, Z. (2020). Catalysts for Clean Energy Conversion and Storage. Front. Mater. 7, 43. doi:10.3389/fmats.2020.00043

CrossRef Full Text | Google Scholar

Xiong, R., He, H., Sun, F., and Zhao, K. (2012). Evaluation on State of Charge Estimation of Batteries with Adaptive Extended Kalman Filter by experiment Approach. IEEE Trans. Vehicular Technol. 62 (1), 108–117.

Google Scholar

Yang, Z., Liu, Q., Zhang, L., Dai, J., and Razmjooy, N. (2020). Model Parameter Estimation of the Pemfcs Using Improved Barnacles Mating Optimization Algorithm. Energy 212, 118738. doi:10.1016/j.energy.2020.118738

CrossRef Full Text | Google Scholar

Zhang, J., and Sanderson, A. C. (2009). Jade: Adaptive Differential Evolution with Optional External Archive. IEEE Trans. Evol. Computat. 13 (5), 945–958. doi:10.1109/tevc.2009.2014613

CrossRef Full Text | Google Scholar

Zhang, Y., Huang, C., and Jin, Z. (2020). Backtracking Search Algorithm with Reusing Differential Vectors for Parameter Identification of Photovoltaic Models. Energ. Convers. Manage. 223, 113266. doi:10.1016/j.enconman.2020.113266

CrossRef Full Text | Google Scholar

Zhou, J., Zhang, Y., Zhang, S., Guo, Y., Yang, Z., Feng, W., et al. (2021). A Novel Maximum Power point Tracking Strategy Based on Enhanced Real-Time Adaptive Step-Size Modified Control for Photovoltaic Systems. Front. Energ. Res. 9, 685415. doi:10.3389/fenrg.2021.685415

CrossRef Full Text | Google Scholar

Zhou, S., Liu, X., Hua, Y., Zhou, X., and Yang, S. (2021). Adaptive Model Parameter Identification for Lithium-Ion Batteries Based on Improved Coupling Hybrid Adaptive Particle Swarm Optimization- Simulated Annealing Method. J. Power Sourc. 482, 228951. doi:10.1016/j.jpowsour.2020.228951

CrossRef Full Text | Google Scholar

Glossary

A_E experiment current

A_S calculated current

BESS battery energy storage system

C_d concentration polarization capacitance (C)

C_p electrochemical polarization capacitance (C)

cfPSO constriction factor particle swarm optimization

D dimension of problem

DE differential evolution

DOL dynamic opposite learning

DOLADE adaptive differential evolution algorithm with a dynamic opposite learning strategy

ETLBO elitist teaching–learning-based optimization

G_max maximal number of generation

GWO grey wolf optimizer

I_L load current (A)

JADE adaptive differential evolution algorithm with an optional external archive

Max maximum value

Mean average value

MFO moth-flame optimization

Min minimum value

N number of experimental data

Np population size

OCV open circuit voltage

P population

PV photovoltaic

R₀ internal resistance (Ω)

R_d concentration polarization resistance (Ω)

R_p electrochemical polarization resistance (Ω)

RMSE root mean square error

rand random numbers in (0, 1)

SD standard deviation

SECM second-order RC equivalent circuit model

SOC state of charge

T sampling time (s)

U₀ resistance voltage (V)

U_d second RC network’s voltage (V)

U_L terminal voltage (V)

U_OCV open circuit voltage (V)

U_p first RC network’s voltage (V)

μCR crossover factor

μF mutation factor