- 1School of Computing, University of South China, Hengyang, China
- 2Engineering and Technology Research Center of Software Evaluation and Testing for Intellectual Equipment of Hunan Province, Hengyang, China
- 3CNNC Key Laboratory on High Trusted Computing, Hengyang, China
- 4Nuclear and Radiation Safety Center, Ministry of Ecological Environment of China, Beijing, China
- 5Institute of Nuclear and New Energy Technology, Tsinghua University, Beijing, China
The verification of nuclear design software commonly uses direct comparison methods. Benchmark questions, classical programs, experimental data, manual solutions, etc., would be used as expected results to compare with program outputs to evaluate the reliability of software coding and the accuracy of the numerical solution. Because nuclear power software numerically simulates complex physical processes, it involves many partial differential equations. It is usually challenging to construct analytical or accurate solutions and is expensive to develop benchmark questions and experimental data. Hence, the quantity of verification examples is small. By using the direct comparison method, verification is complicated, high cost, and inadequate. Entering the validation process without adequate proof will adversely impact the effectiveness and efficiency of validation. Metamorphic testing is an indirect verification technology that cleverly combines the nature of the model with software verification. It evaluates the correctness of the code by examining whether the program satisfies the metamorphic relation. Without manual solutions or benchmark examples, it has broad application prospects in the field of nuclear power. A lightweight verification method based on metamorphic relation has been produced here. Metamorphic relations are identified from physical equations, numerical algorithms, and program specifications. Next, they are explicitly used to system, integration, and unit tests to improve test adequacy. Because no need to develop verification examples, this method can detect code errors as soon as possible at a low cost, improve test efficiency, avoid mistakes remaining in subsequent stages and reduce the overall cost of verification.
Introduction
The development of nuclear power software usually includes the stages of physical equation modeling, numerical method selection, and code programming. Verification evaluates whether the algorithm is suitable for equations and whether the code accurately implements the algorithm. Verification is the prerequisite for validation. Without adequate verification, it will substantially adversely impact the effectiveness and efficiency of validation.
Software verification usually uses direct comparison methods. Benchmark questions, classical programs, experimental data, manual solutions, etc., would be used as expected results to compare with program outputs to evaluate the reliability of software coding and the accuracy of the numerical solution. These verification examples are part of system-level information and can only be used for system and acceptance testing. While failures have been detected in those testing levels, revealing and locating defects in functions and solvers is a great challenge. As a result, the cost is exceptionally high, even leading to the collapse of the entire project. Because nuclear power software numerically simulates complex physical processes, it involves many partial differential equations. It is usually impossible to construct analytical or accurate solutions and is expensive to develop benchmark questions and experimental data. Hence, the small number of verification examples further aggravates nuclear software verification’s difficulty.
In the process of software verification, tester often implicitly check whether the code satisfies the specific characteristics of the physical equation, numerical solution method, and program specification. If the above rules are violated, it indicates that the code has defects and verification is false. Metamorphic testing (MT) is a rapid indirect verification method for qualitative evaluation. MT cleverly combines the evaluation of the model nature with software verification. Without manual solutions or benchmark questions, it assesses the code reliability by examining whether the code satisfies the metamorphic relation (MR). It has broad application prospects in the nuclear field.
The main innovation points in this article include: 1) A lightweight verification method based on metamorphic relation has been developed. It employs MRs to rapidly evaluate the code reliability at a low cost before the traditional methods estimate the solution accuracy expensively. The former is a supplement to the latter. 2) It makes the verification of nuclear power software more reasonable, reveals defects in the early stage of verification, and reduces the total cost of development. 3) The study of MR is helpful to deep insight into the characters of equations and algorithms, improve the quality of code and continuously increase the developer’s confidence in the program. In other words, MRs are the domain knowledge, and the research on them is profit to understand the system better and reuse that knowledge.
Specifically, a group of metamorphic relations is identified from the characteristics of physical equations and numerical algorithms. Then, metamorphic relations are explicitly used to evaluate whether the code keeps the specific rules of equations and algorithms. Two types of code errors can be revealed out quickly and efficiently. The first one is that the code does not accurately implement the numerical algorithm, and the second one is that the numerical method does not correctly solve the physical model.
For the application of this method, the point-depletion computing code, namely NUIT, was used as the experimental object. Without verification examples, the code failures were found by the metamorphic relation. This method significantly alleviates the requirement for verification examples and improves verification efficiency and adequacy.
Direct Comparison Method
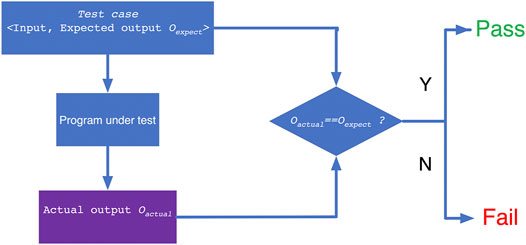
At present, nuclear power software verification usually adopts a direct comparison method, which verifies the correctness of the code by comparing the actual output with the expected result. The working principle is shown in Figure 1.
The expected result mainly employs typical benchmark questions, power plant operating data, and experimental bench data. For example, software package NESTOR is verified by international benchmark questions, Qinshan Nuclear Power Plant Unit 1 and Unit 2 operating data, and Hualong No. 1 Unit bench data (Lu et al., 2018). Furthermore, verification of PCM adopts benchmark questions, CPR1000/M310 power plant data, critical reactor test data, and similar software (Wang et al., 2018). The classical program is also a kind of expected result, such as the ORIGEN program for fuel consumption analysis (Hermann and Westfall 1998), APOLLO (Sanchez et al., 1988) and CASMO (Rhodes, Smith, and Lee 2006) for assembly calculation, MCNP(Brown et al., 2002) for radiation shielding, RELAP (Andrs et al., 2012) for system program and so on.
Oracle Problem
Oracle is a mechanism used to determine whether the execution result of the program under test is correct. It is challenging to construct when the expected result does not exist or the construction cost is exceptionally high; it is called an Oracle problem (Barr et al., 2015). Nuclear power software involves the numerical solution of many partial differential equations. It is usually tricky to construct analytical or accurate solutions. Furthermore, for fourth-generation reactors, such as high-temperature gas-cooled reactors, sodium-cooled fast reactors, molten salt reactors, lead reactors et al., and modern designs, e.g., high-fidelity, one-step method, multi-physics coupling, etc., new-generation software has almost no comparable programs and benchmark questions. In addition, benchmark questions, power plant operating data, and experimental bench data are only applicable to specific reactor types due to differences in the neutron energy spectrum, geometric configuration, and core materials. For verification examples, the development cost is high, the cycle is long, and the quantity is small. Therefore, the Oracle problem of nuclear power software is particularly prominent.
Compared with traditional testing methods, i.e., the direct comparison method, this type of software is called a non-testable system (Patel and Hierons 2018). Oracle problem makes nuclear power software testing insufficient. Hence, defects are challenging to find, which affects the safety and economy of engineering design. The sharp-jump problem is found in the classic burnup program ORIGEN when it calculates the decay chain of 239Pu and 233U (Isotalo and Aarnio 2011). If the half-life of some daughter-nucleus meets a specific relationship with the burnup step length, the calculation error will suddenly increase. Without adequate verification, such situations would remain.
Generally, software verification includes four test levels: unit testing, integration testing, system testing, and acceptance testing. Each level requires differently corresponding expected results. However, benchmark questions are only applicable to acceptance testing, and the expected results are seriously insufficient in other test levels. Code bugs are challenging to find early, making it challenging to locate defects and high costs for debugging and repairing. The characteristics of nuclear power software essentially cause the Oracle problem. Even if developing more benchmark questions, this problem can only be alleviated but cannot be solved. Therefore, there is an urgent need to introduce new software verification technologies.
Metamorphic Testing
Most scientific computing software is untestable software (Kanewala and Bieman 2014). Software verification often implicitly checks whether the code satisfies the specific characteristics of the physical equations, numerical methods, and program specifications. If those characteristics are violated, the code should have errors and could not pass the test. Metamorphic testing is an indirect verification technology that skillfully combines the program’s specific characteristics checking with software verification without constructing verification examples. The correctness of the code is evaluated by examining whether the code meets the metamorphic relation (MR). Its working principle is shown in Figure 2.
MRs are necessary properties of the target function or algorithm in relation to multiple inputs and their expected outputs (Chen et al., 2018; Chen and Tse 2021). For example, a program P implements sine function. It is hard to construct an oracle to determine whether P(x) is correct. However, applying her periodicity, i.e., sin(x) = sin (x+2π), an MR can be obtained as following: if x2 = x1 + 2π, then P (x2) = P (x1). As a result, using a group of inputs that satisfied such input pattern, if twice execution results violate the output pattern, it will indicate that P does not agree with MR. In other words, P conflicts with the basic property of sine. Thus, P has a failure. MRs are essential properties that are meaningful for software verification, and codes should abide by them.
Metamorphic testing is one of the effective means to solve Oracle problems (Chen et al., 1998; Liu et al., 2014; Segura et al., 2018; Kanewala and Yueh Chen 2019). Studies have shown that MT has the advantages of reasonable cost and a more vital ability to expose errors (Hu et al., 2006). It is used for software verification, software validation, and software quality assurance (Segura and Zhou 2018). Furthermore, it appears to be the only technique applicable to all three areas of verification, namely testing, proving, and debugging (Chen and Tse 2021). MT has broad application prospects in the nuclear field.
Lightweight Verification Method Based on Metamorphic Relation
For relieving the Oracle problem, this paper developed a lightweight verification method based on metamorphic relation. The MR hierarchical classification model (Xiaohua et al., 2020) identifies MRs from the specific property of physical equations, numerical algorithms, and program specifications. Then applying them to system testing, integration testing, and unit testing, respectively, to improve the adequacy of testing. Because there is no need to develop verification examples, this method can reveal code failures at the earliest opportunity. As a result, it will improve verification efficiency at a lower cost. In addition, it is also a necessary supplement to the traditional verification technology.
NUIT is a burnup calculation code independently developed by the Institute of Nuclear and New Energy Technology of Tsinghua University (Jian et al., 2020). NUIT implements a variety of burnup algorithms, including the transmutation trajectory analysis method (TTA), the Chebyshev Rational Approximation Method (CRAM), Quadrature group Rational Approximation Method (QRAM), Laguerre Polynomial Approximation method (LPAM), and Mini-Max Polynomial Approximation method (MMPA). For ease of understanding, the rest of this article uses NUIT for discussion.
MR Identification Model
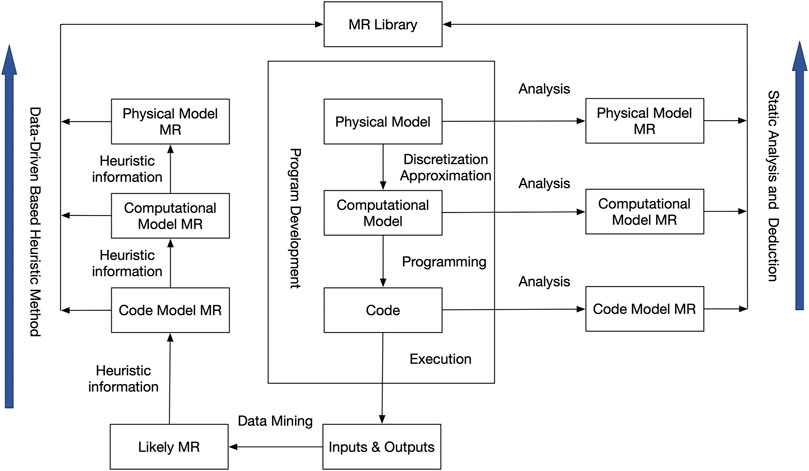
MR is the key in MT. According to current research literature (Sun et al., 2019; Segura et al., 2016), there are several MR identification techniques, such as machine-learning-based, search-based, pattern-based, data mutation-based, and existing MRs’ composition etc. We divide them into two categories, namely static analysis, and dynamic discovery, from the perspective of whether to execute the program under test. The former does not execute the program and derives MR by analyzing physical equations’ properties, numerical algorithms, and program specifications. The latter reveals MR from inputs and outputs. Because these relations are fitted from data, their validity has not been proved theoretically, thus called likely relations. However, they can provide heuristic information for MR identification. As a result, one abstract MR identification model has been constructed, illustrated in Figure 3. This model has four types of MR, i.e., physics model, computational model, code model, and likely MR. Besides them, a single MR should be formally described with the template approach (Segura et al., 2017).
The Verification Processes
It is assumed that a group of MR has been obtained. The lightweight verification method includes two core stages: MR identification and program evaluation. Specifically, we describe the main activities as follows: 1) Analyzing the nature of the physical equation. 2) Investigating the properties of the numerical algorithm. 3) Studying the characteristic of the program specification. 4) Revealing the metamorphic relation by techniques in the identification model, i.e., transforming the above rules into a hierarchical MR model. 5) In accordance with MR, a group of MR test input pairs is generated, and the program under test is evaluated with MR. If the MR is satisfied, the test passes. Otherwise, it indicates that at least a failure in the code.
For demonstrating the details, there are several examples as follows.
Example 1: We are analyzing the nature of the physical equation. In the case of the fission reaction, the density of 135Xe gradually increases and does not change until production and consumption reach a dynamic balance after about 2–3 days. According to this rule, we can identify a physical model MR. Specifically, suppose t is the burnup time, D(t) is the nuclide density of 135Xe, T is the threshold at which the reaction reaches balance. Before balance,
Example 2: One property of the numerical algorithm is that the nuclide density should smoothly change with the burnup step. The corresponding computational model MR is described as follows. Similarly, t1 and t2 is the burnup time, D(t) is the nuclide density, T is the error threshold. If t2 is next to t1,
Example 3: After studying the characteristics of the program specification of the matrix exponent method, we find one rule that the result should not be affected by the nuclide ranking rule in the matrix. Hence, a code model MR is obtained. It assumes that o is the sorting rule, D(o) is the nuclide density when the burnup matrix is sorted by rule o, T is the error threshold. If o1 and o2 are different, then
Automation Execution Algorithm
It supposes that a set of MR has been obtained. The automation execution algorithm is as follows: 1) Reading a metamorphic relation. 2) Generating a set of test inputs according to the input pattern r and driving the program under test to execute to obtain the calculation outputs. 3) Evaluate whether those results comply with the output pattern R. If R is violated, the verification fails, and the process ends. Else 4) checking whether there is still a metamorphic relation that has not been adopted. If not, terminate the process, else do activity 1)–3) repeatedly.
Case Study
The burnup program describes the law of nuclide density changes over time. It is an essential part of the reactor’s physical design. It plays a crucial role in calculating the breeding and consumption of fuel in the reactor and changes in reactivity. The density of a particular nuclide can be expressed by Eq. 1.
The burnup equation can also be rewritten in matrix form, as shown in Eq. 2, where A is the coefficient matrix of the N-order nuclide depletion equation, and N is the number of nuclides.
Experiment
Twenty-eight MRs have been identified from NUIT using the static analysis technique, of which eighteen are physical model MR, and the rest are computational model MR (Meng et al., 2020; Li et al., 2020a; Li et al., 2020b; Li et al., 2021). Specifically, they are listed as follows.
The input parameters of NUIT mainly include initial fuel enrichment, mass, burnup step length, step unit, and the number of steps. The burnup calculation types include pure decay, constant flux, and constant power. The parameters constrained by the calculation type have neutron fluence rate and power. The solver mainly includes TTA and CRAM. The solver parameters include approximate order and truncation threshold. The output parameters mainly include nuclide density, radioactivity, neutron reaction rate, neutron absorption rate, decay heat, and other physical quantities.
By analyzing the physical model MRs, the adjustable input parameters include fuel enrichment, mass, total burnup time, neutron flux, and power. Since the neutron flux and power can be converted to each other, and the obtained properties are equivalent. Thus only power is taken here. The source test case of MT uses the verification example of the user manual. The burnup database adopts the high-temperature gas-cooled reactor HTGR nuclide database. The solver employs CRAM. The initial values of other parameters involve that the fuel enrichment is 8.5 percent, mass is one ton, power is 20 MW. The total burnup time is 340 days, of which the step length of the first stage is 1 day, the second stage is 4 days, and the third stage is 12 days, with twenty steps in each stage. The nuclide density is selected as the output parameter.
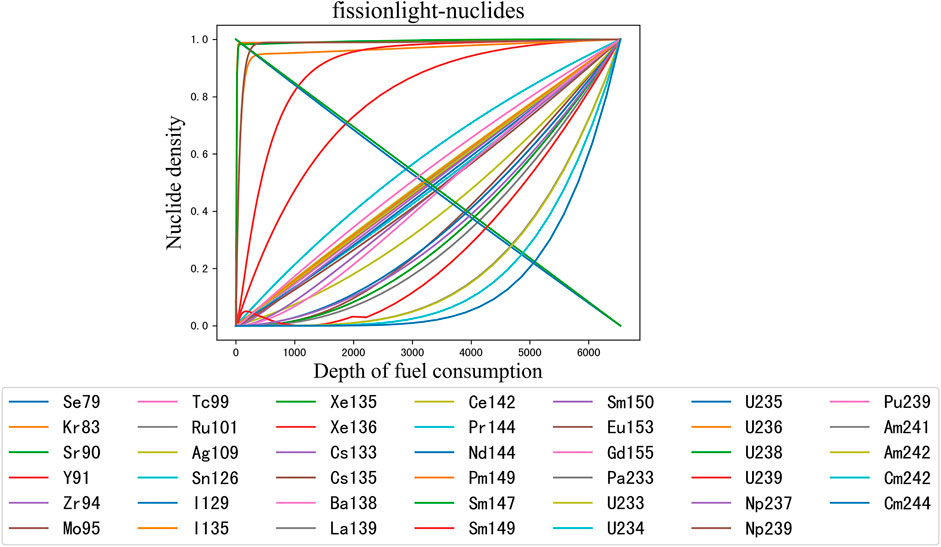
Figure 4 illustrates the trend relation between the density of some nuclides and the burnup level. A linear function y = ax + b can express some relations, such as 135Cs and 235U, the coefficient a is greater than zero in the former, while a is less than zero in the latter. A power function y = ax2+bx + c can also denote ones; for example, 237Np and 135Xe, the parameter a is greater than zero in the former, while a is less than zero in the latter. These observations can guide MR identification.
Assuming that the input pattern of MR is inequality, the single factor approach is used to design test cases, i.e., only one parameter changes at a time. To accurately describe the physical laws, the number of samples is more than 20. Therefore, the design results are as follows: 1) the fuel enrichment is from 1 to 20 percent, increasing by 1 percent each time; 2) The fuel mass is from 500 to 10000 kg, increasing by 500 kg each time; 3) The power is from 20 to 210 MW, increasing or decreasing by 10 MW each time. To sum up, a total of 160 test cases are designed.
Result
A total of forty-six defects were found, of which thirteen bugs were contributed by the lightweight method. After analyzing carefully, we can divide the defects of NUIT into three categories. The first one is that the code does not accurately implement the numerical algorithm. The second one is that the numerical algorithm does not correctly solve the physical equation; It results in the applicable scope of the code being narrower than that agreed in the requirements document. The last one is that the parameters of the algorithm are set inappropriately for specific calculation conditions. Hence, the first type error number is thirteen, and the second type error is three. Half of them are contributed by the lightweight method.
For example, 1) when solving the short half-life nuclides, such as 134Cs, 242Cm, and 244Cm, etc., by the TTA method, it is necessary to shorten the burnup step length; otherwise, the deviation will increase significantly. 2) Since time-consuming and significant deviation, the TTA method is not suitable for solving non-homogeneous burnup equations. 3) Matrix exponent numerical algorithms, like CRAM, QRAM, LPAM, and others, are more stable and reliable in the constant power than constant neutron flux. 4) Similarly, their results of the instantaneous are better than integral.
Discussion
The program model MR is applied for unit testing to evaluate whether the code correctly performs the program design specifications. Next, the computational model MR is employed for integration testing to estimate whether the code accurately implements the numerical solution algorithm. Moreover, the physical model MR is performed for system testing to ensure that the code correctly explains the physical equations.
Compared with the traditional verification model, this paper clearly defines the nature of verification activity. It makes the implicit evaluation of the program’s properties explicating. Furthermore, we can perform qualitative verification on nuclear power software without benchmarks at a low cost by taking advantage of MT. It should be compliance testing before any quantitative examinations at every test level.
The lightweight verification method has the following advantages:
1) It assumes that the program accurately implements the numerical algorithm. Then, the code should maintain the specific properties of the algorithm, such as symmetry, homogeneity, conjugation, error convergence, etc. Similarly, if the numerical algorithm correctly solves the physical equation, it should keep the expected natures of the equation even though there are no verification examples. If the actual outputs violate the above assumptions, there must be bugs in the program under test. Therefore, the lightweight verification method can significantly reduce verification costs and improve verification efficiency.
2) The properties of numerical algorithms and physical equations belong to high-order rules independent of the specific implementation of code. The program should keep these high-order regulations, whether the programming language is Python or C/C + +, whether the mathematical library is Intel MKL, OPENBLAS, or EIGEN. Therefore, lightweight verification has broader applicability and stronger reusability, which is helpful to improve the evaluation level of nuclear power software. It has important practical significance for shortening software certification time.
With advantage 1, the actual test time of NUIT only took 3 months, and there was no development cost of verification example for improvement of the test coverage. Based on advantage 2, the physical MRs are applied at the different solvers of NUIT, such as TTA, CRAM, and others. It reduces the test time significantly. Moreover, MRs identified from NUIT can verify other burnup calculation programs, such as KYLIN-2 developed by NPIC.
To sum up, the lightweight verification method based on MR alleviates the Oracle problem better compared with the traditional direct comparison method. It uses a lower cost to increase the test adequacy, reveal code bugs in early stage of verification, and avoid leaving defects to the subsequent testing level. Since reducing the cost of defect location and repair, improving the efficiency of research and development, it has broad application prospects in nuclear power software verification.
The main limitations of this method come from MR and source test cases. At present, MR identification technology mainly depends on manual analysis and inference, so data-driven MR mining technology is a promising research direction.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
XY: Supervision, Conceptualization, Methodology. ML: Conceptualization, Methodology, Writing an original draft and editing. SY: Methodology, Analysis. JL: Methodology, Analysis. YL: Methodology, Experiment. JS: Conceptualization, Experiment.
Funding
Financial support of National Science and Technology Major Project of China (2019ZX06005001), Natural Science Foundation of Hunan Province of China (2020JJ4519), Scientific Research Project of Department of Education of Hunan Province of China (19C1608), Teaching Reform Research Project of Hunan Province of China (Xiang Jiaotong 2018; No. 436-327).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Andrs, D., Berry, R., Gaston, D., Martineau, R., Peterson, J., Zhang, H., et al. (2012). Relap-7 Level 2 Milestone Report: Demonstration of a Steady State Single Phase Pwr Simulation with Relap-7. Idaho Falls: Idaho National Laboratory.
Barr, E. T., Harman, M., McMinn, P., Shahbaz, M., and Yoo, S. (2015). The Oracle Problem in Software Testing: A Survey. IIEEE Trans. Softw. Eng. 41 (5), 507–525. doi:10.1109/TSE.2014.2372785
Brown, F. B., Barrett, R. F., Booth, T. E., Bull, J. S., Cox, L. J., Forster, R. A., et al. (2002). MCNP Version 5. Trans. Am. Nucl. Soc. 87 (273), 2–3935.
Chen, T. Y., Cheung, S. C., and Yiu, S. M. (1998). Metamorphic Testing: A New Approach for Generating Next Test Cases. Technical Report HKUSTCS98-01. HongKong: Department of Computer Science, Hong Kong University of Science and Technology. Available from: https://www.cse.ust.hk/∼scc/publ/CS98-01-metamorphictesting.pdf.
Chen, T. Y., Kuo, F.-C., Liu, H., Poon, P.-L., Towey, D., Tse, T. H., et al. (2019). Metamorphic Testing. ACM Comput. Surv. 51 (1), 1–27. doi:10.1145/3143561
Chen, T. Y., and Tse, T. H. (2021). “New Visions on Metamorphic Testing after a Quarter of a Century of Inception,” in ESEC/FSE 2021 - Proceedings of the 29th ACM Joint Meeting European Software Engineering Conference and Symposium on the Foundations of Software Engineering, August 2021 (New York, NY: Association for Computing Machinery), 1487–1490. doi:10.1145/3468264.3473136
Hermann, O. W., and Westfall, R. M. (1998). ORIGEN-S: SCALE System Module to Calculate Fuel Depletion, Actinide Transmutation, Fission Product Buildup and Decay, and Associated Radiation Source Terms. Washington, DC: Citeseer.
Hu, P., Zhang, Z., Chan, W. K., and Tse, T. H. (2006). “An Empirical Comparison between Direct and Indirect Test Result Checking Approaches,” in Proceedings of the Third International Workshop on Software Quality Assurance, SOQUA 2006, New York, USA, November 2006 (New York, NY: Association for Computing Machinery), 6–13. doi:10.1145/1188895.1188901
Isotalo, A. E., and Aarnio, P. A. (2011). Comparison of Depletion Algorithms for Large Systems of Nuclides. Ann. Nucl. Energ. 38 (2–3), 261–268. doi:10.1016/j.anucene.2010.10.019
Kanewala, U., and Bieman, J. M. (2014). Testing Scientific Software: A Systematic Literature Review. Inf. Softw. Tech. 56 (10), 1219–1232. doi:10.1016/j.infsof.2014.05.006
Kanewala, U., and Yueh Chen, T. (2019). Metamorphic Testing: A Simple yet Effective Approach for Testing Scientific Software. Comput. Sci. Eng. 21 (1), 66–72. doi:10.1109/MCSE.2018.2875368
Li, J., She, D., Shi, L., and Liang, J. g. (2020). The NUIT Code for Nuclide Inventory Calculations. Ann. Nucl. Energ. 148, 107690. doi:10.1016/j.anucene.2020.107690
Li, M., Wang, L., Yan, S., Yang, X., Liu, J., and Wan, Y. (2020a). “Metamorphic Relations Identification on Chebyshev Rational Approximation Method in the Nuclide Depletion Calculation Program,” in Proceedings of 2020 IEEE 20th International Conference on Software Quality, Reliability and Security Companin(QRS-C), Macau, China, Dec. 2020 (IEEE), 1–6. doi:10.1109/QRS-C51114.2020.00013December 11-14
Li, M., Yan, S., Yang, X., and Liu, J. (2020b). “Metamorphic Testing on Nuclide Inventory Tool.” In Proceedings of the 2020 28th International Conference on Nuclear Engineering, V003T14A001. August 2020, American Society of Mechanical Engineers. doi:10.1115/ICONE2020-16403
Li, M., Wang, L., Yue, W., Liu, B., Liu, J., Liu, Z., et al. (2021). Metamorphic Testing of the NUIT Code Based on Burnup Time. Ann. Nucl. Energ. 153 (April), 108027. doi:10.1016/j.anucene.2020.108027
Liu, H., Kuo, F.-C., Towey, D., and Chen, T. Y. (2014). How Effectively Does Metamorphic Testing Alleviate the Oracle Problem. IIEEE Trans. Softw. Eng. 40 (1), 4–22. doi:10.1109/TSE.2013.46
Lu, Z., Li, Q., Dong, L., Chai, X., Fang, H., and Gong, Z. (2018). Engineering Applicability Strengthening Design and Practice of NESTOR Software Package. Nucl. Power Eng. 39 (1), 161–164. doi:10.13832/j.jnpe.2018.01.0161
Meng, L., Lijun, W., Shiyu, Y., and Xiaohua, Y. (2020). Metamorphic Relation Generation for Physics Burnup Program Testing. Int. J. Performability Eng. 16 (2), 297–306. doi:10.23940/ijpe.20.02.p12.297306
Patel, K., and Hierons, R. M. (2018). A Mapping Study on Testing Non-testable Systems. Softw. Qual J 26 (4), 1373–1413. doi:10.1007/s11219-017-9392-4
Rhodes, J., Smith, K., and Lee, D. (2006). “CASMO-5 Development and Applications,” in Proceedings of the PHYSOR-2006 Conference, ANS Topical Meeting on Reactor Physics, Vancouver BC Canada, January 2006, 144.
Sanchez, R., Mondot, J., Stankovski, Ž., Cossic, A., and Zmijarevic, I. (1988). APOLLO II: A User-Oriented, Portable, Modular Code for Multigroup Transport Assembly Calculations. Nucl. Sci. Eng. 100 (3), 352–362. doi:10.13182/NSE88-3
Segura, S., Duran, A., Troya, J., and Cortes, A. R. (2017). “A Template-Based Approach to Describing Metamorphic Relations,” in Proceedings of the 2nd International Workshop on Metamorphic Testing MET ’17, Buenos Aires, Argentina, May 2017 (IEEE Press), 3–9. doi:10.1109/MET.2017.3
Segura, S., Fraser, G., Sanchez, A. B., and Ruiz-Cortes, A. (2016). A Survey on Metamorphic Testing. IIEEE Trans. Softw. Eng. 42 (9), 805–824. doi:10.1109/TSE.2016.2532875
Segura, S., Towey, D., Zhou, Z. Q., and Chen, T. Y. (2020). Metamorphic Testing: Testing the Untestable. IEEE Softw. 37, 46–53. doi:10.1109/MS.2018.2875968
Segura, S., and Zhou, Z. Q. (2018). “Metamorphic Testing 20 Years Later,” in Proceedings of the 2018 ACM/IEEE 40th International Conference on Software Engineering, Gothenburg, Sweden, May 2018 (IEEE Computer Society), 538–539. doi:10.1145/3183440.3183468
Sun, C.-A., Fu, A., Poon, P.-L., Xie, X., Liu, H., and Chen, T. Y. (2019). METRIC+: A Metamorphic Relation Identification Technique Based on Input Plus Output Domains. IIEEE Trans. Softw. Eng. 47, 1. doi:10.1109/tse.2019.2934848
Wang, C., Yang, S., Peng, S., Li, G., Ma, Y., Chen, J., et al. (2018). Automated Validation of CGN Nuclear Software Package PCM. Nucl. Power Eng. 39 (S2), 43–46. doi:10.13832/j.jnpe.2018.S2.0043
Keywords: nuclear power software, metamorphic relation, lightweight verification method, software verification, metamorphic testing
Citation: Li M, Yang X, Yan S, Liu J, Liu Y and Sun J (2022) A Lightweight Verification Method Based on Metamorphic Relation for Nuclear Power Software. Front. Energy Res. 10:788753. doi: 10.3389/fenrg.2022.788753
Received: 03 October 2021; Accepted: 13 January 2022;
Published: 04 February 2022.
Edited by:
Qian Zhang, Harbin Engineering University, ChinaReviewed by:
Xiaoyuan Xie, Wuhan University, ChinaYu Ma, Sun Yat-sen University, China
Tao Zhang, Macau University of Science and Technology, Macao SAR, China
Copyright © 2022 Li, Yang, Yan, Liu, Liu and Sun. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiaohua Yang, eGlhb2h1YTE5NjNAZm94bWFpbC5jb20=
 Meng Li
Meng Li Xiaohua Yang
Xiaohua Yang Shiyu Yan
Shiyu Yan Jie Liu
Jie Liu Yusheng Liu
Yusheng Liu Jun Sun
Jun Sun