Maximum Power Point Tracking in Power System Control Using Reservoir Computing

This article deals with an innovative approach to maximum power point tracking (MPPT) in power systems using the reservoir computing (RC) technique. Even though extensive studies have been conducted on MPPT to improve solar PV systems efficiency, there is still considerable room for improvement. The methodology consisted in modeling and programming with MATLAB software, the reservoir computing paradigm, which is a form of recurrent neural network. The performances of the RC algorithm were compared to two well-known methods of maximum power point tracking: perturbed and observed (P&O) and artificial neural networks (ANN). Power, voltage, current, and temperature characteristics were assessed, plotted, and compared. It was established that the RC-MPPT provided better performances than P&O-MPPT and ANN-MPPT from the perspective of training and testing MSE, rapid convergence, and accuracy of tracking. These findings suggest the need for rapid implementation of the proposed RC-MPPT algorithm on microcontroller chips for the widespread use and adoption globally.

1 Introduction

Recent advances in technology, industry growth, increasing populations with their proportional energy needs highlight the problem of energy shortage.

Leggett (2021) theorized that failure to meet the global energy quest and the consistent depletion of non-renewable energy resources resulted in renewable energy as a sustainable alternative for energy generation in the future. Solar photovoltaic (PV) technology has been identified as one of the most auspicious energy sources based on the Sun (Dajuma et al., 2016) as a natural resource. Several previous studies posited that solar PV can resourcefully substitute orthodox energy sources in addition to improving environmental conservation (Acakpovi and Asabere, 2017)

According to the International Energy Agency (IEA) forecast, by 2050, PV technology is likely to become a very significant source of energy that will offer about 11–13% of global electricity and would be able to minimize about 2.3 gigatons of carbon dioxide (CO₂) emissions per year. PV has attracted more attention due to the advantages of the sun as a source of energy characterized by inexhaustibility, omnipresence, absence of rotating parts, accessibility everywhere, and minimum required maintenance (Boukenoui et al., 2016).

The PV technology directly converts sunlight into electricity, a phenomenon known as the photovoltaic effect. Furthermore, PV systems’ optimum output power mainly depends on environmental factors such as temperature and irradiation, installation method, and efficiency of the PV cell. In practical operation, a PV system exhibits a peak point on its power-voltage curve known as the maximum power point (Boukenoui et al., 2016; Acakpovi et al., 2018). Maximum power point tracking (MPPT) algorithms are used to determine the highest efficiency output of a photovoltaic system. Having the PV array operating around this MPP at all times is promising for the highest efficiency. However, owing to the sun movement and variation in intensity, operating at MPP is complex and requires a tracking system.

Tracking systems are generally made of power converters with extreme efficiency requirements. The expectation from the tracking systems is to enhance the energy productivity of a PV plant by harvesting the maximum sunshine in a day. The tracking system follows the Sun directions and variations preferably in real time and adjusts necessary parameters to remain in conditions of highest receptivity of solar irradiation throughout a day (Acakpovi et al., 2012; Acakpovi et al., 2017).

Even though some MPPT exist in previous studies, global trends indicate is certainly a big room for improvement in their operation, which can be supported by artificial intelligence implemented on microchips. In this regard, this article explores the application of “reservoir computing” (RC), one of the recent computing paradigms to improve upon existing solar tracking algorithms and enhance PV system efficiency. RC is a new computation framework that can be classified as one of the artificial intelligence techniques, specifically under the recurrent neural networks (RNN) category.

The learning complication on RC seems to be less complex than that of the traditional RNN, making this technique very attractive because the pre-processor, in this case the reservoir, consists of random recurrently connected non-linear elements, and learning actually takes place only at the output layer stage (Soriano et al., 2015; Kudithipudi et al., 2016; Gallicchio and Micheli, 2021; Subramoney et al., 2021).

The rest of the article is organized as follows: Section 2 presents the literature review and relevant background information, Section 3 presents the methodology, mainly the computation approach for reservoir computing. Section 4 deals with the result and data analysis, and Section 5 presents the conclusion.

2 Literature Review

Diverse MPPT systems have been developed in the past, including the perturb and observe (P&O) method (Femia et al., 2007; Piegari and Rizzo, 2010; Abdelsalam et al., 2011; Mamarelis et al., 2014; Piegari et al., 2015). The P&O method consists of introducing some perturbations in the PV array voltage and regularly reading the output power of the PV module, which is compared to previous values. The difference in reading, whether increasing or decreasing output power, is used to determine the direction of the perturbations, which might be reversed whenever necessary. Accurate algorithms are developed in line with P&O to achieve MPPT.

Additionally, Nakir et al. (2016) worked on a new MPPT algorithm for vehicle integrated solar energy system and argued that a significant amount of energy can be economized when electric vehicles surface is covered by PV cells. Their study proposed a new algorithm called smart observation (SO), which was used to achieve better MPP performance under fast-moving conditions compared to previous algorithms.

Liu et al. (2012) and Huang et al. (2016) developed the auto-scaling variable step method. Liu and Huang (2011) further explored the fast- and low-cost analog method. Liu et al. (2012) and Acakpovi (2016b) adopted the particle swarm optimization (PSO) method for a low-power PV system. They concluded that the steady-state performance and tracking speed are enhanced using the PSO approach, and the cost of tracking is reduced. Similarly, a fuzzy-logic control was proposed (Garraoui et al., 2013; Hajighorbani et al., 2014; Chen et al., 2016) and merged with the hill-climbing method. It was found that the fuzzy rule needed to be varied dynamically according to the reading of the sensors to attain good tracking speed and stability, which poses several computational complexities.

Salam et al. (2013), Mellit and Kalogirou (2014), and Rezk and Eltamaly (2015) noted that the traditional MPPTs such as perturbation and observation (P&O), incremental conductance (IncCond), and hill-climbing (HC) methods are not able to recognize the global MPP from the local MPPs especially in situations where there is more than one peak. Hence, lower MPPT efficiency is achieved because the power generated by the PV plant is marginally reduced. Ahmed and Miyatake (2008), Mellit and Kalogirou (2014), and Boukenoui et al. (2016) proposed a technique grounded on the Fibonacci search algorithm for a PV power generation system using partial shading conditions (PSCs). The improved Fibonacci search technique is comparable to the variable step size in the P&O technique. A wide range search is used as a modification carried out with a new function that leads the operating point to the global MPP. Contrarily, this method is limited to ensuring convergence to the global MPP. To overcome this limitation, a power compensation approach has been introduced by Karatepe et al. (2008).

Moreover, an adaptive perceptive particle swarm optimization (APPSO) was proposed by Roy Chowdhury and Saha (2010) and Chowdhury (2021). Under any weather condition, this was meant to track the global MPP. Nevertheless, there are significant complexities when implementing APPSO-based MPPT. Getting the model frame was a challenge and the principle could not be achieved as expected upon testing. Ishaque et al. (2012) came up with an improved PSO-based MPPT algorithm for a PV generation system that functions under PSCs, which can track the GMPP for countless shading circumstances. However, the shortfall of their study is the reliance on the system-specific parameters known as series cell number.

Likewise, Ishaque et al. (2012) proposed a PSO technique that governed the population size inertia (PI) and integrated the learning features by the trial-and-error method. The procedure has effectively tracked the global MPP under partial shading conditions and achieved a higher efficiency of about 99.5%. A universal MPPT-based P&O algorithm was established to detect the global MPP position in the PV array using the power regulation approach (Koutroulis and Blaabjerg, 2012). The complexity of implementing this algorithm, coupled with the cost involved, makes them impracticable.

Many other studies addressed the partial shading issues of a PV system from the perspective of microchip programming and integrating them into complex electronics systems (Acakpovi and Ben Hagan, 2013; Nanda and Mohanty, 2014; Acakpovi and Sunny, 2015).

2.1 Theoretical Basics of Reservoir Computing (RC)

The human brain’s capability to process data forms the basis of neuro-computing. The vital computing units of the nervous system are neurons, and the synapses are the conduits through which communication is sent to other neurons. The brain behaves as a dynamic computational system that is not wired for a definite task but reprocessing, reorganizing, and altering the given prevailing brain structure. Our brains’ computational capability has given rise to the field of Artificial Neural Networks (ANNs). ANNs imitate biological neural networks that can perform several computational functions.

In the field of ANNs, a “unit” is a neuron that can be mathematically represented with equations. McCulloch-Pitts (2021) proposed a simple two-state neuron model, which is the first artificial neuron model. Later on, Li et al. (2016) proposed the realistic integrate-and-fire models, also known as the spiking neuron models, designed to describe and forecast biological processes.

Liquid state machines (LSMs) and the echo state network (ESN) (Jaeger, 2007, 2008) are the two current computing paradigms introduced based on ANN. Both models epitomize a novel class of computing models stimulated by recurrent neural networks. The principal term for these paradigms is reservoir computing (RC) (Jaeger, 2008; Hamedani et al., 2019).

The mathematical modeling of the computing “unit” (neuron) accounts for the major difference between these two models. While in the LSMs, the “unit” is modeled as a spiking integrate-and-fire neuron, in the ESN architecture, the unit is implemented as sigmoid. The spiking neuron model closely looks like the spiking nature of biological neurons and retains the vital neuron behavior. As a result, LSM applications primarily focus on providing an effective biological architecture for generic cortical microcircuits computations.

2.2 Liquid State Machines

A recently introduced novel computational framework is the liquid state machines (LSMs) (Zhang et al., 2015). The “liquid” is considered as the computing core in the recurrent neural network (RNN). A mathematical expression of spiking integrate-and-fire neurons defines each computing unit in the “liquid.” Within time-varying inputs, the LSM framework can perform real-time computations. The LSM’s architecture is made up of three different segments: 1) the processing layer, also known as the readout layer; 2) the liquid’s state space, which means memory; and 3) the pre-processor unit called the “liquid” (Jaeger, 2008; Zhang et al., 2020). The outstanding characteristics of the LSM’s architecture are that only the readout layer is trained to extract the time-varying information from the liquid. Trentin et al. (2015), through an experiment, showed that the readout layer can be trained to accomplish a temporal pattern recognition task.

2.3 Solar Photovoltaic Generator

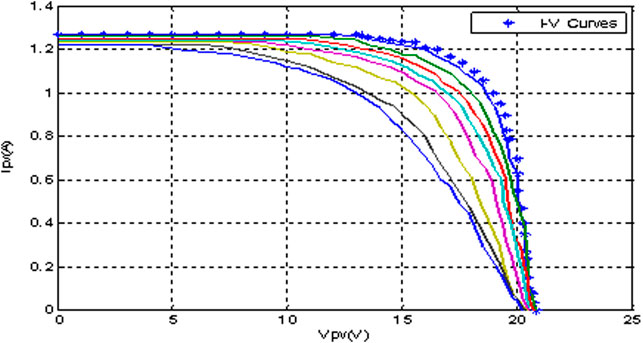
To understand the theoretical dynamics of MPP, the output of a typical PV is used with the characteristics illustrated in Figure 1.

FIGURE 1

FIGURE 1. Characteristics of selected solar panel.

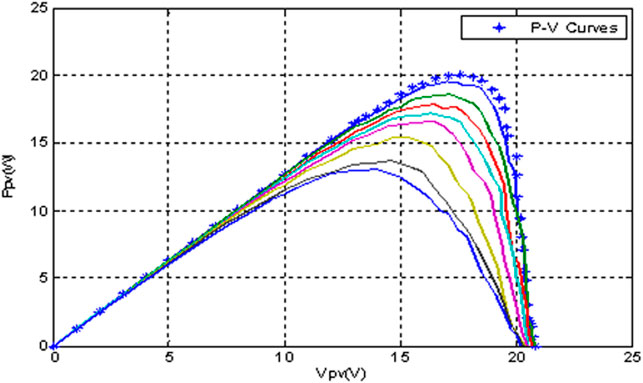
The nature of the curve and the optimal operational points of Vmpp, Impp, and Pmax change when the weather conditions, such as temperature (T) and irradiance (G), shadow and vary. The weather and the consequent varying maximum optimal operational points (MOOPs) cause electrical power system variations not only to the PV generator but also to the tie-grid and consumers (Piegari and Rizzo, 2010; Quamruzzaman and Rahman, 2014; Sahu and Dixit, 2014). During the effect of the non-linear variations, the intrinsic structure of the cell undergoes numerous phenomena that adversely affect the conductivity of the silicon material, which subsequently provoke a drop in the generated power output, as shown in Figures 2, 3 (Nordman et al., 2012; Verma et al., 2016).

FIGURE 2

FIGURE 2. I-V curves showing the effects of weather on photovoltaic solar cell.

FIGURE 3

FIGURE 3. P-V curves showing the effects of changing weather on photovoltaic solar cell.

The P-V curves of Figures 2, 3 clearly show multi-nonlinear optimal power points at different voltages. A proposed circuit is needed to track these optimal power points fast, accurately, and simply.

A typical electrical power system can hardly operate at these varying voltages and optimal power points illustrated in Figures 2, 3 because of its inimicality to power system stability (Chen et al., 2015; Li et al., 2016).

The circuit in Figure 4 represents a proposed actual nature of the circuit used to implement the RC’s maximum power point tracking algorithm in the microcontroller.

FIGURE 4

FIGURE 4. Electrical circuit model to implement MPPT using RC.

The RC MPPT algorithm modifies the input reference voltage (V_ref) and the proportional integral (PI) loop stimulates the panel operating voltage (V_pv) to the set reference voltage. Then, a control PI loop is needed to signal the corresponding duty cycle $\left(\delta \right)$ to a pulse width modulator (PWW) to trigger switching, which is usually achieved with power electronic bipolar transistors (FET, BJT, and MOSFET) (Ahmad et al., 2016; Ajami et al., 2016).

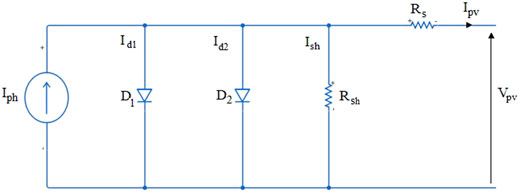
However, for mathematical and computation analysis, a standard solar photovoltaic equivalent circuit in Figure 5 is needed. Herein, the double diode model of the photovoltaic cell is used.

FIGURE 5

FIGURE 5. Double diode equivalent circuit (Bakhoda et al., 2016).

When sunlight illuminates a PV solar cell, a photocurrent (Iph) is generated. This current is, however, subject to losses due to semiconductor imperfections, variations in weather, temperature, irradiance, and shadow, among others (Kumar and Chatterjee, 2016; Nayanar et al., 2016).

Generally, the losses encountered in a PV cell are modeled by a series resistance (Rs) and a shunt resistance (Rsh). Additionally, the model of a PV cell makes use of two diodes with respective saturation currents I_s1 and I_s2 and respective ideality factors n₁ and n₂, as illustrated in Figure 5.

With the assumption that these diodes are performing at their optimum levels to ensure the switching capabilities, their effects are greatly used to depict the variations in the fluctuations in maximum power point both intrinsically electrically and extrinsically environmentally (Kulkarni and Teuscher, 2012; Elsaharty et al., 2016).

An equivalent mathematical equation derived from the equivalent circuit of Figure 5 is presented below:

$I_{pv}=I_{sc}-I_{S1}\left[e\frac{V_{pv}+R_{s }{I}_{pv} }{n_1{V}_t}-1\right]-I_{S2}\left[e\frac{V_{pv}+R_s I_{pv}}{n_2{V}_t}-1\right]-\frac{V_{pv}+R_s{I}_{pv} }{R_{sh}},(1)$

where I_sc is the short circuit current, V_pv is the voltage generated by the solar panel, I_pv is the current generated by the solar panel, R_s is the series resistance of the PV model, R_sh is the shunt resistance of the PV model, I_s the saturation current, V_t is the thermal voltage, $\left(I_{S1}\right)$ represents the $saturationcurrentofdiode$ D1, $\left(I_{S2}\right)$ represents the $saturationcurrentofdiode$ D2, $idealityfactor\left(n_1\right)=1,\text{ and }idealityfactor \left(n_2\right)=1.$

Assuming n₁ and n₂ are performing at optimum switching capabilities, then the corresponding power equation and the duty cycle is obtained as

$P_{pv }=V_{pv}\left\{I_{sc}-I_{S1}\left[e\frac{V_{pv}+R_{s }{I}_{pv} }{n_1{V}_t}-1\right]-I_{S2}\left[e\frac{V_{pv}+R_s I_{pv}}{n_2{V}_t}-1\right]-\frac{V_{pv}+R_s{I}_{pv} }{R_{sh}}\right\},(2)$

$Duty cycle\left(\delta \right)=1- \frac{V_{oc}}{ V_{pv} }.(3)$

RC is well known as a powerful computational tool that supports real-time computation on a continuous variable. Its performance is assessed from the perspective of two properties: separation and approximation.

The liquid or the reservoir is said to have the separation property if the LSM or ESN has different internal states for two different input sequences. Euclidian distance or Hamming distance is used to measure the distance between different states. The measure of the readout capability to produce the desired output from the given liquid states is known as the approximation property (Jaeger, 2008; Kulkarni and Teuscher, 2012; Jayawardene and Venayagamoorthy, 2015; Alomar et al., 2016)

2.4 Application of Reservoir Computing to Maximum Power Point Tracking

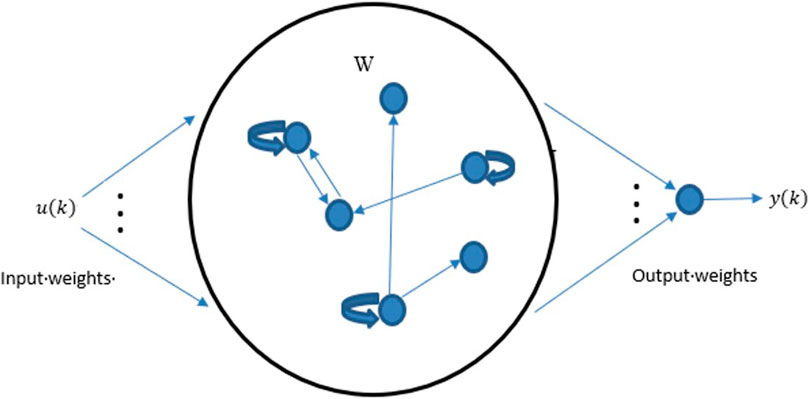
Under the category of the recurrent neural network, the echo state network (ESN) has recently emerged with more reliability and flexibility in training. ESN uses a reservoir, basically a large and sparsely connected RNN for which the weight and connectivity of neurons are randomly assigned and fixed (Jaeger, 2008; Jayawardene and Venayagamoorthy, 2015). Figure 6 illustrates the architecture of ESN.

FIGURE 6

FIGURE 6. Echo state network (ESN) structure.

A reservoir of size N consists of an $N\times 1$ input weight vector v and N neurons with connection weights between them giving an $N \times N$ sparse matrix W. The vector r denotes the readout weights. At a given time n, the “state” of the reservoir consists of the state of all the outputs of each neuron at the considered time, denoted by the $N$ $\times$ 1 state vector X (n). The current state of the reservoir may be updated to the next state as follows:

$\mathit{X}\left(n+1\right)=\text{tanh}\left[\mathit{WX}\left(n\right)+\mathit{V}u\left(n\right)\right].(4)$

In Eq. 4, $u\left(n\right)$ represents the input signal. It has been assumed that all inputs use the $sigmodial\left(\text{tanh}\right)$ as the activation function (Jaeger, 2008; Kulkarni and Teuscher, 2012; Jayawardene and Venayagamoorthy, 2015; Alomar et al., 2016).

Referring to Figure 6, the output function is determined as follows:

$y\left(n\right)=\tanh \left[{\mathit{X}}^{\mathit{T}}\left(n\right)\mathit{r}\right].(5)$

The purpose of the model output, which consists of the Readout training, is to find r such that, for any input $u\left(n\right)$ and its desired output d(n), the mean square error (MSE) determined by Eq. 6 that is minimized:

$MSE=\frac{1 }{L}{\displaystyle \sum }_{n=1}^L\left[tan{h}^{-1}\left(d\left(n\right)\right)-y\left(n\right)\right]^2,(6)$

$r=P^{\text{*}}tan{h}^{-1}\left(d\right).(7)$

In Eq. 6, L represents the duration of the training signals.

A careful analysis of Eqs 6, 7 shows that the problem can be formulated as a linear equation, which can be written in matrix form and solved for the readout as

$P=\left[\begin{array}{c}{X}^T\left(1\right)\\ X^T\left(2\right)\\ X^T\left(3\right)\\ \begin{array}{c}.\\ .\\ .\end{array}\\ X^T\left(L\right)\end{array}\right]\in L\times N,(8)$

where $P^{\text{*}}$ denotes matrix pseudoinverse of P. The matrix P contains, in each row, the state vector X(n) of each time step (Jaeger, 2008; Macausland, 2014).

3 Methodology for Implementing the RC-MPPT

3.1 Modeling of Reservoir Computing to Implement MPPT (RC-MPPT)

The modeling process starts with a training of the echo state network (ESN) algorithm based on refined and documented data in previous studies. Consider a training sequence with input/output of the form below:

$X\left(n\right), J\left(n\right), \dots , X\left(k\right),J\left(k\right).$

The goal is to deduce a train ESN for which the output Y(n) is approximately close to that of the teacher output J(n) while the ESN is triggered by input X(n). The following steps explain the implementation procedure:

Step 1. Design a dynamic reservoir (DR) network (Win, W, Wback) which is not trained yet and has the property of echo state, whose internal units exhibit dynamic and random characteristics as displayed in Figure 7

FIGURE 7

FIGURE 7. Schematic architecture of algorithm implementation.

The weights are generated based on the following basic sub-steps:

(i) Generate a random weight matrix internally and label it as W₀.

(ii) Apply a normalization to the random matrix W₀ based on the equation below to obtain W₁:

${\mathit{W}}_1=\frac{1}{\left|{\mathit{\alpha }}_{\mathit{max}}\right|}\cdot {\mathit{W}}_0.$

${\mathit{\alpha }}_{\mathit{max}}$ is the spectral radius of W₀

(iii) The next stage has to do with scaling W₁ to W₀ by applying the following equation:

$W=\beta W_1,$

where $\beta$ is the spectral radius of $W$.

(iv) Generate randomly, input weights Win, and output backpropagation weights.

Wback leads to the untrained network (Win, W, and Wback).

Step 2. In step two, the ESN network training characteristics are estimated using a simple routine procedure under MATLAB software

(i) Arbitrarily set the state of the network to start.

(ii) Drive the network with the training data as follows:

$X\left(n\right), J\left(n\right), \dots , X\left(k\right),J\left(k\right), n=0,\dots ,T.$

By applying the input data X(n), the output J (n-1) can be computed as follows:

$Y\left(n+1\right)=f\left(W_{in}X\left(n+1\right)+WY\left(n\right)+W_{back}\left(n\right)\right).$

(iii) At the initial time n = 0, the system output is not yet defined, so assume J (0) = 0.

(iv) At any time when bigger than or equal to the washout time T₀, record the compacted data made of input/reservoir/previous-output states (X(n) Y(n) O (n –1)) as an additional row into a state matrix M. At the final stage, the size of the state matrix M should be

$\left(T-T_0+1\right)\times \left(K+N+L\right).$

(v) Likewise, for each time longer than or equal to T₀, record the sigmoid-inverted teacher output tanh⁻¹I(n) in a new row to be added to the teacher collection matrix.

T. The final size of the teacher collection matrix should be

$\left(T-T_0+1\right)\times L.$

Step 3. Computation of output weights.

(i) Multiply the pseudoinverse of M with T, leading to an output matrix (W_out) of size (K + N + L) x L. W_out is given by

${\left(\mathit{W}out\right)}^T ={\mathit{M}}^{-1}\mathit{T}.(10)$

A linear optimization approach was used to determine the pseudoinverse elements according to the Moore–Penrose theorem (Macausland, 2014).

(ii) The next step consists of Transposing (Wout)^t to Wout.

Step 4. Exploitation.

At this stage, all essential elements of the network (Win, W, Wback, Wout) are known and ready for use. While applying the input sequence V(n), the output Y (n+1) can be deduced as follows:

$\mathit{Y}\left(\mathit{n+}\mathrm{1}\right)={\mathit{f}}_{\mathit{act}}\left(\mathit{Wout}\left(\mathit{V}\left(\mathit{n+}\mathrm{1}\right),\mathit{X}\left(\mathit{n+}\mathrm{1}\right),\mathit{J}\left(\mathit{n}\right)\right)\right)(11)$

where ${\mathit{f}}_{\mathit{act}}$ is the activation function. In this case, the function tanh is as illustrated by Jaeger (2008), Kulkarni and Teuscher (2012), Jayawardene and Venayagamoorthy (2015), and Alomar et al. (2016).

Figure 7 represents the internal architecture of the proposed reservoir computing algorithm for MPPT tracking. Based on the descriptions above, the algorithm can be implemented through programming with MATLAB software.

4 Data Analysis and Results

In this section, we examined the simulated results and conducted a comparative analysis between the two well-known methods of maximum power point tracking, namely, Perturbed and Observed (P&O) and Artificial neural network (ANN), to our novel approach of reservoir computing for maximum power point tracking.

4.1 Analysis of Simulated Results for Perturbed and Observed (P&O)

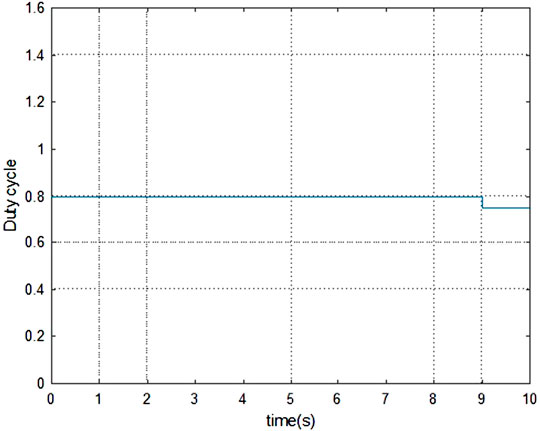
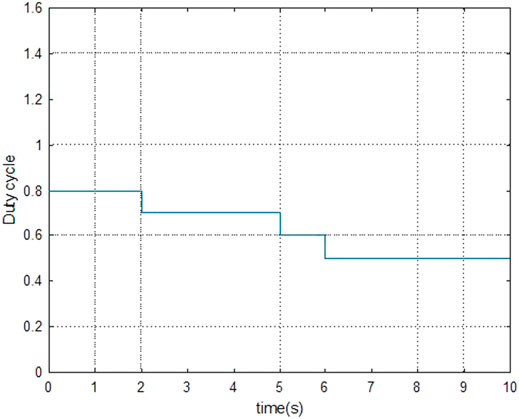
The simulated results of Figure 8,9 show that, for a very small step size of 0.001, the variations of δref are insignificant and the change from 0.8 to 0.75 occurred only after 9 s. On the contrary, when the step size is raised to 0.4, which is close to the reference value of 0.8, the variations were faster, leading to a value of 0.5 after 6 s.

FIGURE 8

FIGURE 8. Variation of the duty cycle for a smaller step size of ∆δ = 0.001.

FIGURE 9

FIGURE 9. Variation of the duty cycle for a bigger step size of ∆δ = 0.4.

Summarily, a smaller step size $\left(\mathrm{\Delta }\delta \right)$ takes a longer time to reach the maximum power point (MPP), making it very slow. However, a bigger $\mathrm{\Delta }\delta$ took a faster time to reach the MPP. It must be noted that a step size (perturbation) can be classified as small or big based on the reference duty cycle $\left(\delta ref\right)$.

However, the challenge is that, with a bigger $\mathrm{\Delta }\delta$, the MPP might easily be missed. A further attempt to backtrack the MPP might also fail, thus keeping the MPP unstable and fluctuating, which clearly violates power system operations and control stability.

4.2 Analysis of Simulated Results of Artificial Neural Network

The implementation was successful. The model converged faster irrespective of the step size that was smaller or bigger. The error margin was also better. Based on the simulation results, the mean square error (MSE) was (10) ^ (−5) as illustrated in Figure 10, when tracking maximum power point compared to the P&O. However, certain local minimum power points were observed, which were not necessarily optimal. Also, for every new characteristic dataset, there was a need for training as previous state memorization and state updates were not possible.

FIGURE 10

FIGURE 10. Mean square error (MSE) for training, validation, and testing of the ANN-MPPT.

4.2.1 Simulation Results of RC-MPPT

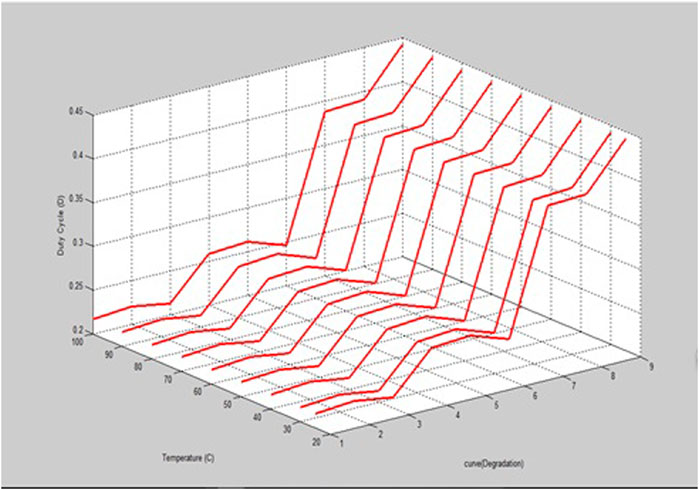
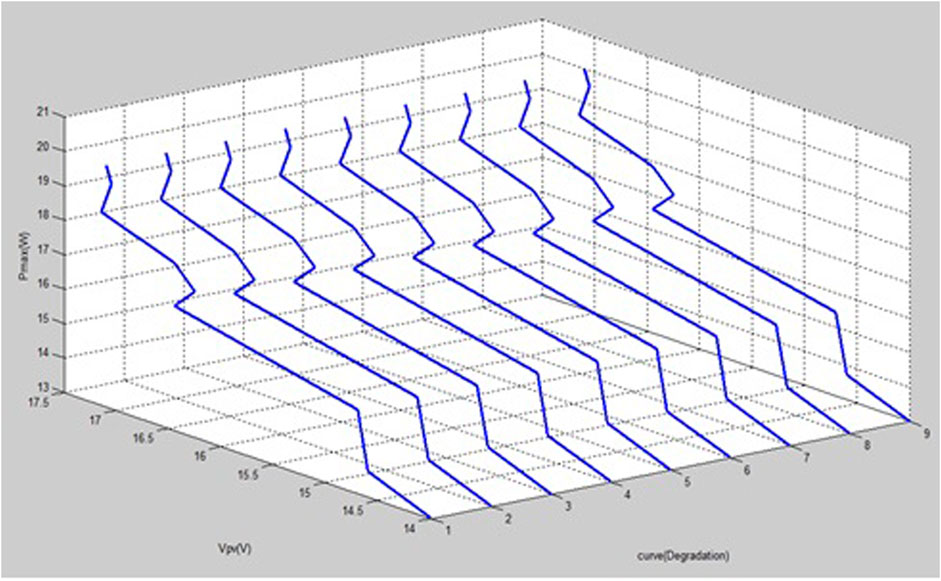
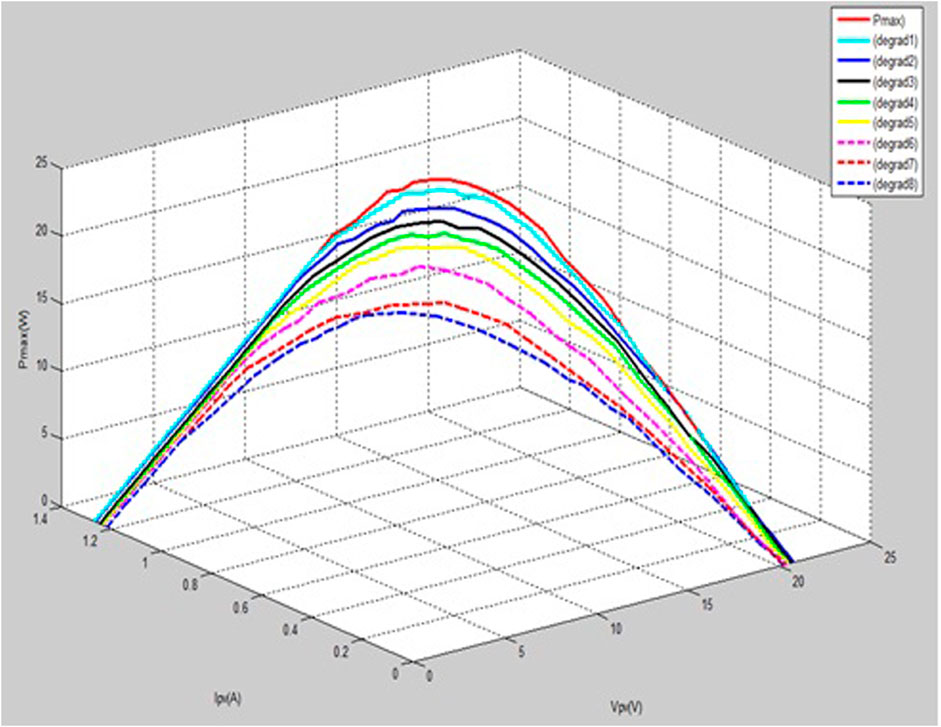
Simulated results implemented using MATLAB were obtained. In order to assess the relationships that exist between the inputs and the outputs using the RC-MPPT, 2D, several 3D curves were plotted as illustrated from Figures 11–14. A summary of the result is shown in Table 1. The MPPT algorithm allows the creation of random networks that simulate and train the readout layer utilizing the echo state network (ESN). The learning algorithm is computed after the data has been normalized. We further compute the matrix pseudoinverse spectral radius. Subsequently, the activation sigmoidal function is used to implement the readout (i.e., the output) layer.

FIGURE 11

FIGURE 11. Ground truth curve showing the output of RC-MPPT.

FIGURE 12

FIGURE 12. Duty cycle against temperature variation in 3D.

FIGURE 13

FIGURE 13. Maximum power against voltage variation in 3D.

FIGURE 14

FIGURE 14. Power (W) against current (A) and voltage (V) illustrating various MPP in 3D.

TABLE 1

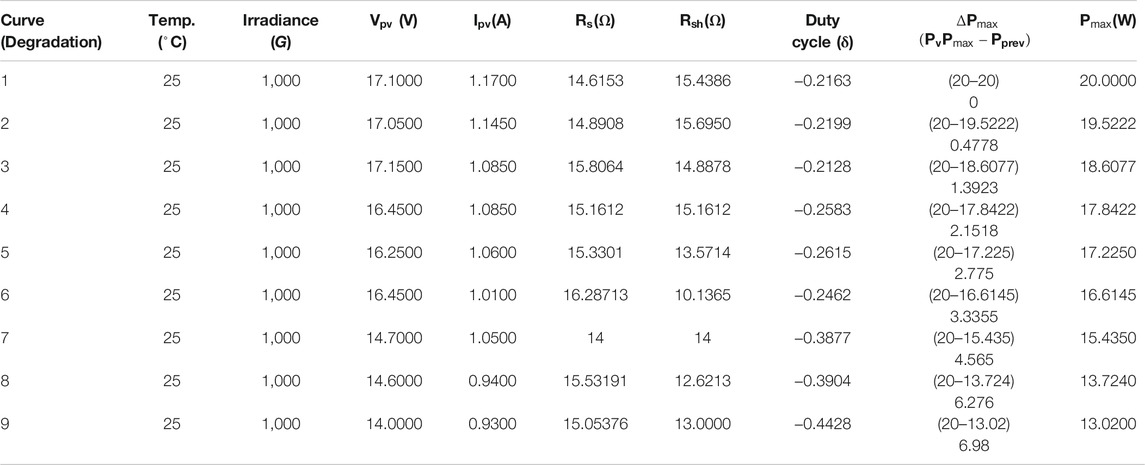
TABLE 1. A summary of the 2D and 3D optimal output points using the RC-MPPT for multiple curves (degradation).

After the exploitation of the various parameters in 2D and 3D, Tables 1, 2 summarize the optimal parameters at every stage for the different sets of data used in the RC-MPPT algorithm. The various relationships, interdependency, and effects on one another were also observed numerically. Interesting relationships exist between these parameters obtained at optimal points for the datasets used.

TABLE 2

TABLE 2. Summary of computational performance.

5 Conclusion

In summary, this article investigated the implementation of reservoir computing for maximum power point tracking of solar PV systems. Reservoir computing is one of the recurrent neural network techniques that had not been applied to MPPT before, though having promising results. The article, therefore, considered a mathematical conceptualization and developed an algorithm to implement the reservoir computing paradigm that was programmed with MATLAB software. The results were compared with two well-established computational approaches that have been used for MPP tracking in the past: P&O and ANN.

Findings revealed that the RC-MPPT presented more advantageous results than the predecessor techniques in terms of lower computational complexity compared to ANN, assured convergence, accuracy of tracking, and least MSE irrespective of the varying complexity in changing environmental conditions. RC is also particularly interesting for MPPT applications because of its non-linear and super high memory or storage characteristics.

The findings from the study highlight very important issues for theory and practice. The improved tracking accuracy associated with other benefits constitutes an extension of knowledge and an improvement of previous AI techniques used to address the same problem. For practice, the algorithm may be implemented on a microchip and made available to users for improved solar PV efficiency. Full implementation of the algorithm on microchips is highly recommended for further studies. Again, further studies should consider comparing the performances of the RC-MPPT to newly emerging AI techniques.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author Contributions

MS and DS have contributed equally to draft the first version of the paper. AA contributed significantly in re-conceptualizing the work, designing experiment set and conducting programming with Matlab. He also reviewed significantly the write-up for English and Format editing. D-GO-M, and RS have equally contributed in reviewing the work and advising on the development of algorithms, their programing and applications to the dataset.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdelsalam, A. K., Massoud, A. M., Ahmed, S., and Enjeti, P. N. (2011). High-performance Adaptive Perturb and Observe MPPT Technique for Photovoltaic-Based Microgrids. IEEE Trans. Power Electron. 26 (4), 1010–1021. doi:10.1109/tpel.2011.2106221

CrossRef Full Text | Google Scholar

Acakpovi, A. (2016b). Performance Analysis of Particle Swarm Optimization Approach for Optimizing Electricity Cost from a Hybrid Solar, Wind and Hydropower Plant. Nternational J. Renew. Energ. Res. (Ijrer) 6 (1), 323–334.

Google Scholar

Acakpovi, A., and Asabere, N. Y. (2017). Exploring the Fundamentals of Solar Photovoltaic Technology and its Modellingin Renewable Energy Systems. Editor S. A. Kale (Accra, Ghana: Nova Science Publishers), 1–37. Available at: https://www.researchgate.net/publication/311675251_Exploring_the_Fundamentals_of_Solar_Photovoltaic_Technology_and_its_Modelling.

Google Scholar

Acakpovi, A., and Ben Hagan, E. (2013). Novel Photovoltaic Module Modeling Using Matlab/Simulink. Int. J. Comput. Appl. 83 (16), 27–32. doi:10.5120/14535-2978

CrossRef Full Text | Google Scholar

Acakpovi, A., Michael, M. B., Asabere, N. Y., and Honvo, J. (2018). Modern Electrical Grid Optimization with the Integration of Big Data and Artificial Intelligence Techniques. in Advances in Energy Research. Editor M. J. Acosta. 29th ed (Accra, Ghana: Nova Science Publishers), 193–234. Available at: https://www.researchgate.net/publication/324220385_Modern_electrical_grid_optimization_with_the_integration_of_big_data_and_artificial_intelligence_techniques.

Google Scholar

Acakpovi, A., Michael, M. B., and Majeed, I. B. (2017). Grid Connected Hybrid Solar and Diesel Generator Set: A Cost Optimization with HOMER. Adv. Sci. Technol. Eng. Syst. J. 2 (4), 92–98. doi:10.25046/aj020412

CrossRef Full Text | Google Scholar

Acakpovi, A., Xavier, F. F., and Awuah-Baffour, R. (2012). “Analytical Method of Sizing Photovoltaic Water Pumping System,” in 2012 IEEE 4th International Conference on Adaptive Science & Technology (ICAST), 65–69. doi:10.1109/icastech.2012.6381067

CrossRef Full Text | Google Scholar

Acakpovi, A., Yaw, N., and Babbo, D. (2015). Low Cost Two-Axis Automatic Solar Tracking System. Commun. Appl. Electro. 3 (8), 46–53. doi:10.5120/cae2015652015

CrossRef Full Text | Google Scholar

Ahmad, J., Spertino, F., Ciocia, A., and di Leo, P. (2016). A Maximum Power point Tracker for Module Integrated PV Systems under Rapidly Changing Irradiance Conditions. Proc. - 2015 Int. Conf. Smart Grid Clean Energ. Tech. ICSGCE 2015, 7–11. doi:10.1109/icsgce.2015.7454261

CrossRef Full Text | Google Scholar

Ahmed, N. A., and Miyatake, M. (2008). A Novel Maximum Power point Tracking for Photovoltaic Applications under Partially Shaded Insolation Conditions. Electric Power Systems Res. 78 (5), 777–784. doi:10.1016/j.epsr.2007.05.026

CrossRef Full Text | Google Scholar

Ajami, A., Alizadeh, R., Elmi, M., Ajami, A., Alizadeh, R., and Elmi, M. (2016). Design and Control of a Grid Tied 6-switch Converter for Two Independent Low Power Wind Energy Resources Based on PMSGs with MPPT Capability. Renew. Energ. 87 (P1), 532–543. doi:10.1016/j.renene.2015.10.031

CrossRef Full Text | Google Scholar

Alomar, M. L., Canals, V., Perez-Mora, N., Martínez-Moll, V., and Rosselló, J. L. (2016). FPGA-based Stochastic echo State Networks for Time-Series Forecasting. Comput. Intell. Neurosci. 2016, 3917892. doi:10.1155/2016/3917892

PubMed Abstract | CrossRef Full Text | Google Scholar

Boukenoui, R., Salhi, H., Bradai, R., and Mellit, A. (2016). A New Intelligent MPPT Method for Stand-Alone Photovoltaic Systems Operating under Fast Transient Variations of Shading Patterns. Solar Energy 124, 124–142. doi:10.1016/j.solener.2015.11.023

CrossRef Full Text | Google Scholar

Chen, Y.-T., Jhang, Y.-C., and Liang, R.-H. (2016). A Fuzzy-Logic Based Auto-Scaling Variable Step-Size MPPT Method for PV Systems. Solar Energy 126, 53–63. doi:10.1016/j.solener.2016.01.007

CrossRef Full Text | Google Scholar

Chen, G., Liu, L., and Huang, S. (2015). Enhanced GSA-Based Optimization For Minimization Of Power Losses In Power System. Mathe. Prob. Eng.. doi:10.1155/2015/527128

CrossRef Full Text | Google Scholar

Chowdhury, S. R. (2021). Particle Swarm Optimization. Centre for VLSI and Embedded Systems Technology. Available at: https://slideplayer.com/slide/8925334/ (Accessed December 13, 2021).

Google Scholar

Dajuma, A., Yahaya, S., Touré, S., Diedhiou, A., Adamou, R., Konaré, A., et al. (2016). Sensitivity of Solar Photovoltaic Panel Efficiency to Weather and Dust over West Africa: Comparative Experimental Study between Niamey (Niger) and Abidjan (Côte d'Ivoire). Cweee 05 (04), 123–147. doi:10.4236/cweee.2016.54012

CrossRef Full Text | Google Scholar

Elsaharty, M., Ashour, H., Rakhshani, E., Pouresmaeil, E., and Catalão, J. (2016). A Novel DC-Bus Sensor-Less MPPT Technique for Single-Stage PV Grid-Connected Inverters. Energies 9 (4), 248. doi:10.3390/EN9040248

CrossRef Full Text | Google Scholar

Femia, N., Granozio, D., Petrone, G., Spagnuolo, G., and Vitelli, M. (2007). Predictive & Adaptive MPPT Perturb and Observe Method. IEEE Trans. Aerosp. Electron. Syst. 43 (3), 934–950. doi:10.1109/taes.2007.4383584

CrossRef Full Text | Google Scholar

Gallicchio, C., and Micheli, A. (2021). Deep Reservoir Computing, 77–95. Pisa, Italy: ScienceDirect/Elsevier

CrossRef Full Text | Google Scholar

Garraoui, R., Sbita, L., and ben Hamed, M. (2013). “MPPT Controller for a Photovoltaic Power System Based on Fuzzy Logic,” in 10th International Multi-Conferences on Systems, Signals & Devices 2013 (SSD13). doi:10.1109/ssd.2013.6564055

CrossRef Full Text | Google Scholar

Hajighorbani, S., Radzi, M. A. M., Ab Kadir, M. Z. A., Shafie, S., Khanaki, R., and Maghami, M. R. (2014). Evaluation of Fuzzy Logic Subsets Effects on Maximum Power point Tracking for Photovoltaic System. Int. J. Photoenergy 2014, 1–13. doi:10.1155/2014/719126

CrossRef Full Text | Google Scholar

Hamedani, K., Zhou, Z., Bai, K., and Liu, L. (2019). The Novel Applications of Deep Reservoir Computing in Cyber-Security and Wireless Communication. Intell. Syst. Comput. doi:10.5772/INTECHOPEN.89328

CrossRef Full Text | Google Scholar

Huang, T. C., Du, M. J., Lin, K. L., Ng, S. S., Chen, K. H., Wey, C. L., et al. (2016). A Direct AC–DC and DC–DC Cross-Source Energy Harvesting Circuit with Analog Iterating-Based MPPT Technique with 72.5% Conversion Efficiency and 94.6% Tracking Efficiency. 2014 Symp. VLSI Circuits Dig. Tech. Pap. 31 (8), 5885–5899. doi:10.1109/VLSIC.2014.6858365

CrossRef Full Text | Google Scholar

Ishaque, K., Salam, Z., Amjad, M., and Mekhilef, S. (2012). An Improved Particle Swarm Optimization (PSO)-based MPPT for PV with Reduced Steady-State Oscillation. IEEE Trans. Power Electron. 27 (8), 3627–3638. doi:10.1109/tpel.2012.2185713

CrossRef Full Text | Google Scholar

Jaeger, H. (2008). A Tutorial on Training Recurrent Neural Networks, Covering BPPT, RTRL, EKF and the “Echo State Network” Approach Michigan, USA: Semantic scholar, 2002.

Google Scholar

Jaeger, H. (2007). Echo State Network. Scholarpedia 2 (9), 2330. doi:10.4249/SCHOLARPEDIA.2330

CrossRef Full Text | Google Scholar

Jayawardene, I., and Venayagamoorthy, G. K. (2015). Reservoir Based Learning Network for Control of Two-Area Power System with Variable Renewable Generation. Neurocomputing 170, 428–438. doi:10.1016/j.neucom.2015.01.089

CrossRef Full Text | Google Scholar

Karatepe, E., Hiyama, T., Boztepe, M., and Çolak, M. (2008). Voltage Based Power Compensation System for Photovoltaic Generation System under Partially Shaded Insolation Conditions. Energ. Convers. Manag. 49 (8), 2307–2316. doi:10.1016/j.enconman.2008.01.012

CrossRef Full Text | Google Scholar

Koutroulis, E., and Blaabjerg, F. (2012). A New Technique for Tracking the Global Maximum Power point of PV Arrays Operating under Partial-Shading Conditions. IEEE J. Photovoltaics 2 (2), 184–190. doi:10.1109/jphotov.2012.2183578

CrossRef Full Text | Google Scholar

Kudithipudi, D., Saleh, Q., Merkel, C., Thesing, J., and Wysocki, B. (2016). Design and Analysis of a Neuromemristive Reservoir Computing Architecture for Biosignal Processing. Front. Neurosci. 9, 502. doi:10.3389/fnins.2015.00502

PubMed Abstract | CrossRef Full Text | Google Scholar

Kulkarni, M. S., and Teuscher, C. (2012). “Memristor-based Reservoir Computing,” in Proceedings of the 2012 IEEE/ACM International Symposium on Nanoscale Architectures - NANOARCH '12, 226–232. doi:10.1145/2765491.2765531

CrossRef Full Text | Google Scholar

Kumar, D., and Chatterjee, K. (2016). A Review of Conventional and Advanced MPPT Algorithms for Wind Energy Systems. Renew. Sustain. Energ. Rev. 55, 957–970. doi:10.1016/j.rser.2015.11.013

CrossRef Full Text | Google Scholar

Leggett, J. (2021). Climate, Energy, Tech, and the Future of Civilisation. Available at: https://jeremyleggett.net/ (Accessed December 14, 2021).

Google Scholar

Li, X., Wen, H., Jiang, L., Lim, E. G., Du, Y., and Zhao, C. (2016). Photovoltaic Modified β-Parameter-based MPPT Method with Fast Tracking. J. Power Electro. 16 (1), 9–17. doi:10.6113/jpe.2016.16.1.9

CrossRef Full Text | Google Scholar

Liu, Y.-H., and Huang, J.-W. (2011). A Fast and Low Cost Analog Maximum Power point Tracking Method for Low Power Photovoltaic Systems. Solar Energy 85 (11), 2771–2780. doi:10.1016/j.solener.2011.08.019

CrossRef Full Text | Google Scholar

Liu, Y.-H., Huang, S.-C., Huang, J.-W., and Liang, W.-C. (2012). A Particle Swarm Optimization-Based Maximum Power Point Tracking Algorithm for PV Systems Operating under Partially Shaded Conditions. IEEE Trans. Energ. Convers. 27 (4), 1027–1035. doi:10.1109/tec.2012.2219533

CrossRef Full Text | Google Scholar

Macausland, R. (2014). The Moore-Penrose Inverse and Least Squares. In Advanced Topics in Linear Algebra Washington, USA: University of Puget Sound (p. 11). Available at: http://buzzard.ups.edu/courses/2014spring/420projects/math420-UPS-spring-2014-macausland-pseudo-inverse.pdf.

Google Scholar

Mamarelis, E., Petrone, G., and Spagnuolo, G. (2014). A Two-Steps Algorithm Improving the P&O Steady State MPPT Efficiency. Appl. Energ. 113, 414–421. doi:10.1016/j.apenergy.2013.07.022

CrossRef Full Text | Google Scholar

McCulloch-Pitts (2021). First Artificial Neurons: The McCulloch-Pitts Model - AI Shack. AI Shack. Available at: https://aishack.in/tutorials/artificial-neurons-mccullochpitts-model/ (Accessed December 14, 2021).

Google Scholar

Mellit, A., and Kalogirou, S. A. (2014). MPPT-based Artificial Intelligence Techniques for Photovoltaic Systems and its Implementation into Field Programmable Gate Array Chips: Review of Current Status and Future Perspectives. Energy 70, 1–21. doi:10.1016/j.energy.2014.03.102

CrossRef Full Text | Google Scholar

Nakir, I., Durusu, A., Akca, H., Ajder, A., Ayaz, R., Ugur, E., et al. (2016). A New MPPT Algorithm for Vehicle Integrated Solar Energy System. J. Energ. Resour. Technol. Trans. ASME 138 (2), 1–9. doi:10.1115/1.4031943/474563

CrossRef Full Text | Google Scholar

Nanda, L., and Mohanty, N. (2014). Convergence of MPPT on Microgrid Connected PV System. Int. J. Innovative Researcch Electr. Electron. Instrumentation Control. Eng. 2 (8), 2321–2004. Available at: www.ijireeice.com.

Google Scholar

Nayanar, V., Kumaresan, N., and Ammasai Gounden, N. (2016). A Single-Sensor-Based MPPT Controller for Wind-Driven Induction Generators Supplying DC Microgrid. IEEE Trans. Power Electron. 31 (2), 1161–1172. doi:10.1109/tpel.2015.2420568

CrossRef Full Text | Google Scholar

Nordman, B., Christensen, K., and Meier, A. (2012). Think Globally, Distribute Power Locally: The Promise of Nanogrids. Computer 45 (9), 89–91. doi:10.1109/mc.2012.323

CrossRef Full Text | Google Scholar

Piegari, L., and Rizzo, R. (2010). Adaptive Perturb and Observe Algorithm for Photovoltaic Maximum Power point Tracking. IET Renew. Power Gener. 4 (4), 317–328. doi:10.1049/iet-rpg.2009.0006

CrossRef Full Text | Google Scholar

Piegari, L., Rizzo, R., Spina, I., and Tricoli, P. (2015). Optimized Adaptive Perturb and Observe Maximum Power point Tracking Control for Photovoltaic Generation. Energies 8 (5), 3418–3436. doi:10.3390/en8053418

CrossRef Full Text | Google Scholar

Quamruzzaman, M., and Rahman, K. M. (2014). A Modified Perturb and Observe Maximum Power point Tracking Technique for Single-Stage Grid-Connected Photovoltaic Inverter. WSEAS Trans. Power Systems 9, 111–118.

Google Scholar

Rezk, H., and Eltamaly, A. M. (2015). A Comprehensive Comparison of Different MPPT Techniques for Photovoltaic Systems. Solar Energy 112, 1–11. doi:10.1016/j.solener.2014.11.010

CrossRef Full Text | Google Scholar

Roy Chowdhury, S., and Saha, H. (2010). Maximum Power point Tracking of Partially Shaded Solar Photovoltaic Arrays. Solar Energ. Mater. Solar Cell 94 (9), 1441–1447. doi:10.1016/j.solmat.2010.04.011

CrossRef Full Text | Google Scholar

Sahu, T. P., and Dixit, T. (2014). “Modelling and Analysis of Perturb & Observe and Incremental Conductance MPPT Algorithm for PV Array Using Ċuk Converter,” in 2014 IEEE Students' Conference on Electrical, Electronics and Computer Science. doi:10.1109/sceecs.2014.6804468

CrossRef Full Text | Google Scholar

Salam, Z., Ahmed, J., and Merugu, B. S. (2013). The Application of Soft Computing Methods for MPPT of PV System: A Technological and Status Review. Appl. Energ. 107, 135–148. doi:10.1016/j.apenergy.2013.02.008

CrossRef Full Text | Google Scholar

Soriano, M. C., Ortín, S., Keuninckx, L., Appeltant, L., Danckaert, J., Pesquera, L., et al. (2015). Delay-based Reservoir Computing: Noise Effects in a Combined Analog and Digital Implementation. IEEE Trans. Neural Netw. Learn. Syst. 26 (2), 388–393. doi:10.1109/tnnls.2014.2311855

PubMed Abstract | CrossRef Full Text | Google Scholar

Subramoney, A., Scherr, F., and Maass, W. (2021). Reservoirs Learn to Learn. Natural Computing Series, 59–76. doi:10.1007/978-981-13-1687-6_3

CrossRef Full Text | Google Scholar

Trentin, E., Scherer, S., and Schwenker, F. (2015). Emotion Recognition from Speech Signals via a Probabilistic echo-state Network. Pattern Recognition Lett. 66, 4–12. doi:10.1016/j.patrec.2014.10.015

CrossRef Full Text | Google Scholar

Verma, D., Nema, S., Shandilya, A. M., and Dash, S. K. (2016). Maximum Power point Tracking (MPPT) Techniques: Recapitulation in Solar Photovoltaic Systems. Renew. Sustain. Energ. Rev. 54, 1018–1034. doi:10.1016/j.rser.2015.10.068

CrossRef Full Text | Google Scholar

Zhang, Y., Li, P., Jin, Y., Choe, Y., Choe, Y., and Member, S. (2015). A Digital Liquid State Machine with Biologically Inspired Learning and its Application to Speech Recognition. IEEE Trans. Neural Netw. Learn. Syst. 26, 2635–2649. doi:10.1109/TNNLS.2015.2388544

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Z., Hong, W.-C., and Li, J. (2020). Electric Load Forecasting by Hybrid Self-Recurrent Support Vector Regression Model with Variational Mode Decomposition and Improved Cuckoo Search Algorithm. IEEE Access 8, 14642–14658. doi:10.1109/access.2020.2966712

CrossRef Full Text | Google Scholar