Allocating the capacity of shared energy storage for wind farm groups based on the over-limit power export risk

Energy storage in wind farms can stabilize the fluctuation of wind power output. Shared energy storage can reduce the construction cost of energy storage devices and stimulate the enthusiasm of wind farms to invest in energy storage. The wind power base is composed of multiple wind farm groups. Existing research methods did not consider how to allocate shared energy storage among wind farm groups in the wind power base. This paper proposes an energy storage capacity allocation method for wind farm groups. Firstly, a bilevel model for the shared energy storage allocation is established. The upper-level model optimizes the shared energy storage allocation of each wind farm group with the goal of minimizing the over-limit power export risk in the wind power base; The lower-level model calculates the over-limit power export of each wind farm group according to the energy storage capacity allocation and transfers the value of over-limit power export to the upper-level model. The bilevel model can be converted to a two-stage model that can be solved sequentially; The wind power base in Belgium is used for numerical simulation to verify the effectiveness of the proposed model. Finally, the sensitivity of confidence level, total energy storage capacity, and risk preference factor are analyzed.

1 Introduction

Integrating renewable energy into the power system makes the power system more environmentally friendly (Kong et al., 2019). However, the substantial volatility of renewable energy is one of the important factors limiting its large-scale grid connection, which directly affects the stable operation of the power system (Ju et al., 2019). In order to use large-scale renewable energy more effectively, researchers all over the world discuss solutions to reduce the threat of large-scale renewable energy to the power system. Some researchers design a dispatching strategy for wind farms with a multiple-stage hybrid energy storage system (Zhang et al., 2018), while other researchers discuss the optimal allocation of energy storage capacity for stabilizing wind power fluctuations (Zhu et al., 2020). Further, some studies reduce curtailed wind energy through energy storage and demand response (Bitaraf and Rahman, 2018). In addition, some studies propose the capacity allocation method using big data (Song et al., 2021). Some studies propose a power smoothing method by using a battery system using the fuzzy control strategy (Cong et al., 2018). The research (Zhang et al., 2019) enhances performances on wind power fluctuations mitigation by optimizing the operation schedule of battery energy storage systems with considerations of operation cost. In addition, some studies deal with the calculation of short and long-term energy storage needs and their dependence on the installed amount of solar energy and wind power (Weiss and Schulz., 2013). Later studies calculate the required energy storage capacity and charging/discharging power ratings for different desired operation scenarios (Lu et al., 2009).

The above studies all refer to the use of energy storage devices in a single wind farm to stabilize volatility, without considering the sharing of energy storage among wind farms. The operation efficiency of energy storage devices is low if the wind farm uses energy storage devices individually. In order to fully tap the application potential of energy storage, some studies propose the concept of shared energy storage (Zhao et al., 2020). Some studies propose a business model for utility-scale shared energy storage systems (Ben-Idris et al., 2021), while other studies analyze the complementary and controllable capabilities of energy storage that promote new energy consumption, and study the multiple energy storage sharing mechanism (Xv et al., 2022). Further, some studies use a hybrid storage system for energy sharing within the prosumers’ community (Mussadiq et al., 2022). In addition, some studies propose a capacity allocation method for photovoltaic microgrid energy storage systems based on time-sharing energy complementarity (Cong et al., 2021). Some studies propose a bi-level optimization problem aiming to improve the use of the shared energy storage for distribution system flexibility (Taşcıkaraoğlu et al., 2018). In addition, some studies propose a shared energy storage strategy among multiple wind farms based on wind power forecasting (Zhu et al., 2018). Later studies establish a cooperative game model in which prosumers and energy storage operators are the main participants to realize capacity optimization of renewable energy and energy storage systems (Tian et al., 2021). Some studies propose a novel shared energy storage planning method considering the correlation of renewable uncertainties on the supply side (Wang et al., 2022). However, how to reasonably allocate the shared energy storage capacity and reduce the over-limit power export risk of wind farm groups is still a problem to be solved.

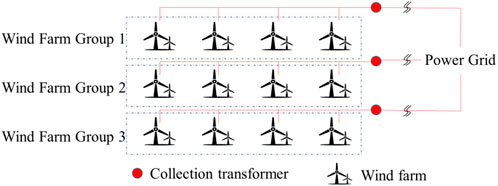
Large-scale wind power base is the main form of wind power. Under the combined effect of multiple factors such as large-scale wind power equipment, cost reduction, and intensified market competition, the wind power base has entered a new stage of installation growth and expansion. Due to the large scale of the wind power base, the wind power base is usually divided into different wind farm groups and connected to the power grid through collection transformers as shown in Figure 1.

FIGURE 1

FIGURE 1. Large-scale wind power base.

The fluctuation of wind power is the main limiting factor for the development of the wind power base. Based on the concept of shared energy storage, this paper proposes an allocation method of shared energy storage capacity for wind farm groups from the perspective of minimizing the over-limit power export risk in the wind power base. The innovations are as follows:

1) Conditional Value at Risk theory is used to characterize the over-limit power export risk of each wind farm group.

2) A bilevel optimization model for shared energy storage capacity allocation in wind farm groups is proposed, which provides a theoretical basis for the reasonable allocation of shared energy storage in wind farm groups.

3) A two-stage solution method for the bilevel optimization model of shared energy storage capacity allocation is proposed, and its equivalence is proved.

The remaining contents of this article are as follows: Section 2 introduces the shared energy storage for wind farm groups. Section 3 introduces the energy storage allocation models and the solution method. Section 4 analyzes the results through simulation. Section 5 gives the conclusion and summarizes the whole article.

2 Sharing energy storage for wind farm groups

The fluctuation of wind power is a threat to the power grid operation. Generally speaking, the long, high-speed, and wide-range fluctuation process is more likely to pose a threat to the power grid operation. In order to reduce the impact of wind power fluctuations, State Grid proposed guidelines for wind farms connected to the power grid, as shown in Table 1.

TABLE 1

TABLE 1. Guidelines for wind farm grid connection.

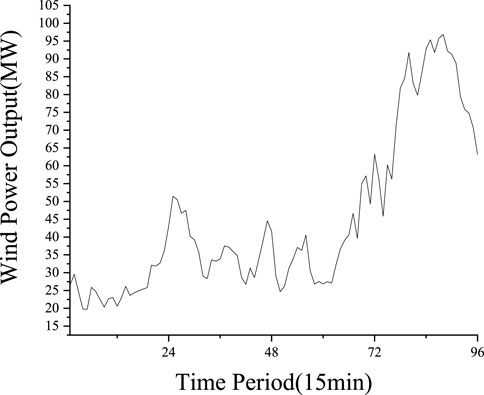
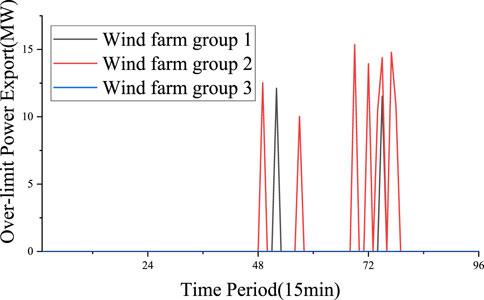
The real data of the wind farm group’s output in Belgium is shown in Figure 2. We can see that the wind farm group’s output has exceeded the limit 8 times a day, and the most serious over-limit power is 14.78 MW. If grid connection is not allowed for the part of over-limit power, 25.5 MWh of wind power will be abandoned per day.

FIGURE 2

FIGURE 2. Wind farm group’s output in Belgium.

We define the over-limit power export risk in wind farms as follows:

$R={\displaystyle \sum }_{s=1}^{NS}{\eta }_s\left(\Delta P_s^{wind}-P_{\mathrm{l}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{t}}\right)(1)$

where, $\Delta P_s^{wind}$ represents power export change of adjacent periods in wind farms. $P_{\mathrm{l}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{t}}$ represents the guideline of power export change shown in Table 1. $NS$ represents the total number of possible scenarios of power export in wind farms. ${\eta }_s$ represents the probability of occurrence of scenario s.

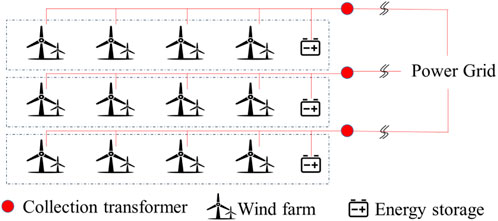
Energy storage can effectively reduce the power fluctuation of wind farm groups so that the power export can meet the guidelines. In other words, energy storage can effectively reduce the over-limit power export risk in wind farm groups and improve wind utilization. Large-scale wind power base usually contains multiple wind farm groups, and each wind farm group is composed of multiple wind farms. We define all wind farms connected to the same collection substation as one wind farm group. As shown in Figure 3, the wind farms inside the wind farm group are connected through the collection station, and then connected to the power grid. In order to reduce the over-limit power export risk, wind farm groups install distributed energy storage independently.

FIGURE 3

FIGURE 3. Distributed energy storage in the wind power base.

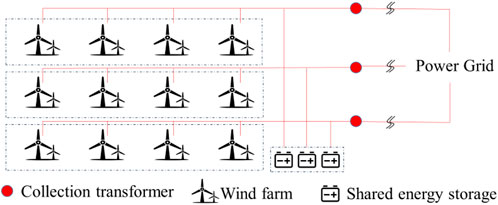
However, the high investment cost of energy storage is the main obstacle for wind farm groups. Figure 4 shows the schematic diagram of shared energy storage in the wind power base. If each wind farm group constructs energy storage independently in the wind power base, the investment will be huge and the energy storage operation efficiency will be low. As wind farm groups belong to the same wind power base, there is only one single stakeholder in the wind power base. Using the concept of sharing energy storage, wind farm groups can jointly invest in energy storage equipment and coordinate operation, which is a new idea for wind farm groups to reduce power fluctuation. In the wind power base, the wind farm groups’ output may vary greatly due to the wake effect. The wake effect refers to the wake area where wind turbines obtain energy from the wind and wind speed decreases downstream. If a downstream wind turbine is located in the wake area, the input wind speed of the downstream wind turbine will be lower than that of the upstream wind turbine. Thus, wind farm groups can jointly use centralized energy storage devices to smooth the wind power output. By reasonably allocating shared energy storage in wind power groups, the wind power base can maximize the use of shared energy storage devices due to the difference of the output power in wind power groups.

FIGURE 4

FIGURE 4. Shared energy storage in the wind power base.

In this way, the wind power base can reduce the over-limit power export risk in a more effective way. If we allocate the shared energy storage to each wind power group, it can be equivalent to that each wind power group has a distributed energy storage to reduce the power fluctuation. However, how to characterize the over-limit power export risk of wind farm groups, and how to reasonably allocate shared energy storage capacity among wind farm groups to minimize the over-limit power export risk of wind farm groups, have become new issues worth studying.

CVaR is an effective method for risk measurement. It can help us understand the expected risk of loss that exceeds a certain value at a certain confidence level. CVaR is widely used in the power system. Some studies use CVaR to describe the risk loss when the real wind power output is beyond the predefined uncertainty set (Zhang et al., 2018). Later studies use CVaR to help the distribution system operator (DSO) to balance the condition risk and the power generation dispatch cost in the power generation dispatch for the lowest total cost (Ren et al., 2019). The advantage of CVaR is that it is not a point probability value, but the weighted average expected value of all losses above the selected probability. In addition, CVaR can be optimized by using the linear programming algorithm. Thus, CVaR is very suitable to characterize the over-limit power export risk.

This paper will use CVaR to characterize the over-limit power export risk of wind farm groups, and allocate the shared energy storage in each wind farm group with the goal of minimizing the over-limit power export risk in the wind power base.

3 Model and methodology

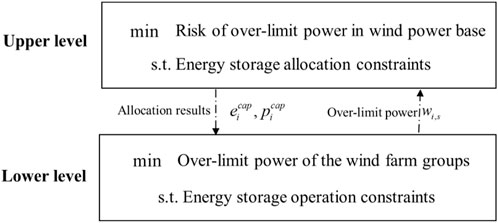
In this section, we introduce a shared energy storage allocation model for wind farm groups in the wind power base based on CVaR. The goal of this model is to minimize the over-limit power export risk in the wind power base. The model framework is shown in Figure 5. The upper-level model minimizes over-limit power export risk in the wind power base with the constraints of energy storage allocation. The upper-level model optimizes the allocation of shared energy storage capacity in each wind farm group and obtains the allocation results of shared energy storage capacity. Then, the upper-level model transfers the allocation results to the lower-level model. The lower-level model minimizes the over-limit power export of each wind farm group according to the allocation results with the constraints of the energy storage operation. The lower-level model obtains the over-limit power export of each wind farm group and transfers it to the upper-level model.

FIGURE 5

FIGURE 5. Model framework.

3.1 Bilevel model for energy storage allocation

3.1.1 Upper-level model

The objective function of the upper-level model based on CVaR is as follows:

$\min \left(1-\mu \right)F^c+\mu CVaR(2)$

where, $\mu$ represents the risk preference factor, $F^c$ represents the over-limit power export of wind farm groups, $CVaR$ represents the over-limit power export risk. The calculation formula of $F^c$ is as follows,

$F^c=\frac{1}{NS}{\displaystyle \sum }_{s=1}^{NS}{\displaystyle \sum }_{i=1}^{NI}{\displaystyle \sum }_{t=1}^{NT}{P}_{ex,s,i,t}(3)$

where, $P_{ex,s,i,t}$ represents the over-limit power export of wind farm $i$ at time $t$ in scenario $s$. $NS$ represents the number of scenarios. $NI$ represents the number of wind farm groups. $NT$ represents the total periods.

The calculation formula of $CVaR$ is as follows,

$CVaR={\displaystyle \sum }_{i=1}^{NI}CVa{R}_i(4)$

$CVa{R}_i={\beta }_i+\frac{1}{NS\left(1-\alpha \right)}{\displaystyle \sum }_{s=1}^{NS}{\varphi }_{i,s},\forall i\in \left[1,...,NI\right](5)$

${\varphi }_{i,s}\ge w_{i,s}-{\beta }_i,\forall i\in \left[1,...,NI\right];s\in \left[1,...,NS\right](6)$

${\varphi }_{i,s}\ge 0,\forall i\in \left[1,...,NI\right];s\in \left[1,...,NS\right](7)$

where, $CVa{R}_i$ represents the over-limit power export risk of wind farm $i$. ${\beta }_i$ represents the VaR value of wind farm $i$ at $\alpha$ confidence level. ${\varphi }_{i,s}$ is the auxiliary variable, which represents the over-limit power export risk over VaR of wind farm $i$ in scenario $s$. $w_{i,s}$ represents the over-limit power export of wind farm $i$ in scenario $s$.

The constrains of upper-level model is as follows:

$e_i^{cap}\ge 0.1\times e_i^N,\forall i\in \left[1,...,NI\right](8)$

$e_i^{cap}\ge 4\times p_i^{cap},\forall i\in \left[1,...,NI\right](9)$

${\displaystyle \sum }_{i=1}^{NI}{e}_i^{cap}\le E^{cap}(10)$

${\displaystyle \sum }_{i=1}^{NI}{p}_i^{cap}\le P^{cap}(11)$

where, $e_i^{cap}$ represents energy storage capacity allocated to wind farm $i$. $e_i^N$ represents the energy storage capacity of wind farm $i$. $p_i^{cap}$ represents max real power output of energy storage allocated to wind farm $i$. $E^{cap}$ represents the shared energy storage capacity. $P^{cap}$ represents the max real power output of shared energy storage.

In order to reduce the impact of wind fluctuations on grid stability, the wind farm is required to be equipped with 10% capacity energy storage, and the charging time should not less than 4 h. To ensure the above requirements, constraints (8)–(9) are added to the model (10)–(11) represents the constraints of the allocation of shared energy storage in wind farm groups.

3.1.2 Lower-level model

The lower-level model minimizes the over-limit power export of the wind farm groups. The objective function of the lower-level model is as follows:

$\min {\displaystyle \sum }_{t=1}^{NT}\max \left(\left|P_{s,i,t}-P_{s,i,t-1}\right|-P_{i,\mathrm{l}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{t}},0\right)(12)$

where, $P_{s,i,t}$ represents the power export of wind farm $i$ at time $t$ in scenario $s$. $P_{i,\mathrm{l}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{t}}$ represents the power export fluctuation limit value to wind farm $i$. The specific definition of $P_{i,\mathrm{l}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{t}}$ are as follows:

$P_{i,\mathrm{l}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{t}}=\left\{\begin{array}{l}3e_i^N\le 30\\ \frac{e_i^N}{10}30<e_i^N\le 100\\ 10100<e_i^N\end{array}\right.(13)$

There are two nonlinear terms in the objective function, absolute value and maximum value, which need to be linearized. Auxiliary variables $P_{ex,s,i,t}$ is introduced to equivalent the objective function to the following linearized form:

$\min {\displaystyle \sum }_{t\in NT}{P}_{ex,s,i,t}(14)$

$P_{ex,s,i,t}\ge P_{s,i,t}-P_{s,i,t-1}-P_{i,\mathrm{l}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{t}}(15)$

$P_{ex,s,i,t}\ge P_{s,i,t-1}-P_{s,i,t}-P_{i,\mathrm{l}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{t}}(16)$

$P_{ex,s,i,t}\ge 0(17)$

The constraints of the lower-level model are as follows:

$P_{s,i,t}=p_{s,i,t}^N+\left(p_{s,i,t}^D-p_{s,i,t}^C\right)(18)$

$e_{s,i,t}=\left(1-s_i\right)e_{s,i,t-1}+\left({\eta }_i^C{p}_{s,i,t}^C-\frac{p_{s,i,t}^D}{{\eta }_i^D}\right),\forall t\in \left[1,...,NT\right](19)$

$0\le p_{s,i,t}^C\le I_{s,i,t}^C{p}_i^{cap},\forall t\in \left[1,...,NT\right](20)$

$0\le p_{s,i,t}^D\le I_{s,i,t}^D{p}_i^{cap},\forall t\in \left[1,...,NT\right](21)$

$SO{C}_{\min }{e}_i^{cap}\le e_{s,i,t}\le SO{C}_{\max }{e}_i^{cap},\forall t\in \left[1,...,NT\right](22)$

$I_{s,i,t}^C+I_{s,i,t}^D\le 1,\forall t\in \left[1,...,NT\right](23)$

$e_{s,i,1}=e_{s,i,T}(24)$

where, $p_{s,i,t}^N$ represents wind power output of wind farm $i$ at time $t$ in scenario $s$. $p_{s,i,t}^D$ represents discharging power of the energy storage of wind farm $i$ at time $t$ in scenario $s$. $p_{s,i,t}^C$ represents charging power of the energy storage of wind farm $i$ at time $t$ in scenario $s$. $e_{s,i,t}$ represents remaining power of the energy storage of wind farm $i$ at time $t$ in scenario $s$. $s_i$ represents self-loss-rate of energy storage of wind farm $i$. ${\eta }_i^C$ and ${\eta }_i^D$ represent charging efficiency and discharging efficiency for energy storage. $SO{C}_{\min }$ and $SO{C}_{\max }$ represent minimum and maximum state-of-charge values for energy storage.

After the wind farm gets the allocated energy storage, its power export depends not only on the output of wind farm but also on the output of energy storage. The power balance constraint can be expressed as constraint (18). Constraints (19)–(24) are energy storage operation constraints.

Since the lower-level model is nonconvex, neither Karush–Kuhn–Tucker optimality conditions nor duality theory can be applied to transform the lower-level model into a set of constraints so as to convert the original bilevel model into an equivalent single-level model. Due to the difficulty in solving the bilevel model, a two-stage solution method is proposed for this bilevel model, which sequentially solve two models.

3.2 Equivalent two-stage model

3.2.1 First-stage model

The objective function of the first-stage model is as follows:

$\min \left(1-\mu \right)F^c+\mu CVaR(25)$

The constraints of the first-stage model are all the constraints of the upper-level model, that is, constraints (8)–(11). And all constraints of the lower-level model, that is, constraints (18)–(24). After solving the first-stage model, we obtain the optimal value ${\overline{e}}_i^{cap}$ and ${\overline{p}}_i^{cap}$.

3.2.2 Second-stage model

The objective function of the second-stage model is as follows:

$\min {\displaystyle \sum }_{t\in NT}{P}_{ex,s,i,t}(26)$

The constraints of the second-stage model are all the constraints of the lower-level model, that is, constraints (18)–(24). In addition, the constraints of the second-stage model also include (27) and (28):

$e_i^{cap}={\overline{e}}_i^{cap}(27)$

$p_i^{cap}={\overline{p}}_i^{cap}(28)$

After solving the first-stage model and the second-stage model sequentially, the energy storage allocation result and the optimal value of CVaR are consistent with the results of the bilevel model in 3.1. The effectiveness of the proposed two-stage model is proved as follows.

3.3 Proof of effectiveness of two-stage model

This section will prove the equivalence of the solution results of the two-stage model and the bilevel model (Li et al., 2016).

Due to all the constraints in the first-stage problem are satisfied in the original bilevel problem, we can infer that any feasible solution to the original bilevel problem also corresponds to a feasible solution to this first-stage problem. The following equation is always true.

${\widehat{f}}_{two-stage}^{one}\le {\widehat{f}}_{bilevel}(29)$

Where ${\widehat{f}}_{two-stage}^{one}$ represents the optimal value of objective function of the first-stage model. ${\widehat{f}}_{bilevel}$ represents the optimal value of objective function of the bilevel model.

Since the objective function of the lower-level model in the bilevel model is the power export fluctuation, which is also a variable in constraint (6) in the upper-level model. The bilevel model can be converted into the following form:

$\min \left(1-\mu \right)F^c+\mu CVaR(30)$

$\begin{array}{l}s.t.\left(2\right)-\left(4\right)\\ \left(6\right)-\left(10\right)\\ \left(14\right)-\left(23\right)\end{array}(31)$

${\varphi }_{i,s}\ge \min \left({\displaystyle \sum }_{t\in NT}{P}_{ex,s,i,t}\right)-{\beta }_i,\forall i\in \left[1,...,NI\right];s\in \left[1,...,NS\right](32)$

Since the following inequality is always true:

$\min \left({\displaystyle \sum }_{t\in NT}{P}_{ex,s,i,t}\right)-{\beta }_i\le {\displaystyle \sum }_{t\in NT}{P}_{ex,s,i,t}-{\beta }_i(33)$

It can be seen from the above formula that the feasible region of the bilevel model is not smaller than that of the first-stage model. We can prove that the following inequality is always true:

${\widehat{f}}_{two-stage}^{one}\ge {\widehat{f}}_{bilevel}(34)$

Since (29) and (34) is always true, we can infer that the following equality is always true:

${\widehat{f}}_{two-stage}^{one}={\widehat{f}}_{bilevel}(35)$

The above formula shows that the optimal objective function value of the two-stage model is equal to that of the bilevel model. The over-limit power export risk of wind farm groups is determined by the results of shared energy storage allocation. Since the optimal objective function of the first-stage model is the same as that of the bilevel model, and the over-limit power export risk of wind farm groups is the same, the results of optimal energy storage allocation of the first-stage model are also the same as those of the bilevel model.

Finally, after the optimal allocation of energy storage is obtained from the first-stage model, the second-stage model optimizes the power fluctuation of wind farm groups according to the energy storage allocation. Because the second-stage model and the lower-level model in the bilevel model have similar structures under the same energy storage allocation scheme, the optimal decision variable values obtained by solving the second-stage model and the lower-level model in the bilevel model must also be the same. This shows that after solving the first-stage model and the second-stage model in sequence, the energy storage allocation and the optimal value of CVaR are completely consistent with the results of the bilevel model. The proof is over.

4 Case study

The case studies are conducted based on the wind power base in Belgian. The wind power base contains three wind farm groups with installed capacity of 250, 150, and 100 MW respectively. Historical wind power output data of the wind power base in Belgian is used as the scenario in the above model, and the time interval is 15 min. The energy storage capacity of three wind farm groups is allocated by using the proposed energy storage allocation method. We use MATLAB with the mixed-integer programming solver Gurobi to solve all the optimization problems (Gurobi Optimizer Reference Manual, 2020).

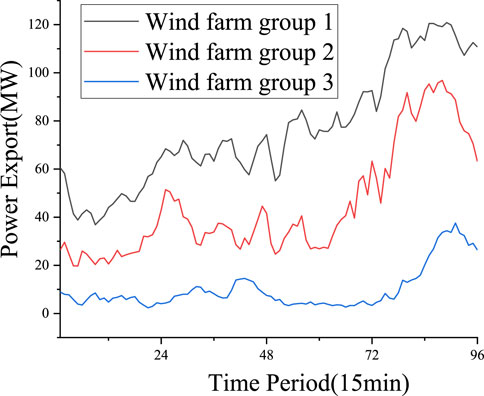
Historical data of wind farm groups in Belgian is shown in Figure 6.

FIGURE 6

FIGURE 6. Historical data of wind power output.

As shown in Figure 7, Wind farm 2 has the highest volatility, followed by wind farm 1, and wind farm 3 has the lowest volatility. The confidence level of over-limit power export risk is 0.9. The total scale of shared energy storage is 100 MWh/50 MW. The charging and discharging efficiency of energy storage is 90%. The self-discharging rate is 0.001.

FIGURE 7

FIGURE 7. Over-limit power export.

4.1 Energy storage allocation results

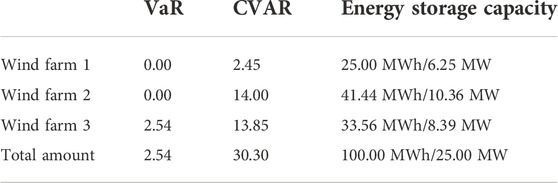
The VaR and CVaR values of wind farm groups and the energy storage allocation results are shown in Table 2.

TABLE 2

TABLE 2. Solution results.

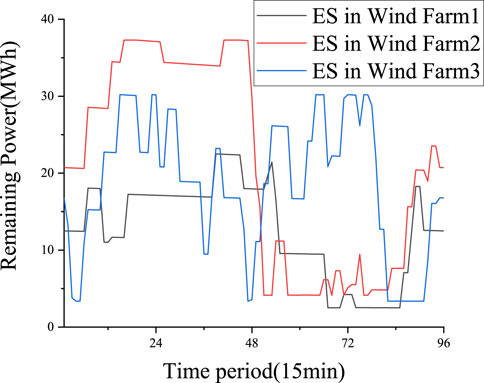
According to the historical output of the wind farm groups, wind farm 2 has the largest fluctuation (6 times out of the limit). If energy storage is allocated only according to the principle of reducing fluctuation, wind farm 2 should get the largest energy storage capacity. However, we have the constraint that the wind farm must be equipped with energy storage with the capacity of 10% of the wind farm installation capacity. The energy storage capacity allocated to wind farm 1 is more than that of wind farm 2 only because the capacity of wind farm 1 is larger. Figure 8 shows the remaining power of energy storage shared by each wind farm.

FIGURE 8

FIGURE 8. The remaining power of energy storage allocated to wind farm groups.

If grid connection is not allowed for the part of power fluctuation exceeding the limit, the three wind farm groups can reduce the wind power curtailment of 7.2 MWh, 10.94 MWh, and 8.23 MWh respectively after energy distribution and storage.

4.2 Sensitivity analysis

4.2.1 Confidence level

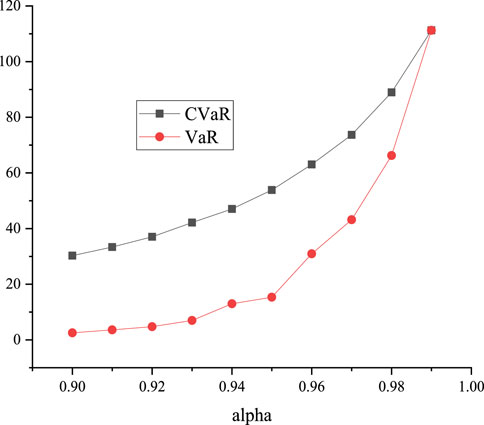
The shared energy storage allocation results under different confidence levels are shown in Table 3. The value of VaR and CVaR under different confidence levels are shown in Figure 9.

TABLE 3

TABLE 3. Solution results.

FIGURE 9

FIGURE 9. VaR and CVaR under different confidence levels.

It can be seen from the figure that, the value of CVaR increases with the increase of confidence level, and the value of VaR also increases. VaR is equal to CVaR when the confidence level is 0.99. This is because the total number of scenarios in the model is 100. When the value of CVaR exceeds the expectation of VaR at 99% confidence level, there is only one scenario representing tail risk, so the value of CVaR is equal to VaR.

4.2.2 Capacity of shared energy storage

In order to further investigate the impact of different shared energy storage capacities on over-limit power export risk, different shared energy storage capacities are set for simulation. When other parameters remain unchanged, the total shared energy storage capacity is taken as 100 MWh to 150 MWh respectively. The value of VaR and CVaR, the energy storage allocation results, and the average daily power exceeding are shown in Figure 10.

FIGURE 10

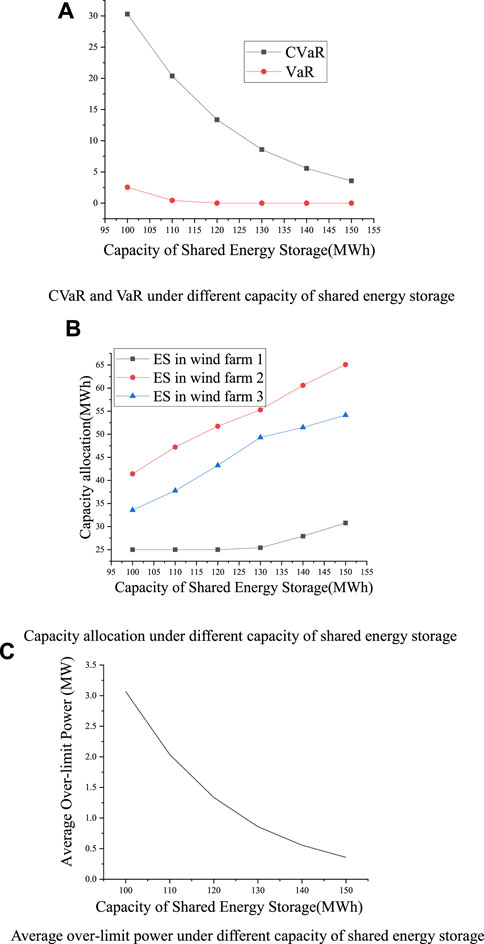
FIGURE 10. Solution results under different capacity of shared energy storage. (A) CVaR and VaR under different capacity of shared energy storage (B) Capacity allocation under different capacity of shared energy storage (C) Average over-limit power under different capacity of shared energy storage.

When the total energy storage capacity reaches 110 MWh, the value of VaR in wind power base is 0. The power export of three wind farm groups will be over-limit at 90% confidence level. The average value of CVaR of the three wind farm groups is less than 20.38. With the increase of the total energy storage capacity, CVaR value of the three wind farm groups will gradually decrease, but the rate of reduction will be slower and slower. It can be seen that when the total energy storage capacity reaches 130 MWh, the energy storage allocated to wind farm 1 will be greater than 25 MWh. We can infer that the energy storage constraint with 10% capacity of the wind farm will no longer work when the total energy storage capacity exceeds 130 MWh. We define the daily over-limit power of the wind farm group as the total amount of over-limit power in a day. It also can be seen that when the total energy storage capacity increases, the average daily over-limit power of wind farm groups will decrease. With the increase of the total shared energy storage capacity, the average daily over-limit power will decrease more slowly. If the over-limit power cannot be connected to the grid, the wind abandonment rate of wind farm groups will decrease with the increase of the total shared energy storage capacity, but the marginal benefit of the total shared energy storage capacity will gradually decrease.

4.2.3 Risk preference factor

Figure 11 shows the value of VaR, CVaR, and daily average over-limit power of wind farm groups under different risk preference factors.

FIGURE 11

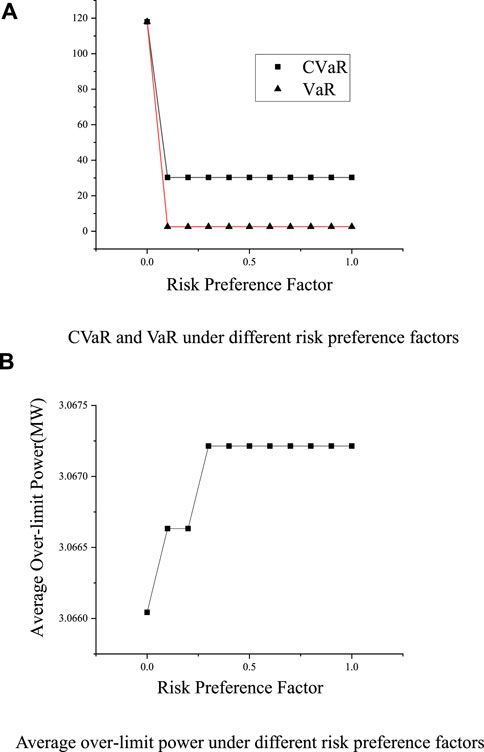
FIGURE 11. Solution results under different risk preference factors. (A) CVaR and VaR under different risk preference factors (B) Average over-limit power under different risk preference factors.

Different energy storage allocation methods under different risk preference factors lead to different values of CVaR. When the risk preference factor is larger, CVaR value of wind farm groups is smaller, and the shared energy storage allocation scheme tends to be more conservative; When the risk preference factor is less than 0.3, the average over-limit power of wind farm increased significantly with the increase of risk preference factor; When the risk preference factor is more than 0.3, the increase of risk preference factor had little impact on the average over-limit power of wind farm.

5 Conclusion

This paper proposes a method to allocate energy storage capacity for wind farm groups based on CVaR. A bilevel model with the objective function of minimizing the over-limit power export risk of wind farm groups is established. Then, a two-stage solution method for the bilevel model is proposed. The effectiveness of the two-stage method is proved. The model and solution algorithm proposed in this paper are used to allocate the energy storage of Belgian wind farm groups. The sensitivity of confidence level, total energy storage capacity and risk preference factors on the optimal allocation of shared energy storage are analyzed. The results show that the proposed method can significantly reduce the over-limit power export risk of wind farm groups and improve the utilization rate of wind energy.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

KS and ZL contributed to the conception and design of the study. WZ organized the simulation, analyzed the results and wrote parts of the manuscript. YL and YG gave suggestions in technical support. JS and HW contributed to write parts of the manuscript.

Conflict of interest

WZ and HW are employed by Zhejiang Huayun Electric Power Engineering Design & Consultation Co., Ltd. YG is employed by State Grid Zhejiang Electric Power Co., Ltd. YL and JS are employed by State Grid Ningbo Power Supply Co.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ben-Idris, M., Brown, M., Egan, M., Huang, Z., and Mitra, J. (2021). Utility-Scale Shared Energy Storage: Business models for utility-scale shared energy storage systems and customer participation. IEEE Electrific. Mag. 9, 47–54. doi:10.1109/mele.2021.3115558

CrossRef Full Text | Google Scholar

Bitaraf, H., and Rahman, S. (2018). Reducing curtailed wind energy through energy storage and demand response. IEEE Trans. Sustain. Energy 9, 228–236. doi:10.1109/tste.2017.2724546

CrossRef Full Text | Google Scholar

Cong, L., Chuanpu, Z., Kuan, W., Lizhu, S., Qingyu, W., and Wenhai, Z. (2021). “Multi-objective capacity optimal allocation of photovoltaic microgrid energy storage system based on time-sharing energy complementarity,” in 2021 International Conference on Power System Technology (POWERCON), Kuala Lumpur, MALAYSIA, 14-16 September 2022, 1123–1129.

CrossRef Full Text | Google Scholar

Cong, Y., Meng, X., Wang, L., and Wang, Y. (2018). “A power smoothing approach based on battery energy storage system for power fluctuations of wind power generation,” in 2018 International Conference on Information Systems and Computer Aided Education (ICISCAE), Changchun, China, July 6-8, 2018, 331–334.

CrossRef Full Text | Google Scholar

Gurobi Optimizer Reference Manual (2020). Gurobi optimizer reference manual. Beaverton, OR, USA: Gurobi Optimization Inc.

Google Scholar

Ju, Y., Sun, G., Chen, Q., Zhang, M., Zhu, H., and Rehman, M. U. (2019). A model combining convolutional neural network and Light GBM algorithm for ultra-short-term wind power forecasting. IEEE Access 7, 28309–28318. doi:10.1109/access.2019.2901920

CrossRef Full Text | Google Scholar

Kong, W., Dong, Z. Y., Jia, Y., Hill, D. J., Xu, Y., and Zhang, Y. (2019). Short-term residential load forecasting based on LSTM recurrent neural network. IEEE Trans. Smart Grid 10, 841–851. doi:10.1109/tsg.2017.2753802

CrossRef Full Text | Google Scholar

Li, Z., Shahidehpour, M., Alabdulwahab, A., and Abusorrah, A. (2016). Bilevel model for analyzing coordinated cyber-physical attacks on power systems. IEEE Trans. Smart Grid 7, 2260–2272. doi:10.1109/tsg.2015.2456107

CrossRef Full Text | Google Scholar

Lu, M. -S., Chang, C. -L., Lee, W. -J., and Wang, L. (2009). Combining the wind power generation system with energy storage equipment. IEEE Trans. Ind. Appl. 45, 2109–2115. doi:10.1109/tia.2009.2031937

CrossRef Full Text | Google Scholar

Mussadiq, U., Kausar, T., Ahmed, S., and Kim, S. M. (2022). “A hybrid storage system for energy sharing and management within prosumers’ community,” in 2022 5th International Conference on Energy Conservation and Efficiency (ICECE), Pakistan, 16th and 17th March, 2022, 1–6.

Google Scholar

Ren, X., Yang, N., Ye, B., Yao, Y., and Gao, C. (2019). “Stochastic planning model for incremental distributio network considering CVaR and wind power penetration,” in 2019 IEEE Innovative Smart Grid Technologies - Asia (ISGT Asia), Chengdu, China, May 21 - Friday, May 24, 2019, 1358–1363.

CrossRef Full Text | Google Scholar

Song, J., Hu, C., and Su, L. (2021). “Distributed wind power and photovoltaic energy storage capacity configuration method under big data,” in 2021 International Conference on Electronic Communications, Internet of Things and Big Data (ICEIB), Xiamen, China, November 4-7, 2022, 318–322.

CrossRef Full Text | Google Scholar

Taşcikaraoğlu, A., Erdinç, O., and Catalão, J. P. S. (2018). “Shared energy storage and direct load control for improved flexibility of distribution system operation,” in 2018 53rd International Universities Power Engineering Conference (UPEC), Glasgow, United Kingdom, 4th-7th September 2018, 1–6.

Google Scholar

Tian, X., Zheng, T., Chen, L., and Xue, X. (2021). “Capacity optimization for wind/photovoltaic prosumers and shared energy storage operator: A cooperative game approach,” in 2021 IEEE 5th Conference on Energy Internet and Energy System Integration (EI2), Taiyuan, China, Held 22-24 October 2021, 2097–2103.

CrossRef Full Text | Google Scholar

Wang, Q., Zhang, X., Yi, C., Li, Z., and Xu, D. (2022). A novel shared energy storage planning method considering the correlation of renewable uncertainties on the supply side. IEEE Trans. Sustain. Energy 13, 2051–2063. doi:10.1109/tste.2022.3179837

CrossRef Full Text | Google Scholar

Weiss, T., and Schulz, D. (2013). “Development of fluctuating renewable energy sources and its influence on the future energy storage needs of selected European countries,” in 2013 4th International Youth Conference on Energy (IYCE), Siófok. Hungary, Thu, 06/06/2013, 1–5.

CrossRef Full Text | Google Scholar

XV, A., He, C., Zhang, M., and Wang, T. (2022). “Day-ahead scheduling with renewable generation considering shared energy storage,” in 2022 4th Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 25th to 28th March 2022, 492–497.

CrossRef Full Text | Google Scholar

Zhang, X., Gu, J., Hua, L., and Ma, K. (2019). Enhancing performances on wind power fluctuation mitigation by optimizing operation schedule of battery energy storage systems with considerations of operation cost. IEEE Access 7, 94072–94083. doi:10.1109/access.2019.2928274

CrossRef Full Text | Google Scholar

Zhang, Y., Han, X., Xu, B., Wang, M., Ye, P., and Pei, Y. (2018). Risk–based admissibility analysis of wind power integration into power system with energy storage system. IEEE Access 6, 57400–57413. doi:10.1109/access.2018.2870736

CrossRef Full Text | Google Scholar

Zhang, Z., Zhang, Y., Huang, Q., and Lee, W. -J. (2018). Market-oriented optimal dispatching strategy for a wind farm with a multiple stage hybrid energy storage system. CSEE J. Power Energy Syst. 4, 417–424. doi:10.17775/cseejpes.2018.00130

CrossRef Full Text | Google Scholar

Zhao, D., Wang, H., Huang, J., and Lin, X. (2020). “Virtual energy storage sharing and capacity allocation,” in 2020 IEEE Power & Energy Society General Meeting (PESGM), Orlando, Florida, 16 – 20 July 2023, 1.

CrossRef Full Text | Google Scholar

Zhu, H., Shi, L., and Wu, F. (2020). “Optimal allocation of energy storage capacity for stabilizing wind power fluctuation,” in 2020 12th IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Nanjing, China, Sept. 20-Sept. 23, 2020, 1–5.

CrossRef Full Text | Google Scholar

Zhu, K., Chowdhury, S., Sun, M., and Zhang, J. (2018). “Grid optimization of shared energy storage among wind farms based on wind forecasting,” in 2018 IEEE/PES Transmission and Distribution Conference and Exposition (T&D), Denver, CO, 16-19 April 2018, 1–5.

CrossRef Full Text | Google Scholar