Research on simplified modeling of large-scale wind farms based on equivalent transfer function and aggregate equivalent

Introduction: In grid-connected research of large-scale wind farms, the problem of long simulation time exists in the research based on detailed model. In order to realize the fast simulation and grid-connected transient research of wind farm, this paper presents a simplified equivalent model of wind farm based on equivalent transfer function and improved capacity weighting method.

Methods: This paper analyzes the mathematical model of wind turbine, corresponding to the strategy of design simplification, and the simplified model is built according to the equivalent transfer function. In addition, this paper considers the equivalent line loss model of collector line, classifies and aggregates the simplified wind turbines, and calculates the equivalent value of the converged wind turbines by using the improved capacity weighting method, the grid-connected simplified modeling of large-scale wind farm is realized.

Results: A model of wind farm-MMC-HVDC flexible grid-connected wind power system is built. The simulation results show that the simplified equivalent model improves the simulation speed greatly while guaranteeing the dynamic characteristics.

Discussion: The simplified equivalent strategy of wind farm can keep the same dynamic performance with the detailed model, and improve the simulation speed, and realize the fast simulation and grid-connected transient research of wind farm.

1 Introduction

In recent years, with the development of economy and energy, environmental problems around the world have become increasingly prominent. Countries around the world are actively developing new types of renewable energy sources. With its lower cost and more mature application technology, wind power has gradually increased its energy share in the power grid. The permanent magnet synchronous motor (PMSG), as a high-performance motor, is widely used in wind power generation because of its response speed, high power factor, and high operational reliability. However, in the permanent magnet synchronous power generation system, since the generator is connected to the power grid through a full-power converter, the rotor speed of the generator is decoupled from the power grid (Singarao and Rao, 2016), and the two operate asynchronously, resulting in a series of transient stability problems. Therefore, it is necessary to establish a grid-connected model of the wind power system based on the simulation platform to simulate and analyze wind power control. At present, the modeling and simulation platform of wind turbines mainly includes MATLAB/Simulink, SCAD/EMTTDC, and PSASP (Sun et al., 2021).

The detailed model of a permanent magnet synchronous power generation system includes a wind turbine, drive shaft, PMSG, full power converter, and their corresponding control systems. However, the detailed model includes electromagnetic, electro-mechanical, and mechanical time scales (Vidyanandan and Senroy, 2013). The high order of the model leads to a slow simulation running speed, which makes it inefficient to analyze the grid-connected wind power system and difficult to optimize the system control strategy. In order to improve the simulation speed of wind power grid connection, some literature reports simplify the wind power system model by reducing the model order. Miao et al. (2015) simplified the converter and grid-connected transformer to simplify the system, but the order of the system is still high. Zhang et al. (2016) simplified part of the PMSG model by equalizing the PMSG with the excitation synchronous motor. Ren et al. (2022) established a reduced-order model applied to the analysis of small disturbance stability. The aforementioned models lack general simplification principles and consider the grid-connected model of a single typhoon power unit, so they all have certain limitations in application scenarios after simplification. Xue et al. (2022) established a full-power wind turbine impedance model that takes into account the dynamics of the machine side system based on a modular, multi-port frequency domain modeling approach to quantitatively analyze the coupling characteristics of the machine side system of a full-power wind turbine, the influencing factors, and the impact on grid stability. The aforementioned model mainly investigates the influence of WTG damping and machine side dynamics on grid stability, which is verified by changing the damping and ignoring the dynamics as a comparison. Similarly, the model mainly considers the grid-connection model of a single unit and is mainly used for the wind turbine design. It cannot be used in wind farm modeling because it is refined modeling of a single unit. In this paper, the simplified modeling of wind farms is realized by equivalent transfer functions on the simplification of wind turbines, and furthermore, the aggregated equivalence at the wind farm level is combined to realize the simplified modeling of wind farms. The current simplified modeling of wind farms mainly focuses on the simplification of WTGs or aggregated equivalence, without focusing on the connection between the analysis of wind farm architecture and the simplification of WTGs. This paper not only simplifies the wind turbine based on the equivalent transfer function to ensure the dynamic characteristics but also analyzes the wind farm architecture, models the wind farm from two aspects for the first time, and validates the modeling strategy based on the actual wind farm project.

With the continuous growth of wind power-installed capacity, the single grid-connected system model is complex, and the capacity is low, which cannot meet the actual wind power grid-connected analysis. Therefore, it is necessary to carry out a certain reasonable equivalent simplification for the grid-connected system of large wind farms to meet the actual simulation requirements. At present, the equivalence simplification of new energy is mainly divided into two parts: clustering among different new energy types and aggregation equivalence of the same type of energy (Wang et al., 2022). Wind farms are mainly composed of wind turbines of the same type, which can be simplified by the aggregation equivalence method. Kim and Sharkawi (2015), based on the conditions of wind speed and access position, used the capacity weighting method to calculate the parameters of equivalent fans so as to realize the equivalent modeling of a single fan in a wind farm. However, this equivalent method ignores the power loss of the collector line, which is relatively ideal. Based on the equivalent fan parameters of the capacity weighting method, the intelligent optimization algorithm is used to identify the equivalent fan parameters in Zhou et al. (2018), which improves the accuracy of the single-machine equivalent model to a certain extent and reduces the dynamic difference before and after the equivalent. Linash et al. (2018) compared and analyzed the detailed models of the two existing equivalent methods, namely, single machine equivalent and multi-machine equivalent, and wind turbines, and found that there was still a gap between the equivalent method and the actual wind farm in terms of theoretical analysis and accuracy. Huang et al. (2015) improved the weighting method and applied it to the parameter aggregation equivalence of wind turbines, which improves the accuracy but still ignores the power loss on transmission lines. Liu et al. (2020) used the improved bird colony algorithm to search and cluster the clustering indexes of 12 state variables of wind turbines, and the K-means algorithm was used to cluster the wind farm, which characterized the external characteristics of the wind farm. However, it focuses on the external characteristics of the wind farm and does not characterize the internal dynamic characteristics of the wind turbine.

Before large-scale wind farms are connected to the grid, it is often necessary to study and analyze their transient characteristics. At present, there are many research studies on wind turbine simplification and wind farm equivalent methods, but there are few literature reports on further reducing the complexity of large-scale wind farms by combining the two methods. The high complexity of wind farms also brings difficulties to wind farm control. For this reason, the simplified modeling of the wind farm is divided into two layers. According to the dynamic characteristics and action time scale of the wind turbine, the simplified principle of each part of the permanent magnet wind turbine system is designed in the lower layer, and the simplified wind turbine model is built based on the equivalent transfer function. The effectiveness of the simplified method is verified by simulation. The upper layer is based on the improved capacity-weighting method for aggregated equivalence of multiple wind turbines, and the parameters of transmission lines and transformers are equivalently calculated considering the power loss of a transmission lines, and the simplified equivalence strategies of the upper and lower layers are integrated to achieve aggregated equivalence modeling of wind farms. A simulation model based on simplified wind farms and modular multilevel converter-high voltage direct current (MMC-HDVC) transmission is built to study the transient characteristics of the grid-connected system by simulating typical transient conditions, and the validity of the equivalent wind farm model is verified.

2 Model and operation principle of a permanent magnet direct-driven wind turbine

A direct-driven wind generation system is a system where the wind turbine directly drives the generator to generate electricity. The wind turbine usually ignores the influence of a yaw-control system, turbine tower, and blade flexibility, including the wind turbine, drive shaft, PMSG, FRC, and their corresponding control systems in modeling (Zhong et al., 2021).

2.1 Wind turbine and PMSG model

At present, the commonly used aerodynamic model mainly adopts the wind energy utilization coefficient model. The mechanical power obtained by the wind turbine capturing wind energy is as follows (Chen et al., 2022):

$\begin{array}{l}{\mathit{P}}_{\mathit{m}}=\frac{\mathit{\rho }{\mathit{S}\mathit{C}}_{\mathit{p}}\left(\mathit{\lambda },\mathit{\beta }\right){\mathit{v}}^3}{2}={\mathit{T}}_{\mathit{m}}{\mathit{\omega }}_{\mathit{m}}\end{array},(1)$

where ρ is the air density, using the standard air density 1.225 kg/m³; S = πR² is the scanning area of the wind turbine; R is the radius of the wind turbine blade, which is easy to measure; v is the wind speed; and C_p is the wind energy utilization coefficient where the value is a function of the blade tip speed ratio λ and the pitch angle β. The expression of λ is as follows:

$\begin{array}{l}\lambda =\frac{{\mathit{\omega }}_{\mathit{m}}\mathit{R}}{\mathit{v}},\end{array}(2)$

where ω_m is the wind turbine speed.

From Eqs 1, 2, the mechanical torque of the wind turbine can be calculated as follows:

$\begin{array}{l}{\mathit{T}}_{\mathit{m}}=\frac{\mathit{\rho }\mathit{\pi }{\mathit{R}}^3{\mathit{C}}_{\mathit{p}}\left(\mathit{\lambda },\mathit{\beta }\right){\mathit{v}}^2}{2\mathit{\lambda }}.\end{array}(3)$

In low to medium wind speed, the pitch angle generally stays around 0 degrees, so the wind turbine can absorb the maximum power.

The optimal blade tip speed ratio uniquely corresponds to the maximum wind energy utilization factor when the pitch angle β of the wind turbine is fixed. When the wind speed changes, the generator speed can be changed according to Eq. 2 to sustain the optimal blade tip speed ratio. Thus, the wind energy utilization factor is always kept at the maximum value, namely, the wind turbine operates at the maximum power, resulting in maximum power point tracking (MPPT) control.

C_p can be expressed as follows:

$\begin{array}{l}\left\{\begin{array}{l}{\mathit{C}}_{\mathit{p}}\left(\mathit{\lambda },\mathit{\beta }\right)=0.5176\left(\frac{116}{\mathit{\alpha }}-0.4\mathit{\beta }-5\right){\mathit{e}}^{-\frac{21}{\mathit{\alpha }}}+0.0068\mathit{\lambda }\\ \frac{1}{\mathit{\alpha }}=\frac{1}{\mathit{\lambda }+0.08\mathit{\beta }}-\frac{0.035}{{\mathit{\beta }}^3+1}\end{array}\right.,\end{array}(4)$

where α is the intermediate variable; C_p uses engineering parameters. Although Cp is a non-linear model, it does not contain dynamic characteristics and can be calculated directly when the pitch angle and blade-tip speed ratio are determined, without increasing the complexity of the system. In order to ensure the accuracy of the wind turbine output power, the corresponding mathematical model is built directly in the process of model building. Once the pitch angle and tip speed ratio are determined, the Cp is determined.

The PMSG converts the wind energy captured by the wind turbine into electrical energy through electromagnetic effects. If we neglect the shafting dynamic effect, the expression of the rotor dynamic equation is as follows (Rosyadi et al., 2022):

$\begin{array}{l}J\frac{\mathit{d}}{\mathit{d}\mathit{t}}{\mathit{\omega }}_{\mathit{m}}={\mathit{T}}_{\mathit{m}}-{\mathit{T}}_{\mathit{e}}-D{\mathit{\omega }}_{\mathit{m}},\end{array}(5)$

where ω_m is the mechanical angular velocity, ω_m = ω_r/p; J is the rotational inertia, a fixed parameter of the turbine; T_m is the electromagnetic torque; and D is the mechanical damping coefficient.

2.2 Full power converter and control system

In a permanent magnet direct-driven wind turbine, a full-power converter converts and controls the output power under a designed control strategy. It is divided into a rotor-side converter and network-side converter, both of which generate PWM signals to achieve the control objective by PI control in a decoupled dq coordinate system. Generally, the wind turbine achieves MPPT control through the control of the rotor-side converter. The grid-side converter is used to maintain the voltage stability on the DC side in the FRC and to support the reactive power of the system.

The rotor-side control strategy is shown in Figure 1. First, the difference between the actual generator speed ω_s and the best reference value ω_s* is input to the PI controller to obtain the q-axis stator current reference value i_sq*. The actual three-phase currents (i_a, i_b, and i_c) are converted into d-axis current i_sd and cross-axis current i_sq by Pike transform. Then, the difference between i_sq* and i_sq is taken as the input for the PI controller to generate the cross-axis stator voltage reference v_sq*. The straight axis uses i_sd* = 0 control, namely, the straight axis reference current i_sd* is set to 0 in the control process. The reference value and the actual value are PI-controlled to generate the straight-axis reference voltage v_1d*. Then, the two-phase static reference voltages v_sα* and v_sβ* are obtained according to the inverse Pike transform. Finally, the PWM signals (S_a, S_b, and S_c) required by the rotor-side converter are generated by the space vector pulse width modulation (SVPWM) method, which regulates the wind turbine torque. In Figure 1, L_sd and L_sq are the dq-axis stator winding inductors, Ψ is the permanent magnetic flux, and θ_s is the electrical angle required in the Park transform calculation.

FIGURE 1

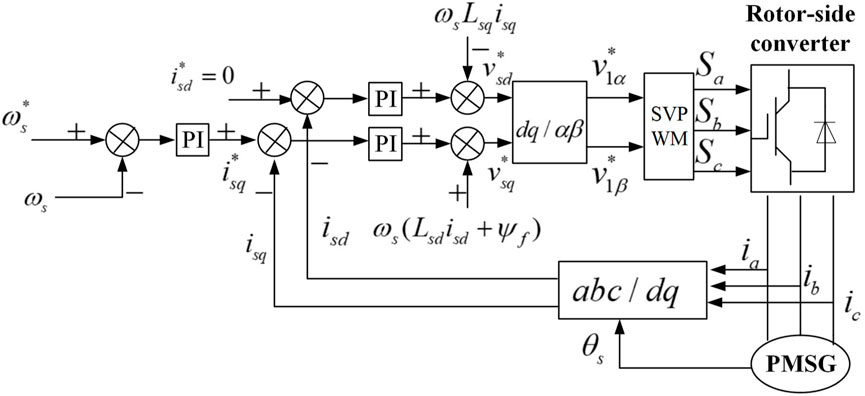
FIGURE 1. Vector control block diagram of the generator side converter shows the control mode on the machine side under the detailed model of the wind turbine, which can be contrasted with the subsequent simplified model.

The rotor-side converter power control strategy generally includes an MPPT control and pitch angle control strategy. In dealing with other conditions, the control strategies can be extended on this basis, such as load shedding control, virtual inertia control, and sag control to enable the wind turbine to support the system frequency.

The network-side control strategy is similar to the rotor-side controller strategy. The control target is to maintain the DC-side bus voltage at a fixed level, which will not be described further.

The pitch angle control system limits the rotor speed of the wind turbine to avoid exceeding the rated value. The pitch angle control system generally includes the main control system and the pitch servo. The main control system generates the reference pitch angle through PI control. Considering the megawatt capacity of the wind turbine, the rotational inertia of its blades is large, so it generates a large moment of inertia. The pitch system contains a rectifier, inverter, and gearbox, and the control section includes flux regulation, position regulation, speed regulation, and torque regulation, which is a complex fourth-order model.

When the wind speed is at low to medium, the pitch angle stays at a minimum of 0° to enable MPPT operation. When the wind speed is higher than the rated wind speed, the speed exceeds the rated speed. The pitch angle reference β_ref is derived by PI control to reduce the wind energy utilization factor C_p, i.e., reduce the mechanical power Pm of the wind turbine to avoid rotor overspeed.

The overall structure of the permanent magnet direct-driven wind generator system is shown in Figure 2.

FIGURE 2

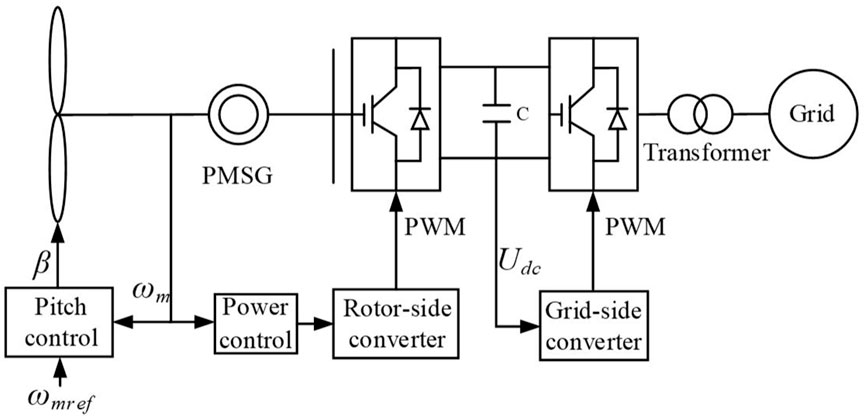
FIGURE 2. Structure and control system of the permanent magnet direct-driven wind power system show the control structure of a permanent magnet direct-driven wind power system, which provides the basis for the control of subsequent wind turbines.

In summary, even though the current model of the permanent magnet direct-driven wind generator system has been simplified, it is still a high-order complex model. Considering pitch control, power control, grid-side converter, PMSG, etc., the model order is as high as 11 orders. For the simulation of a large wind farm transient study, the single machine model is too complex. Hence, further analytical simplification of the model is needed.

3 Wind turbine simplification strategy based on the equivalent transfer function

Wind farms are usually composed of hundreds of wind turbine generators. If the aforementioned modeling is carried out for each wind turbine generator, the establishment of a complete model of the whole wind farm and the simulation analysis and control of corresponding working conditions will take up many hardware resources, and the time cost is huge. Therefore, in this paper, considering the various parts of the wind turbines and their equivalent transfer function model, based on the rational analysis of the original model and reasonable design about the principle of simplification, the simplification of wind turbines is realized, the order of system state equations is reduced, the simulation time is reduced at the same time to ensure a certain degree of accuracy, and the fast simulation is carried out under various working conditions of the wind turbines. It is convenient for wind farms to carry out grid-connection transient process research.

3.1 Simplified model of the equivalent transfer function of wind turbines

Based on the analysis of the structure and control strategy of the permanent magnet direct-driven wind turbine in Section 1, the equivalent transfer function is simplified for its three models and two control systems.

3.1.1 Equivalent simplified model of wind turbines and PMSG

According to Eq. 1, in addition to the structural parameters of the wind turbine itself, the mechanical power output of the wind turbine is mainly related to wind speed v and wind energy utilization coefficient C_p, where C_p depends on the blade tip speed ratio λ and pitch angle β, while the blade tip speed ratio λ is related to rotor speed ω_m and wind speed v according to Eq. 2.

Considering that the simplified model of each part needs to be superimposed and synthesized in the future, the output variable of the equivalent simplified model of the wind turbine is designed as the mechanical torque Tm, and the input variables are the wind speed v, rotor speed ωm, and pitch angle β. Based on the relationship of the aforementioned variables, the structure diagram of the simplified model of the wind turbine is shown in Figure 3A.

FIGURE 3

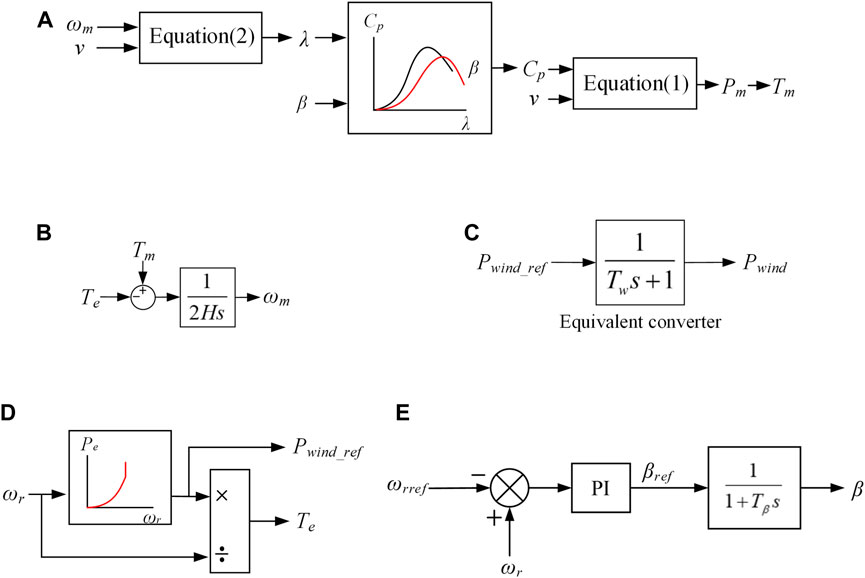
FIGURE 3. (A) Structure diagram of the simplified model which is the simplified aerodynamic part of wind turbine. (B) Simplified part of the permanent magnet synchronous motor. (C) Simplified converter model. (D) Simplified power control module. (E) Simplified pitch angle control model. The aforementioned models are simplified by the equivalent transfer function.

Among them, the relationship between C_p and λ and β can be determined in two ways, namely, the table lookup method and formula method. In order to ensure the equivalent accuracy of the system model while simplifying, the formula method is adopted in this paper, and C_p is determined by Eq. 4.

The dynamic equation of the rotor in PMSG is shown in Eq. 5, which can be regarded as an inertial link, and its inertia time constant is about 6 s. In PMSG, the dynamic response time of the dq axis current is in the order of milliseconds, which is much lower than the dynamic response time of the rotor. At the same time, when the permanent magnet direct-driven wind power system is operating, the energy conversion efficiency is usually above 90%. Therefore, in order to reduce the model order and system complexity, the influence caused by mechanical damping and electromagnetic loss is not included (Ancuti et al., 2020).

In the equivalent simplification of PMSG, the following simplification principles are designed:

• The dynamic response of the dq axis current in PMSG is ignored, that is, the dynamic response under the electromagnetic time scale in PMSG is ignored.

• The influence of mechanical damping and electromagnetic loss in PMSG is ignored.

Based on the aforementioned simplification principles, the rotor dynamic equation expression in PMSG can be simplified as follows:

$\begin{array}{l}J\frac{\mathit{d}}{\mathit{d}\mathit{t}}{\mathit{\omega }}_{\mathit{m}}={\mathit{T}}_{\mathit{m}}-{\mathit{T}}_{\mathit{e}}.\end{array}(6)$

The output variable of the PMSG equivalent simplified model is rotor speed ω_m, and the input variables are mechanical torque T_m and electromagnetic torque T_e. The structure diagram of its transfer function model is shown in Figure 3B. In Figure 3B, H is the inertia time constant, which can be obtained by the rotational inertia of the turbine J, 2H = Jω₀/S_B*p². ω₀ is the rated speed, S_B is the rated capacity, and p is the polar logarithm.

3.1.2 Equivalent simplified model of the converter

In Figure 1, the control block diagram of the converters on the rotor side, the response function of i_sq is,

$\begin{array}{l}\frac{{\mathit{i}}_{\mathit{s}\mathit{q}}\left(\mathit{s}\right)}{{\mathit{v}}_{\mathit{s}\mathit{q}}\left(\mathit{s}\right)}=\frac{1}{{\mathit{L}}_{\mathit{s}\mathit{q}}\mathit{s}+{\mathit{R}}_{\mathit{s}}}\end{array},(7)$

where R_s is stator resistance.

The parameters of rotor speed PI adjustment are k_pw and k_iw, and the PI parameters of the dq axis current are k_pi and k_ii. Then the transfer function between i_sq and i_sq* is

$\begin{array}{l}\frac{{\mathit{i}}_{\mathit{s}\mathit{q}}\left(\mathit{s}\right)}{{\mathit{i}}_{\mathit{s}\mathit{q}}^{*}\left(\mathit{s}\right)}=\frac{{\mathit{k}}_{\mathit{p}\mathit{i}}\mathit{s}+{\mathit{k}}_{\mathit{i}\mathit{i}}}{{\mathit{L}}_{\mathit{s}\mathit{q}}{\mathit{s}}^2+\left({\mathit{R}}_{\mathit{s}}+{\mathit{k}}_{\mathit{p}\mathit{i}}\right)\mathit{s}+{\mathit{k}}_{\mathit{i}\mathit{i}}}\end{array}.(8)$

The reference value of the rotor speed is mainly calculated by the reference electromagnetic power. When MPPT is used for control, the reference electromagnetic power is,

$\begin{array}{l}{\mathit{P}}_{{\mathit{e}}_{\mathit{r}\mathit{e}\mathit{f}}}={\mathit{k}}_{\mathit{o}\mathit{p}\mathit{t}}{\mathit{\omega }}_{\mathit{s}}^3.\end{array}(9)$

Then, according to Eqs 5, 6, the transfer function of P_e and P_{e_ref} is,

$\begin{array}{l}\left\{\begin{array}{l}\frac{{\mathit{P}}_{\mathit{e}}\left(\mathit{s}\right)}{{\mathit{P}}_{{\mathit{e}}_{\mathit{r}\mathit{e}\mathit{f}}}\left(\mathit{s}\right)}=\frac{\mathit{D}\left(\mathit{s}\right)}{{\mathit{L}}_{\mathit{s}\mathit{q}}{\mathit{s}}^3+\left({\mathit{R}}_{\mathit{s}}+{\mathit{k}}_{\mathit{p}\mathit{i}}\right){\mathit{s}}^2+\mathit{D}\left(\mathit{s}\right)}\\ \mathit{D}\left(\mathit{s}\right)={\mathbf{\Psi }}_{\mathit{f}}\left[{\mathit{k}}_{\mathit{p}\mathit{w}}{\mathit{k}}_{\mathit{p}\mathit{i}}{\mathit{s}}^2+\left({\mathit{k}}_{\mathit{p}\mathit{w}}{\mathit{k}}_{\mathit{i}\mathit{i}}+{\mathit{k}}_{\mathit{i}\mathit{w}}{\mathit{k}}_{\mathit{p}\mathit{i}}\right)\mathit{s}+{\mathit{k}}_{\mathit{i}\mathit{w}}{\mathit{k}}_{\mathit{i}\mathit{i}}\right]\end{array}\right..\end{array}(10)$

Generally speaking, the switching frequency of the converter varies from hundreds to thousands Hz, among which the reactance of the filter reactor is usually about 100 μH. Calculation shows that the time constants of the switching dynamic response of the converter and the filtering reactance flux dynamic response are both at the ms level. The dynamic response time constants of the PLL and the internal current loop are both ms, while the time constants of the power control loop are usually 0.2–0.3 s (Geng and Xu, 2011). Therefore, the response of the power control is mainly considered in the dynamic response time of the converter.

Based on the aforementioned time-scale analysis and the detailed transfer function derivation of the converter, the following simplification principles are designed in the simplified converter model:

• The switching dynamics and the dynamic response of each flux, the dynamic response of the phase-locked loop, and the dynamic response of the current inner loop in the converter are ignored.

• The full power converter adopts the qd axis decoupling control, so active power control and reactive power control are separated, and DC side voltage control is ignored.

Based on the aforementioned simplification principle and the fact that the parameters of the inner and outer loop PI controller in the actual wind power system have a bandwidth difference, considering the control bandwidth difference, namely, k_pi>>k_pw, k_ii>>k_iw, and ignoring the electromagnetic loss of the converter, the output power of the wind turbine can be approximated by the transfer function as follows:

$\begin{array}{l}{\mathit{P}}_{\mathit{w}\mathit{i}\mathit{n}\mathit{d}}=\frac{1}{{\mathit{T}}_{\mathit{w}}\mathit{s}+1}{\mathit{P}}_{{\mathit{w}\mathit{i}\mathit{n}\mathit{d}}_{\mathit{r}\mathit{e}\mathit{f}},}\end{array}(11)$

where P_wind is the output power of the wind turbine; P_{wind_ref} is the reference value of the wind turbine output power; and T_w is the equivalent electrical time constant. The time constants of the power T_w as the equivalent electrical time constant of the converter, which mainly consider the response of power control, are usually 0.2–0.3 s. According to different power control strategies, the equivalent time constant can be adjusted appropriately.

The structure diagram of the equivalent transfer function model of the converter is shown in Figure 3C.

3.1.3 Equivalent model of the control system

Under the dq coordinate system decoupling condition, the converter generates a PWM signal through PI control to achieve the control goal. After the converter is simplified and equivalent to a first-order inertial link, the power control loop is simplified. The electromagnetic power of the wind turbine can be directly obtained from the output power reference value P_{wind_ref}, which depends on the overall operation strategy of the wind turbine. P_{wind_ref} is selected according to the rotary speed ω_m to achieve the maximum power capture of the wind turbine. Considering that the equivalent simplified PMSG model requires electromagnetic torque as the input variable, the input variable of power control system model is rotary speed ω_m. The output variables are the reference value P_{wind_ref} of output power and the electromagnetic torque T_e, and the model structure diagram is shown in Figure 3D.

In order to achieve the aforementioned power and the rotor speed does not exceed the rated value, the pitch angle control system is required to assist in the control.

It is known from Section 2.2 that the pitch angle control system includes different control loops, in which the rectifier and inverter can be treated equivalently. In the control loop, because the position loop has the greatest impact on the dynamic performance of the pitch system, the rotary speed loop and speed loop are simplified.

Then, the pitch system can be equivalent to a first-order inertial link based on the transfer function:

$\begin{array}{l}G\left(\mathit{s}\right)=\frac{1}{1+{\mathit{T}}_{\mathit{\beta }}\mathit{s}}\end{array},(12)$

where G(s) is the transfer function of pitch servo; T_β is a time constant and its value can be calculated by the superposition of the inverter time constant of the electric pitch system, time constant of the current sensing unit, and time constant of the speed sensing unit.

Ignoring the dynamic characteristics of the rotary speed loop and speed loop, a theoretical analysis shows that compared with the original detailed model, the dynamic characteristics of the simplified model in the middle- and low-frequency bands are consistent. The dynamic characteristics of the rotary speed loop and speed loop are mainly reflected in the high frequency band, so the accuracy of the pitch system in the high frequency band will be lost to a certain extent. Therefore, the simplified controller of the pitch system is mainly applicable to the pitch angle control in the middle- and low-frequency bands. In the transient analysis of the wind farm, the requirements for the pitch angle control accuracy are slightly lower. The simplified model can meet the requirements, and according to the pitch angle control strategy, it can be applied to all working conditions.

The aforementioned description shows the limitations of the wind turbine simplification strategy based on the equivalent transfer function. Furthermore, the simplified modeling of wind farms is mainly used for the grid-connected transient analysis of wind farms, which is verified in the subsequent simulations. The aforementioned limitations show that the simplified modeling of wind farms cannot be used for the validation of the effect of the refined control strategy of wind farms. This is because the simplified modeling cannot guarantee the accuracy of the pitch angle control and the speed loop control. However, with most of the WTG control strategies, the simplified modeling of the wind farm accurately reflects the dynamic characteristics of the wind farm, which is consistent with the modeling purpose. Further improvements in WTG modeling are needed if accurate control of the pitch angle and speed loop is to be achieved.

The input variable should be set as rotor speed ω_r. The output variable is the pitch angle β. The structure diagram of the pitch angle control system is shown in Figure 3E.

In Figure 3E, ω_rref is the reference value of the rotary speed, generally set as the rated speed; β_ref is the reference value of the pitch angle.

3.1.4 Simplified model based on the equivalent transfer function

Combining the simplified transfer function model in Sections 3.1.1–3.1.3 and connecting its corresponding parts, the simplified model structure diagram is shown in Figure 4.

FIGURE 4

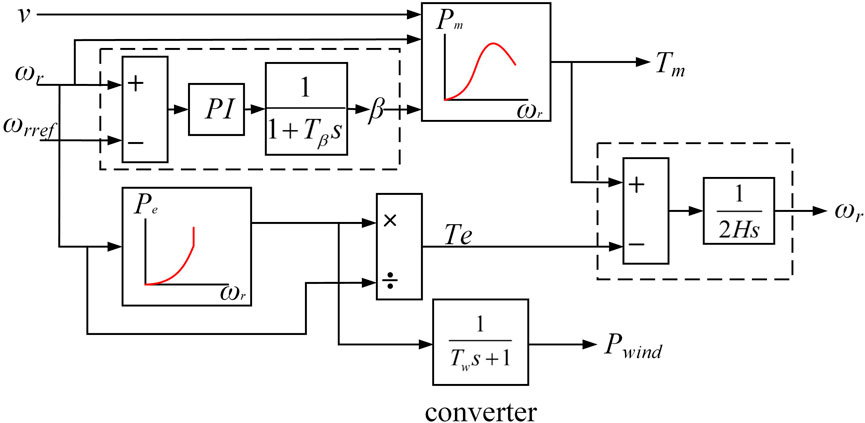
FIGURE 4. Overall simplified structure diagram of the wind turbine integrates the modules in Figure 3 to combine the overall simplified model structure of the wind turbine.

It can be seen from the simplified model structure diagram of the wind turbine unit that after the analysis of the original model and the simplification of the equivalent transfer function, the original complex 11th-order model is simplified to a more concise fourth-order model. At the same time, the accuracy of the fan model is reasonably analyzed to minimize the impact on the dynamic characteristics of the fan.

The specific working principle of the simplified model is as follows: according to the reference power command issued by the power controller, the corresponding reference value of rotary speed ω_rref and the reference value of electromagnetic torque T_e are calculated. The reference value of rotary speed ω_rref and real-time rotary speed ω_r are controlled by PI in the transfer function of the pitch angle to obtain the pitch angle β. The captured mechanical power P_m and mechanical torque of the wind turbine T_m are calculated from the pitch angle β and real-time wind speed v. The real-time rotary speed ω_r is obtained according to the equivalent transfer function of the electromagnetic torque T_e and mechanical torque T_m through PMSG, and the output power of the wind turbine is obtained from the equivalent transfer function of the reference power through the converter.

Based on the aforementioned working principle, the control strategy of the wind turbine in the simplified model can be derived as follows: The output power reference value is obtained according to the original control strategy of the wind turbine, and then the speed reference value is obtained. The difference between the rotational speed reference value and the actual rotational speed is used to obtain the pitch angle reference value through PI control. Under the condition of the given wind speed, the mechanical torque is obtained, and then, the rotational speed of the wind turbine is obtained, finally forming a closed-loop control of rotational speed.

In this paper, the original relatively detailed wind turbine model is analyzed, and the wind turbine model is downgraded on the basis of retaining the dynamic characteristics of the wind turbine as much as possible. When converting the (1)–(9) model into a transfer function, it is necessary to analyze the model according to its own characteristics and design a suitable simplification principle to retain the dynamic characteristics of the model while ignoring the relatively small power loss. The specific function of each part of the model is used as the entry point, while a simple mathematical downgrade is likely to have an impact on the dynamic characteristics of the original model.

On the basis of the original model of the wind turbine, this paper selectively analyzes some of its high-order models and simplifies the dominant and secondary parts. At the same time, the simplified models of each part of the wind turbine are connected through the equivalent transfer function, which makes modeling of the wind turbine more concise and intuitive, while retaining the dynamic characteristics of the wind turbine model as much as possible. A specific follow-up single wind turbine generator set will appear as a simplified model of the equivalent transfer function, which can greatly reduce the complexity and time of simulation, and at the same time, it can ensure the accuracy of simulation to a certain extent, reduce the complexity of wind turbine control, and lay a foundation for wind farm control.

In the simplified modeling of wind farms, the control strategy of wind turbines uses the MPPT control mode, and its simplified control flow is shown in Figure 4. It can be seen that the control model of the wind turbine can run after the wind speed and speed and speed reference values are given. Nowadays, various control strategies for wind turbines are implemented by changing the speed reference value or the pitch angle. By observing each state variable of the wind turbine, the power reference required for the control strategy is calculated and implemented by adjusting the speed reference or pitch angle. In this paper, the speed reference and pitch angle values are not simplified, but only their values are used. Therefore, when the wind turbine adopts different control strategies, the simplified strategy can achieve a certain effect.

3.2 Grid-connected simplified fan model

As shown in the structure diagram of the simplified wind turbine model, the variable input to the power grid by the simplified wind turbine system is only power but not voltage and current, which does not match the connection line of the three-phase power grid. Therefore, it is necessary to design the electrical interface connecting the simplified model and the power grid model.

Considering that only the power of the simplified wind power system varies with the wind speed compared with the grid model, it can be regarded as a power source, and the change in the grid-connected power can be realized through the change in the grid-connected current. Therefore, the electrical interface can be realized through the controlled current source, and the schematic diagram of its structure is shown in Figure 5.

FIGURE 5

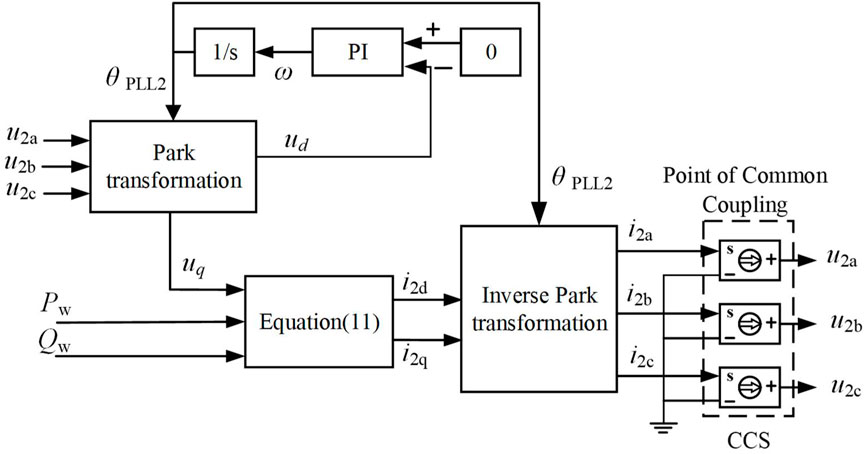
FIGURE 5. Interface module structure of the simplified model and power grid establishes the electrical interface between the simplified model of the wind farm and the grid, allowing the power of the simplified model to be transformed into three-phase voltage and current for grid-connected modeling.

The connection between the simplified model and the power grid is realized mainly through a phase-locked loop, Park transformation, and inverse Park transformation. In order to determine the value of the three-phase current i_2abc, the phase is determined by the voltage of the connection point through the phase-locked loop, and then the dq axis component of the current is obtained according to the output power of the simplified model of the wind turbine through the following formula:

$\begin{array}{l}\left\{\begin{array}{l}{\mathit{i}}_{2\mathit{d}}=\frac{\mathbf{2}}{\mathbf{3}}\frac{{\mathit{P}}_{\mathit{w}}}{{\mathit{u}}_{2\mathit{d}}}\\ {\mathit{i}}_{2\mathit{q}}=-\frac{2}{3}\frac{{\mathit{Q}}_{\mathit{w}}}{{\mathit{u}}_{2\mathit{d}}}\end{array}\right..\end{array}(13)$

Finally, the three-phase current can be obtained through the inverse Park transformation, which can be used as the input signal of the controlled current source to realize the connection between the simplified model of the wind turbine and the power grid model.

At the same time, the loss of the converter and grid-connected interface will be taken into account when the current flows, which will lead to the power difference between the simplified model and the original detailed model; in this regard, P_w is given by the following formula:

$\begin{array}{l}{\mathit{P}}_{\mathit{w}}={\mathit{P}}_{\mathit{w}\mathit{i}\mathit{n}\mathit{d}}-{\mathit{i}}^2{\mathit{R}}_{\mathit{e}\mathit{q}}\end{array},(14)$

where i is the effective value of the three-phase current and R_eq is the equivalent resistance between the converter and the grid-connected interface module, which can be obtained through the inherent parameters of the system.

4 Simplified strategy for wind farms based on aggregation equivalence

Based on the aforementioned simplified modeling of a wind power single machine, the complexity of wind farm modeling is effectively reduced. However, there are usually hundreds of wind power units in large wind farms, and the model is still slightly complex, which needs to be aggregated and equivalent for wind farms. But it is difficult to ensure the accuracy of the model when the single machine equivalent is different from the fan-operating conditions in the field, so it is necessary to divide the field units into several clusters and carry out the equivalent.

In this paper, the wind farm model is divided into a two-layer structure. The lower part simplifies the wind turbines based on the equivalent transfer function; the upper part simplifies the collector lines by analyzing the connection of the wind farm collector system and using the equivalent line loss model. Further, the wind speed conditions and geographical location are considered, the wind turbines in the field are classified and aggregated, and the capacity weighting method is used to calculate the equivalent value of each circuit parameter. The equivalence of large wind farms is realized on the basis of architectural analysis.

4.1 Equivalent parameter calculation

The number of wind turbines in a wind farm is large, with different turbine models and operational variability. Therefore, multiple wind turbine models are equated to a single equivalent wind turbine model based on wind speed in full wind conditions. The generators to be equated in the wind farm are connected to the same busbar by means of a box-type transformer. On the premise that the line impedance between the units is less than the impedance of the transformer connected to the machine end and the line connected to the power grid, the capacity weighting method can be used to conduct the equivalent modeling of the wind farm.

According to the capacity weighting method, the proportion of each generator in the total capacity of the wind farm is the weight δ_i, and the equivalent calculation of the parameters of the wind turbine and generator is carried out according to the weight. The calculation equation of weight δ_i is (Zou et al., 2015)

$\begin{array}{l}{\mathit{\delta }}_{\mathit{i}}=\frac{{\mathit{S}}_{\mathit{i}}}{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{S}}_{\mathit{i}}}\end{array},(15)$

where δ_i is the weight coefficient of the capacity weighting method; S_i is the capacity of the i typhoon power unit in the wind farm; and n is the total number of stroke electric units in the wind farm.

According to the weight δ_i, the equivalent parameters of the wind turbine can be calculated as follows:

$\begin{array}{l}\left\{\begin{array}{l}{\mathit{A}}_{\mathit{e}\mathit{q}}={\displaystyle \sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{A}}_{\mathit{i}}\\ {\mathit{C}}_{{\mathit{p}}_{\mathit{e}\mathit{q}}}={\displaystyle \sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\sigma }}_{\mathit{i}}{\mathit{C}}_{{\mathit{p}}_{\mathit{i}}}\\ {\mathit{V}}_{\mathit{e}\mathit{q}}={\left(\frac{1}{{\mathit{A}}_{\mathit{e}\mathit{q}}{\mathit{C}}_{{\mathit{p}}_{\mathit{e}\mathit{q}}}}{\displaystyle \sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{A}}_{\mathit{i}}{\mathit{C}}_{{\mathit{p}}_{\mathit{i}}}{\mathit{V}}_{\mathit{i}}^3\right)}^{\frac{1}{3}}\end{array}\right.,\end{array}(16)$

where A_i, C_{p_i}, and V_i represent the sweep area, wind energy utilization rate, and captured wind speed of the ith wind turbine in the wind farm, respectively; A_eq, C_{p_eq}, and V_eq represent the sweep area, wind energy utilization rate, and equivalent wind speed after equivalent value, respectively.

The equivalent values of generator parameters are calculated as follows:

$\begin{array}{l}\left\{\begin{array}{l}{\mathit{P}}_{\mathit{e}\mathit{q}}={\displaystyle \sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{P}}_{\mathit{i}},{\mathit{S}}_{\mathit{e}\mathit{q}}={\displaystyle \sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{S}}_{\mathit{i}}\\ {\mathit{R}}_{\mathit{e}\mathit{q}}={\displaystyle \sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\sigma }}_{\mathit{i}}{\mathit{R}}_{\mathit{i}},{\mathit{X}}_{\mathit{e}\mathit{q}}={\displaystyle \sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{\sigma }}_{\mathit{i}}{\mathit{X}}_{\mathit{i}}\\ {\mathit{H}}_{\mathit{e}\mathit{q}}={\displaystyle \sum }_{\mathit{i}=1}^{\mathit{n}}\frac{{\mathit{H}}_{\mathit{i}}}{{\mathit{\sigma }}_{\mathit{i}}}\end{array}\right.\end{array}(17)$

where P_i, R_i, X_i, and H_i represent the active power, stator resistance, stator reactance, and inertia time constant of the ith generator in the wind farm, respectively; P_eq, R_eq, X_eq, and H_eq represent the equivalent active power, stator resistance, stator reactance, and inertia time constant, respectively.

4.2 Calculation of the transmission line and transformer equivalent parameters

The aforementioned method is the conventional capacity weighting method, which only performs capacity weighting but does not consider the internal structure of the wind farm and lacks certain accuracy. In this paper, we adopt the improved capacity weighting method, which considers the calculation of transmission line and transformer equivalent parameters based on the capacity weighting method and analyze the division of the wind farm architecture. The conventional capacity-weighted method lacks analysis of the structure of the wind farm itself, which can indeed enhance its applicability, but a large amount of information is easily lost in the aggregated equivalence of the wind farm, which may cause problems such as inaccurate equivalence of the wind farm and incomplete parameter constraints. The improved capacity-weighted method considers the internal structure of the wind farm and divides the wind farm architecture by combining the transmission lines and transformers connected to the wind turbines, fully retains varied information about the wind farm, and can more perfectly consider the constraints of state variables. Although it further increases the calculation volume, the extra equivalent calculations are negligible compared to the original detailed model in the actual wind farm project.

The connections between the wind turbines and between the turbines and the booster station in large wind farms also appear to be particularly complex and require equivalence calculations of the collector system parameters in the study and analysis. In the wind farm power collection system, the connection between wind turbine and booster station can be divided into two ways: multiple wind turbines with one transformer and one wind turbine with one transformer, and the connection schematic of the wind farm collector system is shown in Figure 6.

FIGURE 6

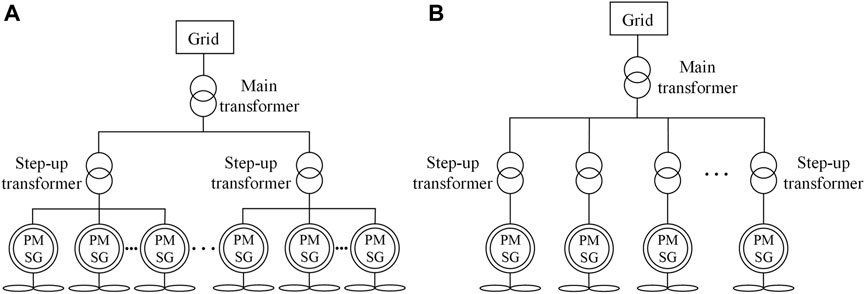
FIGURE 6. Schematic diagram of the connection of the collector system shows two different connections of the wind farm collector system to facilitate the equivalence calculation of the parameters of the subsequent collector system (A) For multiple wind turbines sharing one transformer. (B) One transformer for one wind turbine.

Figure 6A shows several wind turbines connected to the grid through one step-up transformer, and Figure 6B shows each wind turbine connected to the step-up converter station through one transformer, and then through the main transformer to realize the grid connection of wind power. Multiple wind turbine parameters can be equated according to the 3.1 equivalence method, and thus, the rotor side can be considered as a single wind turbine.

From the perspective of the power system, the wind farm access system is concerned with the operating conditions of the wind farm grid connection point. The power flow of the wind farm is a one-way power flow from the wind farm to the external grid. The wind farm is considered as a PQ point in the analysis of the wind farm access system, so the equivalent line loss model can be used to simplify the collection lines in the wind farm (Inés et al., 2018).

S₁, S₂,…, S_n are set as the output power of n wind turbine generator units, respectively; U₁, U₂, …, U_n are set as the terminal voltage of each wind turbine generator unit, respectively, and the impedance of collection lines between two adjacent wind turbine generator units are Z₁, Z₂, …, Z_n, respectively. When equating the collection lines, the wind turbine generator and the wind turbine transformer can be simplified as a current source as a whole. Assuming that the output of each wind turbine generator unit is equal, the current phasors they inject into the collection line are equal, and the losses on each section of the collection line in the wind turbine generator group are as follows:

$\begin{array}{l}\left\{\begin{array}{l}{\mathit{S}}_{{\mathit{L}\mathit{o}\mathit{s}\mathit{s}}_{{\mathit{Z}}_1}}={\mathit{I}}_1^2{\mathit{Z}}_1={\mathit{I}}^2{\mathit{Z}}_1\\ {\mathit{S}}_{{\mathit{L}\mathit{o}\mathit{s}\mathit{s}}_{{\mathit{Z}}_2}}={\left({\mathit{I}}_1+{\mathit{I}}_2\right)}^2{\mathit{Z}}_2=2^2{\mathit{I}}^2{\mathit{Z}}_2\\ ⋮\\ {\mathit{S}}_{{\mathit{L}\mathit{o}\mathit{s}\mathit{s}}_{{\mathit{Z}}_{\mathit{n}}}}={\left({\mathit{I}}_1+{\mathit{I}}_2+\dots +{\mathit{I}}_{\mathit{n}}\right)}^2{\mathit{Z}}_{\mathit{n}}={\mathit{n}}^2{\mathit{I}}^2{\mathit{Z}}_{\mathit{n}}\end{array}\right..\end{array}(18)$

The total loss of the collection line can be expressed as:

$\begin{array}{l}S=\sum {\mathit{S}}_{\mathit{i}}=I\sum \mathit{i}\mathit{Z}\end{array}.(19)$

According to the aforementioned equation, the transmission line in Figure 6 is equated to a series connection of the WTGs and the equivalent line, and the capacity of the equivalent WTGs is

$\begin{array}{l}{\mathit{S}}_{\mathit{e}\mathit{q}}=\sum {\mathit{S}}_{\mathit{i}}\end{array}(20)$

The current injected into the transmission line by the equivalent wind turbine can be expressed as,

$\begin{array}{l}{\mathit{I}}_{\mathit{e}\mathit{q}}=\sum \mathit{n}\mathit{I}\end{array}.(21)$

The impedance of the equivalent transmission line of the wind turbine is represented by Z_eq, so the loss on this line is

$\begin{array}{l}{\mathit{S}}_{\mathit{t}\mathit{o}\mathit{l}\_\mathit{L}\mathit{o}\mathit{s}\mathit{s}}={\mathit{I}}_{\mathit{e}\mathit{q}}^2{\mathit{Z}}_{\mathit{e}\mathit{q}}={\mathit{n}}^2{\mathit{I}}^2{\mathit{Z}}_{\mathit{e}\mathit{q}}\end{array}.(22)$

The equivalent impedance of the transmission line in Figure 6A can be expressed as,

$\begin{array}{l}{\mathit{Z}}_{\mathit{e}\mathit{q}\mathit{a}}=\frac{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{i}}^2{\mathit{Z}}_{\mathit{i}}}{{\mathit{n}}^2}\end{array}.(23)$

Similarly, the equivalent impedance of the transmission line in Figure 6B can be expressed as,

$\begin{array}{l}{\mathit{Z}}_{\mathit{e}\mathit{q}\mathit{b}}=\frac{{\sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{Z}}_{\mathit{i}}}{{\mathit{n}}^2},\end{array}(24)$

where Z_eqa is the equivalent line impedance under the multi-machine one-transformer structure; Z_eqb is the equivalent line impedance under the single-machine one-transformer structure; and Z_i is the impedance of the ith line of the wind farm.

For the equivalence of the transmission line to ground capacitance, since the reactive power to ground capacitance is proportional to the square of the voltage added to the capacitor, and the transmission line voltage is considered to be maintained stable during normal operation of the wind farm, the equivalence of the transmission line to ground capacitance is calculated as follows:

$\begin{array}{l}{\mathit{B}}_{\mathit{e}\mathit{q}}={\displaystyle \sum }_{\mathit{i}=1}^{\mathit{n}}{\mathit{B}}_{\mathit{i}},\end{array}(25)$

where B_eq is the capacitance to ground after equivalence calculation; B_i is the capacitance to ground of the ith line in the wind farm.

After the equivalent calculation of the transmission line, it is also necessary to equate the parameters of the step-up transformer, the voltage drop of the step-up transformer before and after the equivalence should remain the same, and the active and reactive losses of the step-up transformer after the equivalence should be equal to the sum of the active and reactive losses of all step-up transformers before the equivalence; the equivalent parameters of the transformer are calculated as follows:

$\begin{array}{l}{\mathit{Z}}_{\mathit{e}\mathit{q}\mathit{T}}=\frac{{\mathit{Z}}_{\mathit{T}}}{\mathit{n}}\end{array}(26)$

where Z_eqT is the impedance of the step-up transformer after equivalence; Z_T is the impedance of the step-up transformer in the wind farm.

After the improved capacity weighting calculation, the equivalent parameters of large wind farms can be obtained, and the aggregated equivalent modeling of large wind farms is realized.

5 Simulation verification

5.2 Simulation verification of the simplified model of the wind turbine based on equivalent transfer function

5.1.1 Single-machine simulation system

According to the detailed simulation model of a permanent magnet direct-driven wind power system and the grid-connection model of wind turbine based on the simplified equivalent transfer function, the grid-connection simulation system of a single-typhoon power unit with a rated capacity of 5 MW is established. The system structure is shown in Figure 7A. The wind power system is connected to the power grid through transformers and transmission lines. Specific parameters of the wind turbine are shown in Table 1.

FIGURE 7

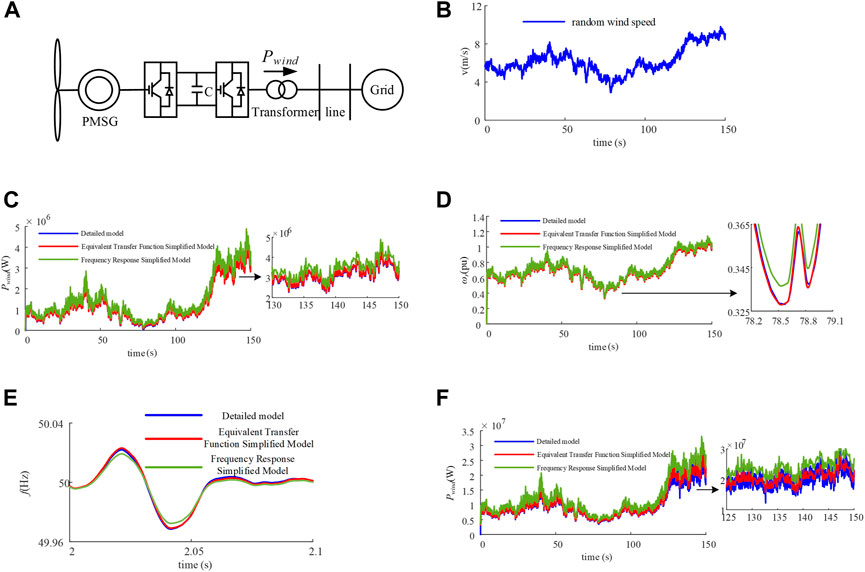
FIGURE 7. (A) Single-machine and multi-machine system simulation analysis shows the simulation structure diagram of a single wind turbine grid-connected system, on which the simulation analysis of the single system is carried out. (B) gives the simulated working conditions for the random wind speed. (C,D) Dynamic simulation analysis of a single wind turbine connected to the grid, and the simplified model of frequency response in other articles is selected to compare with the model in this paper, and the dynamic response characteristics are taken as the grid-connected power and rotor speed. (E) shows Comparison graph of system frequency under load fluctuation, which verifies the effectiveness of the strategy in this paper under the dynamic characteristics of frequency. (F) Comparison graph of the output power of multiple wind turbines under the equivalence strategy of this paper, which verifies the consistent effectiveness of the equivalence method of this paper for the output power.

TABLE 1

TABLE 1. Parameters of wind turbines.

5.1.2 Analysis of simulation results

In order to realize the rapid simulation and grid-connected transient study of wind farms under various working conditions, the turbulent wind speed conditions under the full wind speed range are simulated, and the random wind speed is shown in Figure 7B. In order to make the analysis of simulation results more accurate and comprehensive, it covers all wind speed conditions from the cut wind speed to rated wind speed. When the wind turbine is under MPPT control, the wind turbine can capture the maximum power. However, the PMSG has a rated power limit, and when the wind speed exceeds the rated wind speed, the captured mechanical power of the wind turbine will be reduced to meet the PMSG power limit. This can be achieved with the pitch angle control system. If we consider the grid-connected transient simulation of the wind turbine, the wind speed above the rated wind speed is not much different from the rated wind speed, because the power transferred from PMSG to the grid is the same at this time. The difference is that the pitch angle of the wind turbine changes, which has no effect on the grid-connected transient characteristics. Therefore, the wind speed above the rated wind speed is not included in the simulation experiment.

In order to reflect the accuracy and effectiveness of the simplification strategy in this paper, a simplified model based on the frequency response of the direct-driven permanent magnet wind turbine (LI et al., 2021) is selected as the comparison and analysis. The comparison of the response characteristics of the detailed simulation model, the simplified equivalent transfer function model, and the simplified frequency response model is shown in Figures 7C,D.

Further data analysis is shown in Table 2.

TABLE 2

TABLE 2. Error analysis for simplified models.

Relative data in Table 2 are obtained from relatively detailed model data. It can be seen from both Figures 7C,D and Table 2 that compared with the simplified frequency response model and the detailed model in this paper, the dynamic characteristics of grid-connected power and rotor speed under turbulent wind speed are closer, especially the rotor speed. The control effect of the control strategy with rotor speed as the observation quantity can be more accurate. Although the simulation time of the simplified equivalent transfer function model is slightly longer than that of the simplified frequency response model, compared with the simulation time of the detailed model in this paper, which is about 250 s, the difference between the simulation time of the two models is not significant, that is, they exchange a smaller simulation time for more accurate simulation dynamic characteristics, which is more advantageous in the fast grid connection transient research of wind farms.

In order to verify the effectiveness of the simplified model under various working conditions, considering the grid connected load fluctuation, the load drops suddenly by 0.2 MW in 2 s. The wind turbine uses droop control to participate in frequency modulation. The dynamic frequency response of each model is shown in Figure 7E. It can be seen that the frequency response curves of the detailed model and the simplified model almost coincide with each other for the same load fluctuation, and the frequency response of the equivalent transfer function simplified model and the detailed model is more consistent with that of the frequency response simplified model. This is mainly because the frequency response-simplified model neglects a lot of power losses in the simplification process, and its grid-connected power is relatively large as shown in Figure 7E, and the grid-connected power is more ideal. Under droop control, its power variation makes the frequency fluctuation smaller. However, in the study of grid-connected transient of wind farms, the accuracy of dynamic characteristics is of higher priority in simplification. This verifies the effectiveness of the simplified equivalent transfer function model proposed in this paper in the subsequent grid connection research.

5.2 Simulation analysis of the wind farm based on aggregation equivalence

5.2.3 Multi-turbine simulation system

On the basis of the fan parameters of the stand-alone simulation system in 4.1, seven actual wind turbines are taken as an example and equated to one wind turbine. The equivalent wind turbine parameters are calculated by the equivalent method in Section 3.1. The equivalent parameters are shown in Table 3.

TABLE 3

TABLE 3. Equivalent wind turbine parameters.

The structure diagram of the grid-connected fan system after the equivalent value is shown in Figure 7A. The multiple wind turbines are equivalent to the single wind turbine after equivalent value calculation, and then it is connected to the power grid through converters, transformers, and transmission lines.

Based on the equivalent wind turbine, the equivalent transfer function is simplified. The output power of each equivalent model under turbulent wind speed is shown in Figure 7F.

Under the equivalent output power of multiple wind turbines, the equivalent output power fluctuates greatly under the detailed model because of the turbulent wind speed and the equivalent output power of multiple wind turbines. The simplified frequency response model neglects the power loss which is smaller than the overall output power in the single machine simplification, but it can be evidently seen that the output power is larger than the actual detailed model in the case of a multi-machine equivalent. The equivalent output power of multiple machines based on the simplified equivalent function model is more suitable to the detailed model.

Meanwhile, by comparing the output power in Figures 7C,D,F, it can be seen that the power difference multiple is consistent with the number of wind turbines. It can be seen that based on the simplified wind turbine model, the aggregated equivalent model of multiple turbines at turbulent wind speeds can effectively output the power of the detailed turbine model, which verifies the effectiveness of the aggregation method.

5.2.2 Equivalent simulation of wind farms

Based on the multi-machine equivalent simplified simulation in 4.2.1, multiple wind turbines in large wind farms can be equivalently simplified to reduce the complexity of wind farm simulation.

Taking the Rudong ±400 kV offshore HVDC wind farm project in Jiangsu Province of China as an example, the specific connection diagram of the offshore wind farm is shown in Figure 8A.

FIGURE 8

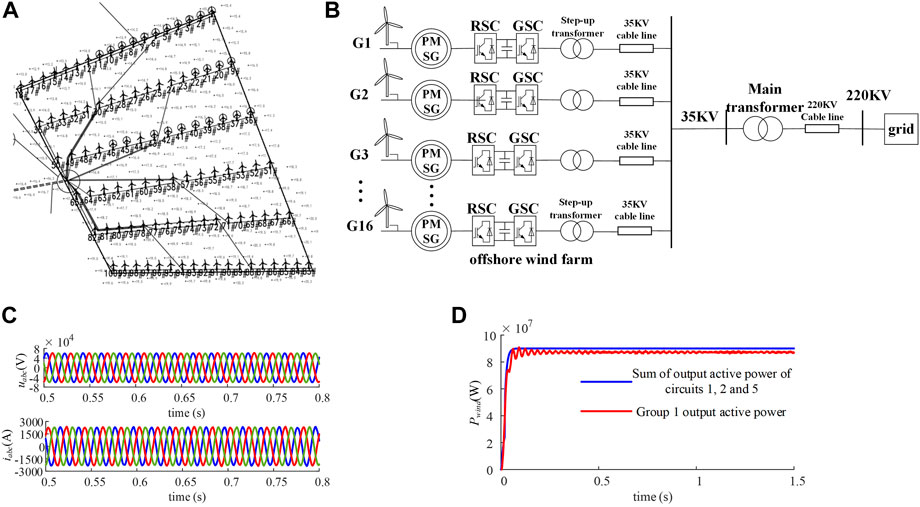
FIGURE 8. Wind farm equivalent simulation. (A) shows connection schematic of the actual wind farm as a model reference for the subsequent wind farm simulation in this paper. (B) shows structure of the wind farm after classification and aggregation, taking into account the wind speed conditions and geographical location. (C,D) analyze the waveforms of wind farm grouping 1, and the effectiveness of the equivalence strategy of this paper to improve the capacity-weighting method is verified by the comparative analysis of grid-connected voltage and current and output power.

In Figure 8A, the parameters of a single wind turbine are shown in Table 1; each wind turbine is equipped with a package transformer to boost to 35 kV, the wind turbines are connected through 35-kV cable transmission lines, and the cable length between the units is between 400 m and 600 m. According to the different geographical locations, the 100 wind turbines are divided into 16 circuits, each loop forms a different loop, which is connected to the offshore boost transformer (main transformer) through a long-distance transmission cable to achieve a 220-kV grid connection.

Considering wind speed and geographical location, the wind turbines of the wind farm are classified and aggregated. First, the 100 wind turbines are divided into 16 circuits, each circuit includes 5–8 wind turbines, and the wind farm structure diagram of 16 circuits is shown in Figure 8B. The aforementioned capacity weighting method is used to calculate the equivalent parameters of the wind turbines, package transformers, and cable lines in each circuit.

According to the connection diagram of the wind farm, the 16 circuits are divided into five groups to achieve a grid-connected connection. The grouping of the wind farm is shown in Table 4.

TABLE 4

TABLE 4. Grouping of wind farms.

On the basis of 16 loops, the wind farms are divided into five groups according to the connection coupling relationship between the loops. On one hand, it can reduce the complexity of wind farm aggregation equivalence, and on the other hand, the grouping is based on the connection relationship between loops, which can be changed flexibly according to the actual engineering situation.

In order to verify the accuracy of each group equivalent simplification, group 1 was selected for waveform analysis in simulation.

Figure 8C shows the voltage and current waveforms of the power grid on the 35-kv cable line in group 1. The voltage and current of the power grid remain stable during operation, and the voltage and current harmonics of the wind farm are lower, with better power quality.

Figure 8D shows the comparison waveform of the output power of group 1 and the sum of the output power of loops 1, 2, and 5. It can be seen from Figure 8D that the final active power output of group 1 is slightly less than the total active power output of the three loops due to the influence of 35-kV cable lines and transformers. At the same time, the total output active power of the three loops is 90 MW, and the number of wind turbines in the three loops is 18, calculated according to the rated power of a single wind turbine of 5 MW, and the output power of the equivalent simplified wind farm is in line with the actual situation.

Figure 8C,D also verify the effectiveness of the aggregation method applied to wind farm modeling. The output power matches the unaggregated wind farm output power while ensuring smooth operation of the wind farm model output power and voltage and current.

Combining 16 circuits and five groups, it can be seen that the equivalent wind farm can operate normally, and the output power conforms to the operation law of the wind farm. For the wind farm model adopted in this paper, the detailed model simulation time of the wind farm is about 102 min, while the simulation time of the wind farm based on the simplified model of the equivalent transfer function and the aggregation equivalent value is about 15 min, which greatly improves the speed of large-scale wind farm modeling and simulation.

Nowadays, offshore wind power is developing rapidly, and the proportion of offshore wind farms in large wind farms is high. Therefore, this paper combines engineering examples and takes offshore wind farms as the object of simulation analysis. However, offshore wind farms are far away from the mainland grid, and various losses in wind power transmission need to be considered. MMC-HVDC becomes a good transmission model as the transmission bridge between offshore wind farms and power grids. Therefore, this paper considers building a grid-connected model of wind farms based on MMC-HVDC to validate the simplified modeling of large wind farms.

The next step is to model the wind farm’s connection to a VSC-HVDC-based electric power transmission, and to set up a typical failure scenario for transient simulation of the system, the simulation results of the simplified wind farm and the detailed wind farm model are compared to verify the effectiveness of the simplified wind farm. The model of the grid-connected system based on the simplified wind farm and MMC-HVDC is shown in Figure 9A.

FIGURE 9

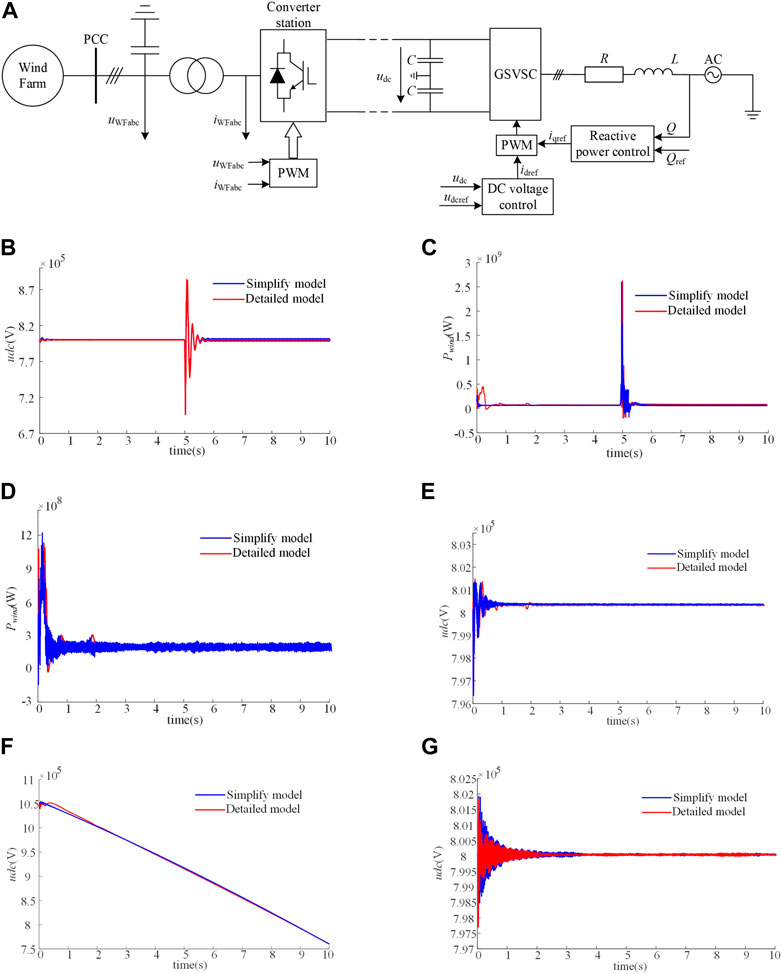
FIGURE 9. Simplified equivalent wind farm grid integration Analysis based on MMC-HVDC. (A) is a simplified equivalent wind farm grid-connected structure diagram based on MMC-HVDC, which provides a model basis for subsequent simulation analysis. (B,C) DC voltage and output power waveforms of the wind farm when a three-phase ground fault occurs in the AC circuit of the wind farm. (D,E) show the output power and DC voltage waveforms of the wind farm when a three-phase ground fault occurs at the grid-connected end. (F,G) DC voltage waveform on the wind farm side and the grid-connected side when a fault occurs on the DC transmission line. The aforementioned waveforms compare the dynamic characteristics of the simplified equivalent model and the detailed model under various operating conditions and verify the validity of the simplified equivalent model.

1) The AC circuit of the wind farm has three-phase ground fault in 4.99–5.01 s The DC voltage and output active power of wind farm are shown in Figures 9B,C.

Set the wind farm three-phase power bus at 4.99–5.01s for a three-phase symmetrical ground fault, fault duration of 0.02s.

Figure 9B shows that when a fault occurs, the voltage on the DC side drops due to voltage sag of the AC bus, which is adjusted by VSC constant DC voltage control after the fault is removed and the voltage is returned to the rated value of 800 kv.

Figure 9C shows that when a fault occurs, the active power output waveform of the wind farm side has a large oscillation, which gradually returns to normal after the fault is removed.

As shown in Figures 9B,C, the dynamic characteristics of the DC side voltage and the output power of the wind farm are similar under the same operating conditions of the simplified model and the detailed model.

2) The three-phase grounding fault which occurred in 4.99–5.01 s of the main AC network at the grid-connected end. The waveform of active power and DC voltage on the wind farm side is shown in Figures 9D,E.

This part of the simulation will set the output three-phase electric power voltage bus bar on the grid side occurs three-phase grounding short-circuit fault, assuming that the system occurs three-phase symmetrical grounding fault during 4.99–5.01 s, and the fault duration is 0.02 s.

As shown in Figures 9D,E, due to the fault isolation characteristics of the VSC-HVDC system, the normal operation of the wind farm is not affected by the fault at the converter station at the receiving end, the active power output of the converter station at the sending end is normal, and the DC side voltage is also stable at the rated value. At this point, it can be seen that the simplified wind farm model and the detailed wind farm model in the steady-state operation performance are not much different; the output of the two active power and DC voltage is similar, and this verifies the effectiveness of wind farm simplification in steady-state operation.

3) DC transmission circuit in 5–10 s, the wind farm-side DC voltage, and grid-side DC voltage waveform are shown in Figures 9F,G.

In this part, when the simulation is set up for 5 s, a DC transmission circuit will break down, and it will continue until the end of the simulation.

As shown in Figures 9F,G, the DC voltage of the sending-end converter station continues to drop after the DC transmission circuit breaks down, while the DC voltage of the receiving-end converter station remains about 800 kv due to the constant DC voltage control. In addition, the DC voltage of the simplified model is close to that of the detailed model, and the voltage fluctuation of the simplified model is a little larger at the receiving end, but the stability is the same as that of the detailed model.

4) Single-pole DC grounding fault occurred in 5–10 s; DC side voltage and wind farm side voltage waveform are shown in Figures 10A,B.

FIGURE 10

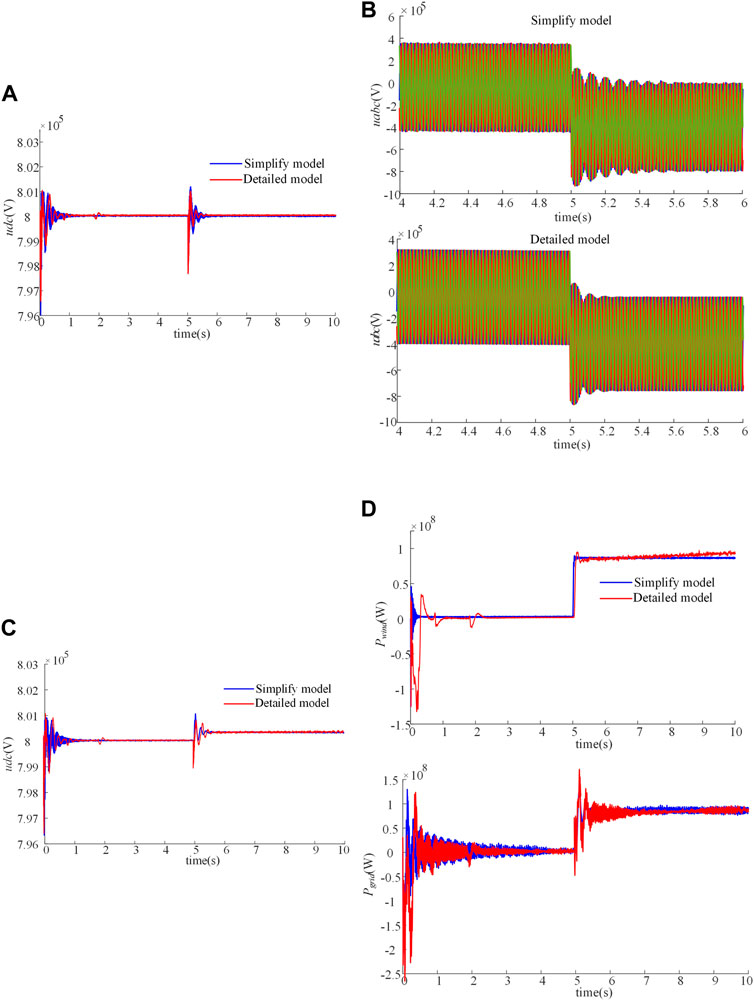
FIGURE 10. Supplementary fault analysis of wind farm grid connection. (A) (B) Waveform of DC-side voltage and wind farm-side voltage during a single-pole DC ground fault (C,D) show the waveforms of DC voltage, wind farm output power, and grid-connected power under the step change of wind speed. The aforementioned section considers the three-phase voltage comparison and wind speed variation of the wind farm as a supplement to the simulation analysis and compares the dynamic characteristics of the simplified equivalent model with the detailed model under various operating conditions to further verify the effectiveness of the simplified equivalent strategy in this paper.

In this part of the simulation, one pole of the DC transmission circuit grounding fault, assuming that 5-s fault occurs, and the same continued until the end of the simulation.

Figures 10A,B shows that the DC voltage dips following a single-pole ground fault in the DC transmission circuit. After fault removal by the constant DC voltage regulation back to 800 kv and maintains stability. The DC component of the AC voltage on the wind farm side decreases, and the overall voltage drops and does not return to the state before the fault, but the AC current remains unchanged.

As shown in Figures 10A,B, the transient characteristics of the simplified model are basically the same as those of the detailed model on the DC side, while on the AC side of the wind farm, the fluctuation time of the simplified model is slightly longer; this may be due to the deviation of the inertial parameters of the simplified model, but the dynamic characteristics of the two models are consistent with the steady-state amplitude.

5) The wind speed of the wind farm changes step-by-step at 5 s. The waveform of DC voltage, active power of the wind farm, and power grid are shown in Figures 10C,D.

This part of the simulation settings is 0–5 s when the wind farm at wind speed 5 at the start, 5 s after the sudden change to 10, to maintain until the end of the simulation.

As can be seen in Figures 10C,D, the output active power of the wind farm increases and the DC voltage increases with the sudden change in wind speed, keeping a new stable operating value.

Comparing the simplified wind farm model with the detailed wind farm model, we can find that under the condition of the step change of wind speed, the observations of both models transition from the same steady state value to another one, and the dynamic characteristics of the transition process are basically the same.

The simulation time of the aforementioned conditions is shown in Table 5, in which the simulation time is the time consumed when the model runs for 10 s. In order to avoid chance, the time-consumption of simulation under all working conditions is calculated. It can be seen that compared with the detailed wind farm model, the simulation time of the simplified wind farm model is relatively less. For large-scale wind farms, the simplified equivalent of wind farm can greatly reduce the time-consumption of grid-connected transient simulation and save the calculation cost.

TABLE 5

TABLE 5. Comparison of the simulation time.

The model of the simplified wind farm connected to the VSC-HVDC transmission system works well under the aforementioned five conditions, and its dynamic wave characteristics are consistent with the detailed model of the wind farm. Therefore, the simplified wind farm can replace the detailed wind farm model to complete the wind farm grid-connected transient simulation research under the HVDC control module and provide a platform for the parameter design of the subsequent protection module.

6 Conclusion

In order to realize the rapid simulation and grid-connected transient research of large-scale wind farms, this paper conducts a two-layer simplified modeling for the wind farm and analyzes the mathematical model of the wind power system in the lower layer. The simplified model of the wind turbine is based on the equivalent transfer function; the upper layer deduces the parameter calculation and the equivalent method of the equivalent wind farm in detail and uses the improved capacity weighting method to calculate the equivalent value of the wind farm. On this basis, combined with the simplified model of the lower wind turbine, the wind farms are grouped according to the wind farm connection structure, and the equivalent parameters are calculated respectively, and the equivalent simplified modeling method of the wind farm is proposed. Taking the Rudong VSC-HVDC-based wind farm in China as an example, the following conclusions are drawn through simulation analysis:

• By analyzing the electromagnetic time-scale dynamic response of the wind power system and taking into account part of the power loss, the simplified model of the wind turbine based on the equivalent transfer function proposed in this paper can effectively replace the detailed model of the wind turbine and effectively reflect the dynamic characteristics of the wind turbine under various operating conditions. The simplified modeling of wind turbines is realized.

• On the basis of simplified modeling of wind turbines, this paper presents a simplified modeling method of large-scale wind farms based on aggregate equivalence, which can not only accurately reflect the dynamic characteristics of the wind farm but, at the same time, the complexity of large-scale wind farm model is effectively reduced and the simulation time is reduced; and the comparison and analysis of the grid-connected transient of the MMC-HVDC simulation model connected the wind farm and the detailed wind farm are carried out; the effectiveness of the simplified wind farm in practical application is verified.

It should be pointed out that the simplified aggregation modeling of wind farms in this paper is mainly used for the transient research of large-scale wind farms connected to the grid, that is, to study the dynamic characteristics of the wind farm model. To enhance the system stability, the dynamic characteristic analysis of the energy storage system, its coupling mechanism with the wind farm dynamics, and a reasonable simplification strategy need further research, which will be our next research direction.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

RD conducted the simulation, wrote the original manuscript, and supported the research financially. CY, RM, HY, JJ, and QS reviewed and corrected the manuscript. All authors read and agreed to the published version of the manuscript.

Funding

This study received funding from the Science and Technology Program of Jiangsu Frontier Electric Technology Co., Ltd. (No. KJ202112). The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article manuscript, or the decision to submit it for publication.

Acknowledgments

All authors acknowledge the Jiangsu Branch Companies from China Three Gorges Renewables (Group) Co., Ltd., and CGN New Energy Holdings Co., Ltd., for providing data of wind turbines for this research.

Conflict of interest

RD, CY, RM, HY, and JJ were employed by Jiangsu Frontier Electric Technology Co., Ltd.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ancuti, M. C., Musuroi, S., Sorandaru, C., Dordescu, M., and Erdodi, G. M. (2020). Wind turbines optimal operation at time variable wind speeds. Appl. Sci. (Basel). 10 (12), 4232. doi:10.3390/app10124232

CrossRef Full Text | Google Scholar

Chen, Y. J., Yang, B., Han, Y. M., He, T. Y., He, P., Meng, X., et al. (2022). Optimal Adaptive inertial droop control-based power system frequency regulation via wind farms. Front. Energy Res. 9. doi:10.3389/fenrg.2021.819398

CrossRef Full Text | Google Scholar

Geng, H., and Xu, D. (2011). Stability analysis and improvements for variable-speed Multipole permanent magnet synchronous generator-based wind energy conversion system. IEEE Trans. Sustain. Energy 2 (4), 459–467. doi:10.1109/TSTE.2011.2146285

CrossRef Full Text | Google Scholar

Huang, P. H., E1 Moursi, M. S., Xiao, W., and Kirtley, J. L. (2015). Subsynchronous Resonance Mitigation for series-Compensated DFIG-based wind farm by using two-degree-of-Freedom control strategy. IEEE Trans. Power Syst. 30 (3), 1442–1454. doi:10.1109/TPWRS.2014.2348175

CrossRef Full Text | Google Scholar

Inés, S., Miguel, M., Javier, M., Francisco, J. R., and Susel, F. (2018). Reconfiguration algorithm to reduce power losses in offshore HVDC transmission lines. IEEE Trans. Power Electron. 33 (4), 3034–3043. doi:10.1109/TPEL.2017.2709259

CrossRef Full Text | Google Scholar

Kim, D. E., and Sharkawi, M. A. (2015). Dynamic equivalent model of wind power plant using an aggregation Technique. IEEE Trans. Energy Convers. 30 (4), 1639–1649. doi:10.1109/TEC.2015.2470531

CrossRef Full Text | Google Scholar

Li, C. P., Zhang, Z. S., Li, J. H., Ma, Y. B., and Zou, J. J. (2021). Design of control strategy and effect evaluation for Primary frequency regulation of wind storage system. Front. Energy Res. 9. doi:10.3389/fenrg.2021.739439

CrossRef Full Text | Google Scholar

Linash, K., Bikash, P., Robin, G., and Kevin, D. (2018). Stability analysis of a PMSG-based large offshore wind farm connected to a VSC-HVDC. IEEE Trans. Energy Convers. 32 (3), 1166–1176. doi:10.1109/TEC.2017.2705801

CrossRef Full Text | Google Scholar

Liu, J. L., Tang, F., Zhao, J. B., Liu, D. C., and Kamwa, I. (2020). Coherency Identification for wind-Integrated power system using virtual synchronous motion equation. IEEE Trans. Power Syst. 35 (4), 2619–2630. doi:10.1109/TPWRS.2020.2968294

CrossRef Full Text | Google Scholar

Miao, F., Shi, H., and Zhang, X. (2015). Modelling of wind turbines coupled in multi-domain and dynamic response analysis. Proc. CSEE 35 (7), 1704–1712. doi:10.13334/j.0258-8013.pcsee.2015.07.019

CrossRef Full Text | Google Scholar

Ren, B., Sun, R., Li, Q., Gan, D., Zhou, Q., and Wang, C. (2022). Equivalent modeling and small-signal stability analysis on PMSG-based large-scale wind farm connected to power system via VSC-HVDC. Electr. Power Autom. Equip. 42 (5), 142–152. doi:10.16081/j.epae.202203023

CrossRef Full Text | Google Scholar

Rosyadi, M., Umemura, A., Takahashi, R., and Tamura, J. (2022). Detailed and Average models of a grid-connected MMC-controlled permanent magnet wind turbine generator. Appl. Sci. (Basel). 12 (3), 1619. doi:10.3390/app12031619

CrossRef Full Text | Google Scholar

Singarao, V. Y., and Rao, V. S. (2016). Frequency responsive services by wind generation resources in United States. Renew. Sustain. Energy Rev. 55, 1097–1108. doi:10.1016/j.rser.2015.11.011

CrossRef Full Text | Google Scholar

Sun, K., Yao, W., Yan, C., and Wen, J. Y. (2021). Impedance modeling and analysis of medium-frequency oscillation caused by VSC-HVDC connected to local Weak grid and DFIG-based wind farms. Front. Energy Res. 9. doi:10.3389/fenrg.2021.693903

CrossRef Full Text | Google Scholar

Vidyanandan, K. V., and Senroy, N. (2013). Primary frequency regulation by Deloaded wind turbines using variable droop. IEEE Trans. Power Syst. 28 (2), 837–846. doi:10.1109/TPWRS.2012.2208233

CrossRef Full Text | Google Scholar

Wang, H., Chen, H. F., Li, Y., and Liu, S. M. (2022). A Review of air conditioning load aggregation in Distribution networks. Front. Energy Res. 10. doi:10.3389/fenrg.2022.890899

CrossRef Full Text | Google Scholar

Xue, T., Lv, J., Wang, K., Lin, H., Wang, H., and Cai, X. (2022). Accurate impedance modeling of an offshore full-power wind turbine system and analysis of the coupling characteristics between machine- and grid-side systems. Proc. CSEE 42 (12), 4303–4319. doi:10.13334/j.0258-8013.pcsee.211122

CrossRef Full Text | Google Scholar

Zhang, L., Zhu, L., Jiang, D., Chen, N., and Zhao, D. (2016). Modelling approach and Implementation of direct-drive wind turbine. Power Syst. Technol. 40 (11), 3474–3481. doi:10.13335/j.1000-3673.pst.2016.11.029

CrossRef Full Text | Google Scholar

Zhong, C., Lv, Y. M., Zhou, Y., and Li, H. Y. (2021). An equivalent rotor speed Compensation control of PMSG-based wind turbines for frequency support in Islanded Microgrids. Front. Energy Res. 9. doi:10.3389/fenrg.2021.717327

CrossRef Full Text | Google Scholar

Zhou, Y., Zhao, L., and Lee, W. J. (2018). Robustness analysis of dynamic equivalent model of DFIG wind farm for stability study. IEEE Trans. Ind. Appl. 54 (6), 5682–5690. doi:10.1109/TIA.2018.2858738

CrossRef Full Text | Google Scholar

Zou, J., Peng, C., Xu, H., and Yan, Y. (2015). A Fuzzy clustering algorithm-based dynamic equivalent modeling method for wind farm with DFIG. IEEE Trans. Energy Convers. 30 (4), 1329–1337. doi:10.1109/TEC.2015.2431258

CrossRef Full Text | Google Scholar