Multilevel optimization of economic dispatching in active distribution network based on ADMM

With the continuous improvement of the penetration rate of renewable energy and the continuous integration of advanced network control technology and measurement equipment, the traditional distribution network is developing into an active distribution network (ADN) with the characteristics of flexible scheduling control, high user interaction, and high energy utilization. This article fully considers the economy of the overall operation of the distribution network, and proposes a hierarchical optimization economic dispatch method for active distribution networks based on the alternating direction multiplier method (ADMM). Firstly, a hierarchical optimization scheduling model of active distribution network is established with the goal of minimizing the overall operating cost of the distribution network. The alternating direction multiplier method algorithm is decomposed into upper and lower layers to solve. The upper layer is optimized with the goal of minimizing the overall operating cost of the distribution network, and the lower layer considers the distribution network. The distributed photovoltaic and energy storage units connected to the internal nodes of the network are optimized with the goal of minimizing the local energy storage operation cost and power purchase cost. The upper and lower layers, through the exchange of limited boundary information, iterate each other until the convergence conditions are met, and the optimal solution is obtained. Finally, a design example is tested to verify the effectiveness and feasibility of the proposed scheduling method.

1 Introduction

Considering the depletion of fossil energy and the serious pollution caused by traditional thermal power units, vigorously developing renewable energy has become an inevitable trend in the development of power systems. Due to the intermittent and fluctuating nature of renewable energy power generation, a large number of access to the distribution network will complicate the operation of the power system. The traditional distribution network is gradually evolving to have flexible scheduling control, high user interaction, ADN with high energy utilization characteristics (Hua et al., 2018; Li et al., 2022; Liu et al., 2022). At this time, the operating cost of the distribution network increases, and the voltage is easily exceeded. Therefore, in order to realize the coordination and efficient utilization of various distributed energy sources in the ADN, it is an urgent problem to improve the optimal scheduling method of the distribution network (Chen et al., 2017; Li et al., 2021).

Distribution network optimization scheduling methods are mainly divided into traditional centralized optimization and distributed optimization. Centralized optimization can realize the efficient operation of power system through centralized collection, processing and calculation of global information, so it is widely used. However, with the rapid development of active distribution network, the huge data acquisition and calculation process have higher and higher requirements for hardware equipment, and it is easy to cause the scheduling failure of the global system due to the excessive amount of data processed by the scheduling center. In this context, distributed optimization scheduling emerged as the times require. By decomposing and coordinating the optimization problem, the goal of global optimization of the system is achieved. It is an ideal way to achieve large-scale active distribution network optimization and scheduling (Dong et al., 2017). However, since ADN involves various costs such as power generation, energy storage and electricity consumption, its economy cannot be ignored.

At present, the use of layered methods to achieve optimal scheduling research emerges one after another. According to the different optimization objectives of each area within the distribution network (Liang et al., 2019), proposes a distributed multi-objective optimal scheduling method for ADN and uses ADMM algorithm to solve it. However, the economics of the overall operation of the distribution network is not considered. In (Zhu, Han, Yang, Xu, Sun, Li), the author proposes a distributed online optimal power flow algorithm, which can quickly coordinate the processing of distributed energy resources only by relying on the exchange of local measurement values and boundary information. However, the economy of the overall operation of the distribution network is not considered (Xie et al., 2022). Further considered the uncertainty of renewable energy output and the randomness of distribution network operation, and proposed a distributed optimization power flow algorithm based on ADMM. However, the above literatures do not fully consider the overall operating economy of the system (Zhang et al., 2021). Proposes a two-stage distributed optimization scheduling strategy with the goal of minimizing operating cost and network loss. The model was decomposed by the alternating direction multiplier method and realized by the interaction of desired information between adjacent regions. Distributed solution (Lin et al., 2022). Proposes a two-layer optimization method for microgrid groups. The upper layer optimizes and dispatches each microgrid based on the ADMM algorithm with the goal of optimizing the economy, and the lower layer optimizes the internal controllable source output of each microgrid. Reasonable distribution. But the system flow problem is not considered enough (Quan et al., 2021). Comprehensively considered the problem of complex power interaction when the active distribution network contains multiple microgrids, and proposed a two-layer distributed optimization scheduling method. Optimization (Shi and Yewen, 2022). Establishes a two-stage double-layer joint optimal scheduling model, which improved the economics of the distribution network while reducing the network loss, and used an improved particle swarm algorithm to solve the problem (Zhu et al., 2022). Establishes a comprehensive energy system dispatch model for the park with the goal of the lowest dispatch cost, and used the objective cascade method combined with the particle swarm algorithm to solve it. By building a wind-solar-storage combined power generation system, the fluctuation of wind-solar output is suppressed and the cost is reduced. The fuzzy adaptive particle swarm algorithm is used for the optimization solution. In order to improve the utilization rate of renewable energy and reduce the power interaction between the upper and lower power grids (Qi et al., 2022), proposes a two-step dynamic hierarchical scheduling strategy with the goal of having the strongest distribution network coordination ability. An economic dispatch method based on data adaptive and robust optimization is proposed to achieve the expected goals of high energy storage power and low load carrying capacity of the distribution network. However, the solution process of the above literature is more complicated and the solution speed is slow.

This article takes full account of the economy of the overall operation of ADN and the impact of the guide price on the internal safe operation parameters and the root node electricity price. With reference to the two-level optimization theory, aiming at the access of a large number of distributed photovoltaic and energy storage units in the ADN, it increases the difficulty of the overall scheduling and operation of ADN. The entire ADN level is divided into upper and lower levels for research. The upper layer optimizes with the goal of minimizing the overall operating cost. According to the guidance price related to network loss, line capacity and voltage constraints, combined with the root node price, a time-sharing price is formed to coordinate the output of various distributed energy sources, and ultimately achieve the optimal overall operating cost. Each node in the lower layer aggregates local distributed photovoltaic and energy storage units, and optimizes them to minimize the operation cost and power purchase cost of local energy storage. The upper and lower layers iterate with each other until the convergence conditions are met, and the optimal solution is obtained.

2 Hierarchical scheduling framework of active power distribution system

2.1 System structure

The structure of the ADN is shown in Figure 1. Active distribution network can realize active control and operation of various internal distributed energy resources (DER), and its ultimate goal is to actively guide and utilize distributed renewable energy (Gan et al., 2015; Wang et al., 2018).

FIGURE 1

FIGURE 1. The structure of ADN.

The schematic diagram of the hierarchical scheduling framework of the radial distribution network is shown in Figure 2. The root node is connected to the upper-level power grid, and distributed photovoltaic power generation units and distributed energy storage units can be installed under the rest of the nodes except the root node according to different needs.

FIGURE 2

FIGURE 2. Radial distribution network structure and hierarchical dispatching framework.

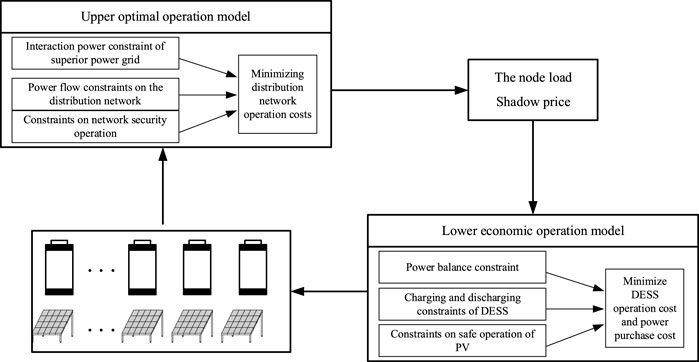
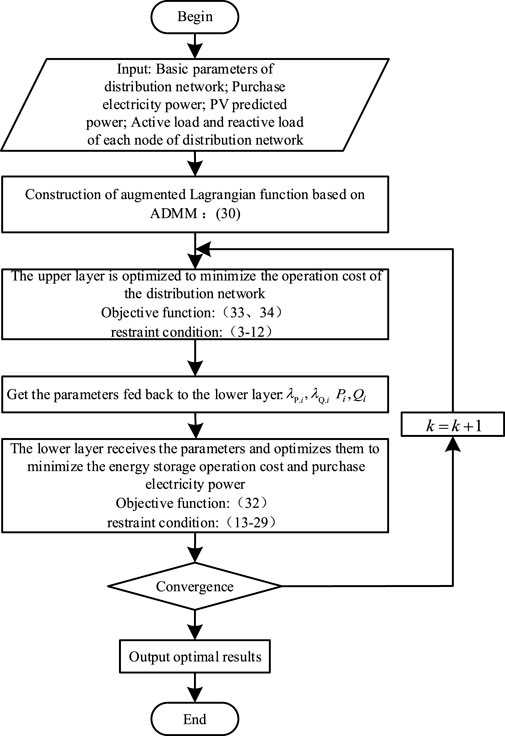
Two-level optimization is widely used in solving complex models, including two-level optimization tasks, and the two are in a nested relationship. The upper layer optimization problem can be understood as a leader, and the lower layer optimization problem belongs to the upper layer, which can be called a follower. The objective functions of the upper and lower layers are independent of constraints and decision variables. The model described in this article aims to optimize the overall operation economy of the distribution network. In the process of solving with the help of ADMM algorithm, it is divided into upper and lower models. The upper model fully considers the constraints of safe operation of the distribution network to minimize the overall operation of the distribution network. The cost is the goal, and the outflow power and guiding price of each node are solved and passed to the lower model. After receiving the solution results of the upper model, the lower model can minimize the operation cost of energy storage and power purchase under the condition of ensuring the safe operation of distributed energy storage and photovoltaics. The cost is the goal, and the output of distributed energy storage and photovoltaics at each node is obtained and fed back to the upper-layer model. The upper and lower models continue to iterate until the convergence conditions are met, and the optimal solution is finally obtained.

2.2 Scheduling strategy design based on guide price

The guide price comprehensively considers various factors, adjusts the current price, and achieves the optimal allocation of resources through artificial control. This article proposes a scheduling strategy based on guide price. When using ADMM algorithm to solve the layered hierarchical optimization scheduling model described in this article, after constructing an augmented Lagrangian function for the established objective function and safe operation constraints, at this time According to the coupling of the dual variables formed by the power flow distribution with the internal safe operation constraints of the distribution network and the electricity price of the root node, it has economic implications. When the dual variable changes, define the dual variable as the leading price. By adjusting the guiding price of each node, combined with the electricity price of the root node of the distribution network, time of use (TOU) price can be formed to guide the output of distributed energy at each node, ensure that the purchase and sale of electricity at each node can be successfully realized, and make the overall distribution network in safe, efficient and economical operation. Under the state, the coordinated management of each node in the distribution network is realized, and finally the effect of distributed control is achieved.

This article fully considers the influence of the guiding price on the internal safe operation parameters of the distribution network and the electricity price of the root node, draws on the double-layer optimization theory, and increases the difficulty of the overall scheduling operation of the distribution network for a large number of distributed photovoltaic and energy storage units connected to the ADN. To solve the problem, the entire distribution network level is divided into upper and lower layers for research. The upper layer is optimized with the goal of minimizing the overall operating cost of the distribution network. According to the guide price related to network loss, line capacity and voltage constraints, combined with the root node electricity price, TOU price is formed to coordinate the output of each distributed energy source, and finally realize the overall operation of the distribution network cost optimal. Each node in the lower layer aggregates local distributed photovoltaic and energy storage units, and optimizes with the goal of minimizing the local energy storage operation cost and power purchase cost. The upper and lower layers are iterated with each other until the convergence conditions are met, and the optimal solution is obtained.

3 Hierarchical optimization scheduling model

The distributed photovoltaic and energy storage units are connected to the internal nodes of the active distribution network, and the optimal scheduling model of the economic operation of the distribution network is established with the goal of minimizing the overall operating cost of the distribution network.

3.1 Objective function

The objective function of ADN economic operation optimization scheduling is:

$f={\displaystyle \sum }_{p=1}^n{C}_{b,p}+{\pi }_P\left({\displaystyle \sum }_{i=1}^m{P}_i+P_{\text{loss}}\right)+{\pi }_Q\left({\displaystyle \sum }_{i=1}^m{Q}_i+Q_{\text{loss}}\right),(1)$

$C_b=k\left(P_{dis}+P_{ch}\right),(2)$

where, $C_b$ is the operating cost of battery energy storage device; k is the operating cost coefficient of energy storage; $P_{dis}$, $P_{ch}$ is the charging and discharging power of energy storage unit respectively; n is the sum of distributed energy storage access nodes; m is the sum of the remaining nodes except the root node; $P_i$, $Q_i$ is the active and reactive power flowing out from the remaining nodes except the root node $P_{\text{loss}}$, $Q_{\text{loss}}$ is the active and reactive network loss inside the distribution network respectively; ${\pi }_{\mathrm{P}}$, ${\pi }_{\mathrm{Q}}$ is the unit active and reactive power bought from outside the distribution network respectively price.

3.2 Constraint condition

The constraints of the optimal scheduling model established in this article mainly include the following aspects:

3.2.1 Upper-level constraints

(1) Branch power flow constraints: All lines in the radial distribution network must meet the system power flow constraints under the safe and stable operation of the distribution network.

$P_{ij}\left(t\right)=P_j\left(t\right)+{\displaystyle \sum }_{h=1}^n\left(r_{jh}{I}_{jh}\left(t\right)+P_{jh}\left(t\right)\right),(3)$

$Q_{ij}\left(t\right)=Q_j\left(t\right)+{\displaystyle \sum }_{h=1}^n\left(x_{jh}{I}_{jh}\left(t\right)+Q_{jh}\left(t\right)\right),(4)$

$V_i\left(t\right)-V_j\left(t\right)=2\left(P_{ij}\left(t\right)r_{ij}+Q_{ij}\left(t\right)x_{ij}\right)+I_{ij}\left(t\right)\left(r_{ij}^2+x_{ij}^2\right),(5)$

$I_{ij}\left(t\right)=\frac{P_{ij}^2\left(t\right)+Q_{ij}^2\left(t\right)}{V_i\left(t\right)}.(6)$

Since formula Eq. 6 is a non-linear equality constraint, the original DistFlow model is non-convex, making it difficult to find the global optimal solution. In order to make the model a convex optimization, the equality constraint is relaxed into an inequality constraint, as shown in formula Eq. 7. At this time, the model is converted into a second-order cone model, which becomes a typical convex optimization problem.

$I_{ij}\left(t\right)\ge \frac{P_{ij}^2\left(t\right)+Q_{ij}^2\left(t\right)}{V_i\left(t\right)},(7)$

where $P_{ij}\left(t\right)$, $Q_{ij}\left(t\right)$ are the active power and reactive power of the branch $ij$ at the beginning of time t; $V_i$ are the square of the node voltage amplitude, $I_{ij}$ are the square of the branch current; $r_{ij}$, $x_{ij}$ are the resistance and reactance of the branch $ij$ respectively.

(2) Node Voltage Constraints

$V_{\min }^2\le V_i\le V_{\max }^2,(8)$

$V_{\max }^2$, $V_{\min }^2$ is the upper and lower limits of the square of the voltage amplitude.

(3) Power Constraint of Upper-Level Grid Tie Line

In order to ensure the safe and stable operation of the distribution network, the distribution network is not allowed to send power backwards to the upper-level power grid.

$P_{01}\left(t\right)\ge 0,(9)$

$Q_{01}\left(t\right)\ge 0.(10)$

respectively $P_{01}\left(t\right)$, $Q_{01}\left(t\right)$ are the active and reactive power transmitted from the higher-level grid to the internal root node of the distribution network in time t.

(4) Node Power Constraints

The active and reactive power flowing out of each node satisfies the following expressions:

$P_i\left(t\right)=P_{L,i}\left(t\right)-P_{PV,i}\left(t\right)-P_{b,i}\left(t\right),(11)$

$Q_i\left(t\right)=Q_{L,i}\left(t\right)-Q_{PV,i}\left(t\right)-Q_{b,i}\left(t\right),(12)$

where $P_i\left(t\right)$, $Q_i\left(t\right)$ are the active and reactive power of outflow node i at time t respectively; $P_i\left(t\right)$, $Q_i\left(t\right)$ are the active and reactive load of node i at time t respectively; $P_{PV,i}\left(t\right)$, $Q_{PV,i}\left(t\right)$ are the active and reactive power output of PV inverter at node i at time t respectively; $P_{b,i}\left(t\right)$, $Q_{b,i}\left(t\right)$ are the active and reactive power output of distributed energy storage at node i at time t respectively.

3.2.2 Lower-level constraints

3.2.2.1 Distributed Photovoltaic Power Generation

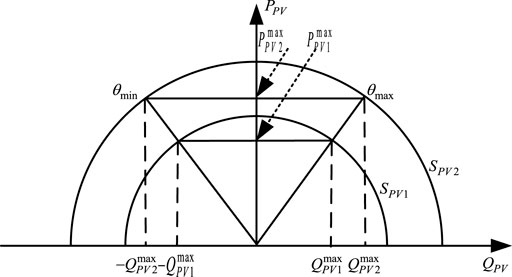
Distributed photovoltaics are connected to each node through photovoltaic inverters. The reactive power adjustment capability of photovoltaic inverters is shown in Figure 3. The capacity of photovoltaic inverters is different, and the apparent power is also different, as shown in $S_{PV1}$ and $S_{PV2}$, the allowable maximum and minimum power factor angles are ${\theta }_{\max }$ and ${\theta }_{\min }$ respectively, so that the maximum active power $P_{PV1}^{\max }$ and $P_{PV2}^{\max }$ of photovoltaic inverters with different capacities can be obtained, and then the maximum reactive power output $\pm Q_{PV1}^{\max }$ and $\pm Q_{PV2}^{\max }$ can be obtained. Under the constraint of formula Eq. 14, as the current output active power of the inverter changes, its reactive power also changes.

FIGURE 3

FIGURE 3. Schematic diagram of PV inverter regulation capability.

In this article, distributed photovoltaics are connected to designated nodes other than the root node, and the photovoltaic units of each node meet the following constraints:

$S_{PV}^t=P_{PV}^t+j{Q}_{PV}^t,(13)$

${\left(P_{PV}^t\right)}^2+{\left(Q_{PV}^t\right)}^2\le {\left(S_{PV}^{\max }\right)}^2,(14)$

$P_{PV}^t\le P_{PV}^{\text{pre}},(15)$

where $P_{\mathrm{w}}^{\text{pre}}$ is the predicted power output of the PV unit; $S_{PV}^{\max }$ is the rated apparent power of the PV unit; and $P_{PV}^t$, $Q_{PV}^t$ is the actual active and reactive power output of the PV unit at time t.

3.2.2.2 Distributed energy storage system

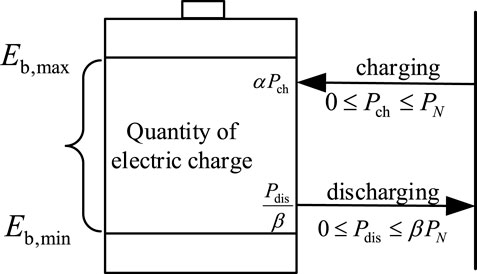
The energy storage unit is connected to each node of the distribution network in a distributed manner. Under the condition of the overall safe and stable operation of the distribution network, the distributed energy storage unit is reasonably and effectively dispatched, so as to reduce the power flow and reduce the network loss. Reduced, low-storage and high-generation arbitrage increases, and the overall operating cost of the distribution network is minimized. Figure 4 shows the distributed energy storage charging and discharging model.

$SOC\left(t+\Delta t\right)=SOC\left(t\right)+\frac{P_{ch}\left(t+\Delta t\right)\cdot \Delta t\cdot \alpha }{E_b},(16)$

$SOC\left(t+\Delta t\right)=SOC\left(t\right)-\frac{P_{dis}\left(t+\Delta t\right)\cdot \Delta t}{E_b\cdot \beta },(17)$

$SO{C}_{b,\min }\le SO{C}_b\left(t\right)\le SO{C}_{b,\max },(18)$

where SOC(t)indicates the remaining power level at time t respectively; EESS indicates the rated capacity of energy storage; $P_c\left(t+\Delta t\right)$, $P_{\text{dis}}\left(t+\Delta t\right)$ are the magnitude of charging and discharging power of DESS at the time $t+\Delta t$ respectively; $\Delta t$ indicates the sampling interval; this article is 1h; $\alpha$, $\beta$ are the charging and discharging efficiency of energy storage respectively.

FIGURE 4

FIGURE 4. DESS charging and discharging model.

The following constraints are met during the operation of DESS:

①The power constraints of DESS

The amount of energy stored at each moment does not exceed the upper and lower limits.

$E_{b,low}\le E_b\left(t\right)\le E_{b,high},(19)$

$E_b\left(t\right)=E_b\left(t-1\right)-\frac{P_{dis}}{\beta }\Delta t+P_{ch}\alpha \Delta t,(20)$

where E_b,low, E_b,high are the upper limit and the lower limit of the stored energy, respectively, E_b(t) is the stored energy at time t.

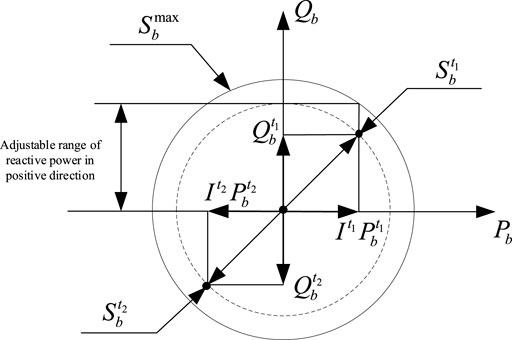
②The power and capacity constraints of DESS

Figure 5 shows the active and reactive capacity diagram of distributed energy storage. In the figure, $S_b^{t_1}$ is the apparent power of distributed energy storage at t1; $P_b^{t_1}$ is the active output for distributed energy storage at t1; $Q_b^{t_1}$ is the reactive power; $S_b^{\mathit{max}}$ is the maximum apparent power.

$S_b^t=P_b^t+j{Q}_b^t,(21)$

${\left(P_b^t\right)}^2+{\left(Q_b^t\right)}^2\le {\left(S_b^{\max }\right)}^2,(22)$

$\left|P_b^t\right|\le P_b^{\max },(23)$

$P_b^t=P_{dis}^t-P_{ch}^t,(24)$

$P_{dis}^t\ge 0,(25)$

$P_{ch}^t\ge 0.(26)$

$P_b$, $Q_b$ is the actual output of the battery energy storage unit; Respectively, $P_{dis}$, $P_{ch}$ is the discharge power and the charging power of the energy storage battery; When the operating cost coefficient of the energy storage battery is greater than 0 and the charging and discharging efficiency is less than 1, and when the optimization power flow problem is optimal, at least one of $P_{dis}$, $P_{ch}$ is equal to 0, which meets the actual operating conditions of the battery energy storage.

FIGURE 5

FIGURE 5. Active and reactive capacity diagram of DESS.

4 Distributed optimization solution based on ADMM

The hierarchical optimization scheduling model of the distribution network established above can be solved by decomposing the upper and lower layers with the help of the ADMM algorithm. The upper layer is optimized with the goal of minimizing the overall operating cost of the distribution network, and each node in the lower layer aggregates local photovoltaic power generation and energy storage. Optimizing with the goal of minimizing local energy storage operating costs and electricity purchase costs. The upper and lower layers are iterated with each other until the convergence conditions are met, and the optimal solution is obtained.

4.1 Solving process

There are many methods for solving distributed optimization problems. ADMM algorithm has decomposability and good convergence, and has been widely used in many different disciplines. It divides the original problem into several sub-problems by constructing an augmented Lagrangian function, adopts asynchronous iteration between sub-problems, and updates the corresponding dual variables, and finally achieves common convergence to solve the original problem (Wang et al., 2019; Chen et al., 2022).

According to the basic theoretical support of the ADMM algorithm, the augmented Lagrangian function of the objective function established in Section 2.1 is first constructed:

$\begin{array}{l}L={\displaystyle \sum }_{p=1}^n{C}_{b,p}+{\pi }_{\mathrm{P}}\left({\displaystyle \sum }_{i=1}^m{P}_i+P_{\text{loss}}\right)+{\pi }_{\mathrm{Q}}\left({\displaystyle \sum }_{i=1}^m{Q}_i+Q_{\text{loss}}\right)\\ +{\displaystyle \sum }_{i=1}^m\left\{{\lambda }_{\mathrm{P}.i}\left[P_i-P_{\mathrm{L}.i}+{\displaystyle \sum }_{j=1}^u{P}_{\text{pv}.j}+{\displaystyle \sum }_{z=1}^w\left(P_{\mathrm{d}.z}-P_{\mathrm{c}.z}\right)\right]+\frac{{\alpha }_i}{2}{‖P_i-P_{\mathrm{L}.i}+{\displaystyle \sum }_{j=1}^u{P}_{\text{pv}.j}+{\displaystyle \sum }_{z=1}^w\left(P_{\mathrm{d}.z}-P_{\mathrm{c}.z}\right)‖}^2\right\}\\ +{\displaystyle \sum }_{i=1}^m\left\{{\lambda }_{\mathrm{Q}.i}\left[Q_i-Q_{\mathrm{L}.i}+{\displaystyle \sum }_{j=1}^u{Q}_{\text{pv}.j}+{\displaystyle \sum }_{z=1}^w{Q}_{\mathrm{b}.z}\right]+\frac{{\beta }_i}{2}{‖Q_i-Q_{\mathrm{L}.i}+{\displaystyle \sum }_{j=1}^u{Q}_{\text{pv}.j}+{\displaystyle \sum }_{z=1}^w{Q}_{\mathrm{b}.z}‖}^2\right\},\end{array}(27)$

Therefore, the optimal scheduling model proposed in Section 2 can be equivalent to the following problems: the active and reactive power flowing out of each node, the active and reactive power of the photovoltaic power generation unit, the charging and discharging power of the energy storage unit and the actual reactive power output and The dual variables are all unknown quantities, so as long as the dual variables reach the maximum value under the constraints, the remaining unknown quantities can reach the minimum value.

$\underset{\left\{{\lambda }_{\mathrm{P}.i},{\lambda }_{\mathrm{Q}.i}\right\}}{\text{Max}}\underset{\left\{P_i,Q_i,P_{\text{pv}.j},Q_{\text{pv}.j},P_{\mathrm{d}.z},P_{\mathrm{c}.z},Q_{\mathrm{b}.z}\right\}}{\text{Min}}L\left(P_i,Q_i,P_{\text{pv}.j},Q_{\text{pv}.j},P_{\mathrm{d}.z},P_{\mathrm{c}.z},Q_{\mathrm{b}.z},{\lambda }_{\mathrm{P}.i},{\lambda }_{\mathrm{Q}.i}\right).(28)$

Constraints are shown in 2.2.1.

For the convenience and high efficiency of solving, firstly, the Lagrange function is decomposed, so that the solution of the above-mentioned optimal dispatching model is divided into upper and lower layers. Each node in the lower layer aggregates the local photovoltaic power generation and energy storage, and optimizes with the goal of minimizing the local energy storage operation cost and power purchase cost at the given electricity price π_P, π_Q of the power grid and the guide pricesλ_P.i, λ_Q.i, P_i, Q_i obtained by the last optimization iteration of the active distribution dispatching center:

$\begin{array}{l}\underset{\left\{P_{\text{pv}.j},Q_{\text{pv}.j},P_{\mathrm{d}.z},P_{\mathrm{c}.z},Q_{\mathrm{b}.z}\right\}}{\text{Min}}\frac{{\alpha }_i}{2}{\displaystyle \sum }_{j=1}^u{P}_{\text{pv}.j}^2+\frac{{\alpha }_i}{2}{\displaystyle \sum }_{z=1}^w\left(P_{\mathrm{d}.z}^2+P_{\mathrm{c}.z}^2\right)+\frac{{\beta }_i}{2}{\displaystyle \sum }_{j=1}^u{Q}_{\text{pv}.j}^2+\frac{{\beta }_i}{2}{\displaystyle \sum }_{z=1}^w{Q}_{\mathrm{b}.\mathrm{z}}^2\\ +{\alpha }_i{\displaystyle \sum }_{j=1}^u{P}_{\text{pv}.j}{\displaystyle \sum }_{z=1}^w\left(P_{\mathrm{d}.z}-P_{\mathrm{c}.z}\right)-{\alpha }_i{\displaystyle \sum }_{z=1}^w{P}_{\mathrm{d}.z}{\displaystyle \sum }_{z=1}^w{P}_{c.z}+{\beta }_i{\displaystyle \sum }_{j=1}^u{Q}_{\text{pv}.j}\\ +\left[{\lambda }_{\mathrm{P},i}^{\left(k-1\right)}+{\alpha }_i\left(P_i^{\left(k-1\right)}-P_{\mathrm{L}.i}\right)\right]{\displaystyle \sum }_{j=1}^u{P}_{\text{pv}.j}+\left[k_{\mathrm{b}}+{\lambda }_{\mathrm{P}.i}^{\left(k-1\right)}+{\alpha }_i\left(P_i^{\left(k-1\right)}-P_{\mathrm{L}.i}\right)\right]{\displaystyle \sum }_{z=1}^w{P}_{\mathrm{d}.z}\\ +\left[k_{\mathrm{b}}-{\lambda }_{\mathrm{P}.i}^{\left(k-1\right)}-{\alpha }_i\left(P_i^{\left(k-1\right)}-P_{\mathrm{L}.i}\right)\right]{\displaystyle \sum }_{z=1}^w{P}_{\mathrm{c}.z}+\left[{\lambda }_{\mathrm{Q}.i}^{\left(k-1\right)}+{\beta }_i\left(Q_i^{\left(k-1\right)}-Q_{\mathrm{L}.i}\right)\right]{\displaystyle \sum }_{z=1}^u{Q}_{\text{pv}.z}\\ +\left[{\lambda }_{\mathrm{Q}.i}^{\left(k-1\right)}+{\beta }_i\left(Q_i^{\left(k-1\right)}-Q_{\mathrm{L}.i}\right)\right]{\displaystyle \sum }_{z=1}^w{Q}_{\mathrm{b}.z}.\end{array}(29)$

The active distribution network dispatch center then optimizes with the goal of minimizing the overall operating cost of the distribution network according to the return of the lower-level aggregates:

$\begin{array}{l}\underset{\left\{P_i,Q_i\right\}}{\text{Min}}\left\{{\pi }_{\mathrm{P}}+{\lambda }_{\mathrm{P}.i}^{\left(k-1\right)}+{\alpha }_i\left[-P_{\mathrm{L}.i}+{\displaystyle \sum }_{j=1}^u{P}_{\text{pv}.j}^{\left(k\right)}+{\displaystyle \sum }_{z=1}^w\left(P_{\mathrm{d}.z}^{\left(k\right)}-P_{\mathrm{c}.z}^{\left(k\right)}\right)\right]\right\}{P}_i+{\pi }_{\mathrm{P}}{P}_{\text{loss}}\\ \left\{{\pi }_{\mathrm{Q}}+{\lambda }_{\mathrm{Q}.i}^{\left(k-1\right)}+{\beta }_i\left[-Q_{\mathrm{L}.i}+{\displaystyle \sum }_{j=1}^u{Q}_{\text{pv}.j}^{\left(k\right)}+{\displaystyle \sum }_{z=1}^w{Q}_{\mathrm{b}.j}^{\left(k\right)}\right]\right\}{Q}_i+{\pi }_{\mathrm{Q}}{Q}_{\text{loss}}.\end{array}(30)$

$\left\{\begin{array}{l}{\lambda }_{\mathrm{P}.i}^{\left(k\right)}={\lambda }_{\mathrm{P}.i}^{\left(k-1\right)}+{\alpha }_i\left[P_i^{\left(k\right)}-P_{\mathrm{L}.i}+{\displaystyle \sum }_{j=1}^u{P}_{\text{pv}.j}^{\left(k\right)}+{\displaystyle \sum }_{z=1}^w\left(P_{\mathrm{d}.z}^{\left(k\right)}-P_{\mathrm{c}.z}^{\left(k\right)}\right)\right],\\ {\lambda }_{\mathrm{Q}.i}^{\left(k\right)}={\lambda }_{\mathrm{Q}.i}^{\left(k-1\right)}+{\beta }_i\left[Q_i^{\left(k\right)}-Q_{\mathrm{L}.i}+{\displaystyle \sum }_{j=1}^u{Q}_{\text{pv}.j}^{\left(k\right)}+{\displaystyle \sum }_{z=1}^w{Q}_{\mathrm{b}.z}^{\left(k\right)}\right].\end{array}\right.(31)$

The optimal output of each distributed unit can be obtained through continuous iteration between the upper-layer active distribution network scheduling center and the lower-layer aggregates until the convergence conditions are met. The solution process is shown in Figure 6.

FIGURE 6

FIGURE 6. Two-layer optimization scheduling solution process.

4.2 Analysis of the influence of guide price on scheduling strategy

In the implementation process of the above method, the upper-level active distribution network dispatch center does not need to know the conventional load of each node in the distribution network, the output of distributed photovoltaic and energy storage, and the specific operating parameters, and only needs to obtain the conventional load and distributed photovoltaic and storage. The total output of energy can realize the regulation of each distributed photovoltaic and energy storage within the distribution network.

By solving the partial derivative $P_{\mathrm{L}.i}$, $Q_{\mathrm{L}.i}$ of the augmented Lagrange function constructed above, the electricity price of each node in the distribution network can be obtained as follows:

$\left\{\begin{array}{l}{\pi }_{\mathrm{P}.i}=\pi +{\lambda }_{\mathrm{P}.i},\\ {\pi }_{\mathrm{Q}.i}=\pi +{\lambda }_{\mathrm{Q}.i}.\end{array}\right.(32)$

According to formula Eq. 32, the electricity price of each node in the distribution network consists of two parts. The first part is the electricity price of the root node of the distribution network, which is given by the upper-level active distribution network dispatch center; the second part is the guide price, which is based on the distribution network. The formation of internal power flow distribution is closely related to the internal network loss and safe operation constraints of the distribution network. The change of guiding price is an adaptive dynamic change process. When the active price of the root node of the distribution network is at the peak time of the day, the characteristics of the distributed photovoltaic output and the arbitrage characteristics of the “low storage and high power generation” of the energy storage unit determine that the output of the energy storage and photovoltaic units will reach the peak of the day, or even high. Load demand for this node. At this time, the injected power of the node is negative, so the node voltage rises to the upper limit or even exceeds the limit. In order to meet the requirements of safe and stable operation inside the distribution network, the active power injection of this node must be limited. It is not difficult to find that the Lagrangian multiplier corresponding to the constraint happens to be the guide price at this time. In the designed hierarchical scheduling framework, the upper-level active distribution network scheduling center also guides the output of the lower-level distributed energy resources according to the adjustment of guide prices.

At this time, the active distribution network dispatch center makes an order dispatch to adjust the price of each node according to the guide price, and finally get the time of use price, so that the electricity purchase price of each node is lower than the root node electricity price, prompting each energy storage unit to reduce the discharge power during this period, thus effectively inhibiting the distribution network. The voltage of each internal node rises, which realizes the coordinated management of each node in the distribution network, and finally achieves the effect of layered control.

5 Case analysis

5.1 Study parameters

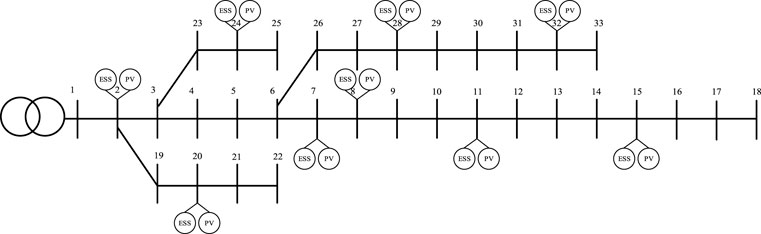
In order to verify the correctness of the distributed optimal scheduling method designed in this paper, the IEEE 33 node example system with distributed photovoltaic and energy storage units as shown in Figure 7 is simulated on WIN10 (2.9 GHz, 16 G) using Matlab 2015b simulation environment, and Cplex solver is called for solution. This example is a typical radial distribution network, with a total load of 3.175 MW + j2.3 MV·A (based on the load data of a typical day in a certain area of China), a reference capacity of 1MVA and a voltage level of 12.66 kV. As shown in Figure 7, distributed photovoltaic and energy storage units are connected to the following nodes, ${\overline{S}}_{PV}$ = 800kVA, ${\overline{S}}_{\mathrm{b}}$ = 80kVA, ${\overline{P}}_{\mathrm{b}}$ = 80kW, ${\overline{E}}_{\mathrm{b}}$ = 160 kW·h. In this example, the energy storage unit is a lithium battery, and its SOC upper and lower limits are 0.1–0.9, with a charge and discharge efficiency of 95%.

FIGURE 7

FIGURE 7. IEEE33 node calculation example system.

5.2 Analysis of simulation results

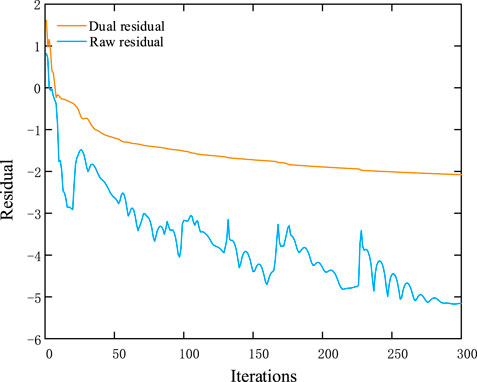
When the established hierarchical optimal scheduling model is solved by ADMM algorithm, the optimization parameters, $\alpha =6$, $\beta =6$ are the convergence of the original residual and the dual residual as shown in Figure 8. It can be seen that after 300 iterations, both of them meet the convergence requirements, which shows that the optimal power flow of the whole distribution network system has been obtained, achieving the goal of the optimal operation economy of the distribution network, and then verifying the effectiveness of the adopted algorithm, and realizing the successful transformation from centralized optimization to layered optimization.

FIGURE 8

FIGURE 8. Residual convergence process.

5.2.1 Analysis of renewable energy output

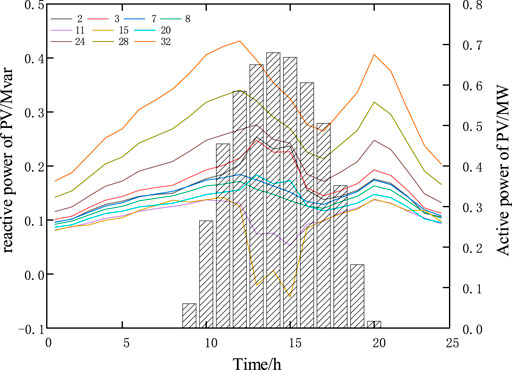
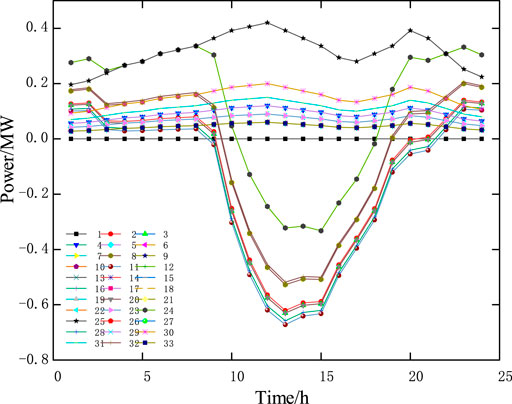
At each node of the new energy access within the distribution network, the active and reactive outputs of distributed photovoltaics and energy storage are shown in Figures 9, 10, respectively, and the comparative analysis of energy storage active output and time-of-use electricity price is shown in Figure 11. It can be seen from the figure that the output of each energy storage unit is closely related to the formulation of the time of use price. During the valley period of electricity price, the energy storage unit acts as a “load” to charge at the minimum cost, which increases the load demand during the valley period, and acts as a load during the peak period of electricity price. The discharge of the “power supply” reduces the demand for power purchases from the upper-level power grid, and ultimately reduces the overall operating cost of the distribution network while achieving load peak shaving and valley filling.

FIGURE 9

FIGURE 9. Output of each PV.

FIGURE 10

FIGURE 10. Output of each ESS.

FIGURE 11

FIGURE 11. Comparative analysis of energy storage active output and TOU price.

5.2.2 Analysis of guide price and operation constraint

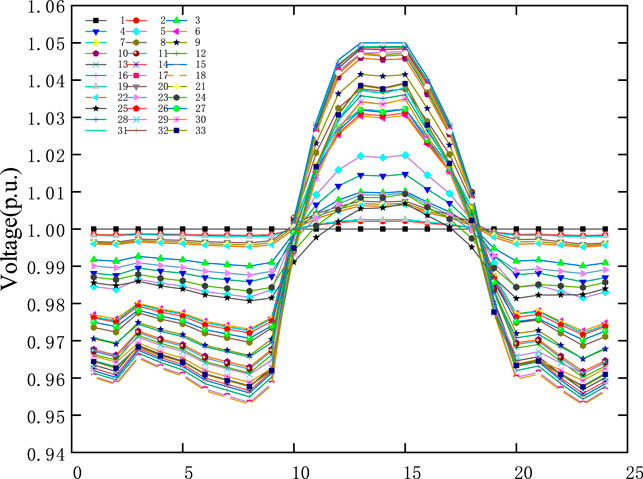
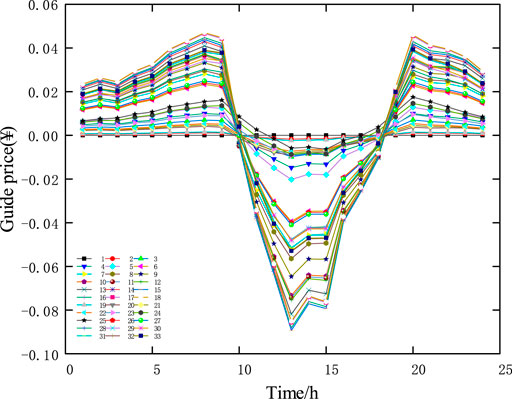
Between 10:00–13:00, the active price is at the peak of the day, and at this time the output of the energy storage and photovoltaic units both reach the peak of the day. At this time, the injected power of the nodes connected to the photovoltaic and energy storage units is negative, so that the voltage of each node increases to the upper limit. As shown in Figure 12. The active power injected into each node is shown in Figure 13. In order to limit the active power injection of these nodes, the active distribution network dispatch center makes command scheduling to adjust the active power guide price of each node, and its change trend is shown in Figure 14. It can be seen that during this period, the guide price of each node is negative, that is, the electricity purchase price of each node is lower than the root node electricity price, which prompts each energy storage unit to reduce the discharge power during this period, thereby effectively suppressing the voltage rise of each node in the distribution network and realizing the Collaborative management of nodes within the distribution network. The comparison of node voltage and guide price is shown in Figure 15.

FIGURE 12

FIGURE 12. Voltage variation of each node.

FIGURE 13

FIGURE 13. Active power injected at each node.

FIGURE 14

FIGURE 14. Guide price of each node.

FIGURE 15

FIGURE 15. Comparative analysis of node15 voltage and guide price.

6 Conclusion

This article proposes a hierarchical optimization scheduling method for active distribution network based on ADMM algorithm. Firstly, a hierarchical optimal scheduling model for active distribution network is established with the goal of minimizing the overall operating cost of the distribution network. With the help of ADMM algorithm, it is decomposed into upper and lower layers to solve, the upper layer is optimized with the goal of minimizing the overall operating cost of the distribution network, and the lower layer considers the distributed photovoltaic and energy storage units connected to the internal nodes of the distribution network, and optimizes with the goal of minimizing the local energy storage operating cost and power purchase cost. The upper and lower layers, through the exchange of limited boundary information, iterate each other until the convergence conditions are met, and the optimal solution is obtained. Moreover, the node guide price related to the internal constraints of the distribution network and the electricity price of the root node of the distribution network are independent of each other, which can be used as a collaborative optimization strategy for each node in the distribution network by the active distribution network dispatch center in the power market environment.

Data availability statement

The datasets presented in this article are not readily available because. This research is supported by the project of Jilin Provincial Science and Technology Department. The data used in this research comes from the power company and is not disclosed due to the confidentiality agreement. Requests to access the datasets should be directed to CL, bGljdWlwaW5nYWJjQDE2My5jb20=.

Author contributions

JQ: Conceptualization, Software, Investigation, Writing—original draft. DM: Conceptualization, Methodology, Writing—review and editing. CL: Writing—review and editing, Validation. YP: Investigation, Writing—original draft. XZ: Data curation. JL: Data curation.

Funding

This work was supported by Joint Foundation of Natural Science Foundation of Jilin Province (No. YDZJ202101ZYTS152).

Conflict of interest

JQ was employed by the company of Inner Mongolia Power Group Co., Ltd., Alxa Electirc Power Supply Company. DM State Grid Jibei Power Company, Zhangjiakou Power Supply Company.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chen, Jiandian, Hou, Zufeng, Zhao, Ruifeng, Bo, Li, Wang, Chao, and Lin, Guihui (2022). Self-optimizing economic dispatch based on active distribution system with multi-microgrid access. Electr. Meas. Instrum., 1–8. http://kns.cnki.net/kcms/detail/23.1202.TH.20211213.1654.006.html.

Google Scholar

Chen, Qi, Wang, Keyou, Li, Guojie, Han, Bei, Xu, Shaojun, and Zechen, Wei (2017). Hierarchical and distributed optimal dispatch of AC/DC hybrid active distribution network. J. CSEE 37 (07), 1909–1918. doi:10.13334/j.0258-8013.pcsee.160266

CrossRef Full Text | Google Scholar

Dong, Lei, Gong, Chengyao, Chen, Naishi, and Pu, Tianjiao (2017). Distributed multi-objective optimal scheduling of active distribution network based on alternating direction multiplier method. Electr. Power Constr. 38 (04), 41–49. doi:10.3969/j.issn.1000-7229.2017.04.006

CrossRef Full Text | Google Scholar

Gan, L., Li, N., Topcu, U., et al. (2015). Exact convex relaxation of optimal power flow in radial networks[J]. IEEE. 2015 (1). doi:10.1109/TAC.2014.2332712

CrossRef Full Text | Google Scholar

Hua, Liangliang, Huang, Wei, Ge, Liangjun, and Liu, Lifu (2018). Bi-level optimal dispatching model of active distribution network considering demand response. Electr. Power Constr. 39 (09), 112–119. doi:10.3969/j.issn.1000-7229.2018.09.014

CrossRef Full Text | Google Scholar

Li, Cuiping, Dong, Zhemin, Li, Junhui, Li, Hongjun, Zhou, Hengyu, and Jin, Qiang (2021). Optimal control strategy of distributed energy storage cluster to improve the new energy consumption capacity of distribution network. Power Syst. Autom. 45 (23), 76–83. doi:10.7500/AEPS20210224004

CrossRef Full Text | Google Scholar

Li, Jingqi, Wang, Dan, Fan, Hua, Yang, Dongjun, Fang, Shangcun, and Sang, Zixia (2022). Hierarchical optimal control method of active distribution network with mobile energy storage. Power Syst. Autom. 46 (10), 189–198. doi:10.7500/AEPS20211008005

CrossRef Full Text | Google Scholar

Liang, Junwen, Lin, Shunjiang, Liu, Mingbo, Song, Yunong, Fan, Guansheng, He, Sen, et al. (2019). Distributed robust optimal scheduling method for active distribution network. Power Grid Technol. 43 (04), 1336–1344. doi:10.13335/j.1000-3673.pst.2018.1375

CrossRef Full Text | Google Scholar

Lin, Yongjun, Xin, Chen, Yang, Kai, Zhou, Shanshan, Bai, Qingfei, and Jiang, Hao (2022). Two-level distributed optimal scheduling of active distribution network with multiple microgrids. J. Syst. Simul. 12. doi:10.16182/j.issn1004731x.joss.21-0573

CrossRef Full Text | Google Scholar

Liu, Rui, Wu, Kuihua, Liang, Feng, Liang, Rong, Wang, Xian, and Yang, Shenquan (2022). Coordinated optimal voltage control of active distribution network with high permeability distributed photovoltaic. J. Sol. Energy 43 (02), 189–197. doi:10.19912/J.0254-0000

CrossRef Full Text | Google Scholar

Qi, Penghui, Hongbo, Wei, Jiang, Xiongfeng, Cao, Wei, Ye, Guinan, and He, Yini (2022). Economic dispatch method of active distribution network based on data adaptive robust optimization. Electr. Meas. Instrum., 1–8. https://kns.cnki.net/kcms/detail/23.1202.TH.20220602.1850.011.html.

Google Scholar

Quan, Ran, Jin, Guobin, Chen, Qing, Li, Guoqing, Pan, Di, and Shi, Chao (2021). Optimal dispatch of DC distribution network with interaction between source network and load storage. Power Syst. acta automatica sinica 33 (02), 41–50. doi:10.19635/j.cnki.csu-epsa.000507

CrossRef Full Text | Google Scholar

Shi, Zhenli, and Yewen, Wei (2022). Multi-objective optimal scheduling of active distribution network based on particle swarm optimization. Electron. Sci. Technol. 1-8. doi:10.16180/j.cnki.issn1007-7820.2022.09.002

CrossRef Full Text | Google Scholar

Wang, Hao, Qian, Ai, Wu, Junhong, Xie, Yinzhe, and Zhou, Xiaoqian (2018). Two-level distributed scheduling method of microgrid group based on alternating direction multiplier method. Power Grid Technol. 42 (06), 1718–1727. doi:10.13335/j.1000-3673.pst.2017.2939

CrossRef Full Text | Google Scholar

Wang, Yin, Ma, Qinfeng, Ouyang, Kefeng, and Zhou, Chuanmei (2019). Economic dispatch method of embedded network loss based on DistFlow power flow model. Comput. Technol. Automation 38 (04), 56–59. doi:10.16339/j.cnki.jsjsyzdh.201904011

CrossRef Full Text | Google Scholar

Xie, Kaijun, Liu, Mingbo, Lu, Wentian, Shen, Z., and Wu, J. (2022). Measurement-based prediction-correction online distributed optimal power flow algorithm for multi-phase active distribution networks. J. Clean. Prod. 362, 131935. doi:10.1016/j.jclepro.2022.131935

CrossRef Full Text | Google Scholar

Zhang, Jin, Hu, Cungang, and Tao, Rui (2021). Two-stage distributed optimal scheduling strategy for active distribution network based on alternating direction multiplier method. China Electr. Power 54 (05), 91–100. doi:10.11930/j.issn.1004-9649.201904021

CrossRef Full Text | Google Scholar

Zhu, Xingxu, Han, Xueshan, Yang, Ming, Xu, Yijing, Sun, Donglei, and Li, Wensheng (2021). A scalable distributed online algorithm for optimal power flow in distribution system. Int. J. Electr. Power Energy Syst., 129. doi:10.1016/j.ijepes.2020.106559

CrossRef Full Text | Google Scholar

Zhu, Ziwei, Huang, Biao, Qiu, Xinyue, and Huang, Chunhui (2022). Optimal dispatching of active distribution network based on stabilizing wind power fluctuation. J. Sol. Energy 43 (05), 90–97. doi:10.19912/J.0254-0096.tynxb.2020-0477

CrossRef Full Text | Google Scholar