- 1Changsha Power Supply Branch, State Grid Hunan Electric Power Co., Ltd, Changsha, China
- 2College of Electrical and Information Engineering, Hunan University, Changsha, China
- 3School of Educational Science, Hunan Normal University, Changsha, China
The integration of renewable power generation introduces randomness and uncertainties in power systems, and the reactive power optimization with interval uncertainty (RPOIU) problem has been constructed to acquire the voltage control strategy. However, the large amount of uncertain data and the coexistence of discrete and continuous control variables increase the difficulty of solving the RPOIU problem. This paper proposes a data-driven hybrid interval reactive power optimization based on the security limits method (SLM) and the improved particle swarm optimization (IPSO) to solve the RPOIU problem. In this method, the large amount of historical uncertain data is processed by data-driven to obtain the boundary of optimal uncertainty set. The control variable optimization is decomposed into continuous variable optimization and discrete variable optimization. The continuous variables are optimized by applying the SLM with the discrete variables fixed, and the discrete variables are optimized by the IPSO with the continuous variables fixed. The two processes are applied alternately, and the values of the control variables obtained by each method are used as the fixed variables of the other method. Based on simulations carried out for the IEEE 30-bus system with three optimization methods, we verified that the voltage control strategy obtained by the data-driven hybrid optimization could ensure that the state variable intervals satisfied the constraints. Meanwhile, the values of the real power losses obtained by the proposed method were smaller than those obtained by the SLM and IPSO. The simulation results demonstrated the effectiveness and value of the proposed method.
1 Introduction
Reactive power optimization is directly related to the security and economy of a power system. There is inherent randomness and volatility with renewable energy resources (RESs), including wind and photovoltaic power, so that the data of the RES output and the power load demand are generally uncertain in the power system. There will be voltage security problems under the effects of these uncertainties. Therefore, it is necessary to construct an uncertain reactive power optimization (URPO) strategy to realize voltage security control while handling the uncertainties. The URPO model incorporates the general reactive power flow (RPF) model with uncertain data, aiming at improving the voltage profile and reducing the loss.
Some approaches have been proposed to solve the URPO model, which is non-convex and non-linear. These approaches mainly include probabilistic programming, robust programming, and interval programming. The probabilistic approach acquires the specific probability distribution of the uncertain data, because it considers them to be random variables. This process represents the RPO model as an expectation model or chance-constrained programming model and obtains the results under a stated confidence level (Arefifar and Mohamed, 2014; Liu et al., 2016). Probabilistic programming requires a large amount of historical data, while the amount of data is generally limited, causing a bias of the empirical distribution. A data-driven modeling approach is introduced to address the issue, and the model is formulated as a two-stage problem, where the first-stage variables find the optimal control for discrete reactive power compensation equipment and the second-stage variables are adjusted to an uncertain probability distribution (Ding et al., 2018). A scenario-based two-stage stochastic optimization framework is also developed in (Saraswat et al., 2020) to minimize the total real power losses in the transmission network. To solve the URPO issue of two conflicting objective functions, the active power loss and voltage deviation are minimized simultaneously, and appropriate probability distribution functions are considered to model the stochastic behavior of wind and solar power generation with the Monte Carlo simulation (MCS) technique (Keerio et al., 2020). These probabilistic processes are quite time-consuming, and the probability distribution of uncertainties is rough due to the limited data.
In contrast, robust programming considers the uncertainties to be from various sets, such as box, cone, or ellipsoid sets, without assuming the probability distribution functions. A two-stage distributed robust optimization model for optimal operation is formulated considering wind-power-uncertainty-based data-driven methods, where the polyhedra-based linearization method is introduced to approximate the second-order cone power flow constraints with a series of linear constraints (Gao et al., 2021). To improve the computational performance, a second-order cone relaxation and decomposition algorithm is proposed to solve the multi-period reactive power optimization problem (Liu et al., 2017). The processes obtain the results with good robustness, while the accuracy of the robust programming model is low due to the linearization. Furthermore, there will be infeasible solutions sometimes because robust optimization is only applicable to convex models, while the general URPO model is non-convex.
The development of interval programming has addressed the issues of probabilistic and robust approaches. This approach expresses the uncertain data as intervals and therefore establishes the RPOIU problem in which the state variables are regarded as intervals. Notably, the control variables include both continuous (generator voltage) and discrete (transformer ratio and reactive power compensation) variables. Interval programming can ensure that the ranges of the state variables are completely confined within the security constraints. The methods for solving the RPOIU problem mainly include intelligent algorithms and mathematical processing. To solve the RPOIU model, the genetic algorithm (GA) is employed as the solution algorithm, where the reliable power flow calculation is used to judge the constraints of the model (Zhang et al., 2017). The improved genetic algorithm (IGA) is proposed to solve the problem that the simple GA is inefficient in the application of power system reactive power optimization, where the coding method, fitness function, initial population generation, and crossover and mutation strategy are modified (Chang and Zhang, 2017; Liu et al., 2022). Particle swarm optimization (PSO) is also widely applied to solve this problem (Li et al., 2017; Khan et al., 2020; Shri et al., 2021). An improved particle swarm optimization and Pareto archive algorithm are combined to solve the multi-objective reactive power optimization problem, and it outperforms the non-dominated sorting genetic algorithm II (NSGA-II) (Liu et al., 2021).
For the application of mathematical processing, the linear approximation method is formulated using the interval Taylor extension to help solve the RPOIU model (Jiang et al., 2014; Zhang et al., 2018b). In order to improve the accuracy of the approximation, the interval sequential quadratic programming method (ISQPM), which employs a second-order interval Taylor expansion, is proposed (Zhang et al., 2019). In addition, the security limits method (SLM) is defined to solve the RPOIU problem, and the model is switched to two deterministic reactive power optimization models (Zhang et al., 2018a).
It is noted again that the coexistence of discrete and continuous variables increases the difficulty of solving the RPOIU problem, and the accuracy when solving the problem by applying a single algorithm is generally low. Considering the above interval approaches, mathematical processing can deal with the continuous variables well, and intelligent algorithms are better at handling discrete variables. Therefore, the problem of mixed-variable processing can be addressed by a co-evolution method, which adopts a mathematical method to deal with continuous variables and an intelligent algorithm to deal with discrete variables to solve the RPOIU problem.
The present work establishes a hybrid interval reactive power optimization algorithm considering the uncertainty of RESs. The algorithm uses interval programming to deal with uncertainties and decomposes the control variable optimization into two subproblems: continuous variable optimization and discrete variable optimization. Since the SLM can reduce the conservation of the interval reactive power optimization algorithm and has a better performance in searching for the optimal solution than other mathematical methods, the SLM is applied for continuous variable optimization. Since the PSO has faster convergence rate and simpler processes, the improved PSO (IPSO) is applied for discrete variable optimization. There are the algorithm alternations between these processes.
The construction of the RPOIU problem is presented in Section 2, followed by the hybrid optimization of the SLM and IPSO for solving the RPOIU problem in Section 3. The simulations employed to demonstrate the performance of the proposed method are presented in Section 4. The conclusions and contributions of this paper are given in Section 5.
2 Modeling of reactive power optimization with interval uncertainty (RPOIU) based on data-driven
As mentioned above, the large amount of historical uncertain data is processed by data-driven to obtain the boundary value of the uncertainties, and the input data of the power grid associated with uncertainties can be described as intervals, including power generation
s.t.
Here
Moreover,
All the variables in the RPOIU model can be divided into state variables and control variables. The state variables include the voltage magnitudes of the load buses, bus angle, and reactive power generation. The control variables include the generator voltage, transformer ratio, and reactive power compensation. Therefore, the formulation of the RPOIU model can be simplified by expressing the vector of state variables as
where
To express the model more conveniently, the bus order of the system is adjusted. Assuming that the slack bus is denoted by index 1, the number of all system buses is n, the number of generator buses is m (including the slack bus), the number of buses with the reactive power capacitor is r, and the number of transformers is k. The generator buses are denoted by index numbers in the range from two to m, the load buses are denoted by index numbers from m+1 to n, and the load buses with the reactive power capacitor are denoted by index numbers from m+1 to m + r. Therefore, the vectors of state and control variables are expressed as
It is noted that the output of the reactive power compensator
3 Hybrid optimization for solving the RPOIU problem based on security limits method (SLM) and improved particle swarm optimization (IPSO)
The hybrid interval reactive power optimization algorithm adopts the SLM and IPSO to process the RPOIU problem alternately. The SLM is applied to deal with the continuous variables in the model to improve the efficiency and optimization effect of the model and ensure that the load voltage is not off-limit in all scenarios. The IPSO is applied to deal with the discrete variables in the model to avoid the problem that the continuous rounding of discrete quantities may lead to inaccurate or even infeasible solutions. It is noted that the power flow equations with interval uncertainties are solved by the optimizing-scenarios method (OSM) (Zhang et al., 2018c).
3.1 SLM-based continuous variable processing
The RPOIU model is solved by the SLM under the condition that the discrete variables
Since the inequality constraints (5)–(9) in the RPOIU model are all univariate, the model can be expressed as follows:
where
To obtain the maximum radii of the interval variables, a vector consisting of the maximum radii of the state variables is defined as
where
According to
Apparently, (15) represents the worst-case security bounds, while the difference between the security limit
where
Assuming that the interval ratio corresponding to
where
where
Therefore, the RPOIU model can be transformed to a deterministic RPO model through Eqs 15–18, expressed as follows:
where
3.2 IPSO-based discrete variable processing
PSO is applied to deal with the discrete variables
The position of each particle in the search space is represented as
where
where
PSO is a global optimization method with a strong global search ability. However, it cannot make full use of the feedback information in the population, resulting in a poor local optimization ability, and the optimal value in the neighborhood of the
where step is the initial step length of the local search. The relationship between the global and local optima is well balanced through the improvement of
The discrete variables are processed by a crossover operation in the IPSO, including the crossover between the particle and itself and the crossover between the particle and optimal individuals. The crossover process can be expressed as follows:
where
3.3 Hybrid optimization based on SLM and IPSO
The RPOIU problem is solved through the hybrid optimization of SLM and IPSO. The values of the continuous variables obtained by SLM are applied as fixed continuous variable values in the IPSO, and the values of the discrete variables obtained by the IPSO are applied as fixed discrete variable values in the SLM. The two methods are applied to solve the RPOIU model alternately, and the values of the control variables are interactive. The final solution of the control variables when solving the RPOIU problem is obtained when the control variable values obtained by the two methods are consistent. Because the discrete variable values obtained by the IPSO are directly used by the SLM, the values of the continuous variables are used for the termination criterion. For convenience, in the example below, when the difference of the continuous variable values between the two methods was less than 0.01, the control variables values were considered to be approximately consistent. Accordingly, the detailed procedure of the hybrid optimization based on the SLM and IPSO is described as follows. It is noted again that the intervals of the state variables are obtained by using the OSM, and they should satisfy the constraints. The flow chart of the proposed method is presented in Figure 1.
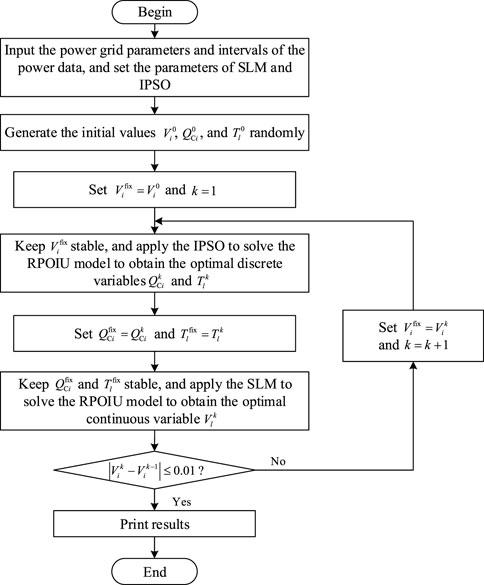
FIGURE 1. Procedure of the hybrid processing based on security limits method (SLM) and improved particle swarm optimization (IPSO) for solving the reactive power optimization with interval uncertainty (RPOIU) problem.
The steps of the proposed algorithm are as follows:
Step (1) Input the power grid parameters and intervals of the power data and set the parameters of SLM and IPSO.
Step (2) Generate the initial values
Step (3) Set
Step (4) Keep
Step (5) Set
Step (6) Keep
Step (7) Determine whether the difference between
4 Simulation results
In this section, the simulations conducted for an IEEE 30-bus system are discussed to demonstrate the effectiveness and superiority of the hybrid optimization based on the SLM and IPSO in solving the RPOIU model problem. The results obtained by the proposed method are compared with those obtained by the SLM and IPSO. All parameters in the simulations were assigned values in a per-unit system, with 100
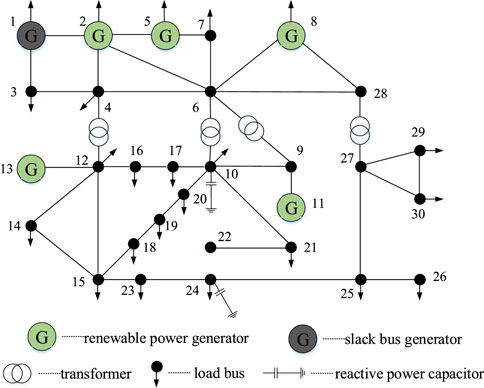
The IEEE-30 bus system included six generators (five renewable power generators), four transformers, and two capacitors. The topology of IEEE 30-bus system is shown in Figure 2. The active power generation and related variable ranges of the generators are shown in Table 1. The settings of the capacitors are shown in Table 2. The voltage magnitudes of the load buses were limited to the range of [0.95, 1.05]. The transformer ratios were limited to the range of [0.9, 1.1] with a step of 0.05. The parameters of SLM and IPSO are set as follows. The iteration precision
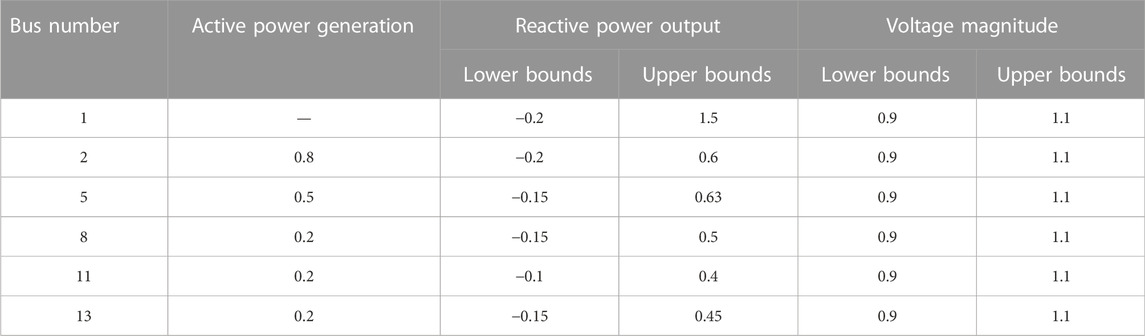
TABLE 1. Active power generation and related variable ranges of generators in IEEE 30-bus system (p.u.).
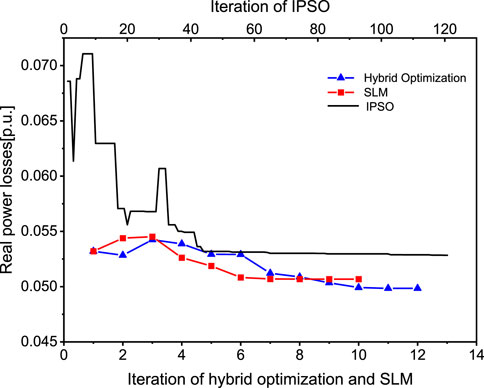
According to the settings specified in Tables 1, 2, the proposed hybrid optimization strategy based on the SLM and IPSO was used to solve the RPOIU model problem for the IEEE 30-bus system, and the results were compared with those obtained by the SLM and IPSO. The results obtained by the hybrid optimization, SLM, and IPSO for the IEEE 30-bus system are presented inFigures 3, 4. Figure 3A; Figure 4A show the voltage magnitude intervals acquired by the hybrid optimization, SLM, and IPSO. The interval bounds were all within the voltage limits. The boundary of state variable intervals obtained by the SLM was closer to the security limits than the hybrid optimization and IPSO. The intervals obtained by the hybrid optimization were close to that obtained by IPSO. Figure 3B; Figure 4B present the reactive power generation intervals acquired by the hybrid optimization, SLM, and IPSO. The interval bounds also were within the limits of the reactive power generation and the interval results obtained by the three methods were close for most of the buses. The results verified the effectiveness of the proposed method for solving the RPOIU problems. The reasons for ensuring the interval results within voltage limits or reactive power generation limits were that the hybrid optimization and SLM both used the security limits to ensure the feasibility of the control variables, and the IPSO determined the feasibility of the control variables by judging whether the state variable intervals satisfied the constraints of the RPOIU model. Figure 5 presents the iterative convergence process of the three algorithms, and the results are shown in Table 3. The hybrid optimization achieved the minimum real power loss, and the IPSO had a relatively large loss of active power compared to the other algorithms. This was because the hybrid optimization could obtain better solutions for the continuous and discrete variables, in contrast to the single optimization, which had difficulty dealing with mixed control variables. It demonstrated that the proposed method had higher accuracy than SLM and IPSO for solving RPOIU models.
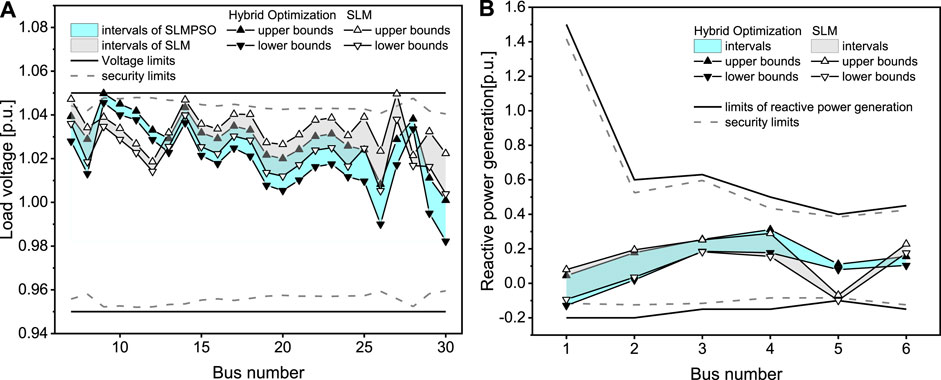
FIGURE 3. Results obtained by the hybrid optimization and SLM for the IEEE 30-bus system: (A) voltage magnitude and (B) reactive power generation.
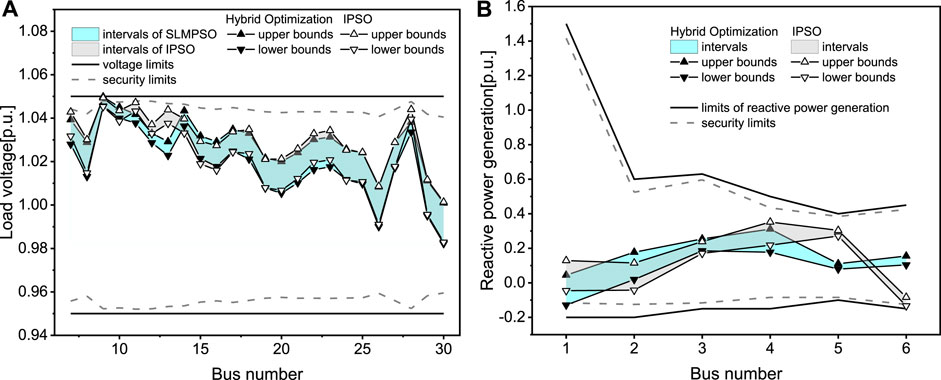
FIGURE 4. Results obtained by the hybrid optimization and IPSO for the IEEE 30-bus system: (A) voltage magnitude and (B) reactive power generation.
5 Conclusion
This paper proposed a data-driven hybrid interval reactive power optimization based on SLM and IPSO for solving the RPOIU problem to address the issue of dealing with mixed control variables. The large amount of uncertain data is expressed as intervals based on data-driven, and the control variable optimization is decomposed into continuous variable optimization and discrete variable optimization. For reducing the conservation of the interval algorithm, the SLM is applied for continuous variable optimization and the IPSO is applied for discrete variable optimization. The two processes are used to solve the RPOIU problem alternately and iteratively until the control variables optimized by the two processes are consistent.
The simulation results obtained by the proposed data-driven hybrid interval reactive power optimization for the IEEE 30-bus system were compared with those obtained by the SLM and IPSO. The proposed data-driven hybrid interval reactive power optimization acquired smaller real power losses than the SLM and IPSO, and it ensured that the interval bounds of the state variables remained within the constraints. The simulation results verified the effectiveness and advantages of the proposed method.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
DC conceptualized the study, contributed to the study methodology, and wrote the original draft. SQ contributed to the writing—review and editing, data curation and investigation. QL contributed to study methodology, data analysis, wrote the original draft and writing-review. WX contributed to software and paper revision. XL contributed to investigation and writing—original draft. YL contributed to supervision and writing—review and editing. HY contributed to the revision of the paper. NK contributed to editing of the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the science and technology project of Changsha Power Supply Branch, State Grid Hunan Electric Power Company Limited (Grant No. 00FCJS2210147), the National Natural Science Foundation of China (Grant No. 52007056), and the Natural Science Foundation of Hunan Province, China (Grant No. 2020JJ5077).
Conflict of interest
Authors DC, SQ, WX and XL were employed by the State Grid Hunan Electric Power Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The authors declare that this study received funding from State Grid Hunan Electric Power Company Limited. The funder had the following involvement in the study: Data curation, investigation, the study methodology, data analysis, and the writing-review\editing.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Arefifar, S. A., and Mohamed, Y. (2014). Probabilistic optimal reactive power planning in distribution systems with renewable resources in grid-connected and islanded modes. IEEE Trans. Ind. Electron. 61 (11), 5830–5839. doi:10.1109/tie.2014.2308144
Chang, S. Y., and Zhang, S. W. (2017). “Research on reactive power optimization algorithm of power system based on improved genetic algorithm,” in Proceedings of the International Conference on Industrial Informatics - Computing Technology, Intelligent Technology, Industrial Information Integration (ICIICII), Wuhan, China, 02-03 December 2017, 21–24.
Ding, T., Yang, Q. R., Yang, Y. H., Li, C., Bie, Z. H., and Blaabjerg, F. (2018). A data-driven stochastic reactive power optimization considering uncertainties in active distribution networks and decomposition method. IEEE Trans. Smart Grid 9 (5), 4994–5004. doi:10.1109/tsg.2017.2677481
Gao, H. J., Wang, J. Y., Liu, Y. B., Wang, L. F., and Liu, J. Y. (2021). An improved ADMM-based distributed optimal operation model of AC/DC hybrid distribution network considering wind power uncertainties. IEEE Syst. J. 15 (2), 2201–2211. doi:10.1109/jsyst.2020.2994336
Jiang, C., Zhang, Z. G., Zhang, Q. F., Han, X., Xie, H. C., and Liu, J. (2014). A new nonlinear interval programming method for uncertain problems with dependent interval variables. Eur. J. Operational Res. 238 (1), 245–253. doi:10.1016/j.ejor.2014.03.029
Keerio, M. U., Ali, A., Saleem, M., Hussain, N., and Hussain, R. (2020). “Multi-objective optimal reactive power dispatch considering probabilistic load demand along with wind and solar power integration,” in Proceedings of the International Conference on Smart Power & Internet Energy Systems (SPIES), Bangkok, Thailand, 15-18 September 2020, 502–507.
Khan, N. H., Wang, Y., Tian, D., Raja, M., Jamal, R., and Muhammad, Y. (2020). Design of fractional particle swarm optimization gravitational search algorithm for optimal reactive power dispatch problems. IEEE Access 8, 146785–146806. doi:10.1109/access.2020.3014211
Li, H., Liu, S., Lu, S., Chen, L., Yuan, X., and Huang, J. (2017). “Reactive power optimization of distribution network including photovoltaic power and SVG considering harmonic factors,” in Proceedings of the International Conference on High Voltage Engineering and Power Systems (ICHVEPS), Denpasar, Indonesia, 02-05 October 2017, 219–224.
Liu, K. Y., Jia, D. L., He, K. Y., Zhao, T. T., and Zhao, F. Z. (2016). “Research on probabilistic reactive power optimization considering the randomness of distribution network,” in Proceedings of the International Conference on Probabilistic Methods Applied to Power Systems (PMAPS), Beijing, China, 16-20 October 2016, 1–6.
Liu, S. Y., Ding, T., Bie, Z. H., Berizzi, A., and Hong, Y. (2017). “A second order cone based relaxation and decomposition algorithm for multi-period reactive power optimization considering uncertain PV integration in active distribution networks,” in Proceedings of the IEEE International Conference on Environment and Electrical Engineering, Milan, Italy, 06-09 June 2017, 1–6.
Liu, X., Zhang, P., Fang, H., and Zhou, Y. (2021). Multi-objective reactive power optimization based on improved particle swarm optimization with ε-Greedy strategy and Pareto Archive algorithm. IEEE Access 9, 65650–65659. doi:10.1109/access.2021.3075777
Liu, Y., Li, L., Li, Y., Li, M., Huang, M., Yu, H., et al. (2022). “Distributed photovoltaic cluster partition and reactive power optimization strategy based on BAS-IGA algorithm,” in Proceedings of the Asia Conference on Power and Electrical Engineering (ACPEE), Hangzhou, China, 15-17 April 2022, 2198–2203.
Saraswat, A., Ucheniya, R., and Gupta, Y. (2020). “Two-stage stochastic optimization for reactive power dispatch with wind power uncertainties,” in Proceedings of the International Conference on Computation, Automation and Knowledge Management (ICCAKM), Dubai, United Arab Emirates, 09-10 January 2020, 332–337.
Shri, S. H., Essa, M. B., and Mijbas, A. F. (2021). “Solving reactive power optimization problem using weight improved PSO algorithm,” in Proceedings of the International Conference on Electrical, Computer, Communications and Mechatronics Engineering (ICECCME), Mauritius, Mauritius, 07-08 October 2021, 1–5.
Zhang, C., Chen, H., Hua, D., Shi, K., Liu, Y., Wang, X., et al. (2018a). “Solution of interval reactive power optimization model through defining security limits,” in Proceedings of the International Conference on Power System Technology (POWERCON), Guangzhou, China, 06-08 November 2018, 1384–1389.
Zhang, C., Chen, H. Y., Liang, Z. P., Guo, M. L., Hua, D., and Ngan, H. (2018c). Reactive power optimization under interval uncertainty by the linear approximation method and its modified method. IEEE Trans. Smart Grid 9 (5), 4587–4600. doi:10.1109/tsg.2017.2664816
Zhang, C., Chen, H. Y., Ngan, H. W., Liang, Z. P., Guo, M. L., and Hua, D. (2017). Solution of reactive power optimisation including interval uncertainty using genetic algorithm. IET Gener. Transm. &. Distrib. 11 (15), 3657–3664. doi:10.1049/iet-gtd.2016.1195
Zhang, C., Chen, H. Y., Shi, K., Liang, Z. P., Mo, W. K., and Hua, D. (2019). A multi-time reactive power optimization under interval uncertainty of renewable power generation by an interval sequential quadratic programming method. IEEE Trans. Sustain. Energy 10 (3), 1086–1097. doi:10.1109/tste.2018.2860901
Keywords: renewable power generation, data-driven hybrid optimization, interval reactive power optimization, security limits method, particle swarm optimization
Citation: Chen D, Qu S, Liu Q, Xiao W, Liu X, Luo Y, Yang H and Kuang N (2023) A data-driven hybrid interval reactive power optimization based on the security limits method and improved particle swarm optimization. Front. Energy Res. 10:1086577. doi: 10.3389/fenrg.2022.1086577
Received: 01 November 2022; Accepted: 01 December 2022;
Published: 19 January 2023.
Edited by:
Xue Lyu, University of Wisconsin-Madison, United StatesReviewed by:
Dongliang Xiao, South China University of Technology, ChinaXueqian Fu, China Agricultural University, China
Copyright © 2023 Chen, Qu, Liu, Xiao, Liu, Luo, Yang and Kuang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Qian Liu, bGl1cWlhbjM2NUBobnUuZWR1LmNu
 Dawen Chen1
Dawen Chen1 Qian Liu
Qian Liu Huaizhi Yang
Huaizhi Yang