Design and assessment of a core-power controller for lithium-cooled space nuclear reactor based on the concept of fuzzy model predictive control

Thanks to its unique characteristics of high power-to-mass ratio, shallow reactivity poisoning, and quick response to reactivity control, power supply system based on lithium-cooled space nuclear reactor is preferred for various exploration missions into outer and deep space. However, due to its nature of few-people or even unmanned on-duty, an intelligent autonomous control of the reactor system, especially an accurate control of the reactor core power following the demanding power output, is of vital importance for such a space nuclear reactor. In this study, a core-power controller for a megawatt ultra-small lithium-cooled space nuclear reactor was designed based on the concept of fuzzy model predictive control (FMPC) combining model predictive control and T-S fuzzy theory. Performance of the FMPC controller was simulated and assessed with the Simulink platform for five typical operation transients including ramp, step and disturbance transient. The results show that the intelligent FMPC controller possesses an excellent load-following ability and anti-interference ability, both of which are of vital importance for space exploration missions. When compared with the classical PID controller, the FMPC controller designed in this study shows also a much better performance with smaller overshoot, lesser adjusting time and lower integral time-squared error.

1 Introduction

Over the past century, human beings have actively carried out various space explorations. Remarkable accomplishments have been achieved, which continuously expanded the boundaries of human knowledge. Many of these accomplishments going to the unknown outer and deep space are largely benefited from the successful development and application of solar cell battery or space radio-isotopic battery, which exploits the energy either from the solar irradiation (Baraskar et al., 2022) or the energy released during decay process of certain radioactive isotopes (Bennett et al., 1996) to provide the necessary power supply. In addition to continuing the deep-space exploration, the next important step will be surface explorations of planetary satellites and other-than-earth planets, among which lunar exploration projects have already been carried out by many countries or international organizations, see for instance in the reviews by Zheng et al. (2008), Ehrenfreund et al. (2012) and Marov and Slyuta (2021). Manned surface exploration of the Mars is also undergoing the process of intense discussions (McNutt et al., 2015). For surface exploration of other-than-earth planets or planetary satellites, traditional solutions of power supply based on solar cell battery or radio-isotopic battery will not be able to meet the needs due to the impact of weak solar light, extreme high or low temperature, dust storms, as well as the demand of a power supply in hundreds of kilowatts or even megawatts and a mission task cycle that can easily last more than 10 years or even decades (Akimov et al., 2012).

Thanks to its unique advantages of high power-to-mass ratio, shallow reactivity poisoning and quick response to reactivity control (IAEA, 2002), a liquid metal-cooled space nuclear reactor, which adopts a fast neutron spectrum reactor core cooled by liquid metal or liquid metal alloys, is the preferred solution to provide the necessary high-power supply also in the environment of lacking or no solar irradiation. As recently reviewed in (Song et al., 2021), worldwide 80% of the prototype designs and 100% of the actual tested space power supply systems are based on various designs of liquid metal-cooled space nuclear reactors. Thanks to its high boiling point and low density, liquid lithium has attracted more and more attentions as the coolant for space nuclear reactor from both industrial and scientific community, see for instance in (Harty and Mason, 1993; Demuth, 2003; Jin, et al., 2022) etc. However, to meet the requirements of safety, reliability, viability, and the long-life expectancy of a space exploration mission, autonomous intelligent control of the reactor are of vital importance when designing the control system of a space nuclear reactor (Zhao at al., 2012). In terrestrial nuclear power plants (NPPs), human operators can manually perform the necessary control functions required for normal and abnormal operating conditions. On the contrary, for space missions into outer and deep space characterized by uncertain environments, rare events, and communication delays, all control functions of the reactor must be performed through a robust control system with very limited or even no human intervention from the Earth (Zhao at al., 2012). The basic requirement is to achieve a fast and accurate control of the reactor core power following the desired power output in different operation modes, including not only steady-state operation at different power levels, but more importantly, also transients between these power levels, and transient modes during startup and emergency shutdown of the reactor.

Thanks to its advantages of stability and maturity, the classical proportional-integral-derivative (PID) control scheme is still widely installed as the standard core-power control scheme in current PWR power plants. However, PID control scheme is not able to well handle the load-following operation modes of a nuclear reactor (Liu et al., 2009). In the past decades, various techniques to enhance the control performance of nuclear reactor have been extensively studied. Advanced control schemes including fuzzy control (Mamdani, 1974), neural network control (Mamdani, 1974), fuzzy PID control (Liu et al., 2009; Zeng et al., 2021) etc. have been proposed. But it is very difficult to design an optimized controller for a nuclear reactor due to its high system complexity and nonlinearity, continuous variations of the reactor parameters with operation time and burn up levels, as well as the inevitable modeling uncertainties of real plant behaviors. In this regard, the methodology of model predictive control (MPC), which has received increased attention as a powerful tool for the control of industrial processing systems (Richalet et al., 1978; Garcia et al., 1989), was also proposed as a suitable strategy for the control of nonlinear, time-varying systems such as nuclear reactors thanks to its unique characteristic of online rolling optimization (Na, 2001; Na et al., 2003; Na et al., 2005; Liu and Wang, 2014). The basic concept of MPC is the utilization of a predictive model describing input, output, and state constraints of the objective system, to solve, at each sampling timestep, an online optimization problem to determine the optimal control actions for a finite future counting from the current time instant (Liu and Wang, 2014). However, once a future trajectory of control moves has been obtained, only the first element of that trajectory is employed as input of the controller. The same optimization calculation will be then conducted at each subsequent time instants. This method has many advantages over the conventional infinite horizon optimal control because it is a suitable control strategy for nonlinear, time-varying systems (Na et al., 2006; Eliasi et al., 2012).

It should be noted, for nonlinear, time-varying systems such as a nuclear reactor core, model predictive controller can be readily defined based on state-space model linearized at locally defined steady-state working points. However, a non-distortive description of the system dynamics can be guaranteed only in the vicinity of these points. Hence, the local predictive controller is only meaningful to system dynamic process near these specific points. Consequently, severe mismatch between the model and the actual plant will significantly worsen the control effect when the control range expands beyond these specific steady-state working points. Fortunately, the nonlinear model of a nuclear reactor core can be divided into multiple linear models according to different core power levels. The reactor power control is a typical so-called multi-model control problem, for which a fuzzy “integration” based on the T-S fuzzy theory (Takagi and Sugeno, 1985) could be employed. Nonlinear feature of the global system can be approximated by a fuzzy “integration” using multiple linear features carefully designed at specific local steady-state working points according to the so-called parallel distributed compensation (PDC) scheme. This methodology of combining model predictive control and fuzzy integration is termed in this study as the so-called fuzzy model predictive control (FMPC). The basic idea is that for each locally linearized state-space model, a MPC controller is designed. Afterwards, the overall controller, which is by its nature still nonlinear, is then obtained via a fuzzy “blending” of all the linear controllers individually designed at local steady-state working points (Ma and Sun, 2000).

In this study, the concept of FMPC was adopted to design the core-power controller of a megawatt ultra-small lithium-cooled space nuclear reactor (Song et al., 2021), which is a prototype design for the space exploration program developed in the framework of the National Key R&D Program of China. Full rated power (FP) of the liquid lithium cooled reactor core is $5.1MW$. The nonlinear reactor core model consisting of equations describing point neutronic kinetics, thermohydraulic behaviors as well as reactivity feedbacks were first linearized at five steady-state working points of relative core power of $20\%$, $40\%$, $60\%$, $80\%$ and $100\%FP$, respectively. For each of the five local state points, a local core-power MPC controller was established based on the linearized state-space equations as the predictive model. The overall core-power controller applicable to the full range of nonlinear reactor core, which is in its nature still nonlinear, was then constructed by a weighted combination of the five local MPC controller via fuzzy integration by using the membership functions specially defined for the selected five steady-state working points. To verify the performance of the FMPC core-power controller, effective, robust, and accurate control of the reactor core power was then realized for five predefined, representative operation transients to space nuclear reactor, including ramp and step transients, as well as disturbance transient. Simulation results show that the intelligent FMPC controller possesses an excellent load-following ability and anti-interference ability, both of which are of vital importance for space exploration missions. When compared with the classical PID controller, the FMPC controller designed in this study shows also a much better performance with smaller overshoot, lesser adjusting time and lower integral time-squared error (ITSE). This study successfully demonstrates the feasibility of FMPC to design sophisticate and effective core-power controller also for nuclear reactors with a fast neutron spectrum.

2 Fuzzy model predictive control

Fuzzy model predictive control (FMPC) is a modern intelligent control methodology combining model predictive control (MPC) (Garcia et al., 1989) and T-S fuzzy theory (Takagi and Sugeno, 1985). In this section, a brief description of model predictive control and T-S fuzzy theory will be provided.

2.1 Model predictive control

In this study, MPC algorithm with linearized state-space equations as the predictive model was adopted. According to the basic principle depicted in Figure 1, a MPC controller consists of a predictive model and an online optimization. The basic idea to calculate a sequence of optimal control moves over a certain number of future timesteps, known as the control horizon $M$, via an online optimization to minimizes an objective function defined over a finite future, known as the predictive horizon $P$ ($P\ge M$). Although a sequence of $M$ optimal control moves are obtained, only the first element of that sequence is implemented to the controlled object. At the next timestep, the control horizon will be shifted forward by one timestep and the same optimization will be repeated with new values of the measured output. This online rolling optimization method is also known as the so-called receding horizon optimal control (Na, 2001). The purpose of taking new measurements into the online optimization at each time steps is to compensate unmeasured disturbances and model inaccuracies, both of which can cause the measured system output to be different from the predicted one by the model (Na et al., 2003). In the following, predictive model and receding horizon optimal control will be briefly described.

FIGURE 1

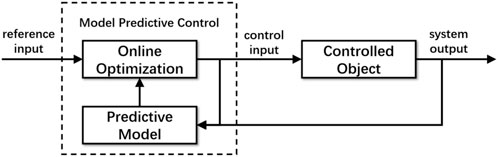
FIGURE 1. Schematic diagram of model predictive control based on linearized state-space equations as predictive model.

2.1.1 Predictive model

Predictive model is used to predict the future output of the controlled object through its historical information, as well as the assumed future control input. In the following, derivation of the predictive model from a linear state-space model will be given. Considering a linear discrete system described by a state-space equation:

$\{\begin{array}{c}x\left(k+1\right)=Ax\left(k\right)+Bu\left(k\right)\\ y\left(k\right)=Cx\left(k\right)\end{array}(1)$

where $x\left(k\right)\in R^n$ stands for the state space of the system at the time $k$, $u\left(k\right)$ and $y\left(k\right)$ are the input and output of the system at the time $k$, respectively. Considering the time horizon of the predictive value of future output are $P$ steps from time $k$, that of the controller input are $M$ steps ($M\le P$) to the controlled object from the time $k$, and the control input remains unchanged thereafter, the following recursion formula can be obtained:

$x\left(k+i|k\right)=A^{i}x\left(k\right)+A^{i-1}Bu\left(k\right)+\cdots +ABu\left(k+i-2\right)+Bu\left(k+i-1\right)=A^{i}x\left(k\right)+{\displaystyle \sum }_{j=0}^{i-1}{A}^{i-1-j}Bu\left(k+j\right)\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}1\le i\le M(2)$

$\begin{array}{ll}\hfill x\left(k+i|k\right)& =A^{i}x\left(k\right)+A^{i-1}Bu\left(k\right)+\cdots +A^{i-M+1}Bu\left(k+M-2\right)+\left(A^{i-M}B+\cdots +B\right)u\left(k+M-1\right)\hfill \\ \hfill & =A^{i}x\left(k\right)+{\displaystyle \sum }_{j=0}^{M-2}{A}^{i-1-j}Bu\left(k+j\right)+{\displaystyle \sum }_{j=M-1}^{i-1}{A}^{i-1-j}Bu\left(k+M-1\right)\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}M<i\le P\hfill \end{array}$

To predict the system output in future $P$ steps, Eq. 2 is combined with the output equation in Eq. 1 to obtain:

$y\left(k+i|k\right)=C{A}^{i}x\left(k\right)+{\displaystyle \sum }_{j=0}^{i-1}C{A}^{i-1-j}Bu\left(k+j\right)\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}1\le i\le M(3)$

$y\left(k+i|k\right)=C{A}^{i}x\left(k\right)+{\displaystyle \sum }_{j=0}^{M-2}C{A}^{i-1-j}Bu\left(k+j\right)+{\displaystyle \sum }_{j=M-1}^{i-1}C{A}^{i-1-j}B\bullet u\left(k+M-1\right)\mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}M<i\le P$

The above equations are written in the vector form to finally yield:

$Y\left(k\right)=Gx\left(k\right)+HU\left(k\right)(4)$

where the definition of $Y\left(k\right)$, $U\left(k\right)$, $G\left(k\right)$, and $H$ are given as:

$\begin{array}{l}Y\left(k\right)\stackrel{\scriptscriptstyle\mathrm{def}}{=}{\left[y\left(k+1|k\right),\cdots ,y\left(k+P|k\right)\right]}_{\left(P\times 1\right)}^T\\ U\left(k\right)\stackrel{\scriptscriptstyle\mathrm{def}}{=}{\left[u\left(k\right),\cdots ,u\left(k+M-1\right)\right]}_{\left(M\times 1\right)}^T\\ G\left(k\right)\stackrel{\scriptscriptstyle\mathrm{def}}{=}{\left[CA,\cdots ,C{A}^P\right]}_{\left(P\times n\right)}^{T}H\stackrel{\scriptscriptstyle\mathrm{def}}{=}{\left[\begin{array}{c}\begin{array}{ccc}{h}_1& 0\cdots & 0\\ ⋮& \ddots & ⋮\\ h_{M-1}& \cdots & 0\end{array}\\ \begin{array}{ccc}{h}_M& h_{M-1}& \dots h_1\\ ⋮& \ddots & ⋮\\ h_P& \cdots & {\displaystyle \sum }_{j=1}^{P-M+1}{h}_j\end{array}\end{array}\right]}_{\left(P\times M\right)}{h}_j\stackrel{\scriptscriptstyle\mathrm{def}}{=}C{A}^{j-1}B,j\ge 1\end{array}(5)$

Eq. 4 in vector form meets the functional requirements of a predictive model. The system state at the current moment $x\left(k\right)$ and the control moves of the future $M$ steps $U\left(k\right)$ are used to predict the output of the system in the future $P$ steps $Y\left(k\right)$.

2.1.2 Receding horizon optimal control

The basic principle of the receding horizon optimal control is depicted in Figure 2. A brief description is given in the following.

FIGURE 2

FIGURE 2. Schematic diagram of receding horizon optimization.

At the present time moment $k$, the purpose of the optimization can be expressed as:

(1). To determine $M$ control moves from the time moment $k$ to $k+M-1$, namely $u\left(k\right),\dots ,u\left(k+M-1\right)$, in such a manner that drastic change of the control moves is suppressed as much as possible;

(2). Meanwhile, to predict future $P$ outputs of the controlled object, namely $y\left(k+1\right),\dots ,y\left(k+P\right)$ in such a manner that they are as close as possible to the expected reference output $w\left(k+1\right),\dots ,w\left(k+P\right)$.

Accordingly, the following quadratic objective function $J\left(k\right)$ can be defined:

$J\left(k\right)={\left(W\left(k\right)-Y\left(k\right)\right)}^T\cdot \mathit{Q}\cdot \left(W\left(k\right)-Y\left(k\right)\right)+U{\left(k\right)}^T\cdot \mathit{R}\cdot U\left(k\right)(6)$

where $W\left(k\right)\stackrel{\scriptscriptstyle\mathrm{def}}{=}{\left[w\left(k+1\right),\cdots ,w\left(k+P\right)\right]}^T$ is the vector form of the expected reference output; $Y\left(k\right)$ and $U\left(k\right)$ are the vector form of the output and control move, respectively. $\mathit{Q}=I_{P\times P}$ and $\mathit{R}=O_{M\times M}$ are the weighting matrixes for output and control move, respectively.

If $Y\left(k\right)$ is substituted with the predictive model expressed in Eq. 4, $J\left(k\right)$ becomes a function of $U\left(k\right)$. The purpose of optimization is then to find an optimal solution of $U\left(k\right)$ to minimize $J\left(k\right)$, which yields:

$\frac{\partial J\left(k\right)}{\partial U\left(k\right)}=0(7)$

With Eq. 7 an analytical expression of the optimal control moves $U\left(k\right)$ can finally be found:

$U\left(k\right)={\left(H^{T}QH+R\right)}^{-1}{H}^{T}Q\left[W\left(k\right)-Gx\left(k\right)\right](8)$

Although future $M$-step optimal control moves is obtained simultaneously, only the first element of $U\left(k\right)$ is implemented:

$u\left(k\right)=d^T\left[W\left(k\right)-Gx\left(k\right)\right](9)$

with $d^T=\left(\mathrm{1,0},\cdots ,0\right){\left(H^{T}QH+R\right)}^{-1}HQ$. When the time base point proceeds to the next moment $k+1$, the control horizon is also shifted forward by one timestep, and the same optimization calculation will then be repeated.

2.2 T-S fuzzy model and parallel distributed compensation control theory

Reactor core power control is a typical so-called multi-model control problem. In this regard, fuzzy control is an effective method to solve multi-model control problems. The T-S fuzzy model is the most common multi-model solution used in the study of fuzzy systems describing large-scale range of linear input-output relations through the IF-THEN rule (Takagi and Sugeno, 1985).

The IF-THEN rule is used to describe the input and output relationship of the nonlinear system near specific local steady-state working point. Let the relative power $n_r$ be the precursor variable, each fuzzy rule of the T-S fuzzy model corresponds to the linearized state-space equation at each working point, and the $i-th$ rule of the fuzzy model can be expressed as follows:

${\mathbf{I}\mathbf{F}n}_r\mathrm{i}\mathrm{s}{M}_i\left(n_r\right)\mathbf{T}\mathbf{H}\mathbf{E}\mathbf{N}\{\begin{array}{c}x\left(k+1\right)=A^{i}x\left(k\right)+B^{i}u\left(k\right)\\ y\left(k\right)=C^{i}x\left(k\right)\end{array}(10)$

in which $M_i\left(n_r\right)$ is the $i-th$ language rule within the fuzzy set corresponding to the precursor variables $n_r$.

For each fuzzy rule of the nuclear reactor power given in Eq. 10, the corresponding local predictive controller is designed by using the MPC method to obtain the $i-th$ control move of the fuzzy controller:

${\mathbf{I}\mathbf{F}n}_r\mathrm{i}\mathrm{s}{M}_i\left(n_r\right)\mathbf{T}\mathbf{H}\mathbf{E}\mathbf{N}{u}^i\left(k\right)={\left(d^i\right)}^T\left[W\left(k\right)-Gx\left(k\right)\right](11)$

Where ${\left(d^i\right)}^T=\left(\mathrm{1,0},\cdots ,0\right){\left({\left(H^i\right)}^T{Q}^i{H}^i+R^i\right)}^{-1}{H}^i{Q}^i$

According to the parallel distributed compensation (PDC) scheme, the global control move of the nonlinear system can be obtained by performing a fuzzy integration of $u^i\left(k\right)$ given in Eq. 11, which yields:

$u\left(t\right)={\displaystyle \sum }_{i=1}^M{\phi }_i\left(n_r\right)u^i\left(t\right)(12)$

where:

${\phi }_i\left(n_r\right)=\frac{M_i\left(n_r\right)}{{\displaystyle \sum }_{j=1}^M{M}_j\left(n_r\right)}(13)$

The control move given in Eq. 12 is then finally the control move implemented to the nonlinear controlled object.

3 Kinetics model of the core of the lithium-cooled space nuclear reactor

In the framework of the National Key R&D Program of China, a prototype design of a megawatt ultra-small lithium-cooled space nuclear reactor to meet the requirements of inherent safety, light weight and long lifetime for typical outer and deep space exploration missions was presented (Song et al., 2021). Principle design of the reactor core is depicted in Figure 3, which adopts liquid lithium circulated by an electromagnetic primary pump as the coolant to transfer the heat released in the reactor core to the secondary Brayton cycle via the primary heat exchanger. In this study, the basic neutronic and thermohydraulic characteristics of the liquid lithium-cooled reactor core were adopted as the object of investigation, for which the most important neutronic and thermohydraulic parameters of the reactor core model are summarized in Table 1. A brief description is also given in the following:

(1) According to the design concept, full rated power (FP) of the reactor core $P_{n0}$ is 5.1 $MW$ and the inlet coolant temperature of the core $T_{c,in0}$ is 1,450 $K$.

(2) For simplification, all the delayed neutrons are averaged into a single group with a total fraction $\beta$ equal to 0.00708. Averaged decay constant of the delayed neutron precursors $\lambda$ is $0.09s^{-1}$. Average prompt neutron generation time $\Lambda$ is $2.45\times {10}^{-8}s$, which is typical for reactor core with a fast neutron spectrum. Feedback influence of the fuel and coolant temperature on the reactivity are considered with the coefficients ${\alpha }_f$ and ${\alpha }_c$, respectively.

(3) All the thermohydraulic characteristics of the reactor core are also considered with lumped parameters. Thermal capacity of the fuel and core coolant are simply taken as constant value. The total thermal capacity of the fuel ${\mu }_f$, which is defined as fuel mass times its heat capacity, is $4.98\times {10}^{4}J/K$. The total thermal capacity of the reactor core coolant ${\mu }_c$, which is defined as coolant mass times its heat capacity, is $4.15\times {10}^{3}J/K$. The effective heat transfer coefficient between fuel and coolant, termed as $\Omega$, is $9.92\times {10}^{5}W/K$. The heat capacity of coolant times mass flow rate of the coolant, termed as $M$, is then $3.4\times {10}^{4}W/K$.

FIGURE 3

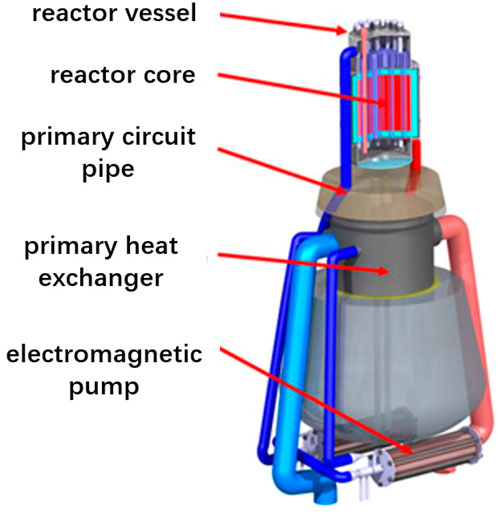
FIGURE 3. Schematic diagram of the ultra-small lithium-cooled space nuclear reactor (Song et al., 2021).

TABLE 1

TABLE 1. Neutronic and thermohydraulic parameters of the core model for the lithium-cooled space nuclear reactor.

Based on the above lumped neutronic and thermohydraulic parameters, the following mathematical model describing the most essential neutronic and thermohydraulic behavior of the liquid lithium-cooled reactor core was able to be established, which yields:

$\{\begin{array}{c}\frac{{dn}_r}{dt}=\frac{\rho -\beta }{\Lambda }{n}_r+\frac{\beta }{\Lambda }{c}_r\\ \frac{d{c}_r}{dt}=\lambda n_r-\lambda c_r\\ \frac{d{T}_f}{dt}=\frac{P_{n0}}{{\mu }_f}{n}_r-\frac{\Omega }{{\mu }_f}{T}_f+\frac{\Omega }{2{\mu }_f}{T}_{c,out}+\frac{\Omega }{2{\mu }_f}{T}_{c,in}\\ \frac{d{T}_{c,out}}{dt}=\frac{2\Omega }{{\mu }_c}{T}_f-\frac{2M+\Omega }{{\mu }_c}{T}_{c,out}+\frac{2M-\Omega }{{\mu }_c}{T}_{c,in}\end{array}(14)$

In the above equation system,

(1) $t$ is the time coordinate.

(2) $n_r$ is the normalized neutron density in the reactor core, which is defined as the actual neutron density relative to the neutron density at full rated power (FP) of the reactor core $P_{n0}=5.1MW$. Since the reactor core power is proportional to the neutron density, the actual reactor core power is then given as $P_{n0}{n}_r$ and $n_r$ also equals the normalized core power relative to the full rated power (FP) $P_{n0}$.

(3) $c_r$ is the normalized equivalent precursor density relative to the neutron density at full rated power.

(4) Temperature of the fuel and coolant are described with lumped parameters, including the average fuel temperature $T_f$, core coolant inlet temperature $T_{c,in}$ and core coolant outlet temperature $T_{c,out}$.

(5) The total reactivity of the reactor core $\rho$ is calculated as follows:

$\rho ={\rho }_{rod}+{\alpha }_f\left(T_f-T_{f0}\right)+\frac{{\alpha }_c}{2}\left(T_{c,out}-T_{c,out0}\right)(15)$

in which ${\rho }_{rod}$ is the reactivity introduced by control rod. It should be noted, since driving mechanism describing the dynamic process of the control rod is not yet available in the current state for the prototype design, no further equation describing the kinetic behavior of the control rod was adopted in this study. Instead, reactivity introduced by control rod ${\rho }_{rod}$ is simply taken. $T_{f0}$ and $T_{c,out0}$ are the initial fuel temperature and initial core outlet coolant temperature, respectively. Therefore, the last two terms in the right hand of the above equation stand for the reactivity feedback from the lumped fuel and coolant temperature, respectively.

Due to the feedback reactivity by fuel and coolant temperature as given in Eq. 15, the reactor core model established in Eq. 14 describing the most essential neutronic and thermohydraulic behavior of the liquid lithium-cooled reactor core is, by its nature, a nonlinear equation system. Before designing a core-power controller according to the concept of model predictive control, the reactor core model needs to be first linearized, for which the following consideration were taken:

(1) At a given moment $t_0$, the reactor core is assumed at a steady state characterized by $n_r=n_{r0}$, $c_r=c_{r0}$, $T_{c,in}=T_{c,in0}$, $T_{c,out}=T_{c,out0}$, $T_f=T_{f0}$.

(2) For a steady state, reactivity of the reactor core is zero, it will yield: $\rho ={\rho }_0=0$.

(3) When the reactor core is subjected to an external disturbance, assuming that the core inlet coolant temperature is unchanged, it will yield: $T_{c,in}=T_{c,in0}$ and $n_r=n_{r0}+{∆n}_r$, $c_r=c_{r0}+{∆c}_r$, $T_f=T_{f0}+∆T_f$, $T_{c,out}=T_{c,out0}+∆T_{c,out}$, $\rho =∆\rho$, in which the symbol $∆$ stands for a small deviation from the steady-state working point characterized by $n_{r0}$.

With the above assumptions, the reactor core model given in Eq. 14 is linearized at the steady-state working point $n_{r0}$, which yields:

$\{\begin{array}{c}\frac{{d∆n}_r}{dt}=-\frac{\beta }{\mathrm{\Lambda }}{∆n}_r+\frac{\beta }{\mathrm{\Lambda }}{∆c}_r+\frac{{\alpha }_f{n}_{r0}}{\mathrm{\Lambda }}∆T_f+\frac{{\alpha }_c{n}_{r0}}{2\mathrm{\Lambda }}∆T_{c,out}+\frac{n_{r0}}{\mathrm{\Lambda }}∆{\rho }_{rod}\\ \frac{d{∆c}_r}{dt}=\lambda {∆n}_r-\lambda ∆c_r\\ \frac{d{∆T}_f}{dt}=\frac{P_{n0}}{{\mu }_f}∆n_r-\frac{\mathrm{\Omega }}{{\mu }_f}{∆T}_f+\frac{\mathrm{\Omega }}{2{\mu }_f}{∆T}_{c,out}\\ \frac{d∆T_{c,out}}{dt}=\frac{2\mathrm{\Omega }}{{\mu }_c}{∆T}_f-\frac{2\mathrm{M}+\mathrm{\Omega }}{{\mu }_c}{∆T}_{c,out}\end{array}(16)$

Furthermore, the state-space variables $x$, control moves $u$ and output $y$ are then defined as the follows:

$x={\left[{∆n}_r,{∆c}_r,{∆T}_f,{∆T}_{c,out}\right]}^{T}u=\left[∆{\rho }_{rod}\right] y={∆n}_r(17)$

Finally, the linearized model is given as:

$\{\begin{array}{c}\dot{x}=A_{c}x+B_{c}u\\ y=C_{c}x+D_{c}u\end{array}(18)$

where the coefficients $A_c$, $B_c$, $C_c$ and $D_c$ are given as the follows:

$A_c=\left[\begin{array}{cccc}\frac{-\beta }{\Lambda }& \frac{\beta }{\Lambda }& \frac{n_{r0}{\alpha }_f}{\Lambda }& \frac{n_{r0}{\alpha }_c}{2\Lambda }\\ \lambda & -\lambda & 0& 0\\ \frac{P_{n0}}{{\mu }_f}& 0& -\frac{\Omega }{{\mu }_f}& \frac{\Omega }{2{\mu }_f}\\ 0& 0& \frac{2\Omega }{{\mu }_c}& -\frac{\left(2M+\Omega \right)}{2{\mu }_c}\end{array}\right](19)$

$B_c={\left[\frac{n_{r0}}{\mathrm{\Lambda }},0,0,0\right]}^T$

$C_c=\left[1,0,0,0\right]$

$D_c=\left[0\right]$

Eq. 18 with the coefficients given in Eq. 19 is the form of the linearized reactor-core model at the steady-state working point characterized by $n_{r0}$. To meet the requirements of model predictive control algorithm, Eq. 18 is then discretized, which yields:

$\{\begin{array}{c}x\left(k+1\right)=Ax\left(k\right)+Bu\left(k\right)\\ y\left(k\right)=Cx\left(k\right)\end{array}(20)$

The coefficients $A$, $B$ and $C$ are given as:

$\begin{array}{c}A=e^{A_{c}T}\\ B=B_c{\int }_0^T{e}^{A_{c}T}dt\\ C=\left[1,0,0,0\right]\end{array}(21)$

in which $T$ is the sampling period. Eq. 20 is the discretized form of the linearized reactor core model at the steady-state working point characterized by $n_{r0}$, which is then used as the predictive model corresponding to this steady state.

4 Design and assessment of the core-power controller based on fuzzy model predictive control

4.1 Design of the fuzzy model predictive control core-power controller

According to the concept of FMPC introduced in Section 2, a “fuzzy” integration of several locally defined MPC controllers at different steady-state working points characterized by different power levels $n_{r0}$ is required to define the overall core-power controller for the lithium-cooled space nuclear reactor. Therefore, to make the control effect of the overall controller in the global range as smoothly as possible, five steady-state working points characterized by $n_{r0}$ of 0.2, 0.4, 0.6, 0.8, and 1.0 are selected as the local state points, at which local MPC controller will be defined. The corresponding language values in the fuzzy set are designated as $M_1$, $M_2$, $M_3$, $M_4$ and $M_5$, which are given with the following triangular membership functions in Eqs 22–26, respectively. The relation between $M_i\left(n_r\right)$ and $n_r$ for the five triangular membership functions are also depicted in Figure 4. Obviously, at the specific $n_{r0}$, the membership function has the value of the unity.

$M_1\left(n_r\right)=\{\begin{array}{c}1n_r<0.2\\ -5\left(n_r-0.4\right)0.2{\le n}_r<0.4\\ 0n_r\ge 0.4\end{array}(22)$

${\mathrm{M}}_2\left({\mathrm{n}}_{\mathrm{r}}\right)=\{\begin{array}{c}\begin{array}{c}0{\mathrm{n}}_{\mathrm{r}}<0.2\\ 5\left({\mathrm{n}}_{\mathrm{r}}-0.2\right)0.2{\le \mathrm{n}}_{\mathrm{r}}<0.4\\ -5\left({\mathrm{n}}_{\mathrm{r}}-0.6\right)0.4{\le \mathrm{n}}_{\mathrm{r}}<0.6\end{array}\\ 0{\mathrm{n}}_{\mathrm{r}}\ge 0.6\end{array}(23)$

$M_3\left({\mathrm{n}}_{\mathrm{r}}\right)=\{\begin{array}{c}\begin{array}{c}0{\mathrm{n}}_{\mathrm{r}}<0.4\\ 5\left({\mathrm{n}}_{\mathrm{r}}-0.4\right)0.4{\le \mathrm{n}}_{\mathrm{r}}<0.6\\ -5\left({\mathrm{n}}_{\mathrm{r}}-0.8\right)0.6{\le \mathrm{n}}_{\mathrm{r}}<0.8\end{array}\\ 0{\mathrm{n}}_{\mathrm{r}}\ge 0.8\end{array}(24)$

$M_4\left({\mathrm{n}}_{\mathrm{r}}\right)=\{\begin{array}{c}\begin{array}{c}0{\mathrm{n}}_{\mathrm{r}}<0.6\\ 5\left({\mathrm{n}}_{\mathrm{r}}-0.6\right)0.6{\le \mathrm{n}}_{\mathrm{r}}<0.8\\ -5\left({\mathrm{n}}_{\mathrm{r}}-1\right)0.8{\le \mathrm{n}}_{\mathrm{r}}<1\end{array}\\ 0{\mathrm{n}}_{\mathrm{r}}\ge 1\end{array}(25)$

$M_5\left(n_r\right)=\{\begin{array}{c}0n_r<0.8\\ 5\left(n_r-1\right)0.8{\le n}_r<1\\ 1n_r\ge 1\end{array}(26)$

FIGURE 4

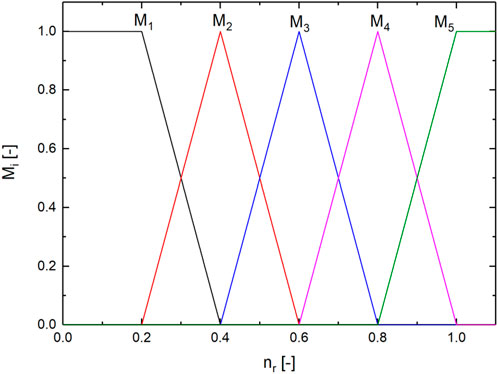
FIGURE 4. Definition of the five membership functions $M_1$ to $M_5$ (A color version of the figure is kindly referred to the online version of the paper).

To assess the performance of the designed FMPC core-power controller, simulations were performed in this study within the Simulink platform embedded in MATLAB software. Simulink block diagram including the five local MPC controllers and the fuzzy integration for the global FMPC controller is then depicted in Figure 5. A brief description of the block diagram is given in the following:

(1) First, it should be noted, since neither an actual lithium-cooled space reactor, nor a full-scope simulator of the reactor are available for the present study, the nonlinear reactor core model derived in Section 3 (Eq. 14 with the corresponding parameters summarized in Table 1) was used in the Simulink simulations as the controlled object, i.e., the module “NuclearReactor” in Figure 5.

(2) The desired relative core power is displayed in the module “Reference” as depicted in Figure 5, while the actual relative core power $n_r$ of the nonlinear “NuclearReactor” is then displayed with the module “out_nr” as depicted in Figure 5. The actual core power $n_r$ will be used in the module “GetWeights” for the fuzzy integration of the five local MPC controllers, in which a weighting factor will be determined for each of the local controller by using the membership functions.

(3) The corresponding local MPC controllers designed for the five selected local state points are designated in Figure 5 with the modules “mpc20,” “mpc40,” “mpc60,” “mpc80,” and “mpc100”, respectively. Construction of the five MPC controllers share the same principle with two inputs “ref” and “mo,” and one output “mv.” “ref” is the desired reference core power, while “mo” is the feedback deviation between the reference core power and the actual core power. For each of the five local MPC controller, its output signal “mv” will then be multiplied with its individual weighting factor, followed by a summation of all the five weighted signals to finally obtain the global control signal for the nonlinear “NuclearReactor”, i.e., “Reactivity” in Figure 5.

(4) The module “Disturbance” depicted in Figure 5 will be used only for the simulation of the disturbance transient, in which a finite reactivity will be added to the reactor core to simulate the case of the reactor core affected by an external disturbance reactivity. For the ramp and step transients, the disturbance reactivity is by default zero.

FIGURE 5

FIGURE 5. Schematic diagram of the designed FMPC controller by Simulink.

4.2 Performance assessment of the fuzzy model predictive control controller for typical transient operation conditions

To verify and assess the performance of the FMPC controller, the following five transient operation conditions representative to a space nuclear reactor were defined and investigated in this study. In all the transients, the reactor core was initially assumed at the steady state of $100\%FP$:

(1) Local ramp transient: 1 $00\%FP\to 90\%FP\to 100\%FP$ ramp change of the reactor core power at a declining and rising rate of $0.1\%FP/s$. The local ramp transient is intended to study the control effect of FMPC controller near the working point at full power operation condition.

(2) Global ramp transient: $100\%FP\to 20\%FP\to 100\%FP$ ramp change of the reactor core power at a declining and rising rate of $0.08\%FP/s$. The global ramp transient is used to simulate the scenario of large-scale power change to reduce the core power to a low power level and the start-up scenario of the reactor core.

(3) There are various unforeseen uncertainties in the space nuclear reactor in the space environment. In the most extreme emergency cases, the reactor core power needs to be reduced to a certain low level as soon as possible to only maintain the necessary power supply needed by the nuclear reactor itself. Therefore, an emergency transient of $100\%FP\to 25\%FP$ fast ramp change of the reactor core power at a declining rate of $0.25\%FP/s$ was also defined.

(4) Besides the above three transients of ramp change, a step transient was also defined with $100\%FP\to 90\%FP\to 100\%FP$ step change of the reactor core power by $10\%FP$.

(5) Last but not the least, a disturbance transient was also defined, in which an external $+20pcm$ reactivity was introduced to the reactor core operating at $100\%FP$. The disturbance transient is used to simulate the scenario of the reactor core disturbed by an external reactivity when the reactor is operating at a steady state of full power.

In all the above five transient operation conditions, the desired objective of the FMPC controller is to enable the reactor core to follow the desired reference power as close as possible during the respective ramp, step or disturbance transient. Figures 6–15 show then the response of the FMPC controller. The adjustment time of the FMPC controller is defined in this study as the total time required for the absolute overshoot of larger than $2\%$ returning to a level lower than $2\%$. As comparative reference, control performance of the classical PID was also included. The main results derived are summarized as the follows:

(1) Figure 6 shows the FMPC control effect for the local ramp transient, during which an excellent load-following performance of the reactor core power was established with the FMPC controller. On contrary, the control effect of PID shows a much higher overshoot. An obvious oscillation of the controlled power was also observed, which is not present with the FMPC controller. As depicted in the enlarged views of Figures 7A,B, with the FMPC controller, the maximal overshoot for the power declining and power rising local ramp change are $-0.32\%$ and $-0.37\%$, respectively. No oscillation was observed, and the absolute maximal overshoot is less than $2\%$, which means the adjusting time of the FMPC controller for the investigated local ramp transient is practically zero.

(2) Figure 8 shows then the FMPC control effect for the global ramp transient. Like the local ramp transient, the FMPC controller also shows an excellent load-following ability better than PID controller. With the FMPC controller, the maximal overshoot for the power declining global ramp change, as shown in Figure 9A, is $-1.71\%$, while the maximal overshoot for the power rising global ramp change, as shown in Figure 9B, is $-2.01\%$. Although this absolute maximal overshoot is slightly larger than $2\%$, it quickly decreases monotonically to a level lower than $2\%$ after an adjusting time of only 2 s.

(3) Figure 10 shows the FMPC control effect for the emergency fast ramp transient. Overall, the actual power level follows well that of the desired reference level. Again, the control effect of the FMPC controller is better than PID controller with smaller overshoot and less adjusting time. The maximum reactivity introduced by the FMPC controller occurs around 300 s, where the reactor power reaches the desired level of $25\%FP$. With the PID controller, an oscillation of the reactor power was observed, which reaches the desired level of $25\%FP$ around 600 s. As depicted in the enlarged view of the area A in Figure 11, the maximum overshoot of $-2.66\%$ occurs at 301 s with the FMPC controller, after which the overshoot decreases monotonically and finally reaches a level of the absolute overshoot lower than $2\%$ at 316 s. The adjusting time of the FMPC controller for the emergency ramp transient investigated is hence 15 s.

(4) Figure 12 shows the FMPC control effect for the step transient. Like the ramp transients, the FMPC controller also shows an excellent load-following ability. With the PID controller, on the other hand, the core power experienced an obvious oscillation and much larger overshoot than with the FMPC controller. As observed in the two enlarged views of the area A and B in Figures 13A,B, with the FMPC controller, the maximal overshoot for the power declining and power rising step change are $-0.54\%$ and $+1.26\%$, respectively. No oscillation was observed, and the absolute maximal overshoot is less than $2\%$, which means the adjusting time of the FMPC controller for the investigated step transient is practically zero.

(5) Figure 14 shows the control effect for the disturbance transient, in which a $+20pcm$ reactivity was introduced at 100 s when the reactor is operated at $100\%FP$. As observed in the upper subfigure of Figure 14, with the FMPC controller, the reactor power experiences a sudden increase then quickly decreases to the desired reference level of $100\%FP$. Similar sudden increase was also observed for the PID controller, however with an oscillation of the reactor power when approaching the desired reference level of $100\%$. As depicted in the lower subfigure, the reactivity introduced by the FMPC controller experiences a local maximum around 100 s then quickly reaches the desired level of $-20pcm$. The reactivity introduced by PID controller experiences an obvious oscillation and a much longer adjusting time to reach the desired level of $-20pcm$.The enlarged view of the area A and B of Figure 14 are depicted in Figures 15A,B, respectively. For the $+20pcm$ disturbance transient, FMPC controller shows an excellent anti-interference capability. The maximal overshoot of $3.43\%$ occurs at 101 s. After an adjusting time of only 2 s, the overshoot quickly decreases to a level less than $2\%$. The maximum overshoot of the PID controller is slightly larger, but the adjusting time is much longer. The maximum reactivity introduced by FMPC controller was $-21.4pcm$ at 108 s, after which the reactivity quickly reached the desired level of $-20pcm$ at about 130 s. With the PID controller, on the other hand, the maximum reactivity introduced was $-24.7pcm$ at 151 s, after which the reactivity reached the desired level of $-20pcm$ at about 300 s. The FMPC controller shows an obvious better anti-interference performance than PID controller.

FIGURE 6

FIGURE 6. Simulation results for the working condition: local ramp transient.

FIGURE 7

FIGURE 7. Enlarged view of the area A and B for the local ramp transient. (A) Local ramp transient around 100 s. (B) Local ramp transient around 250 s.

FIGURE 8

FIGURE 8. Simulation results for the working condition: global ramp transient.

FIGURE 9

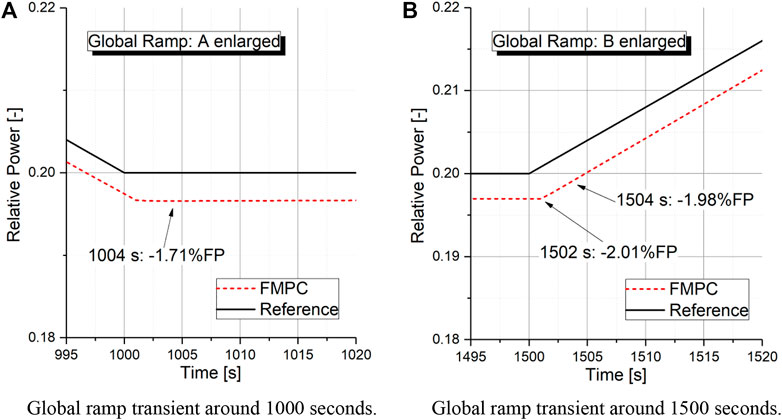
FIGURE 9. Enlarged view of the area A and B for the global ramp transient. (A) Global ramp transient around 1,000 s. (B) Global ramp transient around 1,500 s.

FIGURE 10

FIGURE 10. Simulation results for the working condition: emergency ramp transient.

FIGURE 11

FIGURE 11. Enlarged view of the area A for the emergency ramp transient.

FIGURE 12

FIGURE 12. Simulation results for the working condition: step transient.

FIGURE 13

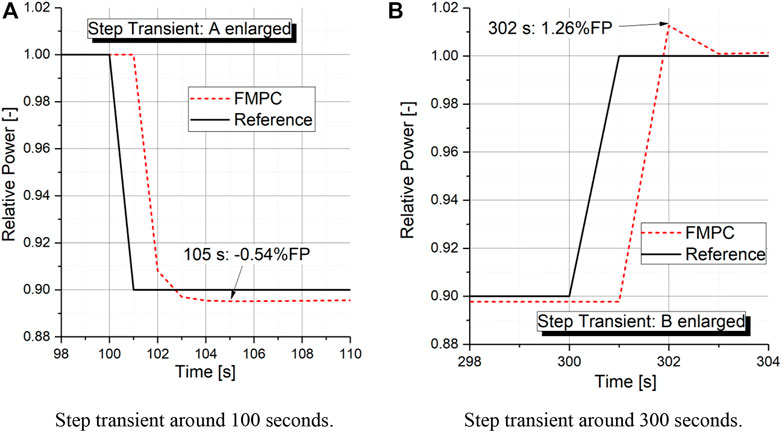
FIGURE 13. Enlarged view of the area A and B for the step transient. (A) Step transient around 100 s. (B) Step transient around 300 s.

FIGURE 14

FIGURE 14. Simulation results for the working condition: disturbance transient.

FIGURE 15

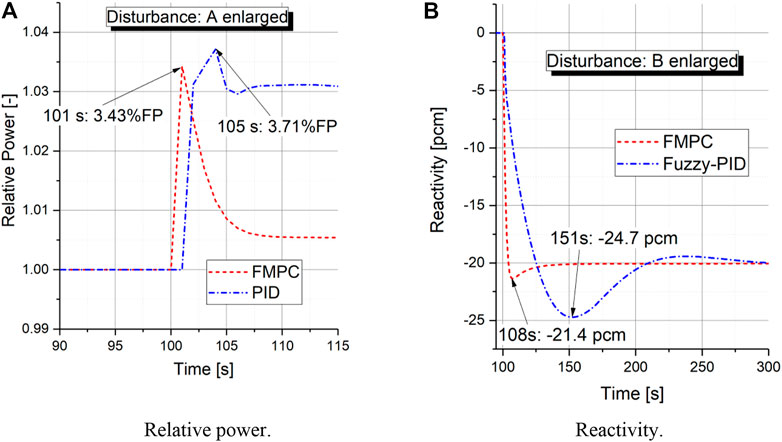
FIGURE 15. Enlarged view of the area A and B for the disturbance transient. (A) Relative power. (B) Reactivity.

Furthermore, the integral time-squared error (ITSE) was applied to evaluate the performance of the FMPC controller and PID controller in each of the above five simulations according to:

$ITSE\left(e,T\right)=\underset{0}{\overset{T}{{\displaystyle \int }}}t{e}^{2}dt(27)$

where $e$ is the deviation between reference core power and the actual core power. Table 2 summarizes then the ITSE values for all the five simulated transient operation conditions. It is obvious that the ITSE values of the proposed FMPC control approach are much lower than those of the PID controller.

TABLE 2

TABLE 2. ITSE values of the FMPC controller and PID controller for the five simulated transient operation conditions.

Finally, to better demonstrate the control effect of the FMPC controller, Table 3 summarizes the most important performance indices of the FMPC controller, including maximal overshoot, adjusting time and maximal reactivity induced for the five investigated transient operation conditions. In conclusion, the core-power controller designed based on fuzzy model predictive control can fulfill various load-following control tasks under typical transient working conditions of the lithium-cooled space nuclear reactor. Furthermore, the fuzzy model predictive control shows also a certain anti-interference capability.

TABLE 3

TABLE 3. Performance indices of the FMPC controller for the five simulated transient operation conditions.

5 Conclusion and outlooks

In this study, a fuzzy model predictive control based on model predictive control and T-S fuzzy theory was designed for the core-power control of a megawatt ultra-small lithium-cooled space nuclear reactor. Firstly, neutronic and thermohydraulic behaviors of the lithium-cooled reactor core described by nonlinear state-space equations were linearized at five steady-state working points characterized by relative core power of $20\%$, $40\%$, $60\%$, $80\%$ and $100\%FP$, respectively. Afterwards, a local model predictive controller was designed for each of the five local steady-state working points based on the state-space equations locally linearized at the specific state points. Finally, all the five local MPC controllers were integrated based on T-S fuzzy theory via the so-called parallel distributed compensation scheme, to build up the so-called fuzzy model predictive control for overall control of the nonlinear reactor core. Five typical operation conditions including both ramp and step transients, as well as a disturbance transient were defined and simulated to assess the performance of FMPC core-power controller. The simulation results show that the FMPC controller has an excellent load-following ability and anti-interference ability, both of which are of vital importance for space exploration missions. When compared with the classical PID controller, the FMPC controller designed in this study shows also a much better performance with smaller overshoot, lesser adjusting time and much lower ITSE values.

Although investigations in this study were conducted for a simplified neutronic and thermohydraulic model of a lithium-cooled space nuclear reactor, it successfully demonstrates the feasibility of fuzzy model predictive control to design sophisticate and effective core-power controller also for typical nonlinear and time-varying nuclear reactors with a fast neutron spectrum. The design method adopted in this study for the core-power controller can be readily extended to other designs of space nuclear reactors, provided more in-depth detailed specifications of specified designs are become available in the future. Nevertheless, it should be pointed out, physical constraints regarding driving mechanism of the control rods are not available for the prototype design of the lithium-cooled space nuclear reactor. Therefore, control constraint is not considered in the FMPC controller designed in this study, which, however, should be included in further investigations if the driving mechanism of the control rods become available. Furthermore, applicability of the fuzzy model predictive control is still worthy further investigations for a wide range of realistic working scenarios of space nuclear reactors, especially for those scenarios of large and abrupt disturbances to the reactor, provided they are become available in the future.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

YY—Conceptualization; Methodology; Project administration; Writing—original draft preparation; Funding acquisition; ZY—Software; Investigation; Data Curation; Visualization; Writing—original draft preparation; BP—Methodology; Writing—original draft preparation; Writing—review and editing; Funding acquisition; YX—Software; Data Curation; Visualization; YD—Software; Writing—review and editing; Project administration.

Funding

This work was financially supported by the University Stability Support Program of Shenzhen (Grant No. 20200803132736020) and the National Key R&D Program of China (Grant No. 2018YFB19006).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akimov, V. N., Koroteev, A. A., and Koroteev, A. S. (2012). Space nuclear power systems: Yesterday, today, and tomorrow. Therm. Eng. 59 (13), 953–959. doi:10.1134/s0040601512130022

CrossRef Full Text | Google Scholar

Baraskar, A., Yoshimura, Y., Nagasaki, S., and Hanada, T. (2022). Space solar power satellite for the Moon and Mars mission. J. Space Saf. Eng. 9 (1), 96–105. doi:10.1016/j.jsse.2021.10.008

CrossRef Full Text | Google Scholar

Bennett, G. L., Hemler, R. J., and Schock, A. (1996). Status report on the U.S. Space nuclear program. Acta Astronaut. 38 (4–8), 551–560. doi:10.1016/0094-5765(96)00038-0

CrossRef Full Text | Google Scholar

Demuth, S. F. (2003). SP100 space reactor design. Prog. Nucl. Energy 42 (3), 323–359. doi:10.1016/s0149-1970(03)90003-5

CrossRef Full Text | Google Scholar

Ehrenfreund, P., McKay, C., Rummel, J. D., Foing, B. H., Neal, C. R., Masson-Zwaan, T., et al. (2012). Toward a global space exploration program: A stepping stone approach. Adv. Space Res. 49 (1), 2–48. doi:10.1016/j.asr.2011.09.014

CrossRef Full Text | Google Scholar

Eliasi, H., Menhaj, M. B., and Davilu, H. (2012). Robust nonlinear model predictive control for a PWR nuclear power plant, Prog. Nucl. Energy, 54, 177–185.

CrossRef Full Text | Google Scholar

Garcia, C. E., Prett, D. M., and Morari, M. (1989). Model predictive control: Theory and practice - a survey. Automatica 25 (3), 335–348. doi:10.1016/0005-1098(89)90002-2

CrossRef Full Text | Google Scholar

Harty, R. B., and Mason, L. S. (1993). 100-kWe Lunar/Mars surface power utilizing the SP-100 reactor with dynamic conversion. AIP Conf. Proc. 271 (2), 1065–1071. doi:10.1063/1.43087

CrossRef Full Text | Google Scholar

IAEA (2002). The role of nuclear power and nuclear propulsion in the peaceful exploration of space. Vienna, Austria: International Atomic Energy Agency.

Google Scholar

Jin, Z., Wang, C., Liu, X., Dai, Z., Tian, W., Su, G., et al. (2022). Operation and safety analysis of space lithium-cooled fast nuclear reactor. Ann. Nucl. Energy 166, 108729. doi:10.1016/j.anucene.2021.108729

CrossRef Full Text | Google Scholar

Liu, C., Peng, J. F., Zhao, F. Y., and Li, C. (2009). Design and optimization of fuzzy-PID controller for the nuclear reactor power control. Nucl. Eng. Des. 239 (11), 2311–2316. doi:10.1016/j.nucengdes.2009.07.001

CrossRef Full Text | Google Scholar

Liu, X., and Wang, M. (2014). Nonlinear fuzzy model predictive control for a PWR nuclear power plant. Math. Problems Eng. 2014, 1–10. doi:10.1155/2014/908526

CrossRef Full Text | Google Scholar

Ma, X. J., and Sun, Z. Q. (2000). Output tracking and regulation of nonlinear system based on takagi– Sugeno fuzzy model. IEEE Trans. Syst. Man. Cybern. B 30 (1), 47–59. doi:10.1109/3477.826946

PubMed Abstract | CrossRef Full Text | Google Scholar

Mamdani, E. H. (1974). Application of fuzzy algorithms for control of simple dynamic plant. Proc. Inst. Electr. Eng. UK. 121 (12), 1585–1588. doi:10.1049/piee.1974.0328

CrossRef Full Text | Google Scholar

Marov, M. Y., and Slyuta, E. N. (2021). Early steps toward the lunar base deployment: Some prospects. Acta Astronaut. 181, 28–39. doi:10.1016/j.actaastro.2021.01.002

CrossRef Full Text | Google Scholar

McNutt, R. L., and Ostdiek, P. H. (2015). Nuclear power assessment study final report. Laurel, MD: The Johns Hopkins University Applied Physics Laboratory.

Google Scholar

Na, M. G. (2001). Design of a receding horizon control system for nuclear reactor power distribution. Nucl. Sci. Eng. 138, 305–314. doi:10.13182/nse01-a2216

CrossRef Full Text | Google Scholar

Na, M. G., Shin, S. H., and Kim, W. (2003). A model predictive controller for nuclear reactor power. Nucl. Eng. Technol. 35 (5), 399–411.

Google Scholar

Na, M. G., Jung, D. W., Shin, S. H., Wook Jang, J., Lee, K. B., and Lee, Y. J (2005). A model predictive controller for load-following operation of PWR reactors. IEEE Trans. Nucl. Sci. 52 (4), 1009–1020. doi:10.1109/tns.2005.852651

CrossRef Full Text | Google Scholar

Na, M. G., Hwang, I. J., and Lee, Y. J. (2006). Inferential sensing and monitoring for feedwater flowrate in pressurized water reactors. IEEE Trans. Nucl. Sci. 53 (3), 2335–2342. doi:10.1109/tns.2006.878159

CrossRef Full Text | Google Scholar

Richalet, J., Rault, A., Testud, J. L., and Papon, J. (1978). Model predictive heuristic control: Applications to industrial processes. Automatica 14, 413–428. doi:10.1016/0005-1098(78)90001-8

CrossRef Full Text | Google Scholar

Song, Y., Zhou, T., Jiang, J., Liu, C., Wang, L., Tan, P., et al. (2021). Progress and prospects on lithium cooled space nuclear reactor power. China Basic Sci. 21 (3), 21–50.

Google Scholar

Takagi, T., and Sugeno, M. (1985). Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man. Cybern. 15 (1), 116–132. doi:10.1109/tsmc.1985.6313399

CrossRef Full Text | Google Scholar

Zeng, E., Jiang, Q., Liu, Y., Yan, S., Zhang, G., Yu, T., et al. (2021). Core power control of a space nuclear reactor based on a nonlinear model and fuzzy-PID controller. Prog. Nucl. Energy 132, 103564. doi:10.1016/j.pnucene.2020.103564

CrossRef Full Text | Google Scholar

Zhao, Z., Jiang, X., Wang, L., and Chen, L. (2012). Neutronics characteristic of conceptual space lithium cooled fast neutron reactor. Atomic Energy Sci. Technol. 46, 374–378.

Google Scholar

Zheng, Y., Ouyang, Z., Li, C., Liu, J., and Zou, Y. (2008). China's lunar exploration program: Present and future. Planet. Space Sci. 56 (7), 881–886. doi:10.1016/j.pss.2008.01.002

CrossRef Full Text | Google Scholar