
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
METHODS article
Front. Energy Res. , 26 December 2022
Sec. Nuclear Energy
Volume 10 - 2022 | https://doi.org/10.3389/fenrg.2022.1058750
This article is part of the Research Topic Benchmark Experiments, Development and Needs in Support of Advanced Reactor Design View all 12 articles
In this paper two major families of methods to deal with the assessment of the rod positioning uncertainty in a lattice are tested: a traditional one described in the International Handbook of Evaluated Criticality Safety Benchmark Experiments (IHECSBE) Handbook and the other one consisting in sampling the position of rods with Monte Carlo techniques (ISO Uncertainty Guidelines). They are applied on a benchmark with tight-packed lattice of UO2 rods that is sensitive to the rod positioning as it is clearly under-moderated. It is shown that the choice of the method has a great impact on the propagated uncertainty, the traditional one leading to a significant overestimation of the overall uncertainty and can also contribute to a bias in the correlation factors that are used for assessing biases due to nuclear data using GLLSM methodologies. The paper briefly describes the tight-packed lattice experimental program performed at the Valduc Research Centre, which is at the origin of these concerns. Then it proposes a simple model on which to apply simulations of rod positioning to be performed with MORET 5 Monte Carlo code using the Prométhée tool. Results demonstrate that use of Monte Carlo methodologies provide more realistic uncertainty estimates in fuel pitch that are consistent with repeatability/reproducibility experiments. The current comparisons use light water reactor systems, which is directly relevant to some small modular reactor designs. However, accurate prediction and estimate of uncertainties in pitch for advanced reactor systems is also relevant. The application of unrealistic uncertainty analysis methods can incur larger margins in advanced reactor design, safety, and operation than are necessary.
For several years now, the criticality community has made efforts to provide documented critical experiments with “best-estimate” uncertainties that could be of interest for the validation of criticality codes. A project named International Criticality Safety Benchmark Evaluation Project (ICSBEP) was created in 1992 for that purpose (Briggs, Scott, and Nouri 2003). In that prospect, experiments from diverse laboratories and covering a wide range of applications were evaluated. A part of the evaluation consists of determining the chemical and geometrical uncertainties. Sometimes just a few parameters can drive the overall uncertainty. When designing experimental programs, people in charge of the design of experiments try to select moderation values as close as possible to the moderation optimum. One of the reasons is that the closer the moderation ratio is to the optimum, the lower the uncertainties in rod positioning and fewer rods are needed to reach criticality. However, in the French tight-packed-lattice experiments, LEU-COMP-THERM-071 (Leclaire 2019a), LEU-COMP-THERM-072 (Leclaire 2019b), and LEU-COMP-THERM-073 (Leclaire 2019c), the experiments have pitches smaller than required for optimal moderation, as they were designed to slightly shift the sensitivity of keff to the epithermal energy range with a view to address the economic needs of nuclear operators with a more compact storage. Therefore, the uncertainty contribution from rod positioning is greater.
In fact, when the spacing between rods corresponds to the fissile medium moderation ratio optimum, the positioning uncertainty is negligible. However, when the spacing between rods is smaller when we get further from the moderation ratio optimum, the impact is much greater. Depending on the pitch between rods, the positioning uncertainty can have a varying effect upon keff. The situation where the moderation ratio is far from the optimum ratio could be encountered in advanced reactor design concepts, including microreactors. During the design and operations, the uncertainty in the positioning of rods due to the tolerance values of grids’ holes and fuel rods is considered in the calculations. A propagation method based on MC sampling can help in determining the best estimate of the overall uncertainty and mitigating overestimation of margins supporting safety and operations.
Moreover, with the growth of advanced tools used to estimate the biases due to nuclear data such as TSUNAMI (Rearden 2004), WHISPER (Brown, Rising, and Alwin 2016), and MACSENS [Fernex], the accurate determination of correlation factors between experimental cases has become an important issue. The determination of such values is conditioned by a thorough evaluation of uncertainties, and the associated random and systematic components of each uncertainty.
To sum this up, different ways of propagating the uncertainty in terms of Δkeff can be envisioned, amongst which what can be called “traditional” ones based on ICSBEP recommendations and other ones based on Monte Carlo (MC) simulations. Depending on the method, the impact on Δkeff can be completely different. The aim of this work is to compare the traditional methods with methods using MC simulations on variable sizes of lattices as proposed in the International Organization for Standardization (ISO) uncertainty guides (referred to in this document as the ISO GUM S1 procedure) (JCGM 2009) (JCGM 2008) and to compare with repeatability/reproducibility experiments allowing access to such uncertainty.
From 1998 to 1999 a series of critical experiments referred to as the tight-packed lattice experimental program was performed using Apparatus B in the Commissariat à l'Energie Atomique (CEA) Valduc Research Centre in France (Duhamel and Girault 2006). The experimental device, shown in Figure 1A, is commonly used for assembling configurations with epithermal and thermal neutron energy spectra. These experiments, designed by L'Institut de Radioprotection et de Sûreté Nucléaire (IRSN), and funded by COGEMA (also formerly AREVA NC and now Orano Cycle) and IRSN, involved UO2 rods at a 1.05-, 1.075-, 1.1- or 1.6-cm square pitch and contributed to the validation of uranium cross sections in thermal and epithermal energy ranges. Twenty-seven critical experiments were performed, evaluated, and analyzed with different criticality software packages. The experiments were slightly sub-critical, the water level being raised until keff = 1 - (βeff/10). The water critical level was obtained by extrapolation of the inverse neutron counting rate.
The first step of the program involved lattices of 1.1-cm square pitched UO2 rods moderated and reflected by water (documented in LEU-COMP-THERM-071). The UO2 rods were a typical design for a pressurized-water reactor (PWR) with a235U enrichment of 4.738 wt%. The main characteristics of the fuel rods are given in Table 1 (uncertainties are indicated as 1σ). The uncertainties of the rods are mainly due to the precision of measurement devices and are therefore assumed to be 90% systematic. The UO2 rods consisted of vertically stacked pellets contained within Zircaloy-4 cladding. The rod diameter corresponded to the industrial fuel pin diameter. The fuel stack length was adjusted to the height of the experimental tank, which was equal to 90 cm. Experimental uncertainties for the rod characteristics are also gathered in Table 1.
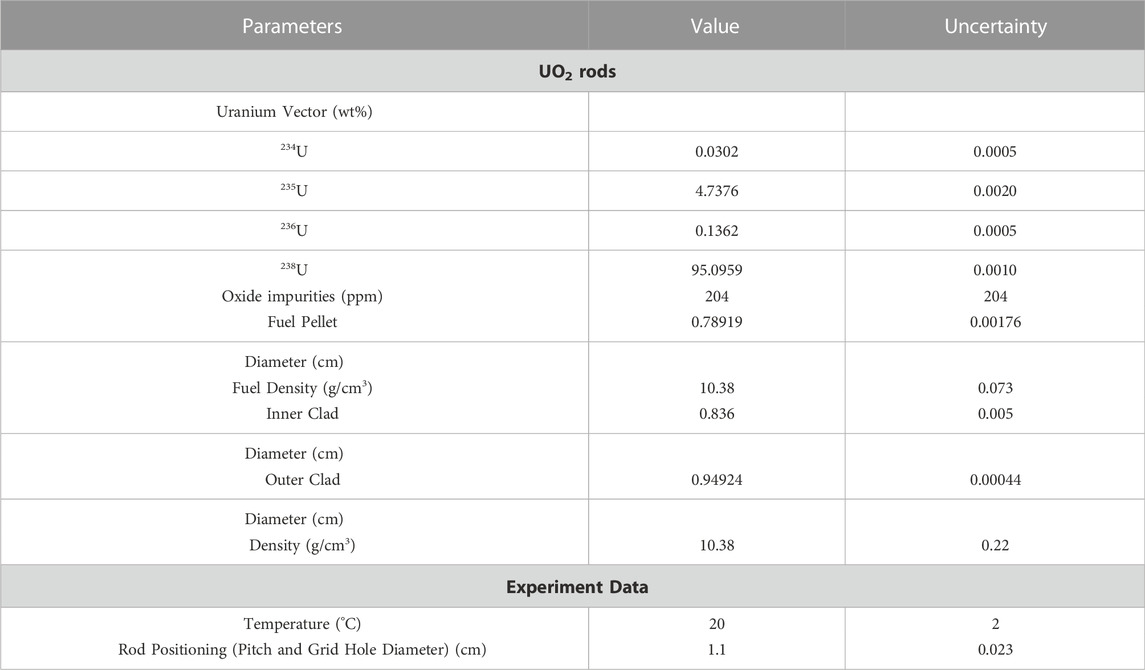
TABLE 1. Primary experiment parameters and uncertainties for LEU-COMP-THERM-071 (Leclaire 2019a).
Sensitivity studies were performed to assess the impact on keff of various experimental uncertainties upon the configuration in accordance with the recommendations of the IHECSBE uncertainty guide (Dean 2008). The effects on keff changes were adopted as the associated components of the keff uncertainty. In order to compare different methods of rod positioning uncertainty, the uncertainties of two revisions (0 and 1) of the LEU-COMP-THERM-071 benchmark are reported in Table 2. The main components of the keff errors are shown in Table 2 for the first series of experiments along with the overall propagated uncertainty, calculated as the square root from sum of squares of its individual components. The differences between revision 0 and revision 1 are mainly associated with the fact that random uncertainties were ignored in revision 0 and are taken into account in revision 1. Moreover, the rod position being the source of large uncertainty, its treatment has been modified using Monte Carlo sampling in revision 1, contributing to a reduction of its propagated value. It can also be seen that for cases with a small pitch the rod positioning has a non-negligible effect on the overall uncertainty.
To test efficiently the different methods, it seems reasonable to define a simple benchmark, shown in Figure 1B, with which they can be tested. This benchmark is made of three different lattices of UO2 rods having the same characteristics as the Valduc rods (see Section 2.1). The variable parameter is the pitch between rods (1.1, 1.3, and 1.6 cm). The smallest pitch corresponds to an under-moderated lattice and the largest pitch to the moderation optimum as can be seen in Figure 2, where is reported the material buckling (Bm2) versus the pitch between rods. The moderation ratio, Vmod/Vox, values are reported in Table 3.
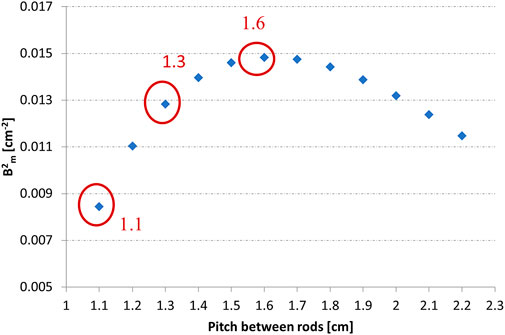
FIGURE 2. Material buckling versus pitch between rods. The pitch between rods correspond with the distance between the centers of two neighboring rods. B2m is the material buckling.
In order to have a keff close to 1, the number of fuel rods is adjusted accordingly. The 1.1-cm pitch lattice comprises an array of 35 × 35 rods, the 1.3-cm lattice an array of 25 × 25 rods and the 1.6-cm pitch lattice an array of 17 × 17 rods. It is to be noticed that the moderation optimum corresponds to a pitch of 1.6 cm between rods for a 4.738 wt% 235U enrichment. The rod plugs were not considered in the model; only the fissile column surrounded by its cladding was retained. The height of rods was then set equal to 89.765 cm. The lattices were centered in a parallelepiped box, containing water, of 130-cm height and side dimensions corresponding to the lattice size plus 20 cm.
Calculations were performed using the MORET 5 Monte Carlo code (Cochet, et al., 2015) and the computing environment Prométhée (Richet et al., 2007).
Calculations were performed using the MORET 5 continuous energy Monte Carlo code. It is a 3D MC code for neutron transport developed at IRSN for criticality safety assessments. It employs continuous energy cross sections derived from JEFF-3.1 evaluated nuclear data files (Koning et al., 2006). Typically, each calculation keff was run to achieve a precision of ±.00010 Δkeff (±10 pcm).
Prométhée is a grid computing environment designed to provide engineering methodologies relevant for any available code. The Prométhée system is composed of a Graphical User Interface (GUI) designed to provide ergonomics features for a computing software input data engineering algorithms (for instance uncertainties propagation methods). Then, calculations are remotely performed on servers. The parameterization of rods’ location in the lattice was performed using Prométhée.
At first look, the origin of the rod positioning uncertainty is mainly linked with the presence of two grids (both upper (A) and lower (B) are shown in Figure 3) drilled with holes with a slightly higher diameter; the spacing between rods is conditioned by the grid plate holes. These two grids ensure the mechanical rigidity of the lattice.
As illustrated in Figure 4, The uncertainty of rods’ positioning is composed of:
• Hole position uncertainty due to error in adjustment of the grid hole piercing device: ±.001 cm manufacturing tolerance;
• The uncertainty of the outer diameter of the rod cladding: ±.00044 cm (1σ);
• The uncertainty of the grid holes’ diameter: ±.0085 cm (1σ); and
• The uncertainty of the gap between the rod and the edge of the grid hole (tolerance of ±.0407 cm): corresponds to a 1σ-uncertainty of ±.023 cm.
All in all, a total 1σ-uncertainty of ±.033 cm is obtained. The different components of the spacing uncertainty are converted in an increase or decrease of the distance between rods.
The way the uncertainty in rod positioning is propagated varies from one evaluator to another and from one calculation code to another. One of the examples given to evaluators in the IHECSBE consists of varying the spacing between all rods from plus or minus the uncertainty of the gap. The reactivity difference between these two calculations divided by two times the square-root of three (representing the correction from a two-sided bounding uncertainty with uniform probability distribution to a standard 1σ Gaussian uncertainty) determines the effective uncertainty in keff. The resultant value is then divided by square root of total number of rods. Historically, this method derived from the use of cell codes to evaluate this type of uncertainty.
As shown in Figure 5, this method was applied by shifting the rods nearer or further away from each other. The spacing between two neighboring rods was assumed to be the same throughout the lattice. Thus, the moderation ratio was varied by the same amount for all the lattice rods. For each lattice size, 2 MC calculations were performed: one, increasing the spacing between rods of a given quantity and another decreasing the spacing by the same amount. The variation was chosen in order to remain within the linearity domain of keff variations yet still large enough not to be influenced by the MC standard deviation of the calculation.
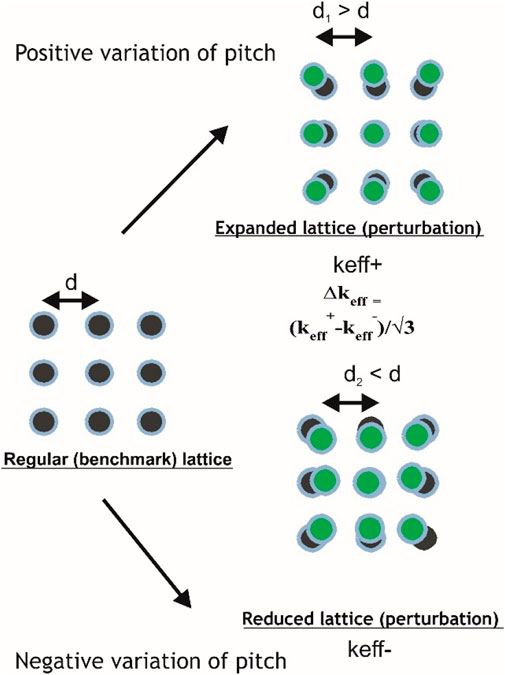
FIGURE 5. Traditional method for evaluation of pitch uncertainty. d is the pitch, d1 correspond with a positive variation of pitch; keff+ is the resulting keff; d2 correspond with a negative variation of pitch. keff− is the resulting keff.
Then, the obtained keff value was scaled to 1σ and, divided by square-root of the number of rods. This factor was derived in Eq. 1:
which assimilated the overall uncertainty to the sum of each rod uncertainty. When assuming that the independent contribution of each rod to the overall uncertainty is the same, the formula can be written as shown in Eq. 2:
The last assumption consists in saying that the variance of the lattice is the total variance divided by N as described in Eq. 3:
For large lattices of rods, assuming that the contribution of the uncertainty of each rod is the same leads to a biased estimation of the uncertainty. A calculation separating the assembly in two zones (internal and peripheral) and assessing separately uncertainties on these two zones should ideally be considered. However, it will not be investigated in this paper.
The “refined traditional” method is a variant of the basic traditional method. The only difference is that the Δkeff is divided by the square-root of an additional factor (kR) to account for the fact that the position of rods is constrained within a grid and that there is a compensation effect for the simultaneous variation of pitch between all rods. This factor (Ivanova, Ivanov, and Bianchi 2014) is called the peak-to-average ratio and is typically constrained between the values of 1.3 and 1.5.
Another variant of traditional methods leans upon the fact that the rod position is constrained within the grids. The rods cannot move outside their grid holes. As a consequence, it is impossible to impose the maximum shift to all the rods at the same time. The average rod position is constrained between two extreme positions that are demonstrated in Figure 6. For that reason, the method could be called “extreme lattice bounds.” The mean variation of rod position is equal to the difference of width between these two lattices divided by the square-root of the total number of rods in the lattice. In fact, in the X direction for instance, only the distance separating the two last rows of rods at the periphery is modified. The modification is equal to the gap between the rod and the grid hole multiplied by √2. As a consequence, the average rod position shift is the gap × √2/√N with N being the total number of rods in the lattice. When propagated in terms of Δkeff, this variation leads to results comparable to traditional methods but slightly lower.
Two kinds of MC simulations were tested during this work. The first one uses the MORET 5 code combined with the Prométhée workbench to do the MC sampling. A first step consisted in comparing the traditional method varying the pitch value according with a chosen distribution law. The variation was then propagated in terms of Δkeff for 100 different rod positioning maps corresponding to 100 different simulations. Then, the distribution of keff was observed.
A second step consisted in comparing the traditional method with a simulation on the position of rod according to ISO GUM S1 standard procedure. Instead of increasing artificially the distance between rods of the same quantity, the position of rods in their holes was sampled independently 100 times (this number was chosen arbitrarily but was found sufficient to have a Gaussian distribution, as shown in Figure 7, which was confirmed by the value of the bootstrap) for the 35 × 35 array and propagated in terms of Δkeff using the ISO GUM S1 standard procedure, which corresponded to a more realistic approach. For this method, the position of each rod was chosen independently from its neighbors. The Δkeff was observed and its statistical parameters (mean and variance) were estimated(Figure 8).
In this section, the position of rods varies independently from the position of neighboring rods (Figure 9), which is more realistic than the use of traditional methods. The position of rods is constrained since they are held by two grids (lower and upper). As explained at the beginning of section IV, the rods can move within their grid holes. Their uncertain position pertains to the external diameter of claddings, the precision of the piercing of grid holes, and to the gap existing between the rods and the grid holes. In fact, with the increase of water level during a critical approach, the rods can move inside their grid holes and their respective positions can be correlated. The overall positioning uncertainty was chosen to follow a uniform distribution. Each rod position was supposed to be completely uncorrelated from that of its neighbors. Thus, the distance between rods was not the same throughout the lattice. The parameterized variable was the position of rods. For each lattice, the input listings were automatically generated with Prométhée tool.
The rods position shifts are given by Eqs 4, 5 in the X and Y lattice directions, respectively. The maximum shift was estimated as being equal to 2 × .0439 cm between two neighboring rods.
The variables r1 and t1 were chosen randomly according with an equiprobable distribution law. This assumption is over-predicting the uncertainty propagation in comparison with a triangular or Gaussian distribution law. By default, this option was retained. The size of the modeled lattice is chosen accordingly with the pitch between rods as defined in section 2.2.
For each lattice, a batch of 100 calculations corresponding to 100 different values of (r1, t1), with a MC precision of ±0.00010 Δk, was launched on 100 different computing nodes via the Prométhée plugin. A fixed number of neutrons per lattice (10,000) was chosen. It has been checked that this number had hardly any impact upon keff. It should be noticed that the observed variance is the sum of both code keff estimate variance (MC codes) and studied rod positioning effect variance. These two random variables being independent, the rod variance is estimated as the difference of observed variance and code variance.
Moreover, the value is known with a small standard deviation (<3 pcm) (Davison, Hinkley, and Schechtman 1986) due to the sample size of 100. The obtained value is far lower than the one obtained using the traditional method. Even if the comparison has been done on a simple benchmark model, the ratio obtained between the uncertainty given by the traditional method and that obtained from the ISO GUM S1 simulations can be transmitted to a configuration close to that model. This procedure applies for the tight-packed lattice program. A rod positioning uncertainty of about 70 pcm is obtained with the traditional method for a 4.738 wt% 235U enrichment and a 35 × 35 rods lattice. For the same rods at the same moderation ratio, the “best estimate” value of the rod uncertainty can be assessed as being closer to 20 pcm.
It should be stressed that the validity of the method leans mainly on the MC sampling. It is conditioned by the number of neutrons per batch and per volume in the geometry. A comparison with a deterministic method would be needed to definitively validate it without potential deviation due to MC sampling of neutrons (including MC Markov chain initial transient).
Another approach consists in using the Monte Carlo N-Particle (MCNP) code, version 6, with the URAN card (Goorley et al., 2013). This card allows selecting universes to randomly translate the geometry inside a lattice cell. The Universe corresponding to the main cell of the lattice is then selected and the rods are randomly shifted within its cell. The same .0439 cm variation is defined as for the previous method involving random sampling. The position of rods is shifted of the following quantities in the X and Y directions according to Eqs 6, 7, respectively.
Here, t1 and t2 are random variables comprised between 0 and 1, and δ1 and δ2 are user-defined variations.
The MORET 5 results for the three lattice pitches of the benchmark are given in Table 4. The JEFF-3.1 evaluation is used for the nuclear data library. Quite similar results are obtained with the two traditional methods, the results of the refined traditional being a little lower. Moreover, for a same pitch variation, the propagated 1σ uncertainty is greater for the lowest pitch, which was predictable since a tight-packed lattice of rods is more sensitive to a pitch variation than a lattice at the moderation optimum.
The calculations were performed for the two methods (MC sampling with MORET 5/Prométhée and URAN card with MCNP) for a rod positioning uncertainty of ± 0.04 cm. The results are reported in Table 4. It can be shown that there is no great influence of the pitch value and that the two methods are quite consistent since there is no significant difference between the results.
For the three pitches of the benchmark and a shift of the position of rods corresponding to the 1σ uncertainty of rod position, calculations were performed with the continuous energy Monte Carlo MORET 5 code and the various methods presented beforehand. These results are reported in Figure 9. It can be shown that the traditional methods lead to higher Δkeff values than the methods based on MC sampling or the URAN card in MCNP6. The reduced uncertainty using the URAN card with MCNP is consistent with similar comparison studies performed for the Neutron Radiography (NRAD) reactor (Bess, Maddock, and Marshall 2014). The discrepancy is more important for smaller pitches. In fact, at moderation optimum, the MC sampling methodology is not necessary since quite consistent results are obtained. This is not the case for tight-packed lattices of rods, however. Moreover, it should be pointed out that the results obtained with MC sampling and those using the URAN card in MCNP6 are perfectly consistent. The question now is to know which method better predicts the uncertainty.
A way to have access to this information is to make comparisons with experimental results. Repeatability/reproducibility experiments can allow such comparison. This was done for another proprietary program called MIRTE (Matériaux en Interaction et Réflexion Toutes Epaisseurs) (Leclaire et al., 2014) whose aim was the validation of the calculation of structural materials in thermal energy spectrum. This program involved the same UO2 rods, with a 1.6-cm square pitch (moderation optimum). The reproducibly experiment consisted in draining the water level from the tank, unloading the baskets containing the rod lattices, shake them, reload them and then perform a new critical approach. Such experiments addressed different uncertainties amongst them such as the critical height uncertainty and the rod position uncertainty. The critical level difference observed between the two experiments, when propagated in terms of Δkeff, corresponded to an insignificant reactivity worth (less than 20 pcm). This value was clearly lower than what was highlighted using traditional methods. It demonstrates that traditional methods are clearly overestimating rod positioning uncertainty. Moreover, the same order of magnitude was obtained as with the MC sampling method. As a result, the results obtained with the MC sampling method or with the URAN card of MCNP 6 are not without experimental validation. One can be confident in the results they provide.
Correlation factors between experiments or between cases of an experimental series are key values for the determination of biases due to nuclear data. For many years now, various tools such as TSURFER for the SCALE 6 package (Wieselquist, Lefebvre, and Jessee 2020), WHISPER for MCNP, and MACSENS (Fernex and Leclaire, 2022) for the CRISTAL package (Gomit et al., 2015) have implemented (or are implementing for MORET) a sensitivity on keff capability and the Generalized Linear Least Squares Methodology (GLLSM) to evaluate biases due to nuclear data (Broadhead et al., 1999). To correctly assess the bias, one needs to know the correlation between experiments (or cases). These values strongly influence the result of the adjustment procedure and therefore the bias. Very accurate-value correlation factors are needed. And for that, a thorough evaluation of uncertainties is required. For each parameter source of uncertainty, it is necessary to know the random and systematic components of the uncertainty to clearly demonstrate the shared uncertainty between cases. Eqs 8–11 show how these factors are calculated.
Establishment of correlations between the uncertainties of a pair of benchmark experiments (called experimental correlations hereafter) is not a trivial task. If an uncertainty component is wholly or partially common for a pair of experiments, the problem is reduced to estimating the component correlation coefficient related to that specific component of the uncertainty.
Where,
In order to demonstrate that correlation factors between experiments are dependent upon the evaluation of experimental uncertainties, an application case is chosen. The tight-packed lattice program, LEU-COMP-THERM-071, is chosen for that aim. We will show how the evaluation of the rod positioning uncertainty can influence the value of correlation factors. Two cases are selected: one with a 1.1-cm square pitch (case 1 of Table 5) and the other with a 1.075-cm square pitch (case 4 of Table 5). The detail of experimental uncertainties is provided with in Table 5. Two scenarios are retained concerning the evaluation of the rod positioning uncertainty: traditional method or Monte Carlo sampling. Cross cut views of the two model lattices are reported in Figure 10.
The rod positioning uncertainty appears to be driving the overall uncertainty. The correlation factors were calculated assuming that the uncertainties pertaining to all parameters are 100% systematic (in fact, the random part of the uncertainty is negligible when compared to the systematic part), except for the rod positioning uncertainty where it is supposed to be random for both scenarios. Even if there is some systematic uncertainty on the grid hole position due to the manufacturing procedure, the rod positioning uncertainty is mainly random. Indeed, the rods are inserted manually in the grids’ holes and lean on their bottom plug. Once positioned in the grids’ holes, they can move randomly within the holes during the critical approach due to the increase of the water level or can even move due to vibrations. Moreover, the positions of rods being not marked in the lattice, from one case to another, the position is resampled, and the positioning uncertainty is random. When looking now at the correlation matrix below, one can see that the correlation factor is strongly dependent on the chosen scenario, for tight-packed lattices of rods. It would not be the case for lattices of rods at moderation optimum.
In this section a first attempt to understand the difference between the traditional methods and the ones using MC simulations (ISO GUM S1) is provided. It is to be noted that it is implicitly assumed while using the traditional methods that the rods are non-correlated in the contribution to overall keff. The traditional methods make the assumption that each rod contributes independently from its neighbors to the overall keff. However, the factor kR (peak to average ratio) is introduced to compensate for that by taking the correlations into account. This factor is purely empirical and depends on the rod lattice size and moderation ratio. In fact, the position of rods is correlated since it is constrained by the presence of grids maintaining them. With the mean free path of neutrons being around 1–2 cm in a thermal spectrum, the neutrons produced in each rod interact with at least two neighbors. Consequently, some covariance terms should contribute negatively to the uncertainty propagation. This is what is observed when doing calculations using MC sampling.
It can be easily concluded from previous sections that the choice of the rod location uncertainty propagation methodology can have a significant impact on the overall uncertainty, especially when the fuel is under-moderated, as it is the case for LEU-COMP-THERM-071. The objective for a good assessment of calculation bias and uncertainty is not necessarily to overestimate this quantity. In criticality-safety assessment, the uncertainty in the positioning of rods due to the tolerance values of grids’ holes and fuel rods is taken into account in the calculations. The same problematics applies on reactor physics design and operations. A propagation method based on MC sampling can help in determining the best estimate of the overall uncertainty, avoiding overestimation of the uncertainty with the traditional method which has historically been used.
Direct applicability of this work applies towards some of the light water small modular reactor and microreactor concepts such as the ACP100 (Danrong et al., 2021), Nuward (OECD, 2021) and Nuscale designs (Weber and Mullin 2020). As the quantity and diversity of these types of reactors expands, questions remain in not just how the uncertainties in pitch will impact reactor physics performance, but also in other core performance parameters including desired uses beyond power generation such as process heat generation for desalination, hydrogen production, or other industrial processes (IAEA 2017).
Overprediction of pitch uncertainties in advanced reactor design could lead to larger than necessary margins required for safety and operations. A simple means to understand this potential impact is to relook at the conversion of the NRAD reactor from highly enriched to low-enriched fuel (Bess, Maddock, and Marshall 2014). The initial critical mass necessary for the converted core was physically greater than computationally predicted, resulting in post-conversion accommodations to incorporate additional fuel rods into a restricted design space to enable the reactor to achieve and maintain at-power operations. While control rod worth and coefficient measurements were not significantly different from their estimates, the available core excess reactivity for operations was much less than the maximum allowed within the safety limits of the technical specifications, and nearly insufficient to enable necessary reactor operations. Uncertainties in the experiment were evaluated, including those for pitch, to estimate the impact upon the bias between computational models and the freshly refueled reactor. Should significantly large uncertainties have been included in the design due to pitch, or any other parameter, the margins between operations and safety would have been even more significantly discrepant, possibly to the point of reactor inoperability.
Therefore, an improved approach is also of interest for advanced reactor designs such as pebble bed reactors using tri-isotropic (TRISO) fuel or other high-temperature gas-cooled reactors (HTGRs), for which the fuel-to-moderator ratio and fuel-to-fuel pitches are random; a sampling MC methodology would help evaluating the uncertainty pertaining to the fuel location. The traditional approach to column and channel pitch in prismatic HTGRs could be on the order of 0.1 %Δkeff (Bess and Fujimoto 2010). While this uncertainty could be minor compared to some more significant uncertainties such as graphite and fuel properties, as manufacturing processes are improved, the approach towards treatment of geometric uncertainties becomes more prominent. However, implementation of a MC sampling methodology for TRISO particle packing in pebbles contributes insignificantly to the overall uncertainty, as expected (Çolak and Seker 2005)(Bess and Dolphin 2013). Similar expectations would apply towards fluoride salt-cooled high-temperature reactor (FHR) designs (Qualls, et al., 2017).
In fast reactor systems, significant contributors to changes in pitch can be seen in thermal expansion or bowing effects (Lum, 2018). Random rod displacement effects are mitigated and negligible if the core assemblies are suitably constrained; however, thermal expansion of grid plates and assemblies further add to the complexity in the evaluation of core neutron leakage and reactivity effects (Pope and Lum 2021). In liquid fuel systems, such as a molten salt reactor (MSR) the impact on pitch could derive from uncertainties in placement of moderator channels and blocks, if used, which can also be more suitably addressed using MC evaluative techniques (Shen, 2019), and should be further investigated as a component of evaluating technological gaps and safety requirements supporting MSR design and deployment (Forsberg 2006)(Elsheikh 2013).
A key aspect in regulation and operation of advanced nuclear reactors will require those designing and deploying the reactors to demonstrate to those regulating the operation and safety of these reactors that all aspects of systems will perform as expected. The impact of uncertainties in rod positioning is only one component of many that will need to be properly understood to satisfy regulatory requirements prior to advanced reactor deployment and operations. Ultimately, the uncertainties addressed in this paper might improve assessment of modular transportation of microreactors or fuel and their ultimate disposal; understanding biases and associated uncertainties when utilizing various methodologies and codes is imperative (Tardy, 2019).
The impact of rod positioning has been tested with various methods: the traditional one recommended historically by the ICSBEP working group, modifications to the traditional method, MC sampling using the MORET 5 code and the Prométhée computing environment, and the MCNP6 code with the URAN card to simulate the uncertain position of rods inside their grids. These methods have been applied on a benchmark involving three critical lattices of Valduc UO2 rods with various pitches (1.1-cm, 1.3-cm or 1.6-cm square pitch) corresponding to different moderation ratios. It has been shown that the traditional methods commonly used by benchmark evaluators does not underestimate the contribution of the rod positioning uncertainty, as it was originally thought. On the contrary, for tight-packed lattices of rods (pitch 1.1 cm), a noticeable positive discrepancy with MC simulations (ISO GUM S1) is highlighted. Moreover, with a good consistency between MC sampling with MORET 5/Prométhée and MCNP 6/URAN being obtained, one can be quite confident in the result. To better estimate such a small effect, it would be necessary to perform calculations with a deterministic code.
At last, the validity of MC sampling calculations is ensured by the comparison with experimental results. Indeed, repeatability/reproducibility experiments were performed in the framework of the MIRTE (Matériaux en Interaction et Réflexion Toutes Epaisseurs) program involving similar rods in a 1.6-cm square-pitched lattice. It can be shown that the uncertain position of rods in their baskets leads to a Δkeff less than ± 0.00020, which is in accordance with the results obtained via MC sampling with MORET 5/Prométhée or MCNP6/URAN. Monte Carlo sampling techniques show improvement in better prediction of actual uncertainties in light water reactor systems, which is directly applicable to many small modular reactor concepts in development. However, the application of such methodologies can apply towards advanced reactor design concepts, including microreactors, to mitigate overestimation of margins supporting safety and operations.
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
NL is the main author of the paper. JB added sections to highlight the interest of such methodology for advanced reactor and complemented the lis references.
The authors wish to thank Yann Richet for the support on the use of the Prométhée tool and are grateful to the Bertrand Cochet for his advice on the use of the code and Alexis Jinaphanh for its support on the calculations.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Bess, J. D., and Dolphin, B. H. (2013). HTR-PROTEUS pebble bed experimental program cores 1, 1A, 2, and 3: Hexagonal close packing with a 1:2 moderator-to-fuel pebble ratio. PROTEUS-GCFR-EXP-001, Rev. 1.
Bess, J. D., and Fujimoto, N. (2010). Evaluation of the start-up core physics tests at Japan’s high temperature engineering test reactor (Fully-Loaded core). HTTR-GCR-RESR-001, Rev. 1.
Bess, J. D., Maddock, T. L., and Marshall, M. A. (2014). Fresh-core reload of the neutron Radiography (NRAD) reactor with uranium(20)-erbium-zirconium-hydride fuel. NRAD-FUND-RESR-001, Rev. 2.
Briggs, J. B., Scott, L., and Nouri, A. (2003). The international criticality safety benchmark evaluation project. Nucl. Sci. Eng. 145 (1), 1–10. doi:10.13182/NSE03-14
Broadhead, B. L., Hopper, C., Childs, R. L., and Parks, C. V. (1999). Sensitivity and uncertainty analyses applied to criticality safety validation: Methods development, 1. Washington, DC: U.S. Nuclear Regulatory Commission. NUREG/CR-6655.
Brown, F. B., Rising, M. E., and Alwin, J. L. (2016). MCNP-WHISPER methodology for for nuclear criticality safety validation. LA-UR-16-23757. Los Alamos, New Mexico, USA: Los Alamos National Laboratory.
Cochet, B., Jinaphanh, A., Heulers, L., and Jacquet, O. (2015). Capabilities overview of the MORET 5 Monte Carlo code. Ann. Nucl. Energy 82, 74–84. doi:10.1016/j.anucene.2014.08.022
Çolak, Ü., and Seker, V. (2005). Monte Carlo criticality calculations for a pebble bed reactor with MCNP. Nucl. Sci. Eng. 149 (2), 131–137. doi:10.13182/NSE04-17
Danrong, S., Qing, L., Dong, Q., Gaojian, D., Chang, Z., Renjie, X., et al. (2021). Key Technology of ACP100: Reactor core and safety design. Nucl. Power Eng. 42 (4), 1–5. doi:10.13832/j.jnpe.2021.04.0001
Davison, A. C., Hinkley, D. V., and Schechtman, E. (1986). Efficient bootstrap simulation. Biometrika 73, 555–566. doi:10.2307/2336519
Dean, V. (2008). ICSBEP guide to the expression of uncertainties. Rev. 5. Paris, France: OECD Nuclear Energy Agency.
Duhamel, I., and Girault, E. (2006). “Criticality experiments with tightly packed lattices of low-enriched UO2 rods,” in Proceeding of the PHYSOR 2006: Advances in Nuclear Analysis and Simulation, Vancouver, September 10-14. Available from: https://www.ans.org/store/item-700323/)
Elsheikh, B. M. (2013). Safety assessment of molten salt reactors in comparison with light water reactors. J. Radiat. Res. Appl. Sci. 6 (2), 63–70. doi:10.1016/j.jrras.2013.10.008
Fernex, F., and Leclaire, N. (2022). A new IRSN tool for nuclear data bias assessment: MACSENS V3.0 GLLSM module. NCSD2022. Anaheim.
Forsberg, C. W. (2006). “Molten-salt-reactor Technology gaps,” in International Congress on Advances in Nuclear Power Plants (ICAPP ’06), Reno, NV, USA, June 4-8. Available at: https://www.ans.org/store/item-700324/.
Gomit, J.-M., Duhamel, I., Entringer, A., Magnaud, C., Damian, F., and Riffard, C. (2015). “Cristal V2.0: A new-generation criticality package,” in Proceeding of the International Conference on Nuclear Criticality Safety (ICNC 2015), Charlotte, NC, September 13-17. Available at: https://www.ans.org/store/item-700400/.
Goorley, T., James, M., Booth, T., Brown, F., Bull, J., Cox, L. J., et al. (2013). Features of MCNP6. LA-UR-13-28114. Los Alamos, NM: Los Alamos National Laboratory.
IAEA (2017). Opportunities for cogeneration with nuclear energy. NP-T-4.1. Vienna, Austria: International Atomic Energy Agency.
Ivanova, T., Ivanov, E., and Bianchi, G. E. (2014). Establishment of correlations for some critical and reactor physics experiments. Nucl. Sci. Eng. 178 (3), 311–325. doi:10.13182/NSE14-24
JCGM (2009). “Evaluation of measurement data – an introduction to the “guide to the expression of uncertainty in measurement” and related documents,” in JCGM 104:2009. Joint committee for guides in metrology (Sèvres, France: Bureau International des Poids et Mesures).
JCGM (2008). “Evaluation of measurement data – supplement 1 to the “guide to the expression of uncertainty in measurement” – propagation of distributions using a Monte Carlo method,” in JCGM 101:2008. Joint committee for guides in metrology (Sèvres, France: Bureau International des Poids et Mesures).
Koning, A., Forrest, R., Kellett, M., Mills, R., Henriksson, H., and Rugama, Y. (2006). The JEFF-3.1 nuclear data library. Paris, France: OECD Nuclear Energy Agency.
Leclaire, N., Duhamel, I., Dauphin, F. X. L., Briggs, B., Piot, J., Rennesson, M., et al. (2014). The MIRTE experimental program: An opportunity to test structural materials in various configurations in thermal energy spectrum. Nucl. Sci. Eng. 179 (4), 429–445. doi:10.13182/NSE14-29
Leclaire, N. (2019a). Low moderated 4.738-wt.%-Enriched uranium dioxide fuel arrays. LEU-COMP-THERM-071, rev. 2.
Leclaire, N. (2019b). Under-moderated 4.738-wt.%-Enriched uranium dioxide fuel rod arrays reflected by water or polyethylene. LEU-COMP-THERM-072, rev. 2.
Leclaire, N. (2019c). Water-reflected under-moderated 4.738-wt.%-Enriched uranium dioxide fuel rod arrays with heterogeneities. LEU-COMP-THERM-073, rev. 1.
Lum, E. S. (2018). Evaluation of run 138B at experimental breeder reactor II, a prototypic liquid metal fast breeder reactor. EBR2-LMFR-RESR-001.
OECD (2021). Nuclear Technology development and economics 2021, small modular reactors: Challenges and opportunities.
Pope, C., and Lum, E. (2021). “Nuclear reactor thermal expansion reactivity effect determination using finite element analysis coupled with Monte Carlo neutron transport analysis,” in Finite element methods and their application. Editors M. Baccouch, and IntechOpen (London, UK. doi:10.5772/intechopen.93762
Qualls, A. L., Betzler, B. R., Brown, N. R., Carbajo, J. J., Greenwood, M. S., Hale, R., et al. (2017). Preconceptual design of a fluoride high temperature salt-cooled engineering demonstration reactor: Motivation and overview. Ann. Nucl. Energy 107, 144–155. doi:10.1016/j.anucene.2016.11.021
Rearden, B. T. (2004). Perturbation theory eigenvalue sensitivity analysis with Monte Carlo techniques. Nucl. Sci. Eng. 146 (3), 367–382. doi:10.13182/NSE03-03
Richet, Y., Heulers, L., Bernard, F., and Gauluet, F. (2007). A flexible calculation environment for criticality parametric modeling, In Proceeding of the International Conference on Nuclear Criticality Safety (ICNC 2007), Saint Ptersburg, Russia.
Shen, D. (2019). Molten-salt reactor experiment (MSRE) zero-power first critical experiment with 235U. MSRE-MSR-EXP-001.
Tardy, M. (2019). Criticality codes biases and associated uncertainties determination for fissile nuclear material transportation using different approaches in 18th International Symposium on the Packaging and Transportation of Radioactive Materials (PATRAM 2019), New Orleans, LA, USA, August 4-9. Available at: https://resources.inmm.org/.
Weber, S. J., and Mullin, E. M. (2020). Severe accident phenomena: A comparison among the NuScale smr, other advanced lwr designs, and operating LWRs. Nucl. Technol. 206, 1351–1360. doi:10.1080/00295450.2020.1756160
Wieselquist, W. A., Lefebvre, R. A., and Jessee, M. A. (2020). “ORNL/TM-2005/39, version 6.2.4,” in SCALE code system (Oak Ridge, Tennessee, USA: Oak Ridge National Laboratory).
CEA Commissariat à l'Energie Atomique
FHR Fluoride salt-cooled High-temperature Reactor
GLLSM Generalized Linear Least Squares Methodology
GUI Graphical User Interface
HTGR High-Temperature Gas-cooled Reactor
ICSBEP International Criticality Safety Benchmark Evaluation Project
IHECSBE International Handbook of Evaluated Criticality Safety Benchmark Experiments
IRSN L'Institut de Radioprotection et de Sûreté Nucléaire
ISO International Organization for Standardization
JFA JFoster and Associates
MC Monte Carlo
MCNP Monte Carlo N-Particle
MIRTE Matériaux en Interaction et Réflexion Toutes Epaisseurs
MSR Molten Salt Reactor
NRAD Neutron Radiography
PWR Pressurized Water Reactor
TRISO Tri-Isotropic
Keywords: ICSBEP, Monte Carlo sampling, positioning uncertainty, prométhée, uran
Citation: Leclaire N and Bess JD (2022) Comparison of two methods for assessment of the rod positioning uncertainty and consequences on the evaluation of correlation factors. Front. Energy Res. 10:1058750. doi: 10.3389/fenrg.2022.1058750
Received: 30 September 2022; Accepted: 12 December 2022;
Published: 26 December 2022.
Edited by:
Yixiang Liao, Helmholtz Association of German Research Centres (HZ), GermanyReviewed by:
Mohammad Alrwashdeh, Khalifa University, United Arab EmiratesCopyright © 2022 Leclaire and Bess. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Nicolas Leclaire, bmljb2xhcy5sZWNsYWlyZUBpcnNuLmZy
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.