
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res., 09 November 2022
Sec. Nuclear Energy
Volume 10 - 2022 | https://doi.org/10.3389/fenrg.2022.1041900
This article is part of the Research TopicExperimental and Numerical Studies on Liquid Metal Cooled Fast ReactorsView all 17 articles
A printed circuit heat exchanger (PCHE) can offer superior performance in area concentration and heat transfer efficiency. A PCHE with a liquid lead–bismuth eutectic (LBE) and supercritical carbon dioxide as working media can use these materials as intermediate heat exchangers in lead–bismuth eutectic-cooled reactors to reduce facility size and improve economy. To ensure the reliability of a numerical simulation for a liquid LBE in PCHE channels, the flow and heat transfer characteristics of a liquid LBE were investigated in a single D-type channel. The existing turbulent Prandtl number
Liquid–metal cooled nuclear reactors are recognized as promising generation-Ⅳ reactors due to their low melting point, high boiling point, excellent heat absorption capacity, high molecular heat conduction, good neutron performance and radiation resistance. Moreover, the liquid lead alloy (typically a liquid lead–bismuth eutectic) offers good passive safety characteristics and superior economy as a coolant for nuclear reactors (Roelofs et al., 2019). The main characteristics of typical lead-based fast reactors (LFRs) worldwide have been summarized by Zhang et al. (2020). They noted the current challenges in their development and discussed the research progress of four main thermohydraulic aspects.
The flow and heat transfer characteristics of liquid lead–bismuth eutectics (LBEs) have been studied extensively by experiments and numerical simulations. An experiment considering a 19-pin hexagonal rod bundle cooled by a forced-convective LBE was completed at the Karlsruhe Liquid Metal Laboratory (KALLA) (Pacio et al., 2016). Their experimental results had good repeatability in the uncertainty range, and correlations for predicting the drag coefficient and Nusselt number
In a nuclear reactor, heat is transferred from the primary circuit to a secondary circuit through an intermediate heat exchanger, and a regenerator is arranged in the second loop. The intermediate heat exchanger and the regenerator take the form of a shell and tube heat exchanger. This configuration requires that both heat exchangers have high heat transfer efficiency, and the safety of the heat exchangers must be guaranteed. Usually, shell and tube heat exchangers are used in conventional nuclear power plants. In recent years, the application of gas Brayton cycle power generation systems in liquid metal reactors has attracted extensive attention. Therefore, the characteristics between liquid metals and gas have been investigated. A numerical simulation method was used to analyse the characteristics of heat transfer and flow resistance between a liquid LBE and helium (Chen et al., 2013). Wang et al. (2017) experimentally investigated the heat transfer characteristics of a liquid LBE and helium in a heat exchanger, and the influences of inlet temperature and inlet fluid mass flow rate on the total heat transfer coefficient were analysed. Liu et al. (2018) designed a noncontact double-wall straight tube heat exchanger for a Kylin-II circuit, and the SST
It is well known that the heat needed to be recovered in the gas Brayton cycle is considerable, so the heat exchange efficiency and size of the regenerator are more prominent (Xu et al., 2020). Compared with shell and tube heat exchangers, printed circuit heat exchangers (PCHEs) have been applied in thermal power and solar power generation systems because of their high heat exchange efficiency, small size and high safety. The development of supercritical carbon dioxide flow and heat transfer characteristics have been classified and summarized in PCHEs according to experimental and numerical simulation results (Huang et al., 2019). An experimental study was conducted on a PCHE regenerator with discontinuous biased rectangular and airfoil fins (Pidaparti et al., 2019), and the local and average heat transfer coefficients and pressure drops under different operating conditions related to the supercritical carbon dioxide (SCO2)-Brayton cycle were measured. Li et al. (2019) studied the influence of inlet temperature and pressure of SCO2 on the overall heat transfer performance of a sawtooth finned PCHE, and an evaluation method was proposed for the overall heat transfer performance considering the influence of operating temperature and pressure. Aneesh et al. (2018) performed a numerical analysis on a simplified numerical model of a single-row PCHE in a helium–helium countercurrent loop and studied the properties of local flow and heat transfer in a periodic channel. Saeed and Kim, 2017 performed a regional optimization of a SCO2 PCHE, which significantly reduced the computation time without affecting the accuracy of the solution.
Most of the literature above has shown PCHEs used as regenerators in the Breton cycle, and the heat transfer characteristics were mainly studied between gases. However, there are few studies on PCHEs as intermediate heat exchangers for primary and secondary circuits of nuclear reactors. The thermal-hydraulic performance of a PCHE was studied with FLiNaK and helium as working fluids (Kim and Sun. 2014), and a reasonable PCHE design method was proposed. FLiNaK and carbon dioxide as working fluids were considered in a PCHE by Kim et al. (2016). They evaluated the influences of the different channel types on economy and proposed the best kinds of channel configuration for PCHEs. To obtain the heat transfer characteristics of SCO2 and liquid metal in PCHEs, Cong et al. (2021) performed a numerical simulation on liquid metal sodium and SCO2 by using SST
At present, model tests and numerical simulations of liquid LBEs are widely performed in circular pipes, annular channels or outside tube bundles. Meanwhile, the heat transfer characteristics of fluids in the D-type channels of PCHEs are mainly focused on fluids such as supercritical carbon dioxide, helium and sodium. Nevertheless, no experimental data or simulation results for the flow and heat transfer characteristics of a liquid LBE in D-type channels have been published thus far. In the current work, to predict the convective heat transfer characteristics of a liquid LBE, a numerical simulation method with the SST
A PCHE is fabricated by flat metal plates with photochemically etched D-type channels. The diameter of the D-type channel is generally 1–2 mm. Compared with shell and tube heat exchangers, the PCHE has a smaller size and superior heat transfer efficiency; the diffusion welding process is used to ensure safety. In this paper, the heat transfer and resistance characteristics of D-type channels with different equivalent diameters are studied by a numerical simulation method. Based on the operational experience of a Russian liquid lead–bismuth reactor, it is believed that the liquid flow rate should be less than 2 m/s because mechanical corrosion can become a serious problem when the fluid velocity is high, especially for liquid heavy metals (Zhang et al., 2013). Therefore, the flow and heat transfer characteristics of the liquid LBE were studied at velocities of 0.2–2.2 m/s in this paper. The structural details of the D-type channel are shown in Figure 1. A shows a straight channel model, B and C show zigzag channels with different angles, and D shows a cross section of the D-type channel. Numerical simulation working conditions and the structural details for the D-type channels are described in Table 1.
In recent years, computational fluid dynamics (CFD) has been widely used in the prediction of flow and heat transfer characteristics of liquid metals. Under the condition of constant wall heat flux, the
To comprehensively assess the applicability of the
Mass equation:
Momentum equation:
Energy equation:
where
Shear‒stress transport (SST) k–ω equations:
where
where
where
At a high Reynolds number,
Turbulent viscosity:
where y is the distance to the next surface.
The constants in the SST
For liquid metals, numerous correlations have been proposed for convective heat transfer calculations by theoretical analysis and experimental research. Universally, the Nusselt number
where
Johnson et al. (1953), Buhr et al. (1968) and Ibragimov et al. (1962) used experimental methods to investigate the heat transfer characteristics of a liquid LBE in a vertical circular pipe, and they obtained experimental data in the range of 200–10,000. The experimental data and their fitted curves are presented in Figure 2. The correlations proposed by scholars are summarized in Table 3; a comparison between the fitted curves of the experimental data and the correlations proposed by scholars is shown in Figure 3.
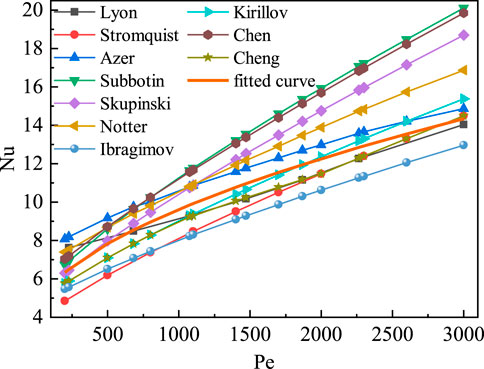
FIGURE 3. Comparison of heat transfer correlations and the fitted curve in Figure 2.
As seen in Figure 2, the calculation results of the correlations proposed by Lyon. (1951), Stromquist (1953), Azer and Chao. (1961), Skupinski et al. (1965), Chen and Chiou. (1981), Sleicher et al. (1973) and Subbotin et al. (1963) are larger than the fitted curve, and the deviations are large. The calculated result of the correlation proposed by Ibragimov et al. (1962) is less than the fitted curve. Therefore, these models are not effective in describing the turbulent heat transfer of liquid metals. The heat transfer correlation proposed by Cheng and Tak. (2006) is in piecewise form. When
The melting point of the liquid LBE is 125°C, and the physical properties of the liquid LBE are only a function of temperature (Organisation For Economic Co-Operation And Development Nuclear Energy Agency, 2015). At atmospheric pressure, the physical parameters of the liquid LBE are completely different from those of conventional fluids such as air and water. The density of the liquid LBE is 12,500–35,000 times that of air and 20,000–55,000 times that of water in the range of 150–1,000°C. The Prandtl number
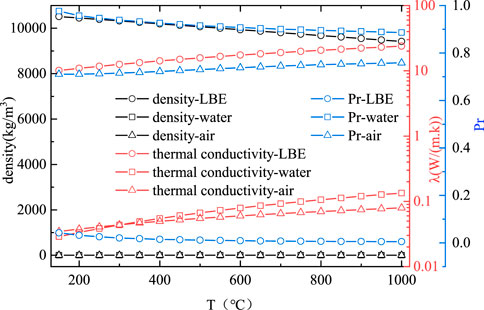
FIGURE 4. Variation in the physical properties of liquid LBE, air and water with different temperatures.
For conventional fluids,
where
To obtain more accurate prediction results, the SST
The
The physical properties of the liquid LBE, such as viscosity, specific heat, thermal conductivity and density, are based on the thermophysical relationships recommended in the guidance manual prepared by the Organization for Economic Cooperation and Development and Nuclear Energy Agency (OECD/NEA) (Organisation For Economic Co-Operation And Development Nuclear Energy Agency, 2015). In this paper, the
The structured mesh with O-type division is adopted for the calculation model, and the grid quantity of meshes ranges between 346,500 and 957,500. The number of boundary layers is set to 10, y+<1, and the
The calculation results show that with the increase in the grid quantity, the difference in liquid LBE pressure drops and
In the present study, 7
To further verify the applicability of the
Taking a D-type straight channel with an equivalent diameter of 3.05 mm as an example, when the fluid velocity varies from 0.2 to 2.2 m/s and the inlet temperature of the liquid LBE and the wall heat flux are constants, the calculated results of the flow and heat transfer characteristics are analysed. Figure 7 shows that the centre flow velocity of the D-type channel reaches the maximum when L/D is equal to 30. If the inlet fluid velocity is less than 1.0 m/s, the flow velocity decreases rapidly. When L/D is equal to 40, the flow velocity reaches a stable value, indicating that the liquid LBE has fully developed. When the fluid velocity is greater than 1.0 m/s, the fluid velocity reaches the maximum value and then maintains the stable value directly. Figure 8 illustrates that if the fluid velocity is low, the thickness of the boundary layer in the channel is large, and the heat transfer coefficient of the fluid fluctuates along the pipe length. When the flow velocity is greater than 1.0 m/s, the heat transfer coefficient of the fluid along the pipe length decreases to a certain value and then tends to be stable.
The liquid LBE in D-type channels with equivalent diameters of 1.53 mm, 3.05 mm, 4.58 mm and 6.1 mm were studied by a numerical simulation method, and the effects of diameters, fluid velocity, inlet temperature and wall heat flux on the heat transfer characteristics were analysed. As seen in Figure 9A, the calculation results show that
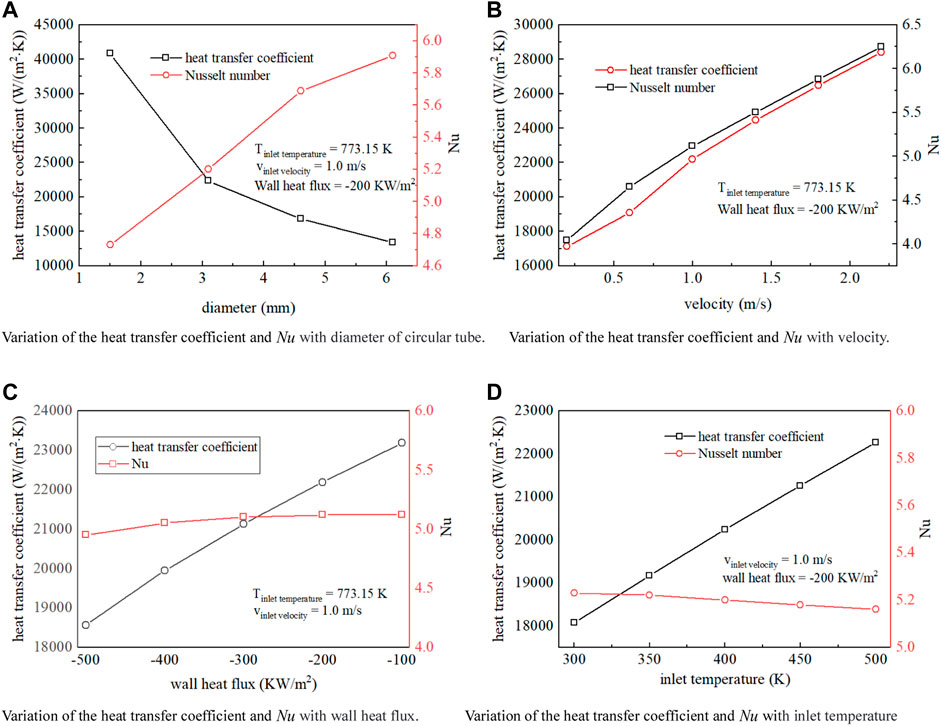
FIGURE 9. Variation of the heat transfer coefficient and
Compared with the circular tube, for the special structural form of the D-type channel, under the condition of constant wall heat flux, the liquid LBE convective heat transfer correlation was proposed. The equation shown in Eq. 17. The application scope of
Generally, the design of a special structure can strengthen the heat transfer characteristics of the fluid. Numerical simulation calculation for the heat transfer characteristics of liquid LBE was performed on the straight channel and the zigzag channel at the same boundary conditions. As seen in Figure 10, the wall temperature of the zigzag channel is higher than that of the straight channel at the same flow velocity. The calculation results also show that the wall temperature decreases with increasing flow velocity, and the wall temperature increases with increasing zigzag channel angle. As shown in Figure 11, with increasing fluid flow velocity,
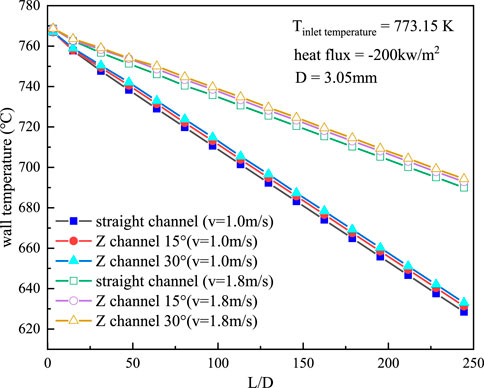
FIGURE 10. Variation in wall temperature along the circular tube for different D-type channels at different velocities.
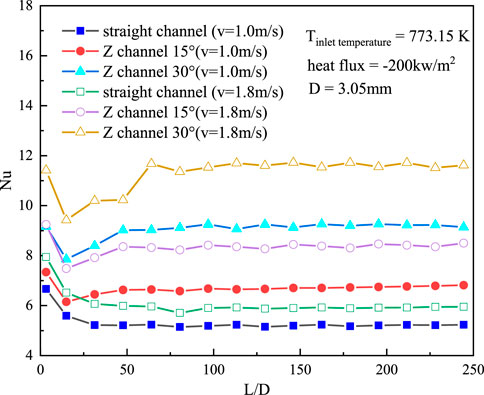
FIGURE 11. Variation in
Although the design of the special structure can strengthen the convective heat transfer of the liquid LBE, it also increases the resistance of the fluid. In the current research, numerical simulation calculations were performed on the resistance characteristics of a straight channel with four equivalent diameters. As seen in Figure 12, at specified boundary conditions, the fluid resistance of liquid LBE increases with the velocity. At the same flow velocity, the smaller the equivalent diameter is, the greater the fluid resistance is. Figure 13 shows the resistance characteristics of the straight channel and zigzag channel. When the equivalent diameter of D-type channels and flow velocity are the same, the resistance of the fluid in the zigzag channel is greater than that in the straight channel, and the larger the angle of the zigzag channel is, the greater the resistance of the liquid LBE is, which is more obvious at high flow velocity. At the same zigzag channel angle, the fluid resistance increases with the flow velocity, which is in accord with the variation tendency of fluid resistance in the straight D-type channel, and the increase in fluid resistance is much larger than that caused by the increase in flow velocity in the straight channel. Therefore, if the design of the D-type channel heat exchanger is performed, the flow velocity of the fluid could not be too high, such as the choice of zigzag channel. It is suggested that the angle of the zigzag channel should not exceed 15°; otherwise, the resistance of the heat exchanger will be very large, resulting in the economic decline of the whole heat exchange system.
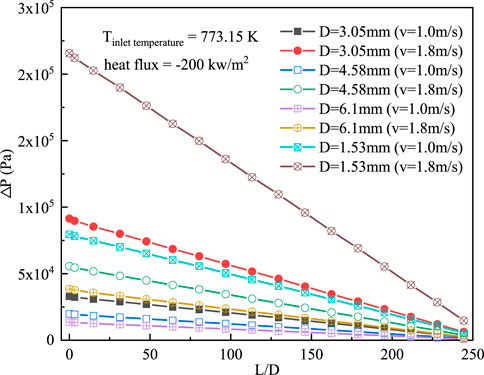
FIGURE 12. Variation in the pressure drop along the circular tube for different diameter channels at different velocities.
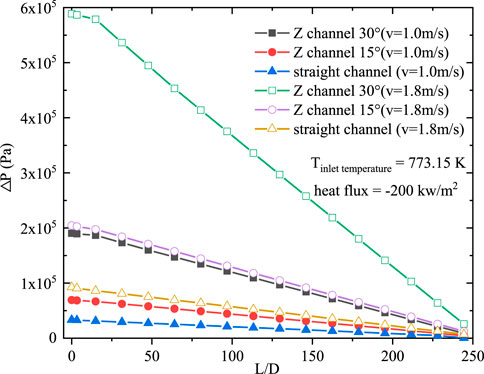
FIGURE 13. Variation in the pressure drop along the circular tube for different D-type channels at different velocities.
In this paper, the SST
1) The
2) To obtain the numerical simulation results of liquid LBE in a circular pipe, the improvement model was proposed in this paper. In addition, the improvement
3) The heat transfer characteristics of liquid LBE were analysed in the current study, including variation of the heat transfer coefficient and
4) The numerical simulation results of liquid LBE in D-type channels show that the heat transfer can be enhanced by reducing the equivalent of the D-channel or adopting a zigzag channel. The zigzag channel could obviously strengthen the heat transfer effect, but the increase in resistance was also particularly prominent. Therefore, it is necessary to comprehensively evaluate the resistance and heat transfer characteristics of zigzag channels when designing PCHEs with special D-type channels.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
HL: experimental data analysis, writing. ZZ: supervision, review and editing. HD: resources, conceptualization. TC: project review.
This research was supported by National Key R&D Program of China (grant number 2020YFB1901804), CNNC’s Pilot-innovation Research Project, National Natural Science Foundation of China (grant number 52176151) and Fundamental Research Funds for the Central Universities of China (grant number 3072022TS1503).
The authors thank them for their financial support.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Aneesh, A. M., Sharma, A., Srivastava, A., and Chaudhury, P. (2018). Effects of wavy channel configurations on thermal-hydraulic characteristics of printed circuit heat exchanger (pche). Int. J. Heat Mass Transf. 118, 304–315. doi:10.1016/j.ijheatmasstransfer.2017.10.111
Aoki, S. (1963). A consideration on the heat transfer in liquid metal. Grafit-Gabrijel D.o.o. doi:10.1016/S0016-5085(13)60330-3
Azer, N. Z., and Chao, B. T. (1961). Turbulent heat transfer in liquid metals-fully developed pipe flow with constant wall temperature. Int. J. Heat Mass Transf. 3 (2), 77–83. doi:10.1016/0017-9310(61)90069-2
Buhr, H. O., Carr, A. D., and Balzhiser, R. E. (1968). Temperature profiles in liquid metals and the effect of superimposed free convection in turbulent flow. Int. J. Heat Mass Transf. 11 (4), 641–654. doi:10.1016/0017-9310(68)90067-7
Chen, C. J., and Chiou, J. S. (1981). Laminar and turbulent heat transfer in the pipe entrance region for liquid metals. Int. J. Heat. Mass Transf. 24 (7), 1179–1189. doi:10.1016/0017-9310(81)90167-8
Chen, F., Huai, X., Cai, J., Li, X., and Meng, R. (2013). Investigation on the applicability of turbulent-Prandtl-number models for liquid lead-bismuth eutectic. Nucl. Eng. Des. 257, 128–133. doi:10.1016/j.nucengdes.2013.01.005
Cheng, X., and Tak, N. I. (2006). Investigation on turbulent heat transfer to lead–bismuth eutectic flows in circular tubes for nuclear applications. Nucl. Eng. Des. 236 (4), 385–393. doi:10.1016/j.nucengdes.2005.09.006
Cong, T., Wang, Z., Zhang, R., Wang, B., and Zhu, Y. (2021). Thermal-hydraulic performance of a pche with sodium and sco2 as working fluids. Ann. Nucl. Energy 157, 108210. doi:10.1016/j.anucene.2021.108210
Duponcheel, M., Bricteux, L., Manconi, M., Winckelmans, G., and Bartosiewicz, Y. (2014). Assessment of RANS and improved near-wall modeling for forced convection at low Prandtl numbers based on LES up to Reτ=2000. Int. J. Heat. Mass Transf. 75, 470–482. doi:10.1016/j.ijheatmasstransfer.2014.03.080
Groetzbach, G. (2003). “Turbulence modeling issues in ADS thermal and hydraulic analyses,” in IAEA Technical Meeting on Theoretical and Experimental Studies of Heavy Liquid Metal Thermal Hydraulics, Karlsruhe, Germany, November 2003 (IAEA-TEC-DOC).
Guo, J., and Huai, X. (2013). Thermodynamic analysis of lead–bismuth eutectic turbulent flow in a straight tube. Energy 57 (1), 600–606. doi:10.1016/j.energy.2013.05.008
Huang, C., Cai, W., Wang, Y., Liu, Y., and Li, B. (2019). Review on the characteristics of flow and heat transfer in printed circuit heat exchangers. Appl. Therm. Eng. 153, 190–205. doi:10.1016/j.applthermaleng.2019.02.131
Ibragimov, M. K., Subbotin, V. I., and Ushakov, P. A. (1962). Investigation of heat transfer for turbulent flow of heavy liquid metals in tubes. J. Nucl. Energy. Parts A/B. React. Sci. Technol. 16 (3), 174–175. doi:10.1016/0368-3230(62)90094-0
Jaeger, W. (2016). Empirical models for liquid metal heat transfer in the entrance region of tubes and rod bundles. Heat. Mass Transf. 53 (5), 1667–1684. doi:10.1007/s00231-016-1929-8
Jaeger, W. (2017). Heat transfer to liquid metals with empirical models for turbulent forced convection in various geometries. Nucl. Eng. Des. 319, 12–27. doi:10.1016/j.nucengdes.2017.04.028
Jischa, M., and Rieke, H. B. (1979). About the prediction of turbulent Prandtl and schmidt numbers from modeled transport equations. Int. J. Heat. Mass Transf. 22 (11), 1547–1555. doi:10.1016/0017-9310(79)90134-0
Johnson, H. A., Hartnett, J. P., and Clabaugh, W. J. (1953). Heat transfer to molten lead-bismuth eutectic in turbulent pipe flow. J. Fluids Eng. 75 (6), 1191–1198. doi:10.1115/1.4015579
Kays, W. M. (1994). Turbulent Prandtl number—Where are we? J. Heat. Transf. 116 (2), 284–295. doi:10.1115/1.2911398
Kays, W. M., Crawford, M. E., and Weigand, B. (2004). Convective heat and mass transfer. New York: The McGraw-Hill Companies, Inc.
Kim, I., and Sun, X. (2014). CFD study and PCHE design for secondary heat exchangers withFLiNaK-Helium for SmAHTR. Nucl. Eng. Des. 270, 325–333. doi:10.1016/j.nucengdes.2014.02.003
Kim, I., Zhang, X., Richard, C., and Sun, X. (2016). Design study and cost assessment of straight, zigzag, S-shape, and OSF PCHEs for a FLiNaK–SCO2 Secondary Heat Exchanger in FHRs. Ann. Nucl. Energy 94, 129–137. doi:10.1016/j.anucene.2016.02.031
Kirillov, P. L., and Ushakov, P. A. (2001). Heat transfer to liquid metals: Specific features, methods of investigation, and main relationships. Int. J. Heat. Mass Transf. 48 (1), 50–59.
Li, H., Deng, T., Ma, T., Ke, H., and Wang, Q. (2019). A new evaluation method for overall heat transfer performance of supercritical carbon dioxide in a printed circuit heat exchanger. Energy Convers. Manag. 193, 99–105. doi:10.1016/j.enconman.2019.04.061
Liu, S., Jin, M., Lyu, K., Zhou, T., and Zhao, Z. (2018). Flow and heat transfer behaviors for double-walled-straight-tube heat exchanger of HLM loop. Ann. Nucl. Energy 120, 604–610. doi:10.1016/j.anucene.2018.06.016
Lyon, R. N. (1951). Liquid metal heat transfer coefficients. Chem. Eng. Prog. 47, 75–79. doi:10.1007/BF00412000
Marocco, Luca, and Garita, Francesco (2018). Large eddy simulation of liquid metal turbulent mixed convection in a vertical concentric annulus. J. Heat. Transf. 140 (7), 072504. doi:10.1115/1.4038858
Marocco, L., Valmontana, A., and Wetzel, T. (2017). Numerical investigation of turbulent aided mixed convection of liquid metal flow through a concentric annulus. Int. J. Heat Mass Transf. 105, 479–494. doi:10.1016/j.ijheatmasstransfer.2016.09.107
Menter, F. R. (1994). Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 32 (5), 1598–1605. doi:10.2514/3.12149
Menter, F. R. “Zonal two equation k-w turbulence models for aerodynamic flows,” in 24th Fluid Dynamics Conference, Orlando,FL,U.S.A, July 1993 (Reston: AIAA). doi:10.2514/6.1993-2906
Organisation For Economic Co-Operation And Development Nuclear Energy Agency (2015). Handbook on lead-bismuth Butectic alloy and lead properties, materials Compatibility, thermal-hydraulics and Technologies. OECD.
Pacio, J., Daubner, M., Fellmoser, F., Litfin, K., and Wetzel, T. (2016). Experimental study of heavy-liquid metal (LBE) flow and heat transfer along a hexagonal 19-rod bundle with wire spacers. Nucl. Eng. Des. 301, 111–127. doi:10.1016/j.nucengdes.2016.03.003
Pidaparti, Sandeep R., Anderson, Mark H., and Ranjan, Devesh (2019). Experimental investigation of thermal-hydraulic performance of discontinuous fin printed circuit heat exchangers for supercritical CO2 power cycles. Exp. Therm. Fluid Sci. 106, 119–129. doi:10.1016/j.expthermflusci.2019.04.025
Reynolds, A. J. (1975). The prediction of turbulent Prandtl and schmidt numbers. Int. J. Heat. Mass Transf. 18 (9), 1055–1069. doi:10.1016/0017-9310(75)90223-9
Roelofs, F., Gerschenfeld, A., Tarantino, M., Tichelen, K., and Pointer, W. D. (2019). “Thermal-hydraulic challenges in liquid-metal-cooled reactors-sciencedirect,” in Thermal Hydraulics aspects of liquid metal cooled nuclear reactors, 17–43. doi:10.1016/B978-0-08-101980-1.00002-8
Saeed, M., and Kim, M. H. (2017). Thermal and hydraulic performance of SCO2 PCHE with different fin configurations. Appl. Therm. Eng. 127, 975–985. doi:10.1016/j.applthermaleng.2017.08.113
Skupinski, E., Tortel, J., and Vautrey, L. (1965). Determination des coefficients de convection d'un alliage sodium-potassium dans un tube circulaire. Int. J. Heat Mass Transf. 8 (6), 937–951. doi:10.1016/0017-9310(65)90077-3
Sleicher, C. A., Awad, A. S., and Notter, R. H. (1973). Temperature and eddy diffusivity profiles in NaK. Int. J. Heat. Mass Transf. 16 (8), 1565–1575. doi:10.1016/0017-9310(73)90184-1
Stromquist (1953). Effect of WETTING on heat transfer characteristics of liquid metals. [Tennessee Univ]. The University of Tennessee. [Technical Report ].
Subbotin, V. I., Papovyants, A. K., Kirillov, P. L., and Ivanovskii, N. N. (1963). A study of heat transfer to molten sodium in tubes. Soviet J. Atomic Energy 13 (4), 991–994. doi:10.1007/BF01480861
Thiele, R., and Anglart, H. (2013). Numerical modeling of forced-convection heat transfer to lead–bismuth eutectic flowing in vertical annuli. Nucl. Eng. Des. 254, 111–119. doi:10.1016/j.nucengdes.2012.09.006
Wang, C., Wang, C., Zhang, Y., Zhang, D., Tian, W., Qiu, H., et al. (2021). Investigation on flow heat transfer characteristic of lead-bismuth eutectic alloy. Atomic Energy Sci. Technol. 55 (5), 822–828. doi:10.7538/yzk.2020.youxian.0356
Wang, Y., Li, X., Huai, X., Cai, J., and Xi, W. (2017). Experimental investigation of a lbe-helium heat exchanger based the ads. Prog. Nucl. Energy 99, 11–18. doi:10.1016/j.pnucene.2017.04.013
Xu, J., Liu, C., Sun, E., et al. (2020). Review and perspective of supercritical carbon dioxide power cycles. Therm. Power Gener. 49 (10), 1–10. doi:10.19666/j.rlfd.202004089
Zhang, J., Kapernick, R. J., Mcclure, P. R., and Trapp, T. J. (2013). Lead-bismuth eutectic technology for hyperion reactor. J. Nucl. Mater. 441 (1-3), 644–649. doi:10.1016/j.jnucmat.2013.04.079
Zhang, Y., Wang, C., Lan, Z., Wei, S., Chen, R., Tian, W., et al. (2020). Review of thermal-hydraulic issues and studies of lead-based fast reactors. Renew. Sustain. Energy Rev. 120, 109625. doi:10.1016/j.rser.2019.109625
Zhao, P., Zhu, J., Ge, Z., Liu, J., and Li, Y. (2018). Direct numerical simulation of turbulent mixed convection of LBE in heated upward pipe flows. Int. J. Heat. Mass Transf. 126, 1275–1288. doi:10.1016/j.ijheatmasstransfer.2018.05.104
Zhu, F., Junmei, W. U., Shi, L., and Guanghui, S. U. (2019). Experimental study on flow and heat transfer characteristic of liquid lead-bismuth eutectic in annular channel. Atomic Energy Sci. Technol. 53 (5), 819–825. doi:10.7538/yzk.2018.youxian.0495
Keywords: printed circuit heat exchange, turbulent Prandtl number, lead-bismuth eutectic, D-type channel, heat transfer correlation
Citation: Liu H, Zhang Z, Du H and Cong T (2022) Numerical study on the heat transfer characteristics of a liquid lead–bismuth eutectic in a D-type channel. Front. Energy Res. 10:1041900. doi: 10.3389/fenrg.2022.1041900
Received: 11 September 2022; Accepted: 24 October 2022;
Published: 09 November 2022.
Edited by:
Songbai Cheng, Sun Yat-sen University, ChinaCopyright © 2022 Liu, Zhang, Du and Cong. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhigang Zhang, emdfemhhbmdAaHJiZXUuZWR1LmNu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.