lp-CMFD acceleration schemes in multi-energy group 2D Monte Carlo transport

The linear prolongation flux update scheme is extended to both regular CMFD acceleration, as well as partial CMFD acceleration in 2D multi energy group Monte Carlo k-eigenvalue neutron transport problems. The acceleration performance of these CMFD variants were investigated in simple 2D slab geometries, first with a monoenergetic case and then with a three group problem on the same geometry based on the monoenergetic cross sections. Flux convergence was determined via an on-the-fly convergence diagnostics developed by Ueki and Brown. It is found that on top of providing better acceleration in general, the linear prolongation scheme is also able to correct for instabilities in the CMFD scheme. Overall, the lp-pCMFD scheme employing a maximum history length is found to have the best performance across the cases presented.

Introduction

In Monte Carlo (MC) calculations of the k-eigenvalue neutron transport problems, fission source iteration may have slow convergence in cases with high dominance ratios. Acceleration methods applied in MC calculations include the Coarse Mesh Finite Difference (CMFD) acceleration scheme, which was originally developed for the acceleration of deterministic neutron transport calculations. The CMFD acceleration scheme employs a diffusion-based calculation on a coarse mesh grid, for which the solution is used to update the transport flux. The use of coarse mesh is suitable efficient diffusion calculation in exceedingly fine mesh calculations or where the fine mesh geometry is complex. The effectiveness of the CMFD acceleration methods employed in MC transport calculations has been demonstrated (Lee et al., 2010; Hunter, 2014; Lee et al., 2014). CMFD variants include partial CMFD (pCMFD), where partial current drift coefficients, as opposed to net currents, are utilised in the diffusion calculation. pCMFD is also known to be unconditionally stable, unlike regular CMFD, though it has shown to be a bit slower in deterministic transport calculations for problems with small and intermediate optical thickness. Several works have also successfully incorporated the pCMFD scheme in place of regular CMFD in continuous energy MC calculations (Yun and Cho, 2010; Jo and Cho, 2018a; Jo and Cho, 2018b).

Another CMFD variant is the linear prolongation CMFD (lp-CMFD) scheme, which is a method first proposed by Wang and Xiao (2018). Where regular CMFD updates the fine mesh flux in a coarse mesh basis after the diffusion step, lp-CMFD uses a linear additive approach from bilinear interpolation of the coarse mesh flux to update the fine mesh scalar flux, thereby resulting in a smoother transport flux update. Employing the linear prolongation in pCMFD results in a lp-pCMFD scheme, which can also be considered. The lp-CMFD scheme has been employed in deterministic transport problems with various spatial discretisation schemes, which demonstrated improved acceleration and stability (Chan and Xiao, 2019a; Chan and Xiao, 2019b; Chan and Xiao, 2019c; Chan and Xiao, 2020a; Chan and Xiao, 2020b). Following the results in deterministic calculations, lp-CMFD and lp-pCMFD schemes has also been employed in 1D slab MC transport calculations (Chan and Xiao, 2021), as well as in a 2D homogenous slab (Abdullatif and Wang, 2022; Than and Xiao, 2022), where its effectiveness relative to regular CMFD is once again demonstrated. Among the CMFD variants investigated in the aforementioned works, the most efficient scheme can vary depending on factors such as the total cross section values.

In this work, we further build on Monte-Carlo simulations of 2D geometries using lp-CMFD based acceleration schemes, with multi energy group and non-homogenous domains. A monoenergetic case will be first studied as a base line and then a three energy group problem based on the monoenergetic case will be investigated. Differences in the performance of each acceleration scheme going from single to multi-energy group will be discussed.

Theory and methodology

The neutron flux ψ(r, Ω, E) is typically split into discrete energy groups (as neutron flux ψ_g(r, Ω)) in neutron transport, where r is the spatial coordinate, Ω is the direction of the neutron velocity, E is the neutron energy and g is the energy group index. The k-eigenvalue time-independent neutron transport equation is thus split into a system of coupled transport equations for each group:

$\begin{array}{cc}\hfill & \mathbf{\Omega }\cdot \nabla {\psi }_g\left(\mathbf{r},\mathbf{\Omega }\right)+{\sigma }_{tg}\left(\mathbf{r}\right){\psi }_g\left(\mathbf{r},\mathbf{\Omega }\right)\hfill \\ \hfill & =\frac{1}{4\pi }\sum _{g^{\prime }}{\sigma }_{s{g}^{\prime }g}\left(\mathbf{r}\right){\varphi }_{g^{\prime }}\left(\mathbf{r}\right)+\frac{1}{4\pi }\sum _{g^{\prime }}{\chi }_g\frac{\nu }{k}{\sigma }_{f{g}^{\prime }}\left(\mathbf{r}\right){\varphi }_{g^{\prime }}\left(\mathbf{r}\right)\hfill \end{array}(1)$

where ϕ_g(r) = ∫ψ_g(r, Ω′) dΩ′ is the scalar flux. σ_tg, σ_sg′g and σ_fg′ are the group discretised total, scattering and fission cross sections respectively. ν is the average fission multiplicity. Xg is the fission energy spectrum. keff is the multiplication factor.

CMFD acceleration schemes aim to solve a simpler diffusion based equation that is obtained by first integrating Eq. 1 over Ω:

$\begin{array}{cc}\hfill & \nabla \cdot {\mathbf{J}}_g\left(\mathbf{r}\right)+{\sigma }_{tg}\left(\mathbf{r}\right){\varphi }_g\left(\mathbf{r}\right)\hfill \\ \hfill & =\sum _{g^{\prime }}{\sigma }_{s{g}^{\prime }g}\left(\mathbf{r}\right){\varphi }_{g^{\prime }}\left(\mathbf{r}\right)+\sum _{g^{\prime }}{\chi }_g\frac{\nu }{k}{\sigma }_{f{g}^{\prime }}\left(\mathbf{r}\right){\varphi }_{g^{\prime }}\left(\mathbf{r}\right)\hfill \end{array}(2)$

where J is the neutron current. Further integrating Eq. 2 over each coarse mesh gives the CMFD equations:

$\begin{array}{cc}\hfill & \sum _{m^{\prime }\in N\left(m\right)}\frac{A_{m{m}^{\prime }}}{V_m}{J}_{gm{m}^{\prime }}+{\sigma }_{\mathit{tgm}}{\varphi }_{gm}\hfill \\ \hfill & =\sum _{g^{\prime }}{\sigma }_{s{g}^{\prime }gm}{\varphi }_{g^{\prime }m}+\sum _{g^{\prime }}{\chi }_g\frac{\nu }{k}{\sigma }_{f^{\prime }gm}{\varphi }_{g^{\prime }m}\hfill \end{array}(3)$

where m is the coarse mesh cell index with volume V_m, with N(m) being the cells neighbouring cell m. J_gmm’ is the group neutron current from cell m to m′ while A_mm’ adjoining surface area between cells m and m′.

Subsequently, a diffusion equation is obtained via Fick’s law with a nonlinear correction term $\widehat{D}$:

$J_{gm{m}^{\prime }}={\tilde{D}}_{gm{m}^{\prime }}\left({\varphi }_{gm}-{\varphi }_{g{m}^{\prime }}\right)+{\widehat{D}}_{gm{m}^{\prime }}\left({\varphi }_{gm}+{\varphi }_{g{m}^{\prime }}\right)(4)$

where

${\tilde{D}}_{gm{m}^{\prime }}=\frac{2D_{gm}{D}_{g{m}^{\prime }}}{h_{m{m}^{\prime }}\left(D_{gm}+D_{g{m}^{\prime }}\right)}(5)$

and

${\widehat{D}}_{gm{m}^{\prime }}=\frac{{\bar{J}}_{gm{m}^{\prime }}-{\tilde{D}}_{gm{m}^{\prime }}\left({\bar{\varphi }}_{gm}-{\bar{\varphi }}_{g{m}^{\prime }}\right)}{{\bar{\varphi }}_{gm}+{\bar{\varphi }}_{g{m}^{\prime }}}(6)$

with $D_{gm}=\frac{1}{3{\sigma }_{\mathit{tgm}}}$. h_mm′ refers to the distance from the center of coarse mesh cell m to the m/m′ surface and the overbars indicate values calculated from the most recent MC fine mesh transport flux.

pCMFD employs partial currents J⁺ and J⁻ instead of the total current J, thus pCMFD equations equivalent to Eq. 4 will be

$J_{gm{m}^{\prime }}={\tilde{D}}_{gm{m}^{\prime }}\left({\varphi }_{gm}-{\varphi }_{g{m}^{\prime }}\right)+{\widehat{D}}_{gm{m}^{\prime }}^{+}{\varphi }_{gm}-{\widehat{D}}_{gm{m}^{\prime }}^{-}{\varphi }_{gm}(7)$

with

${\widehat{D}}_{gm{m}^{\prime }}^{+}=\frac{{\bar{J}}_{gm{m}^{\prime }}^{+}-{\tilde{D}}_{gm{m}^{\prime }}\left({\bar{\varphi }}_{gm}-{\bar{\varphi }}_{g{m}^{\prime }}\right)}{{\bar{\varphi }}_{gm}}(8)$

and

${\widehat{D}}_{gm{m}^{\prime }}^{-}=\frac{{\bar{J}}_{gm{m}^{\prime }}^{-}-{\tilde{D}}_{gm{m}^{\prime }}\left({\bar{\varphi }}_{g{m}^{\prime }}-{\bar{\varphi }}_{gm}\right)}{{\bar{\varphi }}_{g{m}^{\prime }}}(9)$

The overall flowchart of a CMFD-based acceleration is given in Figure 1. After each Monte Carlo transport step, the flux and currents are tallied in the coarse mesh to compute the coefficients in the CMFD or pCMFD calculation. Following the CMFD or pCMFD solution, the MC fine mesh is then updated in either a coarse mesh or fine mesh basis. Updating the fine mesh flux via the linear prolongation method gives rise to the “lp” variant of the acceleration schemes (lp-CMFD and lp-pCMFD), which provides the 4 acceleration scheme variants to be investigated in this work. In regular or CMFD and pCMFD acceleration, the neutron weights w_n are updated according to

${\tilde{w}}_n=\frac{w_n{N}_p{p}_{M\left(n\right)}}{W_n}(10)$

where

$W_n=\sum _{n^{\prime }:M\left(n^{\prime }\right)=M\left(n\right)}{w}_{n^{\prime }}(11)$

to obtain the modified neutron weights ${\tilde{w}}_n$. N_p is the total neutron count, M(n) refers to the coarse mesh cell index from with neutron n originates while

$p_m=\sum _g\frac{{\chi }_g\nu {\sigma }_{fg}{\varphi }_{mg}{V}_m}{{\sum }_{m^{\prime }}{\chi }_g\nu {\sigma }_{fg}{\varphi }_{m^{\prime }g}{V}_{m^{\prime }}}(12)$

is the neutron source fraction, where the scalar flux is updated according to

${\varphi }_{g,fine}^{\mathit{new}}={\varphi }_{g,fine}^{\mathit{old}}\frac{{\mathrm{\Phi }}_{g,coarse}^{\mathit{new}}}{{\mathrm{\Phi }}_{g,coarse}^{\mathit{old}}}(13)$

In lp-CMFD and lp-pCMFD schemes, the CMFD flux is projected back on to the fine mesh flux according to the linear approach described by Wang and Xiao (Wang and Xiao, 2018) the weights are then updated on a fine mesh basis based on the updated fine mesh flux. Instead of Eq. 13, the update of scalar flux is achieved via

${\varphi }_{g,fine}^{\mathit{new}}={\varphi }_{g,fine}^{\mathit{old}}+\mathrm{\Delta }{\varphi }_{g,fine}(14)$

where

$\begin{array}{cc}\hfill \mathrm{\Delta }{\varphi }_{g,fine}& =\frac{x}{{\mathrm{\Delta }}_x}\left(\delta {\mathrm{\Phi }}_{g,i+\frac{1}{2},j-\frac{1}{2}}-\delta {\mathrm{\Phi }}_{g,i-\frac{1}{2},j-\frac{1}{2}}\right)\hfill \\ \hfill & +\frac{xy}{{\mathrm{\Delta }}_x{\mathrm{\Delta }}_y}\left(\delta {\mathrm{\Phi }}_{g,i+\frac{1}{2},j+\frac{1}{2}}-\delta {\mathrm{\Phi }}_{g,i-\frac{1}{2},j+\frac{1}{2}}\right.\hfill \\ \hfill & \left.+\delta {\mathrm{\Phi }}_{g,i-\frac{1}{2},j-\frac{1}{2}}-\delta {\mathrm{\Phi }}_{g,i+\frac{1}{2},j-\frac{1}{2}}\right)\hfill \\ \hfill & +\frac{y}{{\mathrm{\Delta }}_y}\left(\delta {\mathrm{\Phi }}_{g,i-\frac{1}{2},j+\frac{1}{2}}-\delta {\mathrm{\Phi }}_{g,i-\frac{1}{2},j-\frac{1}{2}}\right)+\delta {\mathrm{\Phi }}_{g,i+\frac{1}{2},j-\frac{1}{2}}\hfill \end{array}(15)$

is the bilinear interpolation from the estimated corner node δΦ flux corrections as described in Figure 2.

FIGURE 1

FIGURE 1. Overall flowchart of a Monte-Carlo k_eff calculation with CMFD-based acceleration.

FIGURE 2

FIGURE 2. Illustration of linear interpolation scheme in lp-CMFD.

δΦ is the difference between the CMFD (or pCMFD) solution and the pure Monte Carlo solution that is projected into the coarse mesh. The half integer index values of δΦ are the corner node flux corrections given by

$\delta {\mathrm{\Phi }}_{g,i+\frac{1}{2},j+\frac{1}{2}}=\frac{1}{4}\left[\delta {\mathrm{\Phi }}_{g,i,j}+\delta {\mathrm{\Phi }}_{g,i+1,j}+\delta {\mathrm{\Phi }}_{g,i,j+1}+\delta {\mathrm{\Phi }}_{g,i+1,j+1}\right](16)$

The corner node flux corrections located at the boundary can be calculated in similar fashion according to boundary conditions. Following the fine mesh flux update, the neutron weights can then by updated in the same fashion as in Eqs 10, 12 in a fine mesh basis.

The initial MC iterations are considered to be inactive cycles, as the algorithm is still trying to converge to the true solution. The posterior relative entropy method (Ueki and Brown, 2005; Ueki, 2009) is used to determine the criteria for which the solution is sufficiently stable such that subsequent iterations may be classified as active cycles, from which statistical data such as variance and averages may be subsequently calculated. The Shannon entropy H at each cycle is calculated as

$H=\sum _n{\omega }_n{\log }_2\left({\omega }_n\right)(17)$

where

${\omega }_n=\frac{W_n}{{\sum }_{n^{\prime }}{W}_{n^{\prime }}}(18)$

The posterior relative entropy (PRE) is defined as

$\begin{array}{cc}\hfill H_{\mathit{pre}}\left(\omega ||\omega °\right)& =\sum _n{\omega °}_n{\log }_2\left(\frac{{\omega °}_n}{\frac{1}{2}\left({\omega °}_n+{\omega }_n\right)}\right)\hfill \\ \hfill & +\sum _n{\omega }_n{\log }_2\left(\frac{{\omega }_n}{\frac{1}{2}\left({\omega °}_n+{\omega }_n\right)}\right)\hfill \end{array}(19)$

where ω°_n are the ω_n values at the start of cycle 1 (Ueki and Brown, 2005). H_pre). One advantage of this method is that additional simulations for a reference Shannon entropy stationary convergence is not required.

As illustrated in Figure 3, we use a simple toy model following previous work in Ref. (Than and Xiao, 2022) with a central fissile zone (A) surrounded by a non-fissile zone (B) with vacuum boundary conditions. We study two cases based on this geometry, a monoenergetic case with cross sections listed in Table 1, as well as a three energy group case based on the monoenergetic case with cross sections listed Table 2. There are 500 neutrons per fine mesh for the monoenergetic case and 200 neutrons per fine mesh for the three energy group case in the fissile region A of the simulations, with a 48 × 48 fine mesh and a 24 × 24 coarse mesh for the whole domain. The MC neutron transport simulation codes are developed on the MATLAB platform and executed in parallel using 10 cores on the Intel Xeon W-2255 CPU @ 3.70GHz processor. 10 independent simulations are performed for each of the acceleration schemes: CMFD, pCMFD, lp-CMFD, lp-pCMFD with both a history length of 5 as well as using the full history starting from the first cycle.

FIGURE 3

FIGURE 3. Illustration of the domain used in this work, consisting of two square regions of the indicated dimensions with fissile region A and non-fissile region B.

TABLE 1

TABLE 1. Monoenergetic cross section values used in this work, indicated in units cm⁻¹.

TABLE 2

TABLE 2. Three group cross section values used in this work, indicated in units cm⁻¹. Groups are labeled 1 to 3 in decreasing energy.

Results and analysis

For each case, the k_eff values are recorded over 50 active cycles with an average k_eff of 0.974 ± 0.004 for the monoenergetic case and 0.744 ± 0.005 for the three energy group case. The k_eff is lower in the multi group case as the energy group structure poses as an additional barrier between the generated fission neutrons and the next thermal fission reaction. The suitability of the posterior relative entropy method as condition for the active cycle can be seen from Figures 4, 6. The active cycle flux is sufficiently converged in the sense that is suitable for recording statistical data. Figures 4, 6 further enforce this point, as it can be seen that the k_eff and entropy H values reach within fluctuation range of the stationary value well before the active cycle is declared.

FIGURE 4

FIGURE 4. Shannon entropy progression in single group simulations (top) and multi group simulations (bottom) for each of the acceleration schemes employed, averaged over 10 independent simulations, for either a history length of 5 or maximum (whichever performs better).

Even with just 10 independent simulations for each scheme, the effectiveness of the CMFD-based acceleration methods is clear. From Table 3 it can be seen that CMFD schemes cut the number of inactive cycles by around half, though the base CMFD scheme is unstable when considering long history lengths for both the monoenergetic and multi group case. The CMFD flux did not always converge to the correct solution, thus causing the solution to diverge. This instability is corrected with the implementation of linear prolongation flux update, as the lp-CMFD scheme consistently able to converge properly and yield the expected acceleration. It is however noted that the acceleration obtained in 1D MC transport calculations as reported by Chan and Xiao (2021) was much greater in terms of percentage decrease in inactive cycles required. It is clear that the linear prolongation schemes outperform the regular coarse mesh flux update in all cases investigated in this work. It is also interesting to note that while pCFMD schemes perform about equal or slightly worse than regular CMFD with lower history length, extending the history length yields significantly better results on top of being more stable as mentioned, though in all cases pCMFD is still significantly outperformed by lp-CMFD and lp-pCMFD. Having extended history lengths also resulted in a lower variance in the number of inactive cycles required. For the simple monoenergetic system investigated in this work, the lp-pCMFD acceleration proves to be most efficient, followed by the regular lp-CMFD scheme. For the multi energy group case, lp-CMFD and lp-pCMFD produce similar results.

TABLE 3

TABLE 3. Number of inactive cycles required in the single group simulations for each scheme averaged over 10 independent simulations for each acceleration history length. The standard deviation is indicated in the parenthesis. (*) CMFD with maximum history length did not converge.

The shannon entropy progression presented in Figure 4 shows a similar picture. All CMFD-based schemes converge much faster to the stationary value, while lp-CMFD based schemes are even faster in the monoenergetic case. The speed of shannon entropy convergence appears to be primarily influenced by the flux update scheme employed rather the type of CMFD solver used. The posterior relative entropy progression used for on-the-fly convergence analysis presented in Figure 5 mirrors the shannon entropy progression as expected for a diagnostic metric. The k_eff progression is presented Figure 6. There are a few differences in terms of the entropy of the three group problem. First is the pCMFD case, where the shannon entropy converges to the stationary value about as fast as the lp-pCMFD scheme, but interestingly does not reflect an earlier convergence according to the on-the-fly convergence analysis. In the three group case, the lp-CMFD shannon entropy is able to reach its stationary value the earliest, but as Figures 4, 5 show, the value shows fluctuation at first, thus does not result in an earlier active cycle according to the on-the-fly diagnostics. It is also noted in Table 4 that the improvement due to the linear prolongation scheme is slightly more significant when applied to pCFMD versus regular CMFD. In contrast to what Table 3 and Figure 4 suggest, the unaccelerated calculation converges to the stationary k_eff just as quickly as the accelerated calculations. It is however noted that convergence in k_eff is not deemed to be sufficient for overall stationary solution convergence.

FIGURE 5

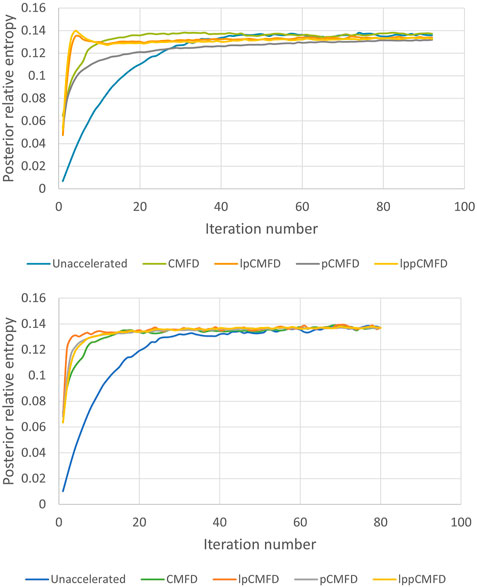
FIGURE 5. Posterior relative entropy progression in single group simulations (top) and multi group simulations (bottom) for each of the acceleration schemes employed, averaged over 10 independent simulations, for either a history length of 5 or maximum (whichever performs better).

FIGURE 6

FIGURE 6. Estimated k_eff progression in single group simulations (top) and multi group simulations (bottom) for each of the acceleration schemes employed for the first 20 cycles, averaged over 10 independent simulations, for either a history length of 5 or maximum (whichever performs better).

TABLE 4

TABLE 4. Number of inactive cycles required in the multigroup simulations for each scheme averaged over 10 independent simulations for each acceleration history length. The standard deviation is indicated in the parenthesis. (*) CMFD with maximum history length did not converge.

Conclusion

In this work, lp-CMFD based acceleration schemes (Wang and Xiao, 2018) are applied to monoenergetic and multi group 2D MC neutron transport calculations with on-the-fly convergence diagnostics (Ueki, 2009). Based on sets of 10 independent simulations, the acceleration given by the CMFD-based schemes in 2D MC neutron transport calculations reduce the inactive cycles required by around half, and is even more efficient with the use of the linear prolongation scheme for flux update. Further, the linear prolongation scheme is able to correct the instability of the CMFD solver at long history lengths. Overall, the linear prolongation-based schemes perform better in both single and multi-group calculations, which lp-pCMFD being the most efficient in single-group and both lp-CMFD and lp-pCMFD yielding similar acceleration in the multi-group simulations.

The shannon entropy of the accelerated schemes also converge much faster than that of the unaccelerated. While the k_eff values in the unaccelerated scheme do converge just as fast as in the accelerated calculations, the slower shannon entropy conversion shows that the overall flux is still much slower to converge without the CMFD-based acceleration schemes.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

YT and SX contributed to conception and design of the study. YT carried out the computational work. YT and SX contributed to writing the manuscript.

Funding

This work was supported by the National Research Foundation Singapore (A-0001360-06-00).

Acknowledgments

The authors thank Chan Yi Meng for the useful resources provided.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdullatif, F., and Wang, D. (2022). “Acceleration of source convergence in Monte Carlo criticality calculation with cmfd schemes,” in International conference on physics of reactors 2022 (PHYSOR 2022), Pittsburgh, PA, 3479–3488.

Google Scholar

Chan, Y., and Xiao, S. (2019a). Convergence study of cmfd and lpcmfd acceleration schemes for k-eigenvalue neutron transport problems in 2-d cartesian geometry with Fourier analysis. Ann. Nucl. Energy 133, 327–337. doi:10.1016/j.anucene.2019.05.035

CrossRef Full Text | Google Scholar

Chan, Y., and Xiao, S. (2020b). A linear prolongating coarse mesh finite difference acceleration of discrete ordinate neutron transport calculation based on discontinuous galerkin finite element method. Nucl. Sci. Eng. 194, 554–571. doi:10.1080/00295639.2020.1752045

CrossRef Full Text | Google Scholar

Chan, Y., and Xiao, S. (2019b). Convergence study of variants of cmfd acceleration schemes for fixed source neutron transport problems in 2d cartesian geometry with Fourier analysis. Ann. Nucl. Energy 134, 273–283. doi:10.1016/j.anucene.2019.06.021

CrossRef Full Text | Google Scholar

Chan, Y., and Xiao, S. (2020a). Implementation and performance study of lpCMFD acceleration method for multi-energy group k-eigenvalue neutron transport problem in hexagonal geometry. Ann. Nucl. Energy 139, 107220. doi:10.1016/j.anucene.2019.107220

CrossRef Full Text | Google Scholar

Chan, Y., and Xiao, S. (2021). Implementation and performance study of the lp-cmfd acceleration scheme for Monte Carlo method based k-eigenvalue neutron transport calculation in 1d geometry. Ann. Nucl. Energy 163, 108562. doi:10.1016/j.anucene.2021.108562

CrossRef Full Text | Google Scholar

Chan, Y., and Xiao, S. (2019c). Theoretical convergence study of lpcmfd for fixed source neutron transport problems in 2d cartesian geometry. Trans. Am. Nucl. Soc. 121, 788–791.

CrossRef Full Text | Google Scholar

Hunter, J. L. (2014). Improvements and applications of the uniform fission site method in Monte Carlo. Massachusetts: Massachusetts Institute of Technology.

Google Scholar

Jo, Y. G., and Cho, N. Z. (2018a). Acceleration and real variance reduction in continuous-energy Monte Carlo whole-core calculation via p-cmfd feedback. Nucl. Sci. Eng. 189, 26–40. doi:10.1080/00295639.2017.1373517

CrossRef Full Text | Google Scholar

Jo, Y. G., and Cho, N. Z. (2018b). Inline critical boron concentration search with p-cmfd feedback in whole-core continuous-energy Monte Carlo simulation. Ann. Nucl. Energy 120, 402–409. doi:10.1016/j.anucene.2018.05.050

CrossRef Full Text | Google Scholar

Lee, M. J., Joo, H. G., Lee, D., and Smith, K. (2014). Coarse mesh finite difference formulationfor accelerated Monte Carlo eigenvalue calculation. Ann. Nucl. Energy 65, 101–113. doi:10.1016/j.anucene.2013.10.025

CrossRef Full Text | Google Scholar

Lee, M. J., Joo, H. G., Lee, D., and Smith, K. (2010). Investigation of cmfd accelerated Monte Carlo eigenvalue calculation with simplified low dimensional multigroup formulation. Int. Conf. Phys. React. PHYSOR 1, 578–590.

Google Scholar

Than, Y. R., and Xiao, S. (2022). lp–cmfd acceleration schemes in 2d Monte Carlo transport. Trans. Am. Nucl. Soc. 126, 268–271.

Google Scholar

Ueki, T., and Brown, F. B. (2005). Stationarity modeling and informatics-based diagnostics in Monte Carlo criticality calculations. Nucl. Sci. Eng. 149, 38–50. doi:10.13182/nse04-15

CrossRef Full Text | Google Scholar

Ueki, T. (2009). Step-refined on-the-fly convergence diagnostics of Monte Carlo fission source distribution. Nucl. Sci. Eng. 163, 99–117. doi:10.13182/nse163-99

CrossRef Full Text | Google Scholar

Wang, D., and Xiao, S. (2018). A linear prolongation approach to stabilizing cmfd. Nucl. Sci. Eng. 190, 45–55. doi:10.1080/00295639.2017.1417347

CrossRef Full Text | Google Scholar

Yun, S., and Cho, N. Z. (2010). Acceleration of source convergence in Monte Carlo k-eigenvalue problems via anchoring with a p-cmfd deterministic method. Ann. Nucl. Energy 37, 1649–1658. doi:10.1016/j.anucene.2010.07.018

CrossRef Full Text | Google Scholar