Research on market trading strategy of multi-microgrid intelligent power distribution system based on Bi-level optimization

With the continuous promotion of the “dual carbon” idea, future power generation will rely heavily on renewable energy sources. As an effective utilization form of clean power sources, it is of positive significance to study the trading strategy of microgrids in the intelligent power distribution system under the influence of carbon quota. In this research, a bi-level optimization method is used to build a trading model of the distribution-side power market, with the upper-level planning aiming to reduce the cost of distribution system operators and the lower-level planning aiming to increase the revenue of microgrids. Secondly, the genetic algorithm and sequential quadratic planning algorithm are applied to the upper and bottom models to determine the optimal clearing strategy for the microgrid and the optimal scheduling scheme for the distribution system operator, respectively. Finally, a typical day is used as an example to analyze in detail the market trading strategy of a multi-microgrid intelligent distribution system under the influence of carbon quota, and the effectiveness of the method described in this paper is verified.

1 Introduction

With the continuous promotion and implementation of the concept of “carbon peaking and carbon neutral,” China has implemented various carbon policies in order to effectively reduce carbon emissions, including carbon quotas, which are an important basis of the carbon trading market (Jin et al., 2021). In the form of power generation, clean power will gradually replace thermal power as the main power source in the future. The new power system needs to have greater power balancing capacity on both the power side and the customer side to undertake more clean power consumption tasks. As an effective carrier for clean power consumption, the microgrid is an important means to revitalize the power regulation potential on the user side. In the future, the intelligent power distribution system will be more friendly to cope with multiple microgrid grid connections, and its regulation method should be based on the originally planned regulation, and build a fair and effective distribution side power market trading mechanism and method, to stimulate the initiative and flexibility of clean power supply grid connection. (State Grid Cooperation of China, 2021; Zhao et al., 2022Yi et al., 2022).

Current research by scholars in China and abroad on distribution-side electricity market trading mechanisms focuses on the following two aspects:

(1) Game theory-based market transaction mechanism

Most of the studies on market transaction mechanisms based on game theory are based on the autonomous operation of micro-networks (Du et al., 2021). For example, (Zhao et al., 2015, Min et al., 2015), used noncooperative game theory to build a general model of the trading model between multiple microgrids, and analyzed and proved the existence of Nash equilibrium of the game; (Le et al., 2016); proposed a new regional grid market-oriented operation model based on game theory to meet the demand of market-oriented reform on the distribution side in the context of high penetration distributed electric energy resources access operation; (Bai et al., 2017, Peilin et al., 2017); uses cooperative game theory to solve the problem of bidding and revenue allocation among multiple microgrids, considering the source-load duality of microgrids; (Zhao et al., 2018, Wenhui et al., 2018); constructs a three-party noncooperative game model based on Nash equilibrium for the wind-fire grid and analyzes the factors affecting the utility of each game party; while (Wang et al., 2019, Xian et al., 2019) establishes a joint game equilibrium model for multi-energy markets and uses a nonlinear complementary approach to solve the bid variance problem of microgrid participation in distribution-side electricity market transactions with uncertain power output.

(2) Optimization theory-based market transaction mechanism

At present, the research methods based on optimization theory mainly focus on two-tier optimization methods and two-stage optimization methods (He et al., 2020). In (Peng et al., 2021), a two-tier model of the optimal bidding strategy of integrated energy service providers is established for the bidding behavior of multiple integrated energy service providers in the integrated energy market, and the impact of each integrated energy service provider’s bidding strategy on the integrated energy market clearing is quantitatively analyzed; (Zhao et al., 2022, Yue et al., 2022); constructs a two-tier optimization model for dynamic pricing and market clearing to study the distribution side market trading strategy taking into account multiple stakeholders. In (Liu et al., 2017), a two-layer optimization model is developed to study the distribution side market trading and bidding mechanism for multiple microgrid operators to participate in the distribution side market bidding. In (Liu et al., 2018), a two-stage robust optimization model with a min-max-min structure is developed for the uncertainty of renewable energy and load within the microgrid to find the scheduling scheme with the lowest operating cost under the worst scenario; (M. H. Moradi et al., 2016), a two-stage optimization model is developed for the power system, where the optimal distribution problem of the microgrid is solved in stage 1, and stage 2 combines Nash equilibrium theory and two-layer The second stage combines Nash equilibrium theory and two-layer planning theory to solve the optimal clearing problem in the distribution side of the electricity market. In (De Gejirifu et al., 2019), the uncertainty of wind storage plants participating in the electricity spot market bidding is considered and modeled by the two-stage optimization idea and stochastic chance constrained planning theory, and the developed model can provide a basis for the wind storage plants to participate in the electricity spot market bidding scheme and the operation plan formulation; (Fazlalipour et al., 2018); considering that the microgrid can be used as a rotating backup resource, a two-stage bidding model for microgrid participation in the joint market of day-ahead market and rotating backup market is established.

Overall, the above study considers the economic benefits of distribution networks and each microgrid operator in the electricity market. However, there is a missing consideration of the influence of carbon quotas, which are an important basis for carbon trading market, on the bidding strategy of each microgrid after the introduction of regional distribution networks.

In this paper, we study the regional distribution-side day-ahead electricity market with the participation of multiple microgrids and use two-layer planning theory to solve the optimal bidding strategy of microgrid operators and the optimal dispatching problem of distribution network operators under the consideration of carbon quotas. The upper-level planning is solved by a genetic algorithm to minimize the cost of the distribution market operator; the bottom-level planning is solved by a sequential quadratic programming algorithm to maximize the revenue of the microgrid, and finally determines the optimal clearing strategy of the microgrid and the optimal dispatching scheme of the distribution network operator. The article concludes with a detailed analysis of the trading strategy of the distribution-side electricity market under the influence of carbon quotas and the participation of multiple microgrids, taking a typical day as an example.

2 Distribution side power market model

2.1 Market structure

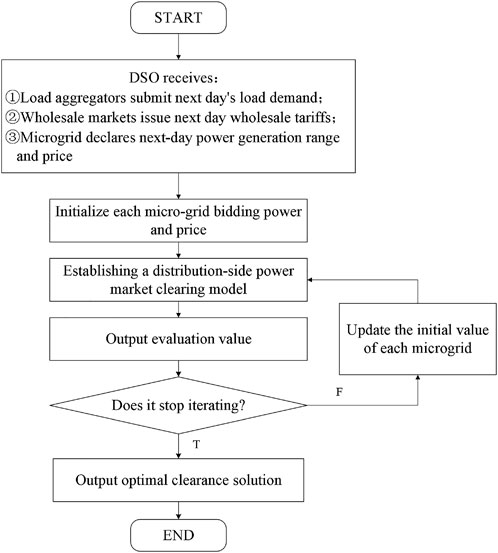
The structure of regional distribution-side electricity market transactions is shown in Figure 1, where market players include: distribution system operators (DSO), microgrid operators, wholesale electricity markets, and load aggregators, and the behavior of each player in the market is:

(1) The DSO is responsible for the operation and clearing of the electricity market and needs to receive the load demand for the next day and information on the offers of the parties, and the DSO can purchase electricity from the microgrid operators and wholesale markets in the region.

(2) The load aggregator, which owns the load resources in the region, is responsible for purchasing electricity from the electricity market and selling it to customers, and it needs to submit to the DSO the load demand $P_{\mathrm{L}}\left(t\right)$ for each period on the second day.

(3) The wholesale power market is required to issue the next day’s wholesale tariff ${\lambda }_{\text{WSM}}\left(t\right)$ to the DSO, and the power purchased by the DSO is required to satisfy the line operating constraint $\left(P_{\text{WSM}}^{\min }\left(t\right),P_{\text{WSM}}^{\max }\left(t\right)\right)$, where $P_{\text{WSM}}^{\max }\left(t\right)$ and $P_{\text{WSM}}^{\min }\left(t\right)$ are the upper and lower limits (kW) of line transmittable power, respectively.

(4) Based on the historical data and the carbon quota issued by the Ministry of Ecology and Environment, microgrid m shall declare the power range $\left(P_{\text{MG},m}^{\min }\left(t\right),P_{\text{MG},m}^{\max }\left(t\right)\right)$ and corresponding quotation for DSO to participate in the bidding for each period on the following day. The power range declared for the microgrid is explained as follows: Firstly, in the electricity market, power generation equipment can be divided into high-carbon power sources and low-carbon power sources according to carbon emissions. Taking microgrids with the same capacity and free carbon allowances, for example, the declared upper limit of microgrids with high-carbon power sources is lower than that of microgrids with low-carbon power sources. Secondly, at present, the primary purpose of accepting clean energy-based microgrids to the grid is to reduce carbon dioxide emissions, so microgrids connected to the grid should contribute to the achievement of carbon emission targets in the regional electricity market, i.e., the declared power limit is the minimum power commitment of the microgrid to meet the carbon emission target.

FIGURE 1

FIGURE 1. Power market construction of distribution system.

The trading process is shown in Figure 2.

FIGURE 2

FIGURE 2. Transaction flow chart.

Step 1. The load aggregators in the region forecast the load demand for each time slot of the next day and declare it to the DSO, the wholesale market issues the wholesale power price for the next day, and each micro-network operator declares the power sales range for each time slot of the next day to the DSO and offers the corresponding price.

Step 2. After receiving the information from each entity, DSO shall establish a power market clearing model to minimize power purchase cost and the constraints of load power, declare the power range of the microgrid and safety operation constraint of the system, etc., and make the dispatch plan for the region by solving the optimal solution of this model.

Step 3. DSO shall promptly announce to each microgrid and wholesale market the regional dispatch plan derived from Step 2, i.e., the winning power $P_{\text{MG},m}\left(t\right)$ and corresponding clearing power price ${\lambda }_{\text{MG},m}\left(t\right)$ of each microgrid and the power purchased by DSO from the wholesale market $P_{\text{WSM}}\left(t\right)$ on the next day.

2.2 Market model

In the electricity market bidding process, from the perspective of the DSO, the objective is to meet the next day’s load demand, ensure the safety of system operation, and minimize the cost of power purchase; from the perspective of the microgrid, the objective is to maximize its revenue through bidding. In this process, the behaviors of microgrids and DSO are independent of each other and affect each other, so this problem can be described as a two-layer planning problem. In this regard, the upper-level optimization problem aims at minimizing the cost of expenses of the distribution system operator, while the bottom-level optimization problem aims at maximizing the profit of the microgrid operator from electricity sales, and determines the market clearing scheme after considering the load power, the declared power of the microgrid, the carbon emission index and the system security constraints. The decision variables are the power purchased by the distribution system operator from each microgrid and the wholesale market and the clearing tariff of the microgrid operator m.

2.2.1 Mathematical model for distribution system operators

The core of the upper-level optimization problem lies in the DSO’s comprehensive consideration of system security constraints based on the offers of all parties to achieve economic optimality. The objective is to minimize the total system power purchase cost, and the upper-level optimization model is.

$\min {\displaystyle \sum }_{t=1}^{N_T}[{\displaystyle \sum }_{m=1}^{N_m}{P}_{\text{MG},m}\left(t\right){\lambda }_{\text{MG},m}\left(t\right)+P_{\text{WSM}}\left(t\right){\lambda }_{\text{WSM}}\left(t\right)](1)$

$\mathrm{s}.\mathrm{t}.{\displaystyle \sum }_{m=1}^{N_m}{P}_{\text{MG},m}\left(t\right)+P_{WSM}\left(t\right)=P_L\left(t\right),\forall t(2)$

$P_{\text{MG},m}^{\mathit{min}}\left(t\right)\le P_{\text{MG},m}\left(t\right)\le P_{\text{MG},m}^{\mathit{max}}\left(t\right),\forall m,\forall t(3)$

$P_{\text{WSM}}^{\mathit{min}}\left(t\right)\le P_{\text{WSM}}\left(t\right)\le P_{\text{WSM}}^{\mathit{max}}\left(t\right),\forall t(4)$

where: $N_T$ denotes the total number of bidding periods, generally taken as 24; $N_{\mathrm{m}}$ denotes the total number of microgrid operators participating in the bidding; $P_{\text{MG},m}\left(t\right)$ denotes the declared power of microgrid m in time slot t (kW); ${\lambda }_{\text{MG},m}\left(t\right)$ denotes the declared power of microgrid m in time slot t ($/kWh); $P_{\text{WSM}}\left(t\right)$ denotes the power purchased by DSO from the wholesale market in time slot t (kW); ${\lambda }_{\text{WSM}}\left(t\right)$ denotes the wholesale power price of the wholesale market in time slot t ($/kWh); $P_{\mathrm{L}}\left(t\right)$ denotes the load demand in the region at time slot t (kW); $P_{\text{MG},m}^{\min }\left(t\right)$ and $P_{\text{MG},m}^{\max }\left(t\right)$ are the lower and upper limits of the declared power of microgrid m at time slot t (kW), respectively; and Eq. 4 represents the upper and lower constraints to be satisfied by the DSO to purchase power from the wholesale market.

(2) Mathematical model of micro-network operators

The goal of micro-network operators is to maximize their interests, and the underlying optimization model is shown below.

$\max {\displaystyle \sum }_{m=1}^{N_m}(P_{\text{MG},m}(t){\lambda }_{\text{MG},m}(t)-({\alpha }_{\text{MG},m}{P}_{\text{MG},m}^2(t)+{\beta }_{\text{MG},m}{P}_{\text{MG},m}(t)+{\gamma }_{\text{MG},m})),\forall t(5)$

$\mathrm{s}.\mathrm{t}.P_{\text{MG},m}\left(t\right)=\left[{\lambda }_{\text{MG},m}\left(t\right)-{\beta }_{\text{MG},m}\right]/2{\alpha }_{\text{MG},m}(6)$

${\alpha }_{\text{MG},m}{P}_{\text{MG},m}^2\left(t\right)+{\beta }_{\text{MG},m}{P}_{\text{MG},m}\left(t\right)+{\gamma }_{\text{MG},m}\le P_{\text{MG},m}\left(t\right){\lambda }_{\text{MG},m}\left(t\right),\forall m,\forall t(7)$

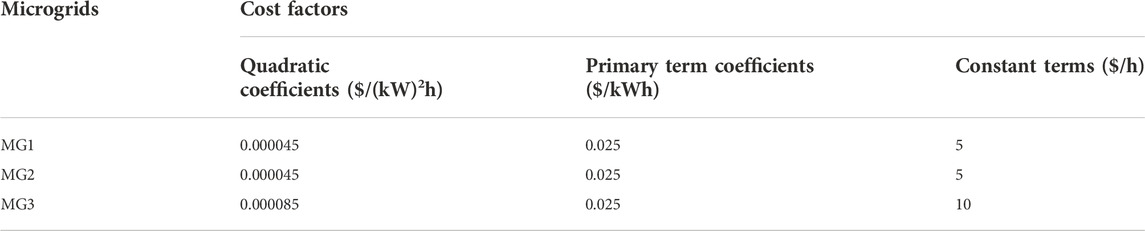
In this paper, the quadratic function is used to approximate the generation cost of microgrid m, ${\alpha }_{\text{MG},m}$, ${\beta }_{\text{MG},m}$ and ${\gamma }_{\text{MG},m}$ denote its quadratic term coefficient ($/(kW)²h), primary term coefficient ($/kWh), and constant term ($/h), respectively; Eq. 6 represents the relationship between the winning power bid and the clearing tariff when the microgrid operator’s revenue is maximized; Eq. 7 ensures that each microgrid benefits from the competitive bidding.

3 Solution method

By analyzing the market model, we can see that any micro-network competes with other micro-networks to win the power bid through competitive bidding, and any party who offers too much or too little will damage its interests; meanwhile, DSO makes the most economical scheduling plan based on each party’s offer and considering various constraints. Therefore, the upper-level optimization problem is essentially a linear programming problem with constraints; since there is competition among multiple subjects in the bottom-level optimization problem, and the introduction of constraint (7) can ensure that each micro-network is profitable in the bidding, this paper simplifies the bottom-level optimization problem to a quadratic programming problem to find the maximum profit of each micro-network. For the distribution-side electricity market model depicted in Figure 1, this paper establishes an embedded algorithm that solves the upper-level problem by genetic algorithm and the bottom-level problem by sequential quadratic programming (SQP) method.

3.1 Upper-level optimization problem

The upper-level optimization problem aims at solving the optimal offer strategy for each microgrid to achieve its economic optimum. It is assumed that the wholesale power price of the next day in the wholesale market is known. The offer price of microgrid m affects its winning power and clearing tariff, and thus its profit.

In this paper, the genetic algorithm is used to solve the upper-level optimization problem, and the offer of each micro-network and the corresponding outgoing power $\left({\lambda }_{\text{MG},m}\left(t\right),P_{\text{MG},m}\left(t\right)\right)$ are taken as the population individuals, and the optimal outgoing of micro-network m can be found through the selection of population individuals.

3.2 Lower-level optimization problem

The lower-level optimization problem aims to find the optimal amount of power cleared from each microgrid and the optimal amount of power purchased by DSO from the wholesale market. In this paper, we assume that the microgrid cost is a quadratic function concerning the generation capacity, so this paper adopts the SQP algorithm to solve the bottom planning problem.

3.3 Approximation $\phi$—mapping

The general form of the Bilevel Programming Problem is shown below.

$\min F\left(x_u,x_l\right),\forall x_u\in X_U,\forall x_l\in X_L(8)$

$\mathrm{s}.\mathrm{t}.x_l\in \mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}\left\{\begin{array}{l}f\left(x_u,x_l\right):g_j\left(x_u,x_l\right)\le 0,\\ j=1,...,J\end{array}\right\}(9)$

$G_k\left(x_u,x_l\right)\le 0,k=1,...,K(10)$

where $F\left(x_u,x_l\right)$ corresponds to the upper-level objective function shown in Eq. 1; $f\left(x_u,x_l\right)$ corresponds to the bottom-level objective function shown in Eq. 5; $x_u$ denotes the upper-level decision variable, i.e., the clearing tariff of the microgrid; $x_l$ denotes the bottom-level decision variable, i.e., the clearing tariff of the microgrid and the wholesale market, $g_j\left(x_u,x_l\right)$ corresponds to the bottom-level constraints shown in Eqs 6, 7; Eq. 10 corresponds to the upper-level constraints shown in Eqs 2–4.

Let function $\phi \left(x_u\right)$ be the mapping of the underlying optimal function values corresponding to any given upper-level decision variable.

$\phi \left(x_u\right)=\min \left\{\begin{array}{c}f\left(x_u,x_l\right):g_j\left(x_u,x_l\right)\le 0,\\ j=1,...,J,x_l\in X_L\end{array}\right\}(11)$

Bringing Eq. 11 into the model (8)-(10) transforms the Bilevel Programming Problem into a single-level form.

$\min F\left(x_u,x_l\right),\forall x_u\in X_U,\forall x_l\in X_L(12)$

$\mathrm{s}.\mathrm{t}.f\left(x_u,x_l\right)\le \phi \left(x_u\right)(13)$

$g_j\left(x_u,x_l\right)\le 0,j=1,...,J(14)$

$G_k\left(x_u,x_l\right)\le 0,k=1,...,K(15)$

In general, $\phi$ - mapping is always scalar-valued regardless of the lower level variable dimension and whether or not there exist multiple lower level optimal solutions. Thus, the calculation of $\phi$ - mapping is not complicated. (Sinha et al., 2020).

In this paper, we apply the $\phi$ - mapping idea in the nested algorithm constructed in the previous section. After updating the algorithm step, the micro-network offers are fixed and a local search is performed in the single-level planning shown in Eqs 12–15 to solve for the corresponding optimal outgoing power for each micro-network offer to update the population.

3.4 Bilevel programming solution method

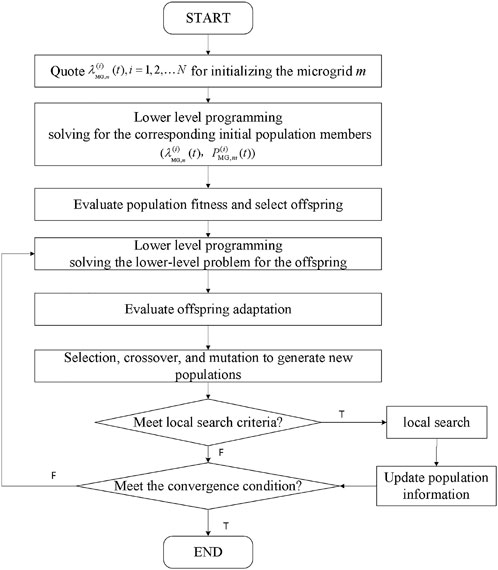
The computational flow for solving the Bilevel Programming Problem in this paper is shown in Figure 3.

(1) Take the N-dimensional random numbers to initialize the microgrid m with the outgoing electricity price;

(2) Using the SQP algorithm in the underlying planning, find the microgrid clearing power $P_{\text{MG},m}^{\left(i\right)}\left(t\right)$ corresponding to ${\lambda }_{\text{MG},m}^{\left(i\right)}\left(t\right)$ , and together with it form the initial population member $\left({\lambda }_{\text{MG},m}^{\left(i\right)}\left(t\right),P_{\text{MG},m}^{\left(i\right)}\left(t\right)\right)$;

(3) Evaluate the fitness of the population members using the objective function and constraints of the upper-level planning.

(4) Selecting the offspring members.

(5) Solve the underlying problem for each child using the SQP algorithm.

(6) Repeat step (3).

(7) Select, crossover, and mutate to generate a new population, perform a local search in its vicinity after every k generation, and update the population if there is an improvement.

(8) Check whether the termination condition is satisfied and if so, stop the iteration to output the winning power and outgoing tariff of each power seller, otherwise return to step (5).

FIGURE 3

FIGURE 3. Calculation flow chart.

4 Example

4.1 Simulation environment

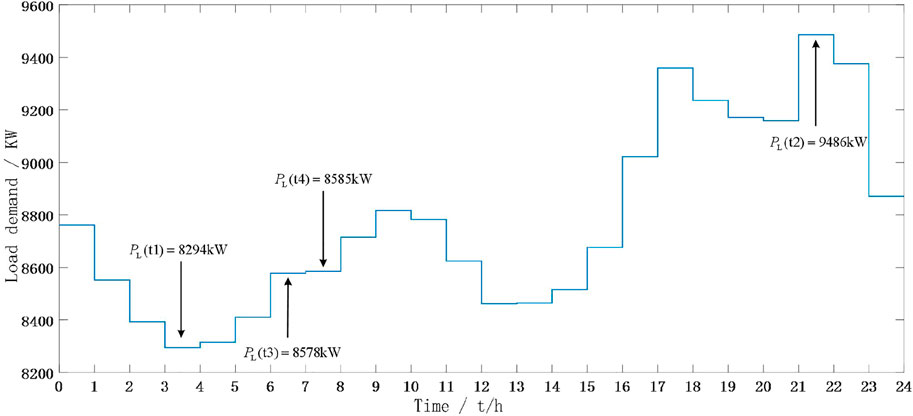
To verify the feasibility of the proposed method, this paper builds a simulation optimization model based on Matlab + cplex, taking a two-layer iterative stopping accuracy of 0.01 and N = 100. The regional load in this paper uses simulated data of a typical day, and the daily load curve is shown in Figure 4.

FIGURE 4

FIGURE 4. Regional daily load curve.

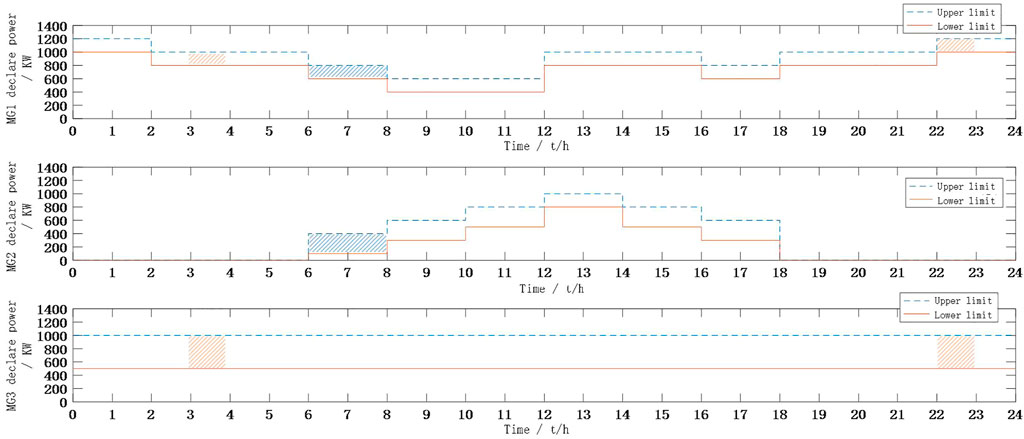
It is assumed that there are three adjacent microgrids (numbered MG1, MG2, and MG3 in order) in the region, and to reflect their differences, it is set that the power generation equipment configured in MG1 is mainly wind power, the power generation equipment configured in MG2 is mainly photovoltaic, and the equipment that can generate stable power is configured in MG3. Given the strong coupling between new energy generation and climatic conditions, considering the climate change in a day and the carbon quota issued by the Ministry of Ecology and Environment, it is assumed that the declared power range of MG1, MG2, and MG3 in a timeshare is shown in Figure 5 (Li et al., 2009), and the generation cost is shown in Table 1. The distribution system operator purchases power from the wholesale market in the range of 0–30 MW, and the wholesale electricity price in the wholesale market is 0.088$/kWh, and the line loss rate is taken as 5%.

FIGURE 5

FIGURE 5. Three microgrids declare next-day power intervals.

TABLE 1

TABLE 1. Power generation costs of three microgrids.

4.2 General analysis

The practical simulation debugging shows that the computational speed of the algorithm in this paper is moderate, and the initial value selection will affect the iteration time, but will not have a large impact on the final result. This paper will focus on the discussion of the bidding.

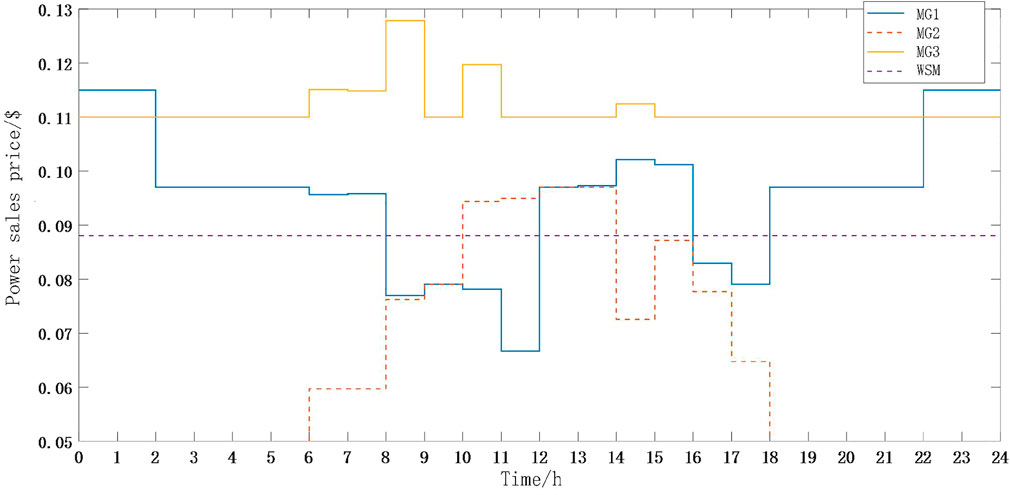
The simulation results are shown in Figure 6 and Figure 7. Figure 6 shows the percentage of electricity sold by each seller to the total load demand on the next day, and Figure 7 shows the price of electricity sold by each seller on the next day. Analysis shows that.

(1) the presence of line losses makes the actual power purchased by the distribution network larger than its actual power demand.

(2) The DSO uses the power interval declared by each microgrid (Figure 5) as a reference to formulate the next-day interval dispatch plan, so the general rule of the distribution-side power market to formulate the clearing power can be summarized as allocation by capacity. Therefore it is crucial that each micro-grid in the day-ahead power market can accurately predict the next day’s generation.

(3) When there is sufficient power in the wholesale market, DSO can also fully respect the willingness of each microgrid to generate power, such as agreeing to the transaction price of MG3 at 0.128$/kWh, which is much higher than the price in the wholesale market, during the period [8:00,9:00] to benefit the microgrid, which can motivate the microgrid with higher generation cost to participate in the market transaction and establish a long-term partnership to cope with the lack of power in the wholesale market. This will provide an incentive for microgrids with higher generation costs to participate in the market and establish long-term partnerships to address the lack of power in the wholesale market and help achieve carbon reduction targets.

FIGURE 6

FIGURE 6. Share of electricity sold by each power seller.

FIGURE 7

FIGURE 7. Price of electricity by each power seller.

4.3 The influence of load changes on different cost microgrid bids

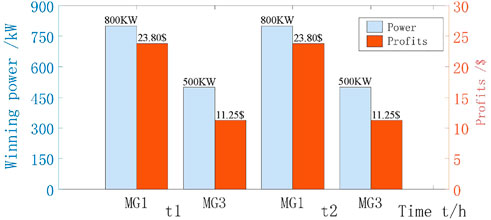
The clearing scheme and profit of microgrids are influenced by the cost of generation. Take the next day’s electricity consumption low time t1 = [3:00,4:00] and peak time t2 = [21:00,22:00], whose load demand is 8294kW and 9486kW respectively, and the power range declared by each microgrid is the same (see Figure 5 at the red shaded mark). Since t1 and t2 are nighttime, so MG2 does not participate in the market bidding. From Figure 7, we can see that the clearing power price of MG1 is 0.097$/kW and MG3 is 0.110$/kWh in both t1 and t2 scenarios, and the winning power and profit of MG1 and MG3 are shown in Figure 8, which shows that.

(1) From the fact that MG1 has the same winning power and profit in both scenarios t1, t2, it is clear that its optimal clearing scenario is not affected by load changes when the declared power range and cost of the microgrid are constant.

(2) In the two scenarios of t1 and t2, the pay-out tariff of MG1 is at a lower level because of its lower generation cost. In the case of the market, competition leads to the fact that MG3 is always unable to raise its price and to ensure the profit of MG3 makes the winning power of MG3 smaller than that of MG1. It is obvious from Figure 8 that MG1 with its low generation cost has a clear advantage in the power market and can achieve maximum profit itself.

FIGURE 8

FIGURE 8. Dispatched power and profit of MG1 and MG3 under t1 and t2 scenarios.

4.4 The influence of different declared power on micro network bidding

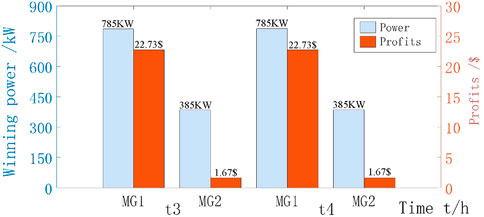
The generation costs of MG1 and MG2 are the same, but their declared power ranges vary with time. Take the scenarios [6:00,7:00] and [7:00,8:00] in Figure 4, where the load demand does not change much, as t3 and t4, respectively, and their load demands are 8,578 kW and 8,585 kW, respectively. The declared power ranges of MG1 are 600–800 kW and MG2 are 100–400 kW (see Figure 5 at the blue shaded mark). The declared power range of MG1 is 600–800 kW and the declared power range of MG2 is 100–400 kW (see Figure 5 at the blue shaded mark). From Figure 7, it can be seen that the clearing tariffs for MG1 and MG3 in t3 and t4 scenarios are 0.096$/kW and 0.06$/kWh, respectively. The clearing tariffs and profits for MG1 and MG2 at t3 and t4 are shown in Figure 9.

FIGURE 9

FIGURE 9. Dispatched power and profit of MG1 and MG2 under t3 and t4 scenarios.

The changes in load demand in scenarios t3 and t4 are small, and the calculated microgrid clearing scheme is approximately the same with the same cost and declared power range, which shows that the algorithm used in this paper has good calculation performance and can guarantee the accuracy of the calculation results.

From Figure 9, it can be seen that the winning bids of MG1 and MG2 with the same cost but different declared power ranges are in line with the law of “capacity-based allocation”. In this scenario, the declared power range of MG2 is lower, and the final price of its electricity clearance is lower than that of MG1 as shown in Eq. 6, which ultimately leads to its low profit because the internal configuration of MG2’s photovoltaic power generation equipment is limited in the morning when the solar energy resources are insufficient, which leads to its insufficient allocation of carbon quotas and ultimately makes the declared power range of MG2 unable to make more profit. Therefore, the microgrid should optimize itself and declare a reasonable power interval to maximize its profit.

5 Conclusion

The day-ahead power bidding problem for a regional distribution market with multiple micro-networks is solved in this paper using a bilevel programming approach. The upper-level planning aims to reduce the cost of the distribution system operator, and the bottom-level planning aims to maximize the revenue of the micro-networks. This helps to identify the best clearing strategy for the micro-networks and the best dispatching scheme for the distribution system operator. The simulation’s findings support this.

(1) The algorithm used in this paper has good computational performance and can ensure that the system can optimize the interests of each power seller and distribution system operator on the basis of economy and safety.

(2) The generation cost and declared power range of the microgrid affect the final clearing result, and the microgrid with a low generation cost and reasonable declared power range has certain advantages in the market.

(3) Under certain conditions, DSO can benefit microgrids with higher generation costs to address the scarcity of power in wholesale markets and help achieve carbon reduction targets.

This paper assumes that each microgrid can accurately predict the next day’s generation interval, but in actual operation, distribution system operators should consider the situation that clean power generation is affected by weather, resulting in the actual generation capacity being different from the interval scheduling plan made before the day, and optimize the market trading rules to ensure the safe and stable operation of the regional distribution system (Fang et al., 2020).

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This study is supported by the National Natural Science Foundation of China under Grant 52107075.

Acknowledgments

I would like to thank my supervisor for his constant encouragement and support. I could not have completed this thesis without his patient guidance.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bai, P, Xia, L, and He, J (2017). Design of bidding mechanism for multiple microgrids[J]. Mod. Electr. Power 34 (06), 22–27. doi:10.19725/j.cnki.1007-2322.2017.06.004

CrossRef Full Text | Google Scholar

De, G., Tan, Z., Li, M., Yang, S., Ma, J., Tan, Q., et al. (2019). Bidding strategy of wind-storage power plant participation in electricity spot market considering uncertainty[J]. Power Syst. Technol. 43 (08), 2799–2807. doi:10.13335/j.1000-3673.pst.2019.0547

CrossRef Full Text | Google Scholar

Du, Y., Li, F., Zandi, H., and Xue, Y. (2021). Approximating nash equilibrium in day-ahead electricity market bidding with multi-agent deep reinforcement learning[J]. J. Modern Power Syst.Clean Ener. 3 (9), 534–544. doi:10.35833/MPCE.2020.000502

CrossRef Full Text | Google Scholar

Fang, X., and Cui, M. (2020). Analytical model of day-ahead and real-time price correlation in strategic wind power offering[J]. J. Modern Power Syst.Clean Ener. 5 (8), 1024–1027. doi:10.35833/MPCE.2019.000598

CrossRef Full Text | Google Scholar

Fazlalipour, P., Ensan, M., and Mohammadiivatloo, B. (2018). Optimal participation of low voltage renewable micro-grids in energy and spinning reserve markets under price uncertainties. Int. J. Electr. Power & Energy Syst. 102, 84–96. doi:10.1016/j.ijepes.2018.04.010

CrossRef Full Text | Google Scholar

He, S., Gao, H., Tian, H., Wang, L., Liu, Y., and Liu, J. (2021). A Two-stage robust optimal allocation model of distributed generation considering capacity curve and rpeal-time price based demand response[J]. J. Modern Power Syst.Clean Ener. 1 (9), 114–127. doi:10.35833/MPCE.2019.000174

CrossRef Full Text | Google Scholar

Jin, T, Chen, M, and Chen, Y (2021). Discussion on carbon quota management of power generation enterprises based on energy consumption level[J]. Shanghai Energy Conserv. (01), 53–59.

Google Scholar

Le, J, Liu, Y, Ye, X, Wu, Z, and Li, Z (2016). Market-oriented operation pattern of regional power network integration with high penetration level of distributed energy resources[J]. Proc. CSEE 36 (12), 3343–3354. doi:10.13334/j.0258-8013.pcsee.152844

CrossRef Full Text | Google Scholar

Li, S, Li, G, Li, Z, and Wu, J (2009). Research on typical curve prediction method of wind farm output[C]. Haikou: Wind Farm Access to Grid Technology Symposium, 255–261.

Google Scholar

Liu, Y, Guo, L, and Wang, C (2018). Economic dispatch of microgrid based on two-stage robust optimization[J]. Proc. CSEE 38 (14), 4013–4022+4307. doi:10.13334/j.0258-8013.pcsee.170500

CrossRef Full Text | Google Scholar

Liu, Y, Guo, L, and Wang, C (2017). Optimal bidding strategy for microgrids in electricity distribution market[J]. Power Syst. Technol. 41 (08), 2439–2476. doi:10.13335/j.1000-3673.pst.2016.2989

CrossRef Full Text | Google Scholar

Moradi, M. H., Abedini, M., and Hosseinian, S. M. (2016). A combination of evolutionary algorithm and game theory for optimal location and operation of DG from DG owner standpoints. IEEE Trans. Smart Grid 7 (2), 1–616. doi:10.1109/TSG.2015.2422995

CrossRef Full Text | Google Scholar

Peng, L, Ma, X, Guo, Z, Lei, J, Yuan, Z, He, S, et al. (2021). Game strategy of integrated energy service providers based on Bi-level optimization[J]. Power Syst. Technol. 45 (02), 460–473. doi:10.13335/j.1000-3673.pst.2020.1013

CrossRef Full Text | Google Scholar

Sinha, A, Lu, Z, Deb, K, and Malo, P (2020). Bilevel optimization based on iterative approximation of multiple mappings. J. Heuristics 26, 151–185. doi:10.1007/s10732-019-09426-9

CrossRef Full Text | Google Scholar

State Grid Cooperation of China, (2021). State Grid Cooperation of China releases the “carbon peak, carbon neutrality” action plan[N]. Beijing: State Grid News, 2021-03-02.

Google Scholar

Wang, X, Zhang, Y, and Zhang, S (2019). Game analysis of multi-energy market considering microgrid bidding[J]. Power Syst. Technol. 43 (09), 3184–3192. doi:10.13335/j.1000-3673.pst.2019.0797

CrossRef Full Text | Google Scholar

Zhao, M, Chen, S, Liu, F, and Huang, X (2015). A game-theoretic approach to analyzing power trading possibilities in multi-microgrids[J]. Proc. CSEE 35 (04), 848–857DOI10. doi:10.13334/j.0258-8013.pcsee.2015.04.011

CrossRef Full Text | Google Scholar

Zhao, W, Yan, H, and He, W (2018). Equilibrium model of electricity market based on non-cooperative game of wind farms, thermal power plants and power grid company[J]. Power Syst. Technol. 42 (01), 103–111. doi:10.13335/j.1000-3673.pst.2017.1337

CrossRef Full Text | Google Scholar

Zhao, Y, Chen, Y, and Sun, W (2022). Region dispatch method and market trading strategy for multi-microgrid distribution system[J]. Power Syst. Technol. 46 (01), 47–56. doi:10.13335/j.1000-3673.pst.2021.0245

CrossRef Full Text | Google Scholar

Zhao, Y, Zhang, X, Zhao, C, Gong, C, Xiao, Y, Li, M, et al. (2022). Dynamic pricing and market clearing strategy for power distribution considering multiple stakeholders[J]. South. Power Syst. Technol. 16 (01), 137–144. doi:10.13648/j.cnki.issn1674-0629.2022.01.015

CrossRef Full Text | Google Scholar