- 1Electric Power Research Institute, Yunnan Power Grid Co. Ltd., China Southern Power Grid, Kunming, China
- 2Yunnan Power Grid Co. Ltd., China Southern Power Grid, Kunming, China
- 3Zhejiang Guozi Robotics Co. Ltd., Hangzhou, China
A new meta-heuristic algorithm called like-attracts-like optimizer (LALO) is proposed in this article. It is inspired by the fact that an excellent person (i.e., a high-quality solution) easily attracts like-minded people to approach him or her. This LALO algorithm is an important inspiration for video robotics cluster control. First, the searching individuals are dynamically divided into multiple clusters by a growing neural gas network according to their positions, in which the topological relations between different clusters can also be determined. Second, each individual will approach a better individual from its superordinate cluster and the adjacent clusters. The performance of LALO is evaluated based on unimodal benchmark functions compared with various well-known meta-heuristic algorithms, which reveals that it is competitive for some optimizations.
1 Introduction
Optimization is almost everywhere in our world, which usually attempts to find the perfect solution for a certain issue. To deal with these issues, various optimization methods have been proposed and have shown a good performance. Most of them fall into two categories: mathematical programming methods and meta-heuristics (Dai et al., 2009). The first type can rapidly converge to an optimum with high convergence stability by utilizing the gradient information (Guo et al., 2014), such as quadratic programming (Wang et al., 2014) and the Newton method (Kazemtabrizi and Acha, 2014). But the mathematical programming methods are highly dependent on the mathematical model of the optimization problem (Mirjalili and SCA, 2016). Furthermore, they are even incapable of addressing a blank-box optimization with only the input and output measurements. In contrast, the meta-heuristic algorithms are more flexible to be employed for different optimization problems since they are highly independent of the mathematical model of the specific problem (Zhang et al., 2017). Furthermore, they are easily applied to an optimization with only the input and output measurements instead of any gradient information or convex transformation. Meanwhile, through the balance between global search and local search, they can effectively avoid falling into the low-quality local optimal solution (Alba and Dorronsoro, 2005). Consequently, meta-heuristic algorithms have become a popular and powerful way to engineer optimization problems.
So far, most meta-heuristic algorithms have been designed from different nature phenomena (Askari et al., 2020), e.g., animal hunting and human learning. Among all of these meta-heuristic algorithms, there is no one able to tackle every optimizing issue with a good performance based on the No-Free-Lunch theorem (Wolpert and Macready, 1997). In fact, each meta-heuristic algorithm can show superior performance in only some kinds of optimization problems compared with most of the other algorithms (Zhao et al., 2019). This is also the main reason why so many different meta-heuristic algorithms have been designed and proposed.
According to the number of searching individuals, the meta-heuristic algorithms can be divided into two categories, including the single-individual-based and population-based algorithms (Mirjalili et al., 2014). It is noticeable that the single-individual-based algorithms with simple searching operations require fewer fitness evaluations and computation time than those of the second category (Mas et al., 2009). However, it is also easily trapped in a low-quality local optimum since the single individual is difficult to increase the solution diversity while guaranteeing an efficient search, such as simulated annealing (SA) (Kirkpatrick et al., 1983) and tabu search (TS) (Glover, 1989). In another aspect, population-based methods (Mirjalili et al., 2014) can effectively improve the optimization efficiency and global searching ability via a specific cooperation between different individuals. In contrast to the single-individual-based algorithms, the population-based algorithms need to consume more computation time to execute adequate fitness evaluations for exploration and exploitation.
The video robot system has the benefits of high strength, high precision, and good repeatability. Meanwhile, it has a strong ability to withstand extreme environments, so it can complete a variety of tasks excellently (Mas et al., 2009). Although the majority of video robots execute these tasks in an isolated mode, increasing attention is being paid to the use of closely interacting clustered robotic systems. The potential benefits of clustered robotic systems include redundancy, enhanced footprint and throughput, resilient irreconcilability, and diverse features in space. A key feature among these considerations is the technology utilized to coordinate the movement of individuals.
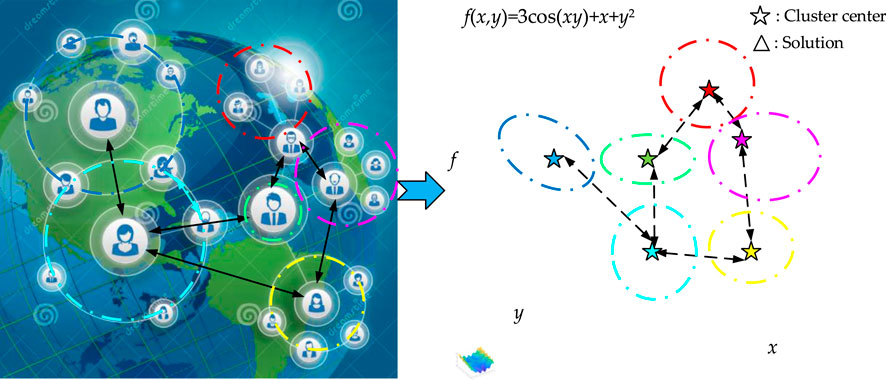
In this article, a new machine learning-based hybrid algorithm named like-attracts-like optimizer (LALO) is also proposed based on solution clustering. Video clustering robots require optimization algorithms for further planning of their routes during population coordination in order to achieve higher efficiency. For this problem, the proposed LALO algorithm can perform the corresponding optimization. It essentially mimics the social behavior of human beings where an excellent person easily attracts like-minded people to approach them (Fritzke et al., 1995; Fišer et al., 2013). Similarly, all the searching individuals in LALO will be divided into multiple clusters by a growing neural gas (GNG) network (Mirjalili et al., 2014) according to their positions. Different from the conventional clustering methods, the topological relations between different clusters can be generated for guided optimization (See Figure 1).
The rest of this article is organized as follows: Section 2 provides the principle and the detailed operations of LALO. The discussions of optimization results in unimodal benchmark functions are given in Section 3. At last, Section 4 concludes this work.
2 Like-attracts-like optimizer
2.1 Inspiration
Like-attracts-like is one of the main parts of social interactions which shows an excellent person easily drives like-minded people to approach them; thus, a group of people with similar features will be formed, as illustrated in Figure 2 (Gutkin et al., 1976). Inspired by this social behavior, a searching individual can represent a person in like-attracts-like, while each cluster can be regarded as a group of people. In this work, the proposed LALO is mainly designed according to the interaction network of different clusters.
2.2 Optimization principle and mathematical model
LALO is mainly composed of two stages: the clustering stage and the searching stage. Particularly, the clustering stage is achieved by the GNG network, and the searching stage is designed by combining the encircling prey of gray wolf optimizer (GWO) depending on the interaction network of the different clusters.
2.2.1 Clustering phase by the GNG network
As a form of unsupervised learning, the GNC network (Fišer et al., 2013) can dynamically adjust its topological structure to match the input data without any desired outputs. It can not only achieve fast data clustering but also keep a topological structure to guide the optimization. In general, the GNC network contains a set of nodes V and a set of edges E without weights, i.e.,
Step 1. Initialize the network from two nodes, in which the positions of these two nodes are randomly generated within the lower and upper bounds of the input data, as
where
Step 2. Randomly select a solution
where
Step 3. Update the age of all the edge links with the nearest node as
where
Step 4. Update the accumulated error of the nearest node as
where
Step 5. Update the positions of the nearest node and its linked nodes as
where
Step 6. If
Step 7. If
Step 8. Insert a new node if the time of network learning is an integral multiple of the inserting rate
where
where
Step 9. Decrease the accumulated errors of all the nodes, as
where
Step 10. Export the network if the conditions for termination are fulfilled; otherwise, switch to Step 2.
2.2.2 Searching phase
In LALO, each individual will approximate a better individual (i.e., the learning target) with a high-quality solution; thus, a potentially better solution can be found with a higher probability. This process is achieved based on the encircling prey of gray wolf optimizer (GWO) (Mirjalili et al., 2014). To guarantee high solution diversity (Gutkin et al., 1976), the learning target (See Figure 3) is selected from the interactive clusters or the best solution so far, according to solution comparison between adjacent clusters as follows:
where
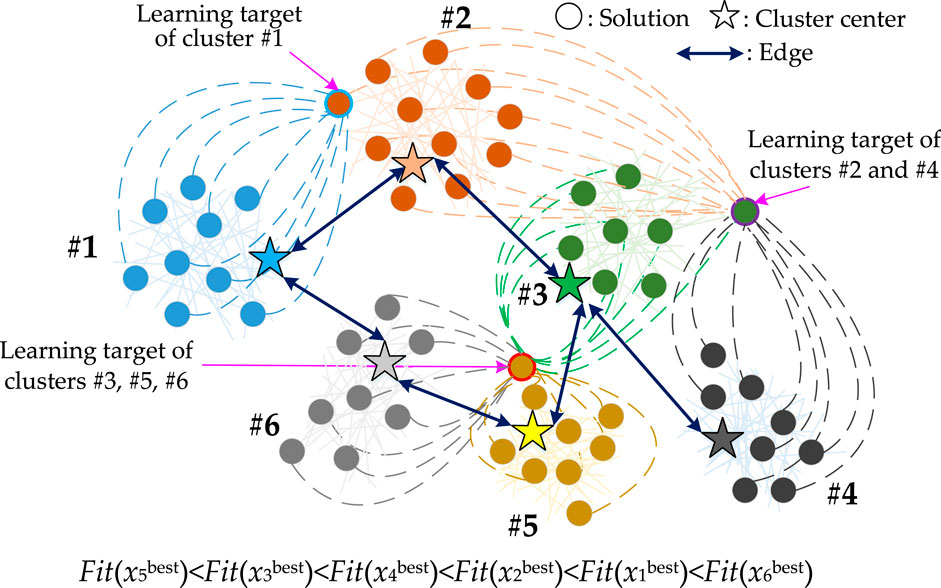
FIGURE 3. Illustration of the learning target-based searching phase of multiple interactive clusters in LALO.
Based on the selected learning target, the position of each individual can be updated as follows (Zeng et al., 2017):
where
2.2.3 Dynamic balance between exploration and exploitation
Like many meta-heuristic algorithms, LALO also requires wide exploration in the early phase (Heidari et al., 2019). As the iteration number increases, the exploration weight should be gradually weakened, while the exploitation weight should be gradually enhanced. To achieve a dynamic balance between them, the cluster number
where
2.2.4 Pseudocode of LALO
To summarize, the pseudocode for LALO is provided in algorithm 1, where T is the iteration number in the GNC network and Tmax is the corresponding maximum iteration number (i.e., the termination condition of the GNC network).
Algorithm 1. Graph construction.
3 Like-attracts-like optimizer for unimodal benchmark functions
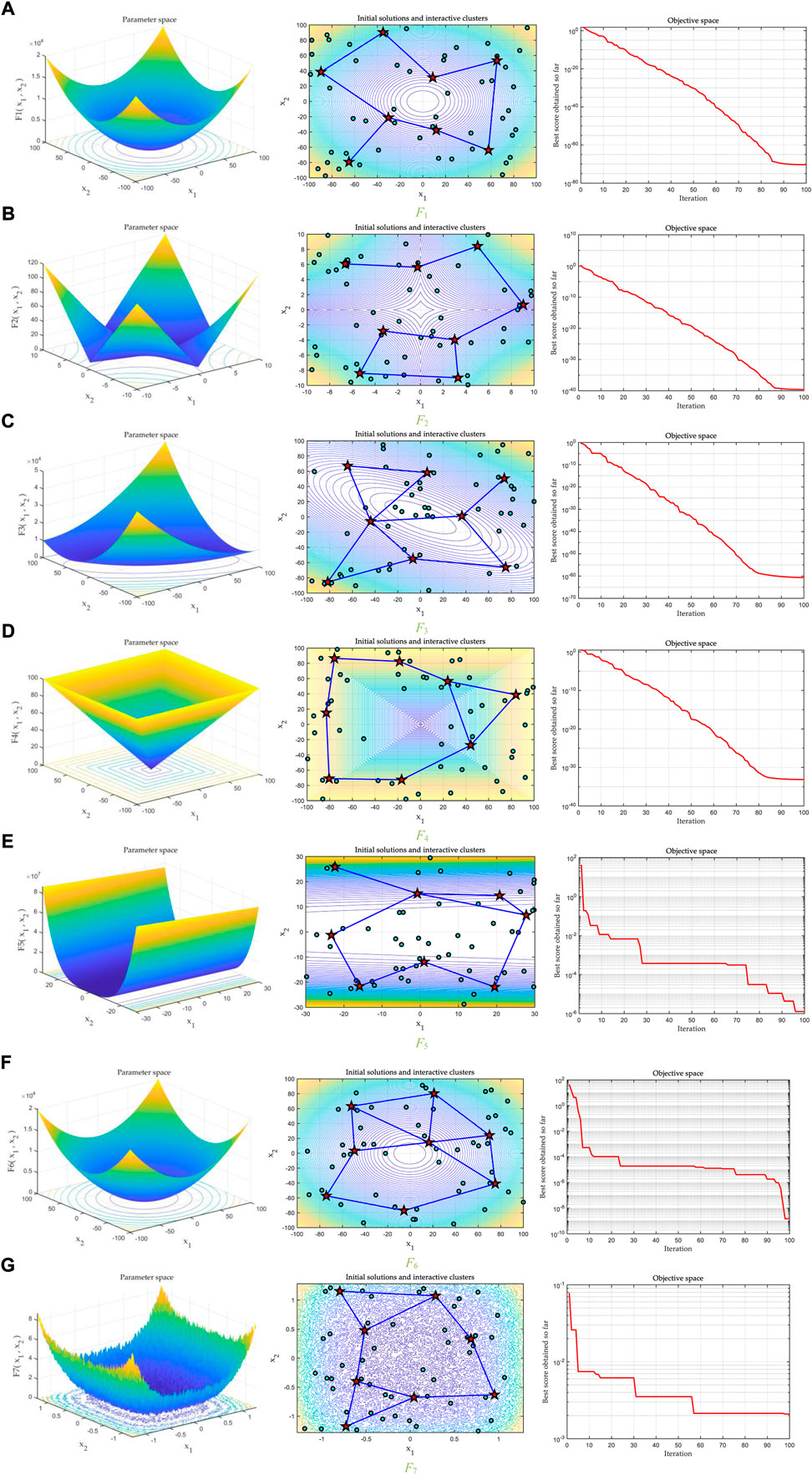
In this section, unimodal features are adopted to test the capability of LALO. Meanwhile, nine well-known meta-heuristic algorithms, namely, GWO (Mirjalili et al., 2014), GA (Holland, 1992), EO (Faramarzi et al., 2020), PSO (Kennedy and Eberhart, 1007), gravitational search algorithm (SSA) (Mirjalili et al., 2017), GSA (Rashedi et al., 2009), evolution strategy with covariance matrix adaptation (CMA-ES) (Hansen et al., 2003), success-history-based parameter adaptation differential evolution (SHADE) (Tanabe and Fukunaga, 20132013), and SHADE with linear population size reduction hybridized with the semi-parameter adaption of CMA-ES (LSHADE-SPACMA) (Faramarzi et al., 2020), are used for performance comparisons, in which their parameters can be referred in Gutkin et al., 1976. To allow for an equitable competition, the maximum suitability rating for each algorithm was set to 15,000. Consequently, the population size and maximum iteration number of LALO are set to be 20 and 750, respectively, while other parameters can be determined via trial and error, as shown in Table 1. To clearly illustrate the searching process for the 2-dimensional benchmark functions, the population size and maximum iteration number of LALO are set to be 50 and 100, respectively; the maximum cluster number is set to be 8.
The unimodal benchmark functions
Figure 4 provides the searching space of the two-dimensional unimodal benchmark functions and the searching process of LALO, where the initial solutions and interactive clusters of LALO are also given. In consequence, the initial interactive clusters are distributed dispersedly, which can achieve wide exploration in the initial phase of LALO. As the iteration number increases, LALO can gradually find a better solution with an enhanced exploitation weight (Storn and Price, 1997; Regis, 2014).
Table 3 shows the average fitness and rank obtained by different algorithms for unimodal benchmark functions in 30 runs. It can be seen that LALO can obtain high-quality optimums on the whole for the unimodal benchmark functions, especially for function F2 with the first rank. Particularly, the average rank of average fitness LALO is the highest among all the algorithms except EO for the seven unimodal benchmark functions (Rao et al., 2011; Jin, 2011; El-Abd, 2017; Jin et al., 2019). This effectively verifies the highly competent exploitation ability of LALO against the other nine meta-heuristic algorithms.
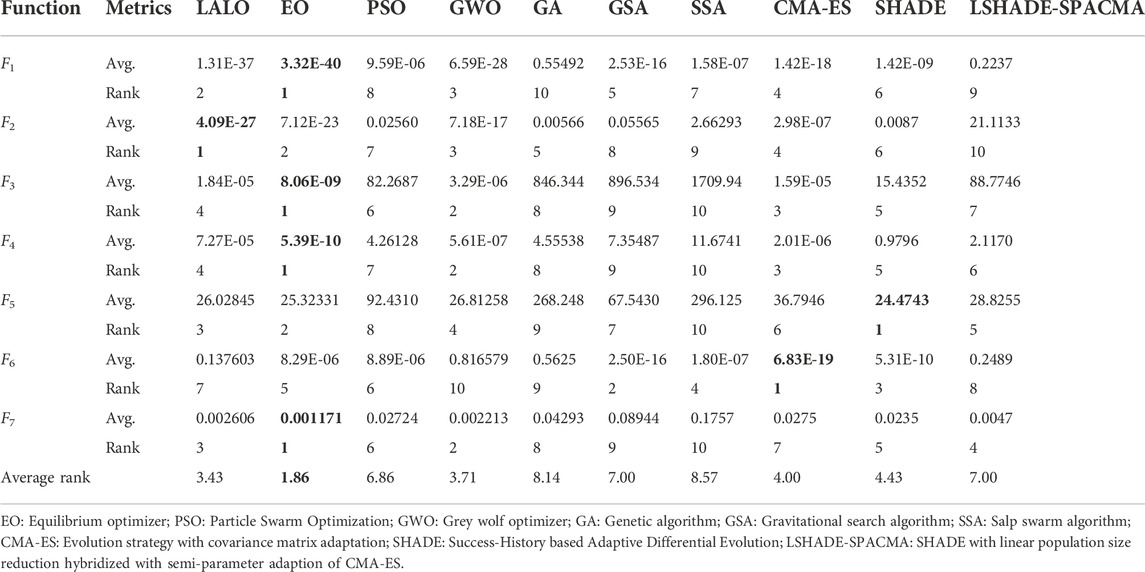
TABLE 3. Average fitness and rank obtained by different algorithms for unimodal benchmark functions in 30 runs.
On the other hand, Table 4 gives the fitness standard deviation and rank obtained by different algorithms for the unimodal benchmark functions in 30 runs. Similarly, the average rank of the fitness standard deviation obtained by EO outperforms the other algorithms for the unimodal benchmark functions, followed by LALO. It reveals the high optimization stability of LALO compared with other algorithms for the unimodal benchmark functions.

TABLE 4. Fitness standard deviation and ranks obtained by different algorithms for unimodal benchmark functions in 30 runs.
Figure 5 provides the box-and-whisker plots of ranks obtained by different algorithms for the benchmark functions from F1 to F7. It can be found from Figure 5A that the ranks of the average fitness obtained by LALO are mainly distributed in the top three for all the benchmark functions, which is the highest among all the algorithms. In contrast, the ranks of average fitness obtained by GA are mainly distributed from 6 to 9, which demonstrate that it easily traps into a low-quality optimum due to premature convergence. Similarly, LALO also performs best among all the algorithms on the ranks of fitness standard deviation, as shown in Figure 5B. This sufficiently indicates that LALO is highly competitive compared to the presented nine meta-heuristic algorithms for the benchmark functions.

FIGURE 5. Box-and-whisker plots of ranks obtained by different algorithms for the benchmark functions from F1 to F7. (A) Rank of average fitness. (B) Rank of fitness standard deviation.
4 Conclusion
This article proposes a novel machine learning-based meta-heuristic algorithm, in which the main contributions can be summarized as follows:
1) The proposed LALO is a novel meta-heuristic algorithm inspired by the social behavior of human beings that states an excellent person easily attracts like-minded people to approach him or her. Compared with the traditional clustering-based meta-heuristic algorithm, LALO can not only divide the searching individuals into multiple clusters by using the GNG network but can also generate the interaction topology between different clusters. Hence, each individual can select its learning target from the interactive clusters; thus, a wide exploration can be implemented in the searching phase.
2) The exploration and exploitation of LALO can be dynamically balanced via adjusting the number of interactive clusters and the searching coefficient. As a result, it can enhance the exploration of LALO in the initial phase, while the exploitation can be gradually strengthened as the iteration number increases.
3) The comprehensive case studies are carried out to evaluate the optimization performance of LALO compared with various meta-heuristic algorithms. On the whole, LALO is highly competitive in the optimum quality and optimization stability for 29 benchmark functions and 3 classical engineering problems. Particularly, the simulation results clearly demonstrate that LALO is more appropriate to handle fix-dimension multimodal benchmark functions, composite benchmark functions, and classical engineering problems.
Due to the superior optimization performance of LALO, it can be applied to various real-world optimizations. Furthermore, it also can be extended into a multi-objective optimization algorithm to search the Pareto optimum solutions for different kinds of multi-objective optimization problems.
Data availability statement
The data analyzed in this study are subject to the following licenses/restrictions: Internal enterprise Data. Requests to access these datasets should be directed to Qmlhb19UYW5nQG91dGxvb2suY29t.
Author contributions
XH, BT, and MZ: writing the original draft and editing. YM and XM: discussion of the topic. LT, XW, and DZ: supervision and funding.
Funding
The authors gratefully acknowledge the support of the research and innovative application of key technologies of image processing and knowledge atlas for complex scenes in the Smart Grid (202202AD080004), the research and innovative applications of key technologies of image processing and knowledge atlas for complex scenes in the Smart Grid (YNKJXM20220019), the practical maintenance of substation inspection robot master station management platform of Yunnan Electric Power Research Institute in 2022–2023 (056200MS62210005), and the Yunnan technological innovation talent training object project (No. 202205AD160005).
Conflict of interest
Authors XH, BT, MZ, YM, XM, and LT are employed by the Electric Power Research Institute of Yunnan Power Grid Co., Ltd., China Southern Power Grid. XW is employed by Yunnan Power Grid Co., Ltd., China Southern Power Grid. DZ is employed by Zhejiang Guozi Robotics Co., Ltd.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Alba, E., and Dorronsoro, B. (2005). The exploration/exploitation tradeoff in dynamic cellular genetic algorithms. IEEE Trans. Evol. Comput. 9, 126–142. doi:10.1109/TEVC.2005.843751
Askari, Q., Younas, I., and Saeed, M. (2020). Political optimizer: A novel socio-inspired meta-heuristic for global optimization. Knowl. Based. Syst. 195, 105709. doi:10.1016/j.knosys.2020.105709
Dai, C., Chen, W., Zhu, Y., and Zhang, X. (2009). Seeker optimization algorithm for optimal reactive power dispatch. IEEE Trans. Power Syst. 24, 1218–1231. doi:10.1109/TPWRS.2009.2021226
El-Abd, M. (2017). Global-best grain storm optimization algorithm. Swarm Evol. Comput. 37, 27–44. doi:10.1016/j.swevo.2017.05.001
Faramarzi, A., Heidarinejad, M., Stephens, B., and Mirjalili, S. (2020). Equilibrium optimizer: A novel optimization algorithm. Knowl. Based. Syst. 191, 105190. doi:10.1016/j.knosys.2019.105190
Fišer, D., Faigl, J., and Kulich, M. (2013). Growing neural gas efficiently. Neurocomputing 104, 72–82. doi:10.1016/j.neucom.2012.10.004
Fritzke, B. (1995). “A growing neural gas network learns topologies,”. In Advances in Neural Information Processing System, G. Tesauro, D. S. Touretzky, and T. K. Leen (Cambridge, MA, USA: MIT Press), 7, 625–632. doi:10.1007/978-3-642-40925-7_38
Guo, L., Wang, G.-G., Gandomi, A. H., Alavi, A. H., and Duan, H. (2014). A new improved krill herd algorithm for global numerical optimization. Neurocomputing 138, 392–402. doi:10.1016/j.neucom.2014.01.023
Gutkin, T. B., Gridley, G. C., and Wendt, J. M. (1976). The effect of initial attraction and attitude similarity-dissimilarity on interpersonal attraction. Cornell J. Soc. Relat. 11, 153–160. doi:10.1080/00224545.1978.9924167
Hansen, N., Müller, S. D., and Koumoutsakos, P. (2003). Reducing the time complexity of the derandomized evolution strategy with covariance matrix adaptation (CMA-ES). Evol. Comput. 11, 1–18. doi:10.1162/106365603321828970
Heidari, A. A., Mirjalili, S., Faris, H., Aljarah, I., Mafarja, M., and Chen, H. (2019). Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 97, 849–872. doi:10.1016/j.future.2019.02.028
Holland, J. H. (1992). Genetic algorithms. Sci. Am. 267, 66–72. doi:10.1038/scientificamerican0792-66
Jin, Y. (2011). Surrogate-assisted evolutionary computation: Recent advances and future challenges. Swarm Evol. Comput. 1, 61–70. doi:10.1016/j.swevo.2011.05.001
Jin, Y., Wang, H., Chugh, T., Guo, D., and Miettinen, K. (2019). Data-driven evolutionary optimization: An overview and case studies. IEEE Trans. Evol. Comput. 23, 442–458. doi:10.1109/TEVC.2018.2869001
Kazemtabrizi, B., and Acha, E. (2014). An advanced STATCOM model for optimal power flows using Newton’s method. IEEE Trans. Power Syst. 29, 514–525. doi:10.1109/TPWRS.2013.2287914
Kennedy, J., and Eberhart, R. “Particle swarm optimization,” in Proceedings of ICNN95-international conference on neural network. IEEE. doi:10.1007/978-0-387-30164-8_630
Kirkpatrick, S., Gelatt, C. D., and Vecchi, M. P. (1983). Optimization by simulated annealing. Science 220, 671–680. doi:10.1126/science.220.4598.671
Mas, I., Li, S., and Acain, J. (2009). Entrapment/escorting and patrolling missions in multi-robot cluster space control. In Proceedings of the IEEE/RSJ international conference on intelligent robots & systems. IEEE. St. Louis, MO, USA.
Mirjalili, S., Gandomi, A. H., Mirjalili, S. Z., Saremi, S., Faris, H., and Mirjalili, S. M. (2017). Salp swarm algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 114, 163–191. doi:10.1016/j.advengsoft.2017.07.002
Mirjalili, S., Mirjalili, S. M., and Lewis, A. (2014). Grey wolf optimizer. Adv. Eng. Softw. 69, 46–61. doi:10.1016/j.advengsoft.2013.12.007
Mirjalili, S., and SCA, (2016). Sca: A sine cosine algorithm for solving optimization problems. Knowl. Based. Syst. 96, 120–133. doi:10.1016/j.knosys.2015.12.022
Rao, R., Savsani, V., and Vakharia, D. (2011). Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Computer-Aided Des. 43, 303–315. doi:10.1016/j.cad.2010.12.015
Rashedi, E., Nezamabadi-pour, H., and Saryazdi, S. (2009). Gsa: A gravitational search algorithm. Inf. Sci. (N. Y). 179, 2232–2248. doi:10.1016/j.ins.2009.03.004
Regis, R. G. (2014). Evolutionary programming for high-dimensional constrained expensive black-box optimization using radial basis functions. IEEE Trans. Evol. Comput. 18, 326–347. doi:10.1109/TEVC.2013.2262111
Storn, R., and Price, K. (1997). Differential evolution-a simple and efficient heuristic for global optimization over continuous space. J. Glob. Optim. 11, 341–359. doi:10.1023/A:1008202821328
Tanabe, R., and Fukunaga, A. (2013). Success-history based parameter adaptation for differential evolution. IEEE Congr. Evol. Comput., Kraków, Poland, 71–78. doi:10.1007/s00500-015-1911-2
Wang, M. Q., Gooi, H. B., Chen, S. X., and Lu, S. (2014). A mixed integer quadratic programming for dynamic economic dispatch with valve point effect. IEEE Trans. Power Syst. 29, 2097–2106. doi:10.1109/TPWRS.2014.2306933
Wolpert, D. H., and Macready, W. G. (1997). No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1, 67–82. doi:10.1109/4235.585893
Zeng, Y., Chen, X., Ong, Y.-S., Tang, J., and Xiang, Y. (2017). Structured memetic automation for online human-like social behavior learning. IEEE Trans. Evol. Comput. 21, 102–115. doi:10.1109/TEVC.2016.2577593
Zhang, Q., Wang, R., Yang, J., Ding, K., Li, Y., and Hu, J. (2017). Collective decision optimization algorithm: A new heuristic optimization method. Neurocomputing 221, 123–137. doi:10.1016/j.neucom.2016.09.068
Keywords: like-attracts-like optimizer, meta-heuristic algorithm, growing neural gas network, dynamic clustering, video robotics cluster control
Citation: Huang X, Tang B, Zhu M, Ma Y, Ma X, Tang L, Wang X and Zhu D (2023) Like-attracts-like optimizer-based video robotics clustering control design for power device monitoring and inspection. Front. Energy Res. 10:1030034. doi: 10.3389/fenrg.2022.1030034
Received: 28 August 2022; Accepted: 20 September 2022;
Published: 09 January 2023.
Edited by:
Bin Zhou, Hunan University, ChinaReviewed by:
Yaxing Ren, University of Lincoln, United KingdomYiyan Sang, Shanghai University of Electric Power, China
Copyright © 2023 Huang, Tang, Zhu, Ma, Ma, Tang, Wang and Zhu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Biao Tang, Qmlhb19UYW5nQG91dGxvb2suY29t
 Xuyong Huang1
Xuyong Huang1 Biao Tang
Biao Tang