Wind-resistant structural optimization of irregular tall building using CFD and improved genetic algorithm for sustainable and cost-effective design

Tall buildings with irregular shapes and considerable heights are gaining popularity in creating the vertical cities around the world. They also considered one of the major energy consumers with little regards to sustainability. Tall building is wind-sensitive structure and shape plays major role in determining wind loads, which usually govern the design of its lateral resisting system. Thus, evaluating wind loads properly and designing an optimal lateral system accordingly are the main challenges attributed to the design process of irregular tall building. This paper presents a computational procedure for the optimal design of wind-resistant irregular tall building to minimize the total weight of structure within design requirements in single digital environment. That is achieved firstly by creating a digital system of computational fluid dynamic (CFD) analysis that is coupled with pressure-load translation (PLT) algorithm to evaluate the wind motions on irregular tall buildings and generate the design wind loads accordingly. Genetic Algorithm (GA) with enhance design constrains function of lateral displacements, inter-story drifts and top acceleration is then developed to perform structural optimization. A numerical example using 70-story twisting reinforced concrete building is implemented to verify the feasibility of the developed computational procedures. Steady and incompressible flow applied at ($0°$) angle of attack was implemented in the CFD model to simulate the wind flow on the studied building. Genetic algorithm with improved design constraints of static and dynamic design requirements was developed to optimize the structure effectively and efficiently. The numerical example demonstrates its effectiveness by achieving 35.71% reduction of concrete volume from the original lateral structural system design. This is also translated into a sustainability value by lessening the embedded carbon dioxide by 4,400 tons.

1 Introduction

Social and economic accelerating development, together with new engineering and construction techniques have inspired architects and engineers to design atypical, complex and slender tall buildings to reflect their creativity and innovation (Alkhatib et al., 2021a). These developments are associated with complexity in wind-induced motions and its attributed structural factors such as low natural frequency, lack of sufficient damping and increment in flexibility and slenderness (Sharma et al., 2018), where wind-induced forces usually govern the design of tall building (Elshaer et al., 2017). Thus, finding a balance between safety, serviceability and economy has been a challenge faced by architects and engineers when designing modern irregular tall buildings. This challenge is leveled up when sustainability factor is added into the equation by producing energy-efficient design.

Because building shapes plays critical role in deriving its aerodynamic characters, modification of tall building forms proved to be effective in mitigating wind-induced loads on tall buildings (Xie, 2014; Elshaer et al., 2017). Several studies investigated different aerodynamic modifications on tall buildings including major modifications such as tapering, twisting and setback (Kim and You, 2002; Kim et al., 2008; Xie, 2014; Bairagi and Dalui, 2018) that have a significant impact architecturally and structurally on building design, or minor modifications such as corner configuration (Zhengwei et al., 2012; Li et al., 2018; Thordal et al., 2020; Mandal et al., 2021), where it has little to no effect on the intent design, yet still shows an effective results in reducing wind responses. While Kim and You (Kim and You, 2002) and Xie (Xie, 2014) found that tapering is more effective in mitigating across-wind responses, Xie (Xie, 2014) further explored twisting shape modification demonstrating that it has and extra advantage of equalizing winds distribution and responses along wind directions. Minor corner modifications, including rounding, chamfering and recession, were also investigated by Tamura et al. (Tamura et al., 1998) and Elshaer et al. (Elshaer et al., 2017) and founded to be effective in reducing wind responses. Li et al. (Li et al., 2018) demonstrated that chamfered corners resulted in an effective reduction of a long-wind loads and recessed corners showed similar effectiveness in reducing across-wind responses, but Mandal et al. (Mandal et al., 2021) proved that rounded corners are more effective in reducing wind loads than chamfered ones. Alkhatib et al. (Alkhatib et al., 2022a) introduced a new computational method to optimize wind loads on irregular tall buildings with minor aerodynamic modifications to the external shape of the buildings. Touloupaki et al. (Atabay, 2009), in the other hands, proposed a parametrical approach to minimize energy consumption of tall building by altering its geometrical form. Hassanli et al. (Hassanli et al., 2018) and Ruiz et al. (Ruiz et al., 2021) investigated the effectiveness of tall building aerodynamic treatements to wind energy harvesting by incorporating wind power system directly into the built environment. Although these studies present a valuable insight by exploiting computational methods to evaluate wind motions on tall buildings properly, altering building configuration is not architecturally and structurally preferred.

Quite the opposite, structural optimization does not rely on the changing of the building external geometries or requires additional cost. However, most of previous research work of structural optimization focused on seismic loading, with little regard to wind loading (Huang et al., 2015; Fu et al., 2018; Alkhatib et al., 2022b). In that context, Chan et al. (Chan and Chui, 2006; Chan et al., 2009) developed a set of structural optimization methods based on Optimally Criteria (OC) for optimal design of tall buildings subjected to wind actions and constraints. Huang (Ming-feng, 2013) as well, proposed a performance-based design approach by employing OC for developing optimal structural design of tall building satisfying wind-resistance requirements. However, Fu (Fu et al., 2018) demonstrated that employing OC approach may lead to inaccurate result of frequency constraint because strain energy does not account for the gradient of internal forces to its design variables and proposed an eigen value approach for computing the sensitivity of frequency constraints. Moreover, OC requires wind-induced constrains to be explicitly expressed in complicated mathematical formulas, making it not practically applicable for industrial application. Additionally, dealing with complex and large-scale models, structural response is naturally a non-linear function to the design variables and OC may not lead to discrete solutions and may trapped into local optima. It is also observed that most of the optimization techniques used today for solving engineering problems accept the design variables to be “continuous” and such characteristics cannot be employed in all engineering problems. For architectural problems, besides the mathematical formulation techniques, using “discrete” variables based algorithm is often deemed necessary (Atabay, 2009; Abd Elrehim et al., 2019).

Taking these interesting studies as a benchmark for this research to address their shortcoming, this study presents a new integrated approach for wind-induced structural optimization of irregular tall building within single digital environment. In the first place, a computational fluid dynamic (CFD) system coupled with pressure-load translation (PLT) algorithm is developed to evaluate wind motions on irregular tall building and generate the corresponding design wind loads. Next in order, structural optimization strategy is developed using Genetic Algorithm, with its ability for global search and efficient parallelism, to find the optimal weight of the structure. More importantly, because lateral drifts and top acceleration are the focus in the design of wind-resistance tall building, an enhanced design constrains penalty function is developed and integrated within GA process. Static and dynamic characteristics of the building are then assessed through finite element (FE) integrated solver to evaluate structural responses against design constraints pre-defined limits.

The paper is structured into 5 sections. Section 1 (this section) describes the topic under investigation and summarizes the related studies with its shortcomings to be addressed in this work. Section 2 demonstrates CFD wind loads generation and improved GA structural optimization methodologies. Section 3 verifies the proposed approaches by implementing a numerical example on real existing irregular tall building where analysis and results are presented and discussed. Finally, Section 5 draws the conclusion of this study and highlights the future recommendation for extending this research work.

2 Optimization methodology

2.1 Computational wind loads evaluation

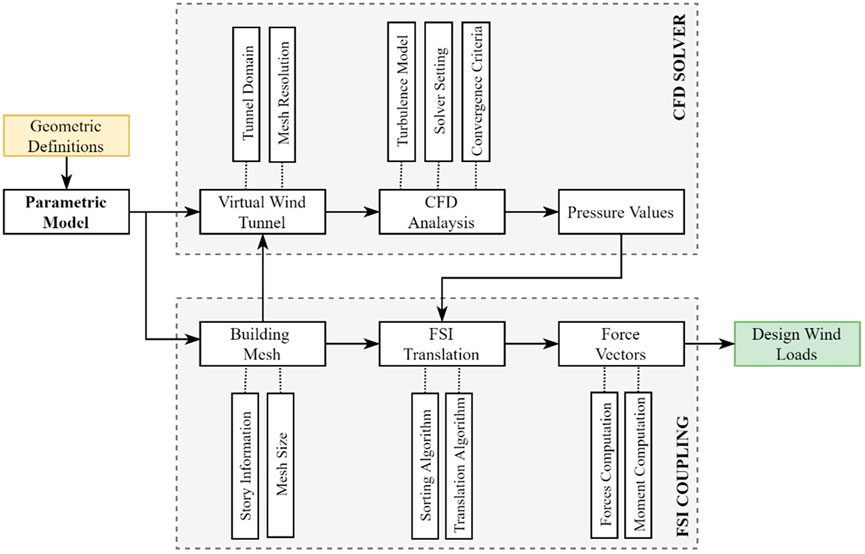
Computational Fluid Dynamic (CFD) has recently extended its applications to architectural problems including tall building aerodynamic studies (Mou et al., 2017; Paul and Dalui, 2021; Sanyal and Dalui, 2022) and this opens an opportunity to utilize CFD in the preliminary stage to evaluate wind motions on irregular tall buildings. However, the idea in this work is to develop an integrated optimization approach where CFD output can be translated into static wind loads acting on each story of a given structure within a single environment in an automated manner. Thus, parametric modelling using Rhino3D (Rutten and McNeel, 2007) and its embedded generative design tool Grasshopper (GH) is employed firstly to generate the initial model representing the bluff body of building exterior shape. OpenFOAM (Weller et al., 1998), an open-source computational fluid dynamic solver that is widely and reliably used in academia and industry to solve computational problems, is utilized to perform the outdoor airflow analysis. However, to run OpenFOAM CFD cases within GH environment, a python wrapper for OpenFoam C++ library is used. Significant parameters to set up CFD environment are defined and evaluated to ensure proper evaluation of wind pressure on the selected building. That includes turbulence models, mesh resolutions, wind profile, wind speed and convergence criteria.

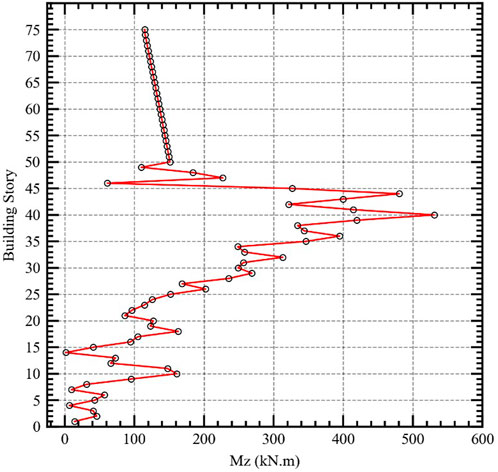
Pressure-Load Translation (PLT) algorithm is then developed to translate CFD output pressures into static wind loads. The PLT technique starts by transforming the pressure exerted by the building exterior façade mesh surfaces into vector forces with respect to its normal directions. Sorting algorithm is written by Python (vanRossum, 1995) to combine and group the collected vectors horizontally and vertically for each story height that is measured by mesh divisions. For each story, two vectors are generated to represent along-wind force (Fy) and across-wind forces (Fx) with respect to building major axis directions, while torsional moments (Mz) are computed as the output of their cross-product to the building’s centroid. Generated Forces and moments are then assigned to the diaphragm center of the structure for each respective story. The overall process of CFD optimal wind loads generation is shown in Figure 1.

FIGURE 1

FIGURE 1. Computational wind loads generation process.

2.2 GA structural optimization methodology

Because satisfying serviceability criteria become more challenging than achieving strength requirement (Chan et al., 2009), also since overall design of tall building is usually governed by lateral stiffness, the output sizes from lateral stiffness serviceability-based optimization are larger than strength based design sizes (Soegiarso and Adeli, 1997; Pezeshk et al., 2000). Hence, only serviceability requirements are employed as constraints for this optimization study, where strength constraints can be dealt with independently (Chan et al., 1995). Practically, strength and capacity design are regularly advised to be performed on a member-by-member approach, with reference to the standard code adopted (Zou and Chan, 2005).

2.2.1 Objective function

In structural design optimization, generally weight of structure is assumed to be the objective function. Considering concrete tall building structure, the objective function can be expressed as minimization of the structural lateral system concrete weigh. Thus, for a 3D structural frame consisting of I = 1,2,3 … , N types of core walls, columns and beams, and j = 1,2,3….M stories, the wind-resistance objective function is formulated as:

To minimize:

$f\left(x\right)={\displaystyle \sum }_{i=1}^N\rho A_i{l}_i$

Limited to:

$b_i^L\le b_i\le b_i^U;h_i^L\le h_i\le h_i^U;t_i^L\le t_i\le t_i^U$

$b_i,h_i,t_i=S_i\in \left\{S\right\}$

Where $\rho$ is concrete density, $A_i$ is sectional area for the ith type of element section, and $l_i$ is the length for ith type of element section. $b_i$, $h_i$ are the width and depth for column/beam section in ith type section respectively and $t_i$ is the thickness of corewall in ith type of section. $S_i$ is the indecies for the section sizes domain defined within $\left\{S\right\}$.

2.2.1.1 Design constraints

General formulation of constrains function for k = 1,2,3 … ,V number of constrains, for j = 1,2,3….,M number of stories is expressed as follow:

$g_k\left(x\right)\le 0$

Giving the problem of wind-resistance optimization, lateral drifts and top acceleration are expressed as the main design constraints restricting their values within recommended limits.

$\frac{u_H}{H}\le {\delta }_{limit};\frac{v_H}{H}\le {\delta }_{limit};\frac{\sqrt{u_H^2+v_H^2}}{H}\le {\delta }_{limit}$

$\frac{u_j-u_{j-1}}{z_j-z_{j-1}}\le {∆}_{limit};\frac{v_j-v_{j-1}}{z_j-z_{j-1}}\le {∆}_{limit};\frac{\sqrt{{\left(u_j-u_{j-1}\right)}^2+{\left(v_j-v_{j-1}\right)}^2}}{z_j-z_{j-1}}\le {∆}_{limit}$

${\widehat{\ddot{x}}}_H\le a_{limit};{\widehat{\ddot{y}}}_H\le a_{limit};{\widehat{\ddot{xy}}}_H\le a_{limit}$

However, GA can only work with unconstrained optimization problem, thus, constrains were transformed into normalized form:

$\frac{\frac{u_H}{H}}{{\delta }_{limit}}-1\le 0;\frac{\frac{v_H}{H}}{{\delta }_{limit}}-1\le 0;\frac{\frac{\sqrt{u_H^2+v_H^2}}{H}}{{\delta }_{limit}}-1\le 0$

$\frac{\frac{u_j-u_{j-1}}{z_j-z_{j-1}}}{{∆}_{limit}}-1\le 0;\frac{\frac{v_j-v_{j-1}}{z_j-z_{j-1}}}{{∆}_{limit}}-1\le 0;\frac{\frac{\sqrt{{\left(u_j-u_{j-1}\right)}^2+{\left(v_j-v_{j-1}\right)}^2}}{z_j-z_{j-1}}}{{∆}_{limit}}-1\le 0$

$\frac{{\widehat{\ddot{x}}}_H}{a_{limit}}-1\le 0;\frac{{\widehat{\ddot{y}}}_H}{a_{limit}}-1\le 0;\frac{{\widehat{\ddot{xy}}}_H}{a_{limit}}-1\le 0$

$u_H,$ $v_H$ are the along-wind and across-wind maximum horizontal displacement at top of the structure and their diagonal vector, ${\delta }_{limit}$ is the allowable limit stipulated by the code (Eurocode H/500), $u_j,v_j$are the along-wind and across wind inter-story drift and their diagonal vector at $j$th floor in respect to floor height $z_j$, ${∆}_{limit}$ is the allowable inter-story drift. ${\ddot{x}}_H,{\ddot{y}}_H$ and $a_{limit}$ are the top story peak acceleration in x and y directions and their recommended limit in a adopted standard, respectively. Threshold of top peak acceleration is computed by employing the lower natural frequency generated by eigenvalue analysis as per ISO 6897 (I S O., 1984) and ISO 10137:2007 (ISO Organization for Standardization, 2007):

${\widehat{\ddot{x}}}_H=\sqrt{2\ln f_{1}T}+\left(0.68+\frac{\ln R}{5}\right)\exp \left(-0.35-0.41\ln f_1\right)$

${\widehat{\ddot{x}}}_H$ is the peak acceleration for $T$ minutes within a return years period $R$, f is the natural frequency of first mode, $\sqrt{2\ln f_{1}T}$ is peak factor, $\left(0.68+\frac{\ln R}{5}\right)$ is adjustment factor and $\exp \left(-0.35-0.41\ln f_1\right)$ is natural frequency acceleration function root mean square. Usually, observation time $T$ is 10 min and return period $R$ is 1, 5 or 10 years. ${\widehat{\ddot{xy}}}_H$ is adopted to evaluate the complex motion of irregular tall building to estimate its corresponding horizontal acceleration as recommended by (Melbourne and Palmer, 1992).

2.2.1.2 Fitness function

In order to calculate fitness value for each individual, and because constrains were normalized, the objective function has to be modified by a violence coefficient, $C$:

$c_k=\{\begin{array}{c}{g}_k\left(x\right)if{g}_k\left(x\right)>0\\ \\ 0if{g}_k\left(x\right)\le 0\end{array}$

Where $C={\displaystyle \sum }_{k=1}^V{c}_k$

The modified objective function can then be written as:

$\mathrm{\Phi }\left(x\right)=f\left(x\right)\left(1+KC\right)$

Where $\Phi \left(x\right)$ is the modified objective function, $f\left(x\right)$ is the actual objective function, $C$ is the violation coefficient and $K$ is a penalty factor with a value depending on the problem. In this case study, $K$ is assumed to be 10 for deflection constrain and 1,000 for drift constrain. The objective function is then required to be transformed into a fitness value. According to (Goldberg, 1989) for optimization minimization problem, to generate fitness value, $\Phi \left(x\right)$ shall be subtracted from large fixed value, so that all fitness values will be positive, and individuals with minimum criteria will have higher fitness values. The fitness value can then be obtained by subtracting the value of unconstrained objective function ${\Phi }_i\left(x\right)$ from the summation of maximum and minimum unconstrained objective function values within a population consisting of all individuals in $i$th generation as follow:

$F_i=\left[{\mathrm{\Phi }}_i{\left(x\right)}_{\mathit{max}}+{\mathrm{\Phi }}_i{\left(x\right)}_{\mathit{min}}\right]-{\mathrm{\Phi }}_i\left(x\right)$

Fitness factor then can be derived as:

${Fc}_i=F_i/F_{avg.}$

$F_{avg.}=\sum F_i/n$

where $n$ is total number of individuals in a population. The overall process of genetic algorithm structural optimization procedures is illustrated in Figure 2.

FIGURE 2

FIGURE 2. Genetic Algorithm optimization process.

3 Numerical example

Case Study: Cayan tower in Dubai, as shown in Figure 3, the tallest twisting tower in the world, present a good example of the current trend of complexity in tall building design. The tower is 306 m in height, with spiral twisting shape of 90° along its height, inspired by human DNA and designed by SOM architectural group (Golasz-Szolomicka and Szolomicki, 2019). The lateral structure system of this concrete building consists of central core wall and perimeter moment frame. To simplify the studied problem, typical story height of 4 m is assumed for all 75 story with total structure height of 300 m.

FIGURE 3

FIGURE 3. Cayan tower dubai (Alkhatib et al., 2022a).

3.1 Wind loads generation

Two versions within the same parametric model are created as illustrated in Figure 4 (a) and (b). The first one is a bluff model representing the exterior shape of the building to be used for CFD wind analysis stage. The other one is element detailed model to be translated into structural model, Figure 4C to be integrated into FE solver for structural responses evaluation during optimization stage.

FIGURE 4

FIGURE 4. Parametric models: (A) Bluff, (B) detailed and (C) structural.

To set up the CFD environment, different parameters and settings adopted to ensure proper analysis and reliable output. In the first place, domain size of virtual tunnel, shown in Figure 5, was determined based on building height (H) with 2.3 H, 10 H, 2.3 H and 2.3 H for windward, leeward, sides and top, respectively as recommended by (Franke et al., 2007). Blockage ratio was then computed at 1.06%, below the threshold ratio of 5%, to provide sufficient space for the air flow to be fully developed (Mou et al., 2017). The Outflow boundary condition was employed to simulate steady and incompressible wind flow. Wall boundary conditions were used to describe the wall of the computational domain and the surface of the studied building. SIMPLE pressure-velocity coupling algorithms was adopted for solver setting, and Second-Order Upwind Scheme was adopted to discretize momentum, turbulent kinetic energy, and turbulence dissipation rate (Meng et al., 2018). Finally, convergence of simulation is assumed to be reached when residuals of x, y, z momentum, k, ε and continuity are less than 10^{–3 39}.

FIGURE 5

FIGURE 5. Computational domain (outer) meshing.

Realizable k—ε turbulence model was adopted to perform numerical simulation. That is because it is sensitive to rapid strain and streamline curvature, flow separation, re-attachment and recirculation (Ozmen et al., 2016), while at the same time, it allows mathematical constrains to fit Reynolds stresses (Tutar and Oguz, 2002). For mesh resolutions, maximum grid size is determined by dividing shortest width of the building over 10 and multiplying the output result by $\sqrt{2}$ for each refinement needed (Alkhatib et al., 2022a). Two staged refinements were done based on similar study (Alkhatib et al., 2022a) as no considerable change of output values is observed for advanced refinement, while reasonable computational time is maintained. The selected mesh size is computed by 1.54 m reaching to a total of 972,660 cell numbers within the computational domain.

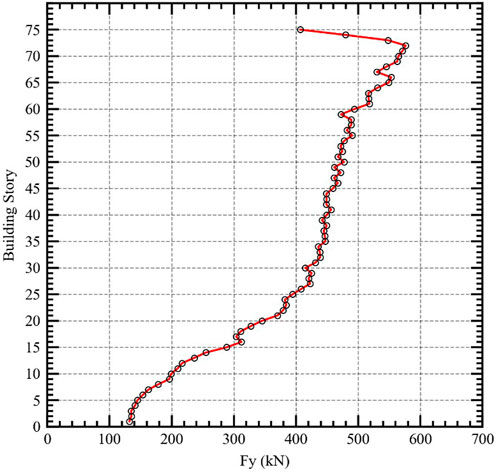
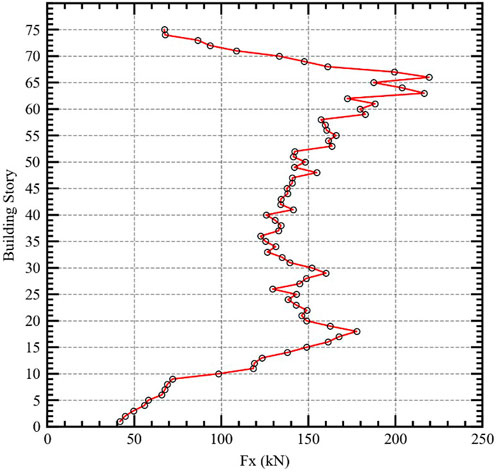
The generated wind loads for the typical $0°$ wind direction that was adopted in this research work are shown in Figure 6, Figure 7 and Figure 8 for along-wind forces (Fy), across-wind forces (Fx) and torsional moment (Mz), respectively. It can be observed that greater forces are generated along the angle of attack in comparison to the across-wind forces. Torsional moment experienced some disruptions due to the nature of the building with its irregular verticality especially at the mid-height of the building.

FIGURE 6

FIGURE 6. Along-wind forces (Fy) along y-direction.

FIGURE 7

FIGURE 7. Across-wind forces (Fx) along x-direction.

FIGURE 8

FIGURE 8. Torsional moment (Mz) around the building’s center.

3.2 GA structural optimization

To implement the developed genetic algorithm technique in the studied example, several configuration and parameters should be established. That includes problem formulation of the investigated problem to suite the optimization algorithm, coding and decoding strategy and controlling parameters.

3.2.1 Problem formulation

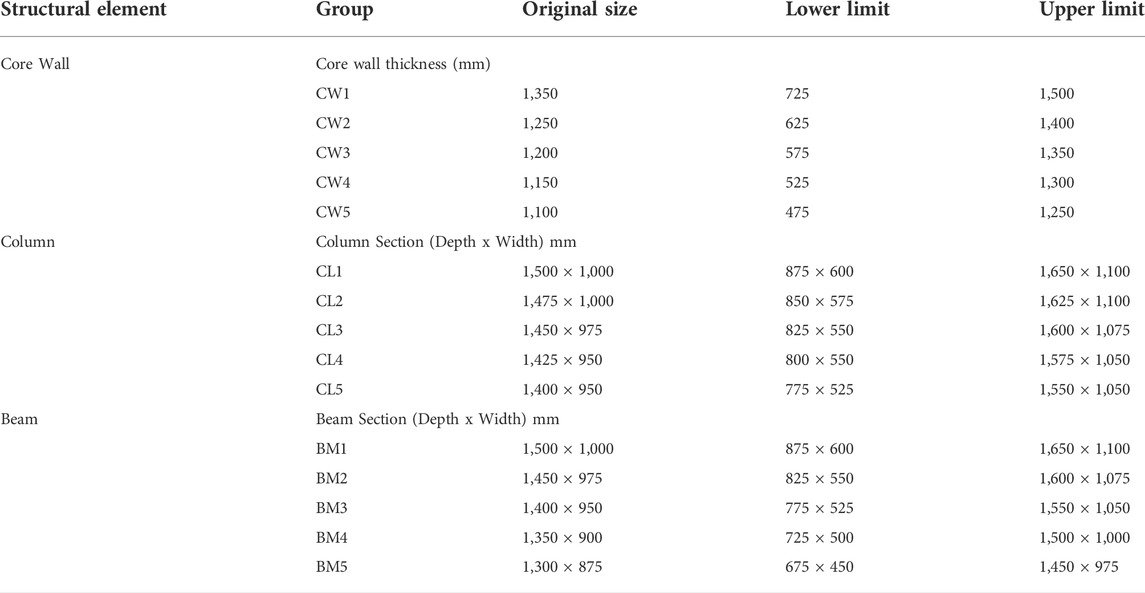
The investigated structure was firstly grouped and arranged to simplify the optimization process. Structure was divided into 5 groups along its height. Group 1, group 2, group 3, group 4 and group 5 represent structural elements from 1st to 15th floor, 16th to 30th floor, 31st to 45th floor, 46th to 60th floor and 61st to 75th floor, respectively as illustrated in Table 1. Since lateral structural system is the aim for this optimization, other structural elements including slab and internal columns are assumed to be constant throughout the height of the structure. Original structural elements are set based on reference structural plan of the case study from (Golasz-Szolomicka and Szolomicki, 2019) and (Marmar et al., 2021) together with engineering experience and judgement. Variation for lower and upper limits are set to be within Eurocode design guidance and standard (Hendy and Smith, 2007). To alleviate long computational processing time by limiting number of design variables, columns and beams are assumed with fixed ratio of 3:2 for depth and width respectively. Thus, sections’ width is changed in proportion to their depth by the fixed ratio. Finally, taking constructability into account, the variance in sections sizes is determined by 25 mm intervals.

TABLE 1

TABLE 1. Structural sections grouping.

Design constraints limitations for structural displacement and inter-story drift are adopted based on Eurocode Standard (Hendy and Smith, 2007). The computed limits are 600 mm and 0.0015 for structural displacement and inter-story drifts, respectively. Top acceleration limit of 0.21 m²/s is generated based on ISO 10137:2007 (ISO Organization for Standardization, 2007) with 1 year return period.

3.2.2 Coding and decoding

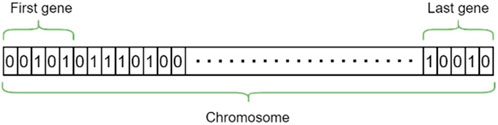
Several ways to represent design variables in GA including real and binary values. This research however adopted binary method, as shown in Figure 9, for its highly efficiency uniform crossover (Hu and Di Paolo, 2008), and faster computing time as it deals with machine original language of 0 and 1. For the 15 design variables represented by the assigned groups, change of design variables sectional area were planned in a set of pool with maximum of 625 mm, 150 mm in section size reduction or increment respectively, and within 25 mm intervals. This will produce a set $\left\{S\right\}$ of 32 sections variance:

$\left\{S\right\}=\left\{625,600,575,\dots ,-125,-150\right\}$

FIGURE 9

FIGURE 9. Binary chromosome representing individual solution.

To produce a binary code for $\left\{S\right\}$, 5 bits is needed for 32 binary coding with (00000) representing first element in set $\left\{S\right\}$and (11111) representing the last element in set $\left\{S\right\}$. For the 15 design variables (groups), each of them is represented by a gene (substring) corresponding to a value from the $\left\{S\right\}$ set and its binary coding. All multi design variables genes are then linked to form chromosome (string). Therefore, for the given 15 design variables with each substring consisting of 5-bits, each individual solution represented by a chromosome (string) having a length of 75-bits of 0’s and 1’s.

3.2.3 GA control parameters

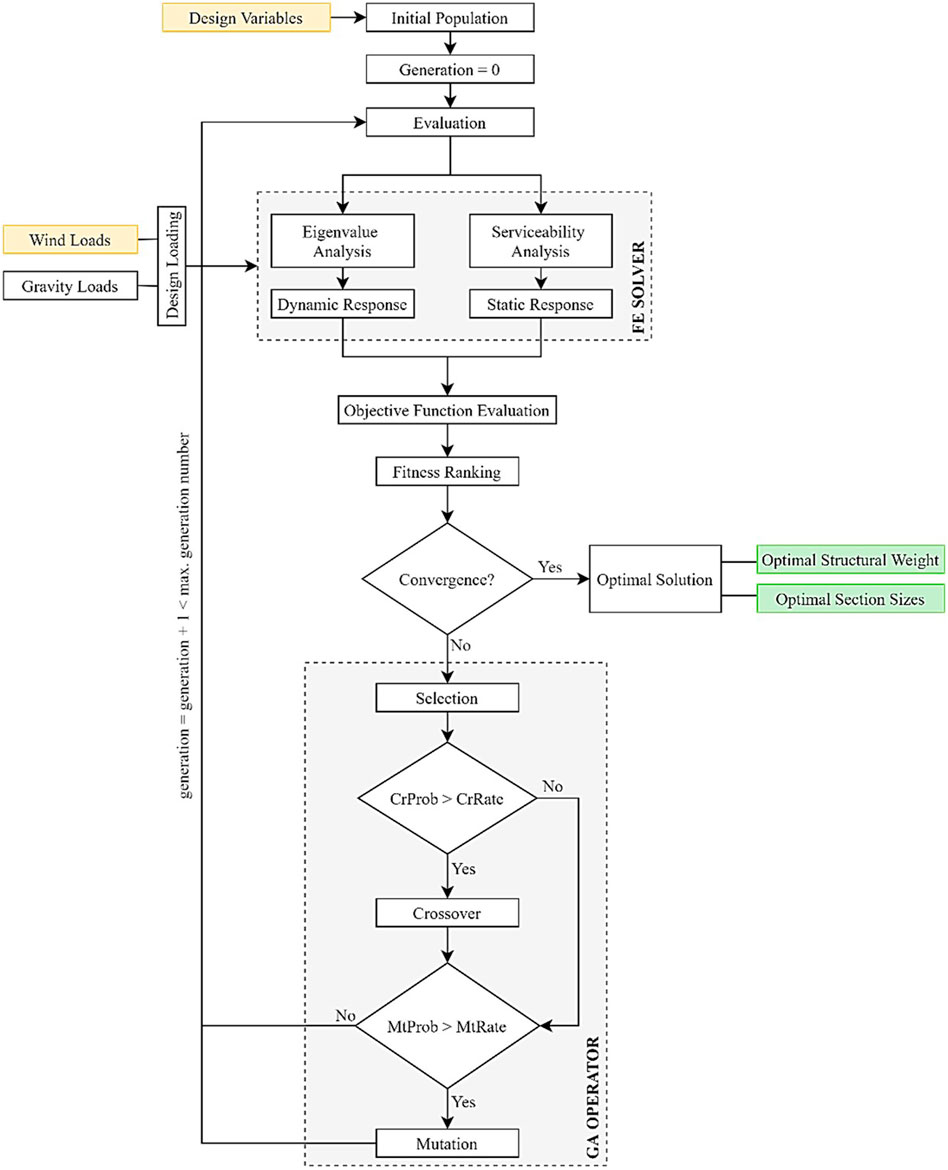
The main controlling parameters for genetic algorithm are population size and generations number. Population size projects number of individuals in each generation, and number of generations projects maximum number of iterations for computational process of genetic algorithm, unless convergence is achieved or stopping criteria is activated. Considering the problem given in this case study, size of design variables, computational time and pre-test of the developed algorithm, population size and number of generations were set to be 50 each. After initial population is randomly created and evaluated, the next generation is produced by undergoing through elitism, crossover and mutation process, as shown in Figures 10, 11.

FIGURE 10

FIGURE 10. Crossover mechanism.

FIGURE 11

FIGURE 11. Mutation mechanism.

Elitism was adopted in the optimization process because of its effectiveness in improving the efficiency of GA (De Jong, 1975). Elitism is achieved by preserving the highest performance individual solution from one generation to another by simply copying the fittest chromosome to the next generation before all individuals in the population undergo crossover and mutation process.

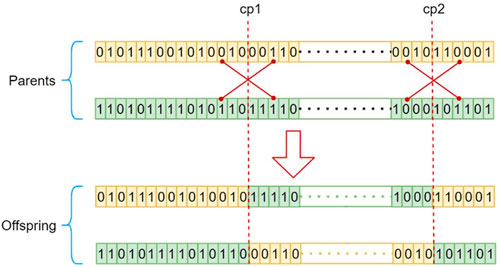
Crossover methods including single-point, multi-point, uniform and variable-to-variable crossover were tested to find the most effective method for the given optimization problem (Hasançebi and Erbatur, 2000). Multi-point crossover was adopted giving that it has a better logic for the optimization problem in hand. In multi-point crossover, parents’ chromosomes (strings) are decomposed to number of substrings at random locations based on the introduced cutting points (cp). Substrings are then swapped and interchanged between parents to produce new offspring. That allows the algorithm to produce new combination of structural sections along structure groups to be evaluated. Crossover rate which decides the possibility of crossover to happen in a given generation is set to be 0.7 as generally implemented in GA optimization.

Mutation was also applied to introduce and maintain diversity in exploration of new solutions. Bit-flip is the method applied in binary coding problems and it is achieved by randomly selecting one individual chromosome from in a given population and randomly flipping one of its gene’s values (from 0 to 1 and vice versa). Mutation rate which decides the possibility of mutation to happen in a given generation is set to be 0.17 as generally implemented in GA optimization.

3.3 Analysis and discussion

Design optimization cycle started by generating the random population and undergoing evaluation process by implementing the above-mentioned objective function and its design contains mathematical formulations. That is involved both static serviceability analysis and dynamic eigen value analysis. The first critical modes of shape are shown in Figure 12. It is observed that due to the complexity of the building form, critical mode of shapes also shows similar complexity in deformation, which cannot be predicted normally as regular shapes. This proves the necessity of the developed formulation to take into account the deformation in both x and y direction, as well as in their diagonal resulted vector direction.

FIGURE 12

FIGURE 12. Eigen-value modal analysis (critical mode of shapes).

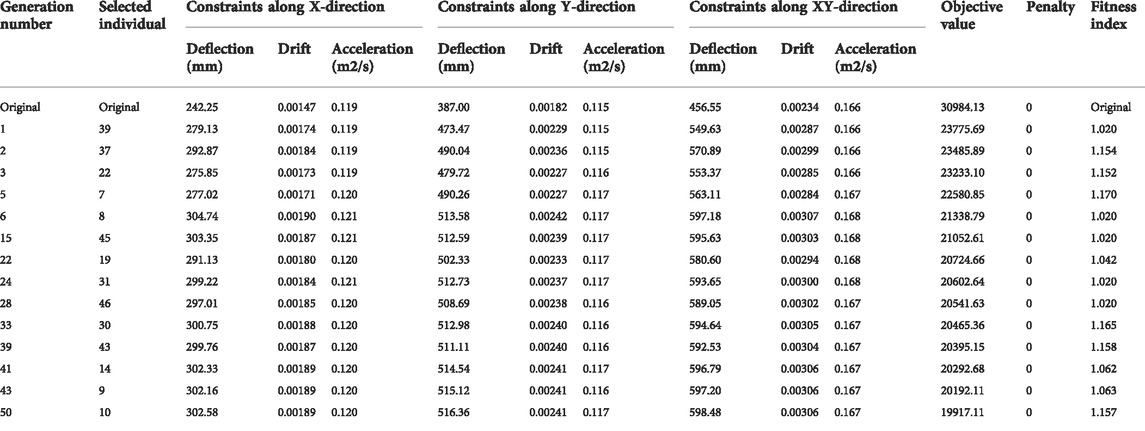
For each generation, the fittest individual within the population is ranked first and documented. That is to allow its use for the second generation if there is no better solution is found, hence algorithm does not lose the best in hand. Summary of the optimization cycle and its associated objective and constraints values are recorded in Table 2. To minimize the lengthy list of the produced 50 generations, and for better result representation, only generations that experienced a change in their individual solutions output are depicted in Table 2.

TABLE 2

TABLE 2. Genetic Algorithm optimization summary.

Several valuable insights can be discussed from the recorded solutions stipulated in Table 2 above. For the design constraints, it was observed that structural displacement governs the design and optimization, while drift and top acceleration still stand far from their limited values. This provides engineers with valuable information on the critical structural response to be dealt with. Besides, it also opens an opportunity for extended optimization by strengthening the structure to the identified critical response and elevating all other design constraints to the level of their maximum allowable limitations. Furthermore, all penalties values for the best ranked recorded solutions are zeros. That demonstrate the competency of the developed algorithm to exclude all potential solutions which violates the design constraints requirements (Ahmed et al., 2022; Aslam et al., 2022; Faraj et al., 2022).

3.3.1 Optimization of structural sections

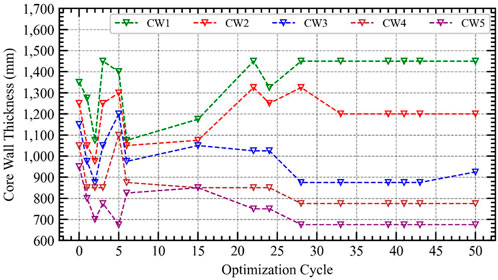
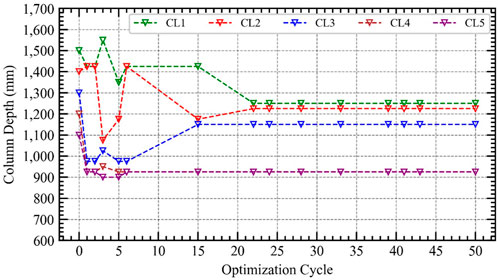
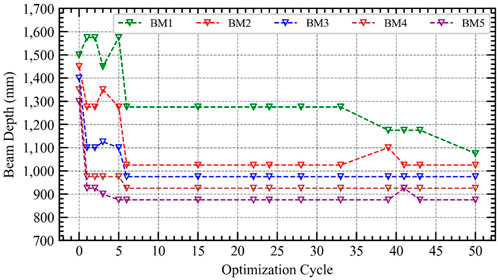
Selected structural sections from the pre-defined variation list for different structural elements are assembled to form an individual solution for the lateral system of the structure. Variation of the sections are shown in Figure 13, Figure 14 and Figure 15 for core-wall, columns and beams sections, respectively. It can be noticed that during the first rounds of generations, section varied greatly in sizes to find an optimum combination that represent the objective function. Another observation is that most of the change in sections occurs among core wall sections. That is justified by the importance of core-wall system in resisting lateral loads in comparison to other structural elements (Khan, 2018; Khan et al., 2019; Alkhatib et al., 2021b; Khan, 2021; Najm et al., 2021; Najm et al., 2022).

FIGURE 13

FIGURE 13. Core-wall section optimization.

FIGURE 14

FIGURE 14. Column section optimization.

FIGURE 15

FIGURE 15. Beam section optimization.

3.3.2 Optimization of structural sections

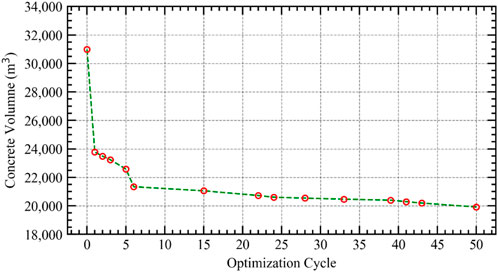
Finally, the recorded weight minimization for every generated solution is shown in Figure 16 in terms of the concrete volume for the lateral structural system (Al-Tayeb et al., 2022; Almeshal et al., 2022; Emad et al., 2022; Saeed et al., 2022). After generating the first population, a huge drop of the structural weight is experienced due to the randomness of the first population where optimization algorithm easily can search for the optimal solution with minimum sections. After that, refinement of the selected solutions is generated through selection procedures and evaluation techniques to further optimize the structural until convergence is reached and all generated solution beyond that represent the same section sizes (Khan, 2017; Najem and Ibrahim, 2018).

FIGURE 16

FIGURE 16. Structural concrete volume optimization.

Optimal sections weight is then compared to the original design to compute the reduction in concrete volume as shown in Table 3. The effectiveness of this optimization approach is validated through the achievable reduction of lateral structural concrete volume by 11,204 cubic meter of concrete that reflects a 36.1% of the total volume from the original sections. Considering the sustainability value in other hand with almost 410 Kg of CO₂ emissions is produced for each cubic meter of concrete, the optimization was able to eliminate a total of 4,400 tons of embedded CO₂ from this process.

TABLE 3

TABLE 3. Structural optimization summary.

4 Conclusion

This study aimed to extend the research and development of structural optimization with focus on irregular tall buildings subjected to wind motions. The developed approach consists of two major procedures. Firstly, an appropriate computational technique to evaluate wind loads on irregular tall building is proposed. That is achieved by integrating parametrical model into computational fluid dynamic analysis, that is coupled with fluid structure interaction algorithm to produce wind forces. The generated forces are then used as an input, together with gravity forces, to perform structural optimization. Structural optimization is developed in this study by employing genetic algorithm with enhanced constraint’s function. Mathematical formulation of the enhanced design constraints is developed with consideration to lateral displacement, drifts and top acceleration for regular and complex motion that may be accounted due to the irregularity of building. Finite element analysis is then performed for each generated solution to evaluate static and dynamic structural responses against the pre-defined objective function.

Existing case study of 75-story building with irregular twisting shape is performed to validate the feasibility of this research work. Only steady and incompressible flow applied at ($0°$) angle of attack was implemented in the CFD model to simulate the wind flow on the studied building. The developed approaches proved to be effective in optimizing the lateral structural system of the studied building. That is experimented by reducing the concrete volume by 35.71% from the original design. Hence, It can be concluded that the adopted computational methods contribute significantly to the performance of design engineers when dealing with complex and irregular structures.

Future studies shall be extended by employing different CFD model including flow type and mesh resolution to improve the accuracy of capturing the wind motions on tall buildings. Moreover, further examination of different evolutionary algorithms, such as Neural Network and Practical Swarm, can be done to measure their effectiveness in dealing with structural optimization problems. Another suggestion, with the benefit of parametrical approach employed in this study, another type of optimization can be developed and integrated within the proposed framework. That includes aerodynamic optimization to mitigate wind motions on the building, and topology optimization. To evaluate different lateral structural system for wind resistance optimal solution.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

Conceptualization, FA, NK, SQ, HN, and MS Methodology, FA, NK, SQ, HN, and MS; software, FA, NK, SQ, HN, and MS; validation, FA, NK, SQ, HN, and MS; formal analysis, FA, NK, SQ, HN, and MS investigation, FA, NK, SQ, HN, and MS; resources, FA, NK, SQ, HN, and MS; data curation, FA, NK, SQ, HN, and MS; writing—original draft preparation, FA, NK, SQ, HN, and MS; writing—review and editing, FA, NK, SQ, HN, and MS; visualization, FA, NK, SQ, HN, and MS; super-vision, FA, NK, SQ, HN, and MS; project administration, MS; funding acquisition, MS. All authors have read and agreed to the published version of the manuscript.

Funding

The research is partially funded by the Ministry of Science and Higher Education of the Russian Federation under the strategic academic leadership program ‘Priority 2030’ (Agreement 075-15-2021-1333 dated 30 September 2021).

Acknowledgments

The authors extend their thanks to the Ministry of Science and Higher Education of the Russian Federation for funding this work.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abd Elrehim, M. Z., Eid, M. A., and Sayed, M. G. (2019). Structural optimization of concrete arch bridges using genetic algorithms. Ain Shams Eng. J. 10, 507–516. doi:10.1016/j.asej.2019.01.005

CrossRef Full Text | Google Scholar

Ahmed, S. N., Hamah Sor, N., Ahmed, M. A., and Qaidi, S. M. A. (2022). Thermal conductivity and hardened behavior of eco-friendly concrete incorporating waste polypropylene as fine aggregate. Mater. Today Proc. 57, 818–823. doi:10.1016/j.matpr.2022.02.417

CrossRef Full Text | Google Scholar

Al-Tayeb, M. M., Aisheh, Y. I. A., Qaidi, S. M. A., and Tayeh, B. A. (2022). Experimental and simulation study on the impact resistance of concrete to replace high amounts of fine aggregate with plastic, Case Stud. Constr. Mater. 17, e01324. doi:10.1016/j.cscm.2022.e01324

CrossRef Full Text | Google Scholar

Alkhatib, F., Alawag, A. M., and Daris, A. (2021). Building information modelling (BIM) and energy performance of building-A review. J. Appl. Artif. Intell. 2, 22–31. doi:10.48185/jaai.v2i1.581

CrossRef Full Text | Google Scholar

Alkhatib, F. H., Kasim, N., Goh, W. I., and Al-masoodi, A. H. H. (2022). Performance-driven evaluation and parametrical design approach for sustainable complex-tall building design at conceptual stage. IOP Conf. Ser. Earth Environ. Sci. 1022, 012047. doi:10.1088/1755-1315/1022/1/012047

CrossRef Full Text | Google Scholar

Alkhatib, F. H., Kasim, N., Goh, W. I., and Al-Masudi, A. A. H. (2021). Multidisciplinary computational optimization: An integrated approach to achieve sustainability in tall building design at early stage-review.” in International Sustainability and Resilience Conference Clim. Change, Malaysia, 2022/05/01, 562

CrossRef Full Text | Google Scholar

Alkhatib, F., Kasim, N., Goh, W. I., Shafiq, N., Amran, M., Kotov, E. V., et al. (2022). Computational aerodynamic optimization of wind-sensitive irregular tall buildings. Buildings 12, 939. doi:10.3390/buildings12070939

CrossRef Full Text | Google Scholar

Almeshal, I., Al-Tayeb, M. M., Qaidi, S. M. A., Abu Bakar, B. H., and Tayeh, B. A. (2022). Mechanical properties of eco-friendly cements-based glass powder in aggressive medium materials today. Proceedings 58, 1582. doi:10.1016/j.matpr.2022.03.613

CrossRef Full Text | Google Scholar

Aslam, F., Zaid, O., Althoey, F., Alyami, S. H., Qaidi, S. M. A., de Prado Gil, J., et al. (2022). Evaluating the influence of fly ash and waste glass on the characteristics of coconut fibers reinforced concrete Structural Concrete n/a.

Google Scholar

Atabay, S. (2009). Cost optimization of three-dimensional beamless reinforced concrete shear-wall systems via genetic algorithm. Expert Syst. Appl. 36, 3555–3561. doi:10.1016/j.eswa.2008.02.004

CrossRef Full Text | Google Scholar

Bairagi, A. K., and Dalui, S. K. (2018). Comparison of aerodynamic coefficients of setback tall buildings due to wind load. Asian J. Civ. Eng. 19, 205–221. doi:10.1007/s42107-018-0018-3

CrossRef Full Text | Google Scholar

Chan, C.-M., and Chui, J. K. L. (2006). Wind-induced response and serviceability design optimization of tall steel buildings. Eng. Struct. 28, 503–513. doi:10.1016/j.engstruct.2005.09.005

CrossRef Full Text | Google Scholar

Chan, C.-M., Grierson, D. E., and Sherbourne, A. N. (1995). Automatic optimal design of tall steel building frameworks. J. Struct. Eng. 121, 838–847. doi:10.1061/(asce)0733-9445(1995)121:5(838)

CrossRef Full Text | Google Scholar

Chan, C. M., Huang, M. F., and Kwok, K. C. S. (2009). Stiffness optimization for wind-induced dynamic serviceability design of tall buildings. J. Struct. Eng. 135, 985–997. doi:10.1061/(asce)st.1943-541x.0000036

CrossRef Full Text | Google Scholar

De Jong, K. A. (1975). An analysis of the behavior of a class of genetic adaptive systems. University of Michigan.

Google Scholar

Elshaer, A., Bitsuamlak, G., and El Damatty, A. (2017). Enhancing wind performance of tall buildings using corner aerodynamic optimization. Eng. Struct. 136, 133–148. doi:10.1016/j.engstruct.2017.01.019

CrossRef Full Text | Google Scholar

Emad, W., Mohammed, A. S., Bras, A., Asteris, P. G., Kurda, R., Muhammed, Z., et al. (2022). Metamodel techniques to estimate the compressive strength of UHPFRC using various mix proportions and a high range of curing temperatures. Constr. Build. Mater. 349, 128737. doi:10.1016/j.conbuildmat.2022.128737

CrossRef Full Text | Google Scholar

Faraj, R. H., Ahmed, H. U., Rafiq, S., Sor, N. H., Ibrahim, D. F., and Qaidi, S. M. A. (2022). Performance of self-compacting mortars modified with nanoparticles: A systematic review and modeling. Clean. Mater. 4, 100086. doi:10.1016/j.clema.2022.100086

CrossRef Full Text | Google Scholar

Franke, J., Hellsten, A., Schlünzen, K. H., and Carissimo, B. (2007). “Best practice guideline for the CFD simulation of flows in the urban environment-a summary,” in 11th conference on harmonisation within atmospheric dispersion modelling for regulatory purposes, United Kingdom, July 2007 Cambridge, UK.

Google Scholar

Fu, J.-Y., Wu, B.-G., Xu, A., Wu, J.-R., and Pi, Y.-L. (2018). A new method for frequency constrained structural optimization of tall buildings under wind loads. Struct. Des. Tall Spec. Build. 27, e1549. doi:10.1002/tal.1549

CrossRef Full Text | Google Scholar

Golasz-Szolomicka, H., and Szolomicki, J. (2019). Architectural and structural analysis of selected twisted tall buildings. IOP Conf. Ser. Mat. Sci. Eng. 471, 052050. doi:10.1088/1757-899x/471/5/052050

CrossRef Full Text | Google Scholar

Goldberg, D. E. (1989). Optimization, and machine learning. Genet. algorithms Search.

Google Scholar

Hasançebi, O., and Erbatur, F. (2000). Evaluation of crossover techniques in genetic algorithm based optimum structural design. Comput. Struct. 78, 435–448. doi:10.1016/s0045-7949(00)00089-4

CrossRef Full Text | Google Scholar

Hassanli, S., Hu, G., Fletcher, D. F., and Kwok, K. C. S. (2018). Potential application of double skin façade incorporating aerodynamic modifications for wind energy harvesting. J. Wind Eng. Industrial Aerodynamics 174, 269–280. doi:10.1016/j.jweia.2018.01.016

CrossRef Full Text | Google Scholar

Hendy, C. R., and Smith, D. A. (2007). Designers’ guide to EN 1992-2.” in Eurocode 2: Design of Concrete Structures: Part 2: Concrete Bridges, 17. London: Thomas Telford.

Google Scholar

Hu, X.-B., and Di Paolo, E. (2008). Binary-representation-based genetic algorithm for aircraft arrival sequencing and scheduling. IEEE Trans. Intell. Transp. Syst. 9, 301–310. doi:10.1109/tits.2008.922884

CrossRef Full Text | Google Scholar

Huang, M. F., Li, Q., Chan, C., Lou, W., Kwok, K., and Li, G. (2015). Performance-based design optimization of tall concrete framed structures subject to wind excitations. J. Wind Eng. Industrial Aerodynamics 139, 70–81. doi:10.1016/j.jweia.2015.01.005

CrossRef Full Text | Google Scholar

ISO Organization for Standardization (2007). Bases for design of structures--serviceability of buildings and walkways against vibrations. Goldberg, Geneva: ISO.

Google Scholar

I S O. (1984). Guidelines for the evaluation of the response of occupants of fixed structures, especially buildings and off-shore structures, to low-frequency horizontal motion (0·063 to 1Hz). The International Organization for Standardization.

Google Scholar

Khan, M. A. (2017). Capturing failures in steel-plated RC beams through a combination of discrete and continuum models Materials Today. Proceedings 4, 9752. doi:10.1016/j.matpr.2017.06.261

CrossRef Full Text | Google Scholar

Khan, M. A., Irfan, S., Rizvi, Z., and Ahmad, J. (2019). A numerical study on the validation of thermal formulations towards the behaviour of RC beams Materials Today. Proceedings 17, 227. doi:10.1016/j.matpr.2019.06.423

CrossRef Full Text | Google Scholar

Khan, M. A. (2021). Toward key research gaps in design recommendations on flexurally plated RC beams susceptible to premature failures. J. Bridge Eng. 26, 04021067. doi:10.1061/(asce)be.1943-5592.0001772

CrossRef Full Text | Google Scholar

Khan, M. A. (2018). Understanding the brittleness of failures in composite RC beam plated at soffit. Mater. Today Proc. 5, 24085–24093. doi:10.1016/j.matpr.2018.10.202

CrossRef Full Text | Google Scholar

Kim, Y.-M., and You, K.-P. (2002). Dynamic responses of a tapered tall building to wind loads. J. Wind Eng. Industrial Aerodynamics 90, 1771–1782. doi:10.1016/s0167-6105(02)00286-6

CrossRef Full Text | Google Scholar

Kim, Y.-M., You, K.-P., and Ko, N.-H. (2008). Across-wind responses of an aeroelastic tapered tall building. J. Wind Eng. Industrial Aerodynamics 96, 1307–1319. doi:10.1016/j.jweia.2008.02.038

CrossRef Full Text | Google Scholar

Li, Y., Tian, X., Tee, K. F., Li, Q.-S., and Li, Y.-G. (2018). Aerodynamic treatments for reduction of wind loads on high-rise buildings. J. Wind Eng. Industrial Aerodynamics 172, 107–115. doi:10.1016/j.jweia.2017.11.006

CrossRef Full Text | Google Scholar

Mandal, S., Dalui, S. K., and Bhattacharjya, S. (2021). Wind induced response of corner modified’U’plan shaped tall building. Wind Struct. 32, 521. doi:10.12989/was.2021.32.6.521

CrossRef Full Text | Google Scholar

Marmar, A., Zouia, S., Ismail, S., and Hallik, A. (2021). Twisted buildings: Concepts and approaches. Archit. Plan. J. 27, 9.

Google Scholar

Melbourne, W. H., and Palmer, T. R. (1992). Accelerations and comfort criteria for buildings undergoing complex motions. J. Wind Eng. Industrial Aerodynamics 41, 105–116. doi:10.1016/0167-6105(92)90398-t

CrossRef Full Text | Google Scholar

Meng, F. Q., He, B. J., Zhu, J., Zhao, D. X., Darko, A., and Zhao, Z. Q. (2018). Sensitivity analysis of wind pressure coefficients on CAARC standard tall buildings in CFD simulations. J. Build. Eng. 16, 146–158. doi:10.1016/j.jobe.2018.01.004

CrossRef Full Text | Google Scholar

Ming-feng, H. (2013). Wind-induced vibration performance-based optimal structural design of tall buildings. Engineer. Mechanics. 30, 240. doi:10.6052/j.issn.1000-4750.2011.08.0519

CrossRef Full Text | Google Scholar

Mou, B., He, B.-J., Zhao, D.-X., and Chau, K. (2017). Numerical simulation of the effects of building dimensional variation on wind pressure distribution. Eng. Appl. Comput. Fluid Mech. 11, 293–309. doi:10.1080/19942060.2017.1281845

CrossRef Full Text | Google Scholar

Najem, H. M., and Ibrahim, A. M. (2018). Influence of concrete strength on the cycle performance of composite steel plate shear walls diyala. J. Eng. Sci. 11, 1. doi:10.24237/djes.2018.11401

CrossRef Full Text | Google Scholar

Najm, H. M., Ahmad, S., and Submitter, Y. (2021). Artificial neural networks for evaluation & prediction of the mechanical properties of waste ceramic optimal concrete exposed to elevated temperature. Social Science Research Network. Available at SSRN 4032028.

Google Scholar

Najm, H. M., Ibrahim, A. M., Sabri, M. M., Hassan, A., Morkhade, S., Mashaan, N. S., et al. (2022). Modelling of cyclic load behaviour of smart composite steel-concrete shear wall using finite element analysis buildings, 12, 850. MDPI

CrossRef Full Text | Google Scholar

Ozmen, Y., Baydar, E., and Van Beeck, J. (2016). Wind flow over the low-rise building models with gabled roofs having different pitch angles. Build. Environ. 95, 63–74. doi:10.1016/j.buildenv.2015.09.014

CrossRef Full Text | Google Scholar

Paul, R., and Dalui, S. (2021). Shape optimization to reduce wind pressure on the surfaces of a rectangular building with horizontal limbs. Period. Polytech. Civ. Eng. 65, 134. doi:10.3311/PPci.16888

CrossRef Full Text | Google Scholar

Pezeshk, S., Camp, C. V., and Chen, D. (2000). Design of nonlinear framed structures using genetic optimization. J. Struct. Eng. 126, 382–388. doi:10.1061/(asce)0733-9445(2000)126:3(382)

CrossRef Full Text | Google Scholar

Ruiz, C. A., Kalkman, I., and Blocken, B. (2021). Aerodynamic design optimization of ducted openings through high-rise buildings for wind energy harvesting. Build. Environ. 202, 108028. doi:10.1016/j.buildenv.2021.108028

CrossRef Full Text | Google Scholar

Rutten, D., and McNeel, R., (2007). Grasshopper3D, others. WA, USA: Robert McNeel & Assoc. Seattle.

Google Scholar

Saeed, A., Najm, H. M., Hassan, A., Qaidi, S., Sabri, M. M. S., and Mashaan, N. S. (2022). A comprehensive study on the effect of regular and staggered openings on the seismic performance of shear walls buildings 12 1293. MDPI

Google Scholar

Sanyal, P., and Dalui, S. K. (2022). Forecasting of aerodynamic coefficients of tri-axially symmetrical Y plan shaped tall building based on CFD data trained ANN. J. Build. Eng. 47, 103889. doi:10.1016/j.jobe.2021.103889

CrossRef Full Text | Google Scholar

Sharma, A., Mittal, H., and Gairola, A. (2018). Mitigation of wind load on tall buildings through aerodynamic modifications: Review. J. Build. Eng. 18, 180–194. doi:10.1016/j.jobe.2018.03.005

CrossRef Full Text | Google Scholar

Soegiarso, R., and Adeli, H. (1997). Optimum load and resistance factor design of steel space-frame structures. J. Struct. Eng. 123, 184–192. doi:10.1061/(asce)0733-9445(1997)123:2(184)

CrossRef Full Text | Google Scholar

Tamura, T., Miyagi, T., and Kitagishi, T. (1998). Numerical prediction of unsteady pressures on a square cylinder with various corner shapes. J. Wind Eng. Industrial Aerodynamics 74, 531–542. doi:10.1016/s0167-6105(98)00048-8

CrossRef Full Text | Google Scholar

Thordal, M. S., Bennetsen, J. C., Capra, S., Kragh, A. K., and Koss, H. H. H. (2020). Towards a standard CFD setup for wind load assessment of high-rise buildings: Part 2-Blind test of chamfered and rounded corner high-rise buildings. J. Wind Eng. Industrial Aerodynamics 205, 104282. doi:10.1016/j.jweia.2020.104282

CrossRef Full Text | Google Scholar

Tutar, M., and Oguz, G. (2002). Large eddy simulation of wind flow around parallel buildings with varying configurations. Fluid Dyn. Res. 31, 289–315. doi:10.1016/s0169-5983(02)00127-2

CrossRef Full Text | Google Scholar

vanRossum, G. (1995). Python reference manual. Amsterdam: Dep. Comput. Sci.

Google Scholar

Weller, H. G., Tabor, G., Jasak, H., and Fureby, C. (1998). A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 12, 620–631. doi:10.1063/1.168744

CrossRef Full Text | Google Scholar

Xie, J. (2014). Aerodynamic optimization of super-tall buildings and its effectiveness assessment. J. Wind Eng. Industrial Aerodynamics 130, 88–98. doi:10.1016/j.jweia.2014.04.004

CrossRef Full Text | Google Scholar

Zhengwei, Z., Yonga, Q., Minga, G., Nankuna, T., and Yongc, X. (2012). “Effects of corner recession modification on aerodynamic coefficients of square tall buildings,” in The seventh international colloquium on bluff body aerodynamics and applications. (Shangha: The International Association for Wind Engineering (IAWE))

Google Scholar

Zou, X.-K., and Chan, C.-M. (2005). Optimal seismic performance-based design of reinforced concrete buildings using nonlinear pushover analysis. Eng. Struct. 27, 1289–1302. doi:10.1016/j.engstruct.2005.04.001

CrossRef Full Text | Google Scholar