A reliable data-driven state-of-health estimation model for lithium-ion batteries in electric vehicles

The implementation of a precise and low-computational state-of-health (SOH) estimation algorithm for lithium-ion batteries represents a critical challenge in the practical application of electric vehicles (EVs). The complicated physicochemical property and the forceful dynamic nonlinearity of the degradation mechanism require data-driven methods to substitute mechanistic modeling approaches to evaluate the lithium-ion battery SOH. In this study, an incremental capacity analysis (ICA) and improved broad learning system (BLS) network-based SOH estimation technology for lithium-ion batteries are developed. First, the IC curves are drawn based on the voltage data of the constant current charging phase and denoised by the smoothing spline filter. Then, the Pearson correlation coefficient method is used to select the critical health indicators from the features extracted from the IC curves. Finally, the lithium-ion battery SOH is assessed by the SOH estimation model established by an optimized BLS network, where the BLS network is formed through its L2 regularization parameter and the enhancement nodes’ shrinkage scale filtrated by a particle swarm optimization algorithm. The experimental results demonstrate that the proposed method can effectively evaluate the SOH with strong robustness as well as stability to the degradation and disturbance of in-service and retired lithium-ion batteries.

1 Introduction

Accompanied by the intensification of ambient pollution and the electrical power crisis, the worldwide automotive market is undergoing an electrification revolution of unprecedented magnitude (Lipu et al., 2021; Qin et al., 2021; Tang et al., 2021; Wang et al., 2021; Wei et al., 2021). Electric vehicles (EVs) represent a crucial technology for significantly mitigating the emission of greenhouse gases, reducing air pollution in densely populated areas, and promoting operation efficiency (How et al., 2020; Tian et al., 2020; Xiong et al., 2020; Hecht et al., 2021; Yin et al., 2021).

Thanks to the extended cycle life, high-quality power density, and reduced self-discharge rate, lithium-ion batteries, as the power source, are extensively implemented in smart grids, portable devices, and EVs (Liu et al., 2021; Zhang et al., 2022a; Jiang et al., 2022). However, the discharging capacity of lithium-ion batteries progressively depreciates with repeated cycling operations owing to the loss of lithium-ion inventory, decomposition of the active material, and drop in conductivity. Moreover, lithium-ion batteries are mandated to be retired for EVs when the discharging capacity drops to about 80% with no damaged batteries, owing to the disadvantages of mileage anxiety, battery security, and other factors (Li and Wang, 2018; Li et al., 2021). Even though retired batteries are not appropriate for continued application in sophisticated EV running environments, they are feasible in stable charging and discharging situations (Yu et al., 2021; Lai et al., 2022). Precise state-of-health (SOH) estimation will deliver a degradation trend for lithium-ion batteries, which will facilitate the monitoring of the degradation for in-service batteries, as well as the reselection and reorganization of retired lithium-ion batteries in the process of cascade utilization. Accordingly, the SOH of lithium-ion batteries, as the critical indicator of the battery output capability, requires detailed investigation and accuracy estimation (Lipu et al., 2018; Sui et al., 2021).

A myriad of research has been focused on SOH estimation and has utilized many methodologies in this domain, which generally belong to direct measurement methods, model-based approaches, and data-based techniques (Sarmah et al., 2019). Open circuit voltage (OCV) and ohmic resistance measurement are commonly implemented for direct measurement of battery SOH in-vehicle battery management systems (BMSs) for the reasons of simplicity and low computational complexity. In order to obtain the intrinsic relationship between SOH and OCV, it is necessary to perform numerous measurements (Wang et al., 2018a). The ohmic internal resistance measurement method calculates the current battery SOH using the definition of the SOH internal resistance (Wang et al., 2018b; Chen et al., 2018). However, the operation temperature, accumulation of error, and sensor noise in the estimation process will introduce substantial deformations of the aging curve. Thus, it is not surprising that there is a large difference between the estimated SOH and practical SOH (Ahn and Lee, 2018; Cui et al., 2018).

Regarding the model-based approaches, degradation models have been developed by profiling the interior mechanisms and characteristics of outside electricity. The most popular models involve the electrochemical model (EM) and equivalent circuit model (ECM) (Ma et al., 2018). For example, Zheng et al. (2016) estimated the capacity using proportional-integral observers based on pseudo-two-dimensional (P2D) EM. However, the P2D model is greatly limited by the low charge-discharge rate. Xiong et al. (2018) utilized the finite analysis method and the genetic algorithm to simplify the P2D model. This model presents the fundamental interpretation for the battery aging caused by electrochemical reactions inside the batteries. Nevertheless, these electrochemical-based aging modeling approaches are not appropriate for practical application owing to the complicated computational process. ECM frequently transforms the problem of SOH estimation into parameter estimation with the combination of extended Kalman filtering (EKF) or particle filtering (PF) and their derivatives. For instance, Guha and Patra (2018) introduced the electrochemical impedance spectrum (EIS) as the key indicator to monitor the capacity and SOH for lithium-ion batteries based on the fractional-order ECM. Shi et al. (2019) established a second-order resistance-capacitance (RC) ECM, and the SOH was estimated using the improved unscented particle filter (UPF). Unfortunately, the identification of all the hidden and intricate non-linear degradation features is challenging, which prevents the construction of an accurate degradation model.

Owing to advancements in machine learning in recent years, there have been widespread applications of data-driven methods in SOH estimation for lithium-ion batteries (Li et al., 2019; Oji et al., 2021; Samanta et al., 2021). The data-driven approach does not demand insight into sophisticated electrochemical reactions in the modeling and SOH estimation processes but converts the SOH estimation problem into a regression prediction program by building a mapping relationship between health indicators (HIs) and discharging capacity or SOH, which offers simple flexibility and excellent nonlinear learning capability (Xu and Xu, 2020). The long short-term memory neural network (LSTM NN) (Zhang et al., 2022b), support vector regression (SVR) (Cai et al., 2020), relevance vector machine (RVM) (Chen et al., 2021), and extreme learning machine (ELM) (Zhao et al., 2022) are frequently utilized data-driven methods to reflect captured HIs for the battery SOH. To achieve higher SOH estimation accuracy, the availability of datasets covering all operating states of the battery is required, which is the principal limitation of data-driven approaches. In addition, it can be observed that the primary problem of data-driven approaches concerns how to obtain reliable and high-quality HIs (Pan et al., 2018).

Currently, HI analysis methods commonly incorporate incremental capacity analysis (ICA), differential pressure analysis (DVA), and so on (Schaltz and Schaltz, 2020; Zhang et al., 2020). The size, location, and distribution of the IC/DV curve peaks fluctuate with battery degradation and represent distinct states of battery health. The ICA method offers a more widespread application than the DVA technique because the latter employs the capacity obtained by integrating current with time as the abscissa, which always generates cumulative errors. The broad learning system (BLS) network is a stochastic vector single-layer neural network learning system proposed by Chen et al. (2019) with the advantages of not having to iteratively update the parameters of certain neural networks, good generalization performance, learning fast, and not producing local optimal solutions. However, the initial parameters of the BLS network affect the performance of this network significantly. The particle swarm optimization (PSO) approach is an advanced parameter optimization algorithm, which has been widely applied to find the global optimal value of network parameters due to its high precision, fast convergence speed, and few parameters (Song et al., 2021).

Based on the above analysis of the research actuality and relevant technical obstacles, an SOH estimation methodology based on the ICA technique and the improved BLS network for in-service and retired batteries is proposed in this work. First, voltage data of the constant current charging stage are utilized to graph the IC curve by smoothing spline filter denoising. HIs of high correlation with battery SOH degradation are generated by IC peaks according to the Pearson correlation analysis method, and then the battery SOH estimation model is constructed using the introduced PSO-BLS network. The PSO-BLS approach refers to the L2 regularization parameter and the shrinkage scale of the enhancement nodes of the BLS network modified by the PSO algorithm in this work. Finally, experiments for SOH estimation are undertaken to verify the feasibility and robustness of the proposed method based on the aging data of in-service and retired batteries measured in the Anqing Normal University (AQNU) laboratory with different charging multipliers. The experimental results demonstrate that the developed PSO-BLS network technique not only guarantees the accuracy of battery SOH estimation but also exhibits excellent robustness and stability. Specifically, several key contributions are presented below.

1) An ICA and improved BLS network-based SOH estimation technology for lithium-ion batteries is developed in this work.

2) An optimized BLS network is constructed through the PSO algorithm using the L2 regularization parameter and the enhancement nodes shrinkage scale of the BLS network.

3) The incremental capacity curves are denoised by the smoothing spline filter based on the voltage data of the constant current charging phase.

The remainder of this study is divided into the following sections. First, the feature extraction and HIs selection will be discussed in detail in Section 2. Then, Section 3 illustrates the monotonic PSO algorithm and BLS network. The procedures and framework of the proposed SOH estimation method are also documented in this section. Section 4 verifies the feasibility, stability, and robustness of the proposed algorithm based on battery aging data with different charging multipliers and different degradation states. Finally, conclusions are discussed in Section 5.

2 Battery aging experiment and feature extraction

2.1 Battery aging experiment

As shown in Figure 1, the high-performance battery measurement system was constructed in the laboratory to execute the charging and discharging aging experiment on the battery with different charging multipliers. The devices mainly included a host, the battery testing device (Neware, CT-4008-5V20A, Shenzhen, China), and the thermostat (Neware, MHW-200, Shenzhen, China).

FIGURE 1

FIGURE 1. Experimental instruments.

Regarding the robustness and effectiveness of the proposed methodology, the experimental objects consist of in-service batteries named N1 and N2, and retired batteries noted as R1 at a constant temperature of 25°C. The current maximum discharging capacity of the batteries N1 and N2 is 2.4 Ah, but for R1 it is only 1.4 Ah. The tested batteries use 18,650 cylindrical ternary lithium-ion batteries, and the specifications of the tested batteries are summarized in Table 1. Batteries N1 and R1 were charged at a constant current of 0.1 C (C is the charge and discharge current measured against the rated capacity) in the designed aging experiments until the terminal voltage achieved 4.2 V, and then controlled at a constant voltage of 4.2 V until the charging current dropped below 48 mA. However, the constant charging current rate of N2 is 0.2 C. In addition, all the tested batteries were discharged under a constant current of 1 C before the battery voltage dropped to 3 V. The SOH of the lithium-ion battery can be defined from the capacity and internal resistance, but the capacity definition method is more accurate and the parameters are easier to obtain. Therefore, the lithium-ion battery SOH is defined from the perspective of capacity in this work, which is defined as:

$SOH=\frac{C_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{d}\mathrm{c}\mathrm{a}\mathrm{p}\mathrm{a}\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{y}}}{C_{\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}\mathrm{c}\mathrm{a}\mathrm{p}\mathrm{a}\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{y}}}\times 100\%,(1)$

where $C_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{d}\mathrm{c}\mathrm{a}\mathrm{p}\mathrm{a}\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{y}}$ and $C_{\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}\mathrm{c}\mathrm{a}\mathrm{p}\mathrm{a}\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{y}}$ are the discharging capacity of the present and the initial times, respectively.

TABLE 1

TABLE 1. Specifications of the experimented battery.

2.2 Incremental capacity curve analysis

IC refers to the charged or discharged capacity within a unit voltage when charging or discharging the battery at a certain current, which is calculated according to the following definition in this work:

$dQ/dV\triangleq \Delta Q/\Delta V,(2)$

$Q=I\times t,(3)$

where $dQ/dV$ denotes the IC value, Q indicates the charging capacity, V is the terminal voltage, I is the charging current, and t represents the charging time for the battery. The IC curve provides insight into the external characteristics of the battery and the sophisticated internal electrochemical mechanism (Jiang et al., 2020). The evolution process of the captured characteristics from the IC curve can be adapted to distinguish the degradation behavior and determine the loss of active material inside the battery (Guo et al., 2021).

In practice, the discharging condition of EVs presents uncertainty and irregularity, while the charging condition usually remains steady with a standard constant current/constant voltage protocol. Therefore, the voltage data of the constant current charging stage are selected to create the IC curve in this work. However, the reported data are frequently contaminated by spurious noise owing to instrument errors, interference factors in the measurement, and other unknown factors. It is extremely challenging to distinguish the significant features based on the original data. To represent the transformation procedure and illustrate the performance of the IC curve better, data denoising using the smoothing spline approach is carried out. Figure 2 shows the comparison before and after denoising the IC curve for one cycle of charging and discharging.

FIGURE 2

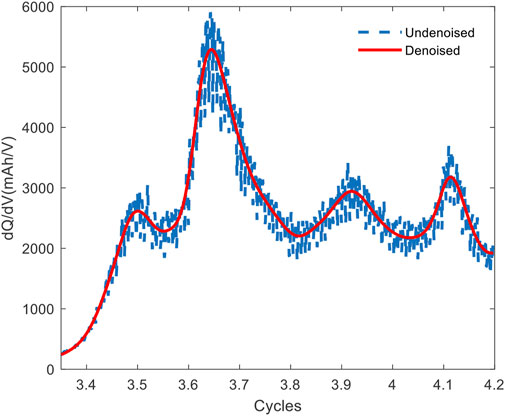
FIGURE 2. Comparison before and after denoising the IC curve for one cycle of charging and discharging.

The spline function, comprising a polynomial spline and a smoothing spline, is a segmented and reduced-order polynomial approximation function, which can be applied to various functions with diverse degrees of nonlinearity (Lin et al., 2020). However, it has been shown that solving polynomial spline coefficients directly by the least-squares method is susceptible to overfitting in theory and practice. Therefore, a smoothing spline adds a penalty value to the residual sum of squares (RSS).

Assume the dataset (x_i, y_i) to fit the model f (x), i = 1, 2, …, n. The general fitting error without adding the smoothing parameter is defined as:

$RSS={\displaystyle \sum }_{i-1}^N{\left\{y_i-f\left(x_i\right)\right\}}^2.(4)$

Then incorporate the smoothing parameter $\lambda$:

$RSS\left(f,\lambda \right)={\displaystyle \sum }_{i-1}^N{\left\{y_i-f\left(x_i\right)\right\}}^2+\lambda {\int \left\{f^{″}\left(t\right)\right\}}^2\mathrm{d}\mathit{t}.(5)$

The natural spline f (x) can be described as:

$f\left(x\right)={\displaystyle \sum }_{j-1}^N{N}_j\left(x\right){\theta }_j,(6)$

where the N_j(x) represents the family of natural splines. Accordingly, Eq. 5 reduces to:

$RSS\left(\theta ,\lambda \right)={\left(y=N\theta \right)}^T\left(y=N\theta \right)+\lambda {\theta }^T{\Omega }_N\theta ,(7)$

${\left\{N\right\}}_{ij}=N_j\left(x_i\right),(8)$

${\left\{{\Omega }_N\right\}}_{jk}=N_j^{″}\left(t\right)N_k^{″}\left(t\right)\mathrm{d}\mathit{t}.(9)$

Therefore, the parameter $\widehat{\theta }$ and fitted smoothing spline are simply calculated by:

$\widehat{\theta }={\left(N^{T}N+\lambda {\Omega }_N\right)}^{-1}{N}^{T}y,(10)$

$\widehat{f}\left(x\right)={\displaystyle \sum }_{j-1}^N{N}_j\left(x\right){\widehat{\theta }}_j.(11)$

In addition, the different charging or discharging rates influence the visibility of the IC curve, for which the higher charging rate would make it hard to observe the IC peaks. Consequently, the robustness of the proposed method is examined through different charging current rates of 0.1 C and 0.2 C, separately. The IC curves of batteries N1, N2, and R1 are displayed in Figure 3.

FIGURE 3

FIGURE 3. The IC curves of batteries N1, N2, and R1.

2.3 Features extraction and the selection of health indicators

It can be clearly observed in Figure 3 that the IC curve shifts downward with the charging and discharging cycles because of the battery deterioration phenomenon. The IC peaks continuously decrease with the maximum discharging capacity reduction of the battery, which exhibits an intense correlation. Generally, the IC curves of lithium-ion batteries comprise several IC peaks. It is, therefore, intuitively seen that the convenient extracted features include the location, height, area, discharging time, and the slope of the left and right sides of each peak based on the battery IC curves.

Consider there is an IC peak ($v_{peak}$, $y_{{\mathit{v}}_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}}}$) between the points of A ($v_A$, $y_{{\mathit{v}}_{\mathrm{A}}}$) and B ($v_B$, $y_{{\mathit{v}}_{\mathrm{B}}}$); the area, discharging time, and left and right gradients of each peak are then, separately, formulated by:

$S={\int }_{\mathrm{A}}^{\mathrm{B}}\frac{\mathrm{d}Q}{\mathrm{d}V}\mathrm{d}V=Q_{\mathrm{B}}-Q_{\mathrm{A}},(12)$

$t_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}}=t_{{\mathit{v}}_{\mathrm{B}}}=t_{{\mathit{v}}_{\mathrm{A}}},(13)$

$k_{\mathrm{l}\mathrm{e}\mathrm{f}\mathrm{t}}=\frac{y_{{\mathit{v}}_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}}}+y_{{\mathit{v}}_{\mathrm{A}}}}{v_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}}+v_{\mathrm{A}}},(14)$

$k_{\mathrm{r}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}}=\frac{y_{{\mathit{v}}_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}}}+y_{{\mathit{v}}_{\mathrm{B}}}}{v_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}}+v_{\mathrm{B}}},(15)$

where S denotes the integration area of the peak, $t_{{\mathit{v}}_{\mathrm{B}}}$ and $t_{{\mathit{v}}_{\mathrm{A}}}$ indicate the discharging time of points B and A, respectively, $K_{left}$ represents the left gradient of the peak, and $k_{right}$ is right gradient.

However, besides the strong correlation between the HIs and the discharging capacity, convenience, reasonableness, and practicality should also be under consideration in the selection of HIs. Accordingly, the location of the peak in the IC curve, as well as the height, is utilized as the battery features in this work. Since there may be more than one peak in the IC curve of the battery, as shown in Figure 3, the estimation results may no longer achieve the optimal performance if all the extracted features are applied to the input datasets of the SOH estimation model. It is therefore worthwhile evaluating the correlation between the features and SOH using the Pearson correlation coefficient to choose the most effective and convenient HIs, which is defined as:

$p=\frac{E\left(XY\right)-E\left(X\right)E\left(Y\right)}{\sqrt{E\left(X^2\right)-E^2\left(X\right)\sqrt{E\left(Y^2\right)-E^2\left(Y\right)}}}(16)$

where X and Y are the sample population. The results are shown in Table 2.

TABLE 2

TABLE 2. The correlation coefficient between preselected features and the battery SOH.

The greater the absolute value of p, the higher the correlation degree between X and Y, while a “–” means that there is a negative correlation between the variable and SOH in Table 2. According to the correlation analysis results of the three different batteries in Table 2, $v_{peak1}$, $y_{{\mathit{v}}_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}2}}$, and $y_{{\mathit{v}}_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}4}}$ are selected as the input HIs of the SOH estimation model for battery N1 since the correlation between them and SOH exceeds 0.95. Similarly, the SOH estimation model based on battery N2 is established using $y_{{\mathit{v}}_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}2}}$, $y_{{\mathit{v}}_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}3}}$, and $y_{{\mathit{v}}_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}4}}$, while for battery R1 it is established using ${\mathit{v}}_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}1}$ and $y_{{\mathit{v}}_{\mathrm{p}\mathrm{e}\mathrm{a}\mathrm{k}1}}$.

3 State-of-health estimation methodology

The proposed PSO-BLS algorithm is described in detail in this section. First, a brief introduction to the PSO algorithm and the BLS network is provided. The procedures for optimizing the hyperparameters of the BLS network by the PSO algorithm are subsequently presented.

3.1 Broad learning system network

A BLS network is a broad learning network constructed based on the random vector functional-link neural network (RVFLNN) (Zhang et al., 2021). Figure 4 presents the architecture of RVFLNN. A traditional RVFLNN directly accepts information from the input data to establish enhancement nodes:

$Y=W·\left[X\Vert \xi \left(X{W}_h+{\beta }_h\right)\right],(17)$

where Y denotes the output of the RVFLNN, X is the input data, $W_h$ and W are the input and output weights, respectively, and ${\beta }_h$ represents the network bias.

FIGURE 4

FIGURE 4. The architecture of RVFLNN.

The BLS first extracts the feature nodes $F^i=\left[F_1,F_2,\dots ,F_i\right]$ from the input data based on the least absolute shrinkage and selection operator (LASSO) sparse feature learning method, which can efficiently characterize the dataset with high computational performance (Ma et al., 2020). The enhancement features $E^i=\left[E_1,E_2,\dots ,E_i\right]$ are then captured through the nonlinear expansion for the enhancement nodes.

Suppose the input dataset X and output matrix Y belong to $R^{N\times C}$. For the n feature mapping and m enhancement mapping, the ith feature node can be represented by (Zhang et al., 2021):

$F_i={\varphi }_i\left(X{W}_{ei}+{\beta }_{ei}\right),i=\mathrm{1,2},\dots ,n,(18)$

where $W_{ei}$ is the random weights, ${\beta }_{ei}$ indicates the bias value, and ${\varphi }_i\left(·\right)$ indicates the activation function of discretionary selection. The sparse autoencoder strategy is applied in the BLS network to optimize the input weights to overcome the unpredictability caused by random initialization:

$\underset{{\widehat{W}}_e}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}:{\Vert F{\widehat{W}}_e-X\Vert }_2+{\lambda }_1{\Vert {\widehat{W}}_e\Vert }_1,s.t.X{W}_e=F,(19)$

where $\stackrel{⌢}{W}$ is the sparse autoencoder solution, $F$ denotes the desired output, and ${\lambda }_1$ is the regular factor of the L1 norm. The alternating direction method of multipliers (ADMM) is adopted to address this optimization problem for the BLS network, which can be expressed as:

$\{\begin{array}{c}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}:f\left(w\right)+g\left(o\right)\\ w-o=0\end{array},(20)$

$f\left(w\right)={\Vert Fw-x\Vert }_2,(21)$

$g\left(w\right)=\lambda {\Vert w\Vert }_1.(22)$

The augmented Lagrangian function of this optimization task is:

$L\left(w,o,\wedge \right)=f\left(w\right)+g\left(o\right)+{\wedge }^T\left(w-o\right),(23)$

where $\wedge$ indicates the Lagrangian multiplier.

The proximal problem can be solved by alternately updating $W$, $o$, and $\wedge$ through:

$w_{k+1}:={\left(F^{T}F+\rho I\right)}^{-1}\left(F^{T}x+\rho \left(o^k=u^k\right)\right),\rho >\mathit{0},(24)$

$o_{k+1}:=S_{\lambda /\rho }\left(w_{k+1}+u_k\right),(25)$

$u_{k+1}:=u_k+\left(w_k-o_{k+1}\right),(26)$

where $S$ is the soft thresholding operator and is expressed by:

$S_k\left(a\right)=\{\begin{array}{c}a=k,a>k\\ 0,\left|a\right|\le k\\ a+k,a<-k\end{array}.(27)$

Therefore, the feature nodes are achieved through continuous iteration of Eqs 24–26, and the jth enhancement node is calculated by:

$E_j=\zeta \left(F^i{W}_{hj}+{\beta }_{hj}\right),j=\mathrm{1,2},\dots ,m,(28)$

where $W_{hj}$ is the random weights, ${\beta }_{hj}$ indicates the bias value, and $\zeta \left(\%\right)$ represents the activation function, which is defined as:

$\zeta \left(\mathrm{x}\right)\frac{1-e^{-2x}}{1+e^{-2x}}.(29)$

Combine the feature node and enhancement node to form the input pattern matrix, and then the broad model can be calculated according to:

$\begin{array}{l}Y=\left[F_1,\dots ,F_i|\zeta \left(F^i{W}_{h1}-{\beta }_{h1}\right),\dots ,\zeta \left(F^i{W}_{hj}-{\beta }_{hj}\right)\right]W\\ =\left[F_1,\dots ,F_i|E_1,\dots ,E_j\right]W\\ =\left[F^i|E^j\right]W\\ =HW\end{array}(30)$

where $H=\left[F^i|E^j\right],$ and the output coefficients matrix $W=H^{+}Y$ is calculated using the ridge regression learning algorithm. The normal L2 regularization can be represented as:

${\text{arg\hspace{0.17em}}}_{\widehat{w}}\mathrm{m}\mathrm{i}\mathrm{n}:{\Vert H\widehat{W}-Y\Vert }_2+{\lambda }_2{\Vert \widehat{W}\Vert }_2,(31)$

where ${\lambda }_2$ is the regular factor of the L2 regularization.

Set the gradient to zero, and W is approximated as:

$W={\left({\lambda }_{2}I+H{H}^T\right)}^{-1}{H}^{T}Y.(32)$

Specifically,

$H^{+}=\underset{{\lambda }_2\to 0}{\lim }{\left({\lambda }_{2}I+H{H}^T\right)}^{-1}{H}^T,(33)$

where I denotes the identity matrix. Without a gradient descent-based learning algorithm, it can be concluded that the training of the BLS algorithm provides faster processing and does not produce local optimum solutions. The BLS framework is displayed in Figure 5.

FIGURE 5

FIGURE 5. The framework of the BLS network.

It can be seen that the L2 regularization parameter and the shrinkage scale of the enhancement nodes are important parameters for the BLS network with the preceding analysis. Because the BLS model does not apply backpropagation to parameter learning but obtains the output weights by pseudo-inversion, this results in the initial parameters of the BLS playing a significant role in the output weights of the network. The PSO algorithm, which is an efficient parameter optimization algorithm, tracks the local optimal solution by searching for the global optimal solution due to the advantages of high precision, prompt convergence, and few parameters. Therefore, the L2 regularization parameter and the shrinkage scale of the enhancement nodes of the BLS network are optimized using the PSO algorithm to augment the precision of the constructed battery SOH estimation model, which enables the BLS network to steadily and reliably yield predicted values.

3.2 Particle swarm optimization algorithm

The PSO algorithm is a global optimization method based on swarm search with inspiration from birds’ flocking or fish schooling, which has been employed in many fields of science and engineering to address nonlinear, nonconvex, and combinatorial optimization projects (Ghorbani et al., 2018). The global optimal solution can be calculated by defining the fitness function and updating the velocity and position of the particles. For a D-dimensional search space, the ith particle of the swarm at time t is represented by a D-dimensional vector $x_i^t={\left(x_{i1}^t,x_{i2}^t,\dots ,x_{iD}^t\right)}^T.$, while the velocity of this particle is $v_i^t={\left(v_{i1}^t,v_{i2}^t,\dots ,v_{iD}^t\right)}^T.$ $p_i^t={\left(p_{i1}^t,p_{i2}^t,\dots ,p_{iD}^t\right)}^T$ denotes the previous best-visited position of the ith particle at time t, and g is the index of the best particle in the swarm. The basic procedures of the PSO algorithm are described as follows (Ren et al., 2021).

For t = 1 to the maximum bound on the number of iterations.

Step 1: Create and initialize a D-dimensional swarm S and the corresponding velocity and position vectors.

$v_i^t={\left(v_{i1}^t,v_{i2}^t,\dots ,v_{iD}^t\right)}^T,(34)$

$x_i^t={\left(x_{i1}^t,x_{i2}^t,\dots ,x_{iD}^t\right)}^T.(35)$

Step 2: Compute the fitness $F_i$ of the particle i by the fitness function.

Step 3: Renew the local optimum and global optimum assumptions, Eqs 19, 20, respectively.

$p_i^{t+1}=\{\begin{array}{c}{F}_i^{t+1},if{F}_i^{t+1}>p_i^t\\ p_i^{t}else\end{array},(36)$

$g=\{\begin{array}{c}{F}_i^{t+1},if{F}_i^{t+1}>g\\ g,else\end{array}.(37)$

Step 4: Update the velocity and position of particles as follows.

$v_{id}^{t+1}=v_{id}^t+c_1{r}_1\left(p_{id}^t-x_{id}^t\right)+c_2{r}_2\left(p_{gd}^t-x_{id}^t\right),(38)$

$x_{id}^{t+1}=x_{id}^t+v_{id}^{t+1},(39)$

where d = 1, 2, …, D denotes the dimension, i = 1, 2, …, S represents the particle index, where S is the size of the swarm, c₁ and c₂ are cognitive and social scaling parameters, respectively, and r₁ and r₂ indicate random numbers in the range [0, 1].

Step 5. Loop steps (2)–(4) until g meets the problem requirements, and then output the optimal solution.

3.3 The framework of the proposed state-of-health estimation method based on the PSO-BLS algorithm

The framework of the proposed model for lithium-ion battery SOH estimation is shown in Figure 6, and the detailed processes of the proposed PSO-BLS network are summarized as follows.

FIGURE 6

FIGURE 6. The framework of the proposed SOH estimation method based on the PSO-BLS algorithm.

(1) Generate training and testing sets.

Suppose the measured historical SOH degradation data and the reported voltage variation data during the constant current charging phase of a lithium-ion battery are described as:

$\mathrm{S}\mathrm{O}\mathrm{H}={\left[\mathrm{S}\mathrm{O}{\mathrm{H}}^1,\mathrm{S}\mathrm{O}{\mathrm{H}}^2,\dots ,\mathrm{S}\mathrm{O}{\mathrm{H}}^m\right]}^T,(40)$

$V=\left[\begin{array}{cccc}{V}_1^1& V_2^2& \cdots & V_n^1\\ V_1^2& V_2^2& \cdots & V_n^2\\ ⋮& ⋮& \ddots & ⋮\\ V_1^m& V_2^m& \cdots & V_n^m\end{array}\right],(41)$

where SOH^m indicates the quantified health state of the battery after m charging and discharging cycles, and $V_n^m$ means the nth sampled voltage value in the mth cycle.

Extract HIs using the ICA method based on the recorded voltage variation data for each constant current charging phase, and then constitute the feature matrix P:

$P=\left[\begin{array}{cccc}{P}_1^1& P_2^2& \cdots & P_n^1\\ P_1^2& P_2^2& \cdots & P_n^2\\ ⋮& ⋮& \ddots & ⋮\\ P_1^m& P_2^m& \cdots & P_n^m\end{array}\right],(42)$

where $P_q^m$ is the captured qth features of the mth cycle using the ICA method, and $0<q<n$.

Based on the HIs and SOH datasets, and according to the proportion of 1:1, the training set and testing set are constructed according to:

$\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{s}\mathrm{e}\mathrm{t}=\left[\begin{array}{ccccc}{P}_1^1& P_2^1& \cdots & P_q^1& \mathrm{S}\mathrm{O}{\mathrm{H}}^1\\ P_1^2& P_2^2& \cdots & P_q^2& \mathrm{S}\mathrm{O}{\mathrm{H}}^2\\ ⋮& ⋮& \cdots & ⋮& ⋮\\ P_1^{m/2}& P_2^{m/2}& \cdots & P_q^{m/2}& \mathrm{S}\mathrm{O}{\mathrm{H}}^{m/2}\end{array}\right],(43)$

$\mathrm{T}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{s}\mathrm{e}\mathrm{t}=\left[\begin{array}{ccccc}{P}_1^{\left(m/2\right)+1}& P_2^{\left(m/2\right)+1}& \cdots & P_q^{\left(m/2\right)+1}& \mathrm{S}\mathrm{O}{\mathrm{H}}^{\left(m/2\right)+1}\\ P_1^{\left(m/2\right)+2}& P_2^{\left(m/2\right)+2}& \cdots & P_q^{\left(m/2\right)+2}& \mathrm{S}\mathrm{O}{\mathrm{H}}^{\left(m/2\right)+2}\\ ⋮& ⋮& \cdots & ⋮& ⋮\\ P_1^2& P_2^2& \cdots & P_q^2& \mathrm{S}\mathrm{O}{\mathrm{H}}^m\end{array}\right],(44)$

where $P=\left[\begin{array}{cccc}{P}_1^1& P_2^2& \cdots & P_q^1\\ P_1^2& P_2^2& \cdots & P_q^2\\ ⋮& ⋮& \ddots & ⋮\\ P_1^{m/2}& P_2^{m/2}& \cdots & P_q^{m/2}\end{array}\right]$ is the training sample and $\left[\begin{array}{c}\mathrm{S}\mathrm{O}{\mathrm{H}}^1\\ \mathrm{S}\mathrm{O}{\mathrm{H}}^2\\ ⋮\\ \mathrm{S}\mathrm{O}{\mathrm{H}}^{m/2}\end{array}\right]$ is the training target when training the SOH estimation model. For testing the model, $P=\left[\begin{array}{cccc}{P}_1^{\left(m/2\right)+1}& P_2^{\left(m/2\right)+1}& \cdots & P_q^{\left(m/2\right)+1}\\ P_1^{\left(m/2\right)+2}& P_2^{\left(m/2\right)+2}& \cdots & P_q^{\left(m/2\right)+2}\\ ⋮& ⋮& \ddots & ⋮\\ P_1^m& P_2^m& \cdots & P_q^m\end{array}\right]$ represents the testing sample and $\left[\begin{array}{c}\mathrm{S}\mathrm{O}{\mathrm{H}}^{\left(m/2\right)+1}\\ \mathrm{S}\mathrm{O}{\mathrm{H}}^{\left(m/2\right)+1}\\ ⋮\\ \mathrm{S}\mathrm{O}{\mathrm{H}}^m\end{array}\right]$ is the testing target.

(2) Parameter identification processes.

Optimize the L2 regularization parameter and the shrinkage scale of the enhancement nodes of the BLS network using the PSO algorithm with the fitness function below based on the training set:

$\mathrm{F}\mathrm{i}\mathrm{t}\mathrm{n}\mathrm{e}\mathrm{s}\mathrm{s}\mathrm{f}\mathrm{u}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}:\frac{1}{m/2}{\displaystyle \sum }_{i=1}^{m/2}{\left(\mathrm{S}\mathrm{O}{\mathrm{H}}^i-\widehat{\mathrm{S}\mathrm{O}{\mathrm{H}}^i}\right)}^2,(45)$

where the $\widehat{SOH}$ is the estimated battery health state. The last column is taken for the training target and the rest for the training samples. Output the improved L2 regularization parameter and the shrinkage scale.

(3) Generate the estimated state of health with the established SOH estimation model using the particle swarm optimization-broad learning system approach.

Develop the SOH estimation model for lithium-ion batteries based on the optimized initial parameters of the BLS network and the testing set, and then generate the estimated battery $\widehat{\mathrm{S}\mathrm{O}\mathrm{H}}$:

$\widehat{\mathrm{S}\mathrm{O}\mathrm{H}}={\left[\widehat{\mathrm{S}\mathrm{O}{\mathrm{H}}^{\left(\frac{m}{2}+1\right)}},\widehat{\mathrm{S}\mathrm{O}{\mathrm{H}}^{\left(\frac{m}{2}+2\right)}},\dots ,\widehat{\mathrm{S}\mathrm{O}{\mathrm{H}}^{\left(m\right)}}\right]}^T.(46)$

It can be detected by theoretical analysis that the proposed PSO-BLS improves the learning ability and generalization capacity of the BLS network, which has the advantages of fewer parameters, fast training speed, strong generalization capacity, and excellent estimation performance.

4 Results and discussion

In this work, the mean square error (MSE), mean absolute percent error (MAPE), root mean square error (RMSE), and correlation coefficient R² are introduced as evaluation factors to demonstrate and discuss the effectiveness of the proposed method more intuitively, and they are respectively defined as:

$MSE=\frac{1}{2}{\displaystyle \sum }_{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2\times 100\%,(47)$

$MAPE=\frac{1}{n}{\displaystyle \sum }_{i=1}^n\left|\frac{y_i-{\widehat{y}}_i}{y_i}\right|\times 100\%,(48)$

$RMSE=\sqrt{\frac{1}{n}{\displaystyle \sum }_{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2\times 100\%},(49)$

$R^2=1-\frac{{\sum }_{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2}{{\sum }_{i=1}^n{\left(y_i-{\overline{y}}_i\right)}^2},(50)$

where $y_i$ and ${\stackrel{⌢}{y}}_i$ represent the reality and estimated values of lithium-ion battery SOH, respectively, n is the number of charging and discharging cycles experienced by the lithium-ion battery at the end of the experiment, and ${\stackrel{⌢}{y}}_i$ indicates the average value of the lithium-ion battery SOH. The computational cost is also used as the metric to quantify the performance of the proposed SOH estimation model. The experiment was performed based on MATLAB 2017b.

The initial L2 regularization factor and the enhancement nodes shrinkage scale of the BLS network are mapped as the positions of particles based on the training set of lithium-ion batteries N1, N2, and R1, separately. Then, the optimized parameters are searched for with Eq. 45 as the PSO fitness function. The optimization processes are shown in Figure 7, and the optimized L2 regularization factor and the enhancement nodes shrinkage scale of the BLS network are documented in Table 3.

FIGURE 7

FIGURE 7. The procedures for optimizing the initial parameters of the BLS network using the PSO algorithm.

TABLE 3

TABLE 3. The optimized parameters of the BLS network by PSO algorithm.

As evidenced in Figure 7, the PSO algorithm can converge nicely on the optimal value in the search process. The SOH estimation models for lithium-ion batteries N1, N2, and R1 are respectively developed using the optimized BLS network, after which one estimates the SOH based on the testing set in order to validate the robustness, stability, and effectiveness of the proposed method. The experimental results are shown in Figure 8.

FIGURE 8

FIGURE 8. The results and absolute error of estimation experiment for batteries N1, N2, and R1.

It can be seen that the proposed method accurately captures the global degradation tendency and estimates the current battery SOH well for the in-service batteries N1 and N2 in Figure 8. However, the sharp effects resulting from instrument noise, measurement errors, and other uncertainties exhibit powerful jitter in the battery discharging capacity curve, which means a great number of unexpected change points. For this category of battery aging state, the proposed method cannot completely track SOH instantaneously, but it is still able to perform a faster and better estimation of the battery SOH while maintaining the estimation error within an acceptable limit. Similarly, the battery R1 undergoes continual lithium-ion deposition and electrolyte loss and forms heavy solid electrolyte interphase (SEI) film, which contributes to the declining discharging capacity and thus becomes unsuitable for powering new EVs. The aging phenomenon is more dramatic for the R1 battery, as seen in Figure 8C, with plenty of mutation and capacity regeneration phenomena. However, an accurate estimation result of the battery SOH is still better with the proposed method. The same conclusion can be obtained from Table 4, where the SOH is calculated utilizing the capacity definition of lithium-ion battery SOH in Eq. 1. The proposed method provides remarkable estimation performance both for in-service and retired batteries. Meanwhile, the excellent experimental results for batteries N1 and N2 with different charging multipliers for the same aging state, and for different aging state batteries R1 and N1 with the same charging multiplier, demonstrate the superior robustness and stability of the introduced method.

TABLE 4

TABLE 4. The statistical errors of SOH estimation results.

Furthermore, to authenticate the effectiveness of the proposed method, the compared experiment is conducted in this work to compare the proposed PSO-BLS network with the conventional BLS network. In addition, SVR transposes complex input samples into a high-dimensional space using the nonlinear transformation, which has a good generalization capability and thus is widely applied in nonlinear regression problems. Instead of considering the Mercer condition when selecting the kernel function, RVM is a supervised learning method similar to SVR, which is more appropriate for nonlinear regression problems with high accuracy. ELM is also a commonly used regression algorithm with strong ability. Therefore, the SVR, ELM, and RVM algorithms are also considered as contrast samples in this study to compete with the proposed PSO-BLS network in the compared experiment. The results are shown in Figure 9; Table 5 records the errors.

FIGURE 9

FIGURE 9. The compared experiment results for batteries N1, N2, and R1.

TABLE 5

TABLE 5. The statistical errors of the compared experiment.

Through comparing the unoptimized BLS network and the commonly utilized SVR and RVM algorithms, it is clear that the estimation performance of the proposed PSO-BLS algorithm is better than other methods both for in-service and retired batteries. In addition, the estimation performance of the individual BLS network is significantly stronger than that of SVR and RVM, based on comparing the experimental results, because of its capability to extract deep information of the battery HIs data. However, the initial parameters of the conventional BLS network are preferentially selected using PSO in this work, which further enhances the nonlinear regression processing capability of the BLS network. A comprehensive evaluation of the proposed method based on error metrics from different perspectives further reveals that the proposed algorithm offers excellent estimation capability of SOH for in-service and retired lithium-ion batteries with high robustness, stability, and self-tuning properties. Consequently, it will facilitate the monitoring of the degradation for in-service cells, and the reselection and reorganization of retired lithium-ion batteries in the process of cascade utilization.

5 Conclusion

A strategy for the SOH estimation of in-service and retired lithium-ion batteries has been presented in this study. First, the IC curves were generated by applying the smoothing spline filter to eliminate the documented data noise based on the voltage data in the constant current charging phase. The HIs, which are highly correlated with the battery SOH, were then identified through screening with the Pearson correlation coefficient method according to the height and position of each IC peak. Finally, the L2 regularization parameter and the enhancement node shrinkage scale of the PSO-optimized BLS network were utilized to estimate the battery SOH for in-service and retired lithium-ion batteries based on the extracted kernel HIs.

The verification experiments were designed to quantify the estimation capability of the proposed method for the nonlinear degradation process of lithium-ion batteries using indicators of different scales based on the aging datasets, which consist of in-service batteries with different charging multipliers and the aging data of retired batteries measured in the laboratory. Furthermore, the proposed PSO-BLS method was investigated and compared with the separate BLS network as well as SVR and RVM methods. The results show that the suggested methodology can effectively estimate the SOH both of in-service and retired batteries with strong robustness and stability to battery degradation and disturbance. It is of great significance to monitor the nonlinear degradation of lithium-ion batteries when employing them, as well as in the recombination of retired lithium-ion batteries during cascade utilization.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

CZ: methodology, data curation, validation, writing-reviewing, and editing. SZ: methodology, software, validation, investigation, writing-original draft preparation, visualization.

Funding

This work was supported by the scientific research foundation for high-level personnel in Jinling Institute of Technology (jit-rcyj-202202) and industry-school cooperative education program of ministry of education (202102355002).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahn, J. H., and Lee, B. K. (2018). High-efficiency adaptive-current charging strategy for electric vehicles considering variation of internal resistance of lithium-ion battery. IEEE Trans. Power Electron. 34 (4), 3041–3052. doi:10.1109/tpel.2018.2848550

CrossRef Full Text | Google Scholar

Cai, L., Meng, J., Stroe, D. -I., Peng, J., Teodorescu, G. R., and Teodorescu, R. (2020). Multiobjective optimization of data-driven model for lithium-ion battery SOH estimation with short-term feature. IEEE Trans. Power Electron. 35 (11), 11855–11864. doi:10.1109/tpel.2020.2987383

CrossRef Full Text | Google Scholar

Chen, C. L. P., Feng, Z. S., and Feng, S. (2019). Universal approximation capability of broad learning system and its structural variations. IEEE Trans. Neural Netw. Learn. Syst. 30 (4), 1191–1204. doi:10.1109/tnnls.2018.2866622

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, L., Lü, Z., Lin, W., Li, J., and Pan, H. (2018). A new state-of-health estimation method for lithium-ion batteries through the intrinsic relationship between ohmic internal resistance and capacity. Measurement 116, 586–595. doi:10.1016/j.measurement.2017.11.016

CrossRef Full Text | Google Scholar

Chen, Z., Shi, N., Ji, Y., Niu, M., and Wang, Y. (2021). Lithium-ion batteries remaining useful life prediction based on BLS-RVM. Energy 234, 121269. doi:10.1016/j.energy.2021.121269

CrossRef Full Text | Google Scholar

Cui, Y., Zuo, P., Du, C., Gao, Y., Yang, J., Cheng, X., et al. (2018). State of health diagnosis model for lithium ion batteries based on real-time impedance and open circuit voltage parameters identification method. Energy 144, 647–656. doi:10.1016/j.energy.2017.12.033

CrossRef Full Text | Google Scholar

Ghorbani, N., Kasaeian, A., Toopshekan, A., Bahrami, L., and Maghami, A. (2018). Optimizing a hybrid wind-PV-battery system using GA-PSO and MOPSO for reducing cost and increasing reliability. Energy 154, 581–591. doi:10.1016/j.energy.2017.12.057

CrossRef Full Text | Google Scholar

Guha, A., and Patra, A. (2018). Online estimation of the electrochemical impedance spectrum and remaining useful life of lithium-ion batteries. IEEE Trans. Instrum. Meas. 67 (8), 1836–1849. doi:10.1109/tim.2018.2809138

CrossRef Full Text | Google Scholar

Guo, Y. F., Huang, K., and Hu, X. Y. (2021). A state-of-health estimation method of lithium-ion batteries based on multi-feature extracted from constant current charging curve. J. Energy Storage 36, 102372. doi:10.1016/j.est.2021.102372

CrossRef Full Text | Google Scholar

Hecht, C., Victor, K., Zurmühlen, S., and Sauer, D. U. (2021). Electric vehicle route planning using real-world charging infrastructure in Germany. eTransportation 10, 100143. doi:10.1016/j.etran.2021.100143

CrossRef Full Text | Google Scholar

How, D. N. T., Hannan, M. A., Lipu, M. S. H., Sahari, K. S. M., Ker, P. J., and Muttaqi, K. M. (2020). State-of-Charge estimation of Li-ion battery in electric vehicles: A deep neural network approach. IEEE Trans. Ind. Appl. 56 (5), 5565–5574. doi:10.1109/tia.2020.3004294

CrossRef Full Text | Google Scholar

Jiang, B., Zhu, J., Wang, X., Wei, X., Shang, W., and Dai, H. (2022). A comparative study of different features extracted from electrochemical impedance spectroscopy in state of health estimation for lithium-ion batteries. Appl. Energy 322, 119502. doi:10.1016/j.apenergy.2022.119502

CrossRef Full Text | Google Scholar

Jiang, B., Dai, H., and Wei, X. (2020). Incremental capacity analysis based adaptive capacity estimation for lithium-ion battery considering charging condition. Appl. Energy 269, 115074. doi:10.1016/j.apenergy.2020.115074

CrossRef Full Text | Google Scholar

Lai, X., Deng, C., Tang, X., Gao, F., Han, X., and Zheng, Y. (2022). Soft clustering of retired lithium-ion batteries for the secondary utilization using Gaussian mixture model based on electrochemical impedance spectroscopy. J. Clean. Prod. 339, 130786. doi:10.1016/j.jclepro.2022.130786

CrossRef Full Text | Google Scholar

Li, D., Zhang, Z., Liu, P., Wang, Z., and Zhang, L. (2021). Battery fault diagnosis for electric vehicles based on voltage abnormality by combining the long short-term memory neural network and the equivalent circuit model. IEEE Trans. Power Electron. 36 (2), 1303–1315. doi:10.1109/tpel.2020.3008194

CrossRef Full Text | Google Scholar

Li, X., and Wang, Z. (2018). A novel fault diagnosis method for lithium-ion battery packs of electric vehicles. Measurement 116, 402–411. doi:10.1016/j.measurement.2017.11.034

CrossRef Full Text | Google Scholar

Li, Y., Liu, K., Foley, A. M., Zulke, A., Berecibar, M., Nanini-Maury, E., et al. (2019). Data-driven health estimation and lifetime prediction of lithium-ion batteries: A review. Renew. Sustain. Energy Rev. 113, 109254. doi:10.1016/j.rser.2019.109254

CrossRef Full Text | Google Scholar

Lin, C. P., Cabrera, J., Denis, Y. W., Yang, F., and Tsui, K. L. (2020). SOH estimation and SOC recalibration of lithium-ion battery with incremental capacity analysis & cubic smoothing spline. J. Electrochem. Soc. 167 (9), 090537. doi:10.1149/1945-7111/ab8f56

CrossRef Full Text | Google Scholar

Lipu, M. S. H., Hannan, M. A., Hussain, A., Hoque, M. M., Ker, P. J., Saad, M. H. M., et al. (2018). A review of state of health and remaining useful life estimation methods for lithium-ion battery in electric vehicles: Challenges and recommendations. J. Clean. Prod. 205, 115–133. doi:10.1016/j.jclepro.2018.09.065

CrossRef Full Text | Google Scholar

Lipu, M. S. H., Hannan, M. A., Karim, T. F., Hussain, A., Saad, M. H. M., Ayob, A., et al. (2021). Intelligent algorithms and control strategies for battery management system in electric vehicles: Progress, challenges and future outlook. J. Clean. Prod. 292, 126044. doi:10.1016/j.jclepro.2021.126044

CrossRef Full Text | Google Scholar

Liu, J., Wang, Z., Hou, Y., Qu, C., Hong, J., and Lin, N. (2021). Data-driven energy management and velocity prediction for four-wheel-independent-driving electric vehicles. eTransportation 9, 100119. doi:10.1016/j.etran.2021.100119

CrossRef Full Text | Google Scholar

Ma, Y., Wu, L., Guan, Y., and Peng, Z. (2020). The capacity estimation and cycle life prediction of lithium-ion batteries using A new broad extreme learning machine approach. J. Power Sources 476, 228581. doi:10.1016/j.jpowsour.2020.228581

CrossRef Full Text | Google Scholar

Ma, Z., Wang, Z., Xiong, R., and Jiang, J. (2018). A mechanism identification model based state-of-health diagnosis of lithium-ion batteries for Energy storage applications. J. Clean. Prod. 193, 379–390. doi:10.1016/j.jclepro.2018.05.074

CrossRef Full Text | Google Scholar

Oji, T., Zhou, Y., Ci, S., Kang, F., Liu, X. X., and Liu, X. (2021). Data-driven methods for battery SOH estimation: Survey and a critical analysis. IEEE Access 9, 126903–126916. doi:10.1109/access.2021.3111927

CrossRef Full Text | Google Scholar

Pan, H., Lü, Z., Wang, H., Wei, H., and Chen, L. (2018). Novel battery state-of-health online estimation method using multiple health indicators and an extreme learning machine. Energy 160, 466–477. doi:10.1016/j.energy.2018.06.220

CrossRef Full Text | Google Scholar

Qin, P., Sun, J., Yang, X., and Wang, Q. (2021). Battery thermal management system based on the forced-air convection: A review. eTransportation 7, 100097. doi:10.1016/j.etran.2020.100097

CrossRef Full Text | Google Scholar

Ren, X., Liu, S., Yu, X., and Dong, X. (2021). A method for state-of-charge estimation of lithium-ion batteries based on PSO-LSTM. Energy 234, 121236. doi:10.1016/j.energy.2021.121236

CrossRef Full Text | Google Scholar

Samanta, A., Chowdhuri, S., and Williamson, S. S. (2021). Machine learning-based data-driven fault detection/diagnosis of lithium-ion battery: A critical review. Electronics 10 (11), 1309. doi:10.3390/electronics10111309

CrossRef Full Text | Google Scholar

Sarmah, S. B., Kalita, P., Garg, A., Niu, X. d., Zhang, X. W., Peng, X., et al. (2019). A review of state of health estimation of Energy storage systems: Challenges and possible solutions for futuristic applications of Li-ion battery packs in electric vehicles. J. Electrochem. Energy 16 (4). doi:10.1115/1.4042987

CrossRef Full Text | Google Scholar

Schaltz, D. E., and Schaltz, E. (2020). Lithium-ion battery state-of-health estimation using the incremental capacity analysis technique. IEEE Trans. Ind. Appl. 56 (1), 678–685. doi:10.1109/tia.2019.2955396

CrossRef Full Text | Google Scholar

Shi, E., Xia, F., Peng, D., Li, L., Wang, X., and Yu, B. (2019). State-of-Health estimation for lithium battery in electric vehicles based on improved unscented particle filter. J. Renew. Sustain. Energy 11 (2), 024101. doi:10.1063/1.5065477

CrossRef Full Text | Google Scholar

Song, B., Wang, Z., and Zou, L. (2021). An improved PSO algorithm for smooth path planning of mobile robots using continuous high-degree Bezier curve. Appl. Soft Comput. 100, 106960. doi:10.1016/j.asoc.2020.106960

CrossRef Full Text | Google Scholar

Sui, X., He, S., Vilsen, S. B., Meng, J., Teodorescu, R., and Stroe, D. I. (2021). A review of non-probabilistic machine learning-based state of health estimation techniques for lithium-ion battery. Appl. Energy 300, 117346. doi:10.1016/j.apenergy.2021.117346

CrossRef Full Text | Google Scholar

Tang, X., Liu, K., Li, K., Widanage, W. D., Kendrick, E., and Gao, F. (2021). Recovering large-scale battery aging dataset with machine learning. Patterns 2 (8), 100302. doi:10.1016/j.patter.2021.100302

PubMed Abstract | CrossRef Full Text | Google Scholar

Tian, N., Fang, H., and Wang, Y. (2020). Real-time optimal lithium-ion battery charging based on explicit model predictive control. IEEE Trans. Ind. Inf. 17 (2), 1318–1330. doi:10.1109/tii.2020.2983176

CrossRef Full Text | Google Scholar

Wang, K., Gao, F., Zhu, Y., Liu, H., Qi, C., Yang, K., et al. (2018). Internal resistance and heat generation of soft package Li4Ti5O12 battery during charge and discharge. Energy 149, 364–374. doi:10.1016/j.energy.2018.02.052

CrossRef Full Text | Google Scholar

Wang, S. L., Fernandez, C., Zou, C. Y., Yu, C.-M., Li, X.-X., Pei, S.-J., et al. (2018). Open circuit voltage and state of charge relationship functional optimization for the working state monitoring of the aerial lithium-ion battery pack. J. Clean. Prod. 198, 1090–1104. doi:10.1016/j.jclepro.2018.07.030

CrossRef Full Text | Google Scholar

Wang, X., Wei, X., Zhu, J., Dai, H., Zheng, Y., Xu, X., et al. (2021). A review of modeling, acquisition, and application of lithium-ion battery impedance for onboard battery management. eTransportation 7, 100093. doi:10.1016/j.etran.2020.100093

CrossRef Full Text | Google Scholar

Wei, Z., Zhao, J., He, H., Ding, G., Cui, H., and Liu, L. (2021). Future smart battery and management: Advanced sensing from external to embedded multi-dimensional measurement. J. Power Sources 489, 229462. doi:10.1016/j.jpowsour.2021.229462

CrossRef Full Text | Google Scholar

Xiong, R., Li, L., Li, Z., Yu, Q., and Mu, H. (2018). An electrochemical model based degradation state identification method of lithium-ion battery for all-climate electric vehicles application. Appl. Energy 219, 264–275. doi:10.1016/j.apenergy.2018.03.053

CrossRef Full Text | Google Scholar

Xiong, R., Pan, Y., Shen, W., Li, H., and Sun, F. (2020). Lithium-ion battery aging mechanisms and diagnosis method for automotive applications: Recent advances and perspectives. Renew. Sustain. Energy Rev. 131, 110048. doi:10.1016/j.rser.2020.110048

CrossRef Full Text | Google Scholar

Xu, W. Y., and Xu, Y. (2020). Data-driven online health estimation of Li-ion batteries using A novel energy-based health indicator. IEEE Trans. Energy Convers. 35 (3), 1715–1718. doi:10.1109/tec.2020.2995112

CrossRef Full Text | Google Scholar

Yin, H., Ma, S., Li, H., Wen, G., Santhanagopalan, S., and Zhang, C. (2021). Modeling strategy for progressive failure prediction in lithium-ion batteries under mechanical abuse. eTransportation 7, 100098. doi:10.1016/j.etran.2020.100098

CrossRef Full Text | Google Scholar

Yu, H., Dai, H., Tian, G., Wu, B., Xie, Y., Zhu, Y., et al. (2021). Key technology and application analysis of quick coding for recovery of retired Energy vehicle battery. Renew. Sustain. Energy Rev. 135, 110129. doi:10.1016/j.rser.2020.110129

CrossRef Full Text | Google Scholar

Zhang, C., He, S. Y., and He, Y. (2022). An integrated method of the future capacity and RUL prediction for lithium-ion battery pack. IEEE Trans. Veh. Technol. 71 (3), 2601–2613. doi:10.1109/tvt.2021.3138959

CrossRef Full Text | Google Scholar

Zhang, M., Hu, T., Wu, L., Kang, G., and Guan, Y. (2021). A method for capacity estimation of lithium-ion batteries based on adaptive time-shifting broad learning system. Energy 231, 120959. doi:10.1016/j.energy.2021.120959

CrossRef Full Text | Google Scholar

Zhang, S., Guo, X., Dou, X., and Zhang, X. (2020). A rapid online calculation method for state of health of lithium-ion battery based on coulomb counting method and differential voltage analysis. J. Power Sources 479, 228740. doi:10.1016/j.jpowsour.2020.228740

CrossRef Full Text | Google Scholar

Zhang, Y., Wik, T., Bergström, J., Pecht, M., and Zou, C. (2022). A machine learning-based framework for online prediction of battery ageing trajectory and lifetime using histogram data. J. Power Sources 526, 231110. doi:10.1016/j.jpowsour.2022.231110

CrossRef Full Text | Google Scholar

Zhao, S., Zhang, C., and Wang, Y. (2022). Lithium-ion battery capacity and remaining useful life prediction using board learning system and long short-term memory neural network. J. Energy Storage 52, 104901. doi:10.1016/j.est.2022.104901

CrossRef Full Text | Google Scholar

Zheng, L., Zhang, L., Zhu, J., Wang, G., and Jiang, J. (2016). Co-estimation of state-of-charge, capacity and resistance for lithium-ion batteries based on A high-fidelity electrochemical model. Appl. Energy 180, 424–434. doi:10.1016/j.apenergy.2016.08.016

CrossRef Full Text | Google Scholar