- 1School of Information Engineering, Henan Institute of Science and Technology, Xinxiang, China
- 2Department of Information Technology, College of Computer and Information Sciences, Princess Nourah Bint Abdulrahman University, Riyadh, Saudi Arabia
- 3Department of Electrical Engineering, Faculty of Engineering, Fayoum University, Fayoum, Egypt
- 4Hourani Center for Applied Scientific Research, Al-Ahliyya Amman University, Amman, Jordan
- 5Faculty of Information Technology, Middle East University, Amman, Jordan
- 6Faculty of Information Technology, Applied Science Private University, Amman, Jordan
- 7School of Computer Sciences, Universiti Sains Malaysia, Pulau Pinang, Malaysia
- 8Department of Information System, Faculty of Computers and Informatics, Suez Canal University, Ismailia, Egypt
- 9Department of Mathematics, Faculty of Science, Zagazig University, Zagazig, Egypt
- 10Faculty of Computer Science and Engineering, Galala University, Suez, Egypt
- 11Artificial Intelligence Research Center (AIRC), Ajman University, Ajman, United Arab Emirates
- 12Department of Electrical and Computer Engineering, Lebanese American University, Byblos, Lebanon
PV cell/module/characteristic array accuracy is mainly influenced by their circuit elements, based on established circuit characteristics, under varied radiation and temperature operating conditions. As a result, this study provides a modified accessible Honey Badger algorithm (HBA) to identify the trustworthy parameters of diode models for various PV cells and modules. This approach relies on modifying the 2D chaotic Henon map settings to improve HBA’s searching ability. A series of experiments are done utilizing the RTC France cell and SLP080 solar module datasets for the single and double-diode models to validate the performance of the presented technique. It is also compared to other state-of-the-art methods. Furthermore, a variety of statistical and non-parametric tests are used. The findings reveal that the suggested method outperforms competing strategies regarding accuracy, consistency, and convergence rate. Moreover, the primary outcomes clarify the superiority of the proposed modified optimizer in determining accurate parameters that provide a high matching between the estimated and the measured datasets.
1 Introduction
Global environmental interests and the persistent increase in energy needs make advanced renewable energy sources universally acceptable. (Li et al., 2022; Xiong et al., 2018; Eid et al., 2021). As a proven start to the effectiveness of renewable energy, solar power has attracted intense deliberation in recent years (Herez et al., 2018). The International Energy Agency has analyzed sustainable energy and finds that more than half of the power needed in the world can be provided by solar energy (Mekhilef et al., 2011). Photovoltaic (PV) methods straight transform solar power into electricity, and it has become one of the most popular sustainable energy production schemes (Siecker et al., 2017). To investigate the dynamic transformation performance of a PV mode, forming the quality of its primary device, i.e., the PV cell, is a crucial issue. Numerous methods have been produced to create PV cells, and the standard widespread procedure is applying similar circuit prototypes. Amongst them, the single diode design and double diode design are the generally utilized circuit designs (Chin et al., 2015). Following choosing a suitable model construction, getting or selecting proper construction parameters is another vital concern. A solar cell model’s precise design and characterization are according to the obtained parameters in that model (Humada et al., 2016; Chin and Salam, 2019).
Practically, two single diodes (SD) and double diode (DD) electrical rotations can adequately represent the solar cell’s style (Pourmousa et al., 2019; Ridha et al., 2022a). To enhance the performance of this method, it is essential to mimic its attitude before launching (Chin et al., 2015). One of the various critical actions in the modeling rule is the parameter identification that illustrates the physics paradigm of the solar partition, based on which it is probable to study the procedure performance and productivity in various situations (Chin et al., 2016). There are five unnamed parameters in the SD design and seven other parameters in the DD design, which must be carefully determined. Precisely determining the parameters enhances the effectiveness and power of the solar cells and presents a leading part in the highest energy point, where the solar cell transfer the total production energy to the load (Dileep and Singh, 2017).
Various methods have been introduced to manage this complicated yet essential problem. They can be organized into two main classes: analytical and optimization methods (Agushaka et al., 2022; Oyelade et al., 2022). The first method, principally based on the manufacturers’ key information points, uses mathematical equalizations to determine the model parameters. The PV parameter extraction becomes an optimization problem in the second method, called the optimization method. It then applies some source points of an addressed current-voltage (I-V) characteristic curve to obtain the parameters (Abbassi et al., 2022a). Consequently, they have gained much attention newly.
In the literature, several efforts are made to handle these problems (Yan et al., 2019); in Kumar et al., 2020), a novel search-based optimization method is proposed to extract the PV parameters. The proposed optimizer is modified to find more accurate solutions by adding an excellent mathematical representation with adaptive weights. The achievement of the presented approach is verified by investigating the determining results with practical effects. A comprehensive statistical investigation demonstrates the advantage of the proposed method. A detailed confusion mutation-based PSO algorithm is introduced in (Liang et al., 2020). Throughout each update in the proposed method, the effectiveness of each new position is assessed and classified as high or low quality. The results confirmed the advantage of the presented method analyzed with other well-known methods in using precision, balance, and speed. In (Chenouard and El-Sehiemy, 2020), a new search method-based bound algorithm is introduced to determine the parameters for three PV models. The measured cells’ determined execution factors for I-V and P-V are similar to the empirical data and competitive with current comparative methods.
An enhanced optimization-based method, called MTLBO, is suggested in (Abdel-Basset et al, 2021) to precisely and probably obtain the unnamed PV parameters. The improvement here is to partition each search section into three levels based on its scoring level. The test results verified the advantage of the suggested method in extracting the parameters of the PV models. The Chaotic Whale Optimization Algorithm is presented in (Oliva et al, 2017) to address the PV parameters. The primary benefit of the offered method is using chaotic theory to calculate and automatically adjust the original parameters of the used method. The outcomes confirmed that the suggested method achieved enhanced precision and accuracy performance. A reliable and robust method for modeling the PV parameters problem is presented in (Qais et al, 2019). The principal objective is to determine the nine-parameter of a three-diode design using the datasheet parameters provided by all industrial applications. The suggested technique obtained more satisfactory outcomes than other similar approaches. It can model any PV design using the provided datasheet information.
Recently, different intelligent search algorithms have been presented and operated to solve the PV parameter estimation problems (Yousri et al, 2020a). Surprisingly, most of these techniques, such as the Particle Swarm Optimizer, Genetic Algorithm, Differential Evolution, Harmony Search, and Cuckoo Search Optimizer, are well-recognized between computer experts and other experts from different disciplines. The methods are adaptable; they evade the local optima trap and give a more reliable solution than the conventional methods. Moreover, the methods have several benefits, making them worthy of addressing any optimization problem. They simulate the problem-addressing procedures utilized by humans and animals. In other terms, a particular algorithm may present promising outcomes when addressing a specific kind of problem. However, that corresponding algorithm may give a poor achievement in a different situation (Yang, 2010). Hence, these causes have motivated researchers to investigate new optimization algorithms for PV parameter estimation problems.
The performance of any optimizer relies on its equilibrium between exploration and exploitation search (Abualigah et al, 2021b; Abualigah et al, 2021a). Exploration indicates the diversification of the optimizer’s solutions to investigate new areas of the search space. In contrast, exploitation introduces the experience to improve the current solutions by exploring nearby their best solutions. Honey Badger Algorithm (HBA) is a newly introduced optimization technique inspired by the intelligent foraging of honey badger (Hashim et al, 2022). The search methods of the honey badger with digging strategies are expressed in the exploration and exploitation stages in HBA. The new optimizer formulates a different procedure and various tools for balancing exploration and exploitation. It has a straightforward structure and contains few control parameters. Notwithstanding its oversimplified creation, the HBA mainly outperforms other optimization methods in many test cases (Ashraf et al, 2022), as in the first proposal. Notwithstanding the encouraging motivation, a complete literature search shows that the HBA has yet to be employed for the PV parameters. Recently, a grouped beetle antennae search (GBAS) algorithm has been proposed to effectively extract the unknown parameters of the single, double, and triple diode s PV models (Sun et al, 2021). The cuckoo search-relevance vector machine (CS-RVM) has been introduced for providing a PV model with measured data over a range of environmental conditions (Ban et al, 2021). The Peafowl optimization algorithm has been reported for identifying the double and triple-diode PV models.
According to the previous discussions, this paper introduces a primary effort to modify the HBA to enhance its performance while handling the PV cell modeling problem. To this point, the two-dimensional Henion map is integrated with HBA to enhance the algorithm’s basic performance in this approach. Accordingly, it is easy to execute and does not need large trial-and-errors to harmonize the parameters. The Chaotic version of HBA (CHBA Alg) is used to select the parameters of PV cells for two main types; single diode and two diodes. An uncomplicated style is used to define the optimal parameter settings values to assure the effective execution of the proposed CHBA. The root-mean-square error (RMSE) among the PV modules production is used. The empirical data is taken as standard measures to decrease the objective function. Moreover, this paper presents parametric restrictions to restrict the investigation within the limitations of the pre-known parameters. The acquired outcomes are assessed and analyzed with other similar algorithms based on generally used benchmarks for validation. In addition, the proposed optimizer has also experimented on three PV modules for various practical purposes at different levels of irradiance and heat. The results showed that the version of the proposed HBA is auspicious, i.e., it produces considerably more precise solutions than other similar methods. Further, the proposed CHBA is positively compatible and efficient for empirical purposes.
The main contribution of this study can be summarized as:
1. Proposed a modified version of HBA using the Hannon map.
2. Apply the modified version of HBA, named CHBA, to estimate the parameters of PV in single and double diode models.
The remaining sections of this paper are presented as follows. Section 2 presents the problem representation and various PV models. The proposed parameter extracting-based HBA method is offered in Section 3. Section 4 shows the empirical results and discussion. Section 5 gives the conclusion and future work directions.
2 Photovoltaic equivalent circuits
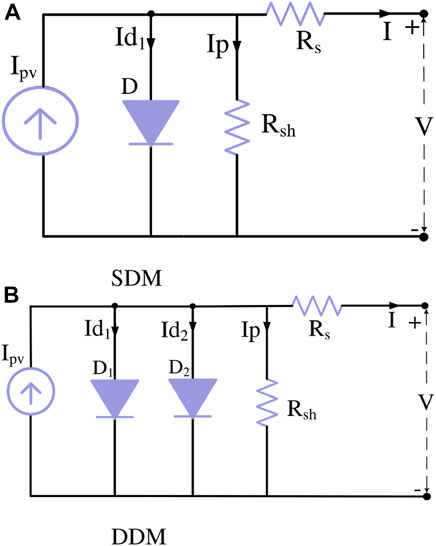
We introduced the essential information of the Photovoltaic equivalent circuits in this section. The single-diode model (SDM) and the double-diode model (DDM) are the two most popular PV models (DDM). For each model, there are different characteristics and structures as given in Figure 1. Such as, the SDM is the simplest PV model; however, its accuracy is less than the efficiency of DDM. DDM emulates the physical performance of PV at irradiation conditions with low-level (Kermadi et al, 2020). In addition, the SD has one diode that generates current and shunts resistance (Rp). In contrast, there are two diodes in DDM; The diffusion current and recombination effects are represented by the first and second diodes, respectively. After that, the combination is performed in the series way with resistance (Rs), and the output current (I) is computed using the law of Kirchhoff’s current as given in the following formula (Yousri et al, 2020a; Abbassi et al, 2022b).where a1 stands for the ideality of the diode. Also, Id1, Io1, and Ip are the diode currents, the saturation diode, and the leakage shunt, respectively. Vt represents the thermal voltage that computed at (T in Kelvin) temperature using
According to the structure of DDM given in Figure 1B, we can be seen that DDM is a generalization of SDM by combining a parallel of the first diode (in SD) with the second diode. This process emulates the physical effects at the P-N junction, so the output current of PV using DDM is given as (Ridha et al, 2022b):
In Eq. 3, a1 and a2 stand for the ideality parameters of the first and second diode, respectively. Io2 is the saturation current. Thus, there are seven parameters in Eq. 3 are required to be estimated. These parameters are the Iph, Io1, Io2, a1, a2, Rs, and Rp). [Vp]Vmp Voltage at maximum power point (MPP) (V) [Vp]Voc Open circuit voltage (V) [Vp]Imp Current at maximum power point (MPP) (A) Moreover, the generated photocurrent is calculated using the radiation value (G) at T as defined in Eq. 4a. Also, the currents of the reverse saturation for Io1,2 are defined in Eq. 4b. In addition, the value of Rp is computed using Eq. 4c and as well as, the open circuit voltage
In Eq. 4, Gs = 1000W/m2 and Ts = 25°C.
[Cp]kiTemperature coefficient of current [Vp]EgBand-gap energy.
3 Formulation of fitness function
Determining the SDM and DDM parameters is seen as a nonlinear optimization issue. The root means square error (RMSE) is the most common objective function used to perform this procedure. It is calculated using the values of the estimated (Iest) and measured (Imeas) currents. The Newton-Raphael method solves nonlinear equations, making the fitness function more accurate for real applications. It is defined as (Ćalasan et al, 2020; Yousri et al, 2019a):
[Vp]nNumber of parallel strings in the array [Vp]ImeasMeasured current (A) [Vp]IestEstimated current (A) [Vp]MLength of the measured dataset [Vp]
To calculate the estimated current (
where dI and dI’ refers to the difference function of I and its first derivative. In case of SDM, dI and dI’ are defined as:
By substituting Eqs 8, 9 in Eq. 7, the
The
3.1 Evaluate the accuracy using lambert form
To justify the accuracy of the developed method to extract the optimal value of the parameters, the Lambert W function (LWF) is applied to measure the currents of SDM and DDM. Therefore, the RMSE has been calculated again for Iest based on the determined parameters and Imeas. When the difference (DiffRMSE) between the RMSE (as in Eq. 6) and RMSE using LWF (i.e., RMSELambert) is large, then this indicates the inaccuracy in determining the parameters. The LWF of SDM is formulated as:
Moreover, the LWF of DDM (Eq. 2) is formulated as (Gao et al, 2016; Gude and Jana, 2022; Ridha, 2020):
[Vp]ILambertCalculated current via Lambert form.
In Eq. 12, ILambert is the output current generated based on LWF. Therefore, RMSELambert is evaluated using the following formula:
[Vp] mNumber of modules in string.
4 Chaotic honey badger algorithm
The two-dimensional Henion map is integrated with HBA to enhance the algorithm’s basic performance in this approach. The descriptions and controlled equations of the proposed algorithm are summarized as follows:
4.1 Honey badger algorithm
The structural properties of the Honey Badger Algorithm (HBA) are detailed in this section. The HBA is one of the most basic optimization techniques derived from honey badger mammal behavior when looking for food. The honey badger utilizes two tactics to catch its meal: to employ his sniffing ability; the second is to excavate to capture the prey. The mammal follows honeyguide birds in the second technique to locate and access the hives. The first method was given the term digging phase, whereas the second principle was given the name honey phase by the algorithm developers (Hashim et al, 2022). The mammal’s mobility is governed by its odor awareness; when the strength of the smell is strong, the mammal’s mobility will indeed be fast, and vice versa (Hashim et al, 2022). The HBA’s primary steps and regulated equations are summarized as follows:
• Initialization step: The first candidate solution is calculated utilizing upper (UB) and lower (LB) limits of the problem space in this phase. The initial solutions are thus randomized sets that may be derived by using the following Eq. (14).
where U is the solutions framework and N represents the number of candidate solutions (honey badgers).
• Updating the candidates’ positions: In this stage, the candidates’ locations Unew are modified strategy, for example, employed, which is either digging or honey phases.
• Digging phase: The movements of the search candidates in this phase are determined by the strength of the predator’s smell and the distance between both the honey badger (agent) and the prey. As seen in Figure 2, the honey badger digs in a circularly polarized shape. The equation for its motion is given below:
where β is a metric of the mammal’s capacity to catch food, Hashim et al. (2022) considered the possible values of β is 6. The r3, 4, 5 are arbitrary variables in the range of 0–1 drawn from a uniformly distributed, In is the intensity. The indicator for the direction of the search is the Fg, and it is generated as follows:
• Honey phase: honey badgers use this approach to modify their place concerning the honey guide bird while searching for beehives. Hashim et al. (2022) defined the honey phase using the following equation:
where r7 is a random number having values between 0 and 1.
• Modeling Intensity In: because the honey badger mammal’s behaviour is regulated by its smell awareness, Hashim et al. (2022) created the following expression for the smell intensity Ini of the victim by each ith candidate:
where prey is the prey’s position and r2 is a random number in the range [0 1].
• Modeling the density variable (σ): the σ is defined by Hashim et al. (2022) as a controller for transmission between the exploration and exploitation phases. To reduce the randomness with time, the developers (Hashim et al, 2022) supposed that β is a regression function during the iterations, as shown below:
where Iter and Itermax refer to the current and the total number of iterations, C is constant that was recommended to be 2.
• Escaping from local solutions: the algorithm developers (Hashim et al, 2022) used an alert (Fg) to indicate the search direction for avoiding becoming tethered to local solutions.
Based on the previous description, the Algorithm 1 describes the main structure of the HBA.
Algorithm 1. Steps of HBA.
Inputs: Agents size N, number of iterations Maxt.
Outputs: The optimal solutions.
Step 1: Calculate the first set of N solutions U with dimension d (i.e., number of unknown variables).
Compute the fitness function of Eq. 13 and the corresponded swarm matrix as the best solutions (prey).
while (Iter ≤ Itermax) do
Upgrade the value of the decreasing factor through Eq. 19.
for (i = 1 to N) do
Compute the intensity through Eq. (18).
if r < 0.5 then
Upgrade the location of Unew through Eq. 15.
else
Upgrade the location of Unew through Eq. 17.
end if
Evaluate the new solutions and compute the Fitt+1 and assign
if Fitt+1 ≤ Fitt then
Set Ui = Unew and Fitt = Fitt+1.
end if
if
Set Ubest = Unew and
end if
end for
end while
Send the recommended solution
4.2 Two-dimensional henon map
In general, the 2D Henon map is one of the most popular discrete-time dynamical systems that simulates the chaotic behavior (Hénon, 1976). The Hénon map is a discrete-time dynamical system that is also known as the Hénon-Pomeau attractor/map. It is one of the most well-studied instances of chaotic behavior in dynamical systems. A point (xn, yn) in the plane is mapped to a new point using the Hénon map. Michel Hénon introduced the map as a simplified version of the Lorenz model’s Poincaré section. In the classical map, an initial plane point will either approach or diverge to infinity from a set of points known as the Hénon weird attractor. The Hénon attractor is a fractal that is smooth in one direction and has a Cantor set in the opposite. Moreover, the main difference between 2D Henon map and others is that it (i.e., 2D Henon) has better pseudo-randomness (Song and Ding, 2014; Bucolo et al, 2022). In addition to, the properties such as uniform non-variation of density variable, and Lyapunov exponent. This support our motivation to apply the 2D Henon map to PV parameter estimation.
The mathematical equation of the Henon map is given as in Eq. 20 and its distribution can be depicted in Figure 3:
4.3 Proposed chaotic honey badger algorithm
The two-dimensional Henon map is applied to adjust the parameters of C and β of Eq. (21), respectively to enhance the performance of the basic HBA optimizer. The updated values of the C and β follow the equation shown below:
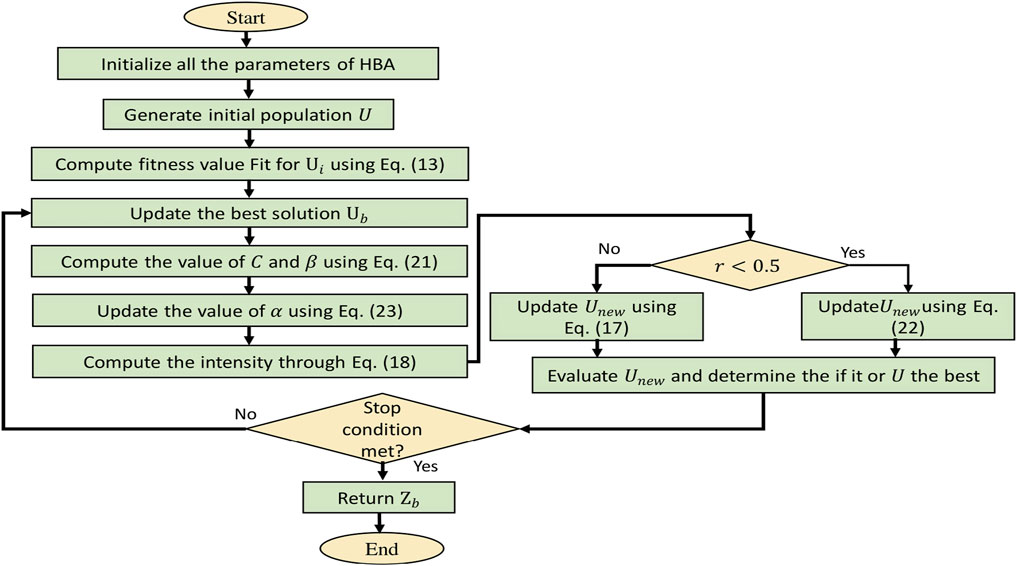
where xt+1 and yt+1 are vectors of the Henon map, t is the current iteration. The 4 and 7 are used to normalize the Henon map vectors to be in the same recommended range by the HBA developer. In section A of the basic HBA, the developers selected the β and C have values of 6 and 2. In the CHBA, the 4 and 7 are selected to provide a wide variety for the variables β and C throughout the iteration numbers in the intervals of [0 7], and [0 4], respectively. The initialization of a Henon map during implementation is 0 (x (1) = 0; y (1) = 0). The attractor of the map has been depicted in Figure 3. The flowchart of the proposed CHBAlg based on the PV parameters estimation process is depicted in Algorithm 2 and the flowchart of Figure 4. Then the digging phase and density variable will be modeled as
Algorithm 2. Pseudo code of CHBA.
Inputs: Agents size N, number of iterations Maxt, the dataset of the I, V of the considered PV cell/module.
Outputs: The optimal solutions.
Step 1: Calculate the first set of N solutions U with dimension d (i.e., the number of unknown variables which are 5 and 7 for SDM and DDM, respectively).
Compute the fitness function of Eq. 13 and the corresponded swarm matrix as the best solutions (prey).
Calculate C, and β based on Hanon map using Eq. 21 with dimensions of 1* Itermax).
while (Iter ≤ Itermax) do
Upgrade the value of the decreasing factor through Eq. (23).
for (i = 1 to N) do
Compute the intensity through Eq. (18).
if r < 0.5 then
Upgrade the location of Unew through Eq. (22).
else
Upgrade the location of Unew through Eq. (17).
end if
Evaluate the new solutions and compute the Fitt+1 and assign
if Fitt+1 ≤ Fitt then
Set Ui = Unew and Fitt = Fitt+1.
end if
if
Set Ubest = Unew and
end if
end for
end while
Send the recommended solution
5 Simulations and discussions
In this section, the proposed CHBA algorithm is examined with three different PV cell/modules to identify the SD and DD PV models’ parameters. The proposed optimizer is compared with a set of recently developed algorithms including barnacles mating optimizer (BMO) (Sulaiman et al, 2020), red fox optimization algorithm (RFSO) (Połap and Woźniak, 2021), electric fish optimizer (EFO) (Yilmaz and Sen, 2020), capuchin search algorithm (CapSA) (Braik et al, 2021), and Aquila optimizer (AO) (Abualigah et al, 2021c) to provide a massive comparison with recent set of meta-heuristics. For unbiased comparison, the conducted algorithms are implemented for 30 independent runs with the number of iterations and population size of 500 and 30, respectively. The number of iterations is selected based on several separate runs, showing that most of the considered algorithms converged around the 500 iterations.
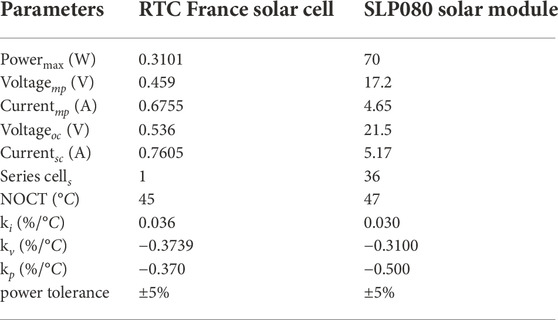
The electric specifications of the considered PV cell and PV module are reported in Table 1.
5.1 Experimental series 1: RTC France silicon solar cell
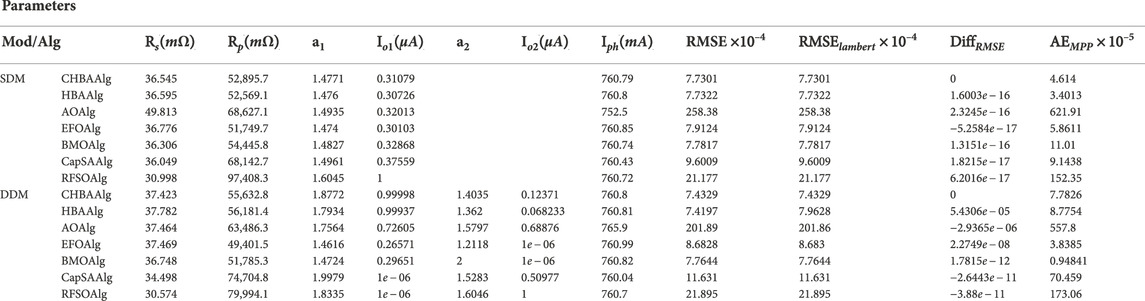
In this part, the performance of the CHBAlg method is computed using 26 (V-I) measured pairs for a commercial RTC France silicon solar cell at 33°C and 1000W/m2. Table 4 shows the parameters of SDM and DDM detected using CHBAlg and other algorithms. The fitness value (RMSE) is used as the main performance metric to evaluate the accuracy of these algorithms. Furthermore, the performance of the determined parameters is assessed by using Lambert forms for SDM and DDM to calculate the RMSElambert and then measure the deviation (DiffRMSE) between the RMSElambert and the obtained RMSE. In the case of the DiffRMSE is large, this indicates inefficient estimated parameters. In addition, the absolute error at MPP (AEMPP) is presented in Table 5 for a more thorough investigation.
In the two test scenarios, RMSE and DiffRMSE using CHBAAlg are smaller than other approaches (HBAAlg, RFSOAlg, BMOAlg, EFOAlg, CapSAAlg, AOAlg), as shown in Table 4 (i.e., SDM and DDM). This demonstrates the developed CHBAAlg approach’s excellent performance and establishes its superiority over other approaches. The CHBAAlg’s AEMPP values indicate its consistency in accurately modeling the PV solar cell. Different statistical measurements are utilized to analyze CHBAAlg’s performance further, as given in Table 2. The Wilcoxon signed-rank test (WSRT) is used to determine whether or not the difference between the CHBAAlg and other approaches is significant, with a significance level of 0.05. It can be seen from the tabled findings that CHBAAlg takes first place according to worst, best, average, and median. Furthermore, its stability is superior to that of other approaches. Traditional HBAAlg can produce outstanding results than the different algorithms. As demonstrated in Table 2, the RMSE and DiffRMSE of CHBAlg are lower than those of other methods (HBAAlg, RFSOAlg, BMOAlg, EFOAlg, CapSAAlg, and AOAlg) for SDM and DDM models. This proves the developed CHBAlg approach’s superiority over other methods by demonstrating its exceptional performance. The AEMPP values of the CHBAlg and HBA show that they are consistent in precisely modeling the PV solar cell. The least RMSE reveals the high accuracy of the identified parameters as the proposed CHBAlg provides the least RMSE; hence it can determine highly accurate results. The average value of the RMSE affirms that the CHBAlg has the highest rank in its reliability as the average RMSE is very close to the best-fetched one. Thereby, the STD of CHBAlg is in the range of 1 × 10–5; meanwhile, the HBA and other algorithms have STD in fields of 3 × 10–4. For the non-parametric statistical analysis, as shown in Table 6, CHBAlg takes the top rank based on the worst, best, median, and average, as seen in the tabular results. Furthermore, it has a higher level of stability than other approaches. Traditional HBAAlg can outperform different algorithms according to the results, and in the best case, it has nearly the same accuracy in Table 3 as CHBAAlg.

TABLE 2. The obtained results by CHBAAlg, and other techniques in the case of SDM and DDM of the RTC cell.
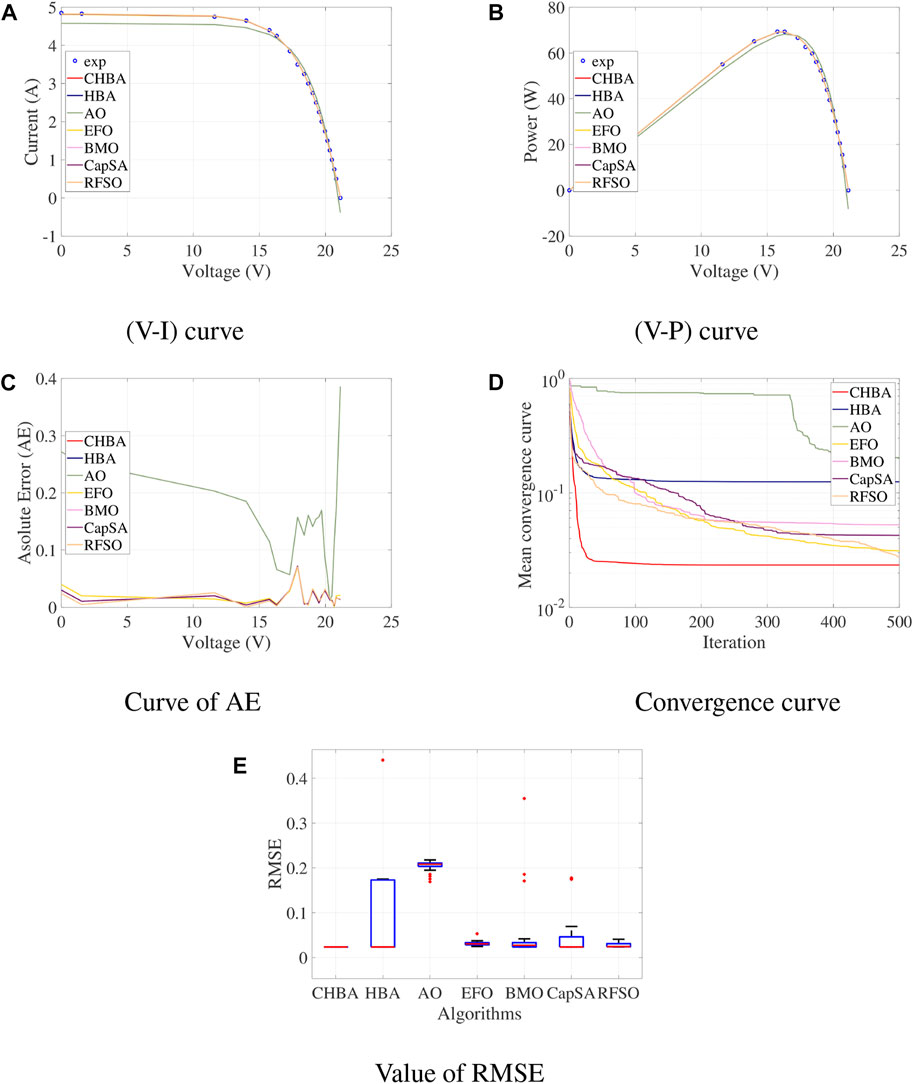
Figures 5, 6 show the current-voltage (V-I), power-voltage (V-P) characteristics, absolute error curve between estimated and measured datasets, the Mean convergence speed of the proposed optimizer compared the state-of-the-art, and the RMSE over 25 runs using SDM and DDM models of RTC France solar cells, respectively, to confirm the certainty of the identified parameters. The following conclusions may be drawn from these graphs: the specified parameters by CHBAlg (Viewed as CHBA, for brief) give a tight match between the measured and identified sets which affirms the accuracy of the identified parameters. The absolute error (AE) curves in Figure 5C, Figure 6C for SDM and DDM models, respectively, the observed AE values between the estimated and measured dataset are less than 0.02 throughout most of the dataset pairs. Accordingly, AE curves indicate the high performance of the developed method to estimate the efficient parameters. On the other hand, the AO optimizer shows a high deviation between the measured and the estimated datasets; hence it has a minor rank in handling this optimization problem. As well as from the mean convergence curve of CHBAlg (viewed as CHBA, for brief) in Figure 5D, Figure 6D, it can be noticed that it can converge to high-quality solutions with faster performance than other methods. Meanwhile, the AO and RFSO are not recommended for solving the PV modeling optimization problem. On the other hand, the HBA converges to fewer quality solutions than HBA and EFO; hence it takes the third rank. Finally, the RMSE boxplots in Figure 5E, Figure 6E show that CHBAlg (Viewed as CHBA, for brief) is very stable in SDM and DDM models. In contrast, AO is the worst method in both models.
For comparing with recent literature, the following Table 4 lists the identified parameters RMSE, DiffRMSE and AEMPP by the recently published techniques including Archimedes Optimization Algorithm (AOA), marine predator algorithm (MPA), EPSO (Yousri et al., 2020b), HCLPSO (Yousri et al., 2019b), PGJAYA (Yu et al., 2019), CWOA (Xiong et al., 2018), PSO-WOA (Xiong et al., 2018), STLBO (Yu et al., 2017), ELPSO (Jordehi, 2018), HFAPS(Beigi and Maroosi, 2018), MLBSA (Yu et al., 2018), TVACPSO (Jordehi, 2016), CPSO (Jordehi, 2016), GA (Jordehi, 2017), CSA (Kang et al., 2018) and ICSA (Kang et al., 2018). The results show that, however, there are other algorithms has the same best RMSE, whereas the proposed optimizer has superiority in achieving minimum AE at the maximum power point. The execution time by all the algorithms is collected as well to highlight all the features of the proposed algorithm. The optimizer has the least execution time.

TABLE 4. The estimated parameters of the SD and DD models of the R.T.C.France cell obtained via the proposed approach and other counterparts.
5.2 Experimental series 2: SLP080 solar module
In this section, the developed method’s performance is tested using a set of twenty-one (V-I) measured pairings for SLP080-12 M module at OAC (G = 1,000 W/m2, and Tamb = 25 °C) (Agwa et al, 2020). The allocated parameters of SDM and DDM by CHBAlg and other techniques are listed in Table 5, with the RMSE value as the major measure for the correctness of the results. In addition, the performance of the determined parameters is assessed by computing the RMSElambert for SDM and DDM models and calculating DiffRMSE). Moreover, for a more detailed study, the absolute error at MPP (AEMPP) is shown in Table 5.

TABLE 5. The determined parameters by the performed optimizers for SDM and DDM of SLP080 solar module.
As demonstrated in Table 5, the RMSE and DiffRMSE of CHBAlg are lower than those of other methods (HBAAlg, RFSOAlg, BMOAlg, EFOAlg, CapSAAlg, AOAlg) for SDM and DDM models. This proves the developed CHBAlg approach’s superiority over other methods by demonstrating its exceptional performance. The AEMPP values of the CHBAlg and HBA show that they are consistent in precisely modeling the PV solar cell. The least RMSE reveals the high accuracy of the identified parameters as the proposed CHBAlg provides the least RMSE; hence it can determine highly accurate results. The average value of the RMSE affirms that the CHBAlg has the highest rank in its reliability as the average RMSE is very close to the best-fetched one. Thereby, the STD of CHBAlg is in the range of 1 × 10–17 and 1 × 10–4, for SDM and DDM, respectively; meanwhile, the HBA and other algorithms have STD in ranges of a × 10–1 and a × 10–3. For the non-parametric statistical analysis, as shown in Table 6, CHBAlg takes the top rank based on the worst, best, median, and average, as seen in the tabular results. Furthermore, it has a higher level of stability than other approaches. Traditional HBAAlg can outperform different algorithms according to the results, and in the best case, it has nearly the same accuracy as CHBAAlg.

TABLE 6. Statistical quantities for the fetched results by CHBAAlg, and other concurrent in case of modeling SDM and DDM models of the SLP080 solar module.
The quality measures of the identified parameters have been measured via drawing the V-I and V-P characteristics, and absolute error curves using the proposed optimizer results and the state of the art as shown in Figures 7, 8 for SDM and DDM, respectively. Moreover, the proposed algorithm convergence speed compared with state-of-the-art and RMSE among the total number of runs, respectively, for SDM and DDM models of SLP080 solar module are displayed in the figures to confirm the certainty of the identified parameters. These curves can be used to draw the following conclusions: The determined parameters using CHBAlg (Viewed as CHBA, for brief) produce a close match between the measured and determined data sets. Figure 7C, Figure 8C show absolute error curves for the SDM and DDM, and it can be noticed that the worst algorithm is AOAlg (Viewed as AO, for brief). However, CHBAlg (Viewed as CHBA, for brief) is the best one. In comparison to the other techniques, CHBAAlg’s (Viewed as CHBA, for brief) mean convergence rate in Figure 7D, Figure 8D is the smallest one, and it is significant. Moreover, from the boxplots of RMSE in Figure 7E, Figure 8E, it can be noticed that CHBAlg (Viewed as CHBA, for brief) is very stable in determining the parameters in the case of SDM and DDM models. Although AOAlg (Viewed as AO, for brief) is the weakest algorithm in both models, BMOAlg and CapSAAlg (Viewed as BMO, CapSA, for brief) come in second and third, respectively.
6 Conclusion and future work
This paper presented a modified version of the Honey Badger Algorithm (HBA) for identifying unknown parameters in PV models with single and double diodes. The proposed method, named chaotic HBA (CHBA), depended on modified HBA using the chaotic 2D Henon map to enhance its ability to find the optimal solution. Under various radiation and temperature settings, the proposed CHBAlg method was tested using two different PV cells/modules: RTC solar cells and SLP080 solar modules.
The accuracy of the developed CHBAlg approach is demonstrated by comparing the acquired findings to well-known state-of-the-art methodologies. The proposed CHBAlg yielded more precise and improved results than the basic HBA in the two situations, with RMSE values of 7.737e-4 and 0.023103 for RTC and SLP080, respectively, in the case of DDM. The RMSE of the CHBA, in the case of SDM, is 7.8398e-4 and 0.023392 for RTC and SLP080, respectively. The consistency of the CHBA’s results was the most notable feature besides the accuracy. As a result, the presented method may be considered a promising search method for identifying the PV models’ unknown parameters in terms of data fitting, precision, and convergence rate. Hence it is evident that the integrated operators with the basic HBA have established their performance and improved the balance between exploration and exploitation.
The proposed method can be applied to various disciplines in the future, such as fuel cells, design issues, machine learning, cloud computing, feature selection, data mining problems, Big Data problems, and other applications.
For the future target, the gradient/Lagrangian-based methods will be integrated for processing the PV modeling optimization problem.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
MA, RA, and MM: Conceptualization, supervision, methodology, formal analysis, resources, data curation, and writing—original draft preparation. LA: Conceptualization, supervision, methodology, formal analysis, resources, data curation, and writing—original draft preparation. OH: Writing—review and editing, project administration, and funding acquisition. SA: Writing—review and editing. DY: data curation, supervision, and writing original draft preparation, methodology, conceptualization, and experimental tests. All authors have read and agreed to the published version of the manuscript.
Funding
Princess Nourah Bint Abdulrahman University Researchers Supporting Project number (PNURSP 2022R197), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abbassi, A., Ben Mehrez, R., Bensalem, Y., Abbassi, R., Kchaou, M., Jemli, M., et al. (2022a). Improved arithmetic optimization algorithm for parameters extraction of photovoltaic solar cell single-diode model. Arab. J. Sci. Eng. 47, 10435–10451. doi:10.1007/s13369-022-06605-y
Abbassi, A., Mehrez, R. B., Touaiti, B., Abualigah, L., and Touti, E. (2022b). Parameterization of photovoltaic solar cell double-diode model based on improved arithmetic optimization algorithm. Optik 253, 168600. doi:10.1016/j.ijleo.2022.168600
Abdel-Basset, M., Mohamed, R., Chakrabortty, R. K., Sallam, K., and Ryan, M. J. (2021). An efficient teaching-learning-based optimization algorithm for parameters identification of photovoltaic models: Analysis and validations. Energy Convers. Manag. 227, 113614. doi:10.1016/j.enconman.2020.113614
Abualigah, L., Abd Elaziz, M., Sumari, P., Geem, Z. W., and Gandomi, A. H. (2021a). Reptile search algorithm (rsa): A nature-inspired meta-heuristic optimizer. Expert Syst. Appl. 191, 116158. doi:10.1016/j.eswa.2021.116158
Abualigah, L., Diabat, A., Mirjalili, S., Abd Elaziz, M., and Gandomi, A. H. (2021b). The arithmetic optimization algorithm. Comput. methods Appl. Mech. Eng. 376, 113609. doi:10.1016/j.cma.2020.113609
Abualigah, L., Yousri, D., Abd Elaziz, M., Ewees, A. A., Al-qaness, M. A., and Gandomi, A. H. (2021c). Aquila optimizer: A novel meta-heuristic optimization algorithm. Comput. Industrial Eng. 157, 107250. doi:10.1016/j.cie.2021.107250
Agushaka, J. O., Ezugwu, A. E., and Abualigah, L. (2022). Dwarf mongoose optimization algorithm. Comput. Methods Appl. Mech. Eng. 391, 114570. doi:10.1016/j.cma.2022.114570
Agwa, A. M., El-Fergany, A. A., and Maksoud, H. A. (2020). Electrical characterization of photovoltaic modules using farmland fertility optimizer. Energy Convers. Manag. 217, 112990. doi:10.1016/j.enconman.2020.112990
Ashraf, H., Abdellatif, S. O., Elkholy, M. M., and El-Fergany, A. A. (2022). Honey badger optimizer for extracting the ungiven parameters of pemfc model: Steady-state assessment. Energy Convers. Manag. 258, 115521. doi:10.1016/j.enconman.2022.115521
Ban, J., Pan, X., and Gu, M. (2021). Electrical characteristics estimation of photovoltaic modules via cuckoo search—Relevant vector machine probabilistic model. Front. Energy Res. 9, 610405. doi:10.3389/fenrg.2021.610405
Barth, N., Jovanovic, R., Ahzi, S., and Khaleel, M. A. (2016). Pv panel single and double diode models: Optimization of the parameters and temperature dependence. Sol. Energy Mater. Sol. Cells 148, 87–98. doi:10.1016/j.solmat.2015.09.003
Beigi, A. M., and Maroosi, A. (2018). Parameter identification for solar cells and module using a hybrid firefly and pattern search algorithms. Sol. Energy 171, 435–446. doi:10.1016/j.solener.2018.06.092
Braik, M., Sheta, A., and Al-Hiary, H. (2021). A novel meta-heuristic search algorithm for solving optimization problems: Capuchin search algorithm. Neural comput. Appl. 33, 2515–2547. doi:10.1007/s00521-020-05145-6
Bucolo, M., Buscarino, A., Fortuna, L., and Gagliano, S. (2022). Multidimensional discrete chaotic maps. Front. Phys. 199, 862376. doi:10.3389/fphy.2022.862376
Ćalasan, M., Aleem, S. H. A., and Zobaa, A. F. (2020). On the root mean square error (rmse) calculation for parameter estimation of photovoltaic models: A novel exact analytical solution based on lambert w function. Energy Convers. Manag. 210, 112716. doi:10.1016/j.enconman.2020.112716
Chenouard, R., and El-Sehiemy, R. A. (2020). An interval branch and bound global optimization algorithm for parameter estimation of three photovoltaic models. Energy Convers. Manag. 205, 112400. doi:10.1016/j.enconman.2019.112400
Chin, V. J., and Salam, Z. (2019). Coyote optimization algorithm for the parameter extraction of photovoltaic cells. Sol. Energy 194, 656–670. doi:10.1016/j.solener.2019.10.093
Chin, V. J., Salam, Z., and Ishaque, K. (2016). An accurate modelling of the two-diode model of pv module using a hybrid solution based on differential evolution. Energy Convers. Manag. 124, 42–50. doi:10.1016/j.enconman.2016.06.076
Chin, V. J., Salam, Z., and Ishaque, K. (2015). Cell modelling and model parameters estimation techniques for photovoltaic simulator application: A review. Appl. Energy 154, 500–519. doi:10.1016/j.apenergy.2015.05.035
Dileep, G., and Singh, S. (2017). Application of soft computing techniques for maximum power point tracking of spv system. Sol. Energy 141, 182–202. doi:10.1016/j.solener.2016.11.034
Eid, A., Kamel, S., and Abualigah, L. (2021). Marine predators algorithm for optimal allocation of active and reactive power resources in distribution networks. Neural comput. Appl. 33, 14327–14355. doi:10.1007/s00521-021-06078-4
Gao, X., Cui, Y., Hu, J., Xu, G., and Yu, Y. (2016). Lambert w-function based exact representation for double diode model of solar cells: Comparison on fitness and parameter extraction. Energy Convers. Manag. 127, 443–460. doi:10.1016/j.enconman.2016.09.005
Gude, S., and Jana, K. C. (2022). A multiagent system based cuckoo search optimization for parameter identification of photovoltaic cell using lambert w-function. Appl. Soft Comput. 120, 108678. doi:10.1016/j.asoc.2022.108678
Hashim, F. A., Houssein, E. H., Hussain, K., Mabrouk, M. S., and Al-Atabany, W. (2022). Honey badger algorithm: New metaheuristic algorithm for solving optimization problems. Math. Comput. Simul. 192, 84–110. doi:10.1016/j.matcom.2021.08.013
Hénon, M. (1976). A two-dimensional mapping with a strange attractor, the theory of chaotic attractors. Berlin, Germany: Springer, 94–102.
Herez, A., Ramadan, M., and Khaled, M. (2018). Review on solar cooker systems: Economic and environmental study for different lebanese scenarios. Renew. Sustain. Energy Rev. 81, 421–432. doi:10.1016/j.rser.2017.08.021
Humada, A. M., Hojabri, M., Mekhilef, S., and Hamada, H. M. (2016). Solar cell parameters extraction based on single and double-diode models: A review. Renew. Sustain. Energy Rev. 56, 494–509. doi:10.1016/j.rser.2015.11.051
Ibrahim, I. A., Hossain, M., Duck, B. C., and Fell, C. J. (2019). An adaptive wind-driven optimization algorithm for extracting the parameters of a single-diode pv cell model. IEEE Trans. Sustain. Energy 11, 1054–1066. doi:10.1109/tste.2019.2917513
Jordehi, A. R. (2018). Enhanced leader particle swarm optimisation (elpso): An efficient algorithm for parameter estimation of photovoltaic (pv) cells and modules. Sol. Energy 159, 78–87. doi:10.1016/j.solener.2017.10.063
Jordehi, A. R. (2017). “Gravitational search algorithm with linearly decreasing gravitational constant for parameter estimation of photovoltaic cells,” in 2017 IEEE Congress on Evolutionary Computation (CEC), Donostia, Spain, 05-08 June 2017 (IEEE), 37–42.
Jordehi, A. R. (2016). Time varying acceleration coefficients particle swarm optimisation (tvacpso): A new optimisation algorithm for estimating parameters of pv cells and modules. Energy Convers. Manag. 129, 262–274. doi:10.1016/j.enconman.2016.09.085
Kang, T., Yao, J., Jin, M., Yang, S., and Duong, T. (2018). A novel improved cuckoo search algorithm for parameter estimation of photovoltaic (pv) models. Energies 11, 1060. doi:10.3390/en11051060
Kermadi, M., Chin, V. J., Mekhilef, S., and Salam, Z. (2020). A fast and accurate generalized analytical approach for pv arrays modeling under partial shading conditions. Sol. Energy 208, 753–765. doi:10.1016/j.solener.2020.07.077
Kumar, C., Raj, T. D., Premkumar, M., and Raj, T. D. (2020). A new stochastic slime mould optimization algorithm for the estimation of solar photovoltaic cell parameters. Optik 223, 165277. doi:10.1016/j.ijleo.2020.165277
Li, D., Yang, B., Li, L., Li, Q., Deng, J., and Guo, C. (2022). Recent photovoltaic cell parameter identification approaches: A critical note. Front. Energy Res. 487, 902749. doi:10.3389/fenrg.2022.902749
Liang, J., Ge, S., Qu, B., Yu, K., Liu, F., Yang, H., et al. (2020). Classified perturbation mutation based particle swarm optimization algorithm for parameters extraction of photovoltaic models. Energy Convers. Manag. 203, 112138. doi:10.1016/j.enconman.2019.112138
Mekhilef, S., Saidur, R., and Safari, A. (2011). A review on solar energy use in industries. Renew. Sustain. energy Rev. 15, 1777–1790. doi:10.1016/j.rser.2010.12.018
Oliva, D., El Aziz, M. A., and Hassanien, A. E. (2017). Parameter estimation of photovoltaic cells using an improved chaotic whale optimization algorithm. Appl. Energy 200, 141–154. doi:10.1016/j.apenergy.2017.05.029
Oyelade, O. N., Ezugwu, A. E., Mohamed, T. I., and Abualigah, L. (2022). Ebola optimization search algorithm: A new nature-inspired metaheuristic optimization algorithm. IEEE Access 10, 16150–16177. doi:10.1109/access.2022.3147821
Połap, D., and Woźniak, M. (2021). Red fox optimization algorithm. Expert Syst. Appl. 166, 114107. doi:10.1016/j.eswa.2020.114107
Pourmousa, N., Ebrahimi, S. M., Malekzadeh, M., and Alizadeh, M. (2019). Parameter estimation of photovoltaic cells using improved lozi map based chaotic optimization algorithm. Sol. Energy 180, 180–191. doi:10.1016/j.solener.2019.01.026
Qais, M. H., Hasanien, H. M., and Alghuwainem, S. (2019). Identification of electrical parameters for three-diode photovoltaic model using analytical and sunflower optimization algorithm. Appl. Energy 250, 109–117. doi:10.1016/j.apenergy.2019.05.013
Ridha, H. M., Hizam, H., Mirjalili, S., Othman, M. L., Ya’acob, M. E., and Abualigah, L. (2022a). A novel theoretical and practical methodology for extracting the parameters of the single and double diode photovoltaic models. IEEE Access 10, 11110–11137. doi:10.1109/access.2022.3142779
Ridha, H. M., Hizam, H., Mirjalili, S., Othman, M. L., Ya’acob, M. E., Ahmadipour, M., et al. (2022c). On the problem formulation for parameter extraction of the photovoltaic model: Novel integration of hybrid evolutionary algorithm and levenberg marquardt based on adaptive damping parameter formula. Energy Convers. Manag. 256, 115403. doi:10.1016/j.enconman.2022.115403
Ridha, H. M., Hizam, H., Mirjalili, S., Othman, M. L., Ya’acob, M. E., and Ahmadipour, M. (2022b). Parameter extraction of single, double, and three diodes photovoltaic model based on guaranteed convergence arithmetic optimization algorithm and modified third order Newton raphson methods. Renew. Sustain. Energy Rev. 162, 112436. doi:10.1016/j.rser.2022.112436
Ridha, H. M. (2020). Parameters extraction of single and double diodes photovoltaic models using marine predators algorithm and lambert w function. Sol. Energy 209, 674–693. doi:10.1016/j.solener.2020.09.047
Siecker, J., Kusakana, K., and Numbi, e. B. (2017). A review of solar photovoltaic systems cooling technologies. Renew. Sustain. Energy Rev. 79, 192–203. doi:10.1016/j.rser.2017.05.053
Song, B., and Ding, Q. (2014). Comparisons of typical discrete logistic map and henon map in Intelligent Data analysis and its Applications. Berlin, Germany: Springer, 267–275.
Sulaiman, M. H., Mustaffa, Z., Saari, M. M., and Daniyal, H. (2020). Barnacles mating optimizer: A new bio-inspired algorithm for solving engineering optimization problems. Eng. Appl. Artif. Intell. 87, 103330. doi:10.1016/j.engappai.2019.103330
Sun, L., Wang, J., and Tang, L. (2021). A powerful bio-inspired optimization algorithm based pv cells diode models parameter estimation. Front. Energy Res. 9, 675925. doi:10.3389/fenrg.2021.675925
Xiong, G., Zhang, J., Shi, D., and He, Y. (2018). Parameter extraction of solar photovoltaic models using an improved whale optimization algorithm. Energy Convers. Manag. 174, 388–405. doi:10.1016/j.enconman.2018.08.053
Yan, Z., Li, C., Song, Z., Xiong, L., and Luo, C. (2019). An improved brain storming optimization algorithm for estimating parameters of photovoltaic models. IEEE Access 7, 77629–77641. doi:10.1109/access.2019.2922327
Yilmaz, S., and Sen, S. (2020). Electric fish optimization: A new heuristic algorithm inspired by electrolocation. Neural comput. Appl. 32, 11543–11578. doi:10.1007/s00521-019-04641-8
Yousri, D., Abd Elaziz, M., Oliva, D., Abualigah, L., Al-qaness, M. A., and Ewees, A. A. (2020a). Reliable applied objective for identifying simple and detailed photovoltaic models using modern metaheuristics: Comparative study. Energy Convers. Manag. 223, 113279. doi:10.1016/j.enconman.2020.113279
Yousri, D., Allam, D., and Eteiba, M. (2019a). Chaotic whale optimizer variants for parameters estimation of the chaotic behavior in permanent magnet synchronous motor. Appl. Soft Comput. 74, 479–503. doi:10.1016/j.asoc.2018.10.032
Yousri, D., Allam, D., Eteiba, M., and Suganthan, P. N. (2019b). Static and dynamic photovoltaic models’ parameters identification using chaotic heterogeneous comprehensive learning particle swarm optimizer variants. Energy Convers. Manag. 182, 546–563. doi:10.1016/j.enconman.2018.12.022
Yousri, D., Babu, T. S., Allam, D., Ramachandaramurthy, V., Beshr, E., Eteiba, M., et al. (2019c). Fractional chaos maps with flower pollination algorithm for partial shading mitigation of photovoltaic systems. Energies 12, 3548. doi:10.3390/en12183548
Yousri, D., Fathy, A., Rezk, H., Babu, T. S., and Berber, M. R. (2021). A reliable approach for modeling the photovoltaic system under partial shading conditions using three diode model and hybrid marine predators-slime mould algorithm. Energy Convers. Manag. 243, 114269. doi:10.1016/j.enconman.2021.114269
Yousri, D., Shaker, Y., Mirjalili, S., and Allam, D. (2022). An efficient photovoltaic modeling using an adaptive fractional-order archimedes optimization algorithm: Validation with partial shading conditions. Sol. Energy 236, 26–50. doi:10.1016/j.solener.2021.12.063
Yousri, D., Thanikanti, S. B., Allam, D., Ramachandaramurthy, V. K., and Eteiba, M. (2020b). Fractional chaotic ensemble particle swarm optimizer for identifying the single, double, and three diode photovoltaic models’ parameters. Energy 195, 116979. doi:10.1016/j.energy.2020.116979
Yu, K., Chen, X., Wang, X., and Wang, Z. (2017). Parameters identification of photovoltaic models using self-adaptive teaching-learning-based optimization. Energy Convers. Manag. 145, 233–246. doi:10.1016/j.enconman.2017.04.054
Yu, K., Liang, J., Qu, B., Cheng, Z., and Wang, H. (2018). Multiple learning backtracking search algorithm for estimating parameters of photovoltaic models. Appl. energy 226, 408–422. doi:10.1016/j.apenergy.2018.06.010
Keywords: PV parameters estimation, honey badger algorithm, chaotic Henon map, single diode circuit, double diode circuit PV cell, PV characteristics assessment
Citation: Almodfer R, Mudhsh M, Alshathri S, Yousri D, Abualigah L, Hassan OF and Abd Elaziz M (2022) Chaotic honey badger algorithm for single and double photovoltaic cell/module. Front. Energy Res. 10:1011887. doi: 10.3389/fenrg.2022.1011887
Received: 04 August 2022; Accepted: 31 October 2022;
Published: 12 December 2022.
Edited by:
K. Sudhakar, Universiti Malaysia Pahang, MalaysiaReviewed by:
Martin P. Calasan, University of Montenegro, MontenegroRamani Kannan, University of Technology Petronas, Malaysia
Copyright © 2022 Almodfer, Mudhsh, Alshathri, Yousri, Abualigah, Hassan and Abd Elaziz. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Samah Alshathri, c2VhbHNoYXRocnlAcG51LmVkdS5zYQ==; Mohamed Abd Elaziz, YWJkX2VsX2F6aXpfbUB5YWhvby5jb20=
 Rolla Almodfer
Rolla Almodfer Mohammed Mudhsh
Mohammed Mudhsh Samah Alshathri
Samah Alshathri Dalia Yousri
Dalia Yousri Laith Abualigah
Laith Abualigah Osama Farouk Hassan8
Osama Farouk Hassan8 Mohamed Abd Elaziz
Mohamed Abd Elaziz