
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Energy Res. , 10 January 2023
Sec. Solar Energy
Volume 10 - 2022 | https://doi.org/10.3389/fenrg.2022.1010745
With the development of renewable energy, the exploitation and utilization of solar energy resources also need continuous progress, but solar radiation data shortage has become a serious concern. A method for estimating global solar radiation has been developed to address this issue. The sunshine-based model is currently the most widely used model due to its high calculation accuracy and few input parameters. This paper will first review 13 subcategories (8 categories in total) of the global solar radiation prediction model based on sunshine. Subsequently, the astronomical factors were introduced to modify empirical coefficients, and 8 new categories of models based on sunshine rate were introduced. The radiation data from 83 meteorological stations in China was used to train and validate the model, and the performance of the model was evaluated by using evaluation indicators, such as coefficient of determination (R2), root mean square error (RMSE), mean absolute bias error (MABE), mean bias error (MBE), and global performance index (GPI). The results show that the R2 value of the unmodified empirical model is in a range of 0.82–0.99, and the RMSE value is in a range of 0.018–3.09. In contrast, with the introduction of the astronomical factor, the model accuracy improves significantly, and the modified power function model (N3) gains its best performance. The R2 of model N3 is in a range of 0.86–0.99, and the RMSE value is in a range of 0.018–2.62. The R2 increases by 0.49%, while the RMSE value 6.44%. Above all, it does not require the input of other meteorological parameters for predicting the value of global solar radiation.
Solar radiation is the source of energy for the movements of the earth’s atmosphere and the causes of all physical phenomena in the atmosphere. Meanwhile, solar radiation is also the main energy source of the earth’s ecosystem and has a significant impact on the development of solar equipment (Sen, 2008). With the continuing depletion of fossil fuels and the aggravation of environmental pollution, the use of renewable energy is becoming important. Therefore, the research and utilization of solar radiation must be expanded (Zhou et al., 2021a). Yet, few ground radiation observation stations have been built in China due to the high costs of solar radiation observation equipment and their maintenance. There are more than 2,000 meteorological data stations in China, but only 122 ground radiation observation stations are found across the country (Chen and Li, 2013). China has a vast land area with various terrains, and the distribution of global solar radiation value varies greatly. Therefore, the observational data from the current stations are insufficient to predict the solar radiation values of other regions.
The commonly used solar radiation prediction methods can be divided into empirical models and data-driven models (Zhou et al., 2021b). Among them, the machine learning model has been widely used to predict solar radiation (Bounoua et al., 2021), and its prediction results are accurate. However, the amount of calculation is large and the calculation process is complicated, making it impossible to predict the radiation data of large-scale stations. The empirical model has become one of the most widely used ones to predict daily global solar radiation due to its relatively high computational accuracy and efficient computational capacity. Hence, it is particularly suitable for large-scale solar radiation calculation tasks (Ustun et al., 2020). Empirical models can be divided into four types according to their input parameters, which include models based on sunshine, temperature, cloud cover, and other meteorological parameters (Mohammadi et al., 2016). The sunshine-based model was the first to be developed among the four types of models. Later, the model based on average daily temperature (Ta) (Sheik and Rao, 2021), cloud cover (CC) (Yakoubi et al., 2021), and other meteorological parameters was developed to improve accuracy (Naserpour et al., 2021). The input of multiple meteorological parameters improves the prediction accuracy of the model, but at the cost of the model’s complexity (Okundamiya and Emagbetere, 2016). Oyewola et al. (2022) evaluated three groups of 20 models based on sunshine duration, temperature and relative humidity. The results show that the mixed model of temperature and relative humidity has the best prediction accuracy. Quansah et al. (2014) evaluated the performance of various models for estimating global solar radiation in Ghana and other tropical regions, and found that models using S and Ta parameters had the smallest values of MBE, MPE, and RMSE. Benamrou et al. (2018) evaluated 10 prediction models of global solar radiation for sunshine duration and temperature, as well as a newly proposed functional model of Fourier series. The results show that the proposed model is more accurate with smaller errors and the best coefficient of determination.
Several new combination models based on sunshine rate by introducing other meteorological parameters have been developed (Ta, relative humidity (RH), CC, atmospheric vapor pressure (Vp), etc.) (Chen et al., 2006b). Falayi et al. (2008) proposed a mixed model of the sunshine rate, RH, Ta, maximum daily temperature (Tmax) and minimum daily temperature (Tmin). Chen and Li (2013) established several models combining sunshine rate, Ta, Vp, RH, and precipitation (Pt). The result showed that when the sunshine duration (S) is available, the introduction of daily average Vp, RH, Pt, and other parameters contributes little to the accuracy of model. The accuracy of the combined model, after the introduction of Ta, has barely improved. Okundamiya and Emagbetere (2016) established a combined model with sunshine rate, Ta, and CC. The model prediction accuracy was better, and the R2 value increased. On the one hand, these models require more input parameters, which significantly increases the difficulty of data acquisition. However, when compared with the sunshine-based model, the accuracy of these models is limited and does not have a significant advantage.
Although different models have advanced significantly, the sunshine-based model has a clear advantage in terms of accuracy and the difficulty of obtaining meteorological parameters. One of the important directions for future large-scale solar radiation prediction tasks is to improve the accuracy of the sunshine-based model without increasing the meteorological parameters (that is, without increasing the difficulty of obtaining meteorological data). Therefore, some researchers proposed to use meteorological factors (including latitude (
This paper reviews more than 100 articles on empirical models for predicting global solar radiation from 1957 to 2021 and divides the models into 13 subcategories (8 categories in total). Based on this, 8 new categories of models have been introduced to explain astronomical factors. By using the radiation data between 1980 and 2016 from 83 meteorological stations in China, we analyzed and studied the global daily solar radiation in different climate zones. The 21 categories of models were trained and validated, and the best model was determined by comparing the evaluation indicators, such as R2, RMSE, MBE, MABE, and GPI, providing guidance to select the best solar radiation prediction model for a specific region. The conclusion showed that from the perspective of GPI indicators, the power function model with astronomical factors has the highest accuracy, good stability, and best overall performance in different climate regions of China. Therefore, the power function model with astronomical factors can forecast global daily solar radiation.
As for the sunshine-based model, its S measurement is accurate, the data it collects is reliable, and it is easier to compare its meteorological parameters with those of others. Moreover, various studies have shown that S has the highest correlation with the value of solar radiation, so the accuracy of global solar radiation based on the sunshine-based model is higher (Nwokolo and Ogbulezie, 2017). Angstrom (1924) was the first to put forward the linear relationship between the ratio of solar radiation to global radiation for clear days and the sunshine rate, and he also established the first monthly average daily global solar radiation calculation model. Prescott (1940) then modified Angstrom’s model by replacing clear-sky radiation with average daily extraterrestrial radiation on a horizontal surface and got a new computational model, which is known as the Angstrom-Prescott model. Garg and Garg (1985) developed linear equations by using the data from eleven stations in India. The equation predicts global solar radiation to an accuracy of 0.5%. Bahel et al. (1986) calculated the monthly average daily global radiation from May 1979 to July 1985 in Dhahran city and established the following model, with its prediction error being lower than 7.5%.
Ogelman et al. (1984) developed the quadratic model equation by fitting the radiation data from Adana and Ankara, Turkey and using the S data from Adana between 1979 and 1981 and Ankara between 1977 and 1981. The predicted data were then compared with the actual measured data, showing that it had a mean absolute relative error of 4.1%. Akinoglu and Ecevit (1990) established a quadratic model that has better performance in predicting global solar radiation. Togrul et al. (2000a) used the data of the Elazig weather station in Turkey to establish the relationship between sunshine rate and the coefficients a and b, and obtained the best results for the linear and logarithmic equations. Almorox and Hontoria (2004) established linear, quadratic, cubic, logarithmic and exponential equations using data from 16 weather stations in Spain, and found that the cubic model had better performance. Katiyar and Pandey (2010) used 5 years data of India to obtain relevant models for four cities. The results show that compared with the linear model, the accuracy of the quadratic and cubic models has not been significantly improved, and the calculation difficulty has increased. Duzen and Aydin (2012) obtained data from seven weather stations in Turkey and evaluated linear, quadratic, cubic, logarithmic, and exponential models. The conclusion is: The cubic and quadratic regression models are the most suitable regression equations.
Assi and Jama (2010) established the linear, quadratic, cubic, single term exponential, logarithmic, linear logarithmic, and power models for Abu Dhabi and Al Ain. The results show that linear and cubic models perform best in the region. Sekhar et al. (2013) obtained linear and quadratic models by using weather data from different cities in Andhra Pradesh, India, and the results showed that the quadratic model is better than the linear model. Suthar et al. (2014) established linear and quadratic models to estimate the global daily solar radiation in India, and the results showed that the quadratic model was more effective. M. Ozturk (2015) established linear, quadratic, cubic, and power function models for Isparta, Turkey, and the cubic model predicted the best results. Liu et al. (2016) established linear, quadratic, and cubic equations for Zhengzhou, China by using the data between January 1995 and December 2004, and the cubic model predicted better results than other models. Ishola et al. (2019) modified the various model coefficients for Ireland, and the results show that the quadratic model works best.
Ampratwum and Dorvlo (1999) established linear, quadratic, logarithmic, and linear-logarithmic model equations. The estimated results of the quadratic model and the linear logarithmic model were better than that of the logarithmic model, but the logarithmic model was simpler and its error was not significantly higher than that of the quadratic model. Exponential and linear exponential models were newly proposed by Bakirci (2009), and they were compared with other empirical equations. The linear-log and linear-exponential models generally give the best results, while the log and exponential models perform worse than the other models. Pant et al. (2019) built quadratic, cubic, logarithmic, linear-logarithmic models to estimate global solar radiation, and the cubic model was the best of all. Akpootu et al. (2019) evaluated the model and found that exponential and linear exponential models were more suitable for estimating global solar radiation. Nadjem et al. (2020) study found that the best model for estimating global solar radiation in southwestern Algeria was a linear exponential model.
Elagib and Mansell (2000) used the data gathered from 16 stations in four different climatic zones in Sudan to establish several new models. The results show that adding geographic parameters to the classical predictors improves global solar radiation estimation. Siva Krishna Rao et al. (2018) used the solar radiation data measured in India from August 2015 to July 2016 to build various models. The results show that the model with the input latitude parameter produces more accurate results. Rensheng et al. (2006) corrected the linear and cubic models by using factors such as longitude, latitude, and altitude. The results show that the latitude can effectively improve the accuracy of the model, and the cos
Researchers have done a lot of research on empirical models and proposed models based on different parameters such as S, Ta, and CC. However, due to the advantages of the simple acquisition of sunshine data, less computation, and high model accuracy, the empirical model based on sunshine duration is still the most widely used empirical model. And a large number of studies have shown that the introduction of other meteorological parameters on the basis of the sunshine model can improve the accuracy of the model, but the performance is not obvious. Because of the multi-parameter input, it is difficult to obtain meteorological data, and the complexity of the model also increases. How to use the least meteorological parameters and improve the accuracy of the model is one of the focuses of the research. On the basis of the sunshine-based model, the introduction of known parameters such as astronomy and geography to improve the accuracy of the model is lacking in current research.
According to the above model introduction, the current empirical models based on sunshine rate can be divided into the following 13 categories. They have been reviewed, and the review results are summarized in Table 1. The detailed introduction of the model is shown in the Supplementary Material.
The research data in this paper is from the daily radiation data dataset of the National Meteorological Data Sharing Center of China and the daily dataset of China’s surface climate data of the National Scientific Meteorological Data Center. The covering period is between 1981 and 2016 while the period records varied from 6 to 35 years. Data includes Daily global radiation on a horizontal surface (H), Daily sunshine duration (S), Ta, Tmax, Tmin, daily maximum pressure, daily minimum pressure, daily average pressure, etc. The theory is used to calculate Maximum possible daily sunshine duration (S0) and extraterrestrial radiation on a horizontal surface (H0) values. The data set is divided into two parts. Two-thirds of them are used for model training, and the rest of them are used for model testing.
Radiation data may have abnormal values due to random errors and instrument errors, which may easily lead to large errors in global radiation calculation. Therefore, the quality of radiation data must be ensured. The data quality control process is as follows: 1) Missing data. If a piece of data is missing, delete it along with all data of that day; 2) If the H is greater than H0 or less than 0.03 time of H0, then remove all data for that day.
China has a vast land expanse from east to west, so it has different climates in different areas. Based on the data of 660 meteorological stations, Liu et al. (2017) proposed a two-step solar radiation zoning method based on support vector machines and k-means clustering, dividing the whole country into five climate zones: zone I: strong radiation and semi-arid zone; zone II: long-sun and arid zone; zone III: semi-humid zone; zone IV: humid zone; zone V: high-humidity and low-sun zone. This paper analyzes the data of 83 meteorological stations in China. Then, according to the climatic zone of each station, the evaluation indicators of each model in different climatic zones are statistically analyzed (Figure 1).
Liu et al. (2015) analyzed the changing rules of the empirical coefficient of the A-P model and found that the coefficient value changes dynamically. This paper firstly takes Mohe data as an example, calculates the empirical coefficients a, b of the A-P model of the site in 1 year, and plots the results in Figures 2, 3. It can be seen from the figure that the empirical coefficients a and b of this site change in a trigonometric function, with the characteristics of fluctuation, which is similar to the change law of astronomical factors. This paper proposes a hypothesis to modify the empirical coefficient of the model to make it more in line with the actual change law, no matter whether it affects the improvement of the model accuracy or not. Therefore, this paper introduces the declination angle to dynamically correct the empirical coefficient of the A-P model, that is, the coefficient a in the original empirical model is corrected to a0+a1sinδ, and the coefficient b is corrected to b0+b1sinδ. Similarly, this process is extended to other models, and 8 new models as shown in Table 2 are proposed.
In this paper, the least square method (Zhou et al., 2019) was used to calculate the model coefficients. The mathematical principles of the least square method are as follows: given a set of data
Minimize the value of Eq. 1, solve the coefficient
The equation of the coefficient matrix A is as follows:
This paper compares the new model with the original one and computes the results by using the least square fitting method. All models are evaluated by using various indicators, and the most suitable model equations for various climate regions in China are obtained. This paper uses the R2, RMSE, MABE, MBE, and GPI methods for data evaluation. The calculation methods are as follows:
(1) determination coefficient
(2) root mean square error
(3) mean absolute bias error
(4) mean bias error
(5) global performance index
Where
R2 is the ratio of the regression sum of squares to the total sum of squares. The model’s performance improves as R2 gets closer to 1. The degree of dispersion between the calculated and measured values is represented by the RMSE, which is always greater than 0, and the smaller the value, the better the result. MABE is a statistic that describes the degree of data dispersion, which can be used to better reflect the actual situation of the predicted error. The smaller the value, the better the result. Models with higher accuracy have higher GPI values.
In this paper, the least squares method is used to fit the solar radiation data of 83 stations under 21 equations, and various evaluation indicators are obtained. The boxplots of each indicator under 21 equations are drawn, and the different results of each indicator in 5 radiation zones, as well as the graphs of the global performance indicators, are also drawn.
As can be seen from the Figure 4, the values of R2, RMSE, MABE, and MBE for these models range from 0.82 to 0.99, 0.018–3.09 MJm−2d−1, 0.014–1.74 MJm−2d−1, −0.71–1.31 MJm−2d−1, the average values are 0.97, 1.34 MJm−2d−1, 0.67 MJm−2d−1, −0.028 MJm−2d−1. Among them, the model S7 and N4 have poorer performances, and the values of the evaluation indicators of the model S7 are all the last digits in each model. The S7 model is in the form of a power function, so it can be seen that the empirical equation in the form of a power function is used to estimate the total solar radiation with poor results. The N4 model is a 1.5th power function model after the correction of the empirical coefficient, and the result is not good. Except for the N4 model, the prediction accuracy of the rest of the new models, after the correction of the empirical coefficients, has improved. Therefore, for the traditional empirical models, the use of the declination angle δ to correct the empirical coefficients can effectively improve the model accuracy.
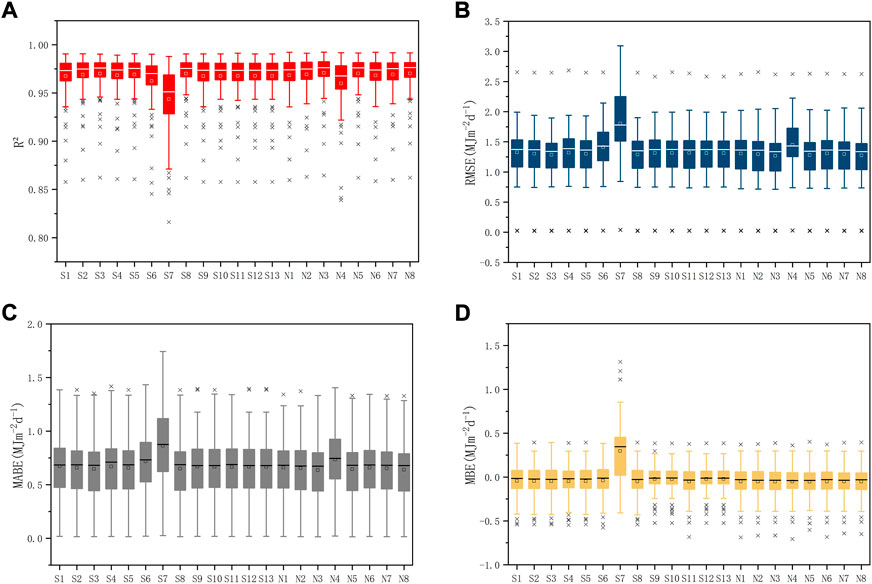
FIGURE 4. Boxplots of evaluation indicators for each model. (A)Boxplots for each model R2; (B)Boxplots for each model RMSE; (C)Boxplots for each model MABE; (D)Boxplots for each model MBE.
Among all the models, the N3 model in the new model has the best performance. The R2, RMSE, MABE, MBE values of this model range from 0.86 to −0.99, 0.018–2.62 MJm−2d−1, 0.014–1.33 MJm−2d−1, −0.67–0.39 MJm−2d−1. The N3 model is a power function model after correcting the empirical coefficients. Compared with the S8 model, it can be seen that the accuracy of the exponential model including the constant term, after the correction of the declination angle δ, has improved. Compared with the N4 model, it can be seen that limiting the exponential value of the exponential model will reduce the prediction accuracy of the model. Different from the value improvements of the uncorrected individual models, the R2 value improvement ranges from 0.076% to 2.89%, and the RMSE value reduction is between 1.36% and 29.8%.
When model S7 is used to predict the H, if it is under cloudy conditions, S equals zero, and the predicted H by the model is also zero. However, in fact, the H must be greater than zero. Therefore, the prediction accuracy of S7 is limited. It can be only used to predict the H on clear days, and it is not applicable in cloudy conditions. As for the yearly H, it produces poor results. In terms of model N4, due to the influence of aerosol concentration and other factors, the variation law between the H and the S of each station is not a definite value. Therefore, the deterministic coefficients of the model reduce the prediction accuracy of the model. As for N3, the constant term of the model is not zero, and it also has the fluctuating characteristics of coefficient changes, which is suitable for prediction under various climatic conditions. The coefficients in N3 can be changed with the change of the station data, which improves the flexibility of the model and makes its prediction result the best among all the models.
It can be seen from Figure 5 that for all models in different partitions, the indicators R2, RMSE, and MABE have the best performance in zone II, and their ranges are 0.95–0.99, 0.72–2.06 MJm−2d−1, and 0.27–1.01 MJm−2d−1 respectively. Zone V has the worst performance, with the ranges of 0.85–0.98, 0.018–3.09 MJm−2d−1, and 0.014–1.74 MJm−2d−1, respectively. For the indicator MBE, the performance of zone I is the best, and its range is −0.41–0.44 MJm−2d−1, and the performance of zone III is the worst, and its range is −0.53–0.71 MJm−2d−1. The newly-built model N3 has the best evaluation performance in each region, while the R2 evaluation model ranks second in Zone I and first in the remaining regions. The average values of R2 are 0.97, 0.98, 0.97, 0.97, and 0.95 in the I-V zones, respectively. The average values of RMSE of I–V zones are 1.44 MJm−2d−1, 1.18 MJm−2d−1, 1.23 MJm−2d−1, 1.27 MJm−2d−1, and 1.34 MJm−2d−1 respectively. The average MABE values of I-V zones are 0.71 MJm−2d−1, 0.56 MJm−2d−1, 0.63 MJm−2d−1, 0.65 MJm−2d−1, and 0.69 MJm−2d−1, and the mean values of MBE are −0.027 MJm−2d−1, −0.063 MJm−2d−1, −0.087 MJm−2d−1, −0.045 MJm−2d−1, and 0.016 MJm−2d−1 respectively. Model S7 has the worst adaptation performance of each evaluation index in the five climatic zones. The average R2 and RMSE values in each zone are 0.96, 0.97, 0.94, 0.93, and 0.90, and 1.86 MJm−2d−1, 1.52 MJm−2d−1, 1.77 MJm−2d−1, 1.96 MJm−2d−1, and 2.13 MJm−2d−1, respectively. The average MABE values of I-V zones are 0.88 MJm−2d−1, 0.70 MJm−2d−1, 0.86 MJm−2d−1, 0.94 MJm−2d−1, and 1.07 MJm−2d−1, and the mean values of MBE are 0.13 MJm−2d−1, 0.11 MJm−2d−1, 0.26 MJm−2d−1, 0.46 MJm−2d−1, and 0.71 MJm−2d−1, respectively.
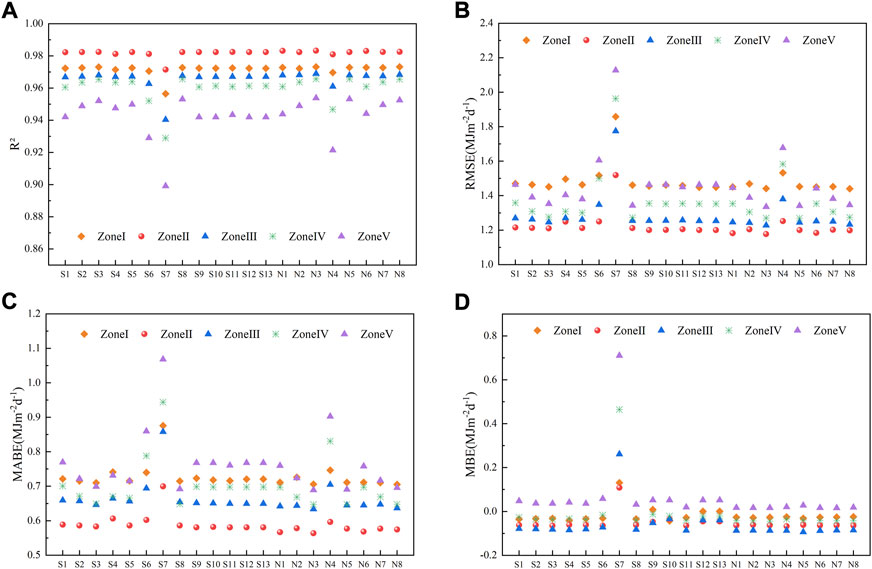
FIGURE 5. The average evaluation index of the models in each climate zone. (A) R2 values of different models in each climate zone; (B) RMSE values of different models in each climate zone; (C) MABE values of different models in each climate zone; (D) MBE values of different models in each climate zone.
Comprehensive analysis. The performance of all models in zone II is generally higher than those in other regions, and their performance in zone V is the worst. Figure 6 shows the distribution of H in Naqu over 37 years. Naqu belongs to zone I (high radiation zone). The reason that the radiation in zone I is high is due to the high atmospheric transparency. As a result, the H on clear and cloudy days varies greatly, as shown in Figure 6, and the distribution of H is much more discrete. Therefore, the prediction accuracy of models decreases. In comparison, zone II belongs to the long sunshine duration zone. The reason why the radiation in zone II is high is because of the long sunshine duration. Take Altay as an example. Figure 7 shows H distribution. It is can be easily found that the distribution of H is much more concentrated. Therefore, the prediction accuracy of the model in zone II is the best. The difference in solar radiation between clear and cloudy conditions is large. We can see from the figure that the distribution of global solar radiation values is more discrete, resulting in the accuracy of each prediction model being lower than that of the stations in zone II. Area II has a long-day and arid area with enough solar radiation and long sunshine duration, and the environment is less affected by other meteorological conditions. As can be seen from Figure 7, the global solar radiation value at the Altay site is more concentrated, so the performance of each model in this zone is the best. Zone V has high humidity and a low solar radiation area. Precipitation, cloud cover, and other factors influence the relationship between global solar radiation and sunshine rate, so each model’s performance in zone V is the worst.
This paper uses four evaluation indicators, but the comprehensive performance of the model cannot be judged by a single evaluation indicator. Therefore, the GPI value is used to rank the model. It can be seen from Figure 8 that model N3 has the best performance with a GPI value of 1.75; model S7 has the worst performance with a GPI value of −49.98. The comprehensive evaluation results are consistent with the above model analysis and regional evaluation results.
This article reviews more than 100 papers on prediction models of global solar radiation based on sunshine rate. By introducing the astronomical factors to modify the empirical coefficients, eight new categories of daily global solar radiation models have been proposed. The radiation data from 83 meteorological stations in China is used to train and validate models of 21 categories. The main conclusions of this study are as follows:
(1) Although different combined models have been developed, the model performances have not improved that much. Furthermore, the difficulties of the acquisition of required meteorological data have increased sharply. Therefore, the sunshine-based models should be the best model for global solar radiation prediction, which yields higher accuracy and less meteorological data.
(2) The power function model with declination angle outperforms all other models. The R2 value is the highest in long-sunshine and arid areas (∼0.98), and the smallest in high-humidity areas (∼0.95). The average value of RMSE is in a range of 1.15–1.44 MJm−2d−1. The maximum and minimum average values of MABE are 0.71 MJm−2d−1 and 0.54 MJm−2d−1 respectively. The minimum and maximum MBE values are -0.091 MJm−2d−1 and—0.027 MJm−2d−1 respectively.
(3) A method is proposed to modify the empirical models by using astronomical factors. The modified models improve R2 by 0.076%–2.89%, and the RMSE value decreases by 1.36%–29.8%, allowing it to predict the more accurate value of daily global solar radiation.
To improve the accuracy of sunshine-based models, this paper introduces the astronomical factor to modify the empirical coefficient, but the changes of empirical coefficients in other kinds of models have not been discussed yet. In the future research, more models will be discussed, such as temperature-based models. Concurrently, this paper only focuses on the influence of the sun’s declination angle. In fact, more astronomical, meteorological, and geographical parameters should be covered, such as the day of the year.
All authors contributed to this work. Methodology, KL and LW; software, LW and YZ; investigation, KL, ZZ, and SF; resources, KL; writing—original draft preparation, LW; writing—review and editing, YZ; supervision, SF and PC All authors have read and agreed to the published version of the manuscript.
This research was funded by the National Natural Science Foundation of China (Nos. 52208033, 52108091), the Shaanxi Province’s 2021 Innovation Capability Support Plan (Project Nos. 2021KRM 100), the Special Scientific Research Plan Project of Shaanxi Provincial Department of Education (Project Nos. 21JK0288), the Key Science and Technology Innovation Team of Shaanxi Province (2022TD-34), the Xi’an Shiyou University Youth Research Innovation Team ConstructionProject (Project Nos. 2019QNKYCXTD22), China Postdoctoral Science Foundation Project (No. 2020M683431) and Natural Science Basic Research Program of Shaanxi Province (Project Nos. 2020JQ-080).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2022.1010745/full#supplementary-material
a, b, c, d, e, Regression coefficients; H, Daily global radiation on a horizontal surface (MJm−2d−1); H0, Extraterrestrial radiation on a horizontal surface (MJm−2d−1); h, Altitude (m); S, Daily sunshine duration (h); S0, CC Maximum possible daily sunshine duration (h) Cloud cover; Ta, Average daily temperature; Tmax, maximum daily temperature; Tmin, minimum daily temperature; Vp, Atmospheric vapor pressure; Pt, Precipitation; RH, Relative humidity; R2, Coefficient of determination; RMSE, Root mean square error (MJm−2d−1); MABE, Mean absolute bias error (MJm−2d−1); MBE, Mean bias error (MJm−2d−1); MPE, Mean percentage error; MRE, Mean relative error; GPI, Global performance index;
Achour, L., Bouharkat, M., Assas, O., and Behar, O. (2017). Hybrid model for estimating monthly global solar radiation for the southern of Algeria: (Case study: Tamanrasset, Algeria). Energy 135, 526–539. doi:10.1016/j.energy.2017.06.155
Adeala, A. A., Huan, Z., and Enweremadu, C. C. (2016). Evaluation of global solar radiation using multiple weather parameters as predictors for South Africa provinces. Therm. Sci. 19, 495–509. doi:10.2298/tsci130714072a
Ajayi, O. O., Ohijeagbon, O. D., Nwadialo, C. E., and Olasope, O. (2014). New model to estimate daily global solar radiation over Nigeria. Sustain. Energy Technol. Assessments 5, 28–36. doi:10.1016/j.seta.2013.11.001
Akinnawo, O. O., Oludotun, J. S. O., Usifo, A. G., and Adejuwon, S. O. (2016). Models for prediction of global solar radiation on horizontal surface for Akure, Nigeria. Glo. Jnl. Pure Appl. Sci. 22, 43–50. doi:10.4314/gjpas.v22i1.6
Akinoǧlu, B. G., and Ecevit, A. (1990). Construction of a quadratic model using modified Ångstrom coefficients to estimate global solar radiation. Sol. Energy 45, 85–92. doi:10.1016/0038-092x(90)90032-8
Akpabio, L. E., and Etuk, S. E. (2003). Relationship between global solar radiation and sunshine duration for Onne, Nigeria. Turkish J. Phys. 27, 161–167.
Akpootu, D. O., Tijjani, B. I., and Gana, U. M. (2019). Sunshine and temperature dependent models for estimating global solar radiation across the Guinea savannah climatic zone of Nigeria. Am. J. Phys. Appl. 7, 125–135. doi:10.11648/j.ajpa.20190705.15
Aksoy, B. (1997). Estimated monthly average global radiation for Turkey and its comparison with observations. Renew. Energy 10, 625–633. doi:10.1016/s0960-1481(96)00035-3
Almorox, J., and Hontoria, C. (2004). Global solar radiation estimation using sunshine duration in Spain. Energy Convers. Manag. 45, 1529–1535. doi:10.1016/j.enconman.2003.08.022
Alsaad, M. A. (1990). Characteristic distribution of global solar radiation for Amman, Jordan. Sol. Wind Technol. 7, 261–266. doi:10.1016/0741-983x(90)90095-j
Ampratwum, D. B., and Dorvlo, A. S. S. (1999). Estimation of solar radiation from the number of sunshine hours. Appl. Energy 63, 161–167. doi:10.1016/s0306-2619(99)00025-2
Andretta, A., Bartoli, B., Coluzzi, B., Cuomo, V., Francesca, M., and Serio, C. (1982). Global solar radiation estimation from relative sunshine hours in Italy. J. Appl. Meteor. 21, 1377–1384. doi:10.1175/1520-0450(1982)021<1377:gsrefr>2.0.co;2
Angstrom, A. (1924). Solar and terrestrial radiation. Report to the international commission for solar research on actinometric investigations of solar and atmospheric radiation. Q. J. R. Meteorol. Soc. 50, 121–126. doi:10.1002/qj.49705021008
Aoun, N., and Bouchouicha, K. (2017). Simple correlation models for estimation of horizontal global solar radiation for oran, northwest Algeria. Int. J. Eng. Res. Afr. 4667, 124–132. doi:10.4028/www.scientific.net/jera.32.124
Aras, H., Balli, O., and Hepbasli, A. (2006). Global solar radiation potential, Part 1: Model development. Energy Sources Part B Econ. Plan. Policy 1, 303–315. doi:10.1080/15567240500398040
Argungu, G. M., Sanusi, Y. A., Dabai, K. A., Abubakar, M., and Roko, A. (2020). Comparative analysis of the performance of six models for the estimation of global solar radiation for katsina, Nigeria. Am. J. Energy Eng. 8, 18–25. doi:10.11648/j.ajee.20200802.11
Assi, A., and Jama, M. (2010). "Estimating global solar radiation on horizontal from sunshine hours in Abu Dhabi–UAE", in: Proceedings of the Advances in Energy Planning, Environmental Education and Renewable Energy Sources, 4th WSEAS International Conference on Renewable Energy Sources. Citeseer, May, 2010, Kantaoui, TN.
Awasthi, J., and Poudyal, K. N. (2018). Estimation of global solar radiation using empirical model on meteorological parameters at Simara Airport, bara, Nepal. J. Inst. Eng. 14, 143–150. doi:10.3126/jie.v14i1.20078
Ayodele, T. R., and Ogunjuyigbe, A. S. O. (2017). Performance assessment of empirical models for prediction of daily and monthly average global solar radiation: The case study of ibadan, Nigeria. Int. J. Ambient Energy 38, 803–813. doi:10.1080/01430750.2016.1222961
Bahel, V., Bakhsh, H., and Srinivasan, R. (1987). A correlation for estimation of global solar radiation. Energy 12, 131–135. doi:10.1016/0360-5442(87)90117-4
Bahel, V., Srinivasan, R., and Bakhsh, H. (1986). Solar radiation for dhahran, Saudi arabia. Energy 11, 985–989. doi:10.1016/0360-5442(86)90029-0
Bakirci, K. (2009). Correlations for estimation of daily global solar radiation with hours of bright sunshine in Turkey. Energy 34, 485–501. doi:10.1016/j.energy.2009.02.005
Bakirci, K. (2017). Prediction of global solar radiation and comparison with satellite data. J. Atmos. Solar-Terrestrial Phys. 152-153, 41–49. doi:10.1016/j.jastp.2016.12.002
Benamrou, B., Mustapha, O., Allaouzi, I., and Ahmed, M. B. (2018). Empirical models for estimating the global solar radiation based on air temperature and sunshine duration. Smart City Appl. 10-11, 1–6. doi:10.1145/3286606.3286856
Benson, R. B., Paris, M. V., Sherry, J. E., and Justus, C. G. (1984). Estimation of daily and monthly direct, diffuse and global solar radiation from sunshine duration measurements. Sol. Energy 32, 523–535. doi:10.1016/0038-092x(84)90267-6
Bounoua, Z., Ouazzani Chahidi, L., and Mechaqrane, A. (2021). Estimation of daily global solar radiation using empirical and machine-learning methods: A case study of five Moroccan locations. Sustain. Mater. Technol. 28, e00261. doi:10.1016/j.susmat.2021.e00261
Cao, F., Li, H., and Zhao, L. (2017). Comparison of the daily global solar radiation from different data sources in Northwest China climate. Int. J. Green Energy 14, 548–554. doi:10.1080/15435075.2017.1307752
Chala, A. A. (2018). Estimating global solar radiation in bale robe town using angstrom-prescott and hargreaves-samani models. J. Energy Technol. Policy 8, 14–40.
Chen, J.-L., and Li, G.-S. (2013). Estimation of monthly average daily solar radiation from measured meteorological data in Yangtze River Basin in China. Int. J. Climatol. 33, 487–498. doi:10.1002/joc.3442
Chen, R., Ersi, K., Yang, J., Lu, S., and Zhao, W. (2004). Validation of five global radiation models with measured daily data in China. Energy Convers. Manag. 45, 1759–1769. doi:10.1016/j.enconman.2003.09.019
Chen, R., Kang, E., Ji, X., Yang, J., and Zhang, Z. (2006a). Trends of the global radiation and sunshine hours in 1961–1998 and their relationships in China. Energy Convers. Manag. 47, 2859–2866. doi:10.1016/j.enconman.2006.03.029
Chen, R., Kang, E., Lu, S., Yang, J., Ji, X., Zhang, Z., et al. (2006b). New methods to estimate global radiation based on meteorological data in China. Energy Convers. Manag. 47, 2991–2998. doi:10.1016/j.enconman.2006.03.025
Coulibaly, O., and Ouedraogo, A. (2016). Correlation of global solar radiation of eight synoptic stations in Burkina Faso based on linear and multiple linear regression methods. J. Sol. Energy 2016, 1–9. doi:10.1155/2016/7870907
Duzen, H., and Aydin, H. (2012). Sunshine-based estimation of global solar radiation on horizontal surface at Lake Van region (Turkey). Energy Convers. Manag. 58, 35–46. doi:10.1016/j.enconman.2011.11.028
El-Metwally, M. (2005). Sunshine and global solar radiation estimation at different sites in Egypt. J. Atmos. Solar-Terrestrial Phys. 67, 1331–1342. doi:10.1016/j.jastp.2005.04.004
El-Sebaii, A. A., Al-Ghamdi, A. A., Al-Hazmi, F. S., and Faidah, A. S. (2009). Estimation of global solar radiation on horizontal surfaces in Jeddah, Saudi Arabia. Energy Policy 37, 3645–3649. doi:10.1016/j.enpol.2009.04.038
El-Sebaii, A., and Trabea, A. (2005). Estimation of global solar radiation on horizontal surfaces over Egypt. Egypt. J. Solids 28, 163–175.
Elagib, N. A., Alvi, S. H., and Mansell, M. G. (1999). Correlationships between clearness index and relative sunshine duration for Sudan. Renew. Energy 17, 473–498. doi:10.1016/s0960-1481(98)00773-3
Elagib, N. A., and Mansell, M. G. (2000). New approaches for estimating global solar radiation across Sudan. Energy Convers. Manag. 41, 419–434. doi:10.1016/s0196-8904(99)00123-5
Falayi, E., Adepitan, J., and Rabiu, A. (2008). Empirical models for the correlation of global solar radiation with meteorological data for Iseyin, Nigeria. Int. J. Phys. Sci. 3, 210–216. doi:10.5897/IJPS.9000218
Feng, Y., Gong, D., Jiang, S., Zhao, L., and Cui, N. (2020). National-scale development and calibration of empirical models for predicting daily global solar radiation in China. Energy Convers. Manag. 203, 112236. doi:10.1016/j.enconman.2019.112236
Garg, H. P., and Garg, S. N. (1985). Correlation of monthly-average daily global, diffuse and beam radiation with bright sunshine hours. Energy Convers. Manag. 25, 409–417. doi:10.1016/0196-8904(85)90004-4
Gbadebo, I. O., and Adeleke, A. E. (2015). Estimation of solar radiation over Ibadan from routine meteorological parameters. Int. J. Eng. Sci. 4, 44–51.
Glover, J., and Mcculloch, J. (1958). The empirical relation between solar radiation and hours of sunshine. Q. J. R. Meteorol. Soc. 84, 172–175. doi:10.1002/qj.49708436011
Gong, Z., Jiang, Y., Yang, H., and Liu, J. (2016). Analysis of daily global solar radiation data for wuhan. MATEC Web Conf. 61, 04013. doi:10.1051/matecconf/20166104013
Gopinathan, K. K. (1988). A general formula for computing the coefficients of the correlation connecting global solar radiation to sunshine duration. Sol. Energy 41, 499–502. doi:10.1016/0038-092x(88)90052-7
Gopinathan, K. K., and Soler, A. (1992). A sunshine dependent global insolation model for latitudes between 60°N and 70°N. Renew. Energy 2, 401–404. doi:10.1016/0960-1481(92)90073-c
Gouda, S. G., Hussein, Z., Luo, S., Wang, P., Cao, H., and Yuan, Q. (2018). Empirical models for estimating global solar radiation in Wuhan City, China. Eur. Phys. J. Plus 133, 517. doi:10.1140/epjp/i2018-12333-2
Hay, J. E. (1979). Calculation of monthly mean solar radiation for horizontal and inclined surfaces. Sol. Energy 23, 301–307. doi:10.1016/0038-092x(79)90123-3
Ishola, K. A., Fealy, R., Mills, G., Fealy, R., Green, S., Jimenez-Casteneda, A., et al. (2019). Developing regional calibration coefficients for estimation of hourly global solar radiation in Ireland. Int. J. Sustain. Energy 38, 297–311. doi:10.1080/14786451.2018.1499645
Jain, P. C. (1990). A model for diffuse and global irradiation on horizontal surfaces. Sol. Energy 45, 301–308. doi:10.1016/0038-092x(90)90015-5
Jain, P. C. (1986). Global irradiation estimation for Italian locations. Sol. Wind Technol. 3, 323–328. doi:10.1016/0741-983x(86)90013-5
Jain, S., and Jain, P. C. (1988). A comparison of the Angstrom-type correlations and the estimation of monthly average daily global irradiation. Sol. Energy 40, 93–98. doi:10.1016/0038-092x(88)90076-x
Jin, Z., Yezheng, W., and Gang, Y. (2005). General formula for estimation of monthly average daily global solar radiation in China. Energy Convers. Manag. 46, 257–268. doi:10.1016/j.enconman.2004.02.020
Kada, B., Bailek, N., Mahmoud, M. E.-S., Alonso, J. A., Slimani, A., and Abdallah, D. (2018). Estimation of monthly average daily global solar radiation using meteorological-based models in adrar, Algeria. Appl. Sol. Energy 54, 448–455. doi:10.3103/s0003701x1806004x
Kalogirou, S. A., Pashiardis, S., and Pashiardi, A. (2017). Statistical analysis and inter-comparison of the global solar radiation at two sites in Cyprus. Renew. Energy 101, 1102–1123. doi:10.1016/j.renene.2016.09.027
Kaplan, A. G., and Kaplan, Y. A. (2020). Developing of the new models in solar radiation estimation with curve fitting based on moving least-squares approximation. Renew. Energy 146, 2462–2471. doi:10.1016/j.renene.2019.08.095
Kaplan, Y. A. (2018). A new model for predicting the global solar radiation. Environ. Prog. Sustain. Energy 37, 870–880. doi:10.1002/ep.12721
Katiyar, A. K., and Pandey, C. K. (2010). Simple correlation for estimating the global solar radiation on horizontal surfaces in India. Energy 35, 5043–5048. doi:10.1016/j.energy.2010.08.014
Khan, M. M., and Ahmad, M. J. (2019). Estimation of global solar radiation using clear sky radiation in Yemen. Int. J. Power Energy Eng. 1, 7–16.
Khogali, A., Ramadan, M. R. I., Ali, Z. E. H., and Fattah, Y. A. (1983). Global and diffuse solar irradiance in Yemen (Y.A.R.). Sol. Energy 31, 55–62. doi:10.1016/0038-092x(83)90033-6
Layi Fagbenle, R. (1993). Total solar radiation estimates in Nigeria using a maximum-likelihood quadratic fit. Renew. Energy 3, 813–817. doi:10.1016/0960-1481(93)90089-y
Lewis, G. (1992). An empirical relation for estimating global irradiation for Tennessee, U.S.A. Energy Convers. Manag. 33, 1097–1099. doi:10.1016/0196-8904(92)90007-j
Lewis, G. (1981). Irradiance estimates for Zambia. Sol. Energy 26, 81–85. doi:10.1016/0038-092x(81)90115-8
Liu, J., Jiang, Y., Gong, Z., and Yang, H. (2016). Estimated Daily Global Radiation for Zhengzhou and Its Comparison With Observations. MATEC Web Conf. 61, 04020–04024. doi:10.1051/matecconf/20166104020
Liu, J., Linderholm, H., Chen, D., Zhou, X., Flerchinger, G. N., Yu, Q., et al. (2015). Changes in the relationship between solar radiation and sunshine duration in large cities of China. Energy 82, 589–600. doi:10.1016/j.energy.2015.01.068
Liu, Y., Zhou, Y., Wang, D., Wang, Y., Li, Y., and Zhu, Y. (2017). Classification of solar radiation zones and general models for estimating the daily global solar radiation on horizontal surfaces in China. Energy Convers. Manag. 154, 168–179. doi:10.1016/j.enconman.2017.10.043
Louche, A., Notton, G., Poggi, P., and Simonnot, G. (1991). Correlations for direct normal and global horizontal irradiation on a French Mediterranean site. Sol. Energy 46, 261–266. doi:10.1016/0038-092x(91)90072-5
Luhanga, P. V. C., and Andringa, J. (1990). Characteristics of solar radiation at Sebele, Gaborone, Botswana. Sol. Energy 44, 77–81. doi:10.1016/0038-092x(90)90069-o
Makade, R. G., Chakrabarti, S., and Jamil, B. (2019). Prediction of global solar radiation using a single empirical model for diversified locations across India. Urban Clim. 29, 100492. doi:10.1016/j.uclim.2019.100492
Manju, S., and Sandeep, M. (2019). Prediction and performance assessment of global solar radiation in Indian cities: A comparison of satellite and surface measured data. J. Clean. Prod. 230, 116–128. doi:10.1016/j.jclepro.2019.05.108
Mbiaké, R., Wakata, A. B., Mfoumou, E., Ndjeuna, E., Fotso, L., Tiekwe, E., et al. (2018). The Relationship between Global Solar Radiation and Sunshine Durations in Cameroon. Open J. Air Pollut. 7, 107–119. doi:10.4236/ojap.2018.72006
Mohammadi, K., Khorasanizadeh, H., Shamshirband, S., and Tong, C. W. (2016). Influence of introducing various meteorological parameters to the Angström–Prescott model for estimation of global solar radiation. Environ. Earth Sci. 75, 219. doi:10.1007/s12665-015-4871-z
Monteiro, A. F. M., Martins, F. B., and Williams, A. (2019). Global Solar Radiation Models in Minas Gerais, Southeastern Brazil. Adv. Meteorology 2019, 1–17. doi:10.1155/2019/9515430
Nadjem, B., Kada, B., Abdel-Hadi, Y. A., Mohamed, E. S., Abdeldjalil, S., Basharat, J., et al. (2020). Developing a new model for predicting global solar radiation on a horizontal surface located in Southwest Region of Algeria. NRIAG J. Astronomy Geophys. 9, 341–349. doi:10.1080/20909977.2020.1746892
Namrata, K., Sharma, S. P., and Seksena, S. B. L. (2016). Empirical models for the estimation of global solar radiation with sunshine hours on horizontal surface for Jharkhand (India). Appl. Sol. Energy 52, 164–172. doi:10.3103/s0003701x16030099
Naserpour, S., Zolfaghari, H., and Zeaiean Firouzabadi, P. (2020). Calibration and evaluation of sunshine-based empirical models for estimating daily solar radiation in Iran. Sustain. Energy Technol. Assessments 42, 100855. doi:10.1016/j.seta.2020.100855
Newland, F. J. (1989). A study of solar radiation models for the coastal region of South China. Sol. Energy 43, 227–235. doi:10.1016/0038-092x(89)90022-4
Nwokolo, S., and Ogbulezie, J. (2017). Performance evaluation of existing sunshine-based computing models for estimating global solar radiation at Lagos, Nigeria. Int. J. Adv. Astronomy 5, 106–116. doi:10.14419/ijaa.v5i2.8308
Ögelman, H., Ecevit, A., and Tasdemiroǧlu, E. (1984). A new method for estimating solar radiation from bright sunshine data. Sol. Energy 33, 619–625. doi:10.1016/0038-092x(84)90018-5
Okundamiya, E., and Emagbetere, J. O. (2016). Evaluation of various global solar radiation models for Nigeria. Int. J. Green Energy 13, 505–512. doi:10.1080/15435075.2014.968921
Olatona, G. I. (2018). Estimating Global Solar Radiation from Routine Meteorological Parameters Over a Tropical City (7.23°N; 3.52°E) Using Quadratic Models. Ann. West Univ. Timisoara - Phys. 60, 45–55. doi:10.2478/awutp-2018-0005
Olomiyesan, B. M., and Oyedum, O. D. (2016). Comparative Study of Ground Measured, Satellite-Derived, and Estimated Global Solar Radiation Data in Nigeria. J. Sol. Energy 2016, 1–7. doi:10.1155/2016/8197389
Onyango, A. O., and Ongoma, V. (2015). Estimation of mean monthly global solar radiation using sunshine hours for Nairobi City, Kenya. J. Renew. Sustain. Energy 7, 053105. doi:10.1063/1.4930530
Ouali, K., and Alkama, R. (2014). A New Model of Global Solar Radiation based on Meteorological Data in Bejaia City (Algeria). Energy Procedia 50, 670–676. doi:10.1016/j.egypro.2014.06.082
Oyewola, O. M., Patchali, T. E., Ajide, O. O., Singh, S., and Matthew, O. J. (2022). Global solar radiation predictions in Fiji Islands based on empirical models. Alexandria Eng. J. 61, 8555–8571. doi:10.1016/j.aej.2022.01.065
Ozturk, M. (2015). An Evaluation of Global Solar Radiation Empirical Formulations in Isparta, Turkey. Energy Sources, Part A Recovery, Util. Environ. Eff. 37, 2474–2486. doi:10.1080/15567036.2012.745037
Pant, B. P., Poudyal, K. N., Acharya, B., and Budha, B. (2019). Empirical Models for the Evaluation of Global Solar Radiation in the Different Sites of Nepal. J. Nep. Phys. Soc. 5, 67–73. doi:10.3126/jnphyssoc.v5i1.26933
Pereira, A. B., and Schiebelbein, L. M. (2018). Performance of Different Models for Estimating the Global Solar Radiation in Brazil. Int. J. Adv. Eng. Res. Sci. 5, 62–69. doi:10.22161/ijaers.5.8.8
Poudyal, K. N. (2016). Estimation of Global Solar Radiation using Modifed Angstrom Empirical formula on the basis of Meterological parameters in Himalaya Region Pokhara, Nepal. J. Inst. Eng. 11, 158–164. doi:10.3126/jie.v11i1.14710
Prescott, J. (1940). Evaporation from a water surface in relation to solar radiation. Trans. Roy. Soc. S. Aust. 46, 114–118.
Prieto, J.-I., and García, D. (2022). Modified temperature-based global solar radiation models for estimation in regions with scarce experimental data. Energy Convers. Manag. 268, 115950. doi:10.1016/j.enconman.2022.115950
Quansah, E., Amekudzi, L. K., Preko, K., Aryee, J., Boakye, O. R., Boli, D., et al. (2014). Empirical Models for Estimating Global Solar Radiation over the Ashanti Region of Ghana. J. Sol. Energy 2014, 1–6. doi:10.1155/2014/897970
Raja, I. A., and Twidell, J. W. (1990a). Distribution of global insolation over Pakistan. Sol. Energy 44, 63–71. doi:10.1016/0038-092x(90)90067-m
Raja, I. A., and Twidell, J. W. (1990b). Diurnal variation of global insolation over five locations in Pakistan. Sol. Energy 44, 73–76. doi:10.1016/0038-092x(90)90068-n
Rehman, S., and Halawani, T. O. (1997). Global solar radiation estimation. Renew. Energy 12, 369–385. doi:10.1016/s0960-1481(97)00057-8
Rensheng, C., Shihua, L., Ersi, K., Jianping, Y., and Xibin, J. (2006). Estimating daily global radiation using two types of revised models in China. Energy Convers. Manag. 47, 865–878. doi:10.1016/j.enconman.2005.06.015
Rietveld, M. R. (1978). A new method for estimating the regression coefficients in the formula relating solar radiation to sunshine. Agric. Meteorol. 19, 243–252. doi:10.1016/0002-1571(78)90014-6
Samanta, S., Patra, P. K., Banerjee, S., Narsimhaiah, L., Chandran, M. a. S., Kumar, P. V., et al. (2019). Generation of common coefficients to estimate global solar radiation over different locations of India. Theor. Appl. Climatol. 136, 943–953. doi:10.1007/s00704-018-2531-4
Samuel, T. D. M. A. (1991). Estimation of global radiation for Sri Lanka. Sol. Energy 47, 333–337. doi:10.1016/0038-092x(91)90026-s
Sarkar, M. N. I., and Sifat, A. I. (2016). Global solar radiation estimation from commonly available meteorological data for Bangladesh. Renewables. 3, 6. doi:10.1186/s40807-016-0027-3
Saud, S., Jamil, B., Upadhyay, Y., and Irshad, K. (2020). Performance improvement of empirical models for estimation of global solar radiation in India: A k-fold cross-validation approach. Sustain. Energy Technol. Assessments 40, 100768. doi:10.1016/j.seta.2020.100768
Sekhar, Y. R., Sharma, K. V., and Rao, A. V. M. S. (2013). New correlations for estimation of monthly average daily solar radiation on a horizontal surface using meteorological data. Int. J. Ambient Energy 34, 160–174. doi:10.1080/01430750.2012.740430
Sen, Z. (2008). Solar energy fundamentals and modeling techniques: Atmosphere, environment, climate change and renewable energy. Berlin Germany: Springer Science & Business Media.
Shahrukh Anis, M., Jamil, B., Azeem Ansari, M., and Bellos, E. (2019). Generalized models for estimation of global solar radiation based on sunshine duration and detailed comparison with the existing: A case study for India. Sustain. Energy Technol. Assessments 31, 179–198. doi:10.1016/j.seta.2018.12.009
Sheik, M., and Rao, C. V. (2021). Empirical models for estimating the global solar radiation of Jubail Industrial City, the Kingdom of Saudi Arabia. SN Appl. Sci. 3, 1–11. doi:10.1007/s42452-020-04043-9
Siva Krishna Rao, K. D. V., Premalatha, M., and Naveen, C. (2018). Method and strategy for predicting daily global solar radiation using one and two input variables for Indian stations. J. Renew. Sustain. Energy 10, 013701. doi:10.1063/1.4995035
Soulouknga, M. H., Coulibaly, O., Doka, S. Y., and Kofane, T. C. (2017a). Evaluation of global solar radiation from meteorological data in the Sahelian zone of Chad. Renewables. 4, 4–10. doi:10.1186/s40807-017-0041-0
Soulouknga, M. H., Falama, R. Z., Ajayi, O. O., Doka, S. Y., and Kofane, T. C. (2017b). Determination of a Suitable Solar Radiation Model for the Sites of Chad. Energy Power Eng. 9, 703–722. doi:10.4236/epe.2017.912045
Srivastava, R. C., and Harsha, P. (2013). Estimating Angstrom-Prescott Coefficients for India and Developing a Correlation between Sunshine Hours and Global Solar Radiation for India. ISRN Renew. Energy 2013, 1–7. doi:10.1155/2013/403742
Suthar, M., Singh, G. K., and Saini, R. P. (2014). Effects of air pollution for estimating global solar radiation in India. Int. J. Sustain. Energy 36, 20–27. doi:10.1080/14786451.2014.979348
Toğrul, I. T., Toğrul, H., and Evin, D. (2000a). Estimation of global solar radiation under clear sky radiation in Turkey. Renew. Energy 21, 271–287. doi:10.1016/s0960-1481(99)00128-7
Toğrul, İ. T., Toğrul, H., and Evin, D. (2000b). Estimation of monthly global solar radiation from sunshine duration measurement in Elaziğ. Renew. Energy 19, 587–595. doi:10.1016/s0960-1481(99)00084-1
Toğrul, I. T., and Toğrul, H. (2002). Global solar radiation over Turkey: comparison of predicted and measured data. Renew. Energy 25, 55–67. doi:10.1016/s0960-1481(00)00197-x
Tsung, K. Y., Tan, R., and Ii, G. Y. (2019). Estimating the global solar radiation in Putrajaya using the Angstrom-Prescott model. IOP Conf. Ser. Earth Environ. Sci. 268, 012056. doi:10.1088/1755-1315/268/1/012056
Uckan, İ., and Khudhur, K. M. (2018). Estimation and comparison of various global solar radiation models on horizontal surface in a hot and dry region. Int. J. Green Energy 15, 358–370. doi:10.1080/15435075.2018.1454322
Ulgen, K., and Hepbasli, A. (2004). Solar Radiation Models. Part 2: Comparison and Developing New Models. Energy sources. 26, 521–530. doi:10.1080/00908310490429704
Ustun, I., Karakus, C., and Yagli, H. (2020). Empirical models for estimating the daily and monthly global solar radiation for Mediterranean and Central Anatolia region of Turkey. Int. J. Glob. Warming 20, 249–275. doi:10.1504/ijgw.2020.10028207
Veeran, P. K., and Kumar, S. (1993). Analysis of monthly average daily global radiation and monthly average sunshine duration at two tropical locations. Renew. Energy 3, 935–939. doi:10.1016/0960-1481(93)90054-k
Woldegiyorgis, T. A. (2019). Estimation of Global Solar Radiation on Horizontal Surface from Sun Shine Hours and Temperature at Kombolcha, Amhara Region, Ethiopia. J. Energy, Environ. Chem. Eng. 4, 39–46. doi:10.11648/j.jeece.20190403.12
Xiao, M., Yu, Z., and Cui, Y. (2020). Evaluation and estimation of daily global solar radiation from the estimated direct and diffuse solar radiation. Theor. Appl. Climatol. 140, 983–992. doi:10.1007/s00704-020-03140-4
Yakoubi, H., El Mghouchi, Y., Abdou, N., Hajou, A., and Khellouki, A. (2021). Correlating clearness index with cloud cover and other meteorological parameters for forecasting the global solar radiation over Morocco. Optik 242, 167145. doi:10.1016/j.ijleo.2021.167145
Yang, H., Jiang, Y., Liu, J., and Gong, Z. (2016). Comparison between Measurements and Models For Daily Global Solar Radiation of Urumuqi. MATEC Web Conf. 61, 04005. doi:10.1051/matecconf/20166104005
Yaniktepe, B., Kara, O., and Ozalp, C. (2017). The global solar radiation estimation and analysis of solar energy: Case study for Osmaniye, Turkey. Int. J. Green Energy 14, 765–773. doi:10.1080/15435075.2017.1329148
Yao, W., Li, Z., Wang, Y., Jiang, F., and Hu, L. (2014). Evaluation of global solar radiation models for Shanghai, China. Energy Convers. Manag. 84, 597–612. doi:10.1016/j.enconman.2014.04.017
Yıldırım, H. B., Teke, A., and Antonanzas-Torres, F. (2018). Evaluation of classical parametric models for estimating solar radiation in the Eastern Mediterranean region of Turkey. Renew. Sustain. Energy Rev. 82, 2053–2065. doi:10.1016/j.rser.2017.08.033
Zhang, Q., Cui, N., Feng, Y., Jia, Y., Li, Z., and Gong, D. (2018). Comparative Analysis of Global Solar Radiation Models in Different Regions of China. Adv. Meteorology 2018, 1–21. doi:10.1155/2018/3894831
Zhou, Y., Liu, Y., Wang, D., and Liu, X. (2021a). Comparison of machine-learning models for predicting short-term building heating load using operational parameters. Energy Build. 253, 111505. doi:10.1016/j.enbuild.2021.111505
Zhou, Y., Liu, Y., Wang, D., Liu, X., and Wang, Y. (2021b). A review on global solar radiation prediction with machine learning models in a comprehensive perspective. Energy Convers. Manag. 235, 113960. doi:10.1016/j.enconman.2021.113960
Keywords: global solar radiation, sunshine-based model, predictive modelling, solar declination, China
Citation: Lan K, Wang L, Zhou Y, Zhang Z, Fang S and Cao P (2023) The applicability of sunshine-based global solar radiation models modified with meteorological factors for different climate zones of China. Front. Energy Res. 10:1010745. doi: 10.3389/fenrg.2022.1010745
Received: 03 August 2022; Accepted: 28 September 2022;
Published: 10 January 2023.
Edited by:
K. Sudhakar, Universiti Malaysia Pahang, MalaysiaReviewed by:
Olanrewaju Oyewola, Fiji National University, FijiCopyright © 2023 Lan, Wang, Zhou, Zhang, Fang and Cao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lingyu Wang, d2FuZ2xpbmd5dTA4MjdAMTYzLmNvbQ==; Yong Zhou, emhvdXlvbmdAeGF1YXQuZWR1LmNu
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.