Application of the improved quasi-static coupled probability theory method to transient safety analysis of an experimental facility

The accelerator-driven sub-critical system is driven by external neutron sources, which are generated by the spallation reaction and maintain the stable operation of the sub-critical core, while the external neutron source increases the complexity of reactor neutron kinetic processes. This article focuses on simulation analysis of neutron space–time kinetics with a dynamic analysis code, which is developed based on the improved quasi-static approximation and Monte Carlo neutron transport method. The amplitude function and shape functions are solved to achieve the dynamics simulation process. Then, the transient responses of beam interruptions and reactivity insertions are calculated and analyzed for an experimental facility. To further verify the correctness and reliability of dynamic behavior, the simulation results are compared with experimental values, and the results show that the normalized neutron fluxes varying with time are in good agreement with the corresponding values. It can be concluded that the improved quasi-static coupled probability theory method can be used to solve the neutron space–time kinetic problem of the experimental facility, and the results are reliable.

1 Introduction

The accelerator-driven sub-critical (ADS) system consists of three parts, namely, the high-energy proton accelerator, the spallation target, and the sub-critical reactor (Li et al., 2017). The working mechanism of the ADS system is to use the high-energy proton beam to bombard heavy nuclei (liquid lead or lead–bismuth alloy), which can produce spallation neutrons as external neutron sources to drive the sub-critical reactor core and maintain the fission reactions. However, the ADS system is different from conventional reactors; it works in a sub-critical state, and external neutron sources will greatly increase the heterogeneity of power distribution and complexity in the neutron process (Gandini and Salvatores, 2002). The energy, position, and spatial distribution of the external neutron source have obvious effects on the neutron flux. Therefore, in the process of transient simulation of introducing reactivity, the flux distribution of the external neutron source and the sub-critical level of the core will be obviously affected (Dulla et al., 2005; Rineiski and Maschek, 2005). Thus, to ensure the reliability of the improved quasi-static coupled probability theory (IQS/MC) method in simulating transient conditions of an experimental facility, carrying out both simulation and experimental research on the beam transient and reactivity insertion is necessary.

Currently, in addition to experimental studies, analytical method and numerical method are mainly used for the simulation analysis of the neutron space–time dynamics characteristic of the accelerator-driven sub-critical system. B. Merk et al. studied the neutron space–time dynamic equation of the accelerator sub-critical reactor based on the multigroup diffusion approximation and deduced the analytic expression of each physical parameter using the Green function method, which has less computation and is easy to implement. However, it was difficult to deal with the multi-energy group and complex boundary conditions and could not simulate the sub-critical problem with an external neutron source (Merk, 2009; Merk and Glivici-Cotruţă, 2012).

The kinetic calculation of ADS is mostly carried out by using the point kinetic model (Cammi et al., 2006; Mikityuk et al., 2007), but the derivation process of the point kinetic model does not consider the external neutron source and the physical phenomena of the external neutron source coupling with the sub-critical reactor. The deterministic numerical method is used to solve the neutron transport equation and obtain the shape function, which has high calculation efficiency, and the SN or PN method are relatively mature, but the calculation results depend on the accuracy of the neutron macroscopic reaction cross section of a sub-critical core with a high energy dispersal spectrum (Chadwick et al., 2011; Shibata et al., 2011). The Monte Carlo method is a numerical method based on the statistical theory that constructs a random probability model to solve the problems. The increasing computer capacity has made the Monte Carlo method an attractive tool to be used in the research studies of the neutron space–time dynamic problem (Hindmarsh, 1980; Bentley et al., 1997; Zhitnik et al., 2005; Mikityuk et al., 2007; Sjenitzer and Hoogenboom, 2013), and this method has been greatly employed in the traditional critical reactor.

In the past work, it was found that in the process of neutron space–time dynamics calculation, the point kinetic method would underestimate the power variations in transient processes, but the IQS/MC method can avoid this problem (Song et al., 2017). The improved quasi-static method is a transient spatial kinetic method that involves factorizing flux into space- and time-dependent, while the shape is both space- and time-dependent. Therefore, in this article, the Monte Carlo method is applied to the IQS method, and the neutron space–time dynamic simulation is carried out for an experimental facility. During the solution of the improved quasi-static method, the neutron flux is decomposed into a shape function and an amplitude function (Suzuki et al., 2005; He et al., 2015), and the time-dependent function mainly reflects in the amplitude changes over time, while the shape function reflects the shape of the spatial and velocity distribution, which changes slowly in a transient process.

The rest of this article is organized as follows: Section 2 introduces the theory of space–time neutron kinetics, the framework of the IQS/MC method, and the development of a transient code. Then, in Section 3, the code is employed to analyze the beam transient process and reactivity insertion process of an experimental facility, and the results calculated by the IQS/MC method are compared with the experimental data. Conclusions are summarized in Section 4.

2 Introduction to the IQS/MC method

In this section, we introduced the theory used in the IQS/MC code, starting from the Boltzmann transport equation written as follows:

$\begin{array}{ll}\hfill \frac{1}{\upsilon \left(E\right)}\frac{\partial \mathrm{\Phi }\left(\mathit{r},E,\mathit{\Omega },t\right)}{\partial t}& +\mathit{\Omega }\cdot \nabla \mathrm{\Phi }\left(\mathit{r},E,\mathit{\Omega },t\right)\mathrm{+}{\mathrm{\Sigma }}_t\left(\mathit{r},E,t\right)\mathrm{\Phi }\left(\mathit{r},E,\mathit{\Omega },t\right)=\iint {\mathrm{\Sigma }}_s\left(\mathit{r};E^{\prime },{\mathit{\Omega }}^{\prime }\to E,\mathit{\Omega };t\right)\mathrm{\Phi }\left(\mathit{r},E^{\prime },{\mathit{\Omega }}^{\prime },t\right)d{E}^{\prime }d{\mathit{\Omega }}^{\prime }\hfill \\ \hfill & +\iint \frac{1}{4\pi }{\chi }_p\left(E\right)\left(1-\beta \right)\nu {\mathrm{\Sigma }}_f\left(\mathit{r},E^{\prime },t\right)\mathrm{\Phi }\left(r,{\mathit{\Omega }}^{\prime },E^{\prime },t\right)d{E}^{\prime }d{\mathit{\Omega }}^{\prime }+{\displaystyle \sum }_{i=1}^{NDG}\frac{1}{4\pi }{\lambda }_i{C}_i\left(\mathit{r},t\right){\chi }_i\left(E\right)+S\left(\mathit{r},E,\mathit{\Omega },t\right).\hfill \end{array}(1)$

Furthermore, the delayed neutron precursor equation is described as follows:

$\frac{\partial C_i\left(\mathit{r},t\right)}{\partial t}=\iint {\beta }_i\nu {\mathrm{\Sigma }}_f\left(\mathit{r},E^{\prime },t\right)\mathrm{\Phi }\left(\mathit{r},E^{\prime },\mathit{\Omega }\prime ,t\right)d{E}^{\prime }d\mathit{\Omega }\prime -{\lambda }_i{C}_i\left(\mathit{r},t\right),(2)$

where $\upsilon$ is the neutron velocity, $\Phi$ is the angle neutron flux, ${\Sigma }_t$ is the macroscopic total cross section, ${\Sigma }_s$ is the double differential scattering cross section, ${\Sigma }_f$ is the macroscopic fission cross section, $S$ is the source term, ${\chi }_p$ is the probability density function for neutrons of exit energy E from all neutrons produced by fission, ${\chi }_i$ is the probability density function for neutrons of exit energy E from all neutrons produced by delayed neutron precursors, $\beta$ is the fraction of fission neutrons that are delayed, $\nu$ is the average number of neutrons produced per fission, ${\lambda }_i$ is the decay constant of the precursor i, ${\beta }_i$ is the fraction of fission neutrons emitted by the delayed neutron precursor group i, $C_i$ is the total number of precursor i in $r$ at time t, NDG is the number of delayed neutron precursor, $r$ is the position vector, $\Omega$ and ${\Omega }^{\prime }$ are the unit vectors (solid angle) in the direction of motion before and after scattering, respectively, E and E′ are the neutron energy before and after scattering, respectively, $t$ is the time, and $\Phi \left(r,E,\Omega ,t\right)$ is the angular neutron flux.

The neutron flux is decomposed into amplitude and shape functions based on the factor method:

$\mathrm{\Phi }\left(\mathit{r},E,\mathit{\Omega },t\right)=n\left(t\right)\cdot \psi \left(\mathit{r},E,\mathit{\Omega },t\right),(3)$

where n(t) is the amplitude function and $\psi \left(r,E,\Omega ,t\right)$ is the shape function. When introducing an amplitude normalization condition Eq. 4,

$\iiint \frac{{\mathrm{\Phi }}^{\ast }\left(\mathit{r},E,\mathit{\Omega }\right)\cdot \psi \left(\mathit{r},E,\mathit{\Omega },t\right)d\mathit{r}dEd\mathit{\Omega }}{\upsilon \left(E\right)}=1,(4)$

where ${\Phi }^{*}\left(r,E,\Omega \right)$ is the neutron importance function obtained by substituting Eq. 3 in Eqs 1, 2 and multiplying by ${\Phi }^{*}\left(r,E,\Omega \right)$ and ${\chi }_p\left(E\right){\Phi }^{*}\left(r,E,\Omega \right)$, respectively. Finally, amplitude function equation systems (5) and (6) can be obtained after integrating Eqs 1, 2 over the whole space and sum over all energy groups.

$\frac{dn\left(t\right)}{dt}=\frac{\rho \left(t\right)-{\beta }_{eff}\left(t\right)}{{\Lambda }_{eff}\left(t\right)}n\left(t\right)+{\displaystyle \sum }_{i=1}^{NDG}{\lambda }_i{C}_i\left(t\right)+q\left(t\right),(5)$

$\frac{d{C}_i\left(t\right)}{dt}=\frac{{\beta }_i\left(t\right)}{{\Lambda }_{eff}\left(t\right)}-{\lambda }_i{C}_i\left(t\right).(6)$

As can be seen, the amplitude function system is similar to the point kinetic equations, which include two differential equations, one for the neutron density $n\left(t\right)$ and the other for precursor concentration $C_i\left(t\right)$. Each term in Eqs 5, 6 can be expressed in the following way:

$\begin{array}{ll}\hfill \rho \left(t\right)=& \frac{1}{F\left(t\right)}\iiint [-\mathit{\Omega }\cdot \nabla \Phi \left(\mathit{r},E,\mathit{\Omega },t\right)-{\Sigma }_t\left(\mathit{r},E,t\right)\Phi \left(\mathit{r},E,\mathit{\Omega },t\right)+\iint {\Sigma }_s\left(\mathit{r};{\mathit{\Omega }}^{\prime },E^{\prime }\to \mathit{\Omega },E;t\right)\Phi \left(\mathit{r},E^{\prime },{\mathit{\Omega }}^{\prime },t\right)d{E}^{\prime }d{\mathit{\Omega }}^{\prime }\hfill \\ \hfill & +\iint {\chi }_p\left(E\right)\nu {\Sigma }_f\left(\mathit{r},E^{\prime },t\right)\Phi \left(\mathit{r},E^{\prime },{\mathit{\Omega }}^{\prime },t\right)d{E}^{\prime }d{\mathit{\Omega }}^{\prime }]{\Phi }^{\ast }\left(\mathit{r},E,\mathit{\Omega }\right)d\mathit{r}dEd\mathit{\Omega },\hfill \end{array}(7)$

${\beta }_{eff}\left(t\right)={\displaystyle \sum }_{i=1}^{NDG}{\beta }_i\left(t\right)=\frac{1}{F\left(t\right)}\int \cdots \int {\chi }_p\left(E\right){\beta }_i\nu {\Sigma }_f\left(\mathit{r},E^{\prime },t\right)\Phi \left(\mathit{r},E^{\prime },{\mathit{\Omega }}^{\prime },t\right){\Phi }^{\ast }\left(\mathit{r},E,\mathit{\Omega }\right)d{E}^{\prime }d{\mathit{\Omega }}^{\prime }d\mathit{r}dEd\mathit{\Omega },(8)$

${\Lambda }_{eff}\left(t\right)=\frac{1}{F\left(t\right)}\iiint \frac{1}{\upsilon \left(E\right)}\Phi \left(\mathit{r},E,\mathit{\Omega },t\right){\Phi }^{\ast }\left(\mathit{r},E,\mathit{\Omega }\right)d\mathit{r}dEd\mathit{\Omega },(9)$

$C_i\left(t\right)=\frac{1}{F\left(t\right){\Lambda }_{eff}\left(t\right)}\iiint \frac{1}{4\pi }{\chi }_i\left(E\right)C_i\left(t\right){\Phi }^{\ast }\left(\mathit{r},E,\mathit{\Omega }\right)d\mathit{r}dEd\mathit{\Omega },(10)$

$F\left(t\right)=\int \cdots \int \frac{1}{4\pi }{\chi }_p\left(E\right)\nu {\Sigma }_f\left(\mathit{r},E^{\prime },t\right)\Phi \left(\mathit{r},E^{\prime },{\mathit{\Omega }}^{\prime },t\right){\Phi }^{\ast }\left(\mathit{r},E,\mathit{\Omega }\right)d{E}^{\prime }d{\mathit{\Omega }}^{\prime }d\mathit{r}dEd\mathit{\Omega },(11)$

$q\left(t\right)=\frac{1}{F\left(t\right){\Lambda }_{eff}\left(t\right)}\iiint S\left(\mathit{r},\mathit{\Omega },E,t\right){\Phi }^{\ast }\left(\mathit{r},E,\mathit{\Omega }\right)d\mathit{r}dEd\mathit{\Omega }.(12)$

The calculation of the amplitude function was coupled with the lumped parameter thermal model for the neutron space–time kinetic process of the ADS system with an external neutron source. According to the conservation of energy, the heat balance of fuel is described as

$m_F{c}_{pF}\frac{d{T}_F\left(t\right)}{dt}=P\left(t\right)-U_{FC}\left(T_F\left(t\right)-T_C\left(t\right)\right),(13)$

and the heat balance of the coolant is described as follows:

$m_C{c}_{pC}\frac{d{T}_C\left(t\right)}{dt}=U_{FC}\left(T_F\left(t\right)-T_C\left(t\right)\right)-2{\omega }_{pC}{c}_{pC}\left(T_C\left(t\right)-T_{C,in}\left(t\right)\right).(14)$

The equation for reactivity is expressed as follows:

$\rho \left(t\right)=\left(T_F\left(t\right)-T_F\left(0\right)\right)\cdot B_F+\left(T_C\left(t\right)-T_C\left(0\right)\right)\cdot B_C.(15)$

In these equations, $m_F$ and $m_C$ are the mass of fuel and coolant in the core, respectively, $c_{pF}$ and $c_{pC}$ are the specific heat capacities of fuel and coolant, respectively, $P\left(t\right)$ is the total thermal power of the core, $T_F\left(t\right)$ is the average fuel temperature, $U_{FC}$ is the heat transfer coefficient between fuel and coolant, ${\omega }_{pC}$ is the coolant mass flow rate, [kg/s], $T_F\left(0\right)$ is the initial fuel temperature, $T_C\left(0\right)$ is the initial coolant temperature, $T_C\left(t\right)$ and $T_{C,in}\left(t\right)$ are the average and inlet coolant temperatures, respectively, and $B_C$ and $B_F$ are the factors of negative feedback of coolant and fuel, respectively.

Meanwhile, the following Eq. 16 of the shape function is obtained:

$\begin{array}{ll}\hfill \frac{1}{\upsilon \left(E\right)}\frac{\partial \psi \left(\mathit{r},E,\mathit{\Omega },t\right)}{\partial t}& =-\mathit{\Omega }\cdot \nabla \psi \left(\mathit{r},E,\mathit{\Omega },t\right)-{\Sigma }_t\left(\mathit{r},E,t\right)\psi \left(\mathit{r},E,\mathit{\Omega },t\right)+\iint {\Sigma }_s\left(\mathit{r};E^{\prime },{\mathit{\Omega }}^{\prime }\to E,\mathit{\Omega };t\right)\psi \left(\mathit{r},E^{\prime },{\mathit{\Omega }}^{\prime },t\right)d{E}^{\prime }{d\mathit{\Omega }}^{\prime }\hfill \\ \hfill & +\iint \frac{1}{4\pi }{\chi }_p(E)[1-\beta )\nu {\Sigma }_f(\mathit{r},E^{\prime },t)\psi (\mathit{r},E^{\prime },{\mathit{\Omega }}^{\prime },t)d{E}^{\prime }{d\mathit{\Omega }}^{\prime }+\frac{1}{4\pi }\frac{{\chi }_i\left(E\right)}{n\left(t\right)}{\displaystyle \sum }_{i=1}^{NDG}{\lambda }_i{C}_i\left(\mathit{r},t\right)\hfill \\ \hfill & +\frac{S\left(\mathit{r},E,\mathit{\Omega },t\right)}{n\left(t\right)}-\frac{\psi \left(\mathit{r},E,\mathit{\Omega },t\right)}{\upsilon \left(E\right)n\left(t\right)}\frac{dn\left(t\right)}{dt}.\hfill \end{array}(16)$

The shape function $\psi \left(r,E,\Omega ,t\right)$ is only weakly dependent on time in the transient process; therefore, the shape function may not require computation at every time step. We assume that the time step in the shape function calculation process is $\Delta t=t_{j+1}-t_j$; after the operation of a fully implicit difference in time, expression (17) is obtained from Eq. 16 as follows:

$\begin{array}{ll}\hfill \mathit{\Omega }\cdot \nabla \psi \left(\mathit{r},E,\mathit{\Omega },t_{j+1}\right)& +{\Sigma }_t\left(\mathit{r},E,t_{j+1}\right)\psi \left(\mathit{r},E,\mathit{\Omega },t_{j+1}\right)-\iint {\Sigma }_s\left(\mathit{r};E^{\prime },{\mathit{\Omega }}^{\prime }\to E,\mathit{\Omega };t_{j+1}\right)\psi \left(\mathit{r},E^{\prime }{\mathit{\Omega }}^{\prime },,t_{j+1}\right)d{E}^{\prime }d{\mathit{\Omega }}^{\prime }\hfill \\ \hfill & -\iint \frac{1}{4\pi }{\chi }_p\left(E\right)\left(1-\beta \right)\nu {\Sigma }_f\left(\mathit{r},E^{\prime },t_{j+1}\right)\psi \left(\mathit{r},E^{\prime },{\mathit{\Omega }}^{\prime },t_{j+1}\right)d{E}^{\prime }d{\mathit{\Omega }}^{\prime }\hfill \\ \hfill & -\frac{1}{4\pi }\frac{{\chi }_i\left(E\right)}{n\left(t_{j+1}\right)}{\displaystyle \sum }_{i=1}^{NDG}{\lambda }_i{C}_i\left(\mathit{r},t_{j+1}\right)=\frac{S\left(\mathit{r},E,\mathit{\Omega },t_{j+1}\right)}{n\left(t_{j+1}\right)}+\frac{1}{\upsilon \left(E\right)\Delta t}\psi \left(\mathit{r},E,\mathit{\Omega },t_j\right)\hfill \\ \hfill & -\frac{1}{\upsilon \left(E\right)}\left[\frac{1}{\Delta t}+\frac{1}{n\left(t_{j+1}\right)}\frac{dn\left(t_{j+1}\right)}{dt}\right]\psi \left(\mathit{r},E,\mathit{\Omega },t_{j+1}\right).\hfill \end{array}(17)$

Eq. 17 is equivalent to solving the non-homogeneous problem of the neutron transport equation.

In order to realize the dynamic calculation process by using the MC code, we use the Taylor formula to represent the shape function of the latter moment with the shape function of the previous moment.

$f(t+\Delta t)=f\left(t\right)+\Delta t\cdot f^{\prime }\left(t\right)+\frac{1}{2}(\Delta t{)}^2\cdot f^{″}(t)+\cdots +\frac{1}{n}(\Delta t{)}^n\cdot f^{\left(n\right)}\left(t\right).(18)$

At the same time, by observing Eq. 14 and comparing it with the neutron transport equation, we can find that the following three terms on the right side of the equal sign are non-homogeneous terms, which can be treated as external neutron sources in MC calculation.

$\frac{1}{\upsilon \left(E\right)}\left[\frac{1}{\Delta t}+\frac{1}{n\left(t_{j+1}\right)}\frac{dn\left(t_{j+1}\right)}{dt}\right]\psi \left(\mathit{r},E,\mathit{\Omega },t_{j+1}\right),(19)$

$\frac{1}{\upsilon \left(E\right)\Delta t}\psi \left(\mathit{r},E,\mathit{\Omega },t_j\right),(20)$

$\frac{S\left(\mathit{r},E,\mathit{\Omega },t_{j+1}\right)}{n\left(t_{j+1}\right)}.(21)$

We set $a=\frac{1}{\upsilon \left(E\right)\Delta t}$, $A=\frac{1}{\upsilon \left(E\right)}\left[\frac{1}{\Delta t}+\frac{1}{n\left(t_{j+1}\right)}\frac{dn\left(t_{j+1}\right)}{dt}\right]$, and $B=\frac{1}{n\left(t_{j+1}\right)}$., and according to the initial shape function $f\left(t_0\right)$ that has been obtained, combined withFormula (19), the shape function $f\left(t_1\right)$ at time t₁ can be obtained.

$B\cdot S-\left[-a\cdot {\psi }^{\prime }\left(t_0\right)+A\cdot {\psi }^{\prime }\left(t_0\right)\right]\to {\psi }_1\left(t_1\right),$

$B\cdot S-\left[-a\cdot {\psi }^{\prime }\left(t_0\right)+A\cdot {\psi }_1^{\prime }\left(t_1\right)\right]\to {\psi }_2\left(t_1\right),$

$B\cdot S-\left[-a\cdot {\psi }^{\prime }\left(t_0\right)+A\cdot {\psi }_2^{\prime }\left(t_1\right)\right]\to {\psi }_3\left(t_1\right)\cdots \cdots ,(22)$

$B\cdot S-\left[-a\cdot {\psi }^{\prime }\left(t_0\right)+A\cdot {\psi }_{n-1}^{\prime }\left(t_1\right)\right]\to {\psi }_n\left(t_1\right),$

$B\cdot S-\left[-a\cdot {\psi }^{\prime }\left(t_0\right)+A\cdot {\psi }_n^{\prime }\left(t_1\right)\right]\to \psi \left(t_1\right),$

where S is the shape function under the action of the external neutron source, ${\psi }^{\prime }\left(t_0\right)$ is the shape function distribution obtained under the action of the fission source at time t = 0, ${\psi }_1\left(t_1\right)$, ${\psi }_2\left(t_1\right)$, $\cdots \cdots$, ${\psi }_n\left(t_1\right)$ are the distribution of the estimated shape function at time t1 in the first, second, … , nth stage, respectively, and ${\psi }_1^{\prime }\left(t_1\right)$, ${\psi }_2^{\prime }\left(t_1\right)$, $\cdots \cdots$, ${\psi }_n^{\prime }\left(t_1\right)$ are the shape functions under the action of ${\psi }_1\left(t_1\right)$, ${\psi }_2\left(t_1\right)$, $\cdots \cdots$, ${\psi }_n\left(t_1\right)$, respectively.

When the calculation of the first transient step is completed, the coefficients a, A, and B in the next transient stage are obtained after updating the amplitude function, and the calculation of the next step is carried out by combining the Formula 17.

$B\cdot S-\left\{-a\cdot {\psi }^{\prime }\left(t_1\right)+A\cdot \left[2\cdot {\psi }^{\prime }\left(t_1\right)-{\psi }^{\prime }\left(t_0\right)\right]\right\}\to \psi \left(t_2\right),$

$B\cdot S-\left\{-a\cdot {\psi }^{\prime }\left(t_2\right)+A\cdot \left[2\cdot {\psi }^{\prime }\left(t_2\right)-{\psi }^{\prime }\left(t_1\right)\right]\right\}\to \psi \left(t_3\right)\cdots \cdots ,(23)$

$B\cdot S-\left\{-a\cdot {\psi }^{\prime }\left(t_{n-1}\right)+A\cdot \left[2\cdot {\psi }^{\prime }\left(t_{n-1}\right)-{\psi }^{\prime }\left(t_{n-2}\right)\right]\right\}\to \psi \left(t_n\right),$

where ${\psi }^{\prime }\left(t_0\right)$, ${\psi }^{\prime }\left(t_1\right)$, ${\psi }^{\prime }\left(t_2\right)$, ……, ${\psi }^{\prime }\left(t_{n-1}\right)$ are the shape function distributions obtained under the action of the fission source at time t = 0, t = 1, t = 2, … … , t = n-1, respectively. Also, $\psi \left(t_1\right)$, $\psi \left(t_2\right)$, $\psi \left(t_2\right)$, ……, $\psi \left(t_n\right)$ are shape functions at time t = 0, t = 1, t = 2, … … , t = n, respectively.

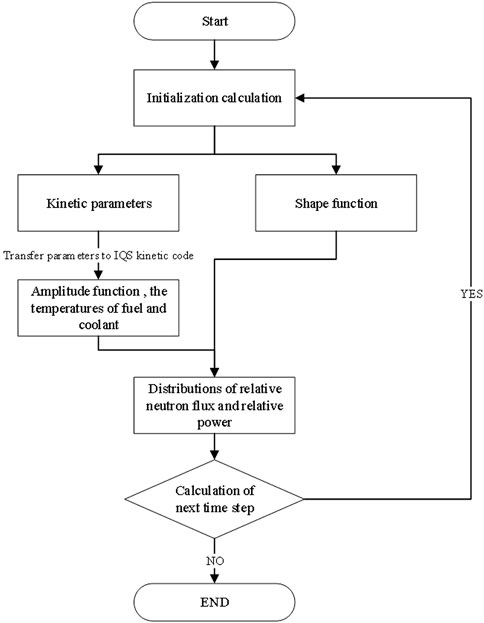
The IQS/MC code was developed based on the aforementioned method in which the IQS dynamic code was used to solve the point reactor kinetic equation, and the Monte Carlo code (Wu et al., 2015) was used to calculate the kinetic parameters and shape function distribution. The IQS dynamic code (Wu et al., 2015) is a solver that can solve the point kinetic equations with an external neutron source. The schematic diagram of the IQS/MC code is shown in Figure 1.

FIGURE 1

FIGURE 1. Schematic diagram of the IQS/MC code.

The calculation process is divided into five stages as follows: in the first stage, the process of proton bombarding the spallation target and the spallation neutron source driving the sub-critical reactor are simulated directly by the MC code, and the energy spectrum distribution and normalized neutron flux distribution at the initial time will be obtained. Then, the IQS/MC calculation process is performed, the kinetic parameters are calculated by the MC code, and the results are passed to the IQS kinetic code for amplitude function calculation. Some results include amplitude function distribution, fuel temperature and coolant outlet temperature changing with time, and updating kinetic parameters that can be obtained while introducing transient conditions or other control conditions. The IQS kinetic code includes the lumped parameter thermal model. Next, the shape function in the next time step is estimated by the shape function in the previous time step and its first derivative. Then, the non-homogeneous term of the shape function equation is passed to the MC code as the external neutron source, and the shape function and kinetic parameters of this time step can be obtained. After that, the amplitude function calculated by the IQS dynamic code is multiplied by the shape function of the corresponding time calculated by the MC code to obtain the normalized neutron flux distribution in the current step. Similarly, the normalized power distribution can be obtained. Finally, the aforementioned process is repeated to perform the coupling calculation of the amplitude function and the shape function in the next time step until the end of the simulation.

The IQS/MC computing platform contains the Monte Carlo transport code and kinetic parameters such as calculation module, IQS dynamic module, thermal module, and control interface module, which can achieve automatic calculation of the transient process and the step-by-step human–computer interaction. The first part is the preparatory work, which can prepare the MC code and relevant input files. The next part is setting thermal parameters, such as the mass of fuel and coolant, specific heat capacities of fuel and coolant, and heat transfer coefficient between fuel and coolant. Next, the calculation of kinetic parameters is performed. Its function is to set the core parameters, calculate the relevant kinetic parameters, and pass the results to the IQS dynamic module. Finally, the transient calculation is performed, which can achieve the automated coupling calculation of amplitude function and shape function.

3 Comparison of simulated results and reference data

Dynamic computation plays an important role in the accelerator-driven sub-critical system, so the purpose of this article is to calculate the kinetic parameter and neutron flux change in the transient process of beam interruptions and reactivity insertion. In the process of beam interruptions, all the control devices are lifted to the highest position at three different sub-critical levels. Also, in the process of reactivity insertion, this article will study the dynamic process of double safety rods in the whereabouts of course.

The correctness of the IQS kinetic code with the external neutron source coupling lumped parameters thermal model has been verified in the literature (Wu et al., 2015). Also, in the past work, we have carried out point kinetic calculation and IQS/MC calculation for the CiADS (China initiative Accelerator Driven System) model with the thermal model. The simulation results show that the IQS/MC method is suitable for transient safety analysis of ADS neutron space–time dynamics (Song et al., 2017). After the CiADS model was calculated by the point kinetic method and the IQS/MC method, an experimental facility is simulated by the IQS/MC method in this article. By comparing the simulated results with the reference data, the reliability of the method can be further verified.

3.1 Beam interruption process

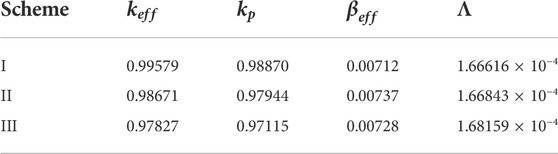
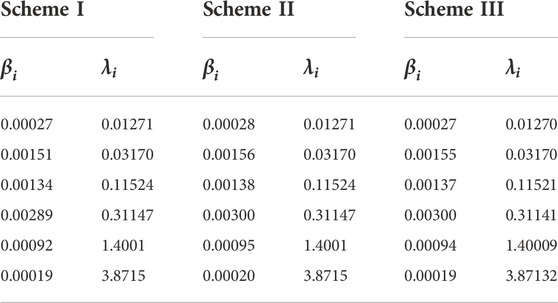
Neutron space–time dynamic parameters of the three sub-critical schemes of the experimental facility including the effective multiplication factor, prompt effective multiplication factor, delayed neutron fraction, and effective neutron generation time are calculated using the MC code, which is shown in Table 1. Also, the grouped effective fraction of delayed neutrons and the decay constant of the precursor are shown in Table 2. Also, the calculation details of neutron kinetic parameters are as follows:

TABLE 1

TABLE 1. Kinetic parameters of the three layout schemes.

TABLE 2

TABLE 2. Grouped delayed neutron effective fraction and decay constant.

The effective multiplication factor, $k_{eff}$, was performed by the MC code using the KCODE option. The prompt effective multiplication factor, $k_p$, can be obtained by adding the “totnu no” option based on the calculation method of $k_{eff}$. The effective delayed neutron fraction, ${\beta }_{eff}$, is the fraction of delayed neutrons in the core at creation, and it is obtained via the following formula in specific calculation. Also, the prompt neutron generation time, $\Lambda =l/k_{eff}$, is easily obtained through the MC code.

${\beta }_{eff}=1-\frac{k_p}{k_{eff}}.(24)$

Figure 2 shows the comparison of the simulation results and reference results of three schemes in the process of beam interruptions, and the neutron flux under a stable state is seen as the reference value of normalized neutron flux. In this calculation process, the time steps of the amplitude function and shape function are 10⁻⁶ s and 10⁻² s, respectively. From the results of normalized neutron flux, it is shown that the variation is almost synchronized with the external neutron source. Also, the relative counts of three layout schemes are rapidly reduced to a stable level compared with the initial state within 10 s. It can be seen that the variation law and range of simulation results are in good agreement with the reference results, which show that the IQS/MC method is reliable in simulating the dynamic behavior of the beam transient.

FIGURE 2

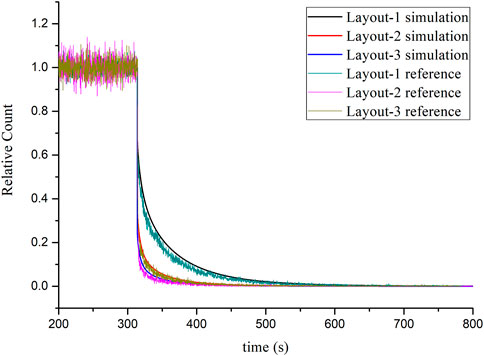
FIGURE 2. Comparison of simulation results and reference results of three schemes in the process of beam interruptions.

3.2 Reactivity insertion process

In the condition of reactivity introduction, this article will study the dynamic behavior of double safety rods inserted into a reactor. The negative reactivity of the safety rod is introduced by means of free falling. We set the total falling distance to 108.65 cm and gravity to 9.8 m/s², so the total free-fall time is 0.47 s. The falling distance is randomly divided into 10 state points: 0, 30, 40, 50, 60, 70, 80, 90, 100, and 108.65 cm in dynamic calculation. In the process of double safety rod falling simulation, the two safety rods fall synchronously, and the time steps of the amplitude function are 10⁻⁶ s.

Figure 3 shows the comparisons for the transient variation of normalized neutron flux between the reference and the simulated values during the process of the double safety rods inserted into the reactor at different sub-critical levels, and the neutron flux under a stable state can be regarded as the reference value of normalized neutron flux. Figure 3 indicates that the trends of the normalized neutron flux after the double safety rod is inserted into the reactor calculated by IQS/MC and reference data are the same, and the difference is less than 3%. The normalized neutron fluxes are rapidly reduced when a double safety rod is inserted, and the values are slowly attenuated to a stable level under the action of delayed neutrons. At the same time, the deeper the sub-critical degree is, the lower the attenuation amplitude of the relative count is. In addition, the reference data in Figure 3 have significant fluctuations and some obvious data peaks. The main reason is that during counting processing, in order to reflect the dynamic behavior of fast-falling processes, the output unit of the detector’s counting is small, so the data fluctuations are more obvious.

FIGURE 3

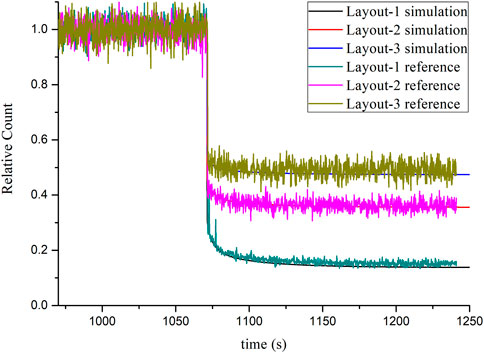
FIGURE 3. Comparison of simulation results and reference results of the three schemes in the double safety rod falling process.

Above all, the simulated and reference values show good agreement on the changing trend under different critical levels in the process of safety rod inserted into the reactor, which indicates that the IQS/MC method has certain reliability on the dynamic response behavior of the safety rod insertion condition of the experimental facility. There are two main reasons to explain the numerical difference between the simulation results and the reference results:

(1) One-thousandth change in the effective multiplication factor of the reactor will have a great impact on stable-level data, so it is the main reason for the difference between simulated and reference data. In order to make the simulated data conform to the reference data better, the initial effective multiplication factor of the reference scheme should be increased, and the adjustment range should not be more than 1%.

(2) The difference in the safety rod value between simulation and reference processes will have a great influence on the change range, which also causes the difference between the simulated data and reference data.

4 Conclusion

The neutron kinetic behavior of the accelerator-driven sub-critical system strongly depends on the characteristics of the external neutron source. In order to study the neutron space–time dynamics of ADS, a method named IQS/MC has been adopted to simulate and analyze the neutron kinetic behavior of an experimental facility.

In this article, the IQS/MC method was used to simulate two transient conditions of beam interruptions and double safety rods inserted into the core of a reactor under three sub-critical layout schemes for an experimental facility, and transient variation of the normalized neutron flux was obtained. In addition, the simulation results were compared with the reference data, and the numerical results calculated by the IQS/MC method were found consistent with the dynamic response behavior changes in the process, which indicates that the method has high reliability and applicability and can provide an important reference for the subsequent design analysis work of the sub-critical facility.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

QG contributed to the conception and design of the study and wrote the sections of the manuscript. ZL organized the structure of the manuscript and gave some suggestions for writing the manuscript. YZ performed the statistical analysis. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was supported by the Guangdong Basic and Applied Basic Research Foundation (Grant Nos. 2020B1515120035, 2021A1515010265, and 2022A1515011462) and the Advanced Core Design and Reactor Shielding Design Technology (Grant No. R-2020ZBREC010).

Conflict of interest

Authors QG, ZL, and YZ were employed by China Nuclear Power Technology Research Institute Co., Ltd.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bentley, C., Demeglio, R., Dunn, M., Goluoglu, S., Norton, K., Pevey, R., et al. (1997). Development of a hybrid stochastic/deterministic method for transient, three dimensional neutron transport. in Paper presented at the American Nuclear Society (ANS) international meeting on advanced reactors safety, Orlando, FL (United States), 1-5 Jun 1997.

Google Scholar

Cammi, A., Luzzi, L., Porta, A. A., and Ricotti, M. E. (2006). Modelling and control strategy of the Italian lbe-xads. Prog. Nucl. Energy 48 (6), 578–589. doi:10.1016/j.pnucene.2006.03.006

CrossRef Full Text | Google Scholar

Chadwick, M. B., Herman, M., Oblozinsky, P., Dunn, M., Danon, Y., Kahler, A., et al. (2011). ENDF/B-VII.1 nuclear data for science and Technology: Cross sections, covariances, fission product yields and decay data. Nucl. Data Sheets 112 (12), 2887–2996. doi:10.1016/j.nds.2011.11.002

CrossRef Full Text | Google Scholar

Dulla, S., Ravetto, P., Rostagno, M. M., Bianchini, G., Carta, M., and D’Angelo, A. (2005). Some features of spatial neutron kinetics for multiplying systems. Nucl. Sci. Eng. 149 (1), 88–100. doi:10.13182/NSE149-88

CrossRef Full Text | Google Scholar

Gandini, A., and Salvatores, M. (2002). The physics of subcritical multiplying systems. J. Nucl. Sci. Technol. 39 (6), 673–686. doi:10.1080/18811248.2002.9715249

CrossRef Full Text | Google Scholar

He, M. T., Wu, H. C., Zheng, Y. Q., Wang, K., Li, X., and Zhou, S. (2015). Beam transient analyses of accelerator driven subcritical reactors based on neutron transport method. Nucl. Eng. Des. 295, 489–499. doi:10.1016/j.nucengdes.2015.10.021

CrossRef Full Text | Google Scholar

Hindmarsh, A. C. (1980). LSODE and LSODI, two new initial value ordinary differential equation solvers. SIGNUM Newsl. 15 (4), 10–11. doi:10.1145/1218052.1218054

CrossRef Full Text | Google Scholar

Li, J. Y., Gu, L., Yu, R., Nadezda, K., and Xu, H. S. (2017). Development and validation of burnup-transport code system OMCB for accelerator driven system. Nucl. Eng. Des. 324, 360–371. doi:10.1016/j.nucengdes.2017.09.012

CrossRef Full Text | Google Scholar

Merk, B. (2009). An analytical approximation solution for a time-dependent neutron transport problem with external source and delayed neutron production. Nucl. Sci. Eng. 161 (1), 49–67. doi:10.13182/NSE161-49

CrossRef Full Text | Google Scholar

Merk, B., and Glivici-Cotruţă, V. (2012). Solutions without space-time separation for ads experiments: Overview on developments and applications. Sci. Technol. Nucl. Installations 2012 (1), 1–11. doi:10.1155/2012/140946

CrossRef Full Text | Google Scholar

Mikityuk, K., Coddington, P., Pelloni, S., Bubelis, E., and Chawla, R. (2007). Comparative transient analysis of critical and subcritical 80-MW Pb-Bi eutectic-cooled reactor systems. Nucl. Technol. 157 (1), 18–36. doi:10.13182/nt07-a3799

CrossRef Full Text | Google Scholar

Rineiski, A., and Maschek, W. (2005). Kinetics models for safety studies of accelerator driven systems. Ann. Nucl. Energy 32 (12), 1348–1365. doi:10.1016/j.anucene.2005.03.007

CrossRef Full Text | Google Scholar

Shibata, K., Iwamoto, O., Nakagawa, T., Iwamoto, N., Ichihara, A., Kunieda, S., et al. (2011). JENDL-4.0: A new library for nuclear science and engineering. J. Nucl. Sci. Technol. 48 (1), 1–30. doi:10.1080/18811248.2011.9711675

CrossRef Full Text | Google Scholar

Sjenitzer, B. L., and Hoogenboom, J. E. (2013). Dynamic Monte Carlo method for nuclear reactor kinetics calculations. Nucl. Sci. Eng. 175 (1), 94–107. doi:10.13182/NSE12-44

CrossRef Full Text | Google Scholar

Song, Y. M., Gao, Q. Y., Xu, Y. C., Wang, K., Yang, Y-W., Zhang, L., et al. (2017). Simulation analysis of neutron time-space kinetics for ADS sub-critical reactor based on IQS/MC method. Atom Energy Sci. Technol. 51 (3), 450–456. doi:10.7538/yzk.2017.51.03.0450

CrossRef Full Text | Google Scholar

Suzuki, T., Chen, X. N., Rineiski, A., Rineiski, A., and Maschek, W. (2005). Transient analyses for accelerator driven system pds-xads using the extended simmer-iii code. Nucl. Eng. Des. 235 (24), 2594–2611. doi:10.1016/j.nucengdes.2005.06.012

CrossRef Full Text | Google Scholar

Wu, C. Y., Song, Y. M., Zhou, J. L., Wen, L., and Zhichao, Z. (2015). Simulation of dynamic properties of ADS subcritical reactor. J. Univ. South China (Science Technol.) 29 (2), 10–13. doi:10.19431/j.cnki.1673-0062.2015.02.004

CrossRef Full Text | Google Scholar

Zhitnik, A. K., Ivanov, N. V., Marshalkin, V. E., Ognev, S. P., Pevnitsky, A. V., Povyshev, V. M., et al. (2005). Code TDMCC for Monte Carlo computations of spatial reactor core kinetics. in Paper presented at the proceedings of the Monte Carlo Method: Versatility Unbounded In A Dynamic Computing World, Chattanooga, Tennessee, USA, April 17-21, 2005.

Google Scholar