
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Energy Res. , 23 September 2022
Sec. Smart Grids
Volume 10 - 2022 | https://doi.org/10.3389/fenrg.2022.1008099
This article is part of the Research Topic Smart Grid Opportunities and Challenges in Integrating Renewable Energies View all 10 articles
 Shahid Aziz Khan1
Shahid Aziz Khan1 Jamshed Ahmed Ansari2
Jamshed Ahmed Ansari2 Rashid Hussain Chandio2
Rashid Hussain Chandio2 Hafiz Mudassir Munir2
Hafiz Mudassir Munir2 Mohammed Alharbi3*
Mohammed Alharbi3* Abdulaziz Alkuhayli3
Abdulaziz Alkuhayli3Electric power industry is continually adopting new techniques to improve the reliability and efficiency of the energy system and to cope with the increasing energy demand and the associated technical challenges. In recent years, the maturation of Artificial Intelligence (AI) led researchers to solve various problems in the power system by using AI techniques. Voltage Source Converter is the result of advancements in the field of power electronics and semiconductors technology, which holds a promising future for the realization of smart grid, renewable energy integration, and HVDC transmission system. Usually hit and trial method or the design engineer’s experience is used for the manual tuning of the PI controllers, which cannot yield superior performance. The process becomes more complicated when multiple grids are involved, such as in VSC-based MTDC grids. This research article use a deep learning optimization technique for the tuning of the VSC controllers, which resulted in quick settling time, better slew rate, less undershoot and low overshoot. The deep learning neural network is trained through the Particle Swarm Optimization (PSO) algorithm to produce the best possible tuned or optimally tuned parameters for the controllers. The optimal tuning of the controller will result in an overall better performance of the converter and the grid. A four-layered deep learning neural network and a three-terminal MTDC grid were designed and simulated in MATLAB/SIMULINK environment.
The power system is undergoing revolutionary changes due to technological advancement, high computational resources, increasing demand, and focus on green energy. Many countries such as China, E. U. members, Australia, etc., are working to shift a significant proportion of their energy consumption from conventional to renewable sources. As a result, there is an increased influx of renewable energy into the system. However, the system cannot readily absorb and distribute this incoming energy. Unlike conventional sources, renewable energy sources cannot be scheduled and are sometimes connected directly to the distributed system instead of the transmission system (Freris and Infield, 2008). The integration of such time variables and distributed sources into the electrical network requires special consideration.
Multi-terminal direct current (MTDC) grids are overlaying their counterparts due to the advantages and flexibility in terms of large-scale integration of remotely located renewable energy resources into the existing AC grids (RODRIGUEZ and ROUZBEHI, 2017). Energy conversion is done through converters such as the matured line commutated converters, the recent voltage source converter, the advanced modular multilevel converter, etc., VSC is a developing technology because of its benefits, such as independent power control, low power loss, dynamic response, etc., (Reed et al., 2003). Inside the VSC converter, PI controllers are used to control the operation of the converter. PI controller is very famous in industrial systems due to its ease of implementation and robustness. The PI controller helps drive the system variables to their target values through the variation of l gain and time constant (O'Dwyer, 2009). The performance of the converter depends on how accurately the controller is tuned. Typically, no specialized or intelligent technique is adopted for the tuning process; instead, the hit and trial method or the engineer’s experience is used to tune the PI controller manually. However, the situation becomes complex when multiple grids are interconnected, such as in MTDC grids. So, with the advancement in grid interconnection, an intelligent technique must be adopted to tune the PI controllers, which can lead to better response and performance. In this research article, a deep learning technique is applied for the tuning of the controllers to yield the best responses in terms of slew rate, settling time, undershoot and overshoot. Although the transformation rate of power generation, transmission, and distribution technology is relatively slow, the power industry researchers are trying to apply AI to every possible section of the power system. For instance, AI has proven to be of great help in power system planning, scheduling, and control (Madan and Bollinger, 1997; Yousaf et al., 2021; Sharma et al., 2022).
The majority of the industrial processes use PI controllers due to their robustness and reliable performance. The recent industrial advancement leads to the development of systems with multipThele and complex closed-loop systems. The performance of these systems greatly depends on how small is the error. So, the tuning of the PI controller is important and directly impacts the overall performance. The control loops for which random tuning may not be sufficient are subjected to various tuning and optimization techniques. A model predictive-based tuning technique was presented in (O’Dwyer, 2003) which was primarily designed to produce quarter decay responses. The Direct Synthesis method (Seborg et al., 2004) is becoming popular amongst engineers due to its ability to tune through a single tuning parameter which has a significant effect on the performance of the closed-loop. The AMIGO tuning rule is based on the 63% step response experiment (Åström et al., 2006) The objective of this method is to minimize error and disturbances. The SIMC optimization or tuning method was obtained through the reduction of the higher models using the half rule approach (Skogestad, 2003).
In (He et al., 2000) an optimal tuning technique based on LQR (Linear Quadratic Regulator) approach is presented. This method is useful for the process that involves time delay and is of low order. The proposed LQr criteria lead to the desired natural frequency and damping ratio. In (Kookos et al., 1999) an online PI controller tuning method for dead time processes is explained, specifically suitable for various chemical processes. This model is an approximation of various complex models such as the first-order plus dead time model having large time constants. A fractional-order proportional and derivative (FOPD) was explained in (Li et al., 2010). This method is specifically beneficial for the application of fractional-order controllers having complicated closed loop. For closed loops systems a droop control optimization (Khan and Ahmed, 2020) technique is also widely used but it doesn’t involve optimization on the controller level.
Moreover, Literature depicts multiple classical and modern optimization or tuning techniques for the PI controller. Due to the widespread industrial applications of the PI or PID controller, it is a well-searched area. More than ninety percent of the industrial system still uses PI or PID controllers due to its ease of implementation and robustness.
Classical techniques are based on assumptions about the plant and output. These assumptions help the controller to reach the optimal setting (Liu and Ansari, 2020). However, classical optimization techniques seem simple and robust, but the desired response may not be obtained due to the assumptions involved.
Ziegler Nichols and Cohen Coons methods are among the classical introductory techniques discovered. The Nichols technique was based on the assumption (Izci, 2021), (Araki and Unbehauen, 2020), while the Coons method involved the FOLPD model (Ziegler and B Nichols, 1942), (Salunkhe et al., 2018). Coons method was built on a better model, but there is no significant difference between the performance of both methods. Specifically, the Nichols method cannot evaluate system parameters in an environment with noisy conditions. The drawback associated with the Coons method under abnormal conditions is the fact that it pushes the system towards instability. It is evident from the literature that complex, intelligent techniques were built from simple logic, such as the Immune algorithm was inspired by the vertebrate immune system. It is a system that protects the internal system from foreign objects. The optimum response is generated based on Learning about the antigen to generate an optimized response (Sebtahmadi et al., 2017).
Ant Colony Optimization technique was inspired by an ant colony and is based on a meta-heuristic approach. This algorithm works like insects looking out for food by following the optimal path (Al-Mogren, 2008), (Dai et al., 2017). Genetic Algorithm (G.A.) navigates the search, similar to the pattern of evolution in nature. It utilizes cost functions and probabilistic rules (Gonçalves et al., 2018). The name genetic comes from the fact that the solution is represented in binary format which is similar to genetic representation (Oshaba et al., 2017). The Differential Evolution (D.E.) technique is used for problems that require numerical optimization. This problem gradient is not known in detail to complete this procedure. The need for a gradient is eliminated because it works in a way that doesn’t require the need for a gradient and results in quality (Geweda et al., 2017).
Another global optimization technique is Evolutionary Programming (E.P.) which involves the steps of initialization, mutation, competition, and reproduction. A quasi-random sequence (QRS) is applied to generate the initial sequence (Liang et al., 2020). Annealing (Badar et al., 2022), Vector Support Machine (SVM) (Kumar et al., 2008) and Surface Method response (Reynoso-Meza et al., 2016) are among the other methods which are not too popular because these are very specifically used for a narrow category of applications.
In one of the popular methods called Particle Swarm Optimization, in search for the optima, a particle population moves through the solution, while keeping track best solution (local and global) (Najeeb et al., 2017). PSO leads to better responses than G.A. The drawback of PSO is its property falls into a local optimum. In this research, the PSO algorithm is used to train the deep learning neural network. The normal way to train the neural network is through the data sets, but in this particular application due to the unavailability of the data set and due to the nature of the problem PSO algorithm is used to train the neural network (Zhao et al., 2015).
Inspired by the biological neural network, in Artificial Neural Network (ANN) there are artificial neurons that can be multilayered. To process the data, a connectionist approach is applied (Ilten and Demirtaş, 2016). AI technology is based fundamentally on ANN, extending to the concepts of deep learning and machine learning. ANN is applied to solve complex nonlinear problems. This research adopted a deep learning technique due to its self-learning capability. The successful implementation of deep learning networks depends upon two key parameters, i.e., hidden layers and neurons in each hidden layer. The performance of the deep learning network depends upon the setting of these two key parameters. However, setting them manually or through the grid search method is time-consuming. PSO algorithm has a great potential to optimize parameter settings (Behera et al., 2016). Apart from industrial processes the applications relating to power system can be found in the literature this research is focused on the power system application and optimization (Ehsan et al., 2021; Shehzad et al., 2021; Chi et al., 2021; Autonomous, 2021; Guasti Junior and Santos, 2021; Lau and Lim, 2018; Fan et al., 2019; Hu and Eberhart, 2002; Dashtdar et al., 2022; Soliman et al., 2021).
The novelty of this research lies in the selection of optimization techniques, i.e., deep learning. The deep neural network is trained through a particle swarm optimization (PSO) algorithm. Previously deep Learning has been applied for image processing, signal processing, computer vision, power system planning, etc., But it has never been applied to the optimization of a VSC controller in a power system setting. This research focuses on the application of deep Learning for power system optimization in a VSC-MTDC grid system.
This work can also be considered an improved version of our previous work, in which fuzzy logic was applied to optimize such systems (Qolomany and Maabreh, 2017). The results of this deep learning optimization are much better than the fuzzy logic technique, so it forms the foundation for applying the artificial intelligence techniques for power system optimization and control. The key contributions of this paper include:
1) An AI-based optimization technique has been exploited for the optimization of power converters Controller (PI tuning).
2) Optimization of the weights and biases of the neural network has been undergone using the Particle Swarm Optimization technique.
3) A step forward towards the application of AI on power systems.
4) Improved performance of the converter in terms of overall stability, overshoot, undershoot, settling time, and slew rate.
5) Increased reliability of the system by combining the benefits of AI-based optimization with the robustness of PI controller.
The paper is structured as follows:
The introduction section focuses on the background and the need for an intelligent and self-learning optimization method for power converters. The second section which is a literature review covers all the significant work already done in this domain. It includes all the optimization techniques that are reported and can be applied to power system problems. It also mentions the drawback of every technique and that is why need to improve the existing techniques. In the third section of the methodology, we covered the steps involved to realize our proposed solution. It focuses on the construction of the deep learning network, mathematical modeling, and how the PSO algorithm is applied to optimize the weights and biases of the neural network itself.
The result and analysis section compares and analyzes the obtained simulated results. From the graphs and table, the superior performance of the proposed solution is proved as compared to other traditional techniques.
The conclusion concludes the contribution of the proposed strategy and it also mentions the future potential research areas in this domain to extend this optimization approach to other converters.
The deep Learning-based optimization process involves the following steps and methodology.
Deep Learning algorithms process the data through various layers of neural network algorithms. In simple words, deep learning refers to the training of the neural network. The neural network consists of several neurons. A neuron can be understood as a building block of a neural network. A network comprises three layers, i.e., input layer, hidden layer, and output layer. The two key hyperparameters that control the network topology include the number of layers and the number of nodes inside each hidden layer.
The input layer is responsible for passing on the initial information to the network. The hidden layer is located between the input and output layer, where all the computations are performed. The outer layer is responsible for producing the results based on the inputs and computations. In the research problem investigated in this article, we have two inputs [error (e) and the derivative of error (de)]. We have three hidden layers, and each hidden layer contains four neurons. The outputs are the optimized parameters for the PI controller, i.e., “Kp” and “Ki.” Figure 1 shows the architecture of the constructed network.
The target value of the error is set at
A feed-forward network architecture was chosen while constructing the neural network (Babaie et al., 2019), (Shehzad et al., 2021). In a feed-forward neural network, the node connections don’t form a cycle. In this case, multiple layers of computational units are connected in a feed-forward manner. Figure 2 shows the interconnections of a feed-forward network with two inputs (
A mathematical representation can help to understand the whole interconnected network and the interaction of these neurons with each other easily. Going forward, the format used to indicate the weights and biases associated with a neuron is as follows
Here, we have two inputs and four neurons in each hidden layer. So, the corresponding weighted matrixes can be written as (Chi et al., 2021),
To compute the pre-activation functions for each neuron of each hidden layer, consider the generic expression of the pre-activation function shown in Eq. 5.
The activation at each layer is equivalent to applying a sigmoid function to the pre-activation of that respected layer. The expression for activation at each layer is depicted in Eq. 6.
Where “g” is called the activation function.
We can compute the pre-activation for each neuron of each layer in the following manner (Autonomous, 2021).
Eqs 7, 8, 9, 10 represent the pre-activation for the four neurons in the first hidden layer.
In short, the pre-activation of the first layer is given by (Guasti Junior and Santos, 2021)
Similarly, the pre-activation and activation functions for the remaining layers can be computed following the above topology.
The normalized mean square error (NMSE) approach is used to optimize the error values. The pseudo-code showing the input arguments to the NMSE handle and the error calculation is given by (Qolomany and Maabreh, 2017).
h = @ (x) NMSE (x, net, inputs, targets);
NMSE = mean (error.^2)/mean [var (target′,1)];
Figure 3 represents the error histogram generated after the training of a controller.
Considering the nature of the research problem, which involves MTDC grids, many variables keep on varying. To improve the accuracy of the deep learning algorithm, a PSO algorithm is used to find the optimum values for the weights and biases of the neural network. It also optimizes the computational time and the fitting regression, along with minimizing the mean square error. PSO was inspired form the swarm movement, which depends upon the individual and neighboring experience. PSO algorithm can be understood via four steps approach. The first step is the initiation and selection of a random population and particle, respectively. In the second step, the fitness of the previous
Where
A three-terminal VSC MTDC system with radial topology has been built in SIMULINK to test the proposed optimization strategy. The whole test system comprises of three AC grids synchronized and connected with each other. The goal of the system is do generate a stable DC output for a HVDC system to ensure the reliable performance. The layout is shown in Figure 5.
The system consists of three AC grids. The apparent power is 200 MVA, 230 kV, and the frequency is 50 Hz.
This section verifies the superior performance of the deep Learning-based optimized PI controller by comparing it with a randomly tuned PI controller. The performance parameters for the designed system include DC voltage, active power, and reactive power. We will compare the parameters like overshoot, undershoot, settling time, etc., to verify the optimal performance.
A smooth output DC voltage ensures the stable operation of the HVDC system and good power quality. To test our designed system for the worst-case scenario, faults were created. Figure 6 shows the response of the DC voltage for a randomly tuned PI controller. While Figure 7 shows the curve obtained after optimizing the PI controller using the proposed deep learning strategy. It is evident that the performance of deep learning optimization is superior in terms of various parameters, as shown in Table 1.
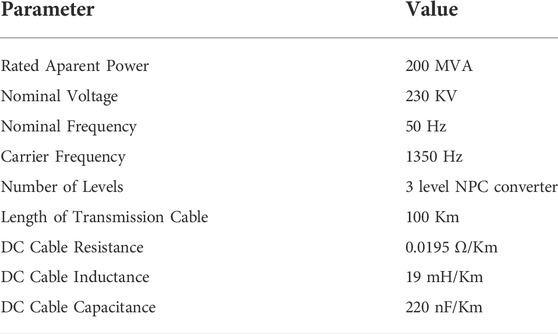
TABLE 1. Shows a comparison of an AI-based optimized PI controller and a PI controller. It is verified from the values of the performance parameters that the responses of the optimized controller are better regarding the mentioned parameters in Table 1.
Considering the time axis at t = 1.5 s, a −0.1p. u step is introduced to the ref, DC voltage. At 2.5 s, a 3-phase to ground fault is created. The proposed deep Learning-based optimized system recovers in 0.083 s, whereas the simple controller recovers in 0.205 s, confirming the superiority of the deep learning optimization PI. Both these graphs show that for a randomly tuned PI controller, the response is not smooth and is oscillating, which can also lead to severe system damage. But after applying the proposed strategy, the graph becomes stable and smooth, even after the fault, ensuring a reliable and stable system.
It should be noted that the simple PI in this paper refers to the classic PI controller which is tuned by hit and trial method or according to the experience of the design engineer. The comparison is between the randomly tuned and the one tuned with the proposed strategy. Other PI tuning techniques are discussed in Section 1 of this paper along with their advantages and disadvantages. Applying all those techniques to pour specific converter problem and then comparing it would result in complexity, so the shortcomings of those methods are highlighted.
The active and reactive power curves are crucial in determining the power quality, reliability, and system stability. The system is tested under transient conditions to verify the reliability of the proposed controller. Figures 8, 9 show the active power responses for a typical PI controller and deep learning-based optimized PI controller, respectively.
It is evident from Table 2 that the performance parameters of deep Learning-based optimized PI controllers are much better than a randomly tuned PI controller. The smooth and constant supply of active and reactive power is crucial for the loads. In the randomly tuned case, the graph shows very unsettling behavior, which is not good for the load and the overall system. By implementing our proposed strategy, In Table 3 we saw that the graph is now better and more stable than the previous version, thus ensuring a more reliable, efficient, and stable system.
Figures 10, 11 depict the reactive power responses for an AI-based optimized and a normal PI controller, respectively. it can be observed that in Table 4 and Table 5 the response of the AI-based optimized controller is smooth and contains less distortion, which helps to maintain the power stability of the system.

TABLE 4. Compares the performance parameters of the two reactive power curves. It is evident that the optimized controller yields a better response regarding the mentioned parameters in Table 3.
Figure 12 shows the real simulated system configuration.
A deep learning optimization technique for the VSC-MTDC was proposed and tested in this article. The proposed technique combines the benefits of artificial intelligence with the PI controller to achieve the best possible system response. A 200 MVA system was tested and the PI controllers were tuned using the deep learning algorithm. Performances with the classical tuning methods were compared and it was confirmed that the proposed strategy yields the best results in terms of overshoot, undershoot etc. To test the reliability of the proposed controllers, the system was tested under normal and transient operating conditions. Results and analysis of the performance parameters confirm the superior performance of the optimized PI controller using deep Learning. As a future trend in the development of a super grid or flexible distribution network, deep learning or AI can be applied to various other aspects of the power systems. This research is limited to two-level VSC topology and cannot be readily applied to MMC or any other converter without proper research and exploration. As a future goal, the optimization of MMC needs further research and exploration.
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
SK and JA did all the software modeling and mathematical calculations. HM and RC helped to analyze the results and compare it with traditional methods. MA and AA helped in writing the paper and reviewing the overall project.
This work was supported by the Researchers Supporting Project number (RSP2022R467), King Saud University, Riyadh, Saudi Arabia.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Al-Mogren, A. S. (2008). Energy adaptive approach in a multi-channel dissemination-based network. New Technol. Mobil. Secur. 2008, 1–6. doi:10.1109/NTMS.2008.ECP.44
Araki, M. (2020). “PID control in control systems, robotics and automation, vol II,” in Encyclopedia of life Support systems (EOLSS), developed under the auspices of the UNESCO. Editor Heinz Unbehauen (Oxford, UK: Eolss Publishers). Available from https://www.researchgate.net/publication/316990192_PID_Controller_Tuning_Techniques_A_Review.
Åström, K. J., Hägglund, T., and Astrom, K. J. (2006). Advanced PID control, 461. Research Triangle Park, NC: ISA-The Instrumentation, Systems, and Automation Society.
Autonomous, Author (2021). Depth-explanation-of-feedforward-in-neural-network-mathematically. Available at https://medium.com/analytics-vidhya/in-depth-explanation-of-feedforward-in-neural-network-mathematically-448092216b63. (Accessed 11 November 2021).
Babaie, M., Sharifzadeh, M., and Al-Haddad, K. (2019). “Adaptive ANN based single PI controller for nine-level PUC inverter,” in 2019 IEEE Electrical Power and Energy Conference (EPEC), 1–6.
Badar, J., Hussain, R., Ahmed Ansari, J., and Munir, H. M. (2022). A detailed review of MMC circuit topologies and modelling issues. Int. Trans. Electr. Energy Syst., 1–17. doi:10.1155/2022/8734010
Behera, S., Subudhi, B., and Pati, B. B. (2016). Design of PI controller in pitch control of wind turbine: A comparison of PSO and PS algorithm. Int. J. Renew. Energy Res. (IJRER) 6 (1), 271–281.
Chi, H. R., Domingues, M. d. F., Kostromitin, K. I., Almogren, A., and Radwan, A. (2021). Spatiotemporal D2D small cell allocation and on-demand deployment for microgrids. IEEE Access 9, 116830–116844. doi:10.1109/ACCESS.2021.3105750
Dai, A., Zhou, X., and Liu, X. (2017). Design and simulation of a genetically optimized fuzzy immune PID controller for a novel grain dryer. IEEE Access 5, 14981–14990. doi:10.1109/access.2017.2733760
Dashtdar, M., Sarada, K., Hosseinimoghadam, S. M. S., Kalyan, C. H. N. S., Venkateswarlu, A. N., Goud, B. S., et al. (2022). Faulted section identification and fault location in power network based on histogram analysis of three-phase current and voltage modulated. J. Electr. Eng. Technol. doi:10.1007/s42835-022-01079-2
Ehsan, Umer, Jawad, Muhammad, Javed, Umar, Zaidi, K. S., Rehman, A. U., Rassõlkin, Anton, et al. (2021). A detailed testing procedure of numerical differential protection relay for EHV auto transformer. Energies (Basel). 14 (24), 8447. doi:10.3390/en14248447
Fan, G. F., Guo, Y. H., Zheng, J. M., and Hong, W. C. (2019). Application of the weighted k-nearest neighbor algorithm for short-term load forecasting. Energies 12 (5), 916. doi:10.3390/en12050916
Geweda, A. E., El-Gohary, M. A., El-Nabawy, A. M., and Awad, T. (2017). Improvement of vehicle ride comfort using genetic algorithm optimization and PI controller. Alexandria Eng. J. 56 (4), 405–414. doi:10.1016/j.aej.2017.05.014
Gonçalves, L. C., Santos, M. F., da Silva, J. L., and Rezende, H. B. (2018). “Development of a PI controller through an ant colony optimization algorithm applied to a SMAR® didactic level plant,” in 2018 19th International Carpathian Control Conference (ICCC), 150–155.
Guasti Junior, W., and Santos, I. P. (2021). “Solving differential equations using feedforward neural networks,” in Computational science and its applications – iccsa 2021. Iccsa 2021. Lecture notes in computer science. (Cham: Springer), 12952. doi:10.1007/978-3-030-86973-1_27
Gupta, T. K., and Raza, K. (2020). Optimizing deep feed-forward neural network architecture: A tabu search based approach. Neural process. Lett. 51 (3), 2855–2870. doi:10.1007/s11063-020-10234-7
He, Jian-Bo, Wang, Qing-Guo, and Lee, Tong-Heng (2000). PI/PID controller tuning via LQR approach. Chem. Eng. Sci. 55, 2429–2439. doi:10.1016/S0009-2509(99)00512-6
Hu, X., and Eberhart, R. (2002). “Multiobjective optimization using dynamic neighborhood particle swarm optimization,” in Proceedings of the 2002 Congress on Evolutionary Computation, 1677–1681.2
Ilten, E., and Demirtaş, M. (2016). Off-line tuning of fractional order PI lambda controller by using response surface method for induction motor speed control.
Izci, D. (2021). Design and application of an optimally tuned PID controller for DC motor speed regulation via a novel hybrid Lévy flight distribution and Nelder–Mead algorithm. Trans. Inst. Meas. Control 43 (14), 3195–3211. doi:10.1177/01423312211019633
Khalid, M. U., Javaid, Nadeem, Ahmad, Almogren, Ahmed, Abrar, Gulfam, Sardar Muhammad, and Radwan, Ayman (2022). Cooperative energy transactions in micro and utility grids integrating energy storage systems. J. Parallel Distributed Comput. 161, 48–62. doi:10.1016/j.jpdc.2021.11.006
Khan, L., and Ahmed, J. (2020). “Unified voltage droop control strategy for VSC-MTDC in HVDC system,” in The 16th IET International Conference on AC and DC Power Transmission (ACDC 2020), 846–851. doi:10.1049/icp.2020.0184
Kookos, I. K., Lygeros, A. I., and Arvanitis, K. G. (1999). On-line PI controller tuning for integrator/dead time processes. Eur. J. control 5 (1), 19–31. doi:10.1016/s0947-3580(99)70134-2
Kumar, S. M. G., Jain, R., and Anantharaman, N. (2008). Genetic algorithm based PID controller tuning for a model bioreactor. Indian Chem. Eng. 50 (3), 214–226.
Lau, M. M., and Lim, K. H. (2018). “Review of adaptive activation function in deep neural network,” in 2018 IEEE-EMBS Conference on Biomedical Engineering and Sciences (IECBES), 686–690.
Li, H., Luo, Y., and Chen, Y. (2010). A fractional order proportional and derivative (FOPD) motion controller: Tuning rule and experiments. IEEE Trans. Control Syst. Technol. 18 (2), 516–520. doi:10.1109/TCST.2009.2019120
Liang, H., Zou, J., Zuo, K., and Khan, M. J. (2020). An improved genetic algorithm optimization fuzzy controller applied to the wellhead.
Liu, S. A. C., and Ansari, J. A. (2020). Centralized fuzzy logic based optimization of PI controllers for VSC control in MTDC network. J. Electr. Eng. Technol. 15, 2577–2585. doi:10.1007/s42835-020-00556-w
Madan, S., and Bollinger, K. E. (1997). Applications of artificial intelligence in power systems. Electr. Power Syst. Res. 41, 117–131. doi:10.1016/S0378-7796(96)01188-1
Najeeb, M., Razali, R., Daniyal, H., Mahmood, A., and Mansor, M. (2017). An intelligent voltage controller for a PV inverter system using simulated annealing algorithm-based PI tuning approach.
Oshaba, A. S., Ali, E. S., and Abd Elazim, S. M. (2017). Speed control of SRM supplied by photovoltaic system via ant colony optimization algorithm. Neural comput. Appl. 28 (2), 365–374. doi:10.1007/s00521-015-2068-8
Qolomany, B., and Maabreh, M. (2017). “Parameters optimization of deep learning models using particle swarm optimization,” in The 13th International Wireless Communications and Mobile Computing Conference IWCMC.
Reed, G., Pape, R., and Takeda, M. (2003). Advantages of voltage sourced converter (VSC) based design concepts for FACTS and HVDC-link applications in 2003 IEEE Power Engineering Society General Meeting, Toronto, Ont., 1816–1821. doi:10.1109/PES.2003.1267437
Reynoso-Meza, G., Sanchis, J., Blasco, X., and Freire, R. Z. (2016). Evolutionary multi-objective optimisation with preferences for multivariable PI controller tuning. Expert Syst. Appl. 51, 120–133. doi:10.1016/j.eswa.2015.11.028
Rodriguez, P., and Rouzbehi, K. (2017). Multi-terminal DC grids: Challenges and prospects. J. Mod. Power Syst. Clean. Energy 5, 515–523. doi:10.1007/s40565-017-0305-0
Salunkhe, S., Phadke, G., Jadhav, S., and Pandeya, A. (2018). “Design and implementation of modified guo tao's algorithm for optimized PI controller for a level control system,” in 2018 4th International Conference for Convergence in Technology (I2CT), 1–4.
Seborg, D. E., Edgar, T. F., and Mellichamp, D. A. (2004). Process dynamics and control. 2nd ed. New York: Wiley.
Sebtahmadi, S. S., Azad, H. B., Kaboli, S. H. A., Islam, M. D., and Mekhilef, S. (2017). A PSO-DQ current control scheme for performance enhancement of Z-source matrix converter to drive IM fed by abnormal voltage. IEEE Trans. Power Electron. 33 (2), 1666–1681. doi:10.1109/tpel.2017.2679118
Sharma, H., Mishra, S., Dhillon, J., Sharma, N. K., Bajaj, M., Tariq, R., et al. (2022). Feasibility of solar grid-based industrial virtual power plant for optimal energy scheduling: A case of Indian power sector. Energies 15, 752. doi:10.3390/en15030752
Shehzad, F., Javaid, N., Almogren, A., Ahmed, A., Gulfam, S. M., and Radwan, A. (2021). A robust hybrid deep learning model for detection of non-technical losses to secure smart grids. IEEE Access 9, 128663–128678. doi:10.1109/ACCESS.2021.3113592
Skogestad, Sigurd (2003). Simple analytic rules for model reduction and PID controller tuning. J. Process Control 13 (4), 291–309. doi:10.1016/s0959-1524(02)00062-8
Soliman, M. S., Belkhier, Y., Ullah, Nasim, Achour, Abdelyazid, Alharbi, Yasser M., Ahmad, Aziz Al, et al. (2021). Supervisory energy management of a hybrid battery/PV/tidal/wind sources integrated in DC-microgrid energy storage system. Energy Rep. 7, 7728–7740. doi:10.1016/j.egyr.2021.11.056
Xu, C., Gordan, B., Koopialipoor, M., Armaghani, D. J., Tahir, M. M., and Zhang, X. (2019). Improving performance of retaining walls under dynamic conditions developing an optimized ANN based on ant colony optimization technique. IEEE Access 7, 94692–94700. doi:10.1109/access.2019.2927632
Yousaf, A., Asif, R. M., Shakir, M., Rehman, A. U., Alassery, F., Hamam, H., et al. (2021). A novel machine learning-based price forecasting for energy management systems. Sustainability 13, 12693. doi:10.3390/su132212693
Zhao, J., Lin, M., Xu, D., Hao, L., and Zhang, W. (2015). Vector control of a hybrid axial field flux-switching permanent magnet machine based on particle swarm optimization. IEEE Trans. Magn. 51 (11), 1–4. doi:10.1109/tmag.2015.2435156
Keywords: optimization, artificial intelligence, deep learning, smart grid, voltage source converter, particle swarm optimization (PSO), smartgrid
Citation: Khan SA, Ansari JA, Chandio RH, Munir HM, Alharbi M and Alkuhayli A (2022) AI based controller optimization for VSC-MTDC grids. Front. Energy Res. 10:1008099. doi: 10.3389/fenrg.2022.1008099
Received: 31 July 2022; Accepted: 17 August 2022;
Published: 23 September 2022.
Edited by:
Muhammad Faizan Tahir, South China University of Technology, ChinaReviewed by:
Srikanth Goud B, Anurag Group of Institutions, IndiaCopyright © 2022 Khan, Ansari, Chandio, Munir, Alharbi and Alkuhayli. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mohammed Alharbi, bW9oYWxoYXJiaUBrc3UuZWR1LnNh
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.