- 1College of Information Engineering, Zhejiang University of Technology, Hangzhou, China
- 2State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources, North China Electric Power University, Beijing, China
- 3College of Electrical Engineering and Automation, Fuzhou University, Fuzhou, China
- 4State Grid Henan Electric Power Research Institute, Zhengzhou, China
Bushing is an indispensable component in high voltage direct current (HVDC) transmission project. As the main insulating material possesses poor thermal conductivity and negative temperature coefficient (NTC) electrical resistivity, HVDC bushing suffers from the distortion of electro-thermal-coupled fields. Therefore, it is urgent to reveal the influence of electrical resistivity-temperature characteristic and thermal conductivity on the DC electric field distribution within bushing insulation, guiding the design and application advanced insulating materials. Here, the simulation of temperature and DC electric field distribution within a 400 kV bushing are carried out. The results show that the optimization of NTC effect and thermal conductivity of an insulating material is able to obtain a more uniform electric field distribution through homogenizing the electric resistivity distribution within bushing insulation. The activation energy of the insulating material has a similar variation trend with the maximum electric field within bushing insulation, which has a potential to represent the temperature dependence of electrical resistivity of insulating materials. It also shows that the reduction of DC electric field by increasing the thermal conductivity has a saturation feature. As a result, the suppression of the NTC effect should be considered together to obtain a smaller electric field within HVDC bushing. The research study provides a new idea to regulate the DC electric field distribution, which is beneficial to the design of advanced insulating materials.
Introduction
High voltage direct current (HVDC) transmission is a key means of consumption and optimal resource allocation of renewable energy (Xiao et al., 2021; Wei et al., 2022). Bushing is an indispensable component of HVDC transmission projects that enables conductors to pass through and are insulated from the transformer tank, the wall of converter valve hall, and other partitions (Setayeshmehr et al., 2006). In recent years, epoxy resin-impregnated paper (RIP)-insulated bushing has developed rapidly by virtue of their non-flammable characteristics compared with oil-impregnated paper-insulated bushing (Wang et al., 2017a). During operation, Joule heat generated by a current-carrying conductor causes a temperature gradient distribution within bushing insulation due to the poor thermal conductivity of RIP (Du et al., 2021). As HVDC transmission is characterized by large current, the heating and the temperature gradient problem within bushing insulation is more severe. It is known that the electrical resistivity of RIP decreases with temperature, denoted as the negative temperature coefficient (NTC) effect, and the distribution of electrical resistivity is uneven within insulation due to the gradient temperature distribution (Cao et al., 2013). Unlike the AC electric field distribution, the DC electric field distribution is mainly influenced by the electrical resistivity distribution. As a result, the electric field is distorted by the uneven temperature distribution, which results in the failures of bushings in converter stations (Liu et al., 2020). Therefore, suppressing the distortion of electro-thermal coupling fields is vital for the safety operation of HVDC RIP bushing.
The enhancement of thermal conductivity of insulating materials is able to suppress the distortion of the DC electric field. Researchers dope AlN, BN, Si3N4, Al2O3, and other insulating fillers possessed with high thermal conductivity into the insulating materials (Zhang et al., 2018; Chen et al., 2019; Zou et al., 2019). As the heat-releasing ability improves, both the hotspot temperature and the temperature gradient decrease within bushing insulation. Indirectly, the electrical resistivity distribution and thus the electric field distribution becomes uniform. It is known that as the doping content of these fillers increases; the insulating performance of composite materials is always weakened (Li et al., 2020), which means that the doping content should be controlled below a certain value. However, whether this doping content has a sufficient effect on the optimization of electric field distribution has not been clearly revealed. Therefore, it is necessary to analyze the relationship between thermal conductivity and electric field distribution within bushing insulation, which is important for the accurate design of the insulating material.
In recent years, researchers have begun to realize that regulating the electrical resistivity-temperature characteristic of insulating materials is also an effective method to suppress the distortion of local electro-thermal-coupled fields. The doping of PTC, GO, SiO2, and other functional fillers into polymeric matrix is able to reduce the temperature dependence of electrical resistivity, obtaining a more uniform electric field distribution within bushing insulation even under a large temperature gradient (Zhang et al., 2014; Du et al., 2020; Teng et al., 2021). A question is then raised: is it possible to suppress the distortion of electric field further through the synergistic regulation of both thermal conductivity and electrical resistivity of insulating materials? If the answer is yes, what would be the optimal parameter? However, there is still a lack of research on the related content.
In this article, the temperature distribution and electric field distribution within a simplified 400-kV bushing insulated with epoxy composites was simulated. The thermal conductivity and electrical resistivity-temperature characteristic of epoxy composites was set as the variables. Then, the individual and collective effect of insulation properties on the electric field distribution was studied. In addition, the regulation strategy aimed at electro-thermal-coupled fields problem was also discussed.
The Experimental method section describes the geometrical model, parameters, equations, and other key information about the simulation. In the Results and discussions section, the influence of temperature gradient, thermal conductivity, and electrical resistivity-temperature characteristic of epoxy composites on the temperature distribution and electric field distribution within bushing insulation is revealed. Finally, conclusion and prospect are given in the Conclusion section.
Experimental method
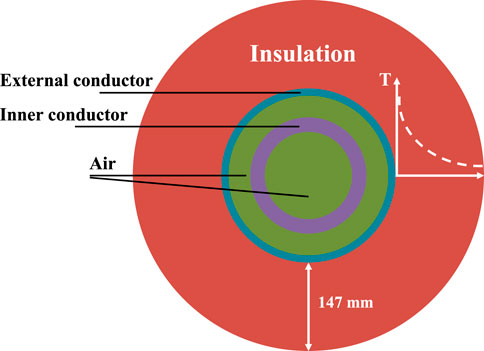
COMSOL Multiphysics FEM software was used to conduct the simulation. The simulation model of the RIP valve-side bushing of a 400-kV converter transformer was constructed to study the temperature distribution and DC electric field distribution within insulation (Zhang et al., 2017). The main body of the model is a coaxial cylindrical structure, including a current-carrying conductor, an outer conductor, and an insulation layer, which can be seen in Figure 1.
When the current passes through the conductor of bushing, heat is generated and then transferred to the outside, which satisfies the following heat balance formula (Sadiku, 2007):
where ρ is the solid density, C is the solid heat capacity at a constant pressure, k is the solid thermal conductivity, μ is the velocity field, T is the temperature, and Q is the heat source. Since the temperature rise within bushing insulation is mainly generated from the current-carrying conductor (Li et al., 2018), the dielectric loss of insulation is ignored. The heat source Q was set as the power loss of the current-carrying conductor.
Since the valve-side bushing connects the valve hall to the valve-side winding of the converter transformer and also passes through the BOXIN, there are three temperature boundaries. The heat will flow out through these boundaries by natural convection, which leads to a temperature gradient distribution inside the insulation governed by the following equation (Bergman et al., 2011):
where q0 is a heat flux that enters the domain and h is the heat transfer coefficient. Considering the ambient temperature and heating loss during the temperature rise test, the heat source power of the current-carrying conductor was set to 1,500 W, the external ambient temperature was set to 50°C, and the transformer tank temperature was set to 90°C (Wang et al., 2017b).
The electric field distribution within bushing insulation is governed by the following equations (Pawar et al., 2012):
where J is the current density, σ is electrical conductivity, Je is injected current density, E is the electric field, and V is the potential. According to the DC withstand voltage test of valve-side bushing, the voltage is selected as 746 kV (Wang et al., 2017a).
As the electrical conductivity is governed by temperature, there is a coupling relationship between the electric field and temperature, through the following equation (Hjerrild et al., 2001):
where A1 is a constant value, φ is the activation energy, e is the charge quantity of carriers, kB is the Boltzmann constant, T is the temperature, and B is the electric field constant.
The simulation variables are the thermal conductivity and electrical resistivity-temperature characteristics of insulating materials. The former indirectly changes the electrical resistivity distribution within the insulation by modifying the temperature distribution inside the insulation. The latter directly changes the electric field distribution within the bushing insulation by influencing the electrical resistivity distribution.
Results and discussion
Effect of temperature gradient
Figure 2 shows the temperature distribution and electric field distribution within bushing insulation with different power losses of the current-carrying conductor. As is seen in Figure 2A, since there is no heat generated from the conductor, the temperature is uniformly distributed when the power loss is 0 W. In this case, the electric field inside the bushing insulation is higher than the outside, which is a typical electric field distribution of coaxial cylindrical electrical equipment (Marzzanti and Marzinotto, 2013). It can be observed that the maximum electric field is 9.0 kV/mm. When the power loss of the current-carrying conductor increases, a temperature gradient distribution is formed due to the combined effect of power loss heating and heat dissipation to the ambient environment. Meanwhile, the electrical resistivity inside the bushing insulation becomes lower than the outside due to the change in temperature distribution, causing the “inversion” phenomenon of the DC electric field distribution in Figure 2B. More severely, the DC electric field distortion becomes more serious, as the temperature gradient enlarges.
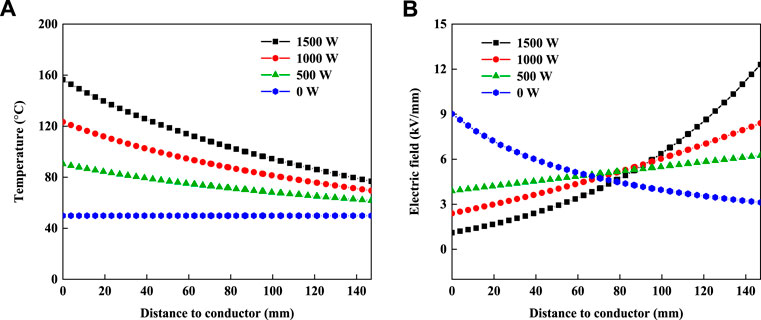
FIGURE 2. Effect of temperature gradient on electric field distribution within bushing insulation: (A) temperature distribution and (B) electric field distribution.
The power loss of the RIP valve-side bushing of a ±400-kV converter transformer is about 1,500 W. At this level of heat generation, the maximum electric field reaches to 12.3 kV/mm near the end shielding of bushing, which increases the risk of failure in this vulnerable area. With the development of the transmission power, this thermal issue will become more serious, which needs to be solved urgently to ensure the economical and reliable operation of HVDC bushings.
Effect of electrical resistivity-temperature characteristic of insulation
It has been proved that the addition of PTC particles into the polymeric insulation material is able to reduce the temperature dependence of electrical resistivity (Teng et al., 2020). As the thermal stability of electrical resistivity increases, the electrical resistivity distribution within bushing insulation becomes uniform, even when subjected to a large temperature gradient. Table 1 gives the parameter of a fitted curve of electrical conductivity-temperature characteristic, which is the inverse of electrical resistivity and is the input of simulation. The values used in this article were obtained from our previous research (Teng et al., 2022).
According to the Arrhenius theory, the activation energy can be used to evaluate the temperature dependence of electrical conductivity for insulating materials, which is a function of temperature at a certain electric field:
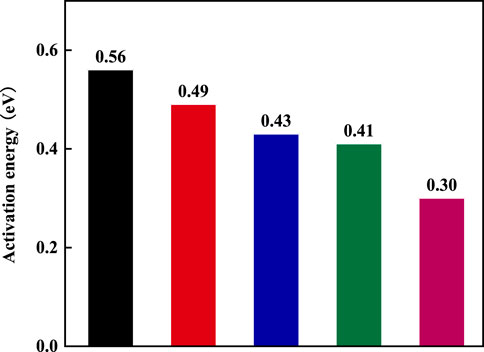
where φ is the activation energy, T is the temperature in Kelvin, and kB is the Boltzmann constant. It is known that the lower the activation energy, the weaker the temperature dependence of electrical resistivity (Huang et al., 2014). As shown in Figure 3, group E has the lowest thermal activation energy of 0.30 eV compared to group A of 0.56 eV, which is consistent with the measured electrical resistivity-temperature characteristic, namely, the electrical resistivity of group E has a narrower range as the temperature rises.
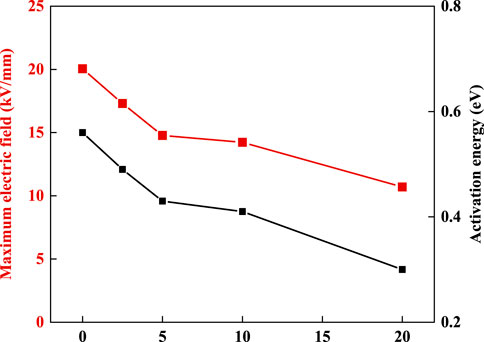
Figure 4 shows the relationship between the maximum electric field within bushing insulation and the activation energy of the insulating material. When the NTC effect of insulating material is suppressed, it can be observed that the maximum electric field decreases. Therefore, the regulation of electrical resistivity-temperature characteristic of insulating materials is essential for the safety and economical operation of HVDC bushings.
More importantly, the trend of the activation energy and the maximum electric field remain essentially the same according to Figure 4. Although the activation energy is often used to characterize dielectric materials, it is usually an ambiguous conception. At the same time, fewer studies have been carried out for the quantitative evaluation indicators of electrical resistivity-temperature characteristic of the insulating material, and thus, the DC electric field. Therefore, it can be considered to use the activation energy to characterize the variability of electric field characteristic within insulation.
As group A is the reference group, Table 2 gives the maximum electric field and activation energy ratio of other groups to group A. It can be observed that the change in the values of the maximum electric field and activation energy is generally consistent when represented by ratio. For example, the maximum electric field of group E decreases by 47% compared with that of group A, while the activation energy decreases by 46%. Therefore, it can be concluded that the activation energy of insulating materials has a potential to represent the electrical resistivity-temperature characteristic of the insulating material and so does the electric field characteristic within bushing insulation.
Effect of thermal conductivity of insulation
It is known that the current-carrying conductor is a huge heat source due to large-flowing current. This heat dissipates to the outside mainly through the insulating material, indicating that the thermal conductivity of the insulating material is an important property for the temperature distribution within bushing insulation. As the thermal conductivity of polymeric materials is poor, many researchers solved this issue by the doping of high-thermal conductivity material, which is able to mitigate the distortion of the DC electric field indirectly. However, these methods usually reduce the insulating performance, which is still hard to satisfy the requirement for engineering application. Based on the abovementioned discussion, it comes up with a problem whether the higher the thermal conductivity, the better the DC electric field distribution within bushing insulation. Therefore, the DC electric field distribution was simulated to reveal the effect of thermal conductivity of the insulating material.
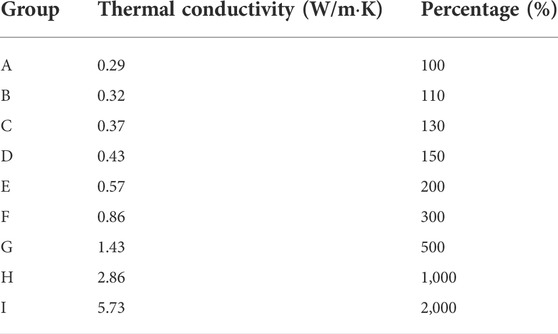
According to Zhao et al. (2018), the thermal conductivity of RIP is about 0.29W/m K, which was selected as the reference and denoted as group A. The thermal conductivity of the optimized groups is shown in Table 3. The percentage listed in Table 3 is the thermal conductivity ratio of the optimized groups to group A. Then, the DC electric field distribution within insulation with different thermal conductivity was simulated using the same electrical resistivity-temperature characteristic.
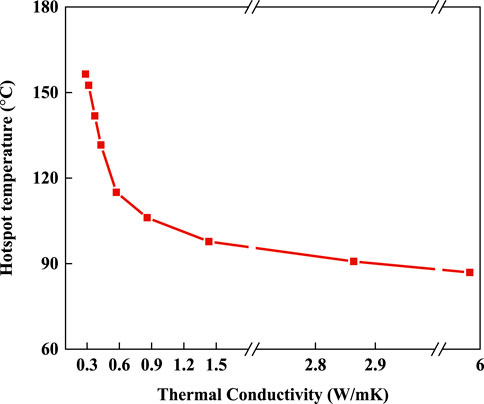
Figure 5 shows the relationship between the thermal conductivity of insulating material and the simulated hotspot temperature within bushing insulation. In general, it can be found that the hotspot temperature decreases gradually as thermal conductivity increases. However, the rate of decline slowed as the thermal conductivity reaches a certain value, which indicates that regulation efficiency decreases with thermal conductivity. When the hotspot temperature is reduced from 156 to 106°C, the thermal conductivity of the insulating material needs to be increased from 0.29 to 0.86W/m K, which is the 300% of the neat RIP material. Meanwhile, when the hotspot temperature is reduced from 106 to 87°C, the thermal conductivity of the insulating material needs to be increased from 0.86 to 5.73W/mK, which is the 2,000% of the neat RIP material.
Boron nitride (BN) particles combine high thermal conductivity and excellent insulating performance, attracting extensive attentions in the field of dielectric materials. High doping content is still unavoidable to obtain a high thermal conductivity of the polymeric material even doping BN particles. For example, 40wt% h-BN microparticles is needed to obtain a thermal conductivity of 0.97W/m K in epoxy composites (Wang et al., 2011). However, researchers also found that the DC breakdown strength decreases by 34.2%, when the doping mass fraction of micron BN particles reaches 15 wt% (Ma et al., 2019). It can be seen that a further increase in thermal conductivity not only has a lower regulating efficiency of hotspot temperature but also has a serious negative effect on the dielectric strength of insulating materials. Therefore, it is an appropriate doping content for the optimal regulation of both the properties.
Figure 6 illustrates the relationship between the thermal conductivity of insulating material and the maximum electric field within bushing insulation. When the thermal conductivity is below 1.5 W/m K, the maximum electric field decreases with thermal conductivity due to the suppression of temperature gradient and thus the uniform distribution of electrical resistivity. As the thermal conductivity increases further, the smaller temperature gradient within bushing insulation has little influence on the electric field distribution within bushing insulation.
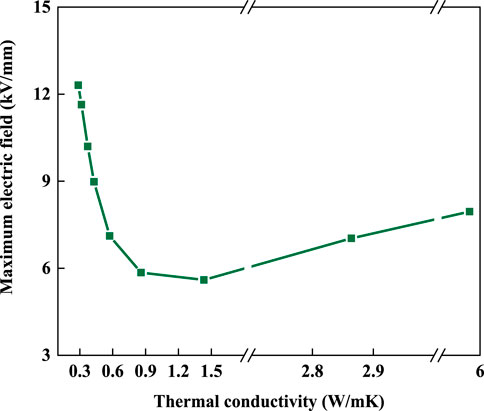
FIGURE 6. Influence of thermal conductivity on the maximum electric field within bushing insulation.
It can be seen in Figure 2B that the electric field distribution within the coaxial cylindrical electrical equipment is nonuniform when the temperature distribution is uniform, in which the electric field inside is higher than the outside. As a result, the electric field distribution is returning to a situation without suffering the temperature gradient as the thermal conductivity increases. As the reversal of electric field distribution disappears gradually, the maximum electric field within bushing insulation increases. Therefore, it should consider the reversal of electric field distribution when regulating the thermal conductivity of insulating materials.
Synergistic effect on the DC electric field distribution
It shows that the reduction of the DC electric field, within insulation regulated by thermal conductivity, has a saturation feature, which means that the increase of thermal conductivity blindly is not an optimal method to suppress the distortion of electric field further. As a result, the synergetic suppression of NTC effect and increase of thermal conductivity should be considered to suppress the distortion of electric field within HVDC bushing. Thus, it is important to reveal the electric field distribution characteristic affected by these factors to serve as a reference for the structural design of advanced insulating materials.
Figure 7 shows the maximum DC electric field within bushing insulation, simulated with different thermal conductivity and optimized electrical resistivity-temperature characteristic. It can be seen that the maximum DC electric field is further reduced, coupled with an optimized electrical resistivity-temperature characteristic of the insulating material. The minimum electric field occurs when the thermal conductivity of the insulating material is 200% that of the unmodified RIP, while the thermal conductivity needs to be increased to 500% of the unmodified RIP without being coupled with the regulation of electrical resistivity-temperature. In that case, the maximum electric field is only 5.2 kV/mm, which is about 42% insulated with unmodified RIP and is also lower than the situation when thermal conductivity is regulated individually (59%). Meanwhile, the radial electric field distribution is almost a straight line, which is beneficial to the safety operation of insulation. According to the abovementioned analysis, it is recommended to suppress the distortion of the DC electric field through the synergistic regulation of both the thermal conductivity and electrical resistivity-temperature characteristic.
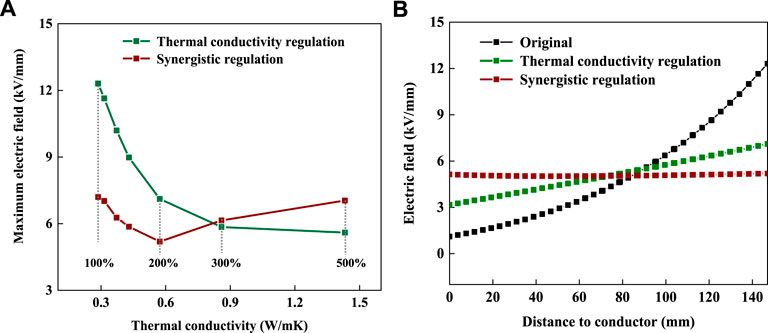
FIGURE 7. Influence of synergistic regulation on the maximum electric field within bushing insulation. (A) maximum electric field; (B) electric field distribution.
On the other hand, it can also be found in Figure 7 that the turning point appears at the position with a lower thermal conductivity, when the insulating material undergoes synergistic regulation, which means that electric field distribution becomes less influenced by temperature distribution. As the flowed current and ambient temperature is variational, the electric field distribution within bushing insulation will become more stable in operation after appropriate design of thermal conductivity and electrical resistivity-temperature characteristic.
Conclusion
In this article, the individual and collective effect of thermal conductivity and the electrical resistivity-temperature characteristic of the insulating material on temperature distribution and DC electric field distribution was studied through the simulation, which has a guiding role in the design of advanced insulating materials. The conclusions are as follows:
1) The temperature gradient causes the distortion of the DC electric field, while suppressing the negative temperature coefficient of electrical resistivity and increasing the thermal conductivity of the insulating material are able to obtain a more uniform DC electric field distribution through homogenizing the distribution of electric resistivity within bushing insulation.
2) The activation energy has a similar variation trend with the maximum electric field within bushing insulation, which has a potential to characterize the temperature dependence of electrical resistivity of insulating materials quantitatively.
3) As the thermal conductivity of insulating material increases, the hotspot temperature within bushing insulation decreases and the descent rate drops, while the maximum electric field declines at the beginning and then rises up later.
4) The synergistic regulation of both the thermal conductivity and the electrical resistivity-temperature characteristic of the insulating material has a better suppression effect of electric field distortion.
5) The simulation of temperature distribution and electric field distribution within electrical equipment is necessary to be conducted to determine the regulation goal of the insulating material, which is important to the efficient and economy design and operation of the insulating material. Further investigations on the design of composite material according to the principle proposed in this article are encouraged.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This study is supported by the State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources (Grant No. LAPS22013) and the National Natural Science Foundation of China (No. 52207032, No. 51977186).
Acknowledgments
The authors are grateful to the reviewers for their constructive comments and suggestions to improve this manuscript.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Bergman, T., Lavine, A., and Incropera, F. (2011). Fundamentals of heat and mass transfer. New York: John Wiley & Sons Press.
Cao, W., Shen, W., He, B. S., and Wu, K. (2013). Structural design for DC bushing core based on the material life. IEEE Trans. Dielectr. Electr. Insul. 20, 281–288. doi:10.1109/TDEI.2013.6451368
Chen, J., Huang, X., Sun, B., and Jiang, P. (2019). Highly thermally conductive yet electrically insulating polymer/boron nitride nanosheets nanocomposite films for improved thermal management capability. ACS Nano 13, 337–345. doi:10.1021/acsnano.8b06290
Du, B., Sun, H., Jiang, J., Kong, X., and Yang, W. (2021). Temperature-dependent electric field distribution in ±800 kV valve-side bushing insulation for A converter transformer. High. Volt. 6, 106–115. doi:10.1049/hve.2019.0385
Du, B., Sun, H., Kong, X., Yang, W., and Li, J. (2020). Improved electric field distribution within bushing insulation by EP/GO nanocomposites with reduced temperature coefficient of conductivity. IEEE Access 8, 176864–176872. doi:10.1109/ACCESS.2020.3026391
Hjerrild, J., Boggs, S., Holboll, J. T., and Henriksen, M. (2001) DC-Field in solid dielectric cables under transient thermal conditions. in Proc. Int. Conf. on Solid Dielectrics, Eindhoven, Netherlands 25-29 June 2001. doi:10.1109/ICSD.2001.955511
Huang, X., Xie, L., Yang, K., Wu, C., Jiang, P., Li, S., et al. (2014). Role of interface in highly filled epoxy/BaTiO3 nanocomposites. Part I-correlation between nanoparticle surface chemistry and nanocomposite dielectric property. IEEE Trans. Dielectr. Electr. Insul. 21, 467–479. doi:10.1109/TDEI.2013.004165
Li, G., Zhou, X., Li, X., Wei, Y., Hao, C., Li, S., et al. (2020). DC breakdown characteristics of XLPE/BNNS nanocomposites considering BN nanosheet concentration, space charge and temperature. High. Volt. 5, 280–286. doi:10.1049/hve.2019.0393
Li, J., Du, B. X., Liang, H., Fu, M., and Gao, Y. (2018). Electrical field distribution in ±600kV converter transformer bushing core with the application of epoxy resin with nonlinear conductivity. in Proc. Int. Conf. on IEEE High Voltage Engineering and Application, Athens, Greece 10-13 September 2018. doi:10.1109/ICHVE.2018.8641890
Liu, X., Chen, M., Liang, C., Tang, H., and Zhang, Q. (2020). Investigation on distribution of electro-thermal coupled field and improved design of ±1100kV converter valve-side bushing. IET Sci. Meas. Technol. 14, 188–197. doi:10.1049/iet-smt.2019.0089
Ma, W., Tian, F., Xiong, W., and Yao, J. (2019). Thermal conductivity and electrical insulation properties of epoxy/BN micro and nano composites. Insul. Mater. 52, 36–42. doi:10.16790/j.cnki.1009-9239.im.2019.07.007
Marzzanti, G., and Marzinotto, M. (2013). Extruded cables for high voltage direct current transmission: Advance in research and development. New Jersey: Wiley-IEEE Press.
Pawar, S., Joshi, K., Andrews, L., I., and Kale, S. (2012). Application of computational fluid dynamics to reduce the new product development cycle time of the SF6 gas circuit breaker. IEEE Trans. Power Deliv. 27, 156–162. doi:10.1109/TPWRD.2011.2170711
Setayeshmehr, A., Akbari, A., Borsi, H., and Gockenbach, E. (2006). On-line monitoring and diagnoses of power transformer bushings. IEEE Trans. Dielectr. Electr. Insul. 13, 608–615. doi:10.1109/TDEI.2006.1657975
Teng, C., Zhou, Y., Li, S., Zhang, L., Zhang, Y., Zhou, Z., et al. (2020). Regulation of temperature resistivity characteristics of insulating epoxy composite by incorporating positive temperature coefficient material. IEEE Trans. Dielectr. Electr. Insul. 27, 512–520. doi:10.1109/TDEI.2020.008600
Teng, C., Zhou, Y., Wu, C., Zhang, L., Zhang, Y., and Zhou, W. (2021). Optimization of the temperature-dependent electrical resistivity in epoxy/positive temperature coefficient ceramic nanocomposites. IEEE Trans. Dielectr. Electr. Insul. 28, 468–475. doi:10.1109/TDEI.2020.009214
Teng, C., Zhou, Y., Zhang, L., Zhang, Y., Huang, X., and Chen, J. (2022). Improved electrical resistivity-temperature characteristics of insulating epoxy composites filled with polydopamine-coated ceramic particles with positive temperature coefficient. Compos. Sci. Technol. 221, 109365. doi:10.1016/j.compscitech.2022.109365
Wang, Q., Liao, J., Tian, H., Liu, P., and Peng, Z. (2017a). Regularity analysis of the temperature distribution of epoxy impregnated paper converter transformer bushings. IEEE Trans. Dielectr. Electr. Insul. 24, 3254–3264. doi:10.1109/TDEI.2017.006685
Wang, Q., Yang, X., Tian, H., Liu, P., and Peng, Z. (2017b). A novel dissipating heat structure of converter transformer RIP bushings based on 3-D electromagnetic-fluid-thermal analysis. IEEE Trans. Dielectr. Electr. Insul. 24, 1938–1946. doi:10.1109/TDEI.2017.006027
Wang, Z., Iizuka, T., Kozako, M., Ohki, Y., and Tanaka, T. (2011). Development of epoxy/BN composites with high thermal conductivity and sufficient dielectric breakdown strength part Ι-sample preparations and thermal conductivity. IEEE Trans. Dielectr. Electr. Insul. 18, 1963–1972. doi:10.1109/TDEI.2011.6118635
Wei, C., Xu, J., Chen, Q., Song, C., and Qiao, W. (2022). Full-order sliding-mode current control of permanent magnet synchronous generator with disturbance rejection. IEEE J. Em. Sel. Top. Ind. Electron Early Access, 1–8. doi:10.1109/JESTIE.2022.3192735
Xiao, D., Chen, H., Wei, C., and Bai, X. (2021). Statistical measure for risk-seeking stochastic wind power offering strategies in electricity markets. J. Mod. Power. Syst. Cle. Early Access, 1–6. doi:10.35833/MPCE.2021.000218
Zhang, L., Deng, H., and Fu, Q. (2018). Recent progress on thermal conductive and electrical insulating polymer composites. Compos. Commun. 8, 74–82. doi:10.1016/j.coco.2017.11.004
Zhang, L., Zhou, Y., Huang, M., Sha, Y., Tian, J., and Ye, Q. (2014). Effect of nanoparticle surface modification on charge transport characteristics in XLPE/SiO2 nanocomposites. IEEE Trans. Dielectr. Electr. Insul. 21, 424–433. doi:10.1109/TDEI.2013.004145
Zhang, S., Zhang, H., Feng, H., Yan, J., Liu, P., and Peng, Z. (2017). Relaxation processes and conduction mechanism of epoxy resin filled with graphene oxide. IEEE Trans. Dielectr. Electr. Insul. 24, 519–527. doi:10.1109/TDEI.2016.005961
Zhao, C., Peng, Z., and Liu, P. (2018). Electric field analysis of 1100kV resin impregnated paper UHVDC wall bushing under different voltage forms. in Proc. Int. Conf. on High Voltage Engineering and Application, Athens, Greece 10-13 September 2018. doi:10.1109/ICHVE.2018.8641868
Keywords: HVDC bushing, epoxy resin-impregnated paper insulation, electric field distribution, thermal conductivity, electrical resistivity-temperature characteristic
Citation: Teng C, Ding Y, Zhang Y, Zhang Y, Huang M and Zhan Z (2022) Investigation on distribution of electro-thermal coupling fields influenced by HVDC bushing insulation properties. Front. Energy Res. 10:1005470. doi: 10.3389/fenrg.2022.1005470
Received: 28 July 2022; Accepted: 15 September 2022;
Published: 30 September 2022.
Edited by:
Dongliang Xiao, South China University of Technology, ChinaCopyright © 2022 Teng, Ding, Zhang, Zhang, Huang and Zhan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Youbing Zhang, eW91YmluZ3poYW5nQHpqdXQuZWR1LmNu; Yunxiao Zhang, emhhbmd5eHRodUAxNjMuY29t; Zhenyu Zhan, emhhbnpoeV9oYS5zZ2NjQGZveG1haWwuY29t
 Chenyuan Teng
Chenyuan Teng Yichao Ding1
Yichao Ding1 Meng Huang
Meng Huang