- 1Institute of Power System Optimization, School of Electrical Engineering, Guangxi University, Nanning, China
- 2Electrical Power Research Institute, Guangxi Power Grid Co., Ltd., Nanning, China
- 3Chengdu Electric Power Investigation and Design Institute, Power China Engineering Co., Ltd., Chengdu, China
- 4Planning and Research Center, Guangdong Power Grid Co., Ltd., Guangzhou, China
Developing a minimum backbone grid in the power system planning is beneficial to improve the power system’s resilience. To obtain a minimum backbone grid, a mixed integer linear programming (MILP) model with network connectivity constraints for a minimum backbone grid is proposed. In the model, some constraints are presented to consider the practical application requirements. Especially, to avoid islands in the minimum backbone grid, a set of linear constraints based on single-commodity flow formulations is proposed to ensure connectivity of the backbone grid. The simulations on the IEEE-39 bus system and the French 1888 bus system show that the proposed model can be solved with higher computational efficiency in only about 30 min for such a large system and the minimum backbone grid has a small scale only 52% of the original grid. Compared with the improved fireworks method, the minimum backbone grid from the proposed method has fewer lines and generators.
1 Introduction
In recent years, as the global climate continues to warm, extreme weather occurs frequently, which seriously affects the reliability of power supply and the national economy. In the power system planning, a minimum backbone grid can be developed. The selected generators and lines in the minimum backbone grid can be reinforced before the extreme weather to ensure the supply of critical loads in extreme weather. After the extreme weather, the power system can be quickly restored to the normal state by the stable power supply of the grid. In summary, developing a minimum backbone grid is beneficial to ensure the uninterrupted power supply of important loads and rapid recovery of core power infrastructure under extreme disaster conditions. It improves the ability of the power grid to respond to low-probability extreme events, which is an important part of resilience in the power grid (Mahzarnia et al., 2020; Trudel et al., 2005; Bie et al., 2017). How to develop a minimum backbone grid from the existing power grid is the core of the research.
At present, the research on developing a minimum backbone grid can be divided into two categories:
One is the heuristic method. The method has been widely used in developing a minimum backbone grid because it is not limited by the non-convexity and non-smoothness of the optimization problem and can quickly obtain a feasible solution. In Yang et al. (2010), a minimum grid model considering the importance of lines and the topology of the grid is constructed, and binary particle swarm optimization is used to solve the model. In Liu et al. (2007), the topological characteristics of scale-free networks are employed to obtain a skeleton-network reconfiguration strategy, and the discrete particle swarm optimization technique is employed to implement the reconfiguration. Rather than providing a detailed restoration path sequence, the strategy aims to obtain several better-performing reconfiguration schemes as the guidance of dispatching operations. In Dong et al. (2015), the authors present a comprehensive index system to measure the survivability of the backbone grid and a new method of constructing the grid considering survivability. The improved biogeographic optimization algorithm provided with strong search ability is used to obtain the optimal solution for the core backbone grid. In Chen, (2021), a risk assessment system of power grid operation involving multi-link uncertain factors is proposed, and a core backbone grid model considering the minimum comprehensive risk index is constructed. The traditional fireworks algorithm is improved to quickly and accurately search the construction scheme of the optimal backbone grid. The above heuristic algorithm is simple and easy to use, compared with the general mathematical programming method. However, it is poor robust and its result is random, which makes it difficult to reproduce and repeatedly check the results in practical applications (Blum and Roli, 2003; Ball, 2011).
The other is the mathematical programming method, which is rarely studied in this research. In Sun et al. (2019), aiming at maximum network restoration efficiency, the optimal backbone grid is formulated as a MILP problem, which can be efficiently solved by commercial solvers such as CPLEX. However, the model cannot ensure the connectivity of the minimum backbone grid, which makes the grid likely to have islands. Then, the backbone grid will be of low reliability, which is not conducive to the survival and rapid recovery of the grid under extreme disaster conditions. Network connectivity is a major bottleneck in the application of mathematical programming methods to this problem. Table 1 compares the method, objective and connectivity method between the existing literature.
In this paper, we also present a mathematical programming method in which a mixed integer linear programming model for a minimum backbone grid is proposed. A minimum number of branches and maximum summation of power flow betweenness objective function is considered in the model. Furthermore, a set of close-form connectivity constraints is formulated to ensure the reliability of the backbone grid. The main contributions of this paper are as follows:
• The minimum backbone grid is described as a MILP model. It considers constraints presented to the practical application requirements such as regional plant constraints.
• Based on the idea of single commodity flow, it considers a set of linear constraints on the grid connectivity, which avoids the island of minimum backbone grid, overcomes the defect that the existing methods are difficult to express the connectivity constraints rigorously, and breaks through the bottleneck of mathematical programming method in the application of this problem.
The simulation results of the IEEE-39 bus system and the French 1888 bus system verify the effectiveness of the proposed model and show that the proposed method has high computational efficiency.
2 Construction planning of minimum backbone grid
The minimum backbone grid is a minimum grid that can ensure the continuous power supply of important loads. The goal is to minimize the scale of the grid, that is, to minimize the number of branches. The backbone grid must satisfy specific constraints such as power balance constraints, line capacity constraints, connectivity constraints, and so on to ensure that it operates under special circumstances. In order to describe the backbone grid quantitatively, some specific constraints to the backbone grid are given as follows:
1) Satisfying the security operation constraints of the power grid;
2) Satisfying the connectivity of network topology;
3) Maintaining specific system load level;
4) Guarantee regional power sources;
5) On basis of satisfying the above constraints, the number of branches in the backbone grid should be the minimum;
The backbone grid also needs to obey special requirements for different situations. This paper gives basic definitions and models that can be expanded on this basis in various situations.
Developing a minimum backbone grid involves determining the critical loads, and selecting essential generators and backbone lines.
2.1 Determining critical loads
The critical loads include the urban emergency dispatch center, core infrastructures such as communication, water supply, and transportation, large densely residential areas, and important customers. Since most critical loads are distributed in the distribution network at a low voltage level, it is necessary to progressively search the corresponding load buses in transmission substations from low voltage to high voltage levels. The range and quantity of the critical loads directly affect the scale of the minimum backbone grid. Excessive critical loads will make the minimum backbone grid too large, resulting in a high investment. Therefore, the proportion of the critical loads should not be too high.
2.2 Selecting essential generators
Selecting essential generators follows the general principles:
1) Trying to ensure each region of the power grid has generators to avoid the blackout in case of regional tie line failure.
2) Preferring to choose the hydro generators in the backbone grid, as the hydro generators have the advantages of simple auxiliary equipment and rapid startup (Adibi and Fink, 2006).
3) The priority of synchronous generators connected to the power grid through a lower voltage level should be higher than that of synchronous generators connected to the power grid through a higher voltage level to ensure that the power locally supplies the backbone load.
2.3 Selecting backbone lines
The principle of backbone line selection is as follows:
1) The two adjacent higher voltage level substations selected into the minimum backbone grid should be connected by lower voltage level lines to strengthen the support between critical areas.
2) According to the characteristics of natural disasters in various regions, some backbone lines should have higher priority. For example, typhoons in some areas generally travel from east to west. In this case, the east-west lines should be preferred in the minimum backbone grid. In the ice disaster scenario, the lines with ice melting devices should be selected as a high priority.
3 Mathematical programming model of minimum backbone grid
3.1 Basic mathematical model
3.1.1 Objective function
The objective function considers two aspects, one is to ensure as few branches as possible, and the other is to preferentially select branches with high importance. The power flow betweenness (Rout et al., 2016) is used as an index to measure the importance of branches.
The objective function is as follows:
where
3.1.2 Constraints
1) Active power balance constraints:
where
2) Generator operating constraints:
where
3) Line capacity constraints:
where
4) DC power flow constraints:
where
5) Phase angle constraint:
where
6) Regional plant constraints:
According to the selection principle of generators, each area has at least one generator, that is
where
7) Spinning reserve constraint:
where
8) Primary frequency reserve constraint:
where
9) Must-in-service line constraints:
where
10) Must-out line constraints:
where
11) Must-on generator constraints:
where
3.2 Connectivity constraints
In the minimum backbone grid model, the connectivity constraint is an important constraint to ensure the reliability and recovery ability of the grid. However, the existing research lacks methods of expressing network connectivity. Network connectivity constraints are widely used in traveling salesman problems, vehicle routing problems, minimum spanning tree problems, and Steiner tree problems (Gollowitzer and Ljubic., 2011). In these problems, single-commodity flow is commonly used to formulate connectivity constraints.
The idea of the single commodity flow constraint is to set the node that sends out the commodity as the root point and the node that requires the commodity as the sink point in a directed graph
where
At the same time, constraint (15) can ensure that the amount of virtual flow passed by each branch does not exceed the actual line capacity.
where
In the minimum backbone grid, a must-on generator in the power grid can be selected as the root point.
3.3 Implementation process of minimum backbone grid
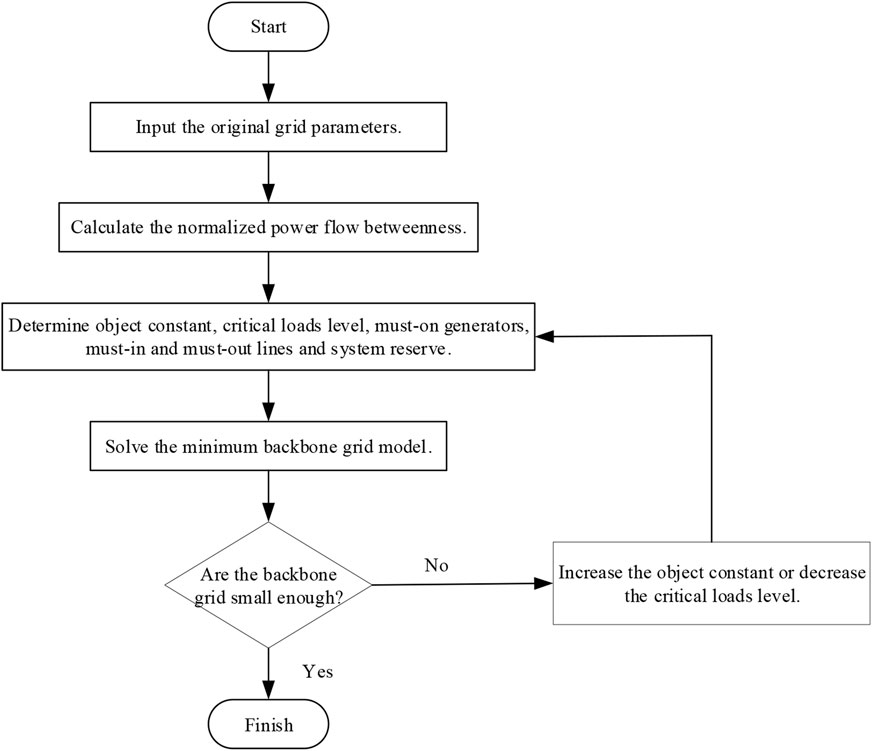
The steps of obtaining a minimum backbone grid are as follows:
1) Input the parameters of the original grid, including line and transformer data, etc.
2) Calculate the normalized power flow betweenness of all branches.
3) Determine object constant, critical loads level, must-on generators, must-in and must-out lines and system reserve.
4) Solve the minimum backbone grid model in Section 3.
5) If the backbone grid is not small enough, increase the object constant or decrease the critical loads level and go to step 3.
The implementation flowchart of the minimum backbone grid is shown in Figure 1:
4 Case studies
To verify the validity of the proposed model, the IEEE-39 bus system (Yeu, 2010) and the French 1888 bus system (Zimmerman et al., 2011) are simulated. All simulations are implemented on a PC with a Core i7 2.9-GHz CPU and 16.0 GB RAM, using mathematical modeling software Pyomo 6.2 and Gurobi 9.5.1 solver to solve the established optimization model, and the convergence gap is set to 0.0001.
4.1 IEEE-39 bus system
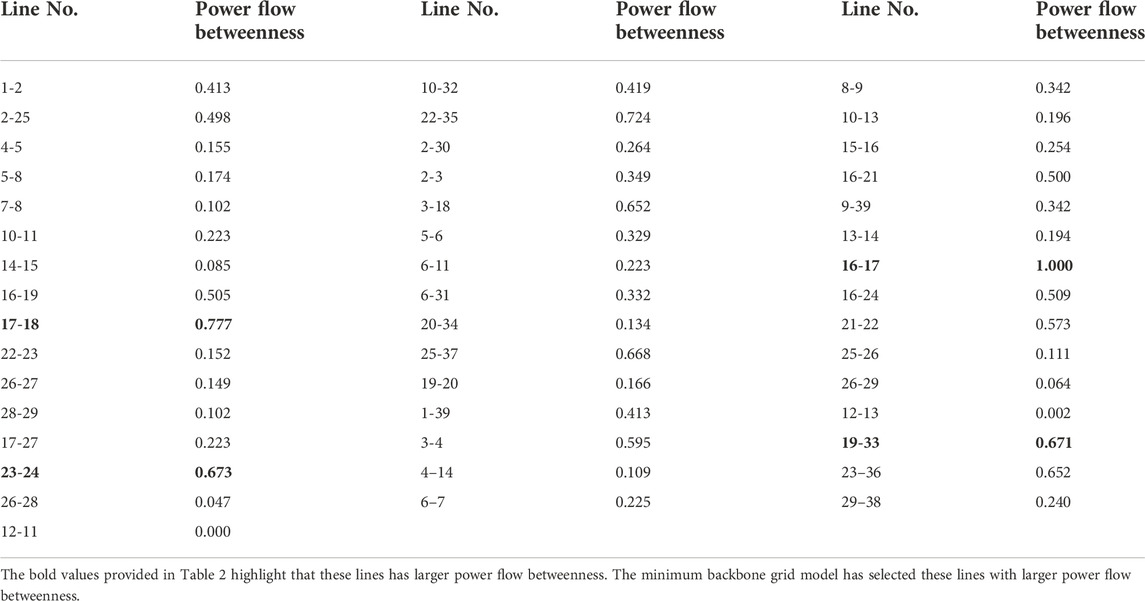
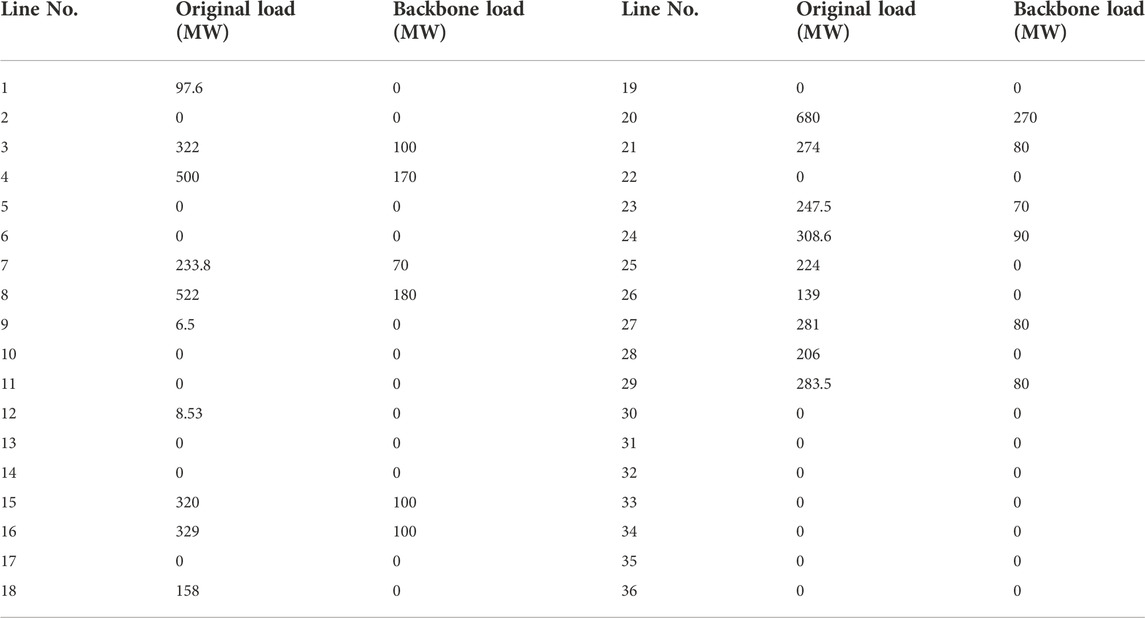
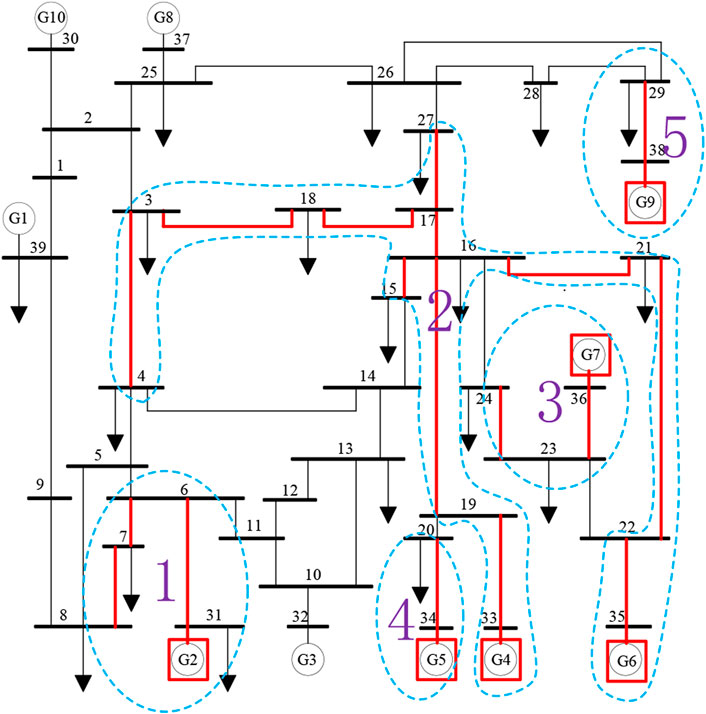
Table 2 shows the normalized power flow betweenness of each line of the IEEE-39 bus system, and Table 3 shows the critical loads in the minimum backbone grid. Due to the small size of the IEEE-39 bus system, regional plant constraints were not considered.
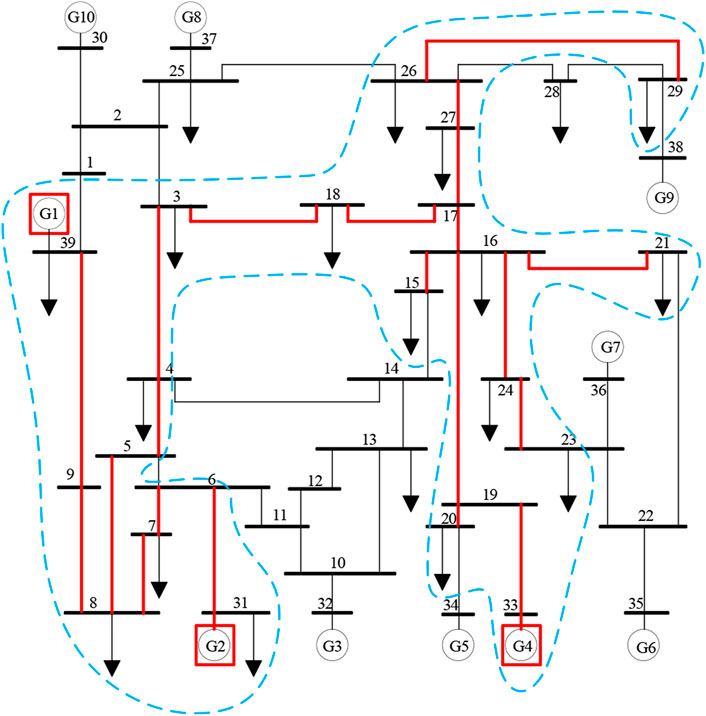
After the calculation, the minimum backbone grid is shown in Figure 2 in red color. Figure 2 shows the grid has 24 lines, 3 generators, which is only 52.17% of the original grid, and all the critical loads in Table 2. Especially, the backbone grid is connected. Reinforcing the 52.17% can ensure the power supply for critical loads of the whole grid under extreme weather. To transmit power to node 29, there are two paths between node 26 and node 29, one is 26-29, and the other is 26-28, 28-29. Line 26-29 is selected by the minimum backbone grid model as expected due to the objective function, that is, the number of lines will be selected as few as possible. In addition, the model has selected lines with larger power flow betweenness, such as lines 16-17, 17-18, 23-24, and 19-33. Other lines with larger power flow betweenness, such as lines 22-35, 25-37, and 23-36, have not been selected because they are outlet lines of unpowered generators. Thus, it can be seen that the objective function is effective and correct.
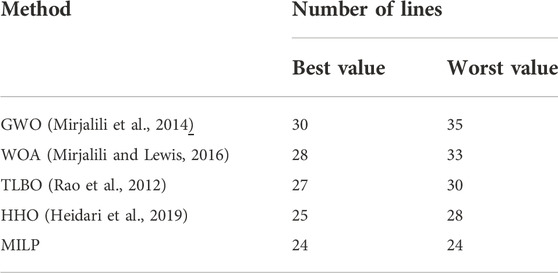
We also compared our proposed MILP method with four heuristic methods. Due to the random results of the heuristic methods, the results listed in Table 4 are obtained based on 100 times running.
From the Table 4, it can be seen that the MILP method has the same lines in minimum backbone grid for every running. By contrast, the heuristic methods have different lines in minimum backbone grid for different running. Furthermore, the MILP method gets the optimal lines which is less than the best value of the heuristic methods in minimum backbone grid.
After removing connectivity constraints (14–18) and retaining other constraints, recalculate the model and the result is shown in Figure 3. There are 18 lines and six generators in the figure. Although the number of lines in this minimum backbone grid is less than that in Figure 2, the minimum backbone grid is not connected and there are five islands. Each island has generator nodes and load nodes to meet power balance. However, the recoverability and reliability of the unconnected grid are low. These five islands are very fragile and very hard to keep frequency or rotor angle stability. They may be blackout following a further disturbance. Once the island is blackout, it will need more time to restore the power grid. This demonstrates the validity of the connectivity constraints proposed in this paper.
4.2 French 1888 bus system
The French 1888 bus system is from the data file (CASE1888RTE) in matpower7.0 and has 2,531 branches. To facilitate the test, the backbone load is set as 15% of the original load. The objective function of the minimum backbone grid model involves two objectives, the minimum number of branches and the maximum summation of power flow betweenness. The purpose of setting
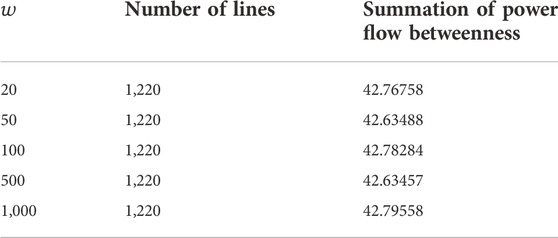
TABLE 5. Number of branches and summation of branch betweenness for backbone grid of the French 1888 bus system with different
As can be seen from Table 5, with the increase of
Table 6 shows the number of constraints and calculation time of the model with and without connectivity constraints. Although considering the connectivity constraints will increase the size of the model, the calculation time is shorter than that of the model without the connectivity constraints. This is because the connectivity constraints tighten the feasible region of MILP, and the algorithm of MILP is easier to find the optimal solution. In addition, for such a large-scale system, the solution can be obtained in an acceptable time, which shows that the mathematical programming method is very efficient.
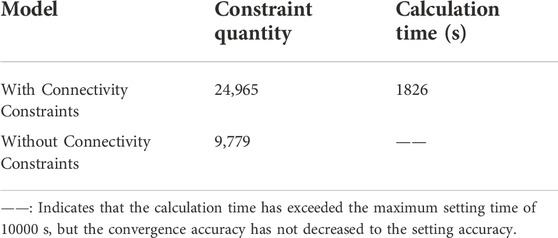
TABLE 6. Number of constraints and computing time for the model with and without connectivity constraints.
Of course, there are some methods to further improve the calculation efficiency of the model, such as further tightening the model according to its characteristics of the model or tuning the parameters of the solver.
5 Conclusion
A mixed integer linear programming model for a minimum backbone grid is proposed in this paper, which considers the practical application requirements. More importantly, the model can ensure network connectivity to avoid islands in the grid, which is an important prerequisite for the practical application of mathematical programming methods in developing a minimum backbone grid. The simulations on the IEEE-39 bus system and the French 1888 bus system verify the validity of the proposed model and show that the minimum backbone grid has a small scale of only 52% of the original grid and the proposed method has high computational efficiency of only about 30 min for such a large system.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
Conceptualization, WM and PL; methodology, WM and PL; software, WM and YH; validation, WM and ZS; resources, WM; data curation, WM and PL; writing—original draft preparation, WM; writing—review and editing, WM, ML, XG, and PL; super-vision, PL. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported in part by the National Natural Science Foundation of China under Grant no. 51967001, 51967002 and 52267006, in part by Guangxi Special Fund for Innovation-Driven Development under Grant no.AA19254034, and in part by Guangxi Key Laboratory of Power System Optimization and Energy Technology Research Grant.
Conflict of interest
Authors ZS and ML were employed by the company Guangxi Power Grid Co., Ltd., YH was employed by the company Power China Engineering Co., Ltd., and XG was employed by the company Guangdong Power Grid Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Adibi, M. M., and Fink, L. H. (2006). Overcoming restoration challenges associated with major power system disturbances - restoration from cascading failures. IEEE Power Energy Mag. 4, 68–77. doi:10.1109/mpae.2006.1687819
Ball, M. O. (2011). Heuristics based on mathematical programming. Surv. Operations Res. Manag. Sci. 16, 21–38. doi:10.1016/j.sorms.2010.07.001
Bie, Z., Lin, Y., Li, G., and Li, F. (2017). Battling the extreme: A study on the power system resilience. Proc. IEEE 105, 1253–1266. doi:10.1109/jproc.2017.2679040
Blum, C., and Roli, A. (2003). Metaheuristics in combinatorial optimization: Overview and conceptual comparison. ACM Comput. Surv. 35, 268–308. doi:10.1145/937503.937505
Chen, Y. (2021). “Construction method of core backbone grid based on improved fireworks algorithm and risk theory,” in 2021 international conference on advanced Technology of electrical engineering and Energy (ATEEE), 62–68.
Dong, F., Liu, D., Wu, J., Ke, L., Song, C., Wang, H., et al. (2015). Constructing core backbone network based on survivability of power grid. Int. J. Electr. Power & Energy Syst. 67, 161–167. doi:10.1016/j.ijepes.2014.10.056
Gollowitzer, S., and Ljubic, I. (2011). MIP models for connected facility location: A theoretical and computational study. Comput. Operations Res. 38, 435–449. doi:10.1016/j.cor.2010.07.002
Heidari, A. A., Mirjalili, S., Faris, H., Aljarah, I., Mafarja, M., and Chen, H. (2019). Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 97, 849–872. doi:10.1016/j.future.2019.02.028
Liu, Y., and Gu, X. (2007). Skeleton-network reconfiguration based on topological characteristics of scale-free networks and discrete particle swarm optimization. IEEE Trans. Power Syst. 22, 1267–1274. doi:10.1109/tpwrs.2007.901486
Mahzarnia, M., Moghaddam, M. P., Baboli, P. T., and Siano, P. (2020). A review of the measures to enhance power systems resilience. IEEE Syst. J. 14, 4059–4070. doi:10.1109/jsyst.2020.2965993
Mirjalili, S., and Lewis, A., (2016). The whale optimization algorithm. Adv. Eng. Softw. 95, 51–67. doi:10.1016/j.advengsoft.2016.01.008
Mirjalili, S., Mirjalili, S. M., and Lewis, A. (2014). Grey wolf optimizer. Adv. Eng. Softw. 69, 46–61. doi:10.1016/j.advengsoft.2013.12.007
Rao, R. V., Savsani, V. J., and Vakharia, D. P. (2012). Teaching–Learning-Based Optimization: An optimization method for continuous non-linear large scale problems. Inf. Sci. 183, 1–15. doi:10.1016/j.ins.2011.08.006
Rout, G. K., Chowdhury, T., and Chanda, C. K. (2016). Betweenness as a tool of vulnerability analysis of power system. J. Inst. Eng. India. Ser. B 97, 463–468. doi:10.1007/s40031-016-0222-z
Sun, L., Lin, Z., Xu, Y., Wen, F., Zhang, C., and Xue, Y. (2019). Optimal skeleton-network restoration considering generator start-up sequence and load pickup. IEEE Trans. Smart Grid 10, 3174–3185. doi:10.1109/tsg.2018.2820012
Trudel, G., Gingras, J. P., and Pierre, J. R. (2005). Designing a reliable power system: Hydro-quebec's integrated approach. Proc. IEEE 93, 907–917. doi:10.1109/jproc.2005.846332
Yang, W. H., Bi, T. S., Huang, S. F., Xue, A. C., and Yang, Q. X. (2010). “Identification of backbone-grid in power grid based on binary particle swarm optimization,” in 2010 international conference on power system Technology, 1–6.
Yeu, R. H. (2010). Small signal analysis of power systems: Eigenvalue tracking method and eigenvalue estimation contingency screening for DSA. Urbana Champagne, IL: University of Illinois at Urbana-Champaign.
Keywords: minimum backbone grid, mixed integer linear programming, connectivity constraints, single-commodity flow, resilience
Citation: Mei W, Sun Z, He Y, Liu M, Gong X and Li P (2023) A mixed integer linear programming model for minimum backbone grid. Front. Energy Res. 10:1004861. doi: 10.3389/fenrg.2022.1004861
Received: 27 July 2022; Accepted: 29 September 2022;
Published: 20 January 2023.
Edited by:
Dan Lu, Alfred University, United StatesReviewed by:
Shunbo Lei, The Chinese University of Hong Kong, Shenzhen, ChinaChen Chen, Xi’an Jiaotong University, China
Copyright © 2023 Mei, Sun, He, Liu, Gong and Li. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Peijie Li, bGlwZWlqaWVAZ3h1LmVkdS5jbg==
 Wenwen Mei
Wenwen Mei Zhiyuan Sun2
Zhiyuan Sun2 Peijie Li
Peijie Li