Lightweight and dynamic authenticated key agreement and management protocol for smart grid

With the development of IoT and 5G, the smart grid, as one of the key component for the smart city, can provide the uninterrupted and reliable electricity service by properly adjusting the electricity supply according to the consumption of users. The advanced metering infrastructure (AMI), as an important part of smart grid system, is a complete network and system for measuring, collecting, storing and analyzing the electricity consumption information of users. The security of AMI plays a vital role in the smooth operation of smart grid. In this paper, we study how to establish the secure communication between two entities in AMI, namely the smart meter and the electricity service provider. Although, there are many authentication and key management protocols for AMI, the high complexity and computation overhead of these protocols hinder their application in the smart grid environment. Based on identity cryptosystem and elliptic curve cryptography (ECC), we put forward a lightweight and dynamic authenticated key agreement and management protocol, which can significantly reduce the computation overhead of the resource-constrained smart meters. In addition, we utilize a one-way key tree technique to efficiently generate and update the group key in the multicast communication. We give a systematic proof to show that our designed protocol not only guarantees the confidentiality and integrity of transmitted messages, but also resists various attacks from an adversary. Finally, we carry out some simulated experiments to demonstrate the high efficiency of our designed protocol.

1 Introduction

As the next generation electricity supply network, the smart grid (Song et al., 2022; Verma et al., 2022) plays an indispensable role in the progress of society and the improvement of life quality. With the development of Industrial Internet of Things (IIoT) (Ge et al., 2021), the research about smart grid has gradually become a hot topic. The smart grid combines communication technology (Liu L. et al., 2022; Mensi et al., 2022), grid technology and computer software to complete the production, distribution and transmission of electricity. AMI, as an important part of smart grid system, generally consists of two entities: one is the electricity service provider and the other is the smart meter device. The smart meter device is usually composed of communication module and sensor module, which can collect and transmit the user’s electricity consumption information in real time. The electricity service provider is usually composed of communication module and control module, which can store and analyze data. On the one hand, the electricity service provider can analyze these data detected by the smart meter in real time to formulate the more reasonable electricity supply strategy, which can effectively improve efficiency, reliability and security of smart grid. On the other hand, the smart meter device can adjust some parameters, such as unit price, based on these messages sent from an electricity service provider.

Although the smart grid has brought great convenience to the people’s lives, it still faces a series of challenges and attacks (He et al., 2017; Kumar et al., 2019b; Peng et al., 2019). The smart gird is vulnerable to various attacks, such as replay attack, impersonation attack and desynchronization attack, which may cause some serious damage to the security of smart grid and the interest of users. Communications between the smart meter and the electricity service provider are carried out via the wired and wireless links, which are easily eavesdropped, modified and intercepted by a malicious adversary. In addition to the external adversary’s attack, the secure problems brought by the insiders are also non-negligible. The transmitted messages between the smart meter and the electricity service provider often contain some confidential and sensitive data. Once these data are obtained by a malicious adversary, it will cause the serious damage to the interest of users. For example, an adversary can analyze the user’s electricity consumption to determine whether the user is at home at the current time, which seriously violates the privacy of users. Therefore, how to ensure the confidentiality of transmitted messages is the first challenge in the smart grid. According to the received messages, the electricity service provider or smart meter device will formulate a electricity distribution strategy or adjust the corresponding parameters, such as updating electricity price or deciding whether to cut electricity. Once a malicious adversary modifies the messages, the electricity service provider or the smart meter may make some inappropriate modifications, decisions, and adjustments based on the modified messages, which will affect the security and stability of entire smart grid. Therefore, how to ensure the integrity of transmitted messages is the second challenge in the smart grid. The encrypted transmission of messages can be carried out by using the secret key generated through the key agreement protocol. In the smart grid, not only the privacy of messages, but also the legitimacy of messages must be ensured. Therefore, before the key agreement, both the service provider and the smart meter should authenticate each other’s identity. However, most of existing authentication protocols contain some complex cryptographic operations, which are not suitable for the resource-constrained smart meter devices. How to reduce the computation overhead of smart meter during the execution phase of protocol is the third challenge in the smart grid.

The authenticated key agreement, as a key establishment method, can not only complete the key agreement, but also authenticate the identity of both parties. There are two ways to implement the authenticated key agreement: the public-key infrastructure and the identity-based cryptography. The method based on the public-key infrastructure needs a certification authority (CA) to generate and manage all certificates for users, where the certificate contains the user’s public key information and other information. By verifying the validity of received certificate sent from its peer, the two communication parties can authenticate each other, which will increase the burden of certificate management and does not apply in the smart grid environment. The identity-based cryptosystem is a more sensible approach to design an authenticated key agreement protocol. However, some previous identity-based authenticated key agreement protocols usually involve some complex cryptographic operations such as bilinear pairing, which are not suitable for the smart meter devices with the limited computation and storage resources. With the rapid development of cloud computing (Gao et al., 2021; Liu Y. et al., 2022), although the resource-constrained smart meter devices can outsource the complex cryptographic operations to the cloud servers with the powerful computation resources (Li H. et al., 2022, 2021), this method not only increases the communication cost and monetary cost of smart meter devices, but also requires adjusting the architecture of entire smart grid. Therefore, one of the most straightforward ways is to design a lightweight authenticated key agreement protocol.

A smart grid system may contain millions of smart meter devices, which will result in the electricity service provider needing to manage millions of session keys at the same time. The electricity service provider not only needs to communicate with a single smart meter, but also potentially needs to carry out the multicast communication with thousands of smart meters. How to generate the group key from session key of multiple smart meters is worth investigating. In addition, once a new smart meter device is added or an old smart meter device is deleted, the group key must be modified accordingly. It is a challenge to design a protocol in which each group member can efficiently compute and update the group key, and the newly added or deleted members do not obtain the updated group key. Therefore, scalability is very important for a key management protocol.

In this paper, in order to solve the above problems, we put forward a lightweight and dynamic authenticated key agreement and management protocol based on identity cryptosystem. Our designed protocol combines the symmetric encryption with the public key encryption, and utilizes ECC and one-way key tree structure (Sherman and McGrew, 2003) to realize authentication, key agreement and group key management and update. The main contributions of this paper can be summarized in three aspects:

• For the resource-constrained smart meter devices, we design a lightweight authenticated key agreement and management protocol based on identity cryptography and ECC. In the execution of designed protocol, each smart meter device only needs to perform several times scalar multiplication and does not need to perform other complex cryptographic operations. The designed protocol not only realizes the mutual authentication between the smart meter and the service provider, but also ensures the confidentiality and integrity of messages transmitted between the two entities.

• For the different communication methods between the smart meter and service provider, including unicast communication and multicast communication, we design a group key generation and update protocol. The service provider can generate a group key based on the session key of each smart meter and update the group key in real time according to the join and exit of smart meter. The service provider and smart meter can efficiently update the group key with the low computation cost. In addition, the designed group key update protocol can realize the forward security and backward security.

• We conduct a comprehensive security analysis to prove that our designed protocol can achieve secure authentication and message transmission, and resist to various attacks. In addition, we carry out some experiments to show that our designed protocol is efficient and lightweight.

The remainder of this paper is organized as follows. Section 2 reviews some related work about the authentication and key management. Section 3 gives a detailed description about system model and security requirements. The background knowledge about ECC is given in Section 4. In Section 5, we describe the designed key agreement and update protocol in detail. A formal security analysis of designed protocol is provided in Section 6. In Section 7, we evaluate the proposed protocol through the numerical analysis and experiments. Finally, we give a conclusion in Section 8.

2 Related work

In this section, we will review some previous authentication and key management protocols in the smart grid. These authentication and key management protocols are constantly modified to achieve a specific security goal and defend against various attacks.

2.1 Some attacks on key management protocols

At first, we introduce some attacks on the previous key management protocols. Wu and Zhou (2011) put forward a novel protocol to solve the secure key management problem in the smart grid, which combined the symmetric encryption technology based on Needham-Schroeder authentication and public key cryptosystem to realize the simplicity and scalability of key management as well as other desirable properties. Their designed protocol not only could resist some common attacks in the smart grid, such as the man-in-the-middle attack and the replay attack, but also could solve the issue of additional vulnerabilities on the session key by utilizing a strict one-time use rule and the fly key generation. However, Xia and Wang (2012) found that the adversary could utilize the man-in-the-middle attack to easily break the Wu’s key management protocol. Based on the previous communication model, the authors designed a new key distribution protocol for the smart grid with the high efficiency as well as the high security, which could resist the impersonation attack, the replay attack and the man-in-the-middle attack. On the one hand, their protocol defined a lightweight directory access protocol (LDAP) server as a third-party, which could significantly reduce operation overhead. On the other hand, when revoking the user’s key, their protocol only needed to remove the related entries of user. Afterwards, Park et al. (2013) pointed out that the Xia’s protocol could not resist the impersonation attack. This meant that the adversary was able to impersonate the responder to the initiator.

2.2 Key management protocols based on ECC

Then, we introduce ECC-based key management protocols. Wan et al. (2014) designed a new scalable key management protocol, which combined the identity-based cryptosystem and the efficient key tree technique to manage the group key and take full advantage of heterogeneity of AMI system. Their protocol could significantly improve the efficiency of key management and resist the desynchronization attack, which was a problem that the previous protocol (Liu et al., 2013) did not solve. Wazid et al. (2017) put forward a three-factor authentication protocol for the remote users in the renewable energy based smart grid environment. The proposed protocol utilized the lightweight cryptographic operations such as one-way hash function, bitwise XOR operation and ECC, which could support the smart meter’s dynamic addition, the flexibility of password and biometric update, the anonymity and untraceability of user. However, this protocol could not flexibly remove the malicious or faulty smart meters. Mahmood et al. (2018) put forward a lightweight authentication protocol based on ECC. The authors used the automated verification tool named ProVerif to analyze the security of proposed protocol and adopted the Burrows-Abadi-Needham (BAN) logic to prove the integrity and completeness of proposed protocol. Although their protocol provided the mutual authentication between the two parties, it didn’t support the anonymity of smart meter. Kumar et al. (2019a) proposed a lightweight authentication and key agreement protocol, which could realize trust, anonymity, integrity and adequate security in the domain of smart energy network. The designed protocol was based on ECC, symmetric encryption, hash function and message authentication code, which could ensure the desired security with the lower computation cost. By utilizing the AVISPA (automated verification of Internet security protocol and application) tool, the authors proved that the designed protocol was semantically secure.

2.3 Key management protocols based on other technologies

Finally, we introduce some key management protocols based on other novel technologies, such as lattice encryption, blockchain and attribute encryption. Chaudhary et al. (2018) designed a lattice-based key exchange protocol to generate the secret session key between the two communication entities. In their protocol, a third party could securely authenticate all entities in network. The encryption algorithm was defined over the quotient ring by using the polynomial vector and simple arithmetic operations, which could ensure the confidentiality and integrity of data. In addition, the authors designed a temporary key-based protocol for detection of suspicious activity to provide the enhanced security. Based on the blockchain technology, Wang et al. (2020) put forward a mutual authentication and key agreement protocol for the smart grid system based on the edge computing, which could support the efficient conditional anonymity and key management, and didn’t need other complex cryptographic primitives. Their designed protocol not only could provide the basic security properties, such as mutual authentication, secure key agreement and resisting replay attack, but also could support the efficient key update and revocation, and the conditional identity anonymity with the low computational overhead and communication overhead. Tomar and Tripathi (2022) designed a mutual authentication and key agreement protocol based on blockchain and fog computing in the smart grid environment, which could overcome some disadvantages of relying on a single trusted authority by creating a blockchain-based distributed environment assisted by cloud servers and fog nodes. The proposed protocol could achieve the default goals and was proven secure under the Real or Random (RoR) model. Based on blockchain and attribute encryption, Li J. et al. (2022) put forward an asymmetric group key agreement protocol for IIoT, which can achieve the efficient access control of participants. The proposed protocol not only realized the automation of access control, but also ensured the tamper resistance and the non-repudiation of agreement process.

Table 1 shows the differences between our proposed protocol and some previous protocols.

TABLE 1

TABLE 1. Comparison with previous protocols.

3 System model and security model

In this section, we will give a detailed description about the system model and security model.

3.1 System model

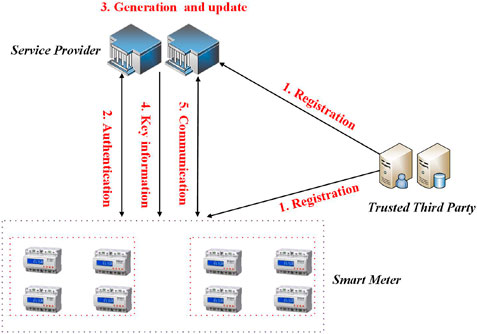
As shown in Figure 1, the system model in the designed protocol consists of three entities as follows:

• Trusted Third Party (TTP) is trusted by all entities in this system, and responsible to produce and publish some system parameters and generate the secret key for each entity based on their identities.

• Service Provider (SP) has the sufficient computation resources and storage resources. The SP will perform mutual authentication with multiple smart meters and negotiate a session key with each smart meter. The SP stores all session keys to generate and update the group key by using a one-way key tree. The SP uses the session key and group key to carry out the unicast communication and multicast communication with the smart meters, respectively.

• Smart Meter (SM) has the limited computation resources and storage resources. Each SM has a session key and a group key. Each SM can communicate with the SP by the session key and use the group key to decrypt the message broadcast by the SP.

FIGURE 1

FIGURE 1. System model.

The overall execution flow of system is as follows:

Once the system is initialized by the TTP, 1) any newly added device SM or SP will register in system with submitting her/his identity to the TTP to obtain a secret key; 2) each SM and SP carry out the mutual authentication and negotiate a session key by using their respective secret keys and other information; 3) the SP divides all SMs into several groups, and uses the session key of each group member and one-way key tree technology to generate the group key of each group. In addition, the SP can update the group key according to the changes of group member; 4) the SP sends some related and necessary key information to the corresponding group members to let them generate and update the group key; 5) SP and SM choose the different communication methods (unicast or multicast) according to the different scenarios.

3.2 Security model and requirements

In this paper, we use the security model adopted by many previous papers (Mahmood et al., 2018). In the designed protocol, we assume that TTP is fully trusted and the secret key of TTP will not be disclosed to the adversary. The adversary can pretend to be any SM or SP during the execution of protocol. We assume that the adversary knows the identity of any SM and SP. The adversary can eavesdrop on these information transmitted on the public channels. In addition, the adversary can retrieve, modify, replay, inject new messages and discard any messages.

The designed authenticated key agreement and management protocol needs to meet the following requirements including confidentiality, integrity, availability (resilience to various attacks) and privacy:

• Confidentiality: In the smart grid, the messages transmitted between the SM and SP usually contain some confidential and sensitive information, which cannot be leaked to the adversary. Once leaked, it will cause serious damage to the interest of users and the security of smart grid. So, the designed protocol should protect the confidentiality of transmitted messages between the SM and SP.

• Integrity: The integrity of transmitted messages is an indispensable attribute of a secure authentication and key management protocol. The SP will make the important decision according to the received information or the SM will make the corresponding operation according to the received information. So, the designed protocol should protect the integrity of transmitted messages between the SM and SP.

• Availability: In the practical applications, various attacks have a serious impact on the security of smart grid. A robust authentication and key management protocol needs to keep availability under various attacks, such as replay attack, impersonation attack and desynchronization attack. The designed protocol should restrict the ability of internal or external users to launch various attacks against other components or networks.

• Privacy: During the process of updating the group key, the newly added or deleted SM may obtain some information about the group key, which cannot be leaked to them. The designed protocol should maintain both forward and backward security. This means that the newly added SM cannot obtain the previous group key and the deleted SM cannot obtain the after group key.

4 Background knowledge

Compared with other public key cryptography algorithms, such as RSA and Elgaml, ECC has some obvious advantages. ECC can achieve the same level of security as other schemes with the smaller scale of secret key. An elliptic curve on a finite field F_q can be represented as: y² = x³ + ax + b mod q, where q is a large prime and a, b ∈ Z_q, 4a³ + 27b² mod q ≠ 0. We define E/F_q as the set of point. Given a point P and an integer n ∈ Z_q, the scalar multiplication can be defined as Q = n ⋅ P. Double-and-add algorithm is an efficient way to compute scalar multiplication, which contains two basic blocks: point addition and point doubling.

Point addition: let P and Q be two points on the elliptic curve, point addition describes the addition of P and Q. There is a straight line between the point P and Q. The line intersects the elliptic curve at another point − F. The output of the addition of P and Q is the point F, where the point F is the reflection of the point − F with respect to the x-axis.

Point doubling: let P be a point on the elliptic curve, point doubling describes the double of the point P. There is one tangent line to the elliptic curve at the point P. The tangent line intersects the elliptic curve at another point − F. The output of the double of the point P is the point F, where the point F is the reflection of the point − F with respect to the x-axis.

Algorithm 1 describes how to compute scalar multiplication, in which the point O is the torsion point.

Algorithm 1. Scalar multiplication.

Input:

 n ∈ Z_q and P ∈ E/F_q.

Output:

 Q = n ⋅ P.

1: Set $n={\sum }_{i=1}^m{n}_{i-1}{2}^{i-1}$ (n_i−1 is 0 or 1).

2: Set Q ← O.

3: for i = 1 to m do

4:  if n_i−1 = 1 then

5:   Q = Q + P.

6:  end if

7:  P = 2P.

8: end for

9: return Q.

4.1 Definition 1 (DDH assumption)

Assume that P is a random point selected from E/F_q and a, b, c are randomly selected from Z_q, the Decisional Diffie-Hellman problem is to distinguish (P, aP, bP, abP) from (P, aP, bP, cP). For any PPT distinguisher $\mathbb{D}$, the advantage is defined as:

$|\mathrm{Pr}\left[\mathbb{D}\left(P,aP,bP,abP\right)\right]-\mathrm{Pr}\left[\mathbb{D}\left(P,aP,bP,cP\right)\right]|<negli\left(\lambda \right).$

where negli () is a negligible function of security parameter λ.

5 Protocol

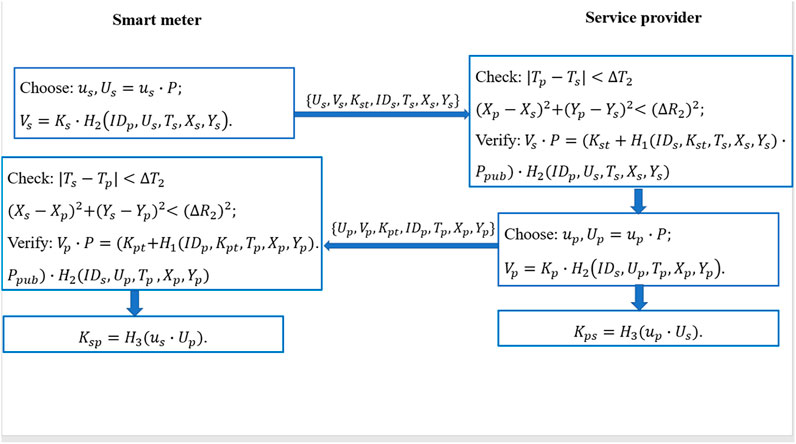
In this section, we will introduce our proposed protocol in detail. As shown in Table 2, we define the mainly used notations in this paper. The designed protocol mainly contain three phases: initialization phase, registration phase and authentication phase. Details of each phase are described as follows:

• Initialization phase: Given a security parameter λ, TTP generates and publishes some system parameters. At first, TTP chooses a λ bits prime q and constructs {F_q, E/F_q, P}, where P is a generator of group E/F_q. Then, TTP randomly chooses a number s ∈ Z_q as the master key and computes P_pub = s ⋅ P. In addition, TTP chooses three hash functions H₁ : {0,1}*× Z_q → Z_q, H₂ : {0,1}*× Z_q → Z_q and H₃ : {0,1}* → Z_q. Finally, TTP publishes {F_q, E/F_q, P, P_pub, H₁, H₂, H₃} as the system parameters and keeps the master key s secret for itself.

• Registration phase:

• The SM firstly chooses a random number r_st ∈ Z_q and computes K_st = r_st ⋅ P. Then, the SM sends K_st to TTP along with its identification ID_s, the current timestamp T_s and the current location (X_s, Y_s) via a secure channel.

• TTP firstly checks whether the two inequalities |T_t − T_s| < △T₁ and ${(X_t-X_s)}^2+{(Y_t-Y_s)}^2<{(△R_1)}^2$ hold. If the two inequalities hold, TTP computes K_ts = s ⋅ H₁(ID_s, K_st, T_s, X_s, Y_s) and sends it to the SM via a secure channel; otherwise, the registration process is aborted.

• The SM verifies the validity of K_ts by checking whether the equation H₁(ID_s, K_st, T_s, X_s, Y_s) ⋅ P_pub = K_ts ⋅ P holds.

• If the verification passes successfully, the SM computes its key K_s = r_st + K_ts.

TABLE 2

TABLE 2. Notations.

For the SP, it can utilize the similar method to randomly choose a number r_pt ∈ Z_q and compute K_pt. Then, the SP sends K_pt along with its identification ID_p, the current timestamp T_p and the current location (X_p, Y_p). TTP can check and return K_tp to the SP. The SP verifies the validity of K_tp by checking whether the equation H₁(ID_p, K_pt, T_p, X_p, Y_p) ⋅ P_pub = K_tp ⋅ P holds. Finally, the SP computes its key K_p = r_pt + K_tp.

• Authentication phase:

• At first, the SM chooses a random number u_s ∈ Z_q and computes U_s = u_s ⋅ P. In addition, the SM computes V_s = K_s ⋅ H₂(ID_p, U_s, T_s, X_s, Y_s). Then, the SM sends these parameters {U_s, V_s, K_st, ID_s, T_s, X_s, Y_s} to the SP.

• The SP firstly checks whether the current time and location of the SM meet the preset conditions by the inequalities |T_p − T_s| < △T₂ and ${(X_p-X_s)}^2+{(Y_p-Y_s)}^2<{(△R_2)}^2$. If all conditions are met, the SP will verify whether the equation V_s ⋅ P=(K_st + H₁(ID_s, K_st, T_s, X_s, Y_s) ⋅ P_pub) ⋅ H₂(ID_p, U_s, T_s, X_s, Y_s) holds.

• If the verification passes successfully, the SP chooses a random number u_p ∈ Z_q and computes U_p = u_p ⋅ P. In addition, the SP computes V_p = K_p ⋅ H₂(ID_s, U_p, T_p, X_p, Y_p). Then, the SP sends these parameters {U_p, V_p, K_pt, ID_p, T_p, X_p, Y_p} to the SM. Finally, the SP computes K_ps = H₃ (u_p ⋅ U_s).

• The SM firstly checks whether the current time and location of the SP meet the preset conditions by the inequalities |T_s − T_p| < △T₂ and ${(X_s-X_p)}^2+{(Y_s-Y_p)}^2<{(△R_2)}^2$. If all conditions are met, the SM will verify whether the equation V_p ⋅ P=(K_pt + H₁(ID_p, K_pt, T_p, X_p, Y_p) ⋅ P_pub) ⋅ H₂(ID_s, U_p, T_p, X_p, Y_p) holds.

• If the verification passes successfully, the SM computes K_sp = H₃ (u_s ⋅ U_p).

Figure 2 shows the entire implementation of the proposed protocol. When the authentication process is completed, the SM and SP negotiate a session key K_i = K_sp = K_ps. The SM and SP can encrypt and transmit messages through the session key. Communications between the SM and SP can be divided into unicast communication and multicast communication according to the number of SMs. When the two parties conduct the secure unicast communication, they only need to use the negotiated session key between the two parties. The detailed process is as follows: Suppose there is a SP and a SM whose identity is ID_i. The session key negotiated by the two parties is K_i. When a message m needs to be transmitted, the SM (SP) utilizes the session key K_i and a symmetric encryption algorithm Enc () such as DES or AES to encrypt the message m into M = Enc (m, K_i). In order to ensure the integrity of message m, we adopt the Hash-based Message Authentication Code (HMAC) to realize it. The SP needs to send {ID_i, M = Enc (m, K_i), HMAC (m, K_i)} to the SM. After receiving the ciphertext of message, the SM firstly utilizes the session key K_i and the corresponding decryption algorithm Dec () to decrypt M to obtain the message m. Then, the SM will recalculate the HMAC of message m and compares it with the received HMAC. If the two HMACs are consistent, the message is complete and has not been tampered with.

FIGURE 2

FIGURE 2. Authentication phase of designed protocol.

When a SP needs to multicast with multiple SMs, it is necessary to generate a group key for these SMs. Then, we will introduce how to generate the group key and how to update the group key.

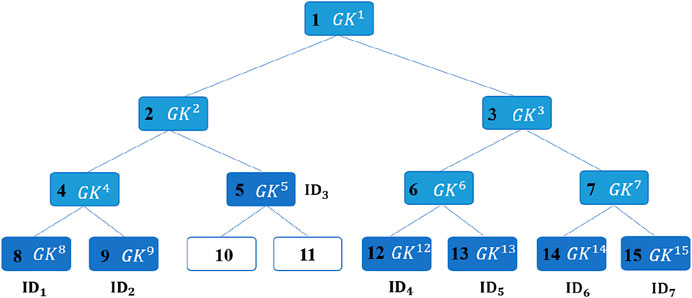
We adopt a method called One-Way Function Tree (OFT) to construct the key tree and generate the multicast key. The OFT is a particular type of binary tree in which each interior node has exactly two children. The value of each leaf node in the OFT is associated with a group member. The value of root node in the OFT is the group key (multicast key). The SP can utilize the group key to securely communicate with all members of this group. The SP can use the session key of all group members to generate the OFT as follows: The value of each leaf node in the OFT is the previously negotiated session key for each SM. For the value of any interior node in the OFT key tree can be generated from the value of its two child nodes. For an interior node v. the value K_v of node v can be defined as K_v = f (K_l) ⊕ f (K_r). f () is a special one-way function, K_l and K_r, respectively represent the value of left child node and the value of right child node, and ⊕ is bitwise exclusive-or.

Each group member not only maintains the value of leaf node, but also stores a list of blinded values for all siblings of nodes along the path from this node to the root. The SP can send these blinded values to the corresponding group members, which enables the corresponding group members to compute the values of node along its path to the root, including the root key and the keys of node along this path. Once a group member (SM) is added or removed, the SP will send the necessary update information to the corresponding group members. According to the received information and locally stored information, each group member will recompute the values of node on its path to the root and obtain a new group key.

For convenience of presentation, we need to number each node in the OFT. When numbering nodes, we view the OFT as a complete tree. In other words, there are some unoccupied leaves for the future group members. Figure 3 shows the overall structure of the OFT. As shown in Figure 3, the value of each leaf node is the session key by running the above authentication protocol. The node with number 5 is a special leaf node that contains two virtual leaf nodes. For each non-leaf node i. the value GKⁱ can be compute as GKⁱ = f (GK²ⁱ) ⊕ f (GK²ⁱ⁺¹). The value of root node GK¹ is the group key.

FIGURE 3

FIGURE 3. An example of OFT key tree.

The OFT is construct by the SP. Then, the SP will broadcasts the blinded value of each sibling node along the path from the member to the root. Each SM can compute the group key according to blinded values. Each blinded value is encrypted by the value of the sibling node, so that only members in the sibling subtree can learn the blinded value. For example, in order to the SM with ID₁ can obtain the group key, the SP needs to send the blinded values {f (GK⁹), f (GK⁵), f (GK³)} to it. To preserve security and privacy, the SP should encrypt f (GK⁹), f (GK⁵), f (GK³) with GK⁸. To preserve integrity, the SP also utilizes HMAC. So, the SP needs to send {Enc (f (GK⁹), GK⁸), Enc (f (GK⁵), GK⁸), Enc (f (GK³), GK⁸), HMAC (f (GK⁹‖f (GK⁵)‖f (GK³), GK⁸)} to the SM with ID₁.

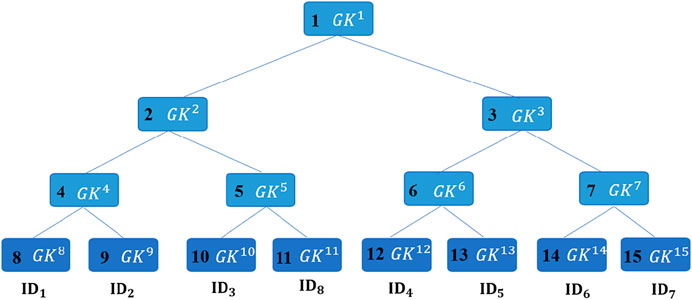
The OFT is dynamic and updatable. When a new SM adds to this group or an existing SM leaves this group, the SP will re-compute the group key and send the updated blinded values to the corresponding SMs. Each SM can update the group key according to the received information. Let’s take the OFT in Figure 3 as an example to show the changes in the OFT after adding a new SM with ID₈. As shown in Figure 4, the two new nodes with numbers 10 and 11 are added to the original OFT. The SM with ID₃ is associated with a leaf node with number 10 and the SM with ID₈ is associated with a leaf node with number 11. The value of node with number 5 is generated from f (GK¹⁰) (the blinded value of ID₃’s session key) and f (GK¹¹) (the blinded value of ID₈’s session key). The original leaf node with number 5 becomes an interior node, which contains two leaf nodes with numbers 10 and 11. Then, the SP needs to send {Enc (f (GK³), GK¹¹), Enc (f (GK⁴), GK¹¹), Enc (f (GK¹⁰), GK¹¹), HMAC (f (GK³‖f (GK⁴)‖ f (GK¹⁰)), GK¹¹)} to the SM with ID₈ to compute the group key. The SP needs to send {Enc (f (GK¹¹), GK¹⁰), HMAC (f (GK¹¹), GK¹⁰)} to the SM with ID₃ to update the group key. The SP needs to send {Enc (f (GK⁵), GK⁴), HMAC (f (GK⁵), GK⁴)} to the SM with ID₁ and ID₂ to update the group key. The SP needs to send {Enc (f (GK²), GK³), HMAC (f (GK²), GK³)} to the SM with ID₄, ID₅, ID₆ and ID₇ to update the group key. Each SM can update the group key with the blinded values of corresponding nodes according to the equation GKⁱ = f (GK²ⁱ) ⊕ f (GK²ⁱ⁺¹).

FIGURE 4

FIGURE 4. SM joining.

When an existing SM leaves this group, the SP can use a similar method to update the group key.

The SP can multicast with multiple SMs by the group key GK. Similar to the unicast communication, the SP utilizes the group key GK, the symmetric encryption algorithm Enc () and authentication code HMAC to broadcast a message m. The SP broadcasts {GID, M = Enc (m, GK), HMAC (m, GK)} to all group members, where GID is the group identity. On receiving the above message, each SM will decrypt the ciphertext to obtain the message m and verify the integrity of m by computing HMAC.

6 Security analysis

In this section, we will conduct the security analysis about the authentication phase and the group key update phase under the security model defined in Section 3. The security analysis about the registration phase is similar to the authentication phase.

6.1 Replay attack

A replay attack means that the adversary can eavesdrop on the exchanged messages and resend some messages at the adversary’s will. In the authentication phase, the SM and the SP can challenge each other. Note that the exchanged messages contain the current timestamp T_s or T_p. In the communications between the two parties, T_s or T_p is not only transmitted in the form of plaintext, but also hidden in V_s = K_s ⋅ H₂(ID_p, U_s, T_s, X_s, Y_s) or V_p = K_p ⋅ H₂(ID_s, U_p, T_p, X_p, Y_p). For example, the adversary generates and sends the fresh timestamp t_s. The adversary expects the SP to return something that matches its secret key in the next message. However, the SP fails to verify the equation V_s ⋅ P=(K_st + H₁(ID_s, K_st, T_s, X_s, Y_s) ⋅ P_pub) ⋅ H₂(ID_p, U_s, T_s, X_s, Y_s) in our designed protocol. Therefore, the replay attack is thwarted. When the SP sends some messages to the SM, in a similar way, we can prove that this process is also resistant to the replay attack due to T_p. This is because the SM fails to verify the equation V_p ⋅ P=(K_pt + H₁(ID_p, K_pt, T_p, X_p, Y_p) ⋅ P_pub) ⋅ H₂(ID_s, U_p, T_p, X_p, Y_p) if the adversary generate a fresh timestamp t_p.

6.2 Impersonation attack

The impersonation attack means that the adversary can be authenticated and communicate with the other parties. That is to say, the adversary can pretend to be the SM (SP) and communicate with the SP (SM). In our designed protocol, the SM and the SP need to carry out the mutual authentication by utilizing the secret key generated by the TTP. If the adversary wants to impersonate the SM, he should generate a valid request {U_s, V_s, K_st, ID_s, T_s, X_s, Y_s} to the SP. However, the process of generating U_s and V_s involves the SM’s private key K_s. Based on the DDH assumption, the adversary cannot recover the private key K_s from the intercepted messages. Similarly, if the adversary wants to impersonate the SP, he should generate a valid response {U_p, V_p, K_pt, ID_p, T_p, X_p, Y_p} to the SM. The process of generating U_p and V_p involves the SP’s private key K_p. Therefore, our designed protocol is resistant to the impersonation attack.

6.3 Desynchronization attack

The desynchronization attack means that the adversary can block message transmission between the SM and the SP to make them lose key synchronization permanently. Once this desynchronization attack is successful, the SM and the SP will no longer communicate with each other. In our designed protocol, the session key is constructed by the random number and timestamp. There is no connection between the newly generated session key and the previously generated session key. Therefore, our designed protocol is resistant to the desynchronization attack. Even if the message is blocked, we can run the designed protocol again to synchronize.

6.4 Unicast and multicast communications security

On the one hand, the unicast key is the session key negotiated between the SM and the SP. The multicast key is generated by using the OFT. The security of session key depends on the security of designed authentication protocol, which we have proven through various attacks. As for the multicast key, according to the construct of OFT, we can know that only the corresponding group members can obtain the group key. Other entities cannot obtain the group key without knowing the relevant key material. On the other hand, it is obvious that our designed protocol can both protect the confidentiality and integrity of messages. By encrypting the content of messages with the session key or the group key, our designed protocol can protect the confidentiality of messages. By computing the HMAC of messages with the session key or the group key, our designed protocol can guarantee the integrity of messages.

6.5 Backward security

Backward security means that when a SM joins the group, it will not be able to calculate the previous group key, even if multiple newly joined SMs collude. When a new SM (leaf node) joins the group, as shown in Figure 4, all values of node on the path from this node to the root in the OFT key tree will be updated. The key tree will add two leaf nodes. The original leaf node will become the parent node of the two leaf nodes, which is an interior node. The newly added node can only receive a blinded value of the original leaf node. All values of node on the path from the leaf node to the root is based on the real value of the original leaf node. However, after updating, all values of node on the path from the leaf node to the root is based on the blinded value of the original leaf node. Without knowing the real value of the original leaf node, the newly joined SM will not recover the previous group key. Even though multiple newly joined SMs collude, they cannot recover the previous group key. This is because they only receive the blinded values of their sibling nodes (the leaf node in the original key tree). The previous group key is computed based on the real values of their sibling nodes. Therefore, no matter how many newly joined smart members collude together, they cannot recover the previous group key.

6.6 Forward security

Forward security means that when a SM is removed from the group, it will not be able to compute the new group key, even if multiple removed SMs collude. Similar to backward security, we can prove that our designed protocol compliant with forward security by the same way. The previous group key is computed based on the blinded values of their sibling nodes. After removing some SMs, the new group key is compute based on the real values of their sibling nodes. Therefore, without knowing the real values of their sibling nodes, no matter how many removed SMs collude together, they cannot obtain the new group key.

7 Evaluation

7.1 Numerical evaluation

We give some numerical analysis about computation cost and communication cost. In the computation cost analysis, we only focus on the number of each entity performs the scalar multiplication and hash algorithm. We ignore other lightweight operations. We denote sm as once scalar multiplication and hash as once hash. At first, in the registration phase, SM/SP needs once sm to compute K_st/K_pt, and once hash and twice sm to complete verification. TTP needs once hash to compute K_ts/K_tp. In terms of communication cost, SM/SP needs to send K_st/K_pt to TTP and TTP needs to return K_ts/K_tp to SM/SP. The bit length of K_st/K_pt is 2λ and the bit length of K_ts/K_tp is λ. In the authentication phase, SM/SP needs five times sm and four times hash to complete authentication and key agreement. SM/SP needs to send {U_s, V_s, K_st}/{U_p, V_p, K_pt} to another entity. The bit length of {U_s, V_s, K_st}/{U_p, V_p, K_pt} is 5λ. We ignore other transmitted data. Table 3 shows the analysis about computation cost and communication cost.

TABLE 3

TABLE 3. Analysis about protocol.

7.2 Experiment evaluation

In this section, we carry out some experiments to show that our designed protocol is lightweight and efficient. In our experiments, we use a computer with Linux Ubuntu 20.04.2 LTS operating system and Intel Core i5 processors with 2.4 GMz and 2G memory to simulate all entities in the designed system, including SM, SP and TTP. Our experiments utilize the C++ programming language to implement our designed protocol and adopt the PBC library to perform scalar multiplication on elliptic curve. The hash function in our experiment is SHA-256.

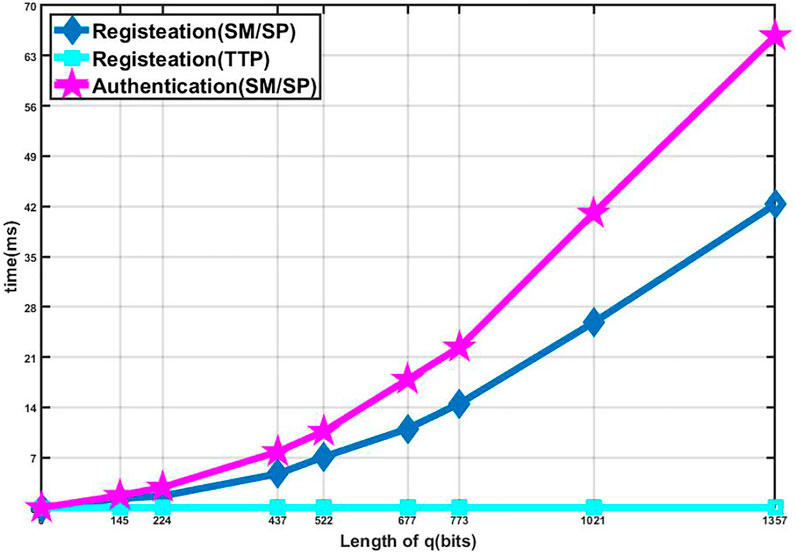
In the first experiment, as the bit length of modulus q increases, we count the time cost in the different stages of each entity. As shown in Figure 5, as the bit length of q increases, the computation overhead of each entity in each stage will also increase accordingly, which also means that the designed protocol has higher security. From Figure 5, we can find that the time cost of TTP is much smaller than that of SM and SP. This is because TTP only communicates with SM or SP and generates the secret key during the registration phase, which only contains once hash algorithm and some lightweight operations in this phase, such as computing the product of two numbers. SM or SP needs to perform multiple scalar multiplications on elliptic curve during the registration and authentication phase. In addition, because the registration phase requires three times scalar multiplications and the authentication phase requires five times scalar multiplications, the time cost of authentication phase is higher than that of the registration phase.

FIGURE 5

FIGURE 5. Time cost under different bit lengths of q.

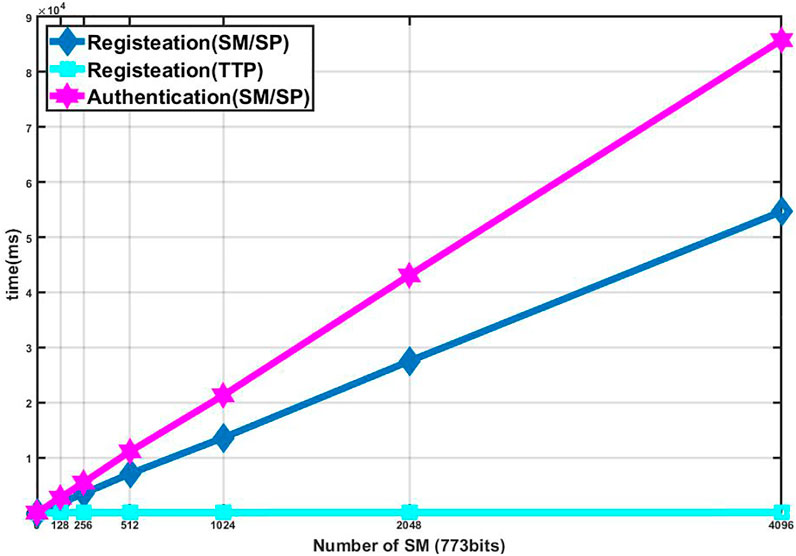
In a second experiment, we show the time cost of each entity when the number of SMs increases. As shown in Figure 6, we can find that, when the number of SMs increases, the time cost of TTP does not change significantly. It shows that TTP can efficiently generate the secret key for each SM in a large-scale smart grid environment.

FIGURE 6

FIGURE 6. Time cost under different numbers of SM.

8 Conclusion

In this paper, we design a lightweight authenticated key agreement and management protocol based on the identity cryptosystem and scalar multiplication on elliptic curve. The designed protocol takes time and geographical factors into account, and can quickly realize the mutual authentication and key negotiation between the two parties in the smart grid. In addition, we design a group key generation and update protocol, which enables the SP and SM to efficiently generate and update the group key in the multicast communication by utilizing a one-way key tree structure. Then, we give an analysis to show that our designed protocol satisfies our given design goals including confidentiality, integrity, and availability. We also prove that the forward and backward security of group key can be guaranteed in the update of group key. Finally, we show the efficiency of proposed protocol through experiments. Our proposed protocol may be not perfect and has some shortcomings. On the one hand, in the current protocol, TTP needs to send the necessary key information to the corresponding SM whenever the group membership changes. If the SM changes frequently, this greatly increases the communication complexity between the two parties. On the other hand, the designed protocol does not take quantum attacks into account, which may have an impact on the security of protocol. In future research, we will explore how to reduce the communication complexity in key update and how to improve the security.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

FZ, TY, and WS contributed to conception and design of the study. FZ and XF organized the database. FZ and TY performed the statistical analysis. FZ wrote the first draft of the manuscript. FZ and TY wrote sections of the manuscript. FZ, TY, WS, and XF contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was supported in part by the National Key Research and Development Program of China (2017YFE0132100) and the National Natural Science Foundation of China (61971305).

Conflict of interest

FZ was employed by China Electric Power Research Institute, State Grid. WS was employed by State Grid Corporation of China. XF was employed by Henan Xj Metering Co, Ltd.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chaudhary, R., Aujla, G. S., Kumar, N., Das, A. K., Saxena, N., and Rodrigues, J. J. P. C. (2018). “Lacsys: Lattice-based cryptosystem for secure communication in smart grid environment,” in 2018 IEEE International Conference on Communications (ICC), 1–6.

CrossRef Full Text | Google Scholar

Gao, X., Yu, J., Chang, Y., Wang, H., and Fan, J. (2021). “Checking only when it is necessary: Enabling integrity auditing based on the keyword with sensitive information privacy for encrypted cloud data,” in IEEE Transactions on Dependable and Secure Computing, 1.

Google Scholar

Ge, X., Yu, J., Zhang, H., Bai, J., Fan, J., and Xiong, N. N. (2021). “SPPS: A search pattern privacy system for approximate shortest distance query of encrypted graphs in IIoT,” in IEEE Transactions on Systems, Man, and Cybernetics: Systems, 1–15.

Google Scholar

He, D., Kumar, N., Zeadally, S., Vinel, A., and Yang, L. T. (2017). Efficient and privacy-preserving data aggregation scheme for smart grid against internal adversaries. IEEE Trans. Smart Grid 8, 2411–2419. doi:10.1109/tsg.2017.2720159

CrossRef Full Text | Google Scholar

Kumar, P., Gurtov, A., Sain, M., Martin, A., and Ha, P. H. (2019a). Lightweight authentication and key agreement for smart metering in smart energy networks. IEEE Trans. Smart Grid 10, 4349–4359. doi:10.1109/tsg.2018.2857558

CrossRef Full Text | Google Scholar

Kumar, P., Lin, Y., Bai, G., Paverd, A., Dong, J., and Martin, A. (2019b). Smart grid metering networks: A survey on security, privacy and open research issues. IEEE Commun. Surv. Tutorials 21, 2886–2927. doi:10.1109/comst.2019.2899354

CrossRef Full Text | Google Scholar

Li, H., Yu, J., Fan, J., and Pi, Y. (2022a). “DSOS: A distributed secure outsourcing system for edge computing service in iot,” in IEEE Transactions on Systems, Man, and Cybernetics: Systems, 1–13.

CrossRef Full Text | Google Scholar

Li, H., Yu, J., Yang, M., and Kong, F. (2021). Secure outsourcing of large-scale convex optimization problem in internet of things. IEEE Internet Things J. 9, 8737–8748. doi:10.1109/jiot.2021.3116127

CrossRef Full Text | Google Scholar

Li, J., Qiao, Z., and Peng, J. (2022b). “Asymmetric group key agreement protocol based on blockchain and attribute for industrial internet of things,” in IEEE Transactions on Industrial Informatics, 1.

CrossRef Full Text | Google Scholar

Liu, L., Zhang, Z., Wang, N., Zhang, H., and Zhang, Y. (2022a). “Online resource management of heterogeneous cellular networks powered by grid-connected smart micro grids,” in IEEE Transactions on Wireless Communications, 1.

CrossRef Full Text | Google Scholar

Liu, N., Chen, J., Zhu, L., Zhang, J., and He, Y. (2013). A key management scheme for secure communications of advanced metering infrastructure in smart grid. IEEE Trans. Ind. Electron. 60, 4746–4756. doi:10.1109/tie.2012.2216237

CrossRef Full Text | Google Scholar

Liu, Y., Yu, J., Fan, J., Vijayakumar, P., and Chang, V. (2022b). Achieving privacy-preserving dsse for intelligent iot healthcare system. IEEE Trans. Ind. Inf. 18, 2010–2020. doi:10.1109/tii.2021.3100873

CrossRef Full Text | Google Scholar

Mahmood, K., Chaudhry, S. A., Naqvi, H., Kumari, S., Li, X., and Sangaiah, A. K. (2018). An elliptic curve cryptography based lightweight authentication scheme for smart grid communication. Future Gener. Comput. Syst. 81, 557–565. doi:10.1016/j.future.2017.05.002

CrossRef Full Text | Google Scholar

Mensi, N., Rawat, D. B., and Balti, E. (2022). Gradient ascent algorithm for enhancing secrecy rate in wireless communications for smart grid. IEEE Trans. Green Commun. Netw. 6, 107–116. doi:10.1109/TGCN.2021.3093821

CrossRef Full Text | Google Scholar

Park, J. H., Kim, M., and Kwon, D. (2013). Security weakness in the smart grid key distribution scheme proposed by xia and wang. IEEE Trans. Smart Grid 4, 1613–1614. doi:10.1109/tsg.2013.2258823

CrossRef Full Text | Google Scholar

Peng, C., Sun, H., Yang, M., and Wang, Y. (2019). A survey on security communication and control for smart grids under malicious cyber attacks. IEEE Trans. Syst. Man. Cybern. Syst. 49, 1554–1569. doi:10.1109/tsmc.2018.2884952

CrossRef Full Text | Google Scholar

Sherman, A. T., and McGrew, D. A. (2003). Key establishment in large dynamic groups using one-way function trees. IIEEE. Trans. Softw. Eng. 29, 444–458. doi:10.1109/tse.2003.1199073

CrossRef Full Text | Google Scholar

Song, E. Y., FitzPatrick, G. J., Lee, K. B., and Griffor, E. (2022). A methodology for modeling interoperability of smart sensors in smart grids. IEEE Trans. Smart Grid 13, 555–563. doi:10.1109/tsg.2021.3124490

CrossRef Full Text | Google Scholar

Tomar, A., and Tripathi, S. (2022). Blockchain-assisted authentication and key agreement scheme for fog-based smart grid. Clust. Comput. 25, 451–468. doi:10.1007/s10586-021-03420-2

CrossRef Full Text | Google Scholar

Verma, G. K., Gope, P., and Kumar, N. (2022). PF-DA: Pairing free and secure data aggregation for energy internet-based smart meter-to-grid communication. IEEE Trans. Smart Grid 13, 2294–2304. doi:10.1109/tsg.2021.3138393

CrossRef Full Text | Google Scholar

Wan, Z., Wang, G., Yang, Y., and Shi, S. (2014). Skm: Scalable key management for advanced metering infrastructure in smart grids. IEEE Trans. Ind. Electron. 61, 7055–7066. doi:10.1109/tie.2014.2331014

CrossRef Full Text | Google Scholar

Wang, J., Wu, L., Choo, K. K. R., and He, D. (2020). Blockchain-based anonymous authentication with key management for smart grid edge computing infrastructure. IEEE Trans. Ind. Inf. 16, 1984–1992. doi:10.1109/tii.2019.2936278

CrossRef Full Text | Google Scholar

Wazid, M., Das, A. K., Kumar, N., and Rodrigues, J. J. P. C. (2017). Secure three-factor user authentication scheme for renewable-energy-based smart grid environment. IEEE Trans. Ind. Inf. 13, 3144–3153. doi:10.1109/tii.2017.2732999

CrossRef Full Text | Google Scholar

Wu, D., and Zhou, C. (2011). Fault-tolerant and scalable key management for smart grid. IEEE Trans. Smart Grid 2, 375–381. doi:10.1109/tsg.2011.2120634

CrossRef Full Text | Google Scholar

Xia, J., and Wang, Y. (2012). Secure key distribution for the smart grid. IEEE Trans. Smart Grid 3, 1437–1443. doi:10.1109/tsg.2012.2199141

CrossRef Full Text | Google Scholar