Verification of CENDL-3.2 and ENDF/B-VIII.0 Evaluated Nuclear Data Library on HTR-10 Benchmark

CENDL-3.2 and ENDF/B-VIII.0 referring to the latest version of CENDL and ENDF/B, respectively, evaluated nuclear data library. To examine the applicability the libraries to high-temperature reactors (HTRs), the HTR-10 benchmark calculations are conducted by adopting CENDL-3.2, ENDF/B-VIII.0, and ENDF/B-VII.1 library. The calculated results are compared with the experimental results. As indicated from the comparison, the results of ENDF/B-VIII.0 show the optimal consistency with the experimental results, and CENDL-3.2 outperforms ENDF/B-VII.1. A semi-quantitative analysis method, on the basis of the sensitivity result, is employed to assess the effect of the cross-section change to $k_{\text{eff}}$. As revealed from the further calculations and analyses, the difference between cross-sections of C-12 (n, γ) channel primarily causes the inconsistent performance of CENDL-3.2 and ENDF/B-VIII.0 on the benchmark.

Introduction

On the basis of the existing experiments and evaluations, the evaluated nuclear data libraries provide necessary data for nuclear science research and engineering design. Several libraries—CENDL (Ge et al., 2020), ENDF/B (Brown et al., 2018), JEFF (Plompen et al., 2020), JENDL (SHIBATA et al., 2011), and TENDL (Koning et al., 2019)—have been developed. After being processed by nuclear data processing codes, e.g., NJOY (MacFarlane and Kahler, 2010) and RXSP (Li et al., 2012), data of the mentioned libraries can be employed for simulations.

CENDL-3.2, the latest version of CENDL, was released by China Nuclear Data Center (CNDC) in 2020. The number of nuclides in CENDL has increased to 272, in which 137 nuclides are inherited from CENDL-3.1, 77 nuclides are partially updated, and 58 nuclides are newly evaluated. The performance of CENDL-3.2 on benchmarks has been evaluated in the report, which is significantly improved, compared with CENDL-3.1 (Ge et al., 2020). As the latest version of ENDF/B, ENDF/B-VIII.0 library was released in 2018. ENDF/B-VIII.0 has major changes for neutron reactions of the vital nuclides for nuclear criticality calculation. In addition, the numbers of nuclide in several sublibraries (e.g., neutron and thermal n-scattering) increase (Brown et al., 2018).

The verification of nuclear libraries by using developed benchmarks is important to their applications and improvement. The performances of CENDL-3.2 were reported to be acceptable by verifications on reactor designs and shielding benchmarks (Shu et al., 2021; Hu et al., 2021; (Zu et al., 2021). More verifications on ENDF/B-VIII.0 were performed, which consisted of critical and shielding benchmark tests (Park et al., 2019; Zhang et al., 2021), as well as sensitivity and uncertainty (S/U) analyses (Hartanto and Liem, 2021).

However, such verification has been rare for high-temperature reactors (HTRs), i.e., one of the generation IV nuclear systems. Graphite serves as moderator, structure material, material of fuel elements, and TRISO particles in HTR (IAEA, 2003). As reported from the research on Very High Temperature Critical Assembly (VHTRC), neutron capture cross-section of carbon strongly impacts the results of criticality calculations (Bostelmann and Strydom, 2017). Therefore, the verification of newly released libraries on benchmarks of HTR is important to the selection of data library for HTR analysis, as well as to the optimization of nuclear data libraries.

In this study, neutron data from CENDL-3.2, ENDF/B-VIII.0, and ENDF/B-VII.1 are processed by NJOY (MacFarlane and Kahler, 2010) and employed for simulating the HTR-10 benchmark. The calculations are conducted by the RMC code (Wang et al., 2015). Two benchmark problems, initial criticality and control rod worth, are calculated, and the results are compared with the experimental results. The comparison finds that the ENDF/B-VIII.0 library show the optimal consistency with the experimental results, and the performance of CENDL-3.2 is better than that of ENDF/B-VII.1. To determine the major difference between CENDL-3.2 and ENDF/B-VIII.0, further calculations and a semi-quantitative analysis method are performed. On the basis of the result of sensitivity analysis, the method can assess the effect of the cross-section change of reaction channels to $k_{\text{eff}}$.

In HTR-10 Benchmark, the HTR-10 benchmark and details of modeling is presented. In Method of Semi-quantitative Analysis, the semi-quantitative analysis method is introduced. In Results and Comparison of Benchmark Problems, the calculation results of libraries are compared with the experimental results. In Further Analyses of Differences, the differences between CENDL-3.2 and ENDF/B-VIII.0 are analyzed.

HTR-10 Benchmark

As a test reactor with 10-MW thermal power, HTR-10 was overall designed and built by Institute of Nuclear Energy Technology, Tsinghua University (Wu et al., 2002). The plant was completed in 2000, and the initial criticality was achieved in the same year. In 2003, the official benchmark document of HTR-10 was released by IAEA (IAEA, 2003).

The simplified vertical and horizontal cross-sections of the core are presented in Figures 1, 2, respectively. The pebble-bed core has a diameter of 1.8 m and a mean height of 1.97 m, which comprises 27,000 spherical fuel elements. A conus region connects the bottom of the core and the discharge tube, whose diameter is 0.5 m. Graphite serves as the major structural material of the core to constitute the top, bottom, and side reflectors, respectively. The side reflector has a thickness of 100 cm, and the channels for control rods, small absorber balls, irradiation, and helium flow are within the reflector (IAEA, 2003).

FIGURE 1

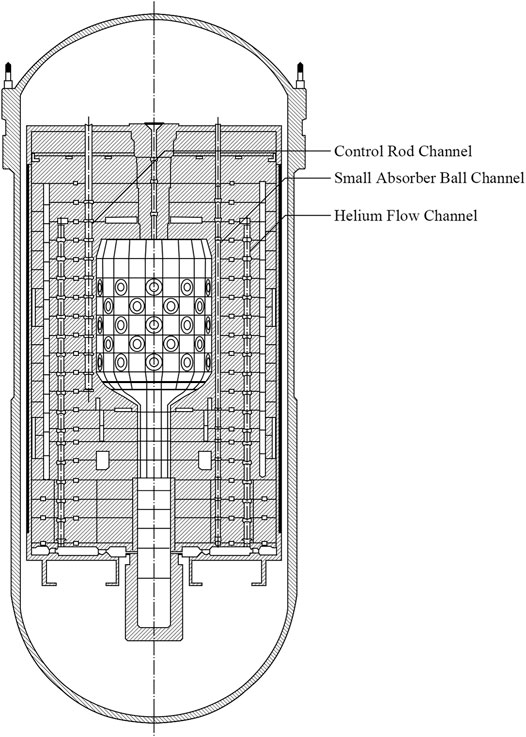
FIGURE 1. HTR-10 reactor vertical cross-section (IAEA, 2003).

FIGURE 2

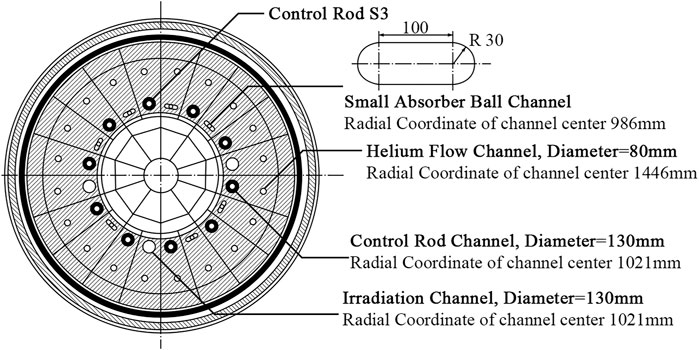
FIGURE 2. HTR-10 reactor horizontal cross-section (IAEA, 2003).

According to Figure 3, the diameter of spherical fuel elements is 6 cm, and the inner fuel part contains numerous TRISO particles (IAEA, 2003). TRISO particle (Petti et al., 2003) consists of a UO₂ kernel and several outer layers, thereby limiting the potential release of radioactive materials. In the benchmark, the discharge tube and the bottom conus region of the reactor core are filled with dummy balls, which are graphite balls with the identical diameter to that of fuel elements. Then, mixed balls, comprising fuel elements and dummy balls at the mix ratio of 57:43, are loaded in the core.

FIGURE 3

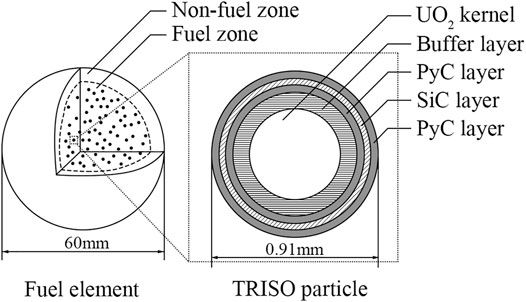
FIGURE 3. HTR-10 spherical fuel element (IAEA, 2003).

Two levels of random distribution are covered in the core of pebble-bed HTR. The first refers to the distribution of TRISO particles in fuel elements, which has been reported to slightly impact macroscopic results of the reactor (Hosseini and Athari Allaf, 2014). Moreover, the second is the distribution of fuel elements, whose effect was also found to be relatively low with the statistical sampling method (Chen et al., 2015). Therefore, this study does not consider the uncertainty of random distribution.

Four benchmark problems are proposed by the benchmark document (IAEA, 2003). However, experimental results are available for two of the benchmark problems, which are initial criticality and control rod worth for the initial core. In this study, the benchmark problems with the experimental results are selected to verify data libraries.

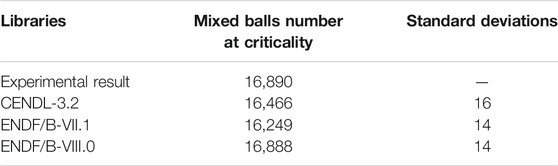
The first selected benchmark problem is initial criticality problem. The indicator of the initial criticality problem is the loading height, or the number of mixed balls, when the criticality is initially achieved. All control rods are withdrawn from the core in such a problem, and the core temperature is 20°C. Because the loading height will be slightly inconsistent under different models of spheres distribution applied, the number of mixed balls is selected as the indicator. Experimental result of this problem was 16,890 balls, indicating that 9,627 fuel balls and 7,263 dummy balls are loaded to achieve criticality.

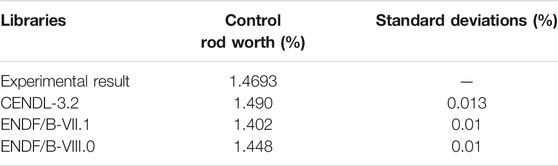
The other benchmark problem refers to the control rod worth problem. The control rod worth problem evaluates the reactivity worth of one fully inserted control rod. The control rods of HTR-10 use Boron carbide (B₄C) as neutron absorber. The whole control comprises five segments connected with stainless steel joints. In the respective segment, annular B₄C is clamped by two layers of stainless steel sleeves. According to this benchmark problem, the core is loaded with 17,000 mixed balls at the mix ratio of 57:43. Only one control rod, in S3 of Figure 2, is inserted to the core for the evaluation of control rod value. The top of the core is defined as z = 0 mm, and the upper boundary of conus region is set to z = 3,518 mm. Moreover, during the experiment, the lower end of the control rod is moved from z = 1,712 mm to z = 3,942 mm. The experimental result of the control rod value of rod S3 is 1.4693%.

It should be noticed that deviations exist between the benchmark definition and the experiment. The density of dummy balls is 1.84 g/cm³ other than 1.73 g/cm³, and the Boron equivalent of impurities in dummy balls reaches 0.125 ppm. In the experiment, the atmosphere of the core is air, not helium.

The three-dimensional model for the Monte Carlo codes of HTR-10 core is built by complying with the benchmark document released by IAEA. The deviations are considered to satisfy the experimental conditions. Furthermore, a random distribution of fuel elements, developed by Discrete Element Method (Li et al., 2009), is employed. The location of all fuel elements remains unchanged in different cases, and only balls in the specified loading heights participate in the calculation. To eliminate the effect exerted by the random distribution on comparisons, the distributions of fuel elements and dummy balls are identical for different libraries at the same loading height. For all cases, the mix ratio of mixed balls is controlled at 57:43.

Method of Semi-quantitative Analysis

The benchmark problems can be calculated by complying with the data of different libraries for verification. However, significant difference may be identified between the results (e.g., $k_{\text{eff}}$) of different libraries. The assessment of the effect by the cross-section change via different reaction channels is conducive to identifying the major difference of libraries for the benchmark. Park et al. quantitatively analyzed the reactivity difference of absorption and fission cross-sections (Park et al., 2019). However, the method in the study is unavailable for light nuclides because the fission cross-section acts as the denominator.

In the present study, the semi-quantitative analysis is conducted to assess the contribution of different reaction channels to the difference of $k_{\text{eff}}$ results. The results of sensitivity analyses and point-wise cross-section data are employed in the method, as expressed below.

S/U analysis of cross-sections is developed for the evaluation of uncertainties propagated from nuclear data to key neutronic parameters (Saltelli et al., 2008). The sensitivity of $k_{\text{eff}}$ is defined as the ratio of relative changes of $k_{\text{eff}}$ and the cross-section.

$S_{{\sigma }_i}=\frac{\partial k_{\text{eff}}/k_{\text{eff}}}{\partial {\sigma }_i/{\sigma }_i},(1)$

where $S_{{\sigma }_i}$ denotes the $k_{\text{eff}}$ sensitivity of ${\sigma }_i$, i.e., the cross-section of a reaction channel of a nuclide.

Eq. 1 indicates that the effect of nuclear data on $k_{\text{eff}}$ can be assessed based on sensitivity result:

$\text{Δ}{k}_{\text{eff}}=k_{\text{eff}}{S}_{{\sigma }_i}\frac{\text{Δ}{\sigma }_i}{{\sigma }_i},(2)$

where $\text{Δ}{\sigma }_i$ denotes a slight change assumed for ${\sigma }_i$, and $\text{Δ}{k}_{\text{eff}}$ represents the corresponding change of $k_{\text{eff}}$.

By the iterated fission probability method (Qiu et al., 2015), the group-dependent sensitivity can be calculated. The point-wise cross-section data should be generated to multi-group cross-sections for further analysis. It is assumed that the difference of neutron flux per lethargy in an energy group can be ignored; then, the multi-group cross-sections can be calculated as follows:

${\sigma }_i=\frac{{{\displaystyle \int }}_{\text{ln}{E}_{i,\text{min}}}^{\text{ln}{E}_{i,\text{max}}}\sigma \left(E\right)\mathrm{d}\left(\text{ln}E\right)}{\text{ln}\left(E_{i,\text{max}}\right)-\text{ln}\left(E_{i,\text{min}}\right)},(3)$

where ${\sigma }_i$ denotes the assessed multi-group cross-section, and $\sigma \left(E\right)$ is from point-wise cross-section data. $E_{i,\text{min}}$ and $E_{i,\text{max}}$ represent the lower bound and the upper bound of the energy group $i$, respectively. By using Eq. 3, group-dependent cross-section can be assessed without calculation of the Monte Carlo code. Error of this assumption decreases with the increase of the number of energy groups, which can be assessed by comparing results of different energy groups’ numbers. It should be noticed that this assumption is not hold for heavy nuclides with strong resonance self-shielding effect. Thus, the evaluation of multi-group cross-sections for heavy nuclides may be still needed.

The sensitivity is further assumed to be constant in the change of the cross-sections. Subsequently, the difference of $k_{\text{eff}}$ caused by a cross-section in an energy group can be approximately calculated by Eq. 4.

$\mathrm{\Delta }{\mathrm{k}}_{\text{eff},i}=k_{\text{eff}}{S}_{{\sigma }_i}{\displaystyle {\int }_{{\sigma }_{i,1}}^{{\sigma }_{i,2}}\frac{\mathrm{d}{\mathrm{\sigma }}_i}{{\sigma }_i}}=k_{\text{eff}}{S}_{{\sigma }_i}\ln \left[\frac{{{\displaystyle \int }}_{\ln E_{i,\min }}^{\ln E_{i,\max }}{\sigma }_2\left(E\right)\mathrm{d}\left(\ln E\right)}{{{\displaystyle \int }}_{\ln E_{i,\min }}^{\ln E_{i,\max }}{\sigma }_1\left(E\right)\mathrm{d}\left(\ln E\right)}\right],(4)$

where ${\sigma }_1$ and ${\sigma }_2$ denote the identical cross-section from two different libraries. The $k_{\text{eff}}$ and the sensitivity are calculated in the same case, in which cross-section ${\sigma }_1$ is applied. However, the $k_{\text{eff}}$ and the sensitivity can change with cross-sections if the difference between two libraries is relatively large. Thus, error can be introduced by this assumption. This error can be assessed by changing the $k_{\text{eff}}$ and the sensitivity of Eq. 4 to the calculation results for cross-section ${\sigma }_2$ and then comparing the two results.

Lastly, the contribution of $k_{\text{eff}}$ difference by the cross-section difference of a reaction channel of a nuclide between two libraries can be assessed by the following:

$\text{Δ}{k}_{\text{eff}}={\displaystyle \sum }_i\text{Δ}{k}_{\text{eff},i}=k_{\text{eff}}{\displaystyle \sum }_i{S}_{{\sigma }_i}\text{ln}\left[\frac{{{\displaystyle \int }}_{\text{ln}{E}_{i,\text{min}}}^{\text{ln}{E}_{i,\text{max}}}{\sigma }_2\left(E\right)\text{d}\left(\text{ln}E\right)}{{{\displaystyle \int }}_{\text{ln}{E}_{i,\text{min}}}^{\text{ln}{E}_{i,\text{max}}}{\sigma }_1\left(E\right)\text{d}\left(\text{ln}E\right)}\right],(5)$

Assumptions are introduced in this procedure, so the error of the result may be relatively high. Thus, the analysis method is suggested as a semi-quantitative method, in which the result can only be exploited to assess the relative magnitude of effects of different reaction channels. However, the difference between contributions of different reaction channels can be of several orders of magnitude. For this reason, by comparing the assessed results of this semi-quantitative analysis, the major difference of libraries for benchmarks can be identified.

Results and Comparison of Benchmark Problems

The calculations of benchmark problems are conducted by the RMC code (Wang et al., 2015). With continuous energy point-wise cross-section data, RMC can achieve a precise result for reactor analysis problems with complex geometry. The approach of random geometry (Liu et al., 2015) is capable of accurately modeling fuel elements and dummy balls in HTR-10.

Neutron data from the three libraries (i.e., ENDF/B-VII.1, ENDF/B-VIII.0, and CENDL-3.2) are processed under the NJOY code (MacFarlane and Kahler, 2010) and subsequently used in the calculation, respectively. The results of benchmark problems and the experimental results are compared. It should be noticed that the thermal n-scattering of graphite is not provided by CENDL-3.2 library, so CENDL-3.2 cases exploit the identical thermal n-scattering data as ENDF/B-VIII.0 cases. The standard deviations of results are analyzed to determine the uncertainty of results.

Initial Criticality and Control Rod Worth present the results of the initial criticality problem and control rod worth problem, respectively.

Initial Criticality

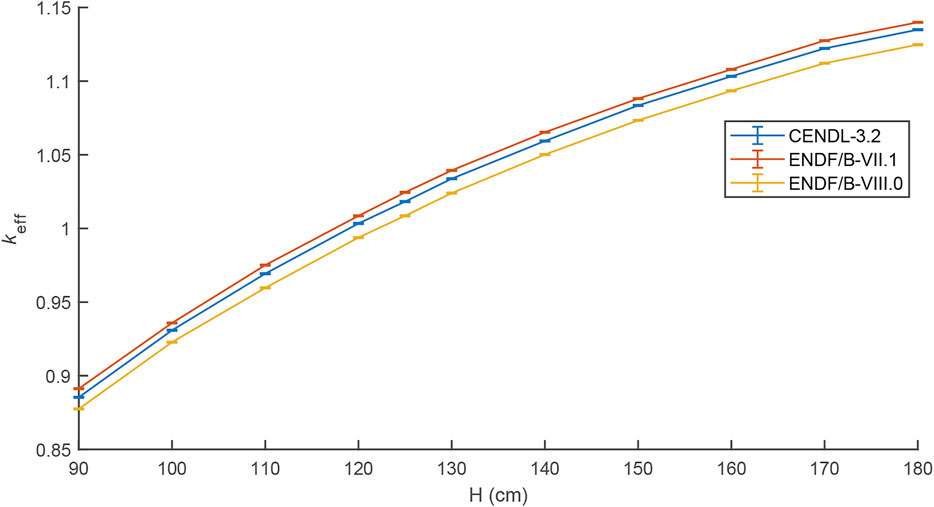
The HTR-10 core with different loading heights (90–180 cm) is calculated, and the results of the three libraries are plotted in Figure 4. The parameters of the calculation are listed in Table 1. The results of the three libraries display the consistent trends, whereas significant $k_{\text{eff}}$ differences are identified. At the respective loading height, the $k_{\text{eff}}$ of ENDF/B-VII.1 is the largest and that of ENDF/B-VIII.0 is the smallest. The result of CENDL-3.2 is between other two libraries. The statistical errors of the calculation results are significantly smaller than the differences between the libraries.

FIGURE 4

FIGURE 4. Curve of loading height and k_eff.

TABLE 1

TABLE 1. Calculation parameters of initial criticality.

The numbers of mixed balls at initial criticality are determined by liner interpolation, which is written as Eq. 6.

$N=N_1+\left(N_2-N_1\right)\frac{1-k_1}{k_2-k_1},(6)$

where $N$ denotes the number of calculated loaded balls at initial criticality. $k_1$ and $k_2$ represent two $k_{\text{eff}}$ closest to 1, whereas $N_1$ and $N_2$ are the corresponding loaded balls numbers.

To assess the standard deviation of $N$, three intermediate values are defined as follows:

$A=\frac{1-k_1}{k_2\mathrm{-}{k}_1},(7)$

$B=\frac{k_2-k_1}{1-k_1},(8)$

$C=\frac{k_2-1}{1-k_1},(9)$

Next, it yields the following:

$N=N_1+\left(N_2-N_1\right)A,(10)$

$A=\frac{1}{B},(11)$

$B=C+1,(12)$

In accordance with the rules of the random error propagation, the standard deviations of the mentioned values can be calculated by the following:

$\sigma \left(N\right)=\left(N_2-N_1\right)\sigma \left(A\right),(13)$

$\sigma \left(A\right)=A^2\sigma \left(B\right),(14)$

$\sigma \left(B\right)=\sigma \left(C\right).(15)$

Moreover, the standard deviation of C is expressed as follows:

$\frac{\sigma \left(C\right)}{C}=\sqrt{{\left(\frac{\sigma \left(k_2\right)}{k_2-1}\right)}^2+{\left(\frac{\sigma \left(k_1\right)}{1-k_1}\right)}^2}.(16)$

The numbers of loaded balls at initial criticality and their standard deviations are determined by Eq. 6 and Eqs 13–16, respectively. The results are listed in Table 2. The calculated number of mixed balls of ENDF/B-VIII.0 library is optimally consistent with the experimental result, whereas that of ENDF/B-VII.1 shows the most significant deviation. The performance of CENDL-3.2 is better than ENDF/B-VII.1. As revealed from the deviations, the three libraries may also provide different results in the calculations of other HTRs. In Further Analyses of Differences, the further determination of differences between CENDL-3.2 and ENDF/B-VIII.0 will be presented.

TABLE 2

TABLE 2. Comparison of initial criticality results.

Control Rod Worth

As presented in Initial Criticality, the large deviations exist between the results of different libraries in the identical situation. To assess the reactivity worth of the control rod, for all libraries, the reactivity of fully inserted rod is set to zero.

The standard deviation of reactivity is analyzed below. The reactivity is defined as follows:

$\rho =\frac{k_{\text{eff}}-1}{k_{\text{eff}}}=1-\frac{1}{k_{\text{eff}}},(17)$

where $\rho$ represents the reactivity corresponding to $k_{\text{eff}}$. Next, the statistical error of $\rho$ can be calculated by Eq. 18:

$\sigma \left(\rho \right)=\sigma \left(\frac{1}{k_{\mathrm{eff}}}\right),(18)$

where $\sigma \left(\rho \right)$ and $\sigma \left(1/k_{\text{eff}}\right)$ denote the standard deviation of reactivity and the reciprocal of $k_{\text{eff}}$, respectively. The latter is expressed as Eq. 19:

$\frac{\sigma \left(1/k_{\text{eff}}\right)}{1/k_{\text{eff}}}=\frac{\sigma \left(k_{\text{eff}}\right)}{k_{\text{eff}}}.(19)$

Subsequently, the standard deviation of control rod worth, other than fully inserted case, can be calculated by Eq. 20:

$\sigma \left(r,z\right)=\sqrt{{\sigma }^2\left(\rho ,z\right)+{\sigma }^2\left(\rho ,\mathrm{FI}\right)},(20)$

where $\sigma \left(r,z\right)$ and $\sigma \left(\rho ,z\right)$ are the standard deviation of control rod worth and reactivity at insert depth z. $\sigma \left(\rho ,\mathrm{FI}\right)$ represents the standard deviation of reactivity of the fully inserted case.

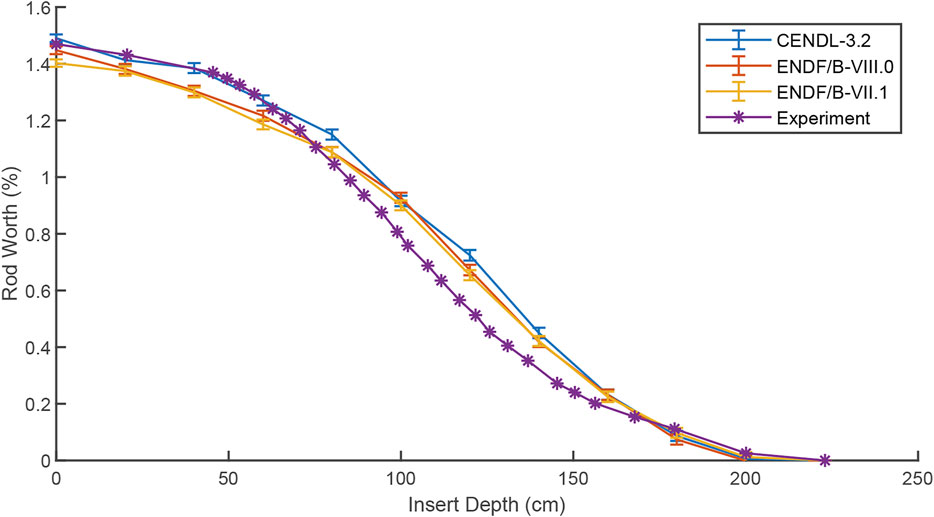
A larger neutron number per cycle is applied for the fully withdrawn case and fully inserted case to improve the accuracy of results. The calculation parameters are listed in Table 3, and the results are presented in Table 4 and Figure 5, in which the experimental results originate from the benchmark document. No significant deviation is observed between calculated control rod worth, using CENDL-3.2 or ENDF/B-VIII.0, as well as the experimental results. However, the results of the three libraries exhibit similar differences to the experimental value during the insertion of the control rod. The differences may be attributed to the difference of actual situation and information provided.

TABLE 3

TABLE 3. Calculation parameters of control rod worth.

TABLE 4

TABLE 4. Comparison of control rod worth results.

FIGURE 5

FIGURE 5. Reactivity worth of control rod S3.

Further Analyses of Differences

In Results and Comparison of Benchmark Problems, the significant differences between the results of different benchmarks are presented. CENDL-3.2 library and ENDF/B-VIII.0 library outperform ENDF/B-VII.1. To identify the nuclides and their reaction channels that primarily cause the difference between the mentioned two libraries, further calculations and analyses should be conducted.

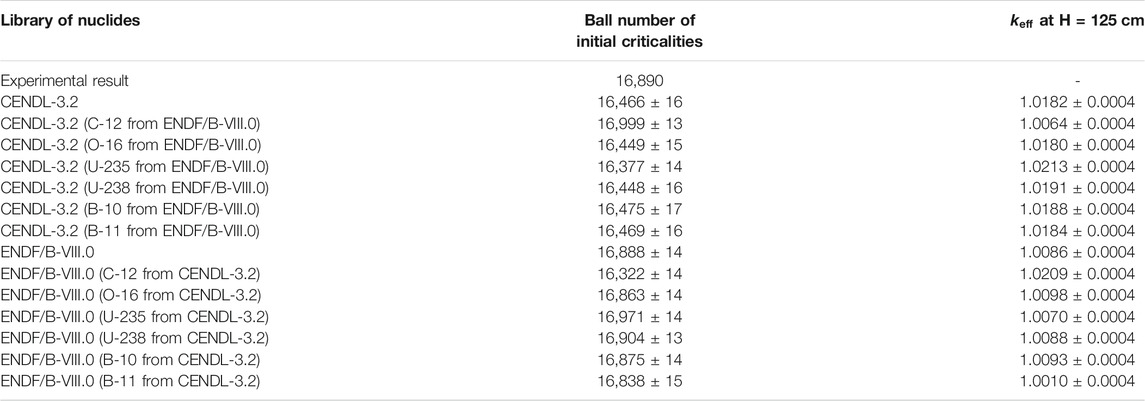
Several calculations of the initial criticality benchmark are conducted with the data of one nuclide from CENDL-3.2 and the data of other nuclides from ENDF/B-VIII.0. Moreover, the calculations are conducted with the data of one nuclide from ENDF/B-VIII.0 and data of other nuclides from CENDL-3.2. The parameters of the mentioned calculations are identical to those listed in Table 1. Table 5 lists the comparison of the calculation results and the results in Initial Criticality

TABLE 5

TABLE 5. Comparison to identify the nuclide causing major impact.

In Table 5, a significant change of the benchmark result can be observed when the cross-section data of C-12 change from one library to the other. Moreover, relatively slight changes are found between cases exploiting cross-section data of a nuclide, other than C-12, from different libraries. As revealed from the mentioned results, the difference between results of initial criticality benchmark, by employing ENDF/B-VIII.0 and CENDL-3.2 library, respectively, is mainly attributed to cross-section of C-12. The result also indicates that similar performance as the other library on pebble-bed HTR could be achieved by the two libraries if the cross-section of C-12 is changed.

To more specifically determine the reaction channel of C-12 most significantly impacting the results, the semi-quantitative analysis method presented in Method of Semi-quantitative Analysis is adopted. The sensitivity analyses are conducted by the RMC code on initial criticality case with ENDF/B-VIII.0 library and CENDL-3.2 library, respectively. The mixed balls number 16890, which is assessed experimentally, is applied for analyses. $k_{\text{eff}}$ sensitivities of the five reaction channels of C-12, which covers elastic scattering, (n, γ), (n, p), (n, d), and (n, α), are analyzed. Point-wise cross-section data from ACE format libraries are applied for the integration of Eq. 4, where ${\sigma }_1$ denotes cross-section from ENDF/B-VIII.0, and ${\sigma }_2$ is from CENDL-3.2.

On the basis of Eq. 4, the effect of the five reaction channels is determined and listed in Table 6. To assess the error introduced by the assumptions in Method of Semi-quantitative Analysis, extra cases are calculated as well. ENDF/B-VIII.0 case means the sensitive, and $k_{\text{eff}}$ is determined by data from ENDF/B-VIII.0 library. ENDF/B-VIII.0 (C-12 from CENDL-3.2) case reveals that all nuclides data except for C-12 originate from ENDF/B-VIII.0 library, and C-12 data are from CENDL-3.2 library. For the elastic scattering channel and the (n, γ) channel, the number of energy groups reaches 44 and 252, respectively, in the sparse and the dense cases. Moreover, for (n, p), (n, d), and (n, α) channels, the reactions occur only under the high neutron energy. Energy from 6 to 20 MeV is uniformly divided by lethargy into energy groups, and the group number of the dense case is twice that of the sparse case.

TABLE 6

TABLE 6. Comparison of assessed results of different cases.

As revealed from the results in Table 6, the errors introduced by multi-group cross-section assessment are relatively low for elastic scattering and (n, γ) channels. However, the sensitivity and $k_{\text{eff}}$ change cause greater errors for the mentioned two channels. The low cross-sections of the (n, p), (n, d), and (n, α) channels cause noticeable statistical error in the Monte Carlo calculation of sensitivity. Hence, the significant differences identified between results of (n, p), (n, d), and (n, α) channels are expected.

Given the results and analysis, the assessment of the effect of the reaction channels is listed in Table 7. Only orders of magnitude of (n, p), (n, d), and (n, α) results are credible as impacted by their large statistical errors. The effect of (n, γ) channel is an order of magnitude larger than the elastic scattering channel, and several orders of magnitude larger than other channels having been analyzed. The negative result of the elastic scattering channel indicates that the difference of cross-section of this channel offsets parts of the effect to $k_{\text{eff}}$ via (n, γ) channel.

TABLE 7

TABLE 7. Assessed effect of C-12 channels.

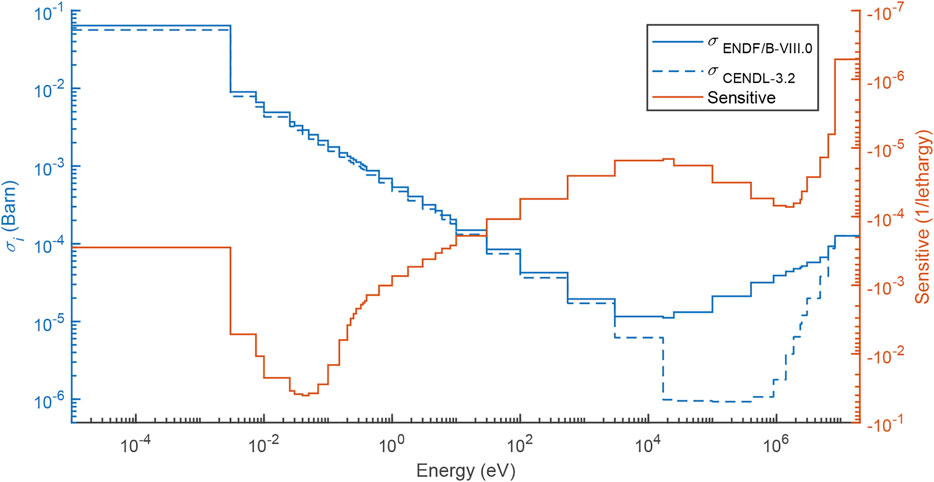
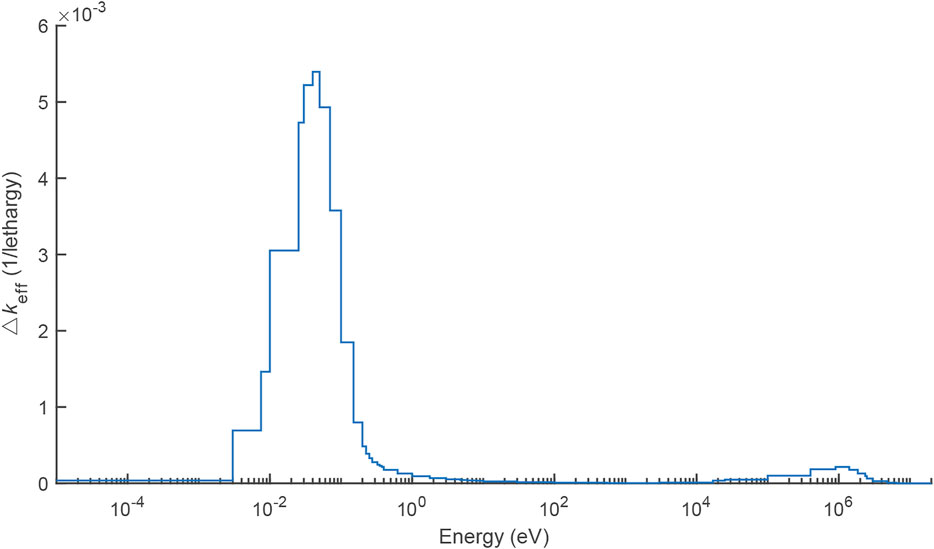
The analysis details of C-12 (n, γ) channel of sparse case using ENDF/B-VIII.0 are illustrated. The sensitivity analysis result and the assessed multi-group cross-sections are plotted in Figure 6, and the effect of the respective group is presented in Figure 7. The multi-group cross-section, which is (n, γ) channel cross-section of C-12 at 20°C, of CENDL-3.2 library is lower than that of ENDF/B-VIII.0 library. The maximal negative sensitivity is identified to range from 10⁻⁸ to 10⁻⁷ MeV. Although the largest deviation of cross-section ranges from 10⁻² to 1 MeV, the range of 10⁻⁸ to 10⁻⁷ MeV mostly contributes to $k_{\text{eff}}$.

FIGURE 6

FIGURE 6. Sensitivity and multi-group cross-sections of C-12 (n, γ) channel.

FIGURE 7

FIGURE 7. Impact to by C-12 (n, γ) channel.

Conclusion and Discussion

In this study, CENDL-3.2 library and ENDF/B-VIII.0 library are verified and compared on the basis of the HTR-10 benchmark. Two benchmark problems with the experimental results are selected for the verification, and the calculation is conducted under RMC code. In the initial criticality benchmark problem, the significant differences between CENDL-3.2, ENDF/B-VIII.0, and ENDF/B-VII.1 are identified. The loading number of mix balls calculated by ENDF/B-VIII.0 library is the closest to the experimental value, whereas that of CENDL-3.2 is the second closest. The ENDF/B-VII.1 shows the worst consistency with the experimental result in the initial criticality benchmark problem. In the control rod worth problem, the performance of ENDF/B-VIII.0 and CENDL-3.2 is similar, whereas ENDF/B-VII.1 library shows a larger difference to the experimental result. In summary, the results of ENDF/B-VIII.0 library are well consistent with the experimental values, whereas the results of CENDL-3.2 are better than those of ENDF/B-VII.1.

Furthermore, the difference between CENDL-3.2 library and ENDF/B-VIII.0 library is determined. As revealed from the calculation results, the difference of C-12 data from the two libraries causes most of the difference of $k_{\text{eff}}$ results. A semi-quantitative method, on the basis of the result of sensitivity analysis, is employed to assess the contribution to that difference via different reaction channels of C-12. The difference of cross-section of (n, γ) channel is reported to mainly cause the different performance of the initial criticality benchmark problem.

Significant difference between $k_{\text{eff}}$ results shows the importance of selecting the appropriate data library on HTR analysis. Further verifications should be conducted to determine the applicability exhibited by the nuclear data libraries on other HTRs.

To avoid overestimation or underestimation of reactivity of HTRs, the optimization of carbon cross-section data is suggested. By complying with the future verification and analysis results, the nuclear data libraries can be optimized for the application on HTRs. The proposed semi-quantitative analysis method may help to assess the influence on $k_{\text{eff}}$ via different reaction channels of nuclides in the future studies.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

TH mainly performed the calculations and analysis and wrote the manuscript. ZL directed the study and strongly supported the modeling. SJ contributed to the establishment of analysis method. KW directed the development of RMC code and supported the numerical calculation.

Funding

This research was funded by the Science Challenge Project (TZ2018001), Project 11775126/11545013/11775127 by the National Natural Science Foundation of China, Young Elite Scientists Sponsorship Program by CAST (2016QNRC001), and Tsinghua University Initiative Scientific Research Program.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bostelmann, F., and Strydom, G. (2017). Nuclear Data Uncertainty and Sensitivity Analysis of the VHTRC Benchmark Using SCALE. Ann. Nucl. Energ. 110, 317–329. doi:10.1016/j.anucene.2017.06.052

CrossRef Full Text | Google Scholar

Brown, D. A., Chadwick, M. B., Capote, R., Kahler, A. C., Trkov, A., Herman, M. W., et al. (2018). ENDF/B-VIII.0: The 8 Th Major Release of the Nuclear Reaction Data Library with CIELO-Project Cross Sections, New Standards and Thermal Scattering Data. Nucl. Data Sheets 148, 1–142. doi:10.1016/j.nds.2018.02.001

CrossRef Full Text | Google Scholar

Chen, H., Fu, L., Jiong, G., and Lidong, W. (2015). Uncertainty and Sensitivity Analysis of Filling Fraction of Pebble Bed in Pebble Bed HTR. Nucl. Eng. Des. 292, 123–132. doi:10.1016/j.nucengdes.2015.05.032

CrossRef Full Text | Google Scholar

Ge, Z., Xu, R., Wu, H., Zhang, Y., Chen, G., Jin, Y., et al. (2020). CENDL-3.2: The New Version of Chinese General Purpose Evaluated Nuclear Data Library. EPJ Web Conf. 239, 09001. doi:10.1051/epjconf/202023909001

CrossRef Full Text | Google Scholar

Hartanto, D., and Liem, P. H. (2021). Sensitivity and Uncertainty Analyses of a High Temperature Gas-Cooled Reactor by Using a 44-group Covariance Library. Ann. Nucl. Energ. 151, 107943. doi:10.1016/j.anucene.2020.107943

CrossRef Full Text | Google Scholar

Hosseini, S. A., and Athari Allaf, M. (2014). Benchmarking of the HTR-10 Reactor's Kinetic Parameters: Effective Delayed Neutron Fraction. Prog. Nucl. Energ. 75, 80–91. doi:10.1016/j.pnucene.2014.04.015

CrossRef Full Text | Google Scholar

Hu, J., Zhang, B., Zong, Z., Liu, C., and Chen, Y. (2021). Verification of CENDL-3.2 Nuclear Data on VENUS-3 Shielding Benchmark by ARES Transport Code. Sci. Technology Nucl. Installations 2021, 1–13. doi:10.1155/2021/6633366

CrossRef Full Text | Google Scholar

IAEA (2003). Evaluation of High Temperature Gas Cooled Reactor Performance: Benchmark Analysis Related to Initial Testing of the HTTR and HTR-10. Vienna, Austria: International Atomic Energy Agency.

Google Scholar

Koning, A. J., Rochman, D., Sublet, J.-C., Dzysiuk, N., Fleming, M., and van der Marck, S. (2019). TENDL: Complete Nuclear Data Library for Innovative Nuclear Science and Technology. Nucl. Data Sheets 155, 1–55. doi:10.1016/j.nds.2019.01.002

CrossRef Full Text | Google Scholar

Li, S., Yu, J., Wang, K., and Et, A. (2012). “R&D on the Nuclear Cross Sections Processing Code RXSP Used for Reactor Analysis,” in The 14th Chinese Conference on Reactor Numerical Calculations and Particle Transport & 2012 Chinese Conference on Reactor Physics (Yinchuan, China.

Google Scholar

Li, Y., Xu, Y., and Jiang, S. (2009). DEM Simulations and Experiments of Pebble Flow with Monosized Spheres. Powder Technology 193, 312–318. doi:10.1016/j.powtec.2009.03.009

CrossRef Full Text | Google Scholar

Liu, S., She, D., Liang, J.-g., and Wang, K. (2015). Development of Random Geometry Capability in RMC Code for Stochastic media Analysis. Ann. Nucl. Energ. 85, 903–908. doi:10.1016/j.anucene.2015.07.008

CrossRef Full Text | Google Scholar

MacFarlane, R. E., and Kahler, A. C. (2010). Methods for Processing ENDF/B-VII with NJOY. Nucl. Data Sheets 111, 2739–2890. doi:10.1016/j.nds.2010.11.001

CrossRef Full Text | Google Scholar

Park, H. J., Kang, H., Lee, H. C., and Cho, J. Y. (2019). Comparison of ENDF/B-VIII.0 and ENDF/B-VII.1 in Criticality, Depletion Benchmark, and Uncertainty Analyses by McCARD. Ann. Nucl. Energ. 131, 443–459. doi:10.1016/j.anucene.2019.04.012

CrossRef Full Text | Google Scholar

Petti, D. A., Buongiorno, J., Maki, J. T., Hobbins, R. R., and Miller, G. K. (2003). Key Differences in the Fabrication, Irradiation and High Temperature Accident Testing of US and German TRISO-Coated Particle Fuel, and Their Implications on Fuel Performance. Nucl. Eng. Des. 222, 281–297. doi:10.1016/S0029-5493(03)00033-5

CrossRef Full Text | Google Scholar

Plompen, A. J. M., Cabellos, O., De Saint Jean, C., Fleming, M., Algora, A., Angelone, M., et al. (2020). The Joint Evaluated Fission and Fusion Nuclear Data Library, JEFF-3.3. Eur. Phys. J. A. 56. doi:10.1140/epja/s10050-020-00141-9

CrossRef Full Text | Google Scholar

Qiu, Y., Liang, J., Wang, K., and Yu, J. (2015). New Strategies of Sensitivity Analysis Capabilities in Continuous-Energy Monte Carlo Code RMC. Ann. Nucl. Energ. 81, 50–61. doi:10.1016/j.anucene.2015.03.026

CrossRef Full Text | Google Scholar

Saltelli, A., Ratto, M., Andres, T., Campolongo, F., Cariboni, J., Gatelli, D., et al. (2008). Global Sensitivity Analysis. The Primer. The Atrium, Southern Gate. Chichester, West Sussex PO19 8SQ, England: John Wiley & Sons.

Google Scholar

Shibata, K., Iwamoto, O., Nakagawa, T., Iwamoto, N., Ichihara, A., Kunieda, S., et al. (2011). JENDL-4.0: A New Library for Nuclear Science and Engineering. J. Nucl. Sci. Technology 48, 1–30. doi:10.1080/18811248.2011.9711675

CrossRef Full Text | Google Scholar

Shu, W., Zu, T., Cao, L., and Wu, H. (2021). Performance of CENDL-3.2 Evaluated Nuclear Data Library for the Shielding Benchmarks. Prog. Nucl. Energ. 136, 103727. doi:10.1016/j.pnucene.2021.103727

CrossRef Full Text | Google Scholar

Wang, K., Li, Z., She, D., Liang, J. g., Xu, Q., Qiu, Y., et al. (2015). RMC - A Monte Carlo Code for Reactor Core Analysis. Ann. Nucl. Energ. 82, 121–129. doi:10.1016/j.anucene.2014.08.048

CrossRef Full Text | Google Scholar

Wu, Z., Lin, D., and Zhong, D. (2002). The Design Features of the HTR-10. Nucl. Eng. Des. 218, 25–32. doi:10.1016/S0029-5493(02)00182-6

CrossRef Full Text | Google Scholar

Zhang, B., Ma, X., Hu, K., Chang, C., Zhou, F., and Chen, Y. (2021). Benchmark Tests for the MATXS-Formatted XMAP Libraries Based on ENDF/B-VIII.0 and ENDF/B-VII.1. Ann. Nucl. Energ. 163, 108584. doi:10.1016/j.anucene.2021.108584

CrossRef Full Text | Google Scholar

Zu, T., Huang, Y., Teng, Q., Han, F., Huang, X., Wan, C., et al. (2021). Application of CENDL-3.2 and ENDF/B-VIII.0 on the Reactor Physics Simulation of PWR. Ann. Nucl. Energ. 158, 108238. doi:10.1016/j.anucene.2021.108238

CrossRef Full Text | Google Scholar