- NARI Group Corporation, Nanjing, China
The stability of wind turbine output is affected by multi-factor disturbances, which makes traditional proportion-integral-differential (PID) control strategy hardly achieve a satisfactory effect. Hence, a pitch control strategy based on fuzzy adaptive particle-swarm-optimization (PSO)-PID is proposed in this paper. Firstly, the models of wind turbine, pitch regulator, and permanent magnet synchronous generator (PMSG) are built. Then, the influence of various disturbances, such as blade deformation, installation errors, and external wind speed, on the wind wheel speed is analyzed. Furtherly, a wind turbine pitch control strategy is devised in detail, in which the PID parameters are initially optimized by PSO and adaptively adjusted by fuzzy controller. Simulations under gust wind and turbulent wind conditions are carried out, and the results show that compared with fuzzy PID and PID, the fuzzy adaptive PSO-PID could reduce errors of wind wheel speed and wind turbine output power effectively.
Introduction
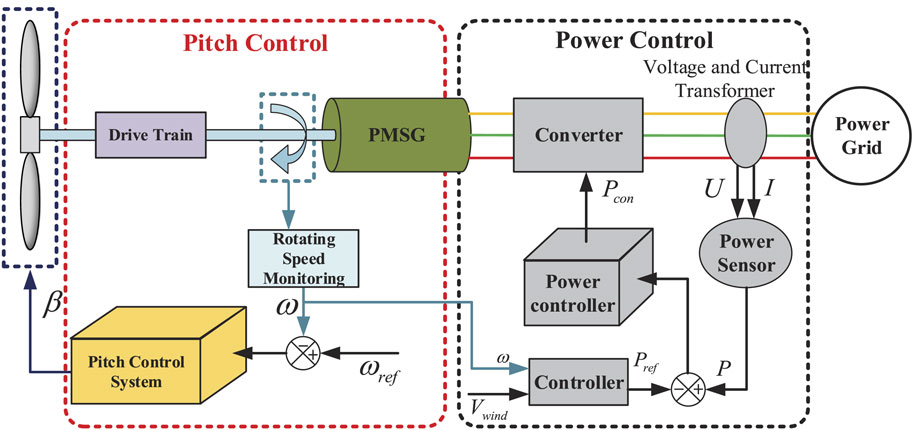
With the aggravation of energy crisis and environmental deterioration of the earth in recent years, the development of renewable energy is more and more urgently demanded. Wind power, an effective mean to deal with the energy crisis, has been widely used in many countries. Its safety and stability are the focuses of attention. The control technology of wind turbines has evolved from a fixed pitch technology to a variable pitch control technology with better efficiency and stability (Mughal and Li, 2015). In a variable pitch control system, the pitch angle changes with the change of wind speed to stabilize wind turbine’s output power when the wind speed is stronger than the rated wind speed (Liu et al., 2018). This could not only maintain the high efficiency but also ensure the safe operation of the wind turbine when the wind speed changes (Barahona et al., 2011). Figure 1 shows the control system of the wind turbine (Xiong et al., 2016), including the pitch control system and the power control system (Xiong et al., 2020 and Xiong et al., 2021).
At present, traditional proportion-integral-differential (PID) control is mostly applied for the pitch regulation in the wind turbine control system. A self-tuning PID control method using reinforcement learning is proposed for the pitch control of large wind turbine generator (Kim et al., 2011). To overcome the shortcomings of conventional PI controller and adapt to nonlinear characteristics of wind turbines, an expert PID controller based on a tracking differentiator is proposed in the literature (Anjun et al., 2011). In the literature (Zahra et al., 2017), a PID controller optimized by particle-swarm-optimization (PSO) is designed to capture the maximum power. However, in actual operation, the wind turbine will be affected not only by the instantaneous wind on the wind turbine but also by many other factors, such as initial parameter error, environmental changes, and blade changes. The factors above bring huge challenges for the pitch control strategy design. In severe cases, it may even cause accidents such as the collapse of the wind turbine tower and the burning of the engine room. Therefore, the adaptive pitch control strategy is particularly important for the stable operation of the wind turbine. A nonlinear PID control strategy is designed in the literature (Liu et al., 2017) to ensure the accuracy and stability of the pitch control system, while the response speed is slow. In the literature (Jafarnejadsani et al., 2013), a pitch regulation strategy is proposed based on radial basis function neural network, which enables the wind turbine’s output to be smoother under different wind speeds. In the literature (Fdaili et al., 2017), PI controller and fuzzy logic control is used to control the blade pitch angle to limit the output power of the wind turbine at high wind speeds. In order to improve the utilization rate of wind energy, an independent pitch system of proportional resonant controller to ensure the rated power output at high wind speeds is adopted in the literature (Wang et al., 2020).
In this paper, the influence of various disturbances, including external wind speed, blade deformation, environmental changes, and initial parameter errors, on the wind turbine is taken into account. An adaptive pitch control strategy for suppressing multi-factor disturbances is proposed. In the proposed control strategy, the initial parameters of PID are optimized PSO algorithm, and fuzzy rules are designed to adjust its parameters dynamically. Then, simulation analysis is performed under rated conditions to validate the design. The results demonstrate that the control strategy could always maintain the wind wheel speed and the wind turbine’s power around rated values and it has higher performance and robustness against disturbance than fuzzy PID control and PID control.
Aerodynamic Characteristics of Wind Turbine
The wind power generation system is mainly composed of a mechanical part and an electromechanical conversion part. Combined with the analysis of aerodynamics and Betz theory, the mechanical power captured by the wind turbine from wind energy could be described by (Yin et al., 2017)
where,
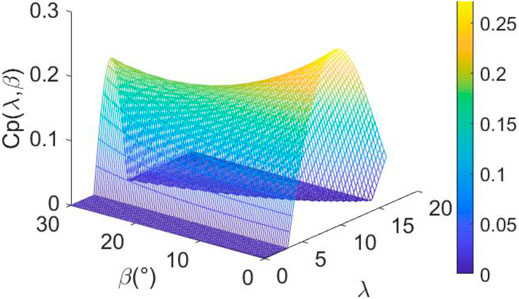
The curve of wind turbine’s power coefficients is shown in Figure 2.
It could be seen from Figure 2 that there is a maximum value of
Model of the Wind Turbine Pitch System
Modeling of Permanent Magnet Synchronous Generator
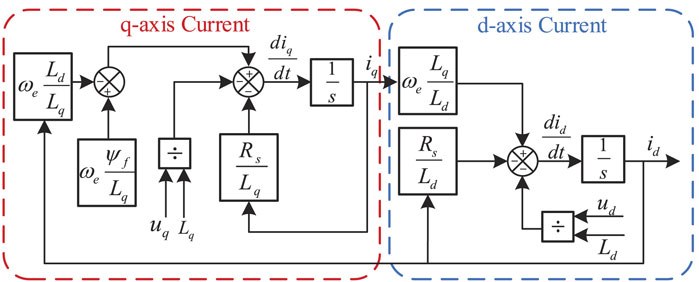
Take the permanent magnet rotor pole centerline as the d-axis and the q-axis ahead of the d-axis by 90° in the direction of rotation of the rotor (Yan et al., 2009). The d–q coordinate system rotates synchronously with the rotor(Liu et al., 2021). Get the mathematical model of the generator in the d–q coordinate system as Eq. 3, and its block diagram is shown in Figure 3.
where,
Modeling of the Transmission System
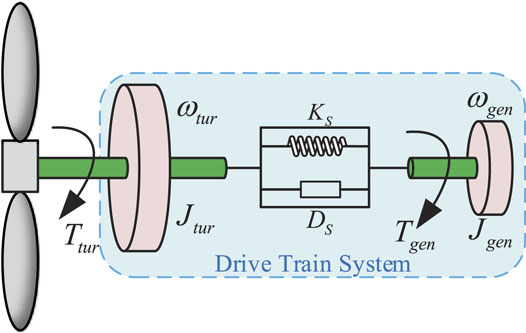
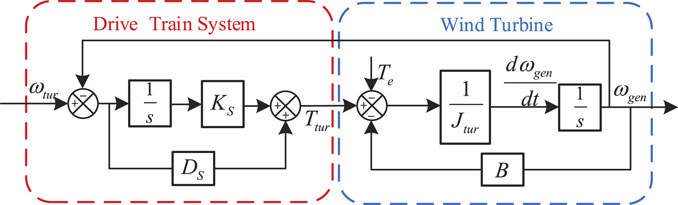
The two-mass model, shown in Figure 4, is often used to model the transmission chain of wind turbines. Particularly, the wind wheel and permanent magnet synchronous generator (PMSG) are, respectively, equivalent to a mass block. Then, a flexible transmission chain connects the two masses. In this way, energy can be converted from mechanical energy to electrical energy.
Using the dynamic model of the spring damping system (Cheng et al., 2019), the model of the drive train system could be expressed as (Mazare et al., 2021)
where,
The wind turbine runs at a certain angular velocity under the action of aerodynamic torque
where,
The block diagram of transmission system is shown in Figure 5.
Modeling of the Pitch System
In this paper, a first-order inertial link is used to simulate the dynamic characteristics of the pitch actuator (Jia et al., 2021). The expression is usually equivalent to
where,
Disturbance Model of Wind Turbine
In actual operation, the wind turbine will be affected by many other disturbance factors, including the blade changes, installation errors, and external wind speed changes.
The blade changes include bending, deformation, and so on. Its disturbance transfer function
where,
The installation errors of the wind turbine include the deviation of the initial pitch angle of each blade and the inclination of the wind turbine tower. Its disturbance transfer function
where,
The wind speed changes include the influence of other wind turbines in the wind farm on the input wind speed. Its disturbance transfer function
where,
In summary, the total disturbance that wind turbines undergo during normal operation is
The Design of Control Strategy
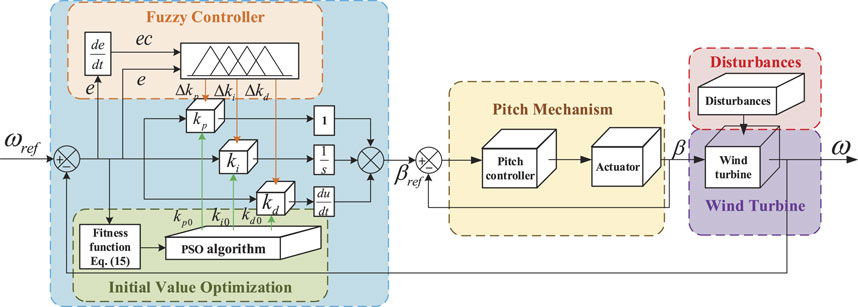
To ensure the stability of the wind turbine, fuzzy control is selected because it could be adaptable to complex and nonlinear systems (Qi and Meng, 2012). However, the fuzzy controller is prone to blind zone and dead zone near the control point, and its steady-state performance is low. Therefore, fuzzy control is difficult to meet the control accuracy requirements. PID control is a commonly used control method in the wind turbine pitch system (Pathak and Gaur, 2019). The combination of PID control and fuzzy control could solve these problems. However, if the initial parameters of PID control are selected improperly, it will cause a large overshoot and a long adjustment time for the system, which will cause the wind turbine’s power to fluctuate too much. The PSO algorithm could be introduced to optimize the initial parameters. A pitch control strategy based on fuzzy adaptive PSO-PID is designed, and its block diagram is shown in Figure 6.
PID Initial Parameters Optimization
The poor PID initial parameters will decrease the system performance, so the PSO algorithm could be introduced to optimize the PID initial parameters. The PSO algorithm is an effective global optimization algorithm. It seeks the optimal value of complex space through information transmission and competition between individuals. The particle swarm searches in an n-dimensional space in particle swarm algorithm. The position of each particle i in space is
where,
The PSO algorithm needs to select a suitable fitness function to achieve the optimal effect of the control. In this paper, the integral time absolute error (ITAE) is selected. Its expression is
where,
The steps of the PSO algorithm for optimizing PID parameters are as follows:
(1) Initialize the position and velocity of the particles, and take a random value within a certain range to generate the first-generation population.
(2) Calculate the fitness of each particle according to the fitness function.
(3) Record the local optimal solution and the global optimal solution.
(4) Update the velocity and position of the particle to move it closer to the optimal solution.
(5) Until the value of the fitness function is less than the set value or the number of iterations reaches the maximum, the optimal individual is output.
PID Parameters Adaptation
The fuzzy adaptive controller takes the deviation E and the deviation change rate EC (de/dt) as the inputs of the controller, shown in Figure 6.
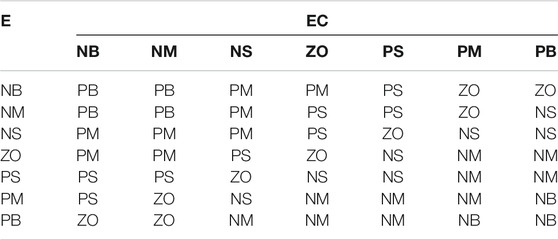
The domain of the input and output of fuzzy control is [−3, 3]. The fuzzy subsets are {NB, NM, NS, ZO, PS, PM, PB}, and the triangle membership function is adopted. The designed fuzzy rules using membership functions are shown in Figure 7.
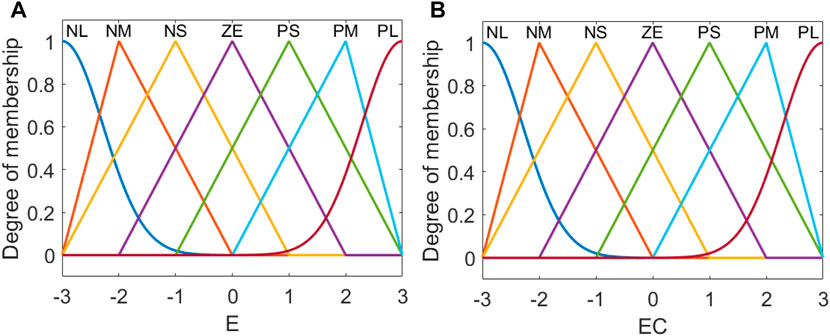
FIGURE 7. Diagram of fuzzy rules using membership functions. (A) is “error E”. (B) is “error rate of change EC”.
Then, the inputs are transformed into the corresponding fuzzy variable value by the fuzzy controller to realize the fuzzification of the inputs. Fuzzy inference is further performed on the fuzzy inputs according to the formulated fuzzy rules. The fuzzy controller rules are shown in Table 1. After defuzzification, the correction value
According to the fuzzy rules, the relationship of inputs (E, EC) and outputs (
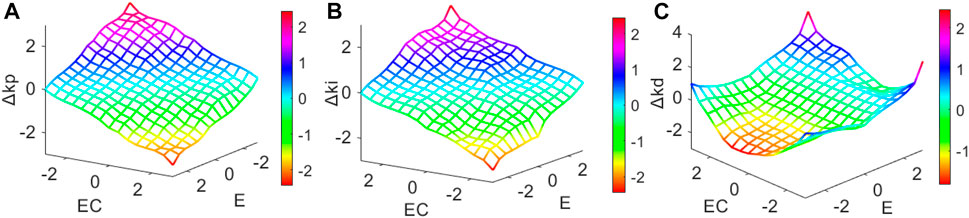
FIGURE 8. The output curve of fuzzy controller. Part label (A) is “the output of Δkp”, part label (B) is “the output of Δki”, part label (C) is “the output of Δkd”.
Simulation and Analysis
To verify the performance of the proposed strategy, control strategy validation and anti-interference analysis are performed by simulation. All of the simulations are based on a 2 MW wind turbine. Its cut-in, rated, and cut-out wind speeds are 3, 11, and 22 m/s, respectively. The wind wheel diameter is 93.4 m. The wind wheel height is 80 m. The length of the blade is 45 m. The rated turning speed of the wind wheel is 12.1 r/min.
Control Strategy Validation
Control strategy validation of the proposed fuzzy PSO-PID is performed by simulation comparison with PID and fuzzy PID. The simulations are conducted under gust wind and turbulent wind, respectively, in both of the cases. Disturbances of blade changes (
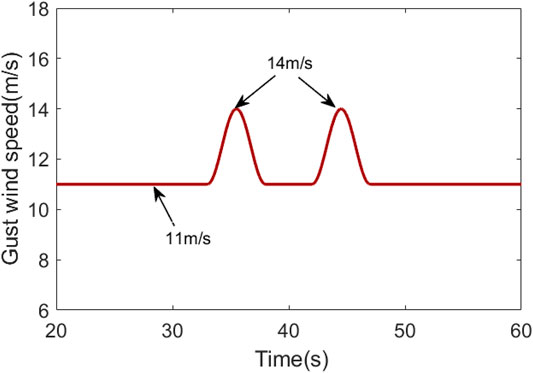
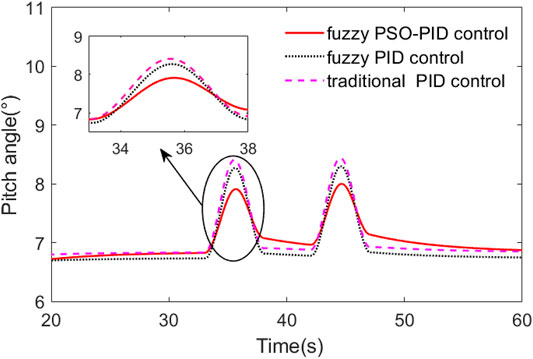
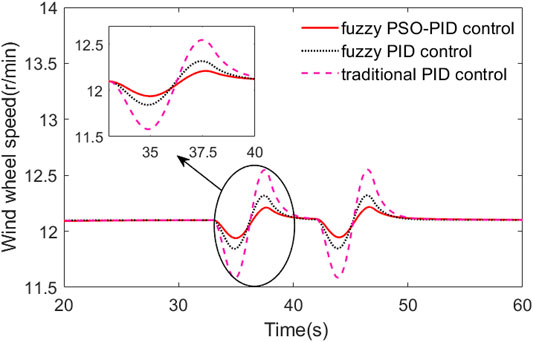
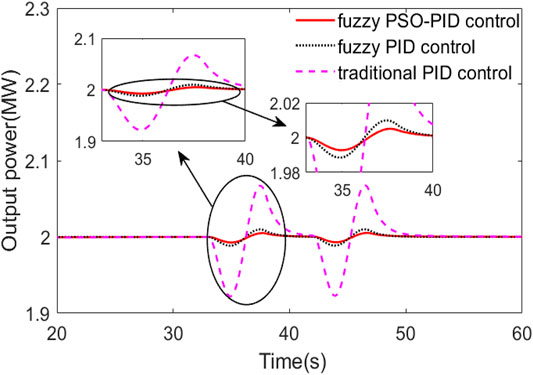
In the gust wind case, the gust wind speed curve is shown in Figure 9, where the maximum gust wind speed is 14 m/s, and the basic wind speed is 11 m/s. The comparison curves of pitch angle, wind wheel speed, and output power are shown in Figures 10–12.
It could be seen from Figure 10 that the maximum value of the pitch angle under fuzzy PSO-PID control is 7.8°. The maximum values of the pitch angle under fuzzy PID control and traditional PID control are 8.2° and 8.3°, respectively. The control method proposed in this paper can reduce the adjustment value of the pitch angle, thereby reducing the loss of the pitch control system.
As can be seen in Figure 11, the sudden increase of wind speed causes the pitch angle to increase first and then decrease, so the speed of the wind wheel shows a trend of first decreasing and then increasing. The fluctuation range of the wind wheel speed is the smallest under the fuzzy PSO-PID control, which is only 0.2 r/min. Under fuzzy PID control and traditional PID control, the fluctuation range is 0.4 and 0.9 r/min, respectively. Fuzzy PSO-PID control reduces the fluctuation range by 50% compared with fuzzy PID control.
As can be seen in Figure 12, the output power of a wind turbine is positively correlated with the wind wheel speed, so its power conversion trend is consistent with the wind wheel speed. The output power is more stable under fuzzy PSO-PID control, while under the traditional PID control, the output power fluctuates up to 0.14 MW. Therefore, fuzzy PSO-PID control has better robustness than fuzzy PID control and traditional PID control.
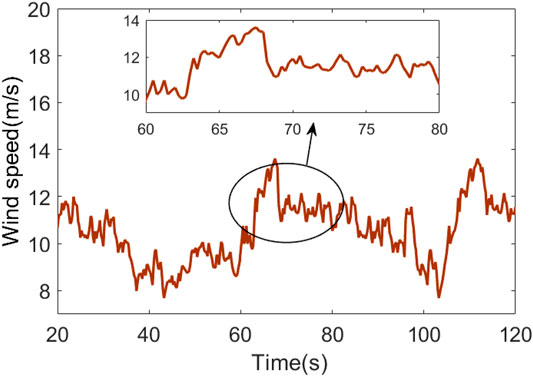
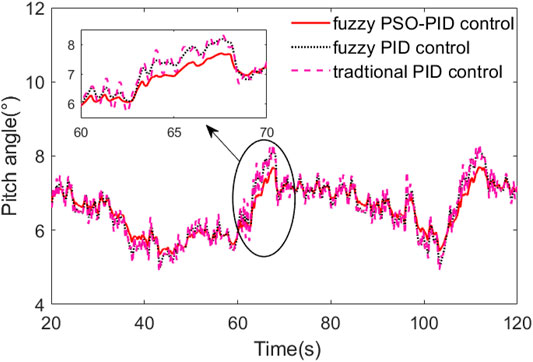
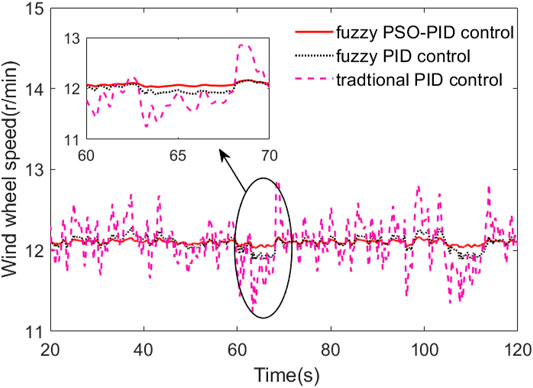
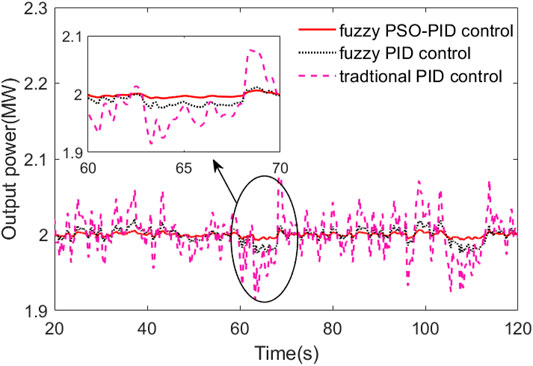
In the turbulent wind case, the turbulent wind speed is shown in Figure 13, where there is a dramatic change in wind speed around 65 s. The comparison curves of pitch angle, wind wheel speed, and output power are shown in Figures 14–16.
It could be seen from Figure 14 that the maximum pitch angle is 7.4° and the minimum pitch angle is 5.9° under fuzzy PSO-PID control between 60 and 70 s where the wind speed changes a lot. The adjustment range of the pitch angle is 2.1° under the fuzzy PID control, and the pitch angle fluctuates sharply and under the traditional PID control. The fuzzy PSO-PID control can reduce the pitch angle adjustment range by about 28.6%.
As can be seen in Figure 15, the wind wheel speed fluctuation under traditional PID control is large, the maximum speed reaches 12.8 r/min, and the minimum speed is only 11.2 r/min. The wind wheel speed is not stable enough under fuzzy control compared with fuzzy PSO-PID control. Under the fuzzy PSO-PID control, the wind wheel speed is basically maintained at 12.1 r/min.
As can be seen in Figure 16, the output power fluctuation is minimal under fuzzy PSO-PID control compared with PID control and fuzzy PID control. And fuzzy PID control is less robust than fuzzy PSO-PID control.
Anti-Interference Analysis
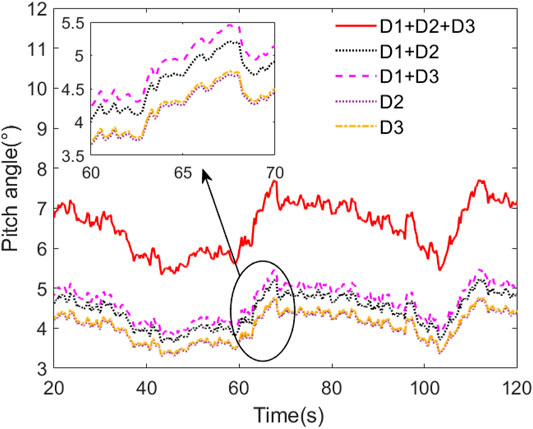
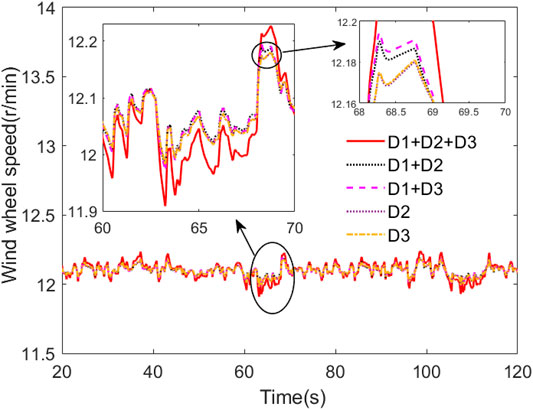
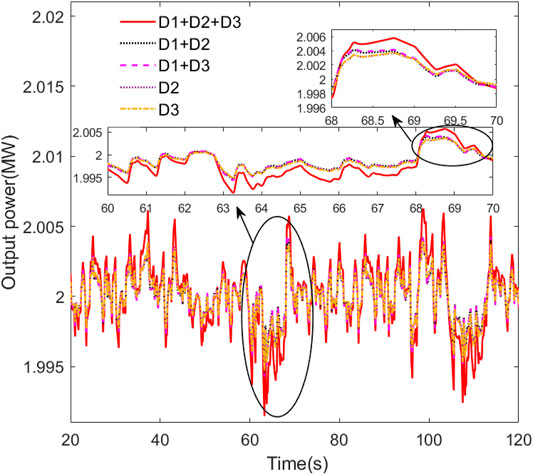
To verify the anti-interference ability of fuzzy PSO-PID control strategy, five different combinations of disturbances,
It could be seen from Figure 17, since all five cases are using the same control strategies, that the change trend of the pitch angle is basically the same. When three disturbances, two disturbances, and one disturbance are applied to the wind turbine, respectively, the values of the pitch angle are around 7°, 5°, and 3°. The more disturbances applied, the greater the pitch angle of the wind turbine to adjust.
It could be seen from Figure 18 that the fluctuation range of wind wheel speed is the largest when disturbance combination
It could be seen from Figure 19 that the output power of the wind turbine under the five combined disturbances is relatively stable. When disturbance combination
Through the control strategy validation and anti-interference simulation, it can be found that using fuzzy PSO-PID control can make the wind wheel speed fluctuation smaller when the pitch angle adjustment range is small, and the wind turbine’s power remains stable at the rated power. And fuzzy PSO-PID control strategy has a better suppression effect on different combinations of disturbances.
Conclusion
In this paper, a fuzzy adaptive PSO-PID is implemented in pitch control for suppressing multi-factor disturbances to improve the stability of wind turbines. In the proposed PID controller, PSO is utilized to optimize its initial parameters, and fuzzy rules are designed to adjust its parameters dynamically. Simulation comparisons with PID control and fuzzy PID control under gust wind and turbulent wind conditions are performed. The results show that in the system with the fuzzy adaptive PSO-PID pitch controller, the pitch angle adjustment range is smaller, and wind wheel speed and output power are smoother. Moreover, the anti-interference capacity of the control is verified by simulations under various combinations of disturbances. Thus, it is demonstrated that the fuzzy adaptive PSO-PID can provide the system with stronger robustness and better performance in suppressing various disturbances.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.
Author Contributions
YS contributed to the conception and design of the study. JL and LG organized the database. LH and YF performed the statistical analysis. JH wrote the first draft of the manuscript and wrote sections of the manuscript. All authors contributed to the manuscript revision and read and approved the submitted version.
Conflict of Interest
The authors were employed by the NARI Group Corporation.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors are grateful for the support by the State Grid Corporation of China Headquarters Management Science and Technology Project (Research on Key Technologies to Improve Wind Turbine Power Generation Efficiency).
References
Anjun, X., Hao, X., Shuju, H., and Honghua, X. (2011). “Pitch Control of Large Scale Wind Turbine Based on Expert PID Control,” in 2011 International Conference on Electronics, Communications and Control (ICECC), Ningbo, China, 9–11.9.2011 (IEEE), 3836–3839. doi:10.1109/ICECC.2011.6068002
Barahona, B., Sorensen, P., Christensen, L., Sorensen, T., Nielsen, H. K., Larsen, X. G., et al. (2011). Validation of the Standard Method for Assessing Flicker from Wind Turbines. IEEE Trans. Energ. Convers. 26 (1), 373–378. doi:10.1109/TEC.2010.2068299
Cheng, J., Li, R., Choobineh, F. F., Hu, Q., and Mei, S. (2019). Dispatchable Generation of a Novel Compressed-Air Assisted Wind Turbine and its Operation Mechanism. IEEE Trans. Sustain. Energ. 10 (4), 2201–2210. doi:10.1109/TSTE.2018.2883068
Fdaili, M., Essadki, A., Nadour, M., and Nasser, T. (2017). “Comparative Study of MPPT and Pitch Angle Control Strategies for a Wind Energy Conversion System,” in 2017 International Renewable and Sustainable Energy Conference (IRSEC), Tangier, Morocco, 4–7. Dec.2017 (IEEE), 1–6. doi:10.1109/IRSEC.2017.8477291
Iqbal, A., and Singh, G. K. (2021). PSO Based Controlled Six-phase Grid Connected Induction Generator for Wind Energy Generation. Trans. Electr. Mach. Syst. 5 (1), 41–49. doi:10.30941/CESTEMS.2021.00006
Jafarnejadsani, H., Pieper, J., and Ehlers, J. (2013). Adaptive Control of a Variable-Speed Variable-Pitch Wind Turbine Using Radial-Basis Function Neural Network. IEEE Trans. Contr. Syst. Technol. 21 (6), 2264–2272. doi:10.1109/TCST.2012.2237518
Jia, C., Wang, L., Meng, E., Chen, L., Liu, Y., Jia, W., et al. (2021). Combining LIDAR and LADRC for Intelligent Pitch Control of Wind Turbines. Renew. Energ. 169, 1091–1105. (prepublish). doi:10.1016/J.RENENE.2021.01.065
Kim, J.-S., Jeon, J., and Heo, H. (2011). “Design of Adaptive PID for Pitch Control of Large Wind Turbine Generator,” in 2011 10th International Conference on Environment and Electrical Engineering (EEEIC), Rome, Italy, 8–11.5.2011 (IEEE), 1–4. doi:10.1109/EEEIC.2011.5874603
Liu, B., Li, Z., Chen, X., Huang, Y., and Liu, X. (2018). Recognition and Vulnerability Analysis of Key Nodes in Power Grid Based on Complex Network Centrality. IEEE Trans. Circuits Syst. 65 (3), 346–350. doi:10.1109/TCSII.2017.2705482
Liu, B., Li, Z., Dong, X., Yu, S. S., Chen, X., Oo, A. M. T., et al. (2021). Impedance Modeling and Controllers Shaping Effect Analysis of PMSG Wind Turbines. IEEE J. Emerg. Sel. Top. Power Electron. 9 (2), 1465–1478. doi:10.1109/JESTPE.2020.3014412
Liu, X., Yu, W., Yang, L., and Ma, Q. (2017). “Research on Variable-Pitch Control Strategy of Wind Turbine Based on the Nonlinear PID,” in 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22.10.2017 (IEEE), 299–303. doi:10.1109/CAC.2017.8242781
Mazare, M., Taghizadeh, M., and Ghaf-Ghanbari, P. (2021). Pitch Actuator Fault-Tolerant Control of Wind Turbines Based on Time Delay Control and Disturbance Observer. Ocean Eng. 238, 109724. doi:10.1016/J.OCEANENG.2021.109724
Mughal, M. H., and Li, G. (2015). “Review of Pitch Control for Variable Speed Wind Turbine,” in 2015 15th Intl Conf on Scalable Computing and Communications and Its Associated Workshops (UIC-ATC-ScalCom), Beijing, China, 10–14.8.2015 (IEEE), 738–744. doi:10.1109/uic-atc-scalcom-cbdcom-iop.2015.148
Pathak, D., and Gaur, P. (2019). A Fractional Order Fuzzy-Proportional-Integral-Derivative Based Pitch Angle Controller for a Direct-Drive Wind Energy System. Comput. Electr. Eng. 78, 420–436. doi:10.1016/j.compeleceng.2019.07.021
Qi, Y., and Meng, Q. (2012). The Application of Fuzzy PID Control in Pitch Wind Turbine. Energ. Proced. 16, 1635–1641. doi:10.1016/j.egypro.2012.01.254
Wang, X., Jiang, Z., Lu, H., Wang, X., Meng, Y., and Li, S. (2020). “Independent Pitch Control Strategy and Simulation for Reducing Unbalanced Load of Wind Turbine,” in 2020 Chinese Control and Decision Conference (CCDC), Hefei, China, 22–24.8.2020 (IEEE), 5535–5539. doi:10.1109/CCDC49329.2020.9164293
Xiong, L., Liu, X., Liu, Y., and Zhuo, F. (2020). Modeling and Stability Issues of Voltage-Source Converter Dominated Power Systems: a Review. Csee Jpes, 1–18. (Early Access). doi:10.17775/CSEEJPES.2020.03590
Xiong, L., Liu, X., Zhang, D., and Liu, Y. (2021). Rapid Power Compensation-Based Frequency Response Strategy for Low-Inertia Power Systems. IEEE J. Emerg. Sel. Top. Power Electron. 9 (4), 4500–4513. doi:10.1109/JESTPE.2020.3032063
Xiong, L., Zhuo, F., Wang, F., Liu, X., Chen, Y., Zhu, M., et al. (2016). Static Synchronous Generator Model: A New Perspective to Investigate Dynamic Characteristics and Stability Issues of Grid-Tied PWM Inverter. IEEE Trans. Power Electron. 31 (9), 6264–6280. doi:10.1109/TPEL.2015.2498933
Yan, G., Wei, Z., Mu, G., Cui, Y., Chen, W., and Dang, G. (2009). Dynamic Modeling and Control of Directly-Driven Permanent Magnet Synchronous Generator Wind Turbine. Proceedings of the CSU-EPSA, 34–39.
Yin, M., Xu, Y., Shen, C., Liu, J., Dong, Z. Y., and Zou, Y. (2017). Turbine Stability-Constrained Available Wind Power of Variable Speed Wind Turbines for Active Power Control. IEEE Trans. Power Syst. 32 (3), 2487–2488. doi:10.1109/TPWRS.2016.2605012
Zahra, B., Salhi, H., and Mellit, A. (2017). “Wind Turbine Performance Enhancement by Control of Pitch Angle Using PID Controller and Particle Swarm Optimization,” in 2017 5th International Conference on Electrical Engineering - Boumerdes (ICEE-B), Boumerdes, Algeria, 29–31.10.2017 (IEEE), 1–5. doi:10.1109/ICEE-B.2017.8192221
Keywords: wind turbine, pitch regulation, fuzzy PSO-PID adaptive controller, disturbances suppression, turbulent wind
Citation: Shao Y, Liu J, Huang J, Hu L, Guo L and Fang Y (2022) The Implementation of Fuzzy PSO-PID Adaptive Controller in Pitch Regulation for Wind Turbines Suppressing Multi-Factor Disturbances. Front. Energy Res. 9:828281. doi: 10.3389/fenrg.2021.828281
Received: 03 December 2021; Accepted: 20 December 2021;
Published: 17 March 2022.
Edited by:
Liansong Xiong, Nanjing Institute of Technology (NJIT), ChinaReviewed by:
Xiaokang Liu, Politecnico di Milano, ItalyLi Rong, Nanjing Institute of Technology (NJIT), China
Copyright © 2022 Shao, Liu, Huang, Hu, Guo and Fang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Junjie Huang, aGpqNDc2MzRAMTYzLmNvbQ==
 Yixiang Shao
Yixiang Shao Junjie Huang
Junjie Huang Yuan Fang
Yuan Fang