- 1Faculty of Electric Power Engineering, Kunming University of Science and Technology, Kunming, China
- 2Electric Power Research Institute of Yunnan Power Grid Co., Ltd., Kunming, China
Wind farm–based frequency regulation of the power system has progressively attracted more attention owing to its higher power generation capacity. Among which the step start-up and adaptive inertial droop control of wind turbines with a maximum power point efficiently regulate the system frequency via fully utilizing the rotational kinetic energy. Besides, the coefficients of adaptive droop control and virtual inertial control will facilitate a significant influence on the frequency support performance and operation status of wind turbines for the power grid. To obtain optimal control parameters, a parameter optimization framework of a step start-up adaptive inertial and droop controller combined with the CGO algorithm is proposed, whose effectiveness is verified by a three-area four-terminal VSC-MT-HVDC–based WFs and AC system in MATLAB/Simulink. As a result, a set of parameters with a satisfactory and comprehensive dynamic control performance can be acquired by the proposed method under both 200 MW and 300 WM load increases compared with the trial-and-error approach.
1 Introduction
In recent years, for the purpose of reducing dependence on fossil fuels, the electric power structure needs to shift more toward renewables to facilitate energy transformation (Zhang et al., 2015; Hou et al., 2017; Meng et al., 2021). Consequently, renewables (Chen et al., 2018; Li et al., 2020; Pabitra and Abhik, 2020; Zhao et al., 2021a) (e.g., solar, wind, hydro energy, etc.) have been wildly developed around the world, upon which the wind energy is increasingly emerging as one of the most mature, promising, and representative renewables, thanks to its unique superior, i.e., clean, reproducible, stable, well-stocked (Liu et al., 2021), and widespread (Díaz and Guedes Soares, 2020).
Yunnan, located in the southwest region of China, is equipped with abundant hydropower and wind power resources. However, the high proportion of installed hydropower also poses new issues for the Yunnan power grid. The water hammer effect (WHE) (Vereide et al., 2017; Al BkoorAlrawashdeh et al., 2021) is a momentous characteristic of the hydraulic turbine governing system, which produces negative damping to the system and thus brings about system oscillation. Furthermore, a typical WHE curve is illustrated in Figure 1 when the degree of guide vane opening of large hydropower units is increased to handle the augment in load demand in the Jin’anqiao hydropower station of Yunnan. It can be transparently seen that WHE causes turbines to produce antithetical performance relative to actual control from Figure 1. That is to say, the output power of turbines will temporarily drop before increasing, which gravely threatens the security and stability of power grid operation, particularly when a large load disturbance occurs in a power system with a high hydraulic turbine capacity. It is noted that the participation of wind farms (WFs) in frequency regulation is an alternative and effective solution to address this tricky obstacle and achieve active power stabilization.
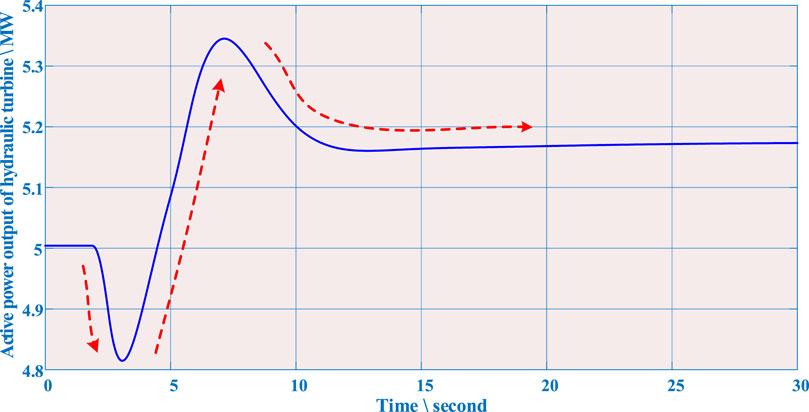
FIGURE 1. Water hammer effect under large hydropower units removal in the Jin’anqiao hydropower station of Yunnan.
However, WFs are mostly distributed far from load centers and need to utilize the voltage source converter–based multi-terminal high voltage direct current system (VSC-MT-HVDCs) to implement electricity transmission (Renedo et al., 2016; Gu et al., 2021). On account of decoupled operation between rotor speed and power system frequency, the doubly fed induction generator–based wind turbine (DFIG-WT) does not directly provide dynamic frequency support for the power grid similar to the inertial response characteristic of synchronous generators (Wang-Hansen et al., 2013; Xiong et al., 2021). Power system inertia is decreased owing to the access of DFIG-WT with a high-penetration level in the power grid, which also raises the frequency regulation pressure (Wang et al., 2019). With a view that the power system frequency fluctuation perhaps causes some serious consequences (Wei Yao et al., 2015; Yang et al., 2015; Golpira et al., 2016; Xiong et al., 2020), e.g., affecting industrial production, triggering relay protection equipment, and even causing frequency collapse phenomena, it is enormously imperative to energetically explore corresponding strategies to realize frequency support from WFs for a secure and stable operation of the alternating current (AC) system.
In the past few decades, multifarious frequency regulation control strategies of the AC system through WFs combined with VSC-MT-HVDCS have been developed (Huang et al., 2021; Zhou et al., 2021), which can be divided into two major categories in general, i.e., indirect and direct methods (MacDowell et al., 2015; Liu et al., 2020; Zhao et al., 2021b). Specifically, indirect active power control introduces large-capacity capacitors in the flexible direct current (DC) transmission system to achieve frequency regulation of the AC side by controlling the voltage of the DC system to release capacitance energy (Zhu et al., 2013; Wen et al., 2016; Gan et al., 2019; Jami et al., 2020; Kadri et al., 2020; Yang et al., 2022). Nevertheless, lack of economy is a pivotal ingredient impeding the widespread application of the indirect method. Comparatively, another one is accomplished by deloading, the discharging kinetic energy of the wind turbine rotor, adjusting pitch angle, etc., (Navalkar et al., 2015; Fu et al., 2017; Boyle et al., 2021; Xiong et al., 2021), whereas deloading operation strategy reserves backup power (Yao et al., 2019) but seriously remedies the efficient engagement of wind resources. Besides, frequently controlling the pitch angle can increase mechanical stress on the wind turbine blades and subsequently endanger the safety of wind turbines (Varzaneh et al., 2014). Accordingly, to implement friendly grid-connected WFs with a fast response to system frequency variation, it is a popular and promising approach to adequately employ the rotational kinetic energy and backup power of wind turbines to simulate the inertial response and primary frequency regulation ability of synchronous turbines. A fuzzy PID control based on maximum power point tracking (MPPT) control is suggested in the literature (Varzaneh et al., 2014) in such a manner that the kinetic energy stored in the rotor inertial is used to control the output power of wind turbines. However, a fuzzy PID control requires real-time–modulating PID parameters according to current system states, and thus, its applicability encountering different scenarios needs to be further validated. The literature reports (Surinkaew and Ngamroo, 2014) considered the uncertainties of wind power and load, which proposed a novel coordinated robust control method for DFIGs and synchronous generators to stabilize system oscillation and adopt an improved firefly algorithm to optimize parameters of the controller. Moreover, a deloading control strategy based on the available margin is developed in reference (Vidyanandan and Senroy, 2013) to furnish primary frequency support for the power system. It is noted that the transitory frequency support perhaps induces the secondary frequency drop (SFD) phenomenon during the recovery process of the wind turbine speed, which is probably worse than the first frequency drop (FFD) if the active power is seriously insufficient. As a consequence, reference (Xiong et al., 2021) attempted to realize appropriate frequency support and alleviate SFD via a two-level combined control strategy of VSC-MT-HVDC–integrated offshore WFs. Nevertheless, the trial and error method was adopted to determine the corresponding parameters of this control mechanism, which extremely imposed a burdensome mission on power grid operators and did not guarantee the control accuracy and stability. Whereupon, for tackling the aforementioned shortcomings, a parameter design framework of a step start-up adaptive inertial droop controller via chaos game optimization (CGO) (Talatahari and Azizi, 2020) is developed to automatically grope the satisfactory control performance and then decidedly mitigate superfluous labor in the new operating circumstances similar to the WHE phenomenon of the Yunnan grid in this article.
Synoptically, this article incorporates five sections as follows. First, Section 1 chiefly introduces the research background, conducts a literature review, and indicates the intentions of this work. Section 2 concisely describes the step start-up adaptive inertial and droop control scheme. Then, the parameter design framework proposed in this article is exhibited in Section 3in detail. The verifications of the presented method are executed in Section 4. Finally, Section 5 thoughtfully illustrates several conclusions and perspectives.
2 Step Start-Up Adaptive Inertial and Droop Control Scheme
The step start-up adaptive inertial and droop control scheme is demonstrated in Figure 2 for a three-area four-terminal VSC-MT-HVDC–based WFs and AC system (Vennelaganti and Chaudhuri, 2018; Xiong et al., 2021). It is noted that the wind turbines are categorized into two clusters according to their rotor speeds to orderly launch after the frequency events (Xiong et al., 2021). Besides, the rotor speed of each wind turbine in both WF 1 and WF2 is determined as 0.90pu, 0.95pu, 0.85pu, 1.00pu, and 1.05pu in sequence, and the discrimination threshold of the two clusters is settled as 0.9pu. Emphatically, the step start-up adaptive inertial and droop control scheme is only applied in WF 1, where all wind turbines operate in MPPT situations. Therefore, the output power reference value
where
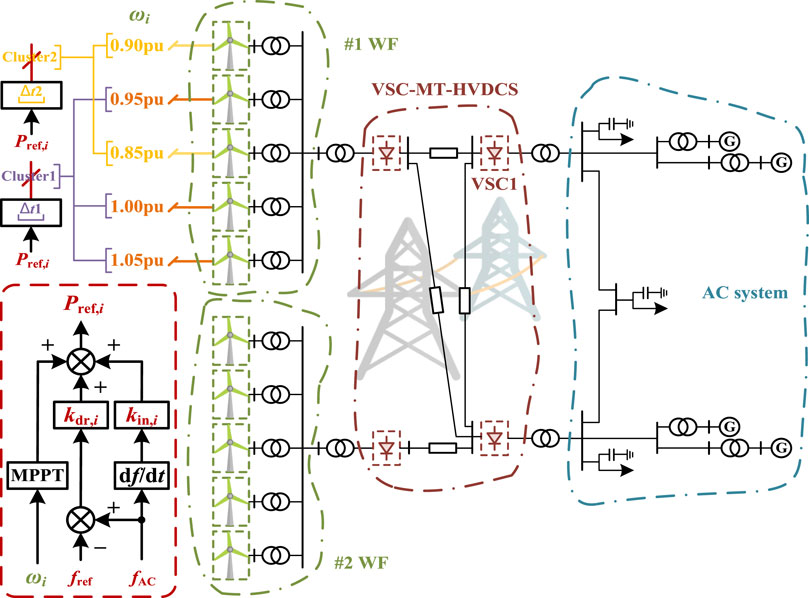
FIGURE 2. Step start-up adaptive inertial and droop control scheme for a three-area four-terminal VSC-MT-HVDC–based WFs and AC system on the WF level.
Additionally, more details about modeling parameters of the whole system, logic of step start-up adaptive inertial and droop control, and the control strategy of VSC stations can be acquired from the literature (Xiong et al., 2021).
3 Parameter Design of the Step Start-Up Adaptive Inertial and Droop Controller via CGO
3.1 Fundamental Principle of CGO
Over the past few decades, omnifarious meta-heuristic algorithms have been proposed, which are triumphantly applied in mathematical and engineering fields thanks to their particular preponderances, e.g., low dependence on models and gradient information of practical problems. Inspired by the fractal configuration and fractal self-similarity issues of the chaos game theory, Talatahari et al. (Talatahari and Azizi, 2020) developed the latest meta-algorithm, namely CGO, whose primary mechanisms can be generalized as follows:
where
Moreover, more information on CGO can be directly obtained from the literature (Talatahari and Azizi, 2020), e.g., pseudo-code, flowchart, corresponding parameter values, etc.
3.2 Parameter Optimization Framework of the Step Start-Up Adaptive Inertial and Droop Controller Based on CGO
In this section, a parameter optimization framework of the step start-up adaptive inertial and droop controller combined with the CGO algorithm is provided. This is based upon a suitable fitness function which is extremely crucial to obtain a set of optimal control parameters and then efficaciously stabilize the grid frequency under different operation conditions (e.g., load decrease or increase). Hence, three indexes about grid frequency
And then, each indicator is allocated a weight factor according to the relative importance and order of magnitude. Finally, the objective function is demonstrated in Eq. 11.
Additionally, parameters of the controller for different wind turbines within the same cluster are identically designed for reducing the dimensions of problem space and enhancing the search efficiency of CGO. Therefore, unknown parameters can be further refined as
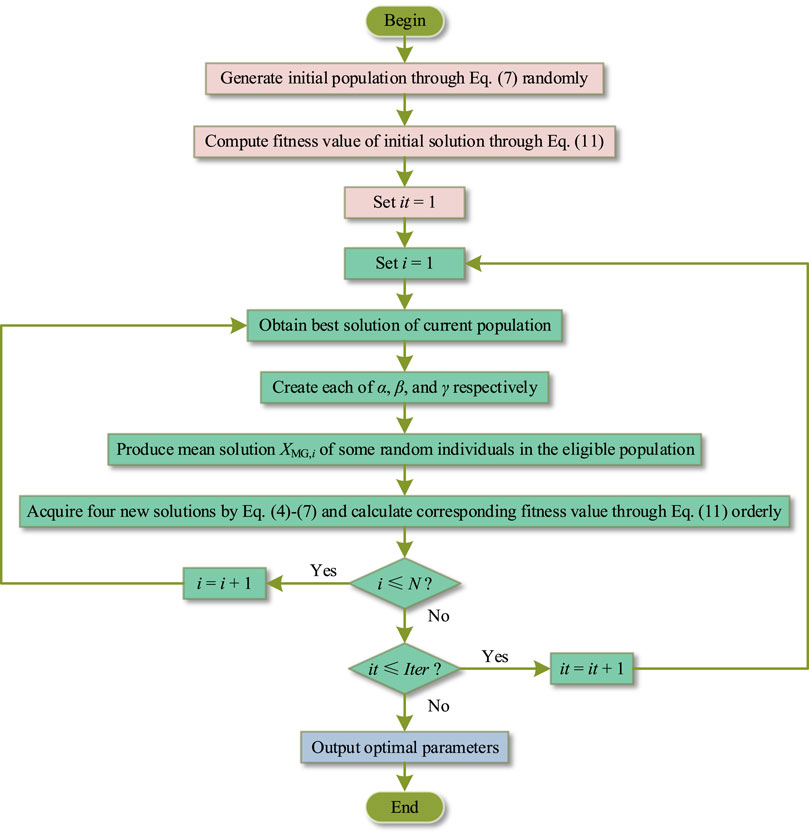
FIGURE 3. Parameter optimization framework for the step start-up adaptive inertial and droop controller based on CGO.
4 Case Studies
In this section, two frequency events, i.e., load increases 200 and 300 MW, are employed to evaluate the performance of the proposed method in chapter 3 via a three-area four-terminal VSC-MT-HVDC–based WFs and AC system shown in Figure 2. Besides, all case studies are implemented by the MATLAB/Simulink 2019b environment through a personal computer with Intel(R) Core(TM) i5 CPU at 2.9 GHz and 16 GB of RAM. DAESSC with variable step is selected as the solver. Meanwhile, N and Iter are settled as 5 and 8, respectively. In particular, all case studies are independently run 10 times to acquire a set of optimal parameters. Furthermore, wind turbine cluster 1 immediately participated to regulate the system frequency after the frequency event appeared (
As a result, optimal parameters obtained by three different methods are tabulated in Table 2, i.e., without WFs participating in frequency regulation (without FSC), trial-and-error (Xiong et al.), and the proposed method upon which the symbol “/” indicates no value. Note that the symbol “/” is applicable for the rest tables of this article.
Furthermore, the dynamic process of the measured frequency and active power in VSC1 acquired by different strategies are elaborately portrayed in Figure 4. One can demonstrably see that the frequency fluctuation of CGO is smaller than that of trial-and-error after the frequency event. Particularly, shown in Figures 4A,C, the CGO-based parameter optimization strategy can efficiently restrain the frequency drop (i.e., SFD and TFD) when the rotor speeds of wind turbines in clusters 1 and 2 start to restore at 10 and 15 s, respectively. Meanwhile, compared with without the FSC strategy, Figures 4B,D unquestionably indicate that more active power generated by WFs with FSC is transmitted to the AC system through VSC1 and thus to compensate the power shortage caused by frequency events occurring at 5 s.
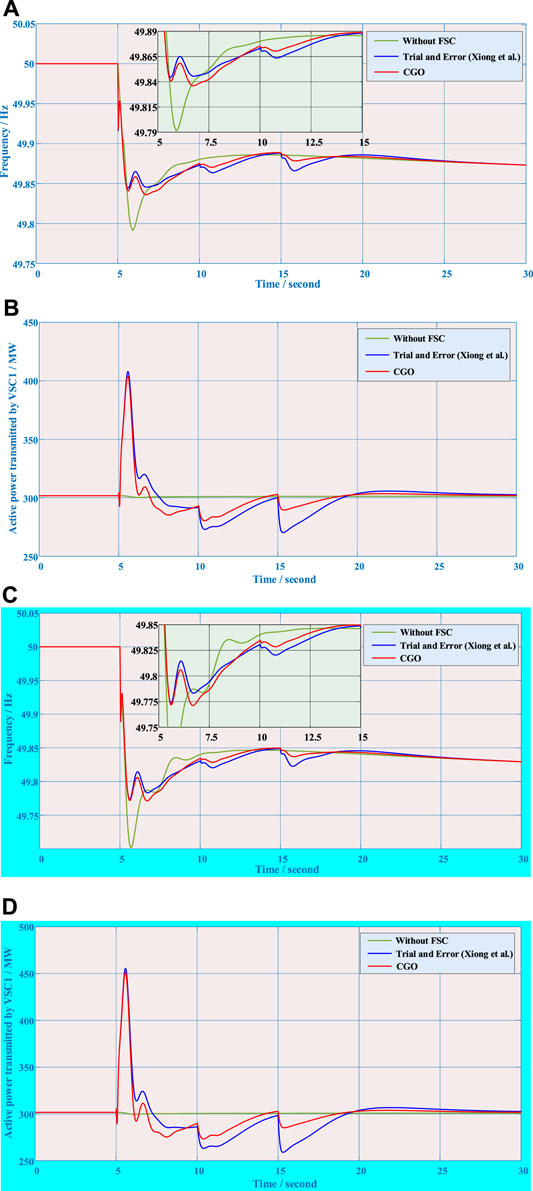
FIGURE 4. Frequency and transmitted active power of VSC1 under two frequency events: (A) Frequency under a 200-MW load increase; (B) transmitted active power under a 200-MW load increase; (C) Frequency under a 300-MW load increase; (D) transmitted active power under a 300-MW load increase.
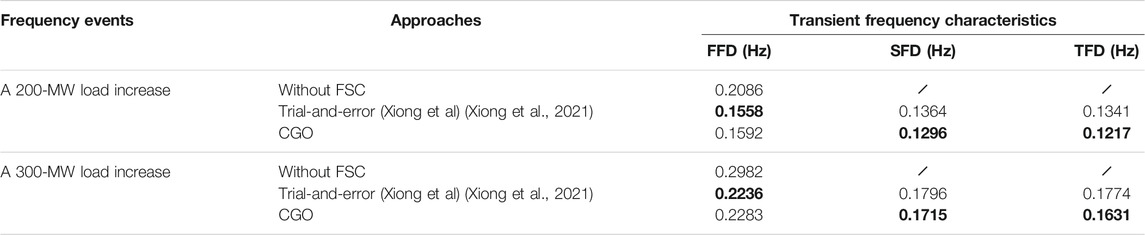
Besides, as illustrated in Table 3, three transient frequency characteristics (Delkhosh and Seifi, 2021; Xiong et al., 2021) (i.e., FFD, SFD, and tertiary frequency drop (TFD)) are used here to further concretely quantify and compare the control performance of three designed approaches. Among which the optimal value is highlighted in bold. Both under the 200 and 300 MW load increases, it is pellucidly observed that although FFD with CGO is more than that with trial-and-error, SFD and TFD with CGO are superior to those with trial-and-error, respectively. Specifically, TFDs with CGO only are 0.1217 and 0.1631 Hz while TFDs with trial-and-error reach up to 0.1341 and 0.1774 Hz under the 200 and 300 MW load increases, respectively.
5 Conclusion
In general, the several main conclusions can be described as follows:
• A parameter optimization framework of the step start-up adaptive inertial and droop controller combined with the CGO algorithm is developed to effectively accomplish frequency support via wind farms for the power system;
• A reasonable objective function is carefully designed by considering three essential factors of system frequency, i.e., integral of frequency deviation and frequency variation rate, and maximum frequency deviation point;
• The optimal control parameter is obtained by a three-area four-terminal VSC-MT-HVDC–based WFs and AC system under a 200 MW load increase, which is also applicable under a 300 MW load increase. Particularly, TFD with CGO merely equals to 0.1631 Hz while that of trial-and-error reaches up to 0.1774 Hz under a 300 MW load increase.
The proposed parameter optimization with CGO can significantly alleviate frequency fluctuation and improve power quality under designed frequency events in this article. Thus, it may also be suitable for other frequency events, e.g., WHE, load demand decrease, etc.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
YC carried out the conceptualization, writing of the original draft, and formal analysis; BY was responsible for supervision, and review and editing of the manuscript; YH conducted formal analysis, software, and supervision; TH was responsible for project administration and resources; PH conducted investigation and validation; XM carried out the reviewing and editing and methodology; XH performed visualization and validation.
Funding
This study received funding from the Key Project of China Southern Power Grid Co., Ltd. (YNKJXM20191240). The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.
Conflict of Interest
Author TH, PH, XM, XH are employed by Electric Power Research Institute of Yunnan Power Grid Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors gratefully acknowledge the support of Key Project of China Southern Power Grid Co., Ltd. (YNKJXM20191240).
Abbreviations
AC alternating current; CGO chaos game optimization; DFIG-WT doubly fed induction generator–based wind turbine; DC direct current; FFD first frequency drop; MPPT maximum power point tracking; MPP maximum power point; SFD secondary frequency drop; TFD tertiary frequency drop; VSC-MT-HVDCs multi-terminal high voltage direct current system; WHE water hammer effect; WFs wind farms; without FSC without WFs participating in frequency regulation.
References
Al Bkoor Alrawashdeh, K., Al-Samrraie, L. a. A., Al-Bsoul, A., Abdullah, A., Lymoon, A., Gul, E., et al. (2021). Investigation of the Influence of Dimensions and Material of the Pipes on the Water Hammer Effect in Microbial Fuel Cells Wastewater Treatment Plants. Sustainable Energ. Tech. Assessments 44, 100990. doi:10.1016/j.seta.2020.100990
Boyle, J., Littler, T., Muyeen, S. M., and Foley, A. M. (2021). An Alternative Frequency-Droop Scheme for Wind Turbines that Provide Primary Frequency Regulation via Rotor Speed Control. Int. J. Electr. Power Energ. Syst. 133, 107219. doi:10.1016/j.ijepes.2021.107219
Chen, J., Yao, W., Zhang, C., Ren, Y., and Jiang, L. (2018). Design of Robust MPPT Controller for Grid-Connected PMSG-Based Wind Turbine via Perturbation Observation Based Nonlinear Adaptive Control. Renew. Energ. 101, 34–51. doi:10.1016/j.renene.2018.11.048
Díaz, H., and Guedes Soares, C. (2020). Review of the Current Status, Technology and Future Trends of Offshore Wind Farms. Ocean Eng. 209, 107381. doi:10.1016/j.oceaneng.2020.107381
Delkhosh, H., and Seifi, H. (2021). Power System Frequency Security index Considering All Aspects of Frequency Profile. IEEE Trans. Power Syst. 36 (2), 1656–1659. doi:10.1109/tpwrs.2020.3047510
Fu, Y., Zhang, X., Hei, Y., and Wang, H. (2017). Active Participation of Variable Speed Wind Turbine in Inertial and Primary Frequency Regulations. Electric Power Syst. Res. 147, 174–184. doi:10.1016/j.epsr.2017.03.001
Gan, W., Ai, X., Fang, J., Yan, M., Yao, W., Zuo, W., et al. (2019). Security Constrained Co-planning of Transmission Expansion and Energy Storage. Appl. Energ. 239, 383–394. doi:10.1016/j.apenergy.2019.01.192
Golpira, H., Seifi, H., Messina, A. R., and Haghifam, M.-R. (2016). Maximum Penetration Level of Micro-grids in Large-Scale Power Systems: Frequency Stability Viewpoint. IEEE Trans. Power Syst. 31 (6), 5163–5171. doi:10.1109/tpwrs.2016.2538083
Gu, M., Meegahapola, L., and Wong, K. L. (2021). Coordinated Voltage and Frequency Control in Hybrid AC/MT-HVDC Power Grids for Stability Improvement. IEEE Trans. Power Syst. 36 (1), 635–647. doi:10.1109/tpwrs.2020.2983431
Hou, P., Hu, W., Soltani, M., Chen, C., Zhang, B., and Chen, Z. (2017). Offshore Wind Farm Layout Design Considering Optimized Power Dispatch Strategy. IEEE Trans. Sustain. Energ. 8 (2), 638–647. doi:10.1109/tste.2016.2614266
Huang, S., Wu, Q., Liao, W., Wu, G., Li, X., and Wei, J. (2021). Adaptive Droop-Based Hierarchical Optimal Voltage Control Scheme for VSC-HVdc Connected Offshore Wind Farm. IEEE Trans. Ind. Inf. 17 (12), 8165–8176. doi:10.1109/tii.2021.3065375
Jami, M., Shafiee, Q., Gholami, M., and Bevrani, H. (2020). Control of a Super-capacitor Energy Storage System to Mimic Inertia and Transient Response Improvement of a Direct Current Micro-grid. J. Energ. Storage 32, 101788. doi:10.1016/j.est.2020.101788
Kadri, A., Marzougui, H., Aouiti, A., and Bacha, F. (2020). Energy Management and Control Strategy for a DFIG Wind Turbine/fuel Cell Hybrid System with Super Capacitor Storage System. Energy 192, 116518. doi:10.1016/j.energy.2019.116518
Li, R. S., Wong, P., Wang, K., Li, B., and Yuan, F. F. (2020). Power Quality Enhancement and Engineering Application with High Permeability Distributed Photovoltaic Access to Low-Voltage Distribution Networks in Australia. Prot. Control. Mod. Power Syst. 5 (3), 183–189. doi:10.1186/s41601-020-00163-x
Liu, Y., Jiang, H., Peng, J., and Aziz, S. (2020). A Grouping-Based Frequency Support Scheme for Wind Farm under Cyber Uncertainty. IEEE Access 8, 178044–178054. doi:10.1109/access.2020.3016356
Liu, Z., Fan, S., Wang, Y., and Peng, J. (2021). Genetic-algorithm-based Layout Optimization of an Offshore Wind Farm under Real Seabed Terrain Encountering an Engineering Cost Model. Energ. Convers. Management 245, 114610. doi:10.1016/j.enconman.2021.114610
MacDowell, J., Dutta, S., Richwine, M., Achilles, S., and Miller, N. (2015). Serving the Future: Advanced Wind Generation Technology Supports Ancillary Services. IEEE Power Energ. Mag. 13 (6), 22–30. doi:10.1109/mpe.2015.2461331
Meng, Y., Yan, S., Wu, K., Ning, L., Li, X., Wang, X., et al. (2021). Comparative Economic Analysis of Low Frequency AC Transmission System for the Integration of Large Offshore Wind Farms. Renew. Energ. 179, 1955–1968. doi:10.1016/j.renene.2021.07.137
Navalkar, S. T., van Solingen, E., and van Wingerden, J.-W. (2015). Wind Tunnel Testing of Subspace Predictive Repetitive Control for Variable Pitch Wind Turbines. IEEE Trans. Contr. Syst. Technol. 23 (6), 2101–2116. doi:10.1109/tcst.2015.2399452
Pabitra, K. G., and Abhik, B. (2020). Stability Enhancement of Wind Energy Integrated Hybrid System with the Help of Static Synchronous Compensator and Symbiosis Organisms Search Algorithm. Prot. Control. Mod. Power Syst. 5 (2), 138–150. doi:10.1186/s41601-020-00158-8
Renedo, J., Garcia-Cerrada, A., and Rouco, L. (2016). Active Power Control Strategies for Transient Stability Enhancement of AC/DC Grids with VSC-HVDC Multi-Terminal Systems. IEEE Trans. Power Syst. 31 (6), 4595–4604. doi:10.1109/tpwrs.2016.2517215
Surinkaew, T., and Ngamroo, I. (2014). Coordinated Robust Control of DFIG Wind Turbine and PSS for Stabilization of Power Oscillations Considering System Uncertainties. IEEE Trans. Sustain. Energ. 5 (3), 823–833. doi:10.1109/tste.2014.2308358
Talatahari, S., and Azizi, M. (2020). Optimization of Constrained Mathematical and Engineering Design Problems Using Chaos Game Optimization. Comput. Ind. Eng. 145, 106560. doi:10.1016/j.cie.2020.106560
Varzaneh, S. G., Gharehpetian, G. B., and Abedi, M. (2014). Output Power Smoothing of Variable Speed Wind Farms Using Rotor-Inertia. Electric Power Syst. Res. 116, 208–217. doi:10.1016/j.epsr.2014.06.006
Vennelaganti, S. G., and Chaudhuri, N. R. (2018). Selective Power Routing in MTDC Grids for Inertial and Primary Frequency Support. IEEE Trans. Power Syst. 33 (6), 7020–7030. doi:10.1109/tpwrs.2018.2854647
Vereide, K., Svingen, B., Nielsen, T. K., and Lia, L. (2017). The Effect of Surge Tank Throttling on Governor Stability, Power Control, and Hydraulic Transients in Hydropower Plants. IEEE Trans. Energ. Convers. 32 (1), 91–98. doi:10.1109/tec.2016.2614829
Vidyanandan, K. V., and Senroy, N. (2013). Primary Frequency Regulation by Deloaded Wind Turbines Using Variable Droop. IEEE Trans. Power Syst. 28 (2), 837–846. doi:10.1109/tpwrs.2012.2208233
Wang, Q., Li, F., Tang, Y., and Xu, Y. (2019). Integrating Model-Driven and Data-Driven Methods for Power System Frequency Stability Assessment and Control. IEEE Trans. Power Syst. 34 (6), 4557–4568. doi:10.1109/tpwrs.2019.2919522
Wang-Hansen, M., Josefsson, R., and Mehmedovic, H. (2013). Frequency Controlling Wind Power Modeling of Control Strategies. IEEE Trans. Sustain. Energ. 4 (4), 954–959. doi:10.1109/tste.2013.2257898
Wei Yao, W., Lin Jiang, L., Jinyu Wen, J., Qinghua Wu, Q., and Shijie Cheng, S. (2015). Wide-area Damping Controller for Power System Interarea Oscillations: A Networked Predictive Control Approach. IEEE Trans. Contr. Syst. Technol. 23 (1), 27–36. doi:10.1109/tcst.2014.2311852
Wen, J., Liu, J., Long, Y., and Yao, W. (2016). Solution to Short-Term Frequency Response of Wind Farms by Using Energy Storage Systems. IET Renew. Power Generation 10 (5), 669–678. doi:10.1049/iet-rpg.2015.0164
Xiong, L., Liu, X., Zhang, D., and Liu, Y. (2020). Rapid Power Compensation Based Frequency Response Strategy for Low Inertia Power Systems. IEEE J. Emerging Selected Top. Power Electronics 9 (4), 4500–4513. doi:10.1109/JESTPE.2020.3032063
Xiong, Y., Yao, W., Wen, J., Lin, S., Ai, X., Fang, J., et al. (2021). Two-level Combined Control Scheme of VSC-MTDC Integrated Offshore Wind Farms for Onshore System Frequency Support. IEEE Trans. Power Syst. 36 (1), 781–792. doi:10.1109/tpwrs.2020.2998579
Yang, B., Jiang, L., Yao, W., and Wu, Q. H. (2015). Perturbation Estimation Based Coordinated Adaptive Passive Control for Multimachine Power Systems. Control. Eng. Pract. 44, 172–192. doi:10.1016/j.conengprac.2015.07.012
Yang, D., Jin, Z., Zheng, T., and Jin, E. (2022). An Adaptive Droop Control Strategy with Smooth Rotor Speed Recovery Capability for Type III Wind Turbine Generators. Int. J. Electr. Power Energ. Syst. 135, 107532. doi:10.1016/j.ijepes.2021.107532
Yao, Q., Liu, J., and Hu, Y. (2019). Optimized Active Power Dispatching Strategy Considering Fatigue Load of Wind Turbines during De-loading Operation. IEEE Access 7, 17439–17449. doi:10.1109/access.2019.2893957
Zhang, X., Yu, T., Yang, B., Zheng, L., and Huang, L. (2015). Approximate Ideal Multi-Objective Solution Q(λ) Learning for Optimal Carbon-Energy Combined-Flow in Multi-Energy Power Systems. Energ. Convers. Management 106, 543–556. doi:10.1016/j.enconman.2015.09.049
Zhao, X., Lin, Z., Fu, B., and Gong, S. (2021). Research on Frequency Control Method for Micro-grid with a Hybrid Approach of FFR-OPPT and Pitch Angle of Wind Turbine. Int. J. Electr. Power Energ. Syst. 127, 106670. doi:10.1016/j.ijepes.2020.106670
Zhao, Y., An, A., Xu, Y., Wang, Q., and Wang, M. (2021). Model Predictive Control of Grid-Connected PV Power Generation System Considering Optimal MPPT Control of PV Modules. Prot. Control. Mod. Power Syst. 6 (4), 407–418. doi:10.1186/s41601-021-00210-1
Zhou, B., Fang, J., Ai, X., Yang, C., Yao, W., and Wen, J. (2021). Dynamic Var reserve-constrained Coordinated Scheduling of LCC-HVDC Receiving-End System Considering Contingencies and Wind Uncertainties. IEEE Trans. Sustainable Energ. 12 (1), 469–481. doi:10.1109/TSTE.2020.3006984
Zhu, J., Booth, C. D., Adam, G. P., Roscoe, A. J., and Bright, C. G. (2013). Inertia Emulation Control Strategy for VSC-HVDC Transmission Systems. IEEE Trans. Power Syst. 28 (2), 1277–1287. doi:10.1109/tpwrs.2012.2213101
Nomenclature
Iter maximum iteration of CGO
N number of population for CGO
α stochastic coefficient for imitating the movement constraints of solution
Keywords: wind farms, frequency regulation, droop control, virtual inertial control, chaos game optimization
Citation: Chen Y, Yang B, Han Y, He T, He P, Meng X and He X (2022) Optimal Adaptive Inertial Droop Control–Based Power System Frequency Regulation via Wind Farms. Front. Energy Res. 9:819398. doi: 10.3389/fenrg.2021.819398
Received: 21 November 2021; Accepted: 03 December 2021;
Published: 12 January 2022.
Edited by:
Bin Zhou, Hunan University, ChinaCopyright © 2022 Chen, Yang, Han, He, He, Meng and He. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yiming Han, MzczNDgyNzUzQHFxLmNvbQ==
 Yijun Chen1
Yijun Chen1 Bo Yang
Bo Yang Yiming Han
Yiming Han