Tian Fei1
Zhang Erfeng- 1School of Energy and Power Engineering, Jiangsu University, Zhenjiang, China
- 2School of Mechanical Engineering, Nantong University, Nantong, China
- 3Yatai Pump & Valve Co. Ltd., Taixing, China
Submersible mixer is the core machinery of sewage treatment, which has a profound effect on the efficiency and performance of the submersible mixing system of sewage treatment. This paper summarizes the scientific research results of submersible mixer in recent years from four aspects: structure and energy characteristics of submersible mixer, numerical simulation calculation method, flow field characteristics, and factors affecting the flow field characteristics. The existing published literature indicates that the structure of submersible mixer for sewage is complicated and the parameters of energy characteristics are special. Few experimental studies are conducted, and mostly numerical calculations are based on clear water as the medium. The mixture model based on the Euler–Euler method is the multiphase flow model currently applied in the field of submersible mixer research. Many factors affect the mixing effect of a submersible mixer, such as installation factors (the location and angle of installation) and impeller design parameters (blade gap, hub-tip ratio, blade angle, etc.), all having a significant impact on the mixing performance. Meanwhile, the development and trends of submersible mixer technology are prospected, and the future directions of further research are proposed: establishing a more suitable numerical calculation method for submersible mixer based on the Euler–Lagrange model; constructing the calculation model with real fluid—solid-liquid two-phase flow as the medium; exploring the influence of various parameters on flow field characteristics of mixing fluid; getting the mixing mechanism of submersible mixer; promoting the development of submersible mixer; and realizing the efficient and stable operation of submerged mixing system.
Introduction
Environmental protection is a prerequisite for the coordinated development of economy, society, and environment, an important social and economic development strategy of all countries and an important and arduous task facing national construction. Water pollution has caused serious water loss in China, and the harmless treatment of sewage is an important measure to protect the environment and maintain green mountains on Earth. Therefore, it is important to study and develop efficient submersible agitators for wastewater (Li et al., 2007).
Submersible mixer for sewage (hereinafter referred to as submersible mixer (as shown in Figure 1) is a submerged device of mixing and pushing flow, is suitable for mixing various types of sewage treatment, which can mix and stir the surrounding water to improve the efficiency of sewage treatment (Gu et al., 2015), and is the core machinery in sewage treatment, with the advantages of small size, high efficiency, and strong turbulence (Yi and Zhai, 2003). In the treatment process, its power consumption accounts for more than 50% of the total power consumption of the whole wastewater treatment process (Kissel and Effenberger, 2010; Brehmer and Kraume, 2012). Its performance directly affects the efficiency, effectiveness, and stability of the whole wastewater treatment system (Qiu, 2021).
FIGURE 1. Submersible mixer.
The study of the submersible mixer not only aims at the structure and performance of the submersible mixer itself but also includes the flow characteristics in the impeller of the submersible mixer and the movement of fluid in the mixing pool of the submersible mixer. As the whole fluid is continuous and interacts with each other, the mixing effect and efficiency are affected by the combination of mixer and pool wall. The research on mixers is complicated.
Scholars from various countries have carried out much research on the working mechanism, flow field characteristics, and other aspects of submersible mixers and achieved certain research results. This paper summarizes the structural characteristics of submersible mixers. It reviews and analyses the current status and progress of domestic and international research in terms of the structure and energy characteristics of submersible mixers, numerical simulation research methods of submersible mixers, flow field characteristics and key factors affecting the flow field characteristics, respectively. It also points out the shortcomings in the research on submersible mixers and the areas that need further in-depth research. It provides a technical reference for relevant personnel to carry out research on submersible mixers.
Structure and Energy Characteristics of Submersible Mixers
The submersible mixer is mainly composed of a submerged motor, sealing mechanism, runner, hand hoist mechanism, electrical control, and so on (as shown in Figure 2). The impeller of the submersible mixer rotates the agitated liquid under the drive of the electric motor to generate a rotating jet and mixes it with shear stress along the jet surface so that liquids other than the jet can be agitated by friction. Volume flow is formed during extreme mixing. A mass flow mode is applied to obtain the agitated and pushed conveyance of controlled fluid (Xu, 2006; Yan et al., 2009; Weixing and Shouqi, 2010b).
FIGURE 2. Structural diagram of submersible mixer.
The rotational speed of submersible mixers is generally 100–1,500 r/min, which is divided into three types according to the impeller speed and the main function: low speed, medium speed, and high speed. The rotating speed of a low-speed submersible mixer is lower than 120r/min, which is mainly used to form long-distance flow pushing, improve fluid flow rate, and prevent sedimentation. The impeller speed range of the medium speed submersible mixer is 120 r/min ∼350 r/min, which mainly focuses on pushing the flow between far and near distances to improve the fluid flow rate and prevent deposition. The rotating speed of the impeller of the high-speed submersible mixer is higher than 350 r/min, which mainly focuses on the short-distance push flow to improve the fluid mixing effect and prevent deposition (GB/T 33566-2017, 2017).
During the operation of the submersible mixer, the fluid in the pool is subjected to the action of convection and vortex splitting, and the effect of uniform mixing is achieved by mixing, which is usually in a turbulent state (Tian et al., 2014a). In the turbulent flow field, there are vortices of different sizes, and the fluid energy is stored in these vortices. Shear forces are formed at the boundary of large-scale vortices to split the large-scale vortices into multiple small-scale vortices. At the same time, the energy of large-scale vortices is transferred to small vortices, and there is energy loss in the process of energy transfer in the meantime. The vortex phenomenon has a significant impact on the effect of pushing the flow. The fewer the number of vortices, the larger the scale of individual vortices, the steadier the flow regime, the lower the energy consumption of vortices, and the better the effect of pushing the flow and mixing (Zhang et al., 2020a). Therefore, the design and the installation of submersible mixers and the matching of the pool should be fully considered to reduce the vortex energy consumption.
Wastewater contains a large amount of suspended organic matter, sediment, mineral fertilizers, and microorganisms with a complex composition (Yan et al., 2009; GB 18918-2002, 2002; Jishui Paishui Sheji Shouce (Disanban), 2016; GB 50318-2017, 2017; Ma and He, 2003); the volume of the pool being agitated is typically large (Chen et al., 2016; Gong et al., 2017; Shi et al., 2019; Chen et al., 2020a); and the development of the flow field is also influenced by factors such as boundaries (Peng et al., 2009; Tian, 2012), making the flow field situation highly complex. Generally, the velocity flow field distribution diagram and axial effective propelled distance, effective disturbance radius of water section, operating power, efficiency, and so on are used to express the conversion characteristics of submersible mixers to the water flow energy. These are the external manifestations of the internal flow law of submersible mixer (CJ/T 109-2007, 2007; GB 37485-2019, 2019).
The velocity flow field distribution diagram can indicate the velocity distribution in the flow field and show the effective range of the fluid stirred by the submersible mixer (Figure 3).
FIGURE 3. Velocity flow field distribution.
Axial effective propelled distance refers to the effective distance that submersible mixer pushes the water along the axial direction in the effective area of the water body’s push-flow mixing work (maintaining the flow velocity greater than or equal to 0.3 m/s), expressed by the symbol Ly (CJ/T 109-2007, 2007).
Effective Disturbance Radius of Water Section
The effective radius of the submersible mixer that disturbs the cross section of the water body in the effective working area of the water body’s push-flow mixing (maintaining the flow rate greater than or equal to 0.3 m/s) is expressed by the symbol Ry (CJ/T 109-2007, 2007). These two parameters investigate the mixing effect of submersible mixers from a macro perspective.
Operating power was proposed in 2019, which refers to the input power acting on each cubic meter of water when the water velocity is not less than 0.3 m/s under the specified test conditions, expressed by symbol E. The calculation formula is as follows (GB 37485-2019, 2019):
where E is the operating power, P is the input power of the motor, and V is the equivalent effective volume.
Efficiency
In 2012, Tian Fei and other scholars used the power definition and momentum conservation to deduce the efficiency calculation formula of the submersible mixer. It is concluded that the mixer’s efficiency is directly proportional to the 3/2 power of the water thrust and inversely proportional to the impeller diameter and shaft power of the submersible mixer. The calculation formula is as follows (Tian et al., 2012a):
where η is the efficiency, F is the water thrust of the submersible mixer, D is the impeller diameter, P1 is the shaft power, and k is the coefficient, deduced by scholars as different.
The special working environment and matching conditions determine that the design of a submersible mixer is different from other fluid machineries such as water pumps and turbines.
Numerical Simulation Calculation Method
The experimental study of submersible mixer is difficult to conduct due to the large size of the pool, the complex internal flow field, the difficulty of measurement, and the high cost.Therefore, experimental research on submersible mixers is not well conducted. Currently, the numerical simulation method is applied to study the characteristics of the flow field. It can analyze the flow field and predict the performance of the flow field inside the impeller of the submersible mixer and the pool, with a short period, high efficiency, and low cost, and provide guidance for engineering applications and optimization of the design (Tian et al., 2013a).
In 1982, Harvey first introduced computational fluid dynamics to the prediction of two-dimensional flow fields in stirred tanks (Harvey and Greaves, 1982a; Harvey and Greaves, 1982b). Numerical simulation studies then developed rapidly, from two-dimensional to three-dimensional numerical simulations and from single-phase to multiphase flows. Research tools were no longer limited to experimental schemes, and the theoretical data no longer depended on experimental empirical data. Recently, as the development of grid technology has enabled the numerical study of more complicated geometric models, computational fluid dynamics functions have become more complete and powerful.
Treatment Method of Mixing Area
In the numerical simulation of the mixing field, for solving the problem of relative motion in the stationary and rotating regions, research scholars have proposed some different solutions, which are primarily black box model method, inner-outer iterative procedure, multiple reference frame method, sliding grid method, and so on (Zhou et al., 2004).
Black Box Model Method
Also known as the impeller boundary condition method, this method deducts the blade area from the calculation domain during calculation. The blade’s effect is virtualized, and the time-averaged velocity and turbulence parameters are used to replace the actual effect of the blade on the fluid. The data of boundary conditions are generally obtained by experimental methods. The model method does not need to consider the grid of the impeller part and has a small amount of computation, which is suitable for the calculation of the steady-state flow field. Harvey verified the feasibility of this method for the first time (Harvey and Greaves, 1982a). However, its boundary conditions need to rely on the support of experimental data, and it is difficult to carry out numerical calculations in complex situations.
Inner-Outer Iterative Procedure
The inner and outer iterative procedure adopts the method of considering the calculation domain separately and divides the calculation domain into two overlapping parts of the inner ring and the outer ring. The calculation of the inner ring is carried out in the reference system rotating at the speed of the impeller, and the calculation of the outer ring is carried out in the static coordinate system. Through the alternating iterative calculation of the two regions, a convergence result is finally obtained. Compared with the black box model method, the inner and outer iterative procedure does not require experimental data, can realize the simulation of the whole mixing area, and has succeeded in calculating some mixing fields. Wang Weijing et al. used an improved internal and external iteration procedure to perform an overall numerical simulation of the Rushton turbine baffled stirred pool. The results are basically consistent with the experimental values (Wang and Mao, 2002). However, this method is not popularly used in commercial software because it requires trial-and-error iterations in the calculation, and the convergence speed is slow.
Multiple Reference Frame Method
The multiple reference frame method (MRF) was proposed by Issa et al. (Issa et al., 1994), which is a calculation method applied to steady-state flow fields. This method divides the mixing area into the impeller area and the mixing pool area. Each area uses an independent reference system for calculation: the impeller area uses the coordinate system of the impeller rotation, and the mixing pool uses the static coordinate system. MRF can simulate the whole flow field of submersible mixer with small amount of calculation and is widely used in many commercial software. At present, the numerical simulation of steady flow field of submersible mixer is mainly based on MRF method. Peng Zhenzhen et al. used FLUENT software to numerically simulate the three-dimensional flow field of a submersible mixing pool with the MRF method and achieved good results (Peng et al., 2009). Tian Fei et al. used the MRF method to perform numerical simulation of the three-blade submersible mixer and verified the matching between submersible mixer and the sewage treatment pool (Tian et al., 2012b). Zhang Haisheng et al. conducted numerical simulations using the MRF method to study the hydraulic performance of submersible mixers at different placement angles and arrived at the optimal placement angle (Zhang et al., 2021). Chen Yunfan et al. used the MRF method for numerical simulation to verify the feasibility of the streamline method and the loop quantity distribution method applied to the design of submersible mixer blades (Chen et al., 2020b).
Sliding Grid Method
The flow field generated by the impeller of the submersible mixer is a periodic flow field (Van’t Riet et al., 1976), and the steady-state calculation method cannot completely reflect this flow field. In 1993, Luo proposed the sliding grid method (Luo et al., 1993). The division method of this method is the same as the MRF method, and it is also divided into the impeller area and the mixing pool area. The sliding grid method is an unsteady calculation method. In this method, the grid of the impeller part rotates with time, so there is mutual sliding of the grid at the interface between the impeller and the mixing pool. At present, this method is widely adopted by general commercial software. Zhou Guozhong et al. used the sliding grid method to numerically simulate the flow field near the paddle in a stirred pool (Zhou et al., 2002). Jin Jianhua et al. used the sliding grid method to numerically simulate the three-dimensional two-phase flow of a submersible mixer (Jin and Zhang, 2014). Tian Fei et al. used the sliding grid method to analyze the internal pressure pulsation characteristics of the submersible mixer and achieved good results (Tian et al., 2014b).
Numerical Calculation Method of Turbulence Model
The fluid ejected from the impeller of the submersible mixer has not only an axial velocity and radial velocity but also a certain tangential velocity (rotational velocity). Rotational velocity makes the radial and axial pressure gradient and affects the entire flow field. So, this jet is a rotating jet. The rotational jet is a composite flow of free jet plus rotation, and its flow situation is relatively sophisticated, mostly in a turbulent state (Tian, 2012). Currently, three types of numerical simulation of turbulence are used in engineering: direct numerical simulation (DNS); Reynolds-averaged equation (RANS), and large eddy simulation (LES) (Liang, 2012). DNS is used to solve the N-S equations directly without introducing any closed model within the grid size at the turbulent scale (Wang, 2016). DNS method would require high computational tools, and thus the DNS method is presently not directly applied to engineering numerical calculations to solve practical problems in engineering. RANS is used to solve the time-averaged Reynolds equation. The controlling equation for the time-averaged physical quantities is obtained by averaging the time of the non-stationary N-S equation. This control equation contains the unknown quantity of the time average of the pulsation, so the number of equations obtained will be less than the number of unknown quantities. Then, it is necessary to assume a closed model, using the lower-order time average to represent the unknown higher order to determine the function of some quantity to make the equation closed. At present, the RANS method has become the most widely used numerical simulation method of turbulence, which is also applied extensively in the numerical simulation of submersible mixers (Wang et al., 2016). LES is a direct solution of the N-S equation. Its basic idea is to accurately solve the motion at all turbulence scales above a certain scale, which enables capturing many large-scale effects and anthropomorphic structures that occur in non-stationary and non-equilibrium processes that the RANS method is unable to do while overcoming the huge computational overhead of DNS method due to the requirement to solve for all turbulence scales. Thus, it is considered the most promising direction for developing a numerical simulation of turbulence. Nevertheless, LES has not been widely used in engineering because the computational overhead is still substantial (Zhang et al., 2008).
Boundary Conditions
For delineating boundary conditions in the numerical simulation of the submersible mixer, the contact surface between pool and atmosphere is relatively unusual. The liquid surface is a free liquid surface. The more popular setting of the free liquid surface boundary conditions has three treatments: no-slip wall, VOF, and rigid-lid assumption. Wang Li et al. used the VOF method, but this method is more cumbersome, and human factors are particularly critical when dealing with function problems (Wang et al., 2007). He Zigan et al. applied simple rigid-lid assumption to the setting of free liquid level in large eddy simulation. By comparing the numerical simulation results with the test results, the limitation of the benchwork assumption near the solid wall was revealed (He et al., 2000).
Tian Fei et al. used FLUENT software to study the numerical simulation of the free liquid surface of the pool set to wall, VOF model, and rigid-lid assumption for three cases, respectively. They found that, in these three models, only the flow field near the pool surface has a significant effect. Among the three models, the numerical simulation of the pool surface as no-slip wall surface was the most difficult to converge, and the computational time was longer. The calculation of the free liquid surface treatment of pool surface using the VOF model required a higher computer configuration and accounted for more computational memory. The rigid-lid assumption was closer to the actual situation and easier to converge, with lower requirements for the computer. Nevertheless, the authors also suggested that the rigid-lid assumption is not realistic for liquid surfaces with relatively large free surface undulations (Fei et al., 2013).
Multiphase Flow Model
Practical application scenarios of submersible mixers are mainly for the movement of multiphase flows. The role of a submersible mixer in the wastewater treatment process is to provide the required circulating flow rate to keep the mixture in the pool in suspension (Liu et al., 2010), where the flow is relatively complex. Compared to the study of single-phase flow, the study of multiphase flow is more difficult. Currently, two major treatments are used in the study of numerical simulation of solid-liquid two-phase flow: Euler–Euler model and Euler–Lagrange model (Liu and Liu, 2018).
Euler–Euler Model
In the Euler–Euler model, the solid and liquid phases are treated as a continuous medium mixed. The solid and liquid phases are placed in the Euler coordinate system for solution (Bao et al., 2005). The Euler–Euler model contains a variety of calculation models. The mixture model is commonly used when studying solid-liquid two-phase flow in FLUENT. The mixture model is a simplified multiphase flow model. The model assumes that the velocity is locally balanced on a short time and space scale. An interphase interaction model must be added to calculate the homogeneous multiphase flow with strong coupling. Jin Jianhua et al. investigated the flow field characteristics of submersible mixers in solid-liquid two-phase flow based on the mixture model (Jin and Zhang, 2014). Tian Fei et al. studied the three-dimensional flow field of submersible mixers based on the rigid-lid assumption using the mixture model (Tian et al., 2014c).
Euler–Lagrange Model
The Euler–Lagrange model regards the fluid as a continuous phase and uses the continuity equation, momentum equation, and energy equation of the Euler method to establish the governing equation. The solid is regarded as a discrete phase, and the Lagrange equation of the discrete phase is established. Momentum, energy, and mass are exchanged between the discrete phase and the continuous phase. Typical Euler–Lagrange models include discrete phase model (DPM) and discrete element model (DEM). Lang Tao et al. investigated the flow characteristics of a sewage pump with a front-mounted stirring device using a DPM model (Lang et al., 2015). Shao Ting et al. used the CFD-DEM method to simulate the solid-liquid suspension system in the stirred kettle (Shao et al., 2013). Shao Wenbo, Shi Weidong, and Xia Cheng et al. conducted a numerical simulation study based on the fully coupled CFD-DEM method for multistage mixed-flow and cyclonic pumps and compared it with the experimental results to verify the accuracy of the computational model (Shao et al., 2020; Shi et al., 2020; Cheng et al., 2021).
The Euler–Euler model has the advantages of shorter solution time and simpler operation (Yang and Zhou, 2017) but ignores the interaction between the solid and liquid phases, which weakens the realism of the non-homogeneous structure in the solid-liquid two-phase flow and is not able to characterize the various properties at the particle level. In contrast, the Euler–Lagrange model takes into account the effects of components of different particle sizes on turbulent diffusion and the effects of turbulent diffusion and pulsation on the motion of the particle population and can trace the complex motion of the particle population and visualize the motion and changes of solid-phase particles in a visual form. Nevertheless, tracking the particle population by the Euler–Lagrange model requires many computer resources and a long solution time (Liu and Liu, 2018).
Research on Flow Field Characteristics
The research on the flow field characteristics of submersible mixers can be divided into research on the flow field characteristics inside the impeller and research on the flow field characteristics inside the mixing pool.
Flow Field Characteristics Inside the Impeller
The research on the characteristics of the flow field inside the impeller is mainly to analyze and study the speed field and pressure field inside the impeller. The research in this area is of great significance to the performance analysis and structural design of the impeller. Tian Fei et al. studied the internal flow field characteristics of the 2-blade submersible mixer and the internal pressure pulsation characteristics by numerical simulation using FLUENT as the calculation software. It is found that the fluid flow velocity near the blade working surface is low and the pressure is high, the back of the blade will form a high-speed zone and a negative pressure zone, and the fluid velocity and pressure gradient from the blade working surface to the back of the blade is apparent. Impeller import and export axis surface velocity is parabolic distribution, import and export velocity ring volume value is small, and the change is smoother. The blade exit axis surface velocity changes gently, approximately equal axial velocity distribution, blade inlet axis surface velocity is linear distribution, and blade import and export velocity ring volume is linear, regular distribution (Tian et al., 2013a).
The fluid inside and near the impeller is greatly affected by the periodic rotation of the impeller. Both the high-pressure low-speed zone and the low-pressure high-speed zone periodically change with the rotation of the impeller. The frequency of pressure pulsation at the inlet and outlet of the impeller and its interior is dominated by the rotation frequency of the impeller, and the pressure pulsation amplitude difference at the inlet of the impeller is greater than the pressure pulsation amplitude difference at the outlet of the impeller (Tian et al., 2014b).
Characteristics of the Flow Field Inside the Pool
The research on the internal flow field characteristics of the submersible mixing pool is of great significance for the design optimization of the submersible mixer and the evaluation of the mixing effect. At present, there is much research on the single-phase flow of submersible mixers but few studies on multiphase flow.
Single-Phase Flow
Peng Zhenzhen et al. used the effective axial advancing distance and the effective diffusion radius to judge the hydraulic performance of submersible mixers. The numerical simulation results show that the rotating impeller produces a high-speed jet, which is pushed forward and divided into two streams. One stream flows to the liquid level and returns to the back of the impeller to form a circulating vortex. The other stream is pushed forward until it hits the pool wall and turns back to form a large circulating vortex. The effective diffusion radius near the blade area is ≥ 2 m. The fluid away from the blade area to the pool wall also rotates around the x-axis but with smaller velocity values (Peng et al., 2009). Xu Qiao et al. used numerical simulation methods to compare the mixing flow fields of the axial flow pump impeller and submersible mixer impeller and found that the flow fields in the two pools are basically similar, showing the characteristics of axial thrust and radial diffusion. However, there are also certain differences. The submersible mixer impeller works better than the axial flow pump impeller in the area where the flow rate is less than 0, and the mixing effect is better (Qiao, 2018). Xu Weixing and others used FLUENT software to analyze the stirred flow field. It was found that the liquid is thrown out by the high-speed rotating impeller on the one hand and compressed by the impeller on the other hand, which forms a high-speed flow area near the impeller with a strong axial component and forms a rotating jet. It advances forward in accordance with an elliptical isovelocity line. The velocity along the centerline is faster than that in other directions. The liquid is conveyed by volume flow (Weixing and Shouqi, 2010a; Weixing and Shouqi, 2010b; Xu and Yuan, 2011a; Xu and Fan, 2011). Tian Fei and others studied the flow field characteristics of the conventional submersible mixer, new-type two-way submersible mixer, and new-type two-impeller submersible mixer. They found that the mixing performance of the two new-type submersible mixers is obviously better than that of the conventional submersible mixer with the same impeller, and the axial effective propelled distance is larger, which is suitable for mixing in a large water pool (Tian et al., 2019). Zhang Xiaoning et al. used the dynamic grid module and UDF module in FLUENT software to numerically simulate the mixing flow field of the swing submersible mixer. They found that the mixing effect of the swing submersible mixer is better than that of the non-swing submersible mixer (Zhang et al., 2017).
Tian Fei et al. summarized and further studied the jet characteristics of submersible mixers on the basis of previous studies. By analyzing and comparing the velocity flow field diagrams in the pools stirred by the four submersible mixers, it is concluded that the jet of the submersible mixer belongs to the submerged non-free turbulent circular cross section rotating jet. As shown in Figure 4, the fluid in the pool flows under the combined action of the submersible mixer and the pool wall. The fluid flows from the suction surface of submersible mixer blades and is pushed out from the impeller working surface after the action of the impeller. As the fluid flows downstream, the perturbation radius of the jet of the submersible mixer increases, the range of the mixing area becomes wider, and the flow velocity at the center of the jet of the mixer gradually decreases. When the fluid moved to the pool wall, the fluid spread to both sides to form a backflow, and two obvious large vortices appeared between the backflow fluid and the jet. Most of the fluid is sucked back into the working area of the impeller due to the backflow, forming the circulation of the fluid in the stirred pool. The fluid flow in the pool is more complicated, and there are three phenomena of entrainment, wall attachment, and vortex (Tian, 2012; Fei et al., 2014).
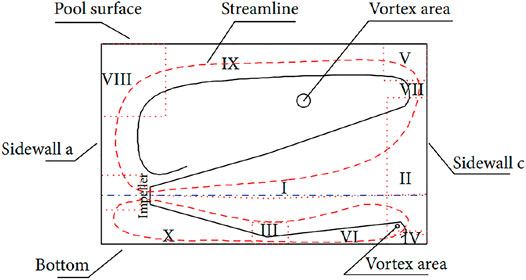
FIGURE 4. Flow diagram in pool. (I) Free jet region; (II) the region impacting with sidewall c; (III) the region impacting with the bottom of the pool; (IV) the region impacting with the bottom of the pool; (V) the region impacting with the surface of the pool; (VI) the region of the bottom of the pool wall jet; (VIII) the region of radial wall jetting with the sidewall c; (IX) the region of radial wall jetting with the pool surface.
Błoński conducted a comparative study on the performance of submersible mixers under three methods (experiment, numerical simulation, and theoretical calculation) and found that the jet of a submersible mixer was divided into three areas. As shown in Figure 5, the first area is the core area. In this area, the streamline is similar to the shape of a cone, the bottom diameter is equal to the diameter of the impeller, and the length of the area is 4–5 times the diameter of the impeller. The second zone is the transition zone, which is responsible for stronger mixing. The cone angle is approximately 2π/15 radians. The third area is the diffusion area, where momentum loss occurs and the velocity field tends to be unified (Błoński et al., 2021).
FIGURE 5. Immersed free stream.
Solid-Liquid Two-Phase Flow
The mixing fluid of the submersible mixer is usually clear water-sludge solid-liquid two-phase flow. Compared with the flow field of single-phase flow, the study of solid-liquid two-phase flow will focus on the distribution, velocity, trajectory, and suspension characteristics of the solid phase inside the pool.
Jin Jianhua et al. used FLUENT software as a tool to study the flow field under two conditions: single-phase flow with clean water and two-phase flow with sewage-sludge as media. The results show that the overall flow law of the flow field is roughly the same under both conditions, and the mixing radius increases with the advance distance of the flow. However, the axial push-flow velocity of the sewage-sludge two-phase flow is less than the flow velocity of the clean water single-phase flow, and the high-velocity area above 1 m/s is also small. At a certain distance downstream of the mixing flow field, the mixing radius is small, and precipitation is formed at the bottom of the pool. In addition, there are obvious deposits directly under the mixer (Jin and Zhang, 2014). Tian Fei et al. used FLUENT software to compare and study the flow field characteristics in the two cases of clear water flow and solid-liquid two-phase flow. The study found that the velocity distribution of the flow field in the two cases is similar. However, in the solid-liquid two-phase flow, due to the influence of solid particles, the velocity of the flow field will increase in the low-velocity zone. In contrast, in the high-speed zone, the velocity of the flow field will decrease. The concentration of solid particles near the pressure surface of the blade is greater than that near the suction surface. Moreover, it was found that, in the dead zone inside the pool, the concentration of solid particles in the dead zone near the pool was higher than that in the upper dead zone of the pool (Tian et al., 2014c).
Research on Key Factors Affecting Flow Field Characteristics
In practical engineering applications, fluid movement is relatively complicated. The jet will collide with the wall of the pool and produce rebound, backflow, vortex, and other phenomena (Tian et al., 2012a). The flow field characteristics of the mixing tank are influenced by several factors, including installation factors of installation position and angle of submersible mixer and impeller design parameters of hub-tip ratio, blade angle, impeller diameter, number of blades, and so on. These factors directly affect the mixing effect and have intuitive guidance for the engineering application of submersible mixers.
Installation Factors
Installation Position
The distance between the installation position and the bottom of the pool stipulated in the measurement of the specific power of the submersible mixer is 1/3 of the effective water depth (GB/T 33566-2017, 2017). However, in practical application, the installation position of the submersible mixer needs to be adjusted according to the actual situation, and various positions have a different impact on the characteristics of the flow field. Xu Weixing et al. used the method of numerical simulation. They used clean water as the medium to compare the flow field distribution in the pool when the installation depth of the submersible mixer was 3 and 5.72 m. It was found that when a submersible mixer is installed near the bottom of the pool, a high-speed flow zone can be formed on the bottom of the pool, which will flush it with jets. This will help prevent the deposition of solid particles at the bottom of the pool so that the medium in the pool can be averaged (Xu and Yuan, 2011b). Tian Fei et al. used numerical simulation methods to study the external characteristics of submersible mixers at four different positions in the pool and analyzed the velocity cloud diagram inside the pool. The results show that when the center axis of submersible mixer impeller is 600 mm from the bottom of the pool, the blade is at least 200 mm from the bottom of the pool, the distance ratio between the left and right walls is 4 : 3, the mixing efficiency and the average velocity of the pool are the highest, and the fluid is stirred the most stable (Tian et al., 2013b). Jin Jianhua used numerical simulation methods to numerically simulate the three-dimensional flow in a two-phase environment of sewage and sludge. It is concluded that reducing the installation position of the mixer can increase the flow rate at the bottom of the pool and reduce the sedimentation of sludge. Moreover, it was found that when the central axis of the impeller is 0.4 m away from the bottom of the pool, there is no obvious sludge deposition, and the density distribution is uniform (Jin and Zhang, 2014).
Installation Angle
Tian Fei et al. used numerical simulation to study the flow field distribution in the pool at different installation angles for two submersible mixers at the same depth and concluded that the installation position and angle of submersible mixers have a great influence on the flow field in the pool and the average flow velocity of the whole pool (Tian et al., 2012c). Based on Star-ccm + virtual simulation platform, Chen Yunfan et al. carried out numerical simulation of the full flow field with water as the research medium and studied the impact of the layout on the mixing effect of the hypoxic pool mixtures when using two submersible mixers. Analyzing the flow field, it was found that the mixing effect of the overall pushing was better than that of the distributed pushing, and the area of the low-speed area was smaller. On the basis of the overall pushing flow, the mixing flow field under three installation angles was studied, and combined with the actual situation of the pool, it was finally determined that the mixer with 45° installation angle would run more safely and stably (Chen et al., 2020a). Zhang Xiaoning et al. studied the velocity distribution of the flow field in the mixing pool with water as the medium and horizontal installation angles of 30°, 45°, 60°, and 90°. It is concluded that the different horizontal installation angles of submersible mixer have a great influence on the flow field in the pool. Among the four schemes studied, the layout angle of 45° has the best effect. In addition, a new method for evaluating the performance of submersible mixer, effective mixing domain method, is presented; that is, the hydraulic performance of submersible mixer can be evaluated by calculating the effective mixing volume (≥0.1 m/s) of water pushing mixing (Zhang et al., 2014). Zhang Zhi et al. used FLUENT software to numerically simulate and theoretically analyze the flow field of the submersible mixer at different installation angles to obtain the effect of different installation angles on the push-flow effect and found that adjusting the installation angle of the submersible mixer can improve the flow state inside the pool, increase the average flow velocity, and reduce the dead zone rate at the bottom, while reasonably changing the installation angle can also reduce the vortex energy consumption. They proposed that the analysis of the dead zone rate using the grayscale correlation method is more accurate than the average velocity method (Zhang et al., 2020a).
Impeller Design Parameters
Blade Gap
Xu Shun et al. found that the blade gap has some influence on the mixing effect of the submersible mixer. Through numerical simulation, the flow field under six working conditions with blade gap of 1, 3, 6, 8, 10, 14 mm was studied and analyzed. It was found that the shaft power and outlet flow were not affected by the blade gap, and the effective mixing ratio increased first and then decreased with the increase in blade gap. The maximum effective mixing ratio, maximum thrust, and minimum effective energy consumption per unit were achieved when the blade gap was 6 mm (Xu et al., 2017).
Hub-Tip Ratio
The hub-tip ratio is the ratio of the diameter of the hub to the diameter of the impeller. It is an important parameter in the design of the impeller of the submersible mixer and has an important influence on the hydraulic performance of the submersible mixer. Xu Weixing et al. used numerical simulation methods to compare the flow fields when the hub-tip ratio was 0.2, 0.3, and 0.4. It is concluded that the impeller with a smaller hub has higher speed, more uniform speed distribution, and better mixing effect (Xu and Yuan, 2010; Xu and Yuan, 2011b; Weixing and Jianping, 2011).
Blade Angle
Blade angle is an important parameter in the impeller design, which has a significant influence on the stirring effect and pressure distribution on the impeller surface. Xu Shun and Ren Xiangxuan used numerical simulation to analyze the flow field under three models with a blade angle of −4°, 0°, and 4°. The results show that, with the increase of blade angle, the area of effective mixing area increases, and the mixing effect is better. The shaft power and thrust of the submersible mixer are continuously increased, and the area of high pressure on the pressure surface of the blade is constantly increased when the blade angle is increased from −4° to 4° degrees. In addition, with the increase of blade angle, the effective energy consumption per unit also increases (Xu et al., 2017; Ren et al., 2021).
Impeller Diameter
The impeller diameter is a fundamental parameter of the impeller, and the optimal matching relationship exists between the outer diameter of the impeller and the rotational speed under the same power. Chen Bin et al. used STAR-CCM + simulation software to conduct a full flow field constant numerical simulation of the submersible mixer and analyzed the average flow velocity in the pool with various impeller diameters in the operation of the circular inspection pool and the square pool. It was found that, in the circular inspection pool, the larger the impeller diameter of the submersible mixer at the same power, the better the effect of push flow, as shown in Figure 6A. In the square pool, the average fluid flow velocity in the pool would first increase and then decrease with the increase of impeller diameter, as shown in Figure 6B. It means that in a square pool, the increase of impeller diameter may deteriorate the mixing effect of submersible mixer. As the impeller diameter is excessive, the cross section of the mainstream is large, the return channel area is reduced, and the total resistance is increased. Thus, the efficiency of the submersible mixer will be declined. Therefore, it is necessary to conduct a more detailed analysis when selecting a submersible mixer in a square pool (Chen et al., 2018).
FIGURE 6. Average flow velocity in two kinds of pools with different impeller diameters.
Number of Blades
The number of blades of submersible mixer is usually 2–3 blades. Zhuang Yufang et al. used numerical simulation to study the effect of the number of blades on the push-flow performance of the submersible mixer. It was found that the push-flow effect of the three-blade submersible mixer and two-blade submersible mixer is basically the same in the circular pool, but there are certain discrepancies as shown in Figure 7A. When the impeller diameter is 1.1–3.1 m, under the same power, the three-blade submersible mixer pushes the flow better than the two-blade effect. When the impeller diameter is greater than 3.1 m later, the two-blade submersible mixer has a better effect of push flow. In the square pool, two-blade and three-blade submersible mixer impeller diameter and speed curve trend are identical. The effect of push flow is enhanced with the increase in impeller diameter and then weakened, as shown in Figure 7B. However, while the impeller diameter is from 1.7 to 4.3 m, the two-blade submersible mixer has a better push-flow effect. When the impeller diameter is in the range of 1.1–1.7 m or greater than 4.3 m, the three-blade submersible mixer has a better push-flow effect (Zhuang, 2018).
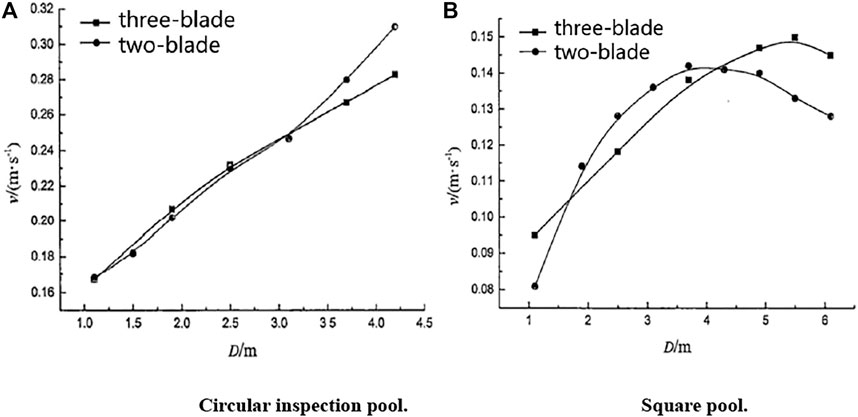
FIGURE 7. Comparison of the average velocity in the pool of three-blade and two-blade submersible mixer.
Impeller Speed
Tian Fei et al. conducted a three-dimensional numerical simulation of the flow field inside the stirred wastewater treatment pool with the same submersible mixer under various rotational speeds using the RNG k -ε turbulence model and SIMPLE algorithm with FLUENT software. By analyzing the velocity field at different cross sections in the pool, it was obtained that, with the increase in impeller speed, the fluid stirred more and more sufficiently in the whole pool, and the effective disturbance radius of the water body cross section became increasingly large. Moreover, it was found that the power of the mixer was proportional to the third power of the mixer speed for the same pool with the same mixer (Tian et al., 2011).
Other Factors
Pool Structure
Column structures are commonly found in large underground sewage mixing pools. The shape and distribution of the column and the shape of the pool have a great influence on the mixing effect. Shi Shuzhou et al. studied the flow field when the columns are square and cylindrical by numerical simulation. It was found that the overall flow velocity of the cylinder was higher, and the flow field distribution was more uniform. The shape resistance of the square column near the column was significantly higher than that of the cylinder, and the fluid flow around the column was poor. The distribution of the column should be well-coordinated with the installation position of the submersible mixer to avoid the loss of the thrust caused by the direct jet network of the mixer. In addition, the simulation analysis on the corner of the pool with right and round corners was carried out. The results show that the smooth transition can minimize the generation of vortices. The flow state in the pool with round corners was more uniform, the overall flow rate was higher, the dead zone area was smaller, and sludge was not easy to deposit (Shi et al., 2019).
Pool Shape
Shi Weidong et al. used the numerical simulation method to simulate the operation of the same submersible mixer in rectangular, straight circular tube, progressive circular tube, and abrupt circular tube four pool types of pools to compare the different power consumption. It was found that the fluid flow in the straight circular tube pool is relatively stable, the effect of fluid flow in the progressive circular tube pool is the second, and the fluid flow in the abrupt circular tube pool is the worst. In the power consumption, the abrupt change circular tube pool within the submersible mixer consumes the most power, the smallest power consumption within the progressive circular tube pool. The authors recommended the application of progressive circular tube pools and circular straight tube pools in the engineering design (Shi et al., 2009).
Diversion Shell
A diversion shell is widely used in fluid machinery and is a device for diversion. After installing the diversion shell, a submersible mixer can produce stable axial flow, reduce the shaft power, and improve efficiency. Using FLUENT as the fluid calculation software, Shi Weidong et al. simulated and analyzed the flow of submersible mixer with diversion shell by combining numerical simulation with experimental verification. It was found that the fluid velocity of submersible mixer with a diversion shell was obviously transferred along the axis, and the radial diffusion was relatively small, which had obvious axial diversion and reduced the effect of the boundary of the pool wall on the fluid in the pool (Shi et al., 2011). Using CFX as the fluid calculation software, Xu Qiao et al. compared the flow field of the submersible mixer with and without the diversion shell by numerical simulation. It was found that the trend of the axial flow velocity is the same in both cases, manifesting as the phenomenon of axial push flow and radial diffusion. However, the model with a diversion shell had a higher axial flow velocity, and the model without a diversion shell had a higher velocity in the reflux zone and a better reflux effect (Qiao, 2018). Using ANSYS-CFX as the fluid calculation software, Xiao Xia et al. studied the flow field distribution of diversion shells at the front and back ends of large and small pools, respectively, by combining numerical simulation with experimental verification. It was found that adjusting the diversion shell to the front can increase the effective advancing distance of the mixer and increase the mixer’s efficiency. In small pools, adjusting the diversion shell to the back can increase the effective advancing distance and overall mixing volume and increase the efficiency of the submersible mixer in the pool (Xia et al., 2019).
Outlook
In recent years, domestic numerical simulation of submersible mixer research has been a significant development. In the future, the following directions deserve attention in the research on submersible mixers:
1) Application of numerical calculation method based on the Euler–Lagrange model to numerical simulation of solid-liquid two-phase flow in the submersible mixer. At present, there are few studies on numerical simulation of submersible mixer in solid-liquid two-phase flow, and the main application is the Euler–Euler model. The numerical simulation method based on the Euler–Lagrange model is more suitable for the practical application of submersible mixer and has been widely used and verified by experiments in the field of water pump, mixing sink (Sun, 2015; Zhang et al., 2020b; Cao et al., 2020; Chen et al., 2021; Li et al., 2021; Quan et al., 2021; Shi et al., 2021). Referring to other research methods of hydro-machinery and combining with the characteristics of the submersible mixer itself, the development of a numerical simulation model suitable for the study of multiphase flow in the submersible mixer will become the main research content in the future.
2) Flow field characteristics of submersible mixer with the solid-liquid two-phase flow as a medium. The flow field characteristics of submersible mixers in water medium have been studied maturely. However, there are some deficiencies in the study of the flow field characteristics of submersible mixer with the solid-liquid two-phase flow as the medium, especially the distribution of solid phase, motion track, and velocity characteristics in two-phase flow. In practical application, the sewage tank usually contains unfiltered small sediment, microorganisms, and other objects. The solid medium will affect the flow field characteristics of the submersible mixer, such as the wear, oscillation, and unstable operation of the impeller of the submersible mixer. For the mixing flow field, there are also effects such as sludge deposition in the mixing dead zone and poor mixing effect.
3) The calculation model based on real fluid—solid-liquid multiphase flow is built to explore the influence of various parameters on the flow field characteristics of mixing fluid in a submersible mixer. At present, the research on the factors influencing the flow field characteristics of submersible mixers in single-phase flow is mature. However, there are few studies on the factors influencing the flow field characteristics in solid-liquid two-phase flow. In the case of two-phase flow, the influence of various parameters of solid phase, such as density, hardness, and volume, on the flow field characteristics should be the focus of future research.
Author Contributions
TF and ZE contributed to the conception and design of this paper. YC collated and collected the literature. TF wrote the first draft of the manuscript. TF, ZE, and YC wrote all parts of the manuscript. SW was responsible for the calibration and modification of the manuscript. All authors participated in the revision, reading, and approval of the submitted version of the manuscript.
Funding
The authors would like to acknowledge the support received from the National Key R&D Program Project (no. 2020YFC1512405), the National Natural Science Foundation of China (no. 51979125), and Six Talent Peaks Project of Jiangsu province (JNHB-192).
Conflict of Interest
Author ZC is employed by Yatai Pump and Valve Co. Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Bao, Y., Gao, Z., and Shi, L. (2005). Recent Research Progress of Multiphase Stirred Reactors [J]. Chemical Industry and Engineering Progress 24 (10), 1124–1130.
Błoński, D., Szulc, P., Machalski, A., and Rogula, J. (2021). Numerical Simulation and Experimental Investigation of Submersible Sewage Mixer Performance [J]. J. Phys. Conf. Ser. 1741 (1), 012007.
Cao, W., Xu, Y., Zhang, H., and Wang, X. (2020). Analysis of Gas-Liquid Two-phase Flow Characteristics of Mining Multistage Emergency Drainage Pump. J. Drainage Irrigation Machinery Eng. 38 (12), 1189–1195.
Chen, B., Chen, Y, Zhang, H., Wang, Y., and Xia, C. (2021). Cavitation Characteristics of High-Speed Submersible Axial-Flow Pump[J]. J. Drainage Irrigation Machinery Eng. 39 (2), 109–115.
Chen, B., Wang, B., Zhang, H., Wang, Q., and Wang, Z. (2016). Effects of Propeller Layout Position on Flow Characteristics in Oxidation Ditch [J]. J. Drainage Irrigation Machinery Eng. (Jdime) 34 (3), 227–231.
Chen, B., Zhuang, Y., Chen, K., Chen, X., and Yang, J. (2018). Influence of Impeller Diameter on Hydraulic Characteristics of Submersible Propeller [J]. China Water & Wastewater 34 (5), 57–60.
Chen, Y., Cai, X., Zhang, H., Chen, Y., Wang, Y., and Xu, Y. (2020). Calculation and Analysis of Airfoil Optimization in Artificial Flow[J]. J. Drainage Irrigation Machinery Eng. 38 (2), 170–175.
Chen, Y., Chen, Y., Zhang, H., Wang, Y., and Xia, C. (2020). Influence and Optimization of Mixer's Arrangement of Flow Field of Anoxic Pool [J]. J. Drainage Irrigation Machinery Eng. 38 (10), 1045–1050.
Cheng, X., Zhao, R., Shi, W., Zhang, D., and Gao, X. (2021). Numerical Investigation of Particle Induced Erosion in a Mixed Pump by CFD-DEM Coupled Method [J]. J. Eng. Thermophys. 42 (2), 357–369.
Fei, T., Shi, W., and Hua, J. (2014). Matching Criterion of Submersible Mixer and Pool [J]. Adv. Mech. Eng. 2014, 1–5.
Fei, T., Wei-Dong, S., and Hua, J. (2013). “Comparison of Sewage Treatment Mixer in Three Pool Face Boundary Conditions [Z],” in Frontiers of mechanical engineering and materials engineering II : Part 2, Hong Kong, 979–983.
Gb 18918-2002 (2002). Discharge Standard of Pollutants for Municipal Waste-Water Treatment Plant: [S].
Gb 37485-2019 (2019). Minimum Allowable Values of Energy Efficiency and Energy Efficiency Grades for Submersible Mixers of Wastewater: [S].
Gong, F., Pan, M., and Tang, L. (2017). Numerical Simulation of Submersible Agitator inside Two-Dimensional Flow Field [J]. J. Hubei Univ. Technol. 32 (1), 93–96.
Gu, Y., Gaoxiao, Q., Jiaobanqi, De. Y., and Yu, Y. (2015). “Research and Application of High-Efficiency Submerged Agitator [Z].” in Proceedings of the First Cross-Straits (Fujian-Taiwan) Water Technology Exchange Conference. Fujian: Quanzhou, 72–73.
Harvey, P. S., and Greaves, M. (1982). Turbulent Flow in An Agitated Vessel - 1. A Predictive Model [J].
Harvey, P. S., and Greaves, M. (1982). Turbulent Flow in An Agitated Vessel - 2. Numerical Solution and Model Predictions [J].
He, Z., Rodi, W., and Frohlich, J. (2000). Large Eddy Simulation of Turbulent Flows in Smooth and Rough Open Channels [J]. Journal of Hydrodynamics 15 (2), 191–201.
Issa, R., Luo, J. Y., and Gosman, D. (1994). “Prediction of Impeller Induced Flows in Mixing Vessels Using Multiple Frames of Reference,” in Proceedings of the 4th European Conf on Mixing, IMechE Symposium Series No 136, F.
Jin, J., and Zhang, H. (2014). A Numerical Simulation of Submersible Mixer in Three-Dimensional Flow with Sewage-Sludge Two-phase [J]. China Rural Water and Hydropower (10), 159–162.
Jishui Paishui Sheji Shouce (Disanban) (2016). Water Supply and Drainage Design Manual (Third Edition)] [J]. Water Wastewater Inf. 2016 (1).
Kissel, R., and Effenberger, M. (2010). Empfehlungen für die Auswahl von Rührwerken für Gärbehälter [J].
Lang, T., Shi, W., Chen, K., Li, W., and Cheng, C. (2015). Research on the Flow Field and Abrasion Characteristics in Sewage Pump with Pre-mixing Device [J]. Fluid Machinery 43 (11), 29–33.
Li, W., Wang, L., Shi, W., Chang, H., and Wu, P. (2021). Numerical Simulation and Performance Prediction of Solid-Liquid Two-phase Flow of Alkaline Pump Based on Full Factor Test[J]. J. Drainage Irrigation Machinery Eng. 39 (9), 865–870.
Li, W., Liu, X., and Wu, C. (2007). Application and Summary of Biologic Disposal High Efficiency Blender [J]. Journal of Agricultural Mechanization Research (7), 181–182.
Liang, T. (2012). Numerical Simulation on Agitated Flow Field of Submersible Mixer and Study on Impeller Optimization Design [D]. Shandong: Shandong University.
Liu, H., and Liu, Y. (2018). Guyebeng Liangxiangliu Ji Mosun Yanjiu Xianzhuang Ji Zhanwang [Research Status and Prospect of Two-phase Flow and Wear of Solid-Liquid Pump] [J]. South Agric. Machinery 49 (23), 8–11.
Liu, X., Wang, W., Zhao, J., and Chang, J. (2010). “The Numerical and Experimental Study on the Hydraulic Characteristics of Submersible Mixer [Z],” in 2010 International Conference on E-Product E-Service and E-Entertainment [v7], Henan, China, 6007–6011.
Luo, J. Y., Gosman, A. D., Issa, R. I., Middleton, J. C., and Fitzgerald, M. K. (1993). Full Flow Field Computation of Mixing in Baffled Stirred Vessels [J]. Chem. Eng. Res. Des. 71, 342–344.
Ma, S., and He, X. (2003). Brief on the Pollutant Discharge Standard of Municipal Wastewater Treatment Plant [J]. Water and Wastewater Engineering 29 (9), 89–94.
Peng, Z., Zhao, H., Guo, C., Wang, W., and Zeng, D. (2009). Qianshuijiaobanji Sanwei Liuchang de Shuzhi Moni. Numerical Simulation of 3-Dimensional Flow Field in Submersible Mixer [J]. Water Wastewater Eng. 35 (z2), 340–342.
Qiao, X. (2018). Design of Impeller of Submersible Mixer Based on Characteristics of Stirring Flow Field [D]. Yangzhou: Yangzhou University.
Qiu, S. P. (2021). Qianshuijiaobanji zai Shuichuli Lingyude Yingyong Yanjiu. [Research on Application of Submerged Agitator in Water Treatment Field] [J]. Shandong Water Resour. (5), 23–25.
Quan, H., Kang, L., Guo, Y., Cheng, J., Yu, X., and Quan, S. (2021). Effect of Solid Concentration on Circulation Flow and Hydralic Characteristics in Vortex Pump[J]. J. Drainage Irrigation Machinery Eng. 39 (6), 555–561.
Ren, X., Tang, F., Xu, Y., Shi, L., and Shang, X. (2021). Performance Analysis of Blade Angle of Submersible Agitator [J]. South-to-North Water Transfers Water Sci. Technol. 19 (4), 805–813.
Shao, T., Hu, Y., Wang, W., Jin, Y., and Cheng, Y. (2013). Simulation of Solid Suspension in a Stirred Tank Using CFD-DEM Coupled Approach [J]. Chin. J. Chem. Eng. 10, 1069–1081.
Shao, W., Zhao, R., and Zhang, D. (2020). Erosion of Multistage Mixed Flow Pump Based on Fully Coupled CFD-DEM Method [J]. J. Hydrodynamics 35 (5), 640–648.
Shi, G., Liu, Z., Li, H., and Yang, X. (2021). Pressure Fluctuation Characteristics of Gas-Liquid Two-phase Flow in Multiphase Pump[J]. J. Drainage Irrigation Machinery Eng. (1), 23–29.
Shi, S., Wang, Y., Xie, J., and Liu, Y. (2019). Application of CFD Simulation in Submersible Agitator Layout and Optimization of Operating Conditions [J]. Water Wastewater Eng. 45 (9), 36–40.
Shi, W., Shi, Y., Gao, X., Zhang, D., Lang, T., and Zhao, T. (2020). Simulation and Experiment on Flow Characteristics of Large Particles in Vortex Pump Based on DEM-CFD [J]. Trans. Chin. Soc. Agric. Machinery 51 (10), 176–185.
Shi, W., Tian, F., Cao, W., Chen, B., and Zhang, D. (2009). Numerical Simulation of Mixer Power Consumptions in Different Ponds [J]. J. Drainage Irrigation Machinery Eng. 27 (3), 140–144.
Shi, W., Tian, F., and Chen, B. (2011). Flow Analysis and Measurement of Wastewater Treatment Mixer with Dome [J]. Transactions of the Chinese Society for Agricultural Machinery 42 (3), 96–99.
Sun, Y. (2015). Numerical Simulation and Analysis of Flow Field and Solid—Liquid Suspension in Stirred Tanks [D]. Ma’anshan, China: Anhui University of Technology.
Tian, F., Shi, W. D., He, X. H., Jiang, H., and Xu, Y. H. (2013). Study on Installation of Submersible Mixer [J]. IOP Conf. Ser. Mater. Sci. Eng. 52 (2). doi:10.1088/1757-899x/52/2/022024
Tian, F., Shi, W. D., Jiang, H., Lu, X. N., and Chen, B. (2012). Study on Velocity Distribution in a Pool by Submersible Mixers [J]. IOP Conf. Ser. Earth Environ. Sci. 15 (5). doi:10.1088/1755-1315/15/5/052031
Tian, F., Shi, W., Jiang, H., and Zhang, Q. (2014). A Study on Two-phase Flow of Multiple Submersible Mixers Based on Rigid-Lid Assumption [J]. Adv. Mech. Eng. 2014 (Pt.2), 531234.
Tian, F. (2012). Jet Characteristics and Experimental Research of Submersible Mixer [D]. Jiangsu: Jiangsu University.
Tian, F., Shi, W., Chen, B., and Cao, W. (2011). “Mixing Performance Investigation of Sewage Treatment Mixer under Multi-Rotational Speed [Z],” in Proceedings of the Fourth National Conference on Hydraulic Machinery and Systems, Lanzhou, 494–497.
Tian, F., Shi, W., Lu, X., Zhang, D., and Lang, T. (2014). Analysis of Characteristics of Pressure Fluctuation inside Submersible Mixer [J]. J. Drainage Irrigation Machinery Eng. (7), 606–610.
Tian, F., Shi, W., Lu, X., Chen, B., and Ou, M. (2012). Numerical Simulation of Submersible Mixer with Three Blades [J]. J. Drainage Irrigation Machinery Eng. 30 (1), 11–14.
Tian, F., Shi, W., Xu, L., and Shao, P. (2014). Jet Characteristics of Submersible Mixer [J]. J. Ningxia Univ. (Natural Sci. Edition) (3), 221–228.
Tian, F., Shi, W., Zhang, D., Cao, W., and Zhou, Q. (2019). Flow Filed Characteristics of New-type Multi-Impeller Submersible Mixer [J]. J. Drainage Irrigation Machinery Eng. 37 (3), 232–236.
Tian, F., Shi, W., Zhang, Q., Zhang, D., and Zhang, G. (2013). Inner Flow Characteristics at Impeller of Submersible Mixer with Two Blades [J]. J. Jiangsu University(Natural Sci. Edition) 34 (4), 395.
Tian, F., Shi, W., Lu, X., Chen, B., and Xu, Y. (2012). Theoretical Calculation and Simulation Analysis of Submersible Mixer Effciency for Wastewater Treatment[J]. Trans. Chin. Soc. Agric. Eng. 28 (12), 50–54.
Van't Riet, K., Bruijn, W., and Smith, J. M. (1976). Real and Pseudo-turbulence in the Discharge Stream from a Rushton Turbine. Chem. Eng. Sci. 31 (6), 407–412. doi:10.1016/0009-2509(76)80024-3
Wang, C., Yuan, L., Li, Z., and Gao, Z. (2016). Recent Progress in the Numerical Simulation of Solid-Liquid Suspensions in Stirred Reactors [J]. J. Beijing Univ. Chem. Technology(Natural Sci. Edition) 43 (1), 1–12.
Wang, F. (2016). Research Progress of Computational Model for Rotating Turbulent Flow in Fluid Machinery [J]. Trans. Chin. Soc. Agric. Machinery 47 (2), 1–14.
Wang, L., Changyong, T., and Moxing Shiyongxing Fenxi ji Yixing Vof Shuzhimoni, (2007). Applicability Analysis of Commonly Used Turbulence Models and VOF Numerical Simulation of Airfoils [D]. Huazhong: Huazhong University of Science and Technology.
Wang, W., and Mao, Z. (2002). Numerical Simulation of the Whole Flow Field in a Stirred Tank with a Rushton Turbine Using the Improved Inner-Outer Iterative Procedure [J]. The Chinese Journal of Process Engineering 2 (3), 193–198.
Weixing, X., and Jianping, Y. (2011). “Optimization Design of Submersible Mixer Based on Simulation Study of AgitatedFlow Field [Z],” in 2011 Third International Conference on Measuring Technology and Mechatronics Automation [v2B], Shanghai, China, 807–810.
Weixing, X., and Shouqi, Y. (2010a). “CFD Analysis on Agitated Flow Field of Submersible Mixer [Z],” in 2010 ASME International Mechanical Engineering Congress and Exposition, Vancouver, British Columbia, Canada, 8890–8894.
Weixing, X., and Shouqi, Y. (2010b). “Numerical Simulation of Agitated Flow Field of Submersible Mixer Based on Computational Fluid Dynamics [Z].” in Mechanical Engineering and Green Manufacturing, Xiangtan, China, 1543–1546.
Xia, X., Lan, F., and Liu, X. (2019). Influences of Diversion Hood Position on Working Efficiency of a Push-Flow Submersible Agitator Based on CFX. [J]. Machinery 46 (7), 71–75.
Xu, S., Tang, F., Wang, W., Liu, Y., and Xu, Q. (2017). Influence of Different Blade Gaps on Flow Field of Submersible Mixer [J]. China Water & Wastewater 33 (1), 106–109.
Xu, W. (2006). Qianshuijiaobanqi Yelun Sheji ji Jiaoban Liuchang Shuzhi Moni. [Design Theory of Submerged Agitator Impeller and Numerical Simulation of Agitation Flow Field] [D]. Zhenjiang: Jiangsu University.
Xu, W., and Fan, M. (2011). “Structure Reverse Design and CFD Analysis on Agitated Flow Field of Submersible Mixer [Z],” in Manufacturing Science and Technology, Singapore, 23–29.
Xu, W., and Yuan, S. (2011). Optimization Design of Submersible Mixer Based on a Simulation Study of Agitated and Engineering Application [J]. China Rural Water and Hydropower 2011(6), 32–35.
Xu, W., and Yuan, S. (2011). Simulation Study on Agitated Flow Field of Submersible Mixer Based on Fluent [J]. Machinery Des. Manufacture 2011(9), 155–157.
Xu, W. X., and Yuan, S. Q. (2010). Numerical Analysis of Agitated Flow Field of Submersible Mixer. Amr 139-141, 2681–2684. doi:10.4028/www.scientific.net/amr.139-141.2681
Yan, J., Huang, D., and Teng, G. (2009). Research on Rural Domestic Sewage Disposal of Biologic Disposal High Efficiency Blender [J]. Journal of Anhui Agricultural Sciences 37 (20), 9606.
Yang, F., and Zhou, S. (2017). Progress of Solid-Liquid Suspension in Stirred Vessel [J]. CIESC Jorunal 68 (6), 2233–2248.
Yi, C. L., and Zhai, H. W. (2003). The Application of Submersible Agitator in Sewage Treatment [J]. J. Luohe Vocational Tech. Coll. 2 (2), 17–18.
Zhang, D., Mei, J., Zhao, R., Huang, J., and Jin, Y. (2020). Response Surface Method-Based Optimization of Impeller of Fluoroplastic Two-phase Flow Centrifugal Pump. J. Drainage Irrigation Machinery Eng. 38 (9), 898–903.
Zhang, H., Zheng, Y., Zhang, Z., Kan, K., and Xuying, M. O. (2021). Influence of Placement Angle of Sewage Mixer on its Hydraulic Characteristics[J]. J. Drainage Irrigation Machinery Eng. 39 (5), 483–487.
Zhang, X., Wang, Y., and Zhao, G. (2017). Yaobaixing Qianshui Jiaobanqi de Shuzhi Moni Yanjiu. Numerical Simulation Research of Swing Submersible Mixer [J]. China Sci. Technol. Inf. (17), 837.
Zhang, X., Zhao, J., and Wang, W. (2014). Influence of Submersible Mixer Installation Angle with the Mixing Effect [J]. J. Beijing Inst. Civil Eng. Architecture (4), 48–51.
Zhang, Z., Cui, G., and Xu, C. (2008). Tuanliu Dawo Shuzhimoni de Lilun yu Yingyong. [Theory and Application of Large Eddy Simulation of Turbulence] [M]. Beijing, China: Tsinghua University Press.
Zhang, Z., Yuan, Z., Jiang, J., and Li, C. (2020). Influence of Wastewater Mixer Setting Angle on Flow Field in Sewage Treatment Pool. J. Drainage Irrigation Machinery Eng. 38 (3), 272–276.
Zhou, G., Shi, L., and Wang, Y. (2002). CFD Prediction of Flow Near the Agitator in Stirred Tank [J]. Journal of Chemical Engineering of Chinese Universities 16 (1), 17–22.
Zhou, G., Shi, L., and Wang, Y. (2004). Computational Fluid Dynamics Progress in Stirred Tank Reactors [J]. Chemical Engineering 32 (3), 28–32.
Keywords: submersible mixer, numerical simulation, flow field characteristics, multiphase flow, CFD
Citation: Fei T, Erfeng Z, Chen Y, Weidong S and Chenghua Z (2022) Review of Numerical Simulation Research on Submersible Mixer for Sewage. Front. Energy Res. 9:818211. doi: 10.3389/fenrg.2021.818211
Received: 19 November 2021; Accepted: 22 December 2021;
Published: 01 February 2022.
Edited by:
Xiaojun Li, Zhejiang Sci-Tech University, ChinaCopyright © 2022 Fei, Erfeng, Chen, Weidong and Chenghua. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhang Erfeng, MTYwMzA3MzA0M0BxcS5jb20=; Shi Weidong, d2RzaGlAdWpzLmVkdS5jbg==